채프 다이나믹 RCS의 빠른 추정을 위한 Multi-Layer Perceptron을 이용한 대리모델

Ⅰ. 서 론

현대 전장에서 다양한 위협으로부터 자산을 보호하는 레이다 대응 방법의 연구는 필수적이다. 대표적으로 채프, Flare, Nixie, 그리고 Decoy가 있다^[1]. 이 중 채프는 세계 2차 대전부터 전통적으로 레이다의 추적 및 식별을 방해하기 위한 레이다 전자방해책으로 가장 일반적으로 사용되었으며^[2],[3], 금속성 물질로 코팅된 섬유 다발을 다량으로 공중에 투하/발사하여 전자기 산란으로 상대방을 기만하는 데 사용된다.

하지만 실제 환경에서 채프의 레이다 반사단면적(RCS, radar cross-section)을 측정할 경우 수 많은 미세한 입자를 공중에 뿌리기 때문에 회수하여 재실험이 어렵고 환경문제 등이 발생한다. 이러한 문제로 채프 실시험이 제한적으로 실시되며 그 결과 역시 접근이 제한되어, 그동안 채프에 대한 연구는 수치해석 기법을 이용하는 경우가 대부분이다. 또한 AI를 활용한 채프의 연구는 채프를 방사하는 위치에 따른 기만 효율을 연구하는 것이 전부였다^[4],[5].

기존의 연구에서 채프운의 다이나믹 RCS는 채프의 동특성을 해석하고 그에 따른 전자기 특성을 계산하여 얻었다. 이때 동특성은 실제 환경과의 유사성을 위해서 환경에 따른 채프의 움직임 변화와 채프 간의 충돌을 반영한 CFD-DEM^[6]을 통해 해석하였고 이런 동특성을 반영한 채프들의 전자기 특성을 근사화 기법인 GEC(generalized equivalent conductor)를 통하여 계산하였다^[7].

GEC는 근사화 기법이기 때문에 비교적 짧은 계산 시간으로 RCS를 계산할 수 있지만, CFD-DEM은 수치해석 기법 중 하나로 매우 많은 계산 시간과 리소스가 요구된다. 본 논문에서는 CFD-DEM과 GEC를 통해서 얻은 다이나믹 RCS와 환경변수를 인공지능 모델로 학습하여 일련의 수치해석 기법들의 적용 없이 빠르게 다이나믹 RCS를 얻을 수 있도록 한다. 이때 학습에 사용하는 모델은 인공지능 회귀 기법^[8],[9] 중 하나인 MLP(multi-layer perceptron)를 사용한다.

Ⅱ. 기존의 채프운 동특성 및 RCS 예측 기법^[10],[11]

CFD-DEM은 CFDs(computational fluid dynamics)와 DEM (discrete element method)을 결합한 방법이다. 먼저, CFDs를 이용하여 채프 섬유 사이의 유체역학을 고려한 채프에 대한 동적 방정식을 계산하고, DEM을 이용하여 채프를 6개의 자유도를 가지는 노드로 설정하여 채프 간의 충돌에 따라 움직임을 계산한다. 위 두 가지 방법의 결합으로 채프들의 위치와 방향을 계산할 수 있다.

GEC는 채프들이 균일한 방향과 분포라고 가정한 EC (equivalent conductor)의 발전된 형태로, 임의의 방향을 가정하여 채프운을 유효 물질로 채프의 분포를 대체하여 표현한 것이다. 채프운을 유효 물질로 대체함으로써 유효 유전율, 부피, 계산 구역을 얻게 되므로 채프운의 RCS를 추정할 수 있다. 그림 1과 같이 기존에는 파라미터 풍향, 풍속, 초기 각도, 시간에 따른 채프운의 위치와 방향을 구하고 운용 주파수, 채프운의 거리, 채프의 수, 채프의 직경에 따른 채프운의 RCS를 GEC로 추정한다.

그림 1. | Fig. 1. 기존 RCS 추정 방법 | Previous RCS estimation method.

Download Original Figure

Ⅲ. 제안하는 다이나믹 RCS 대리모델

3-1 MLP 기본 개념^[12]

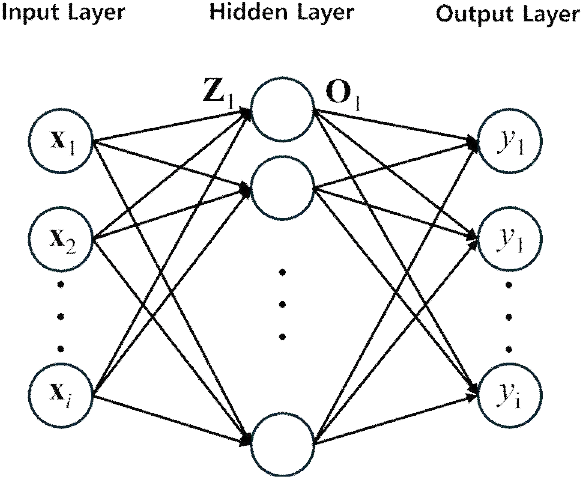
MLP는 기본적으로 입력, 은닉, 그리고 출력 계층으로 이루어져 있고 이 장에서 MLP는 그림 2와 같이 은닉 계층이 하나의 층을 가진다고 가정한다. 각 계층은 노드로 이루어져 있으며, 각 노드는 다음 계층의 모든 노드와 연결되어있다. MLP의 가장 큰 특징은 모든 연속함수를 근사화가 가능하다는 점이다.

그림 2. | Fig. 2. MLP 계층구조 | MLP architecture.

Download Original Figure

i개의 훈련 패턴(x_i, t_i)을 가지고 있다고 가정한다. 여기서 i는 패턴 수를 뜻하고, x_i는 i번째 훈련 패턴의 N차원 입력 벡터이고, t_i는 실제 측정한 값을 말한다. 여기서 입력 벡터 x_i를 입력했을 때, 입력 벡터에 따른 MLP의 예측값을 y_i라 한다. 입력 계층에서 은닉 계층으로 전달되는 은닉 계층의 입력은 식 (1)과 같다.

$$Z_i(l)={\displaystyle \sum _{k=1}^{N+1}{w}_i^{(k)}}(l,k)\cdot x_i(k)$$

(1)

여기서 l은 은닉 계층의 노드 수, k는 입력 계층의 노드 수 그리고 $w_i^{(h)}(l,k)$는 입력 계층에서 출력 계층 사이의 가중치를 나타낸다. 은닉 계층에서 출력되는 값들은 비선형 활성화 함수를 거쳐 식 (2)와 같다.

$$O_i(l)=f\left(Z_i(j)\right)$$

(2)

여기서 j는 다음 계층의 노드 수, 함수 f는 활성화 함수를 나타낸다. 출력 계층에서는 입력에 대한 직접적인 연관성과 학습 데이터의 비선형성을 모두 학습하기 위해 입력 계층의 출력과 은닉 계층 출력의 합으로 식 (3)과 같이 표현된다.

$$y_i(m)={\displaystyle \sum _{k=1}^{N+1}{w}_i^{(h)}}(m)\times x_i(k)+{\displaystyle \sum _{j=1}^L{w}_i^{(\text{out})}}(m,j)\times O_i(j)$$

(3)

여기서 m은 다음 계층의 노드 수, L은 출력의 차원 그리고 $w_i^{(\text{out})}(m,j)$은 은닉과 출력 계층 사이의 가중치이다. MLP에서 학습은 역전파^[13]를 통해서 가중치와 threshold를 업데이트하여 출력되는 결과를 수정한다.

3-2 MLP를 이용한 개선된 방법

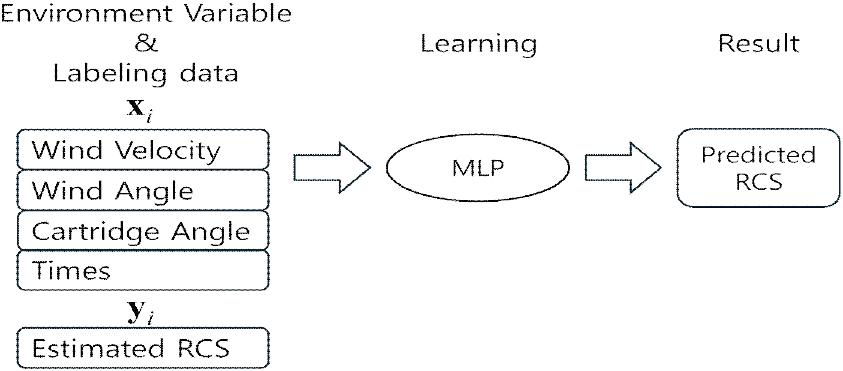
앞서 언급했던 것처럼 기존 RCS 추정은 CFD-DEM으로 계산된 채프운의 동특성에 따라 근사화 기법인 GEC로 RCS를 추정하는 방식이다. 본 논문에서 그림 3과 같은 새로운 접근 방법을 제안한다. 동특성에 따른 채프운을 얻은 후 GEC로 추정한 RCS 결과를 환경변수와 함께 MLP를 이용하여 학습한다. 이때 환경변수는 표 1과 같고, 채프운을 얻을 때와 같은 파라미터를 사용하였다. 훈련에 사용하는 라벨링 데이터의 경우 파라미터와 시간에 따라 RCS를 예측해야 하므로 (case×time)의 데이터를 가진다.

그림 3. | Fig. 3. 제안된 RCS 예측 방법 | Proposed RCS prediction method.

Download Original Figure

표 1. | Table 1. 입력 데이터셋과 출력 데이터셋 | Input dataset and ouput dataset.

Parameter	Dataset	Steps
Wind velocity (m/s)	0～10	1
Wind angle (°)	0～90	45
Cartridge angle (°)	0～45	1
Time (s)	0～5	0.1
Total	1,518×50 (case×time)

Download Excel Table

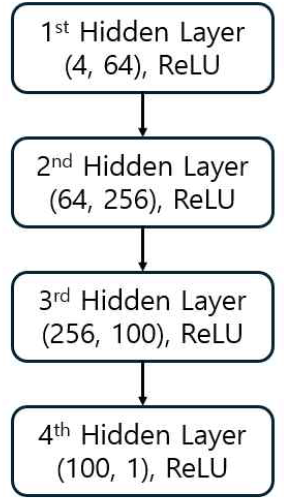
따라서 수치적인 해석방법 없이 RCS를 예측함으로써 시간 단축을 이루고자 한다. 한편, 본 연구에 적용한 MLP 모델의 은닉 계층구조는 그림 4와 같다. 설정한 데이터셋 중에서 학습에는 90 %, 검증에는 10 %로 설정하여 예측하였다. 모델의 성능은 다음의 MSE(mean square error)와 R2 Score를 통해 평가하였다. MSE는 예측값과 라벨링 데이터 사이의 이상치를 설명할 수 있고, R2 score는 예측값이 라벨링 데이터을 얼마나 설명할 수 있는지를 측정할 수 있다.

$$MSE={\displaystyle \sum _{i=1}^N\frac{{\left(y-\widehat{y_i}\right)}^2}{N}}$$

(4)

$$R2=\frac{{\displaystyle \sum _{i=1}^N{\left(\widehat{y_i}-y\right)}^2}}{{\displaystyle \sum _{i=1}^N{\left(\widehat{y_i}-\overline{y}\right)}^2}}$$

(5)

그림 4. | Fig. 4. 은닉 계층구조 | Architecture of the hidden layers.

Download Original Figure

여기서 y는 라벨링 데이터, $\overline{y}$는 라벨링 데이터의 평균, $\widehat{y_i}$는 예측값이다.

3-3 MLP 예측 결과

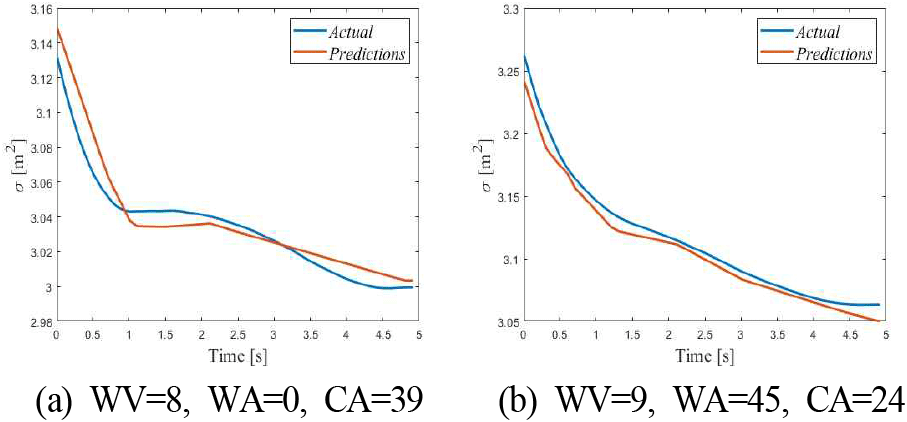
앞에서 제안된 방법에 대한 성능 MSE, R2 score와 걸린 시간을 표 2에 나타내었다. 그리고 그림 5는 풍속(WV, wind velocity), 풍향 (WA, wind angle), 카트리지 초기 각도(CA, cartridge angle)에 대한 시간에 따른 RCS 예측 그래프이다. 빨간색 곡선의 Actual은 CFD-DEM & GEC를 통해 계산된 RCS를 나타낸 것이며, 파란색 곡선의 Prediction은 MLP를 통해 추론한 RCS이다. 표 2와 같이 기존의 CFD-DEM & GEC 모델보다 본 논문에서 제안된 MLP를 이용한 모델이 기존보다 약 44 % 더 빠르며, 높은 정확도를 보여주는 것을 알 수 있다.

표 2. | Table 2. 모델의 성능 평가 및 소요 시간 | Model performance and computation time.

Model	MSE	R2 score	Time (s)
MLP	0.0016	0.9307	10.69
Preprose model	-	-	19.28

Download Excel Table

그림 5. | Fig. 5. MLP를 이용한 RCS 예측 | Predicted RCS using MLP.

Download Original Figure

Ⅳ. 결 론

기존에는 수치해석 기법인 CFD-DEM과 근사화 기법인 GEC를 통해 RCS를 얻음으로써 시간을 단축하였다. 채프운의 동특성에 따라 위치와 방향을 계산하는데 많은 컴퓨터 리소스와 계산 시간이 필요하다. 그래서 본 논문에서는 수치해석 기법을 사용하지 않고 인공지능 회귀 기법인 MLP를 사용하여 새로운 채프운의 RCS 추정 방법을 제안하였다. 또한 본 논문에서는 AI를 통해 해석 시간을 단축하게 되었고 이로써 RCS를 추정할 수 있는 가능성을 확인하였다. 제안한 방법으로 해석할 경우 MSE=0.0016, R2 score=0.9307의 성능을 가지며, 해석시간은 약 44 % 향상되었다. 추후 연구를 통해서 활성화 함수에 따른 성능 비교와 모델에 따른 성능 비교를 통해서 정확도를 증가시킬 예정이다. 또한, 주파수와 같은 파라미터를 가변하여 다양한 경우에서 RCS 예측을 진행할 예정이다.