고속 이동체의 탐지를 위한 광대역 균일빔 기반 빔스캐닝 방향 탐지 연구

Ⅰ. 서 론

현대전에서는 외부 위협으로부터 항공기를 보호하기 위한 전자전의 역할이 대두되고 있다^[1],[2]. 특히, 미사일과 같은 초고속 이동체의 위협에 대응하기 위해 C, X, Ku 밴드 등 다양한 레이다 신호에 대한 광대역 고속 방향 탐지 및 재밍 기술이 요구된다. 기존의 RWR(radar warning receiver) 기반 방향 탐지 및 재밍방식은 광각 커버리지를 위해 낮은 이득을 가진 안테나를 활용하므로 방향 탐지 해상도가 낮다^[3],[4]. 또한, 재밍을 위한 목표 EIRP(effective isotropic radiated power)를 구현하기 위해서는 고출력 신호원이 요구되므로 항공기 페이로드가 크게 증가한다^[5],[6]. 이러한 문제를 해결하기 위해 최근 배열 안테나를 활용한 방향탐지 및 재밍방식이 제안되었다^[7],[8]. 이러한 배열 안테나 기반 방식은 아날로그, 디지털, 하이브리드 빔포머를 활용한 방식으로 세부 구분될 수 있으며, 각 방식에 따라 요구되는 ADC/DAC 컨버터와 주파수 상향/하향 변환기의 수가 다르다^[9]~[12]. 디지털 빔포머는 동시 다중빔 생성, 널링과 부엽 억제와 같은 정교한 빔포밍이 가능하지만, ADC/DAC 컨버터와 주파수 상향/하향 변환기를 포함한 RF chain이 안테나 소자 수만큼 필요하므로 배열 소자 수가 많을수록 소요되는 비용과 차지하는 공간이 크다. 특히, C, X, Ku 밴드 모두를 포함하는 광대역 주파수 상향/하향 변환기는 큰 부피를 가지므로 항공기 탑재를 고려할 때, 최소한의 RF chain을 활용하는 빔포머가 요구된다. 아날로그 빔포머는 정교한 빔포밍 구현이 어렵다는 단점이 있으나, 안테나 채널 수에 상관 없이, 하나의 RF chain으로 운용될 수 있으므로 소요 비용이 작고, 요구되는 공간이 작다는 장점이 있다. 따라서 항공기 탑재를 고려할 때, 아날로그 빔포머가 선호되며, 아날로그 빔포머 기반 방향 탐지 방식은 목표 빔 커버리지 내에 여러 빔을 순차적으로 생성한 후, 가장 큰 수신 전력이 들어온 빔을 입사 방향으로 추정하는 빔스캐닝 방식을 활용한다^[9]. 그러나 광대역에서 기존의 Bartlett 빔포머를 활용할 경우, 생성된 빔은 주파수가 높아질수록 빔폭이 좁아지므로, 빔커버리지 내에서 좁은 빔으로 빔스캐닝을 하기 위해선 많은 빔을 생성해야 한다. 또한, 요구되는 빔이 늘어날수록 탐지 시간이 증가하므로, 고주파 대역에서 탐지 시간이 지연된다는 문제가 생긴다^[13],[14].

본 논문에서는 광대역에서 동일한 빔 스캔 속도를 도출하기 위해 광대역 균일빔(FIB, frequency-invariant beamforming) 방향탐지 및 재밍 기술을 제안한다. 제안된 기술을 활용할 경우 모든 주파수에서 동일한 빔폭을 가지므로, 주파수와 관계없이 동일한 빔 스캔 속도를 도출할 수 있다. 균일빔 생성 가중치는 IFT(inverse Fourier transform) 방식을 활용하여 계산하며^[15], 생성하고자 하는 목표 패턴의 반전력 빔폭(HPBW, half power beamwidth), SLL(side lobe level)에 따라 방향 탐지 성능을 비교 및 분석하였다. 제안된 방식의 성능을 검증하기 위해 3:1 광대역의 동작 대역을 갖는 16×1 배열 안테나를 활용하였으며, 전파 무반사실에서 측정된 각 배열 소자의 AEP(active element pattern)을 활용하여 균일빔을 생성하고, 빔스캐닝을 통해 탐지 성능을 분석하였다. 검증 결과, 제안된 방식은 ±45° 범위에서 5개의 빔을 활용하여 6° 이하의 RMSE (root-mean square)를 도출하였으며, 이를 통해 주파수에 독립적인 빠른 빔조향 기반 방탐, 재밍의 유효성을 검증하였다.

Ⅱ. 빔스캐닝 방향 탐지 알고리즘

배열 안테나의 방향 탐지 성능을 분석하기 위해서 입사 신호를 모델링을 하였다^[16]. 특정 각도 θ에서 입사하는 평면파에 의한 배열 안테나의 응답을 나타내는 조향 벡터(steering vector)는 식 (1)과 같다.

여기서 M은 배열 안테나 소자 수를 나타내며, T는 전치행렬을 의미한다. 또한 위상차 ϕ는 식 (2)와 같이 정의된다.

이때 λ는 파장을 나타내고, d는 배열 안테나 간격을 나타내며, i는 배열 소자 index로, 1부터 M 사이에서 자연수값을 가진다. 입사 각도가 θ_inc일 때, 배열 안테나의 입력 신호 벡터 x는 식 (3)으로 표현된다.

여기서 s는 신호, n은 소자별 noise 벡터이며, 각 벡터의 차원은 M×1이다. 배열 안테나의 output 신호 y는 입력 신호 x와 가중치 벡터 w의 각 항들의 곱 및 합하여 식 (4)와 같이 나타낼 수 있다.

이때 H는 켤레 전치 행렬을 의미하는 에르미트 행렬을 나타낸다. 가중치 벡터 w는 적용 알고리즘에 따라 달라지며, 일반적으로 사용되는 Bartlett 빔포머의 경우, 식 (5)와 같이 조향 벡터로 결정될 수 있다.

또한 수신 신호의 power는 식 (6)에서와 같이 구할 수 있다.

아날로그 빔포머 기반 빔스캐닝을 할 경우, 빔 개수 N_beam개의 빔을 생성하고 각각의 조향 벡터로 수신 신호를 식 (7)과 같이 계산한다.

수신 신호들 중 가장 큰 신호가 수신된 조향각을 추정각도(θ_estt)로 결정되며, 신호 오차는 식 (8)에서 나타내었듯이,

로 결정된다. 또한 모든 주파수와 입사 신호에서의 방향 탐지 오차는 식 (9)에서 나타낸 것과 같이, RMSE로 나타내었다.

이때, N_θ는 입사 신호 개수, N_f는 주파수 개수를 나타내고, f는 주파수 인덱스를 나타낸다.

앞서 설명한 방향 탐지 평가지표 RMSE를 바탕으로 빔스캐닝 기반 방향 탐지 알고리즘의 성능을 분석하기 위해 시나리오 예제를 제시하였다. 방향 탐지를 위한 배열 안테나의 소자 수는 16개를 가정하였고, 신호의 주파수는 6~18 GHz에서 121개의 주파수 샘플링으로 가정하였다. 빔 커버리지는 ±45°이며, 입사 신호는 커버리지 내에서 1° 단위로 입사된다고 가정하였으며, 각각 입사 신호에 대해서 빔스캐닝을 수행하고 스캔 결과를 기반으로 θ_est와 θ_err를 도출하였다.

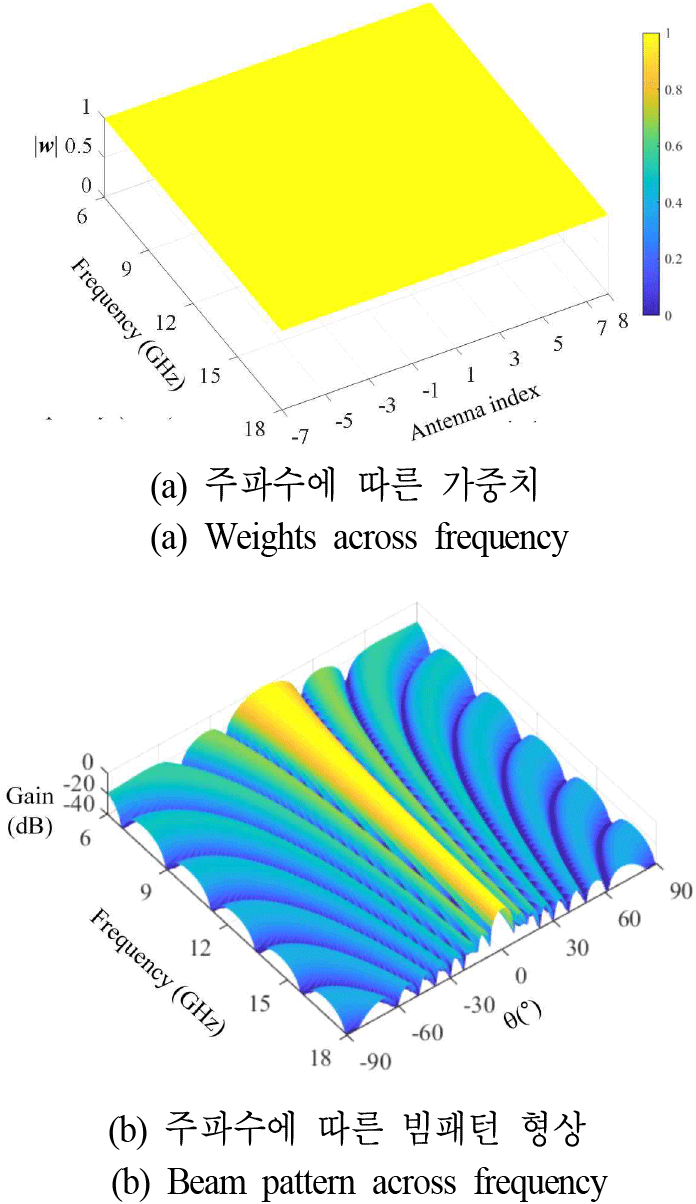
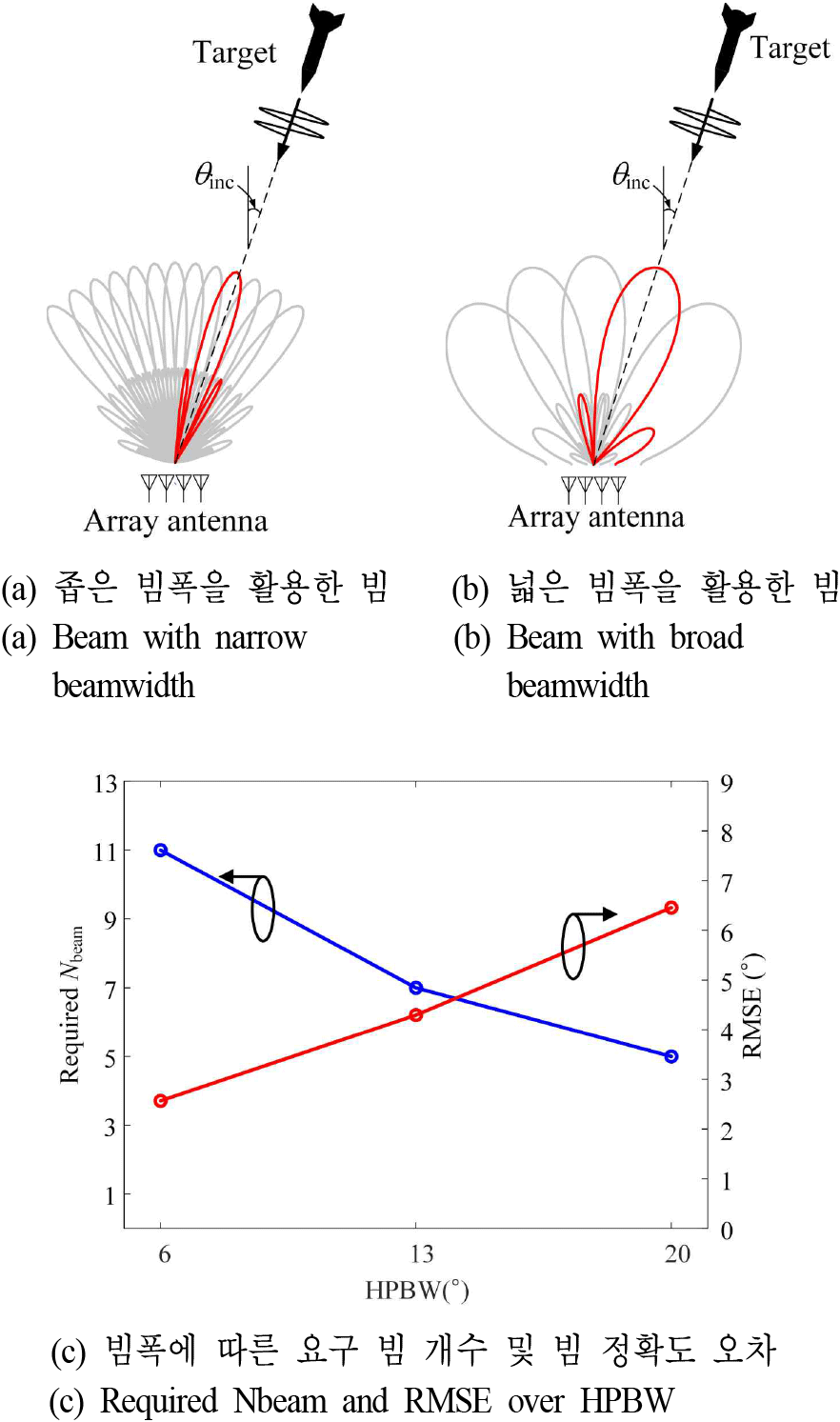
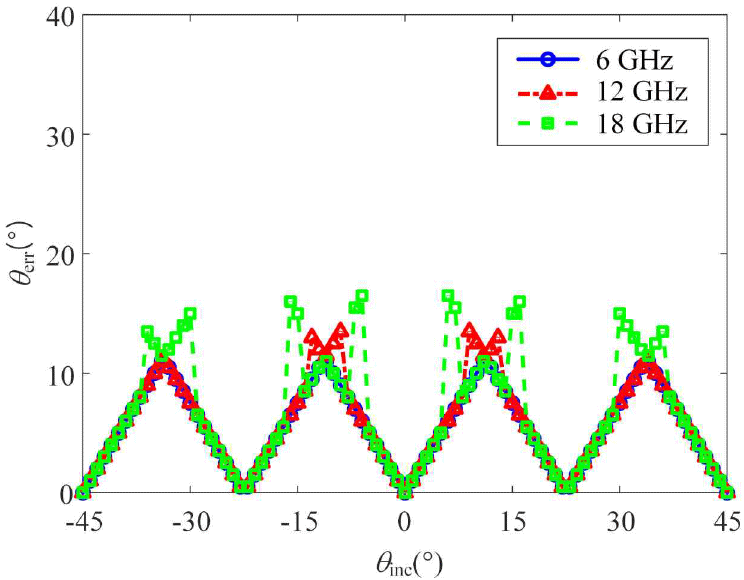
그림 1(a)는 16소자로 구성된 배열 안테나에 대하여 Bartlett 빔포머의 가중치의 크기를 나타낸 그래프로, 모든 주파수 및 안테나 소자에 동일한 크기의 배열 가중치를 가진다. 해당 배열 가중치를 배열안테나에 인가하여 주파수에 따른 빔패턴을 그림 1(b)에 나타내었다. 저대역에서는 상대적으로 빔폭이 크고 주파수가 올라갈수록 빔폭이 좁아지므로, 주파수에 따라 다른 N_beam개의 빔을 생성해야한다. 특히, 18 GHz에서 빔폭은 전면방향 기준 6°를 가지며, 빔 커버리지인 ±45°를 스캔하기 위해 최소 11개의 이상의 많은 빔을 생성해야므로, 탐지 시간이 오래 걸린다는 문제가 있다. 반면 6 GHz에서는 빔폭은 전면방향 기준 18°이며 5개의 빔만으로 빔 커버리지를 스캔할 수 있다. 그림 2(a) 및 그림 2(b)에서와 같이, 빔폭에 따라 목표 빔커버리지를 커버하기 위해 요구되는 빔 개수가 다르며, 빔폭이 좁을수록 많은 빔이 요구된다. 그림 2(c)는 빔폭에 따라, 빔스캐닝을 위한 요구 빔 개수와 방향 탐지 정확도를 나타낸 그래프로, 빔폭이 6°인 경우 목표 빔커버리지를 스캔하기 위해 11개 이상의 빔이 요구되나, RMSE 오차는 약 2.57°로 상대적으로 낮은 오차를 가진다. 반면 빔폭이 20°인 경우, 5개의 빔만으로, 목표 커버리지를 커버할 수 있으며 약 6.4°의 RMSE를 가지는 trade off 관계를 가진다. 그러나, 고속이동체를 빠르게 탐지하기 위해서는 적은 빔 개수를 활용하여 빔스캐닝을 해야 한다. 그림 3에서는 6~18 GHz에서 모두 5개의 빔(−45°, −22.5°, 0°, 22.5°, 45°)으로, isotropic 방사패턴을 가정한 ideal source를 가정하여 빔스캐닝을 시행하였고, 해당 방향 탐지 결과를 나타내었다. 6 GHz에서의 방탐 최대 오차는 11°이며 이는 입사각이 두 빔이 교차되는 조향각들의 중앙값인 −34°, −11°, 11°, 34°일 때 발생하였다. θ_err가 11°일 경우, 23°의 빔폭을 가지는 빔을 활용하여 θ_est방향으로 재밍할 때 목표물이 HPBW 내에 위치하므로 충분한 EIRP를 확보할 수 있다. 반면, 18 GHz에서의 최대 오차는 16.5°으로 해당 θ_est방향으로 재밍 시 HPBW 영역으로부터 벗어난 곳에 목표물이 위치하므로, 재밍을 위한 EIRP를 만족하기 위해서 높은 전력이 요구된다. 18 GHz에서 증가한 오차는 신호가 각각의 빔 사이에 누락된 영역에서 입사될 경우, 주빔이 아닌 부엽에서 신호가 수신되어 최대 전력이 다른 빔에서 발생했기 때문이다. 따라서, 고속 이동체 탐지를 위해 생성가능한 빔 개수가 제한되는 환경에서, 고대역에서 좁은 빔폭으로 인해 탐지 오차가 증가하는 것을 방지하기 위해 동작 주파수 내에서 적절한 빔폭을 균일하게 생성할 수 있는 균일빔 알고리즘 적용이 요구된다.

균일빔을 생성하기 위해 우선 균일하게 생성하고자하는 목표 패턴 설정이 요구된다. 목표 패턴을 생성하기 위해서 bandpass filter 형태의 식 (10)를 활용하였다.

이때 h는 filter의 계수를 나타내며, h의 설정에 따라 패턴의 형상이 결정되므로 목표 패턴을 생성하기 위해서 적절한 값이 선택되어야 한다. 적절한 h를 도출하기 위해, window 함수를 적용할 수 있으며, 본 연구에서는 MATLAB에 내장된 Taylor window 함수를 활용하여 h를 도출하였다. 또한 ω는 각주파수, Δx_tgt는 filter 간격, M_tgt는 filter의 크기를 나타내고, m_tgt는 filter index를 나타낸다. x축을 따라 무한 길이의 이산 배열을 가정하면 빔 응답 B(ω,θ), D(mΔx, ω)와 지수함수 형태의 위상 항들과의 선형합으로 표현할 수 있다.

이때 Δx는 안테나 간격, m은 안테나 index를 나타낸다. 또한 (ω/c)Δxsinθ를 ω1로 치환할 경우, 빔응답은 식 (12)와 같이 DFT 형태로 나타낼 수 있다.

FIB 가중치 D(mΔx, ω)는 식 (13)와 같이 $\tilde{M}$ 개의 주파수 샘플에 대하여 IDFT를 적용하여 구할 수 있다.

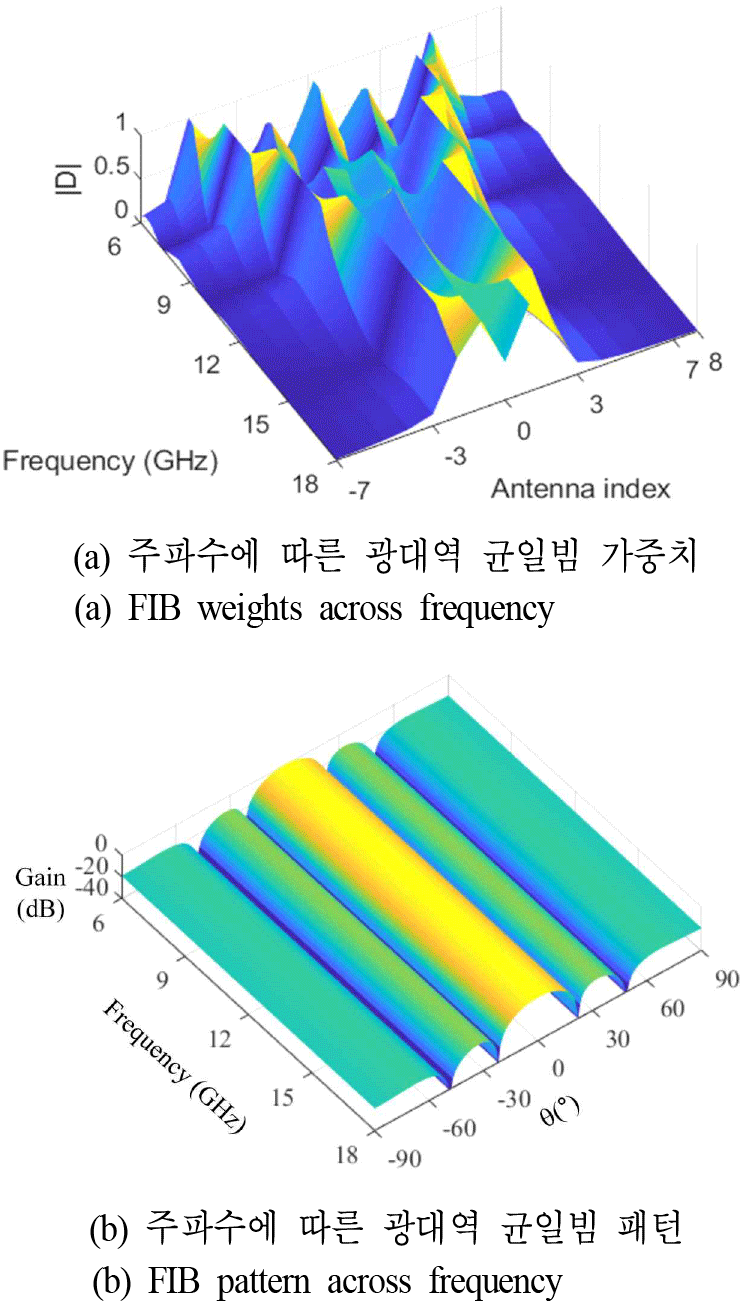
이때 ω₁는 $\tilde{m}$에 대하여 ${\omega }_1=-\pi +2\tilde{m}\pi /\tilde{M}$로 나타낼 수 있다. 식 (12)에서의 D의 차원은 $\tilde{M}\times \tilde{M}$이며 $\tilde{M}$은 안테나 소자 수(M)보다 더 크므로, 배열 안테나에 적용하기 위해 소자 수와 동일하게 차원 일치가 요구된다. 따라서 D에 적절한 window 함수가 요구되며, 본 연구에서는 rectangular window를 활용하였다. 따라서 windowing 이후의 균일빔 가중치 D의 차원은 $M\times \tilde{M}$이며 계산된 균일빔 가중치를 활용하여 균일빔을 생성한다. 그림 4(a)에 각 배열 안테나 소자에 인가되는 균일빔 가중치를 나타내었으며, 주파수에 따라 가중치가 다른 것을 확인할 수 있다. 주파수가 높을수록 배열 중심에 있는 소수의 안테나에 가중치가 집중되고, 주파수가 낮아질수록 많은 배열 소자로 가중치가 분산되는 것을 확인할 수 있다. 계산된 가중치를 배열 안테나에 인가한 빔패턴을 그림 4(b)에 나타내었고, 6~18 GHz에서 주파수에 관계없이 균일한 패턴을 생성하였다.

균일빔 성능은 목표 패턴의 형상에 따라 바뀌며, 빔폭이 좁을수록, SLL이 클수록 빔패턴이 유지되는 대역폭이 줄어든다. 그림 5(a)는 빔폭은 23°로 모두 동일하고, SLL이 각각 7, 13, 19 dB인 목표 패턴을 나타낸 그래프이다. 16개의 배열 소자를 활용하여, 각 목표 패턴 정보를 기반으로 광대역 균일빔을 생성하였다. 그림 5(b)에 45° 조향 시 목표 SLL에 따른 HPBW 특성을 나타내었으며, 목표 SLL이 7 dB인 경우, 최대 오차는 2°이고, 평균 23.29°, 표준편차 1.03°로 광대역에서 균일한 빔이 생성되었다. 반면 SLL이 19 dB인 경우, 6 GHz에서 최대 5°로 저대역에서 균일빔이 깨지는 것을 확인할 수 있다.

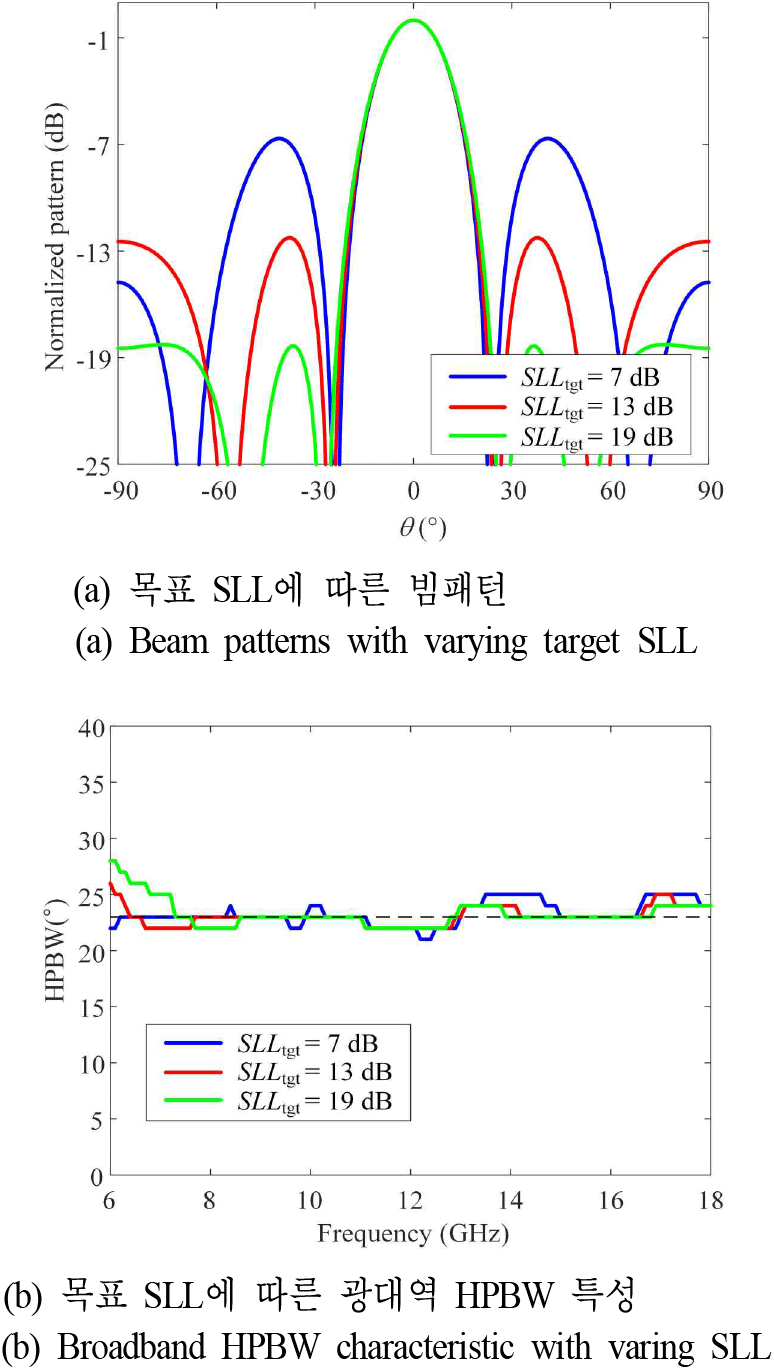
그림 6(a)는 목표 빔폭이 15°, 23°, 31°인 목표 패턴을 나타낸 그래프로 각 패턴의 SLL은 7 dB 이상이다. 31개의 배열 소자를 가정하여 각 목표 패턴 정보를 기반으로 균일빔을 생성하고, 5개의 빔(−45°, −22.5°, 0°, 22.5°, 45°)을 활용하여 빔스캐닝을 하였으며 방향 탐지 결과를 그림 6(b)에 나타내었다.

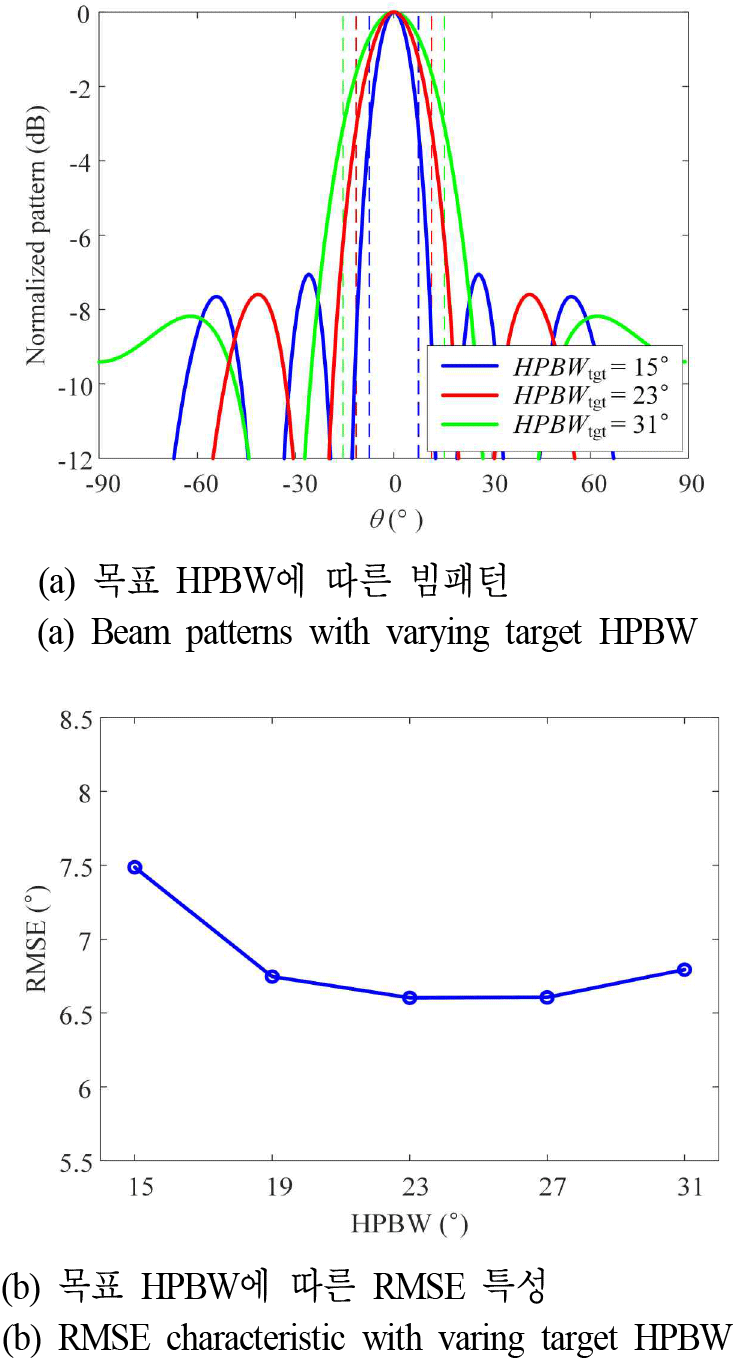
빔폭이 15°인 빔을 활용할 경우, 좁은 빔폭으로 인한 빔 사이 빈 영역으로 인해 RMSE가 증가하였으며, 빔폭이 31°의 경우, 빔 사이에 빈 영역은 없으나, 낮은 이득으로 인해 SNR(signal-noise-ratio)이 낮아져, RMSE가 빔폭이 다소 증가하였다. 빔 사이 간격(22.5°)과 유사한 빔폭을 가지는 23°인 경우 빔 사이 빈 영역이나, 불필요한 중첩 영역이 없으며, 적절한 이득을 가지므로, 낮은 RMSE를 가진다.

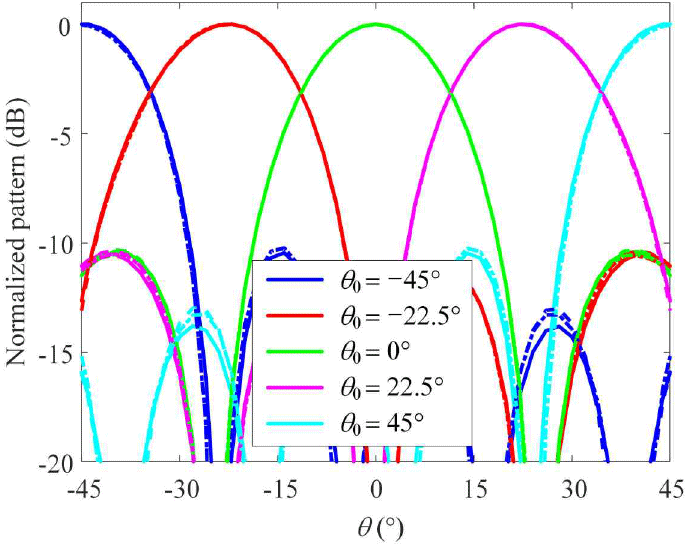
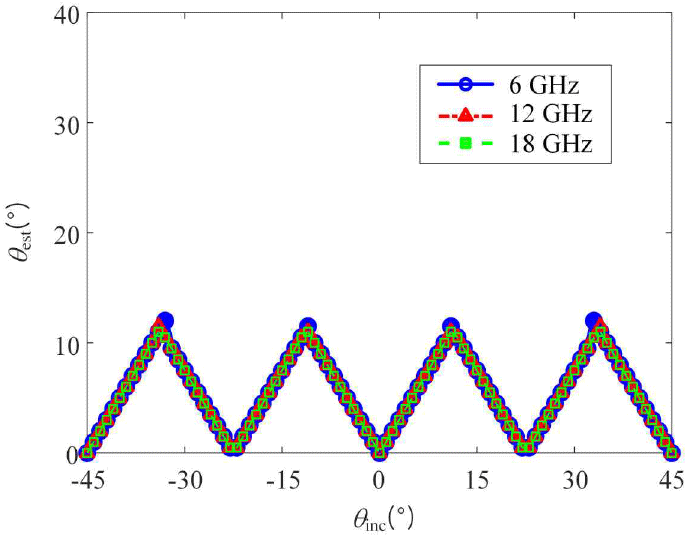
해당 분석 결과를 바탕으로, 16개의 배열 소자를 활용하여 23°의 빔폭을 가지고, 7 dB 이상의 SLL을 만족하는 5개의 빔(−45°, −22.5°, 0°, 22.5°, 45°)으로 균일빔 기반 빔스캐닝 방향 탐지를 시행하였다. 6~18 GHz에서 생성된 5개의 빔을 그림 7에 나타내었다. 6, 12, 18 GHz에서의 빔패턴은 각각 실선(−), 파선(--), 일점 쇄선(-.)으로 나타내었다. 각 목표 주파수에서 방향별로 나타낸 패턴의 주빔들은 목표 패턴과 매우 유사하게 생성되었으며 해당 빔들을 활용하여 빔스캐닝을 하였고, 이에 따른 방향 탐지 결과를 그림 8에 나타내었다. 목표 주파수 내에서 12.5° 이하의 오차가 발생하였으며, 식 (9)을 활용하여 계산한 모든 입사 신호에 대한 RMSE는 균일빔을 적용하지 않을 때는 8.3°이고, 균일빔을 적용할 경우 6.5°으로, 균일빔을 적용하지 않았을 때보다 1.8° 작은 오차를 가진다.

Ⅲ. 균일빔 빔스캐닝 방향 탐지 성능 검증을 위한 배열 안테나 설계 및 알고리즘 검증

알고리즘 검증을 위해 6~18 GHz에서 동작하는 16×1 비발디 배열 안테나를 설계하였다. 배열 형상은 그림 9(a)에 나타내었고 190×45×36 mm로 6 GHz 기준 3.8×0.9×0.72λ의 크기를 가진다. 해당 배열 안테나는 재밍 시, 높은 전력이 인가되므로, 이를 견디기 위해 금속 3D 프린팅 기법을 활용하여 full metal 구조로 설계하였으며, 유지보수를 고려하여 배열 소자를 접지판에 탈착 가능하도록 설계하였고, 해당 부분은 볼트로 고정하였다. 또한, 가장자리에 방사 특성 왜곡을 방지하기 위해 양 끝에 더미 소자를 배치하였으며, 더미 소자는 50 ω 종단저항으로 연결하였다. 제작된 배열 안테나는 무반사실에서 그림 9(b)에 나타낸 것과 같이 근접장 스캐너를 활용하여 측정하였다. 원전계 측정을 하기 위해서는 16×1 배열의 큰 aperture로 인해 긴 원거리장 영역 확보가 요구되므로, 상대적으로 작은 공간에서 측정이 가능한 근접장을 측정하였고, 측정된 데이터를 활용하여 원전계로 변환하였다^[17]. 또한, 중심 소자의 능동 반사 계수(active S parameter)의 시뮬레이션 결과와 측정 결과는 그림 10(a)에 나타내었다. 저대역에서 리플이 존재하며 이는 3D 프린팅 공정으로 인해 소자 상단부의 안테나 정렬이 흐트러졌기 때문이다. 그러나 중, 고대역에서는 시뮬레이션과 유사하게 −10 dB를 만족하고 시뮬레이션과 측정값의 주파수에 대한 평균은 각각 −17.08 dB, −15.72 dB이다. 그림 10(b)는 주파수에 따른 배열 중심소자의 AEP의 이득을 나타내었으며 측정결과와 시뮬레이션 결과가 유사하며, 측정된 이득은 최소 −1.96 dBi, 최대 7.07 dBi이다.

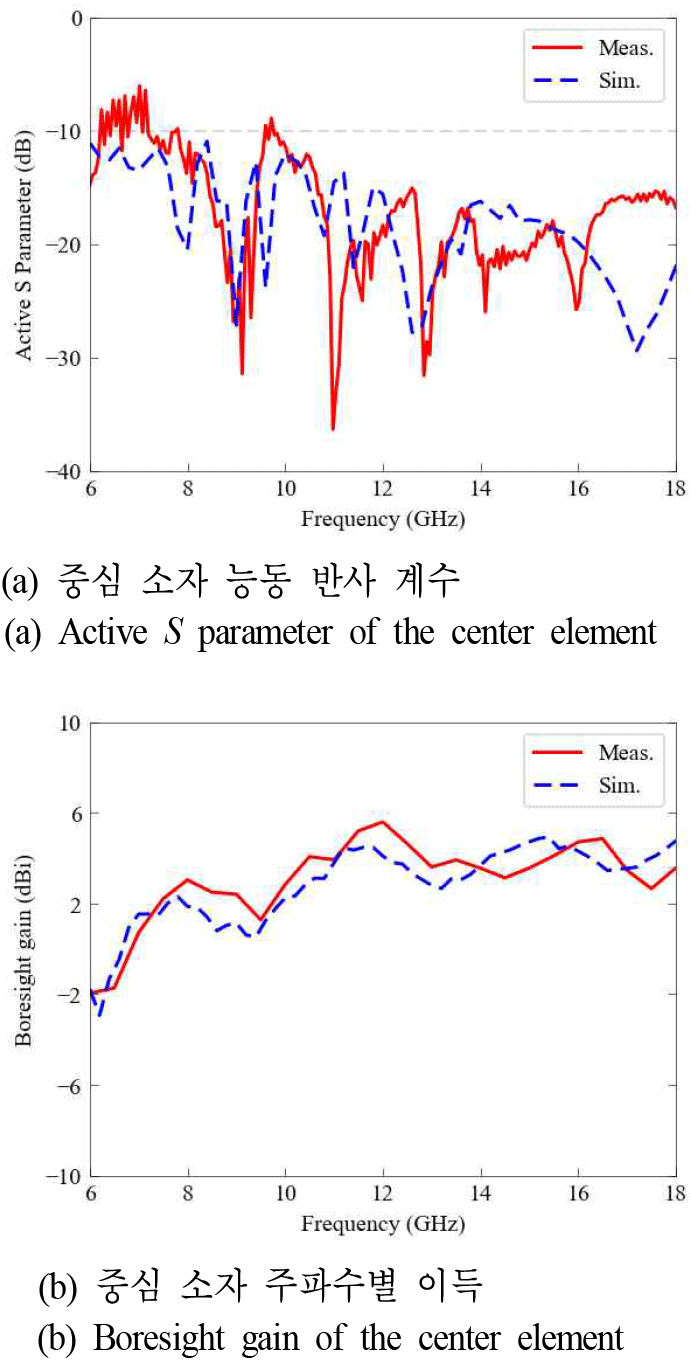
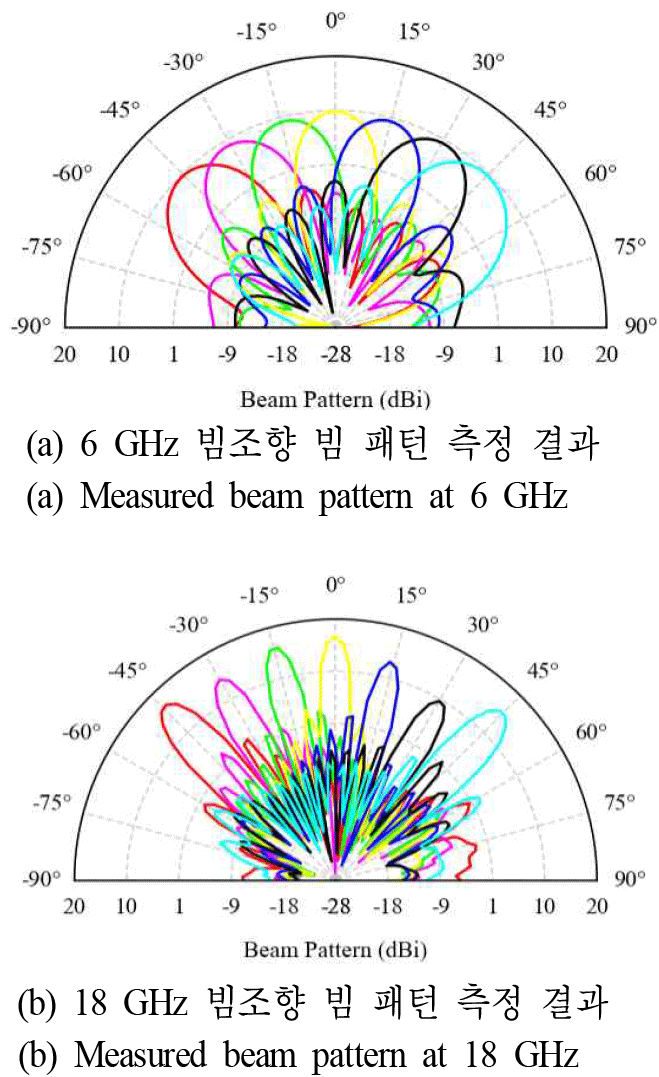
그림 11은 측정된 배열 안테나의 ±45° 범위 내에서 빔조향 패턴을 나타낸 그래프이며, 6 GHz에서는 0° 조향 시, 합성이득과 HPBW은 각각 10.2 dBi, 9°이고 45° 조향 시, 각각 10 dBi, 13°이다. 또한, 18 GHz에서는 합성 이득과 HPBW은 0° 조향 시 각각 16.8 dBi, 3°이고 45° 조향 시 15.4 dBi, 4°를 가진다. ±30°에서 이득은 각각 14.45, 10.1 dBi로 좌우 비대칭이 존재하며, 이는 45° 기울어진 안테나 소자 형상으로 인해 좌우 비대칭 구조에 의해 발생하였으나, 10 dBi 이상의 높은 이득을 유지하였다.

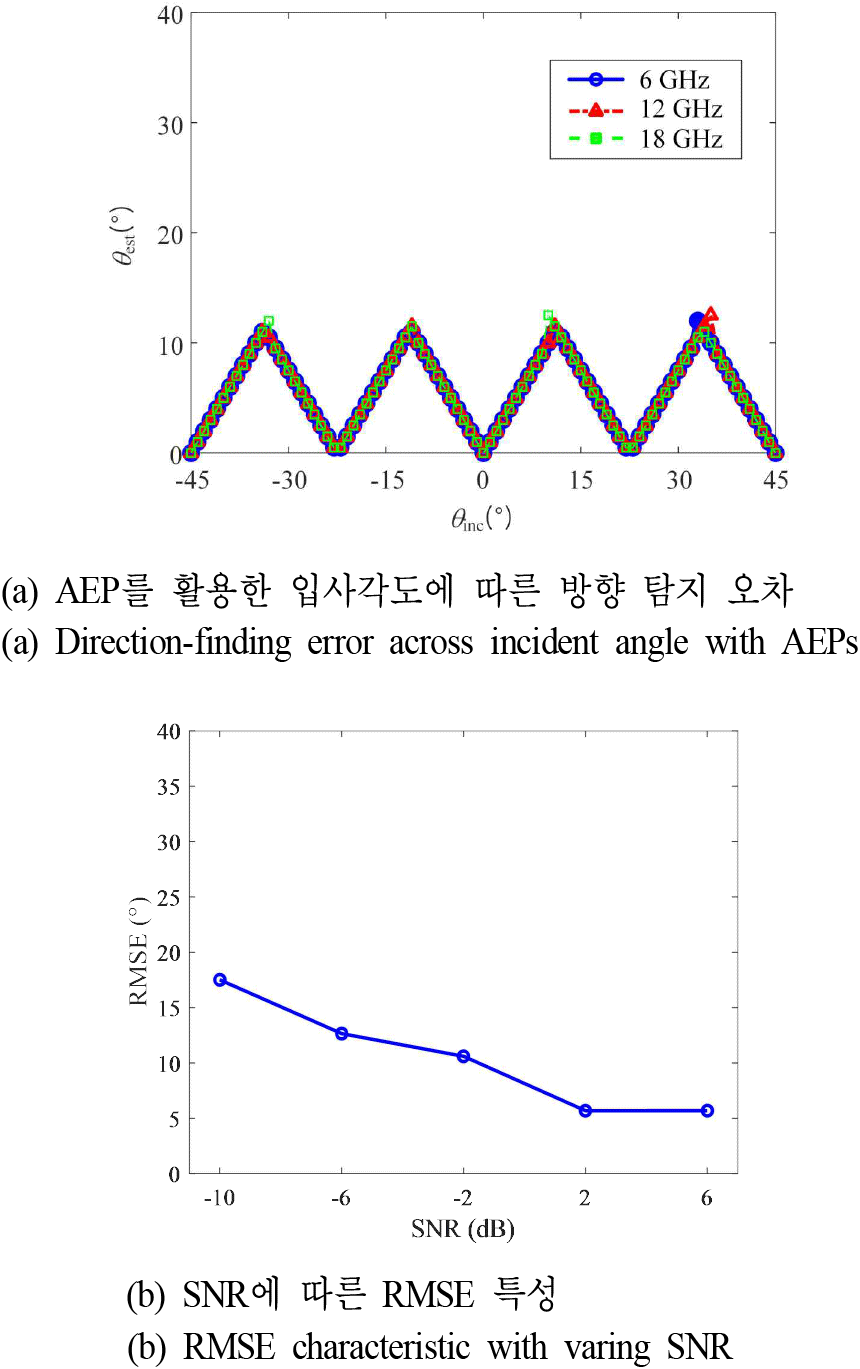
해당 배열 안테나의 AEP 측정 데이터를 활용하여, 균일빔 기반 빔스캐닝 방향 탐지 성능을 분석하였다. 6~18 GHz 광대역에서 노이즈 없이, 1° 간격으로 입사된 각 입사 신호의 방향을 추정하였으며, 이를 그림 12(a)에 나타내었다. 각 주파수에서 모두 균일하게 조향 방향과 동일한 방향에서 최저 0° 오차를 나타내며, 최대 오차는 12.5°로 이론상 최대 오차와 동일한 값을 가진다. 식 (9)를 활용하여, 동작 주파수에서, N_f가 121개인 경우에 ±45°의 범위에서 총 91개의 입사신호에 대해 계산한 결과 RMSE는 6°를 가지며, isotropic source를 활용한 그림 8의 결과와 유사한 결과를 가진다. 또한, 그림 12(b)에 SNR을 −10°부터 6°까지 변화시켜가며, SNR에 따른 RMSE를 분석하였다. SNR이 증가할수록 RMSE는 감소하고, SNR이 0 dB 이상일 경우, RMSE는 6.08°로 6°에 수렴하는 것을 확인하였다. 이를 통해 SNR에 따른 주파수에 독립적인 빠른 빔스캐닝 기반 방탐, 재밍의 유효성을 검증하였다.

Ⅳ. 결 론

본 논문에서는 고속 이동체가 방사하는 전파의 방향을 탐지하기 위해 광대역 균일빔 기반 빔스캐닝 방향 탐지 기술을 제안하였다. 빔스캐닝 방식의 경우, 빔폭에 따라, 탐지 정확도와 탐지 속도 간의 trade off 관계가 있으나, 고속 이동체를 고속으로 탐지하기 위해서 적은 빔 개수로 운용하면서도, 균일빔 기반의 넓은 빔폭을 광대역에서 활용하여 탐지 정확도를 개선하였다. 빔스캐닝 기반 방향 탐지 알고리즘의 성능을 분석하기 위해 시나리오 예제를 제시하였고, 이를 검증하기 위해 16×1 배열 안테나를 설계 및 제작하였다. 해당 안테나는 3:1 광대역에서 중심소자의 AEP는 최대 이득은 7.07 dBi이며, 합성이득은 18 GHz에서 최대 0° 조향 시 16.8 dBi를 가진다. 빔 개수는 5개(−45°, −22.5°, 0°, 22.5°, 45°)로 가정하였으며, 목표 패턴의 빔형상은 23°의 빔폭과 10 dB의 SLL을 가지는 빔패턴을 활용하였다. 배열 소자의 AEP는 무반사실에서 측정되었으며, 측정된 AEP을 활용하여, 균일빔 기반 빔스캐닝을 적용하였다. 그 결과, 노이즈가 없을 때는 isotropic source와 동일하게, 최대 오차는 10°이며 RMSE는 6°으로 계산된다. 또한, SNR의 변화에 따라 RMSE를 분석하였으며, SNR이 0 dB 이상인 경우, RMSE는 6°로 수렴하였다. 이를 통해 제안된 방식은 0 dB 이상의 SNR 환경에서 주파수에 독립적인 빠른 빔스캐닝 기반 방탐, 재밍의 유효성을 검증하였다. 탐지 정확도를 추가적으로 개선하기 위해서, 가장 큰 전력이 수신된 빔의 방향을 입사 방향으로 추정하는 기존 방식과 함께, 상위 두 빔의 수신 전력이 유사한 경우에는 두 빔의 중앙각을 입사 방향으로 추정하는 방법을 고려할 수 있다.