자유 공간 빔 집중 측정용 렌즈의 이론적 분석 및 초점거리 추정

Ⅰ. 서 론

최근 국내에서는 위성용 메쉬 반사판 안테나에 대한 개발이 진행 중이다. 안테나 설계를 위해서는 메쉬 시편의 전기적 특성을 측정할 필요가 있으며, 자유 공간 측정(free-space measurement)^[1] 방식은 시편에 비접촉식으로 산란계수를 측정할 수 있어, 소재의 기계적 변형이 전기적 특성에 미치는 영향을 분석하기에 적합하다. 측정에는 혼 안테나 등에 렌즈를 사용하여 가우시안 빔(Gaussian beam) 이론을 활용해 시편의 특정 영역에 빔을 집중시키는 빔 집중(focused beam) 방식도 사용되고 있다^[2],[3]. 그러나 기존 렌즈 분석 연구들은 계산 과정이 복잡하거나, 파장 대비 렌즈가 두꺼운 경우(electrically thick) 발생하는 회절 및 위상 오차를 정확히 예측하지 못하는 한계가 있었다^[4],[5].

본 논문에서는 자유 공간 빔 집중 측정용으로 설계한 렌즈를 대상으로, 기하 광학(geometrical optics) 방법 및 공간 스펙트럼 방법(angular spectrum method)을 사용하여 이론적 분석을 수행하고, 전자기 시뮬레이션을 통해 렌즈를 투과한 전계 분포의 결과를 비교․분석하여 초점거리를 추정한다.

Ⅱ. 본 론

렌즈는 준광학 이론(quasi-optical theory)^[3],[6]에 기반하여 설계하였다. 주파수 대역은 X-band 중심주파수인 10.3 GHz로 설정하였다. 렌즈의 재질로는 PTFE(ϵ_r=2.1)를 사용하였다. 지름은 200 mm이고, 렌즈 양면을 쌍곡면(hyperboloid)으로 설정하였다. 쌍곡면은 한 초점에서 방사되는 광선이 렌즈를 투과하였을 때 평면파가 형성된다는 특징이 있으며 공식은 식 (1)으로 표현된다. 여기서 n은 렌즈의 굴절률이고, f는 초점거리로서 입력 안테나와 시편의 빔 웨이스트(beam waist)에 의해 각각 f₁=110 mm, f₂=370 mm로 설계하였다.

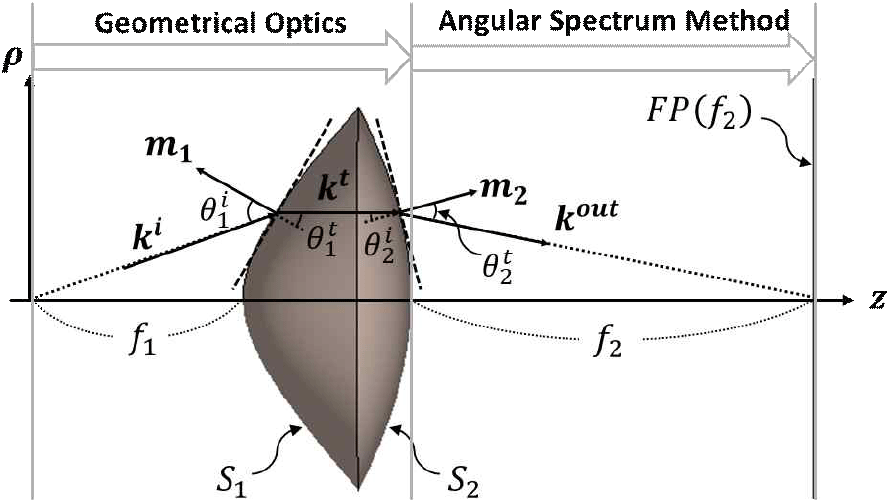
이론적 해석을 위해 그림 1에서 도시한 형상 및 파라미터들을 정의하였다. 렌즈 및 소스가 x, y축에 대해 회전 대칭을 이루므로 원통좌표계(ρ,ϕ,z)를 도입하고, 구조가 ϕ방향으로 변하지 않아, 2차원 평면 구조로 단순화하였다. 전파 소스는 가우시안 빔 모델^[6]을 따르며, 렌즈에 입사되는 전기장 $E_1^i$과 진행 벡터 $k_1^i$는 식 (2)로 표현할 수 있다.

그림 1. | Fig. 1. 이론적 분석을 위한 렌즈의 형상 및 파라미터 | Geometry and parameters of lens for theoretical analysis.

Download Original Figure

렌즈 표면의 법선벡터는 식 (3)과 같이 쌍곡선 형상 S₁의 기울기(gradient)를 이용하여 얻을 수 있다.

입사각과 투과각은 $k_1^i$, m₁의 벡터 내적 및 Snell의 법칙으로부터 식 (4)와 같이 구할 수 있다. 식 (5)를 이용하여 TE와 TM 각 편파의 투과계수를 계산한 뒤, 산술 평균하여 T₁을 구하고 렌즈 내부 필드를 계산하였다.

렌즈 내부에서는 두께 t(ρ)만큼 z축으로 전파되어, S₂에서의 입사파는 식 (6)으로 표현된다. 동일한 방법으로 투과계수 T₂를 구하여 렌즈를 통과한 필드를 얻고, 이를 수직 단면에서의 필드로 바꾸기 위해 자유공간에서 렌즈 두 번째 쌍곡면의 두께 차이인 l(ρ)만큼 추가로 전파하여 최종 렌즈 투과 필드는 식 (7)과 같이 표현된다.

필드가 자유 공간에서 전파하는 과정은 공간 스펙트럼 방법(angular spectrum method)를 사용하였다. 이는 필드를 주파수 영역으로 변환하여 전파한 후에 다시 공간 영역으로 변환하여 필드의 분포를 확인할 수 있는 방법이다^[2]. 원통좌표계의 대칭성을 이용하여 한켈 변환(Hankel transform)을 사용하면 공간 스펙트럼 함수 F_out으로 정의할 수 있고, 최종적으로 z축 방향으로 거리 d에 따라 전파되는 전계는 역 한켈 변환을 통해 식 (8)로 도출되었다.

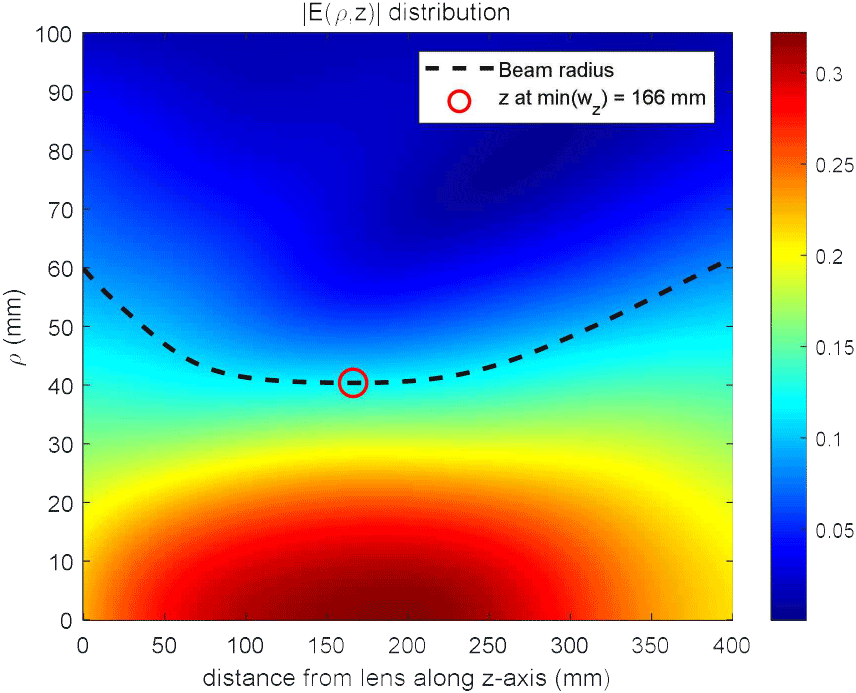
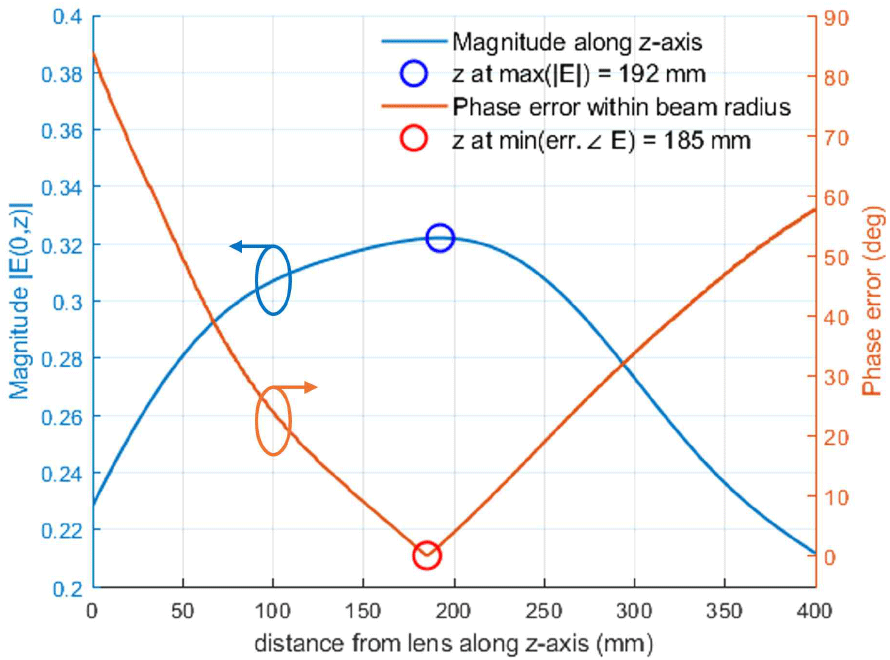
이론적 분석 결과, 렌즈를 투과한 전계 분포는 그림 2와 같으며, 빔의 집중 현상을 확인하였다. ρ축 기준 전계 최대값의 1/e로 감소하는 거리인 빔 반경(beam radius)이 최소가 되는 거리는 166 mm로 도출되었다. 그림 3은 z축 방향에서 거리에 따른 전계 크기 및 빔 반경 범위에서의 위상 오차를 확인하였으며, 전계 세기 최대 및 위상 오차 최소가 되는 거리는 각각 192, 185 mm로 도출되었다.

그림 2. | Fig. 2. 렌즈를 투과한 전계 분포의 이론적 결과 | Theoretical result of electric field distribution through the lens.

Download Original Figure

그림 3. | Fig. 3. z축 방향으로 거리에 따른 전계 세기 및 빔 반경 범위에서의 위상 오차 | Electric-field magnitude along z-axis and phase error within the beam radius region.

Download Original Figure

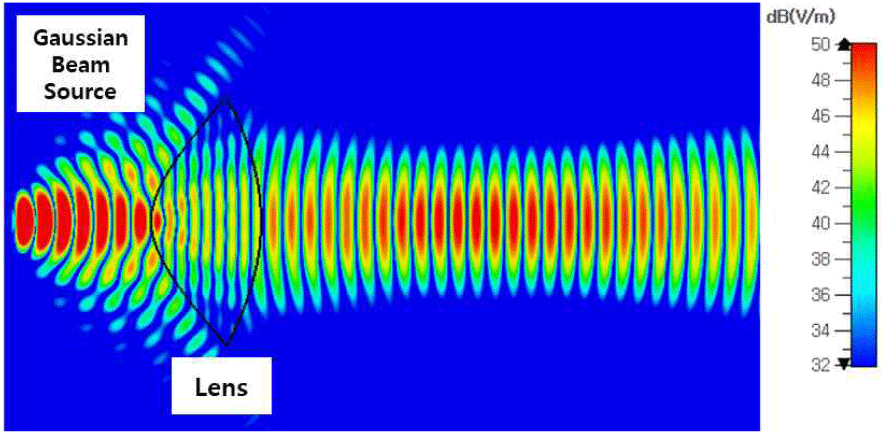
다음으로, 정확한 초점거리를 추정하기 위해 전자기 시뮬레이션을 수행하였다. 시뮬레이션은 CST MWS (microwave studio)를 사용하였고, 소프트웨어에 내장된 가우시안 빔 소스를 인가하였으며, 그 결과는 그림 4에 나타났다. 렌즈를 투과한 빔이 특정 영역에 집중되는 모습을 확인할 수 있다.

그림 4. | Fig. 4. 전계 분포 시뮬레이션 결과 | Simulation result of electric field distribution.

Download Original Figure

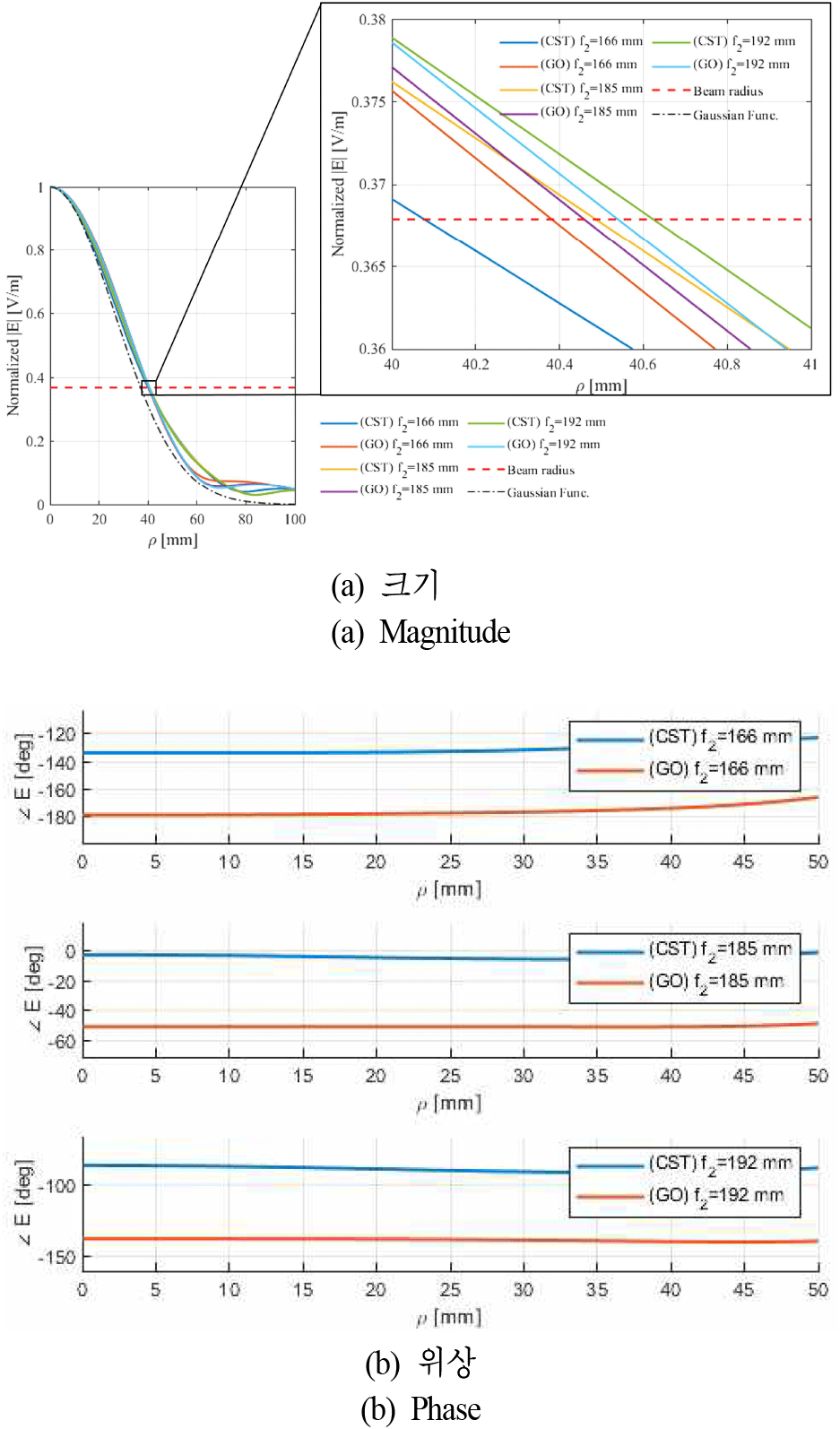
그림 5에서는 예상한 초점거리에 따른 전계를 이론과 시뮬레이션 결과를 비교한 것이다. 크기를 기준으로 빔 웨이스트는 약 40.5 mm로 나타났으며, 초점거리가 166, 185, 192 mm일 때 빔 웨이스트의 차이는 각각 약 0.3, 0.02, 0.08 mm에 불과하여 거의 동일함을 확인하였으며, 위상 오차는 이론적 분석 기준으로 각각 5°, 0.2°, 2°를 보였고, 시뮬레이션 기준으로 6°, 3°, 5°를 확인하였다. 이로써, 이론과 시뮬레이션 결과가 가장 근접하고, 위상 오차가 최소인 185 mm를 초점거리로 추정하였으며, 이는 그림 1의 f₂에도 같은 거리를 의미한다. 추정된 초점거리는 설계값인 370 mm의 절반 수준으로 감소하였는데, 이는 (i) 파장 대비 두꺼운 두께로 인한 중심부와 가장자리 간 위상 오차, (ii) X-band 대역 특성상 회절 효과, (iii) 두 곡면을 각각 설계 후 결합한 구조적 특성 등이 복합적으로 작용한 결과로 판단된다.

그림 5. | Fig. 5. 초점거리에 따른 전계 비교 | Electric field comparison by focal length.

Download Original Figure

Ⅲ. 결 론

본 연구에서는 빔 집중 자유공간 측정을 위해 설계한 렌즈를 대상으로, 기하 광학 및 공간 스펙트럼 방법을 결합한 이론 분석과 전자기 시뮬레이션을 수행하여 렌즈 투과 후의 전계 분포를 기술하고, 시편 위치까지의 초점거리를 예측하였다. 그 결과, 가우시안 빔 반경을 기준으로 위상 오차가 가장 적은 거리를 초점거리로 추정하였으며, 설계값과 추정값 간 차이는 렌즈 두께에 따른 위상 오차, 주파수 대역에 의한 회절 효과 등이 작용했을 것으로 보인다.