Rényi 엔트로피 최소화를 이용한 ISAR 요동 보상

ISAR 영상은 레이다가 고정된 상태에서 움직이는 표적의 궤도를 따라 전자기파를 송수신하여 형성된 영상이다. 이 과정을 수식적으로 살펴보기 위해 표적의 운동궤적을 모형화해보면 다음과 같다.

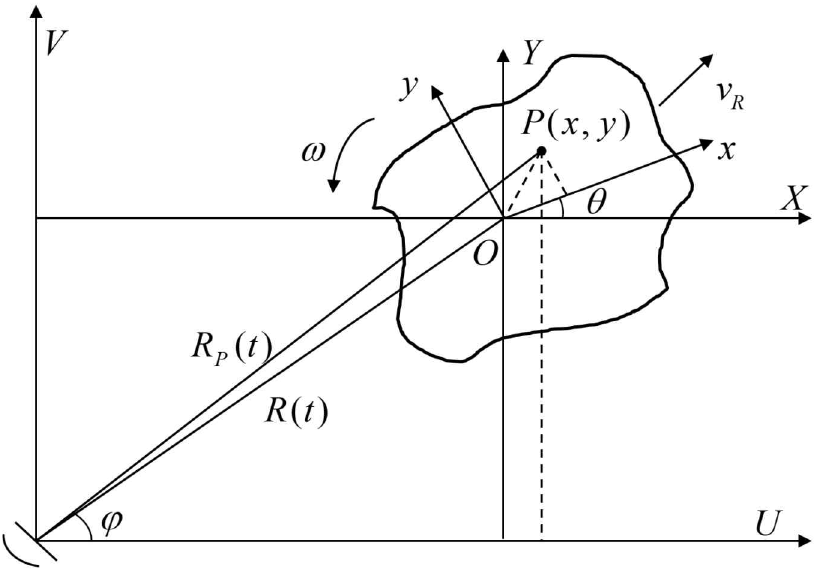
그림 1은 U−V좌표계의 원점에 위치한 레이다로부터 표적 P가 시간 t에 따라 운동하는 모습을 기하학적으로 나타낸 것이다. R_p (t)는 레이다와 표적 사이의 거리를 나타내며 식 (1)과 같이 정리된다^[19].

그림 1. | Fig. 1. 표적의 운동에 대한 기하학적 도시 | Geometry of a target motion.

Download Original Figure

식 (1)에서 x와 y는 x-y 좌표계에서 표적 P의 좌표를 나타낸다. 식 (1)을 살펴보면 표적에 포함된 두 가지 운동성분이 확인된다. 첫 번째 운동성분은 U−V 좌표계에 대하여 시간 t가 진행될 때 표적 P가 위치한 x-y 좌표계 전체가 R(t)의 거리만큼 이동하는 병진운동 성분이 존재한다. 두 번째 운동성분은 x-y 좌표계 내에서 표적 P가 시간 t에 따라 θ(t)의 회전운동 성분을 가지게 된다. θ(t)는 ωt이며 이 때 ω는 각속도이다. 여기서 θ(t)가 매우 작은 값을 갖게 된다면 식 (2)와 같은 근사화가 성립한다^[20].

식 (2)는 식 (1)의 근사식이며, 표적의 초기 위치를 R(0)로 설정하고 레이다 LOS 방향의 속도를 v_R, 가속도를 a_R로 나타낸 식이다. 식 (3)은 표적으로부터 수신된 신호 모델이다^[19].

식 (3)에서 rect는 사각함수, A_i는 i번째 산란점의 크기, c는 빛의 속도, B는 대역폭, f_c는 중심주파수, t_m은 느린시간(slow-time), N은 산란점의 개수, T_obs는 표적 관찰 시간을 각각 나타낸다. 식 (3)을 주파수 방향으로 푸리에 변환하면 거리 압축 데이터가 형성되며 이에 거리정렬 과정을 적용하면 R_p(t)에 포함된 v_R와 a_R를 제거할 수 있다. 이 때 신호 모델은 식 (4)와 같다^[19].

식 (4)에서 FT는 푸리에 변환 연산을, sinc는 sinc 함수를 나타낸다. A_i는 식 (4)는 거리(range) 축에서 sinc 함수의 위치가 시간에 따라 변하지 않는 거리 정렬된 형태를 보이지만, 위상 성분에 포함된 v_RO와 a_RO가 시간 t_m에 관계되기 때문에 yωt_m항에 영향을 주게 된다. 결국 Doppler 주파수와 느린시간 사이의 푸리에 변환 관계에 영향을 주는 요소로 인해 수직 방향의 푸리에 변환을 수행하면 초점이 맞지 않는 ISAR 영상이 형성된다. 따라서 거리 압축 데이터의 위상성분에서 yωt_m항을 제외한 시간에 따라 변화하는 항을 효과적으로 제거할 수 있는 위상보정 과정 혹은 요동 보상 과정이 요구된다.

Shannon 엔트로피(SE, Shannon entropy)는 확률 분포의 불확실성을 정량화하는 가장 보편적인 척도로 널리 활용되어 왔다. 그러나 SE는 단일한 기준에 의해 정의되므로, 분포의 다양한 특성을 충분히 반영하기에는 한계가 있다. 이에 반해 Rényi 엔트로피는 차수 α라는 매개변수를 도입함으로써, 분포의 여러 측면을 유연하게 강조할 수 있다는 장점을 가진다. Rényi 엔트로피는 α값에 따라 희귀 사건이나 우세한 사건에 대한 민감도를 조절할 수 있다. 예를 들어, α가 큰 경우에는 확률이 높은 사건의 영향이 강조되어 분포의 집중도를 평가하는 데 유용하며, α가 작은 경우에는 낮은 확률을 갖는 사건들의 기여도가 상대적으로 커져 분포의 다양성을 반영할 수 있다. 이러한 특성은 SE가 모든 사건을 동일한 기준으로 처리하는 것과 차별화되는 중요한 특징이다.

2-2장에서는 Rényi 엔트로피를 이용한 ISAR 영상의 위상 보정 과정을 수식적으로 살펴보고자 한다. ISAR 영상을 이산 데이터 형식으로 정리하면 식 (5)와 같다^[14].

식 (5)에서 m은 느린시간, n은 거리빈(range bin), k는 Doppler 주파수를 각각 나타낸다. ϕ(m)은 식 (4)에서 표현된 시간에 따라 변화하는 위상 오차 성분을 의미한다. f(m,n)은 식 (4)를 의미하며 g(k,n)은 위상 보정된 f(m,n)의 푸리에 변환식으로 ISAR 영상을 나타낸다.

Rényi 엔트로피는 식 (6)과 같이 정의된다^[18].

식 (6)에서 p_i는 확률밀도함수를 나타내며 α는 Rényi 엔트로피의 변수로 표현된다. ISAR 영상을 정규화하여 영상 전체를 확률밀도함수로 바라볼 때 Rényi 엔트로피는 식 (7)과 같다.

식 (7)의 값을 최소로 만드는 ϕ(m)을 찾으려면 식 (9)를 만족해야 한다.

식 (7)을 미분하여 정리하면 식 (10)과 같이 ϕ(m)와 a(m)의 식으로 표현된다.

식 (9)와 식 (11)로부터 위상 오차 성분 ∠a(m)은 식 (12)와 같이 구할 수 있다.

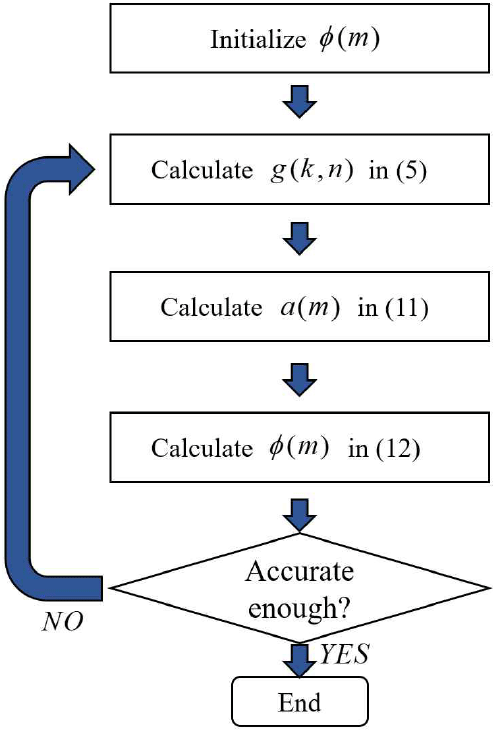
2-2장에서는 Rényi 엔트로피를 이용한 ISAR 영상의 위상 보정 과정으로부터 위상 오차 성분을 식 (12)의 형태로 도출하였다. 식 (11)을 살펴보면 식 (12)가 g(k,n)에 포함된 항임을 확인할 수 있다. 따라서 식 (11)은 그림 2와 같이 고정점 반복법(FPI, fixed-point iteration)을 이용하여 해결 가능하다. 반복 알고리즘을 탈출하기 위한 조건은 식 (13)과 같이 설정할 수 있다^[14].

그림 2. | Fig. 2. 제안된 위상 보정 알고리즘 | Flow chart of the proposed algorithm.

Download Original Figure

식 (13)에서 max는 최댓값 추출 연산자이고, ϕ_i(m)는 i번째 반복을 진행했을 때 구한 위상 오차 성분이며, μ는 문턱 값으로서 이전 위상 오차 성분과 현재 위상 오차 성분의 차이와 비교를 통해 반복 알고리즘을 탈출한다. 본 논문에서 μ는 0.01로 설정하였다.

한편, 식 (6)으로부터 Rényi 엔트로피와 변수 α는 종속 관계가 있음을 알 수 있다. α값이 1에 수렴할 때 Rényi 엔트로피는 SE로 표현된다. α값이 2에 수렴하는 경우 Rényi 엔트로피는 충돌 엔트로피(collision entropy)와 같아진다. 결국 Rényi 엔트로피는 엔트로피의 일반적인 형태로 간주할 수 있다. 따라서 ISAR 영상의 Rényi 엔트로피 위상 보정 과정은 α값의 변화에 영향을 받는다. Rényi 엔트로피의 최적의 α를 찾기 위해 ISAR 영상에 대한 SE 값을 비용함수로 설정하여 전역 최적화를 수행하였다. SE의 경우 값이 작을수록 무질서도가 감소하며 초점이 맞는 ISAR 영상을 보이기 때문에 α의 변화에 따라 비용함수가 최소가 되는 α값을 통해 Rényi 엔트로피를 최적화할 수 있다. 임의의 기동 표적에 대한 서로 다른 시나리오 10개를 설정하고 α값에 따른 각 ISAR 영상의 SE를 측정하고 평균을 계산하였다. 각 시나리오마다 특정 α의 위치에서 SE가 최적화되었고 비용함수가 최소가 되는 α의 값은 1.5 부근으로 확인되었다. 따라서 본 논문에서는 Rényi 엔트로피의 α값을 1.5로 설정하여 모든 실험을 수행하였다.

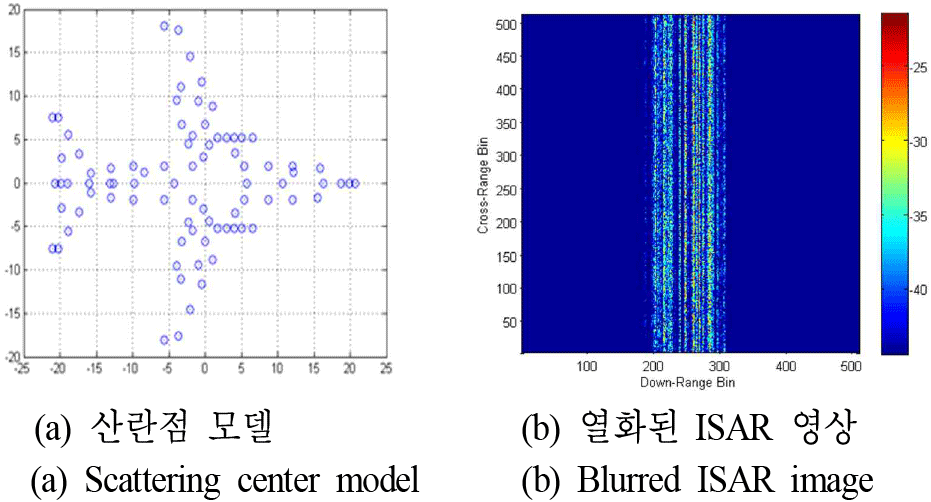
본 실험에서는 제안한 알고리즘의 성능을 분석하기 위해서 88개의 산란점으로 구성된 보잉(Boeing)-747 모델(그림 3(a))을 표적을 기반으로 기동 시나리오에 대한 ISAR 신호를 구성하였다. ISAR 영상은 좁은 대역폭 및 좁은 관측각도 조건하에서 고속-푸리에 변환(FFT, fast Fourier transform)을 기반으로 형성하였으며 시뮬레이션은 MATLAB 프로그램을 이용하였다. 실험에서의 모든 계산은 AMD Ryzen 9 5900X(12-Core, 3.70 GHz) CPU 환경에서 MATLAB R2021a를 이용하여 수행하였다. 표적의 움직임에 따른 병진운동 성분이 위상 오차에 반영되어 해당 ISAR 신호에 대해 Doppler 방향으로 FFT하면 그림 3(b)와 같이 초점이 맞지 않는 ISAR 영상이 생성된다.

그림 3. | Fig. 3. 보잉-747 모델과 ISAR 영상 | A model of Boeing-747 aircraft and its ISAR image.

Download Original Figure

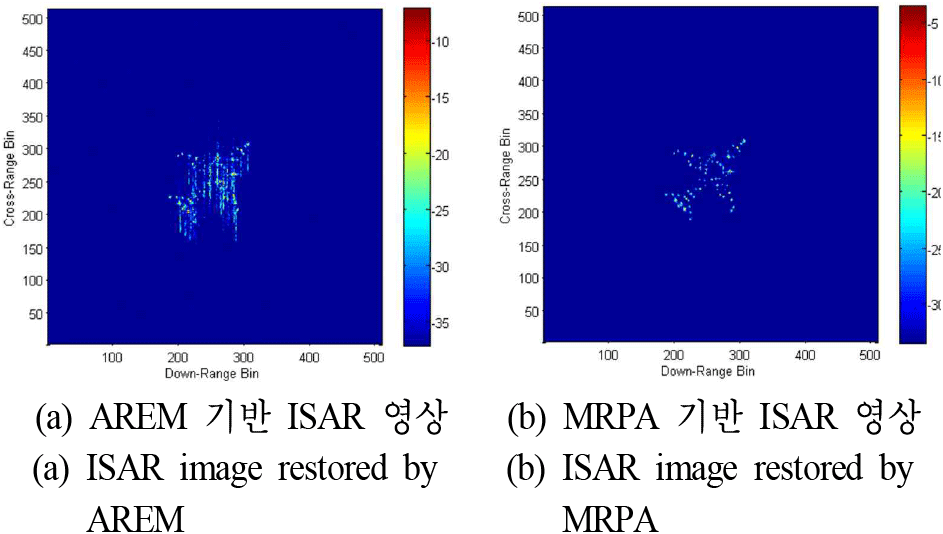
제안한 기법의 성능을 비교 분석하기 위해서 기존에 널리 알려진 ISAR 자동초점 기법인 엔트로피 최소화 기반 ISAR 위상 오차 보상 알고리즘(AREM, ISAR autofocusing based on Rényi entropy minimization)을 선정하였다^[5]. 위상 오차가 존재하는 ISAR 신호에 대해 AREM를 통해 획득한 ISAR 영상은 그림 4(a)와 같다. 그림 3(b)에 비해서는 열화가 많이 개선되었지만 여전히 잔존하는 위상 오차로 인해 초점이 잘 맞지 않는 것을 확인할 수 있다. 한편, 동일한 ISAR 신호에 MRPA를 적용하여 복원된 ISAR 영상은 그림 4(b)와 같다. MRPA를 통해 각 산란점들의 에너지가 분산되지 않고 초점이 잘 맞는 ISAR 영상을 형성하였음을 확인할 수 있다. 각 자동초점 기법을 통해 획득한 ISAR 영상을 정량적으로 분석하기 위해 영상 품질 지표로서 SE를 측정하였다. AREM과 MRPA을 통해 형성된 각 ISAR 영상의 SE는 7.5 및 6.9로 계산되었다. 정량 지표 결과를 통해 MRPA 기법이 기존 AREM 보다 자동초점 성능이 우수함을 확인할 수 있다.

그림 4. | Fig. 4. AREM과 MRPA 기법을 통해 복원된 ISAR 영상 | ISAR images obtained by AREM and MRPA.

Download Original Figure

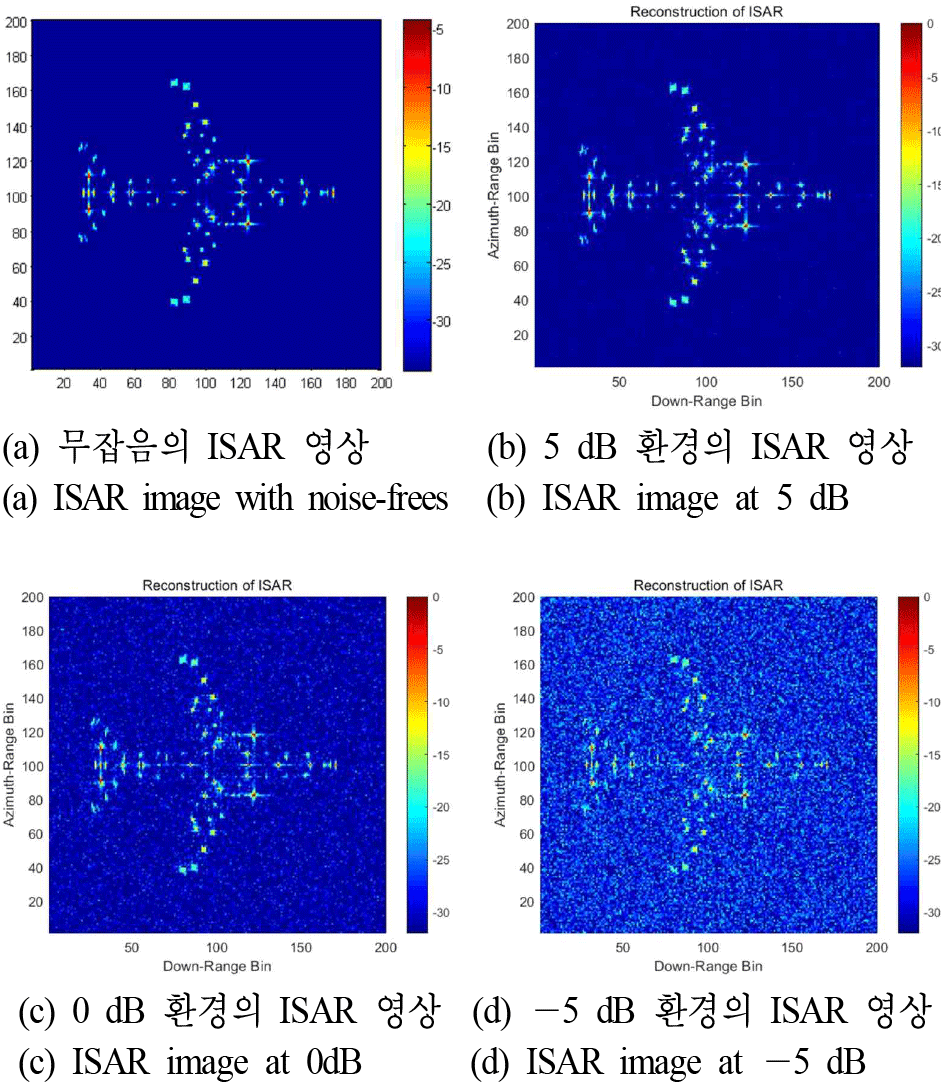
본 실험에서는 다양한 SNR 실험 환경에서 MRPA의 자동 초점 성능을 분석하였다. 먼저, 그림 3(a)의 동일한 보잉-747 모델에 대하여 위상 오차가 존재하지 않는 이상적인 환경에서 ISAR 영상(그림 5(a))을 획득하였다. 이후 위상 오차 성분을 구축하기 위해 Doppler 방향으로 [−π,π] 범위 내에서 랜덤하게 위상을 형성하였다. 생성 오차 성분을 그림 5(a)의 원본 데이터의 위상 신호에 삽입하고 Doppler 방향으로 FFT하면 초점이 맞지 않는 ISAR 영상이 생성된다. 위상 오차가 반영된 ISAR 신호에 대해 잡음 환경을 구축하기 위해 가우시안 잡음을 추가하였다. 구체적으로, SNR이 −5, 0, 5 dB인 가우시안 잡음을 주파수 영역의 ISAR 신호에 각각 삽입하였으며, 각 ISAR 신호에 대해 MRPA 기법을 적용한 결과를 그림 5에 도시하였다. 그림 5(b)는 SNR이 5 dB이며 그림 5(a)의 원본 영상과 매우 유사함을 확인할 수 있다. 그림 5(c)는 SNR이 0 dB이며 표적 주변으로 잡음이 발생하지만 산란점은 초점이 잘 맞는 것을 관측할 수 있다. 그림 5(d)는 SNR이 −5 dB의 열악한 잡음 환경에서 복원된 ISAR 영상을 나타낸다. 각 SNR 환경에서 MRPA 기법을 통해 형성된 ISAR 영상들의 SE는 7.2, 8.5 및 9.5로 계산되었다. 실험 결과를 통해 MRPA 기법은 잡음에 강인함을 확인하였다.

그림 5. | Fig. 5. 다양한 잡음 환경에서 복원된 ISAR 영상 | ISAR images obtained by MRPA various SNR.

Download Original Figure