모노펄스 레이다 추정각도의 최빈값과 산란점들 각도의 원형 평균과의 관계

Ⅰ. 서 론

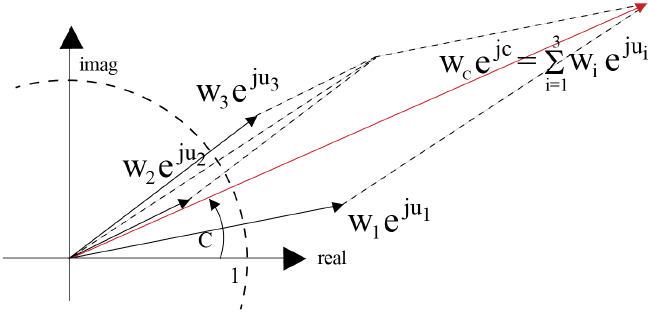
단일 점표적의 경우 무지향성 두 안테나에서의 기저대역(baseband) 측정값을 z₀, z₁라고 하고, sum/delta 신호를 각각 ∑=z₀+z₁, Δ=z₀−z₁로 표시하자. 그림 1에 이들을 복소평면에 보였다. 이제 z₀, z₁ 사이의 각도를 u=arg(z₁)−arg(z₀)라고 하면 tan(u/2)=|Δ|/|∑|, Δ/∑= (|Δ|/|∑|)e^−jπ/2이므로

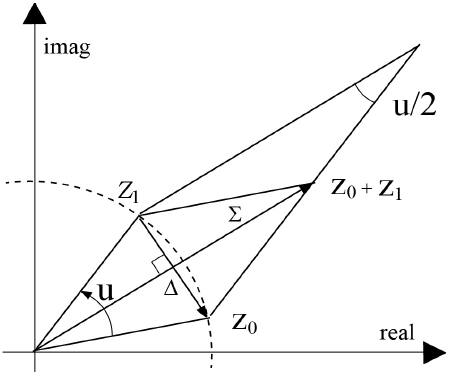
로 표현할 수 있다^[1]. 즉 두 안테나에서 받은 평면파의 위 상차는 ∑, Δ값으로부터 식 (1)에서 구할 수 있고, 평면파의 도래각(angle of arrival), θ는 sin θ=u/(kd)로부터 얻을 수 있다. 여기서 k, d는 각각 파수(wave number), 안테나 사이의 거리를 의미한다.

모노펄스 레이다로 N_t개의 산란점을 가지고 있는 큰 표적(extended target)의 각도를 측정하려고 할 경우, 고해상도가 아닌 일반 레이다를 사용하게 되면 이들 산란점들은 분해되지 않고(unresolved) 같은 거리셀, 같은 도플러 셀 안에 존재하게 된다. 이때 두 안테나에서의 측정값은 식 (2)와 같다.

여기서 A, s, n 은 각각 배열응답 행렬, 신호, 덧셈잡음을 의미하며 식 (3)과 같이 표현할 수 있다

여기서 CN은 circular complex normal을 의미하며, 산란점 i의 안테나 1에 대한 안태나 2의 위상은 u_i로, 산란점 신호의 크기 및 위상은 각각 w_i, ϕ_i로 표시하였다.

이때 w_i는 매 시행 시 변하지 않는 결정적 장애모수(deterministic nuisance parameter)이고, ϕ_i는 레이다와 산란점까지의 거리에 따라 변하는 확률적 장애모수(random nuisance parameter)이다.

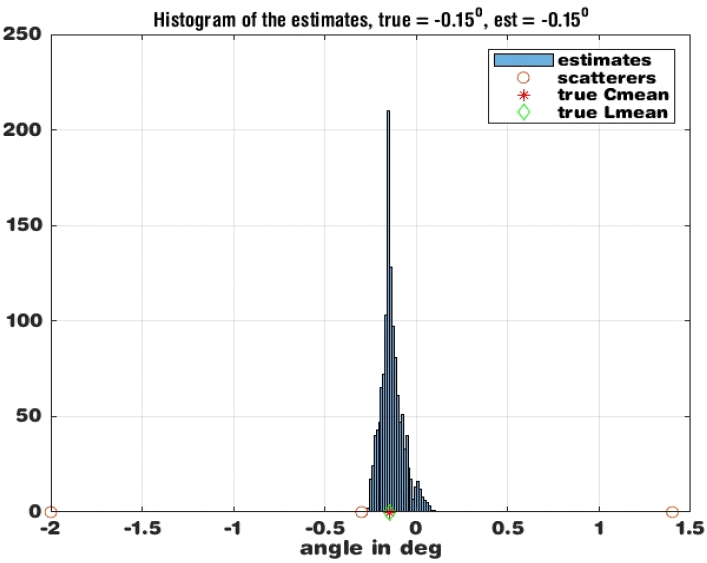
본 논문에서는 ϕ_i가 무작위(random)인 다중 N_t 산란점의 경우, 모노펄스 레이다로 추정한 식 (1)의 최빈값 (mode)이 가중치 원형 평균값(weighted circular mean), ${\displaystyle \sum _{i=1}^{N_t}{w}_i{e}^{-j{u}_i}}$임을 증명하였다 (그림 1). 이와 같은 사실은 지금까지 공개된 참고문헌(예를 들어 참고문헌 [1] 및 참고문헌[2])에 알려진 바 없다. 그림 2에 가중치 원형평균값의 의미를 보였다. 참고로 선형평균값 $\left({\displaystyle \sum _{i=1}^{N_t}{w}_i{u}_i}\right)/\left({\displaystyle \sum _{i=1}^{N_t}{w}_i}\right)$은 u_i가 크지 않을 경우 원형 평균값과 거의 차이가 없는데, 각도와 같이 방향성이 있는 값들의 평균값을 다룰 떄는 원형평균값이 더 적합함이 잘 알려져 있다^[3].

Ⅱ. 통계량 (Statistic) 분포의 유도

산란점의 개수가 N_t 일 때 두 안테나에서 받은 측정값을

라고 하고 식 (5)의 함수

를 정의하자. 또한 ϕ_i가 균일분포(uniform distribution) ϕ_i~U(−π,π)라고 가정하고, ϕ 의 퍼짐(range or spread)을 식 (6)과 같이 정의하며,

f(ϕ)의 정의역 (domain)이 식 (7)과 같다고 하자.

이 경우 0≤r≤R일때 확률변수 c=f(ϕ)의 확률밀도함수는 식 (8)과 같이 표현할 수 있다.

편의상 우선 N_t=3인 경우를 고려하자. 이제 p_c (c|sp(ϕ)=r)을 구하기 위하여 f(ϕ)의 3차원 정의역 (domain) D를 식 (9)와 같이 6개의 (1 ≤i≤6)1차원 정의역으로 분해(partition)하자:

여기서 σ_i는 (1, 2, 3)의 여섯개의 순열(permutation)로서 σ₁=(1,2,3), σ₂=(2,3,1), σ₃=(3,1,2), σ₄=(1,3,2), σ₅=(2,1,3), σ₆=(3,2,1) 를 의미한다.

이제 정의역이 D_i 로 한정된 함수 f를 $f_i\left({\varphi }_{{\sigma }_i\left(2\right)}\right)$라고 하면, 확률변수의 함수(function of random variables)에 관한 잘 알려진 정리^[4]를 사용하여

임을 알 수 있다. 여기서 f_i,j는 f_i를 M개의(monotonic) 1:1 함수로 분해한 j번째 함수이다.

함수 f_i를 각각 f_i (0), f_i (r)를 지나는 직선으로 근사하면 M=1이 되고, 식 (11)은 식 (12)와 같이 간략화된다.

여기서 $b=\left|f_i\left(0\right)-f_i\left(r\right)\right|c_{\min }^{\left(i\right)}=\min \left(f_i\left(0\right),f_i\left(r\right)\right),c_{\max }^{\left(i\right)}=\max \left(f_i\left(0\right),f_i\left(r\right)\right)$이다.

이제^[4], 106쪽의 order statistic의 퍼짐에 관한 정리 2.2를 n=N_t=3인 경우, −π≤r≤π의 균일분포에 대하여 적용하고 적분하면 식 (13)을 얻는다.

이제 마지막으로 식 (10), 식 (12) 및 식 (13)을 식 (8)에 대입하면 p_c(c|sp(ϕ)≤R)를 구할 수 있다.

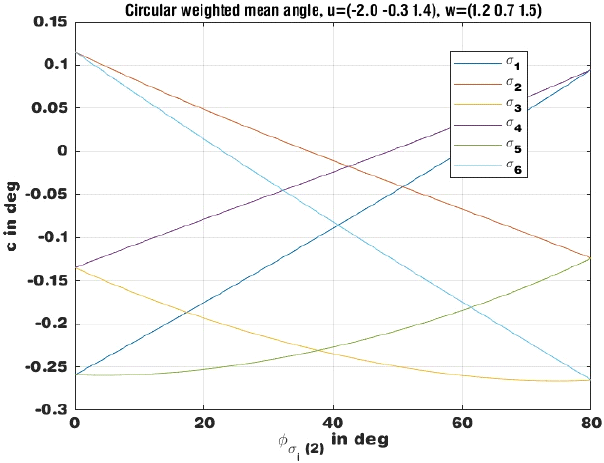
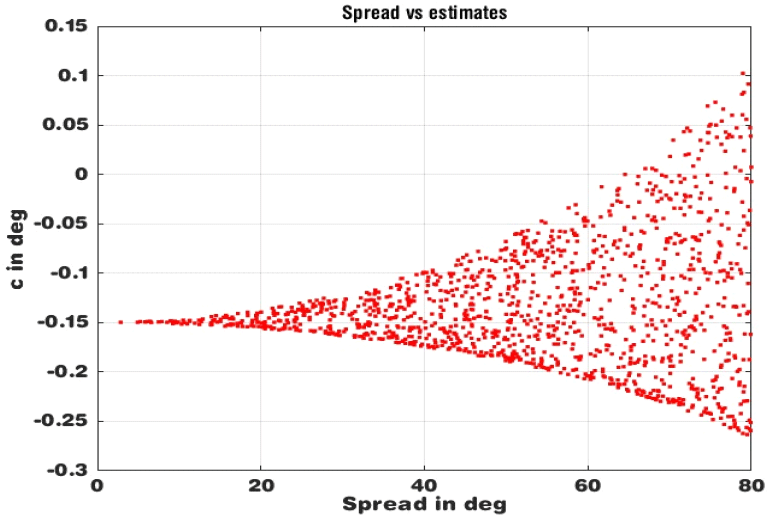
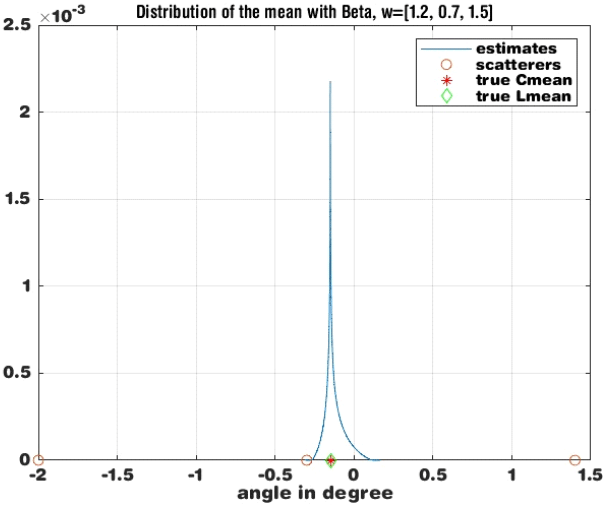
그림 3~그림 5에 u=[−2.0, −0.3, 1.4], w=[1.2, 0.7, 1.4]의 경우를 보였다.

그림 3은 R=80°일 때 f_i (ϕ), $\varphi ={\varphi }_{{\sigma }_i\left(2\right)}$,

을 보인 것으로서

그림 4에 0≤r≤R=80° 각각에 대하여 식 (10) 및 식 (12)를 보였다. 왼쪽의 수렴하는 값, −0.15는 식 (14)에 r=ϕ=0을 대입한 값,

으로서 u의 원형 가중치 평균값임을 알 수 있다.

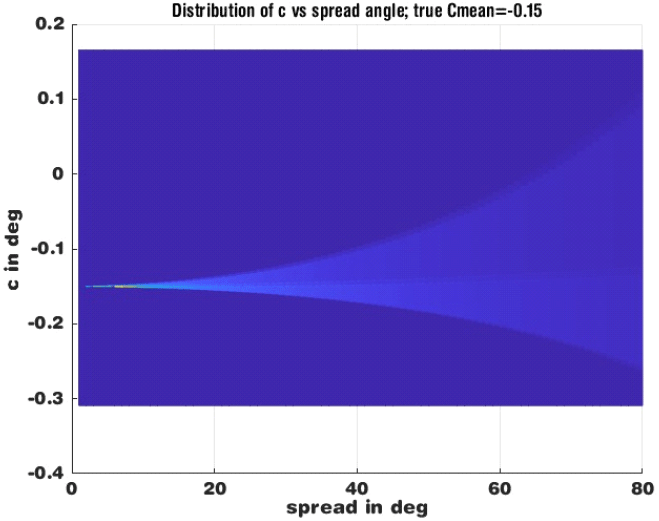
그림 5에 식 (8)의 결과를 보였다. c=f(ϕ)의 분포의 최빈값은 u의 원형 가중치 평균값, −0.15에서 나타난다. 또한 각도들이 작을 경우 선형평균(Lmean)과 원형평균 (Cmean)이 거의 일치함을 볼 수 있다. 하지만 분포 c가 비대칭(skew)이어서 c의 평균값은 최빈값보다 약간 오른 쪽에 위치할 것이다.

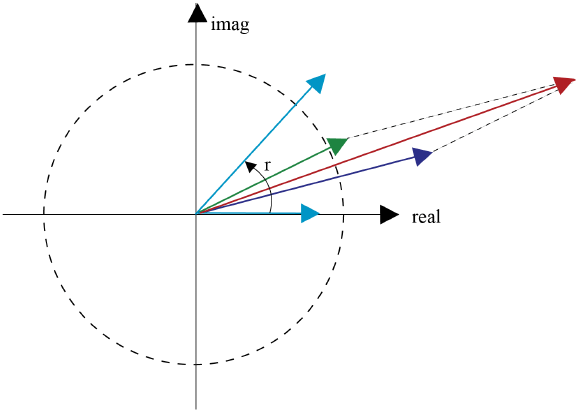
이상에서 설명을 쉽게 하기 위하여 정의역이 1차원으로 분해되는 N_t=3인 경우를 고려하였는데, N_t > 3일 경우는 N_t! 순열 각각에 대하여 ${\varphi }_{{\sigma }_i\left(N_t-1\right)}-{\varphi }_{{\sigma }_i\left(1\right)}$로 고정하고, $w_i\exp \left(-j{\varphi }_{{\sigma }_i\left(2\right)}\right),\mathrm{...}{w}_i\exp \left(-j{\varphi }_{{\sigma }_i\left(N_t-1\right)}\right)$는 변화시키며 하나의 합벡터로 취급하면 지금까지 다룬 N_t=3인 경우가 된다.

예를 들어 그림 6에서 N_t=4인 경우를 보였는데, 총 24개의 순열에 대하여 양쪽 (하늘색) 벡터를 각도 r로 고정하고 중앙의 두 벡터 (초록색, 파란색)를 2-D 공간에서 변화시키되 합벡터 (붉은색)으로 취급한다.

Ⅲ. 모의실험

Ⅱ 절에서 유도한 결과를 검증하기 위하여 균일분포를 따르는 ϕ_i~U(−π, π)를 발생시켜서 sp(ϕ) < 80°를 선택하여 그림 7및 그림 8에 그림 4및 그림 5에 해당하는 산포도와 히스토그램을 그렸다. 두 경우 모두 이론적으로 얻은 결과와 일치함을 볼 수 있다.

Ⅳ. 결 론

다중 산란점의 위상이 균일분포를 가질 때 일반적 모노펄스 원리로 추정한 위상의 분포함수를 정의역 분해방식을 이용하여 적분식(식 (8))으로 표현하고, 근사과정을 거쳐서 수치해석적으로 얻었다(그림 5). 이 결과는 다시 모의실험으로 검증하였다. 여기서 추정한 위상의 최빈값은 각각 산란점 위상값의 가중치 원형 평균값이라는 점을 알 수 있었다. 본 연구의 의의는 모노펄스레이다에 의한 미분해 다수 산란점들의 각도추정값이 적절함을 엄밀하게 확인하는 데 있다.