Ⅰ. 서 론
항공기 레이다는 지상 클러터의 영향을 피하기 위해 MPRF(Medium Pulse Repetition Frequency)를 사용하는 것이 효과적이다. MPRF를 사용하였을 경우, 거리와 도플러 모두 모호성이 존재하게 되므로, 처음 표적을 탐지해야 하는 탐색 모드에서는 다수개의 PRF를 사용하여 모호성을 해결하고, 실제 거리와 속도를 계산하는 것이 일반적이다[1]~[3]. 그러나 추적 시에는 표적의 거리와 속도를 예측할 수 있기 때문에, 이에 적합한 파형을 선택할 수 있다.
파형 선택을 위해 고려되어야 할 조건은 사이드 로브에 의한 클러터 신호, 송신신호 및 메인 로브 클러터에 의한 이클립스(eclipse) 영역이다[4],[5]. 이 영역 내에서는 신호 대 클러터 비(Signal to Clutter Ratio: SCR)가 낮아서 표적을 탐지할 수 없기 때문이다. 따라서, 예측되는 표적신호가 이 영역에 겹치지 않도록 선택하여야 한다. 참고문헌 [6]에서 제안된 기법은 추적모드에서 매 추적마다 사이드 로브 클러터(Side Lobe Clutter: SLC)의 전력 분포위치와 형태를 파악함으로써 PRF 후보군을 선정하기 때문에 계산량이 많고 복잡하다.
본 논문은 추적의 실시간성을 위해 적은 계산량으로 효율적인 PRF를 선택할 수 있도록 일반적으로 적용 가능한 클리어(clear) 영역을 제안하고, 클러터로부터 자유로운 구역을 찾아 PRF 후보군을 계산하고, 그 중에서 가장 최적(optimal)의 PRF를 선정하는 기법을 보였다. 표적의 예측치에 대한 불확실성을 고려하여 허용구역의 중점에서 가장 가까운 PRF를 최종적으로 선택하였다. 더 나아가 본 논문에서는 실시간성을 강화하기 위한 ‘준최적화(quasi-optimization)’기법을 제안하였다.
Ⅱ. 제한조건
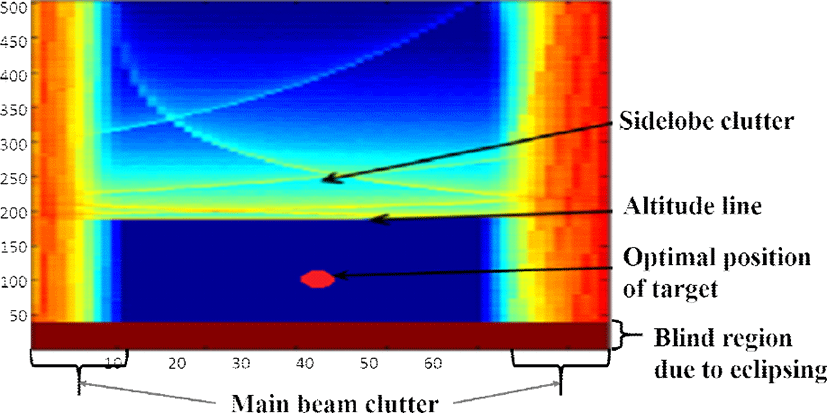
그림 1은 MPRF를 사용하는 항공기에서의 지상클러터 파워를 나타내는 전형적인 RD 맵에 나타낸 것이다[6].
거리방향으로는 고도(altitude line)에서 큰 클러터 파워가 나타나며, 사이드로브 클러터에 의해 반복적인 곡선 패턴이 나타난다. 거리방향의 0~40은 송신 펄스에 의해 블라인드되는 영역으로 펄스 도플러 레이다의 전형적인 모습이다. 속도방향에서 나타나는 블라인드는 메인 로브 클러터에 의해 나타나며, 그림에서는 0 주파수로 보상하였으므로 0(또는 PRF) 근처에서 나타난다. 본 논문에선 이러한 클러터 상황을 가정하였다. 그림에서는 붉은 점으로 표시된 곳이라고 할 수 있다.
거리영역에서 중요한 제한 조건은 최소 탐지거리와 고도이다. 추적을 위하여 예측되는 표적은 클러터 파워가 낮은 클리어 영역에 위치해야 한다. 즉, 송신 펄스에 의한 블라인드(최소 탐지거리) 이후에 위치해야 하고, 항공기 고도 이후에서는 SLC가 나타나기 때문에 고도 이전에 위치해야 한다. 따라서, 예측 표적에 대한 거리영역의 제한 조건을 정리하면 식 (1)과 같고, 이를 그림 2에 나타냈다.
거리영역의 시간 단위는 샘플링 시간 tsub를 이용하여, 거리영역을 빈(bin) 단위로 표현했고, 최소 탐지거리 빈을 Nc, 항공기 고도(km)를 거리 빈 Nh 으로 나타냈다. 또한, Nt는 표적의 위치 빈, n은 폴딩(folding) 정수, NPRI 는 모호하지 않은 거리(unambiguous range) 빈, Next는 압축 및 CFAR(Constant False Alarm Rate) 등 신호처리에 필요한 여분의 빈이다. 이를 NPRI에 대해 정리하면 다음과 같다.
다음 속도영역에서는 예측되는 표적이 일정한 고도로 비행하는 수평비행(level flight)을 가정하였을 때, 지상 클러터의 도플러 주파수(fd)를 살펴봄으로써 클리어 구역을 구할 수 있다[6],[7]. fd는 메인 로브 클러터 주파수를 0으로 보상한 클러터들의 도플러 주파수이다.
여기서 va는 항공기 진행방향으로의 속도, H는 항공기 고도, R은 거리, θ는 항공기에서의 방위각이다. SLC 곡선의 점근선은 에서 나타난다. PRF가 점근선의 간격 보다 작으면, 점근선이 폴딩되어 각각 아래와 같이 나타난다.
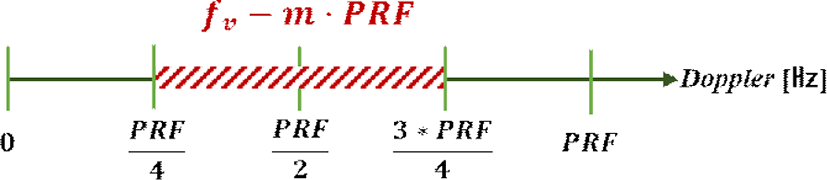
이로부터 PRF/2를 기준으로 클리어 영역이 존재하며, PRF에 따라 변경됨을 알 수 있다. 또한, 고도 이하 영역의 폴딩에 의한 SLC는 충분히 작을 것이며, 이는 그림 1을 통해서도 확인할 수 있다. 따라서 본 논문에서는 속도영역의 제한 조건을 식 (6)과 같이 제안하였으며, 이를 그림 3에 나타냈다.
여기서 fv는 예측되는 표적의 도플러 주파수이다. PRF는 PRI의 역수이므로 위 부등식을 NPRI에 대하여 정리하면 다음과 같다.
본 논문에 사용된 파라미터 값을 표 1에 정리하였다.
Ⅲ. 알고리즘
식 (2)와 (7)을 공통으로 만족하는 NPRI를 구하기 위한 m의 범위는 다음과 같고, 그림 4와 같이 나타낼 수 있다.
예를 들어, 표적이 35 km에서 600 m/s의 속도로 예측되며, 제한 조건이 NC=21, Next=20, Nh=104 라고 가정했을 때, 거리 영역의 n 을 1부터 증가시키며, 가능한 [n,m] 세트를 계산하면 [2,3], [3,2], [4,1], [5,1]이며, 각각의 세트에 대해 NPRI 후보군을 계산할 수 있다. n의 범위는 레이다의 최대 탐지거리로부터 결정되며, 본 논문에서는 5로 제한하였다.
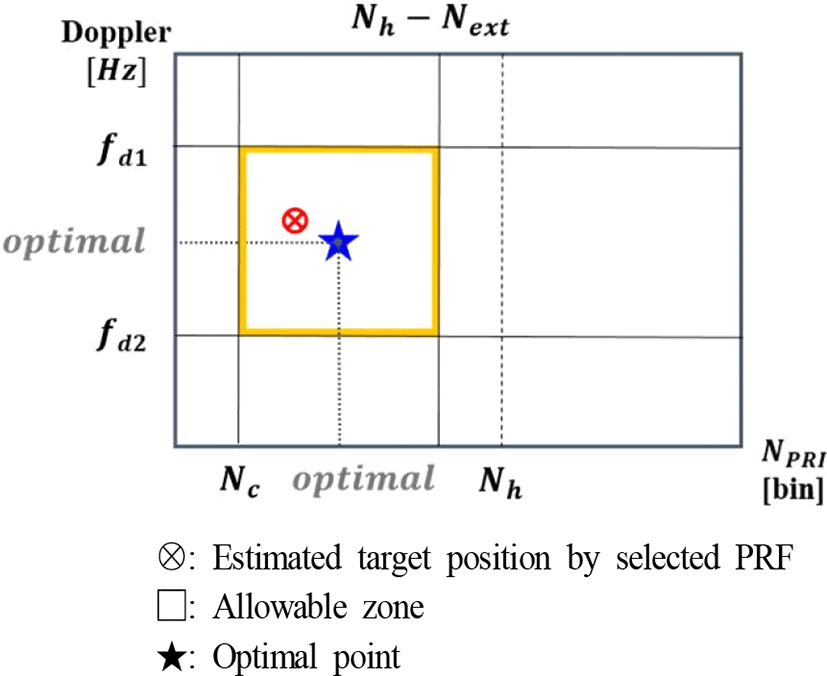
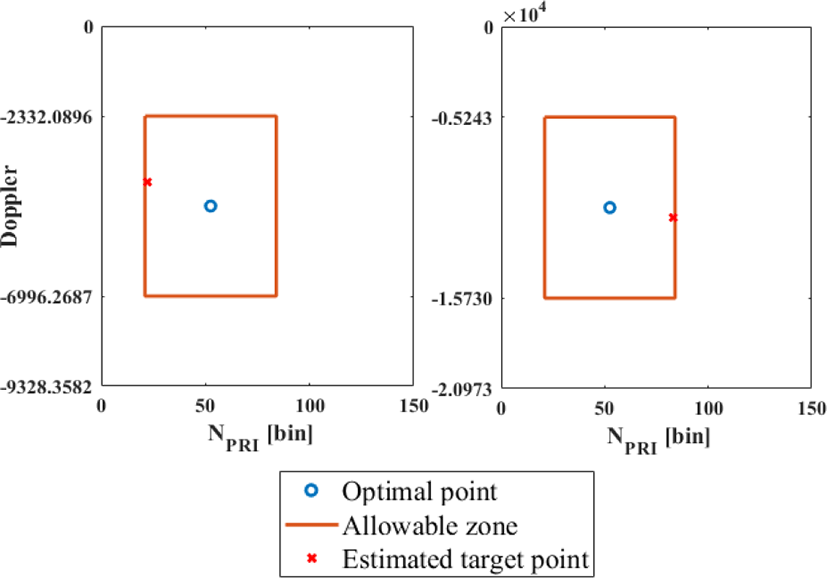
제한 조건을 만족하는 [n, m, NPRI] 후보군 중 예측 표적의 위치가 허용구역의 중심에 가장 가까운 PRF를 최적으로 선택하는 것이 좋다. 이는 표적에 대한 예측치의 불확실성을 고려했기 때문이다. 위 예시에서 허용구역의 중심과 가장 가까운 후보군은 [2, 3, 341]이다. 이처럼 정수 n, m을 1부터 차례대로 증가시킴으로써 최적의 PRF를 선택 하는 과정을 ‘최적화 과정’이라고 할 수 있다.
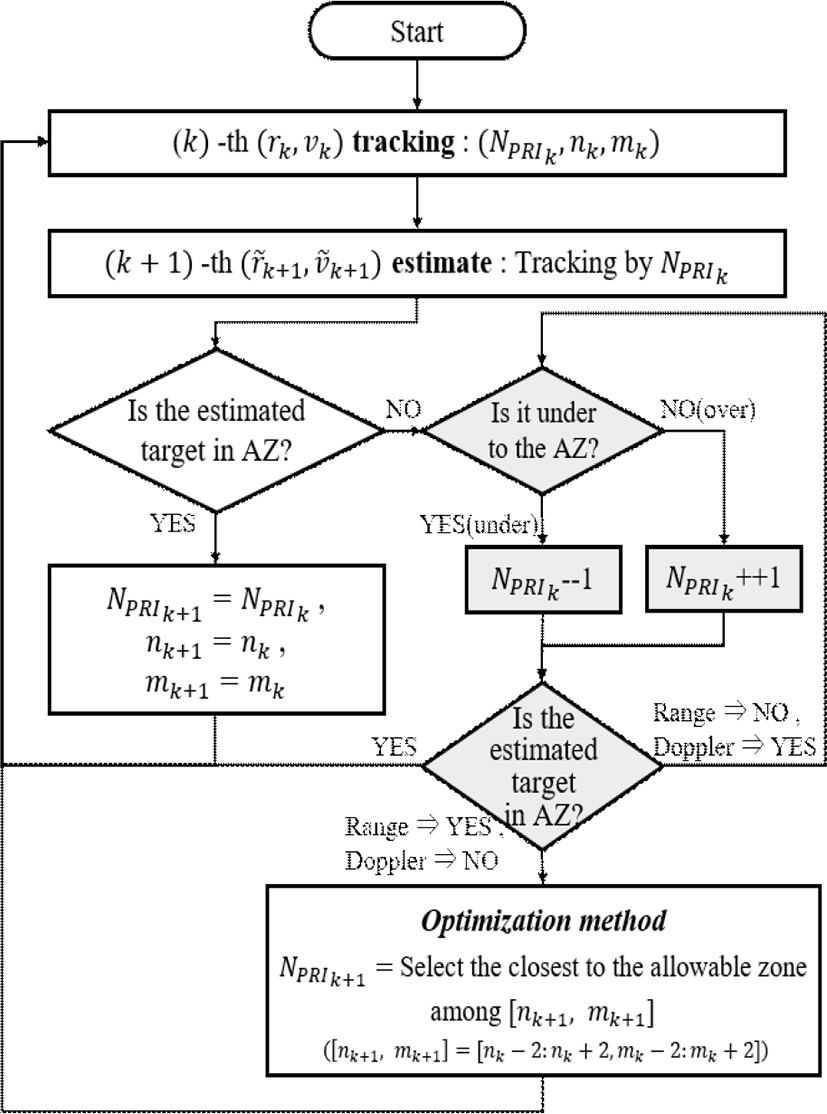
본 논문에서는 추적의 실시간성을 고려하여 ‘준최적화 과정’을 제안한다. 이는 최적화 과정을 수행하기 전에 이전 추적에 사용된 데이터를 이용하는 것이다. k 번째 예측 표적의 거리, 속도가 rk, vk 일 때, 초기 추적은 최적화 과정을 통해 [nk, mk, NPRIk]를 얻는다. t초 후의 표적은 k+1번째 예측 표적의 거리, 속도를 이용했을 때 허용구역 내에 존재한다면, k번째 데이터를 그대로 사용한다. 하지만 허용구역 내에 존재하지 않을 경우, NPRIk를 하나씩 조정함으로써 허용구역 내에 존재하도록 조정하는 것이다. 이러한 기법은 실시간 추적 시 계산량을 크게 감소시킬 수 있다. 조정을 수행해도 속도영역의 허용구역을 벗어난다면, [nk±2, mk±2]에 한하여 최적화 과정을 수행한다. 본 논문에서 기술한 PRI 선택과정을 그림 5에 순서도로 나타냈다.
Ⅳ. 시뮬레이션 결과
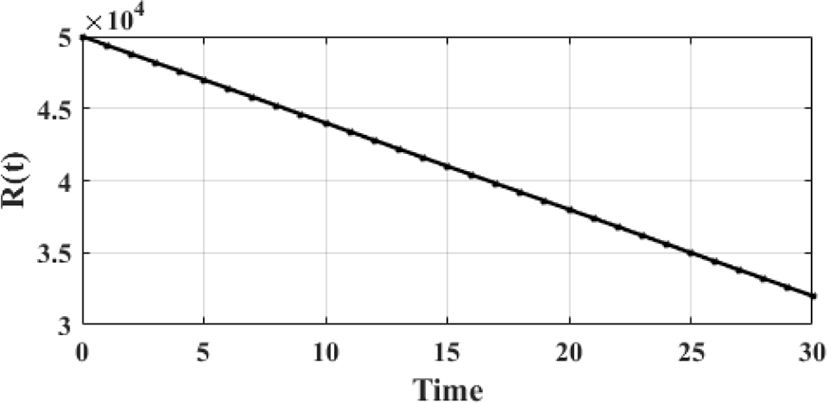
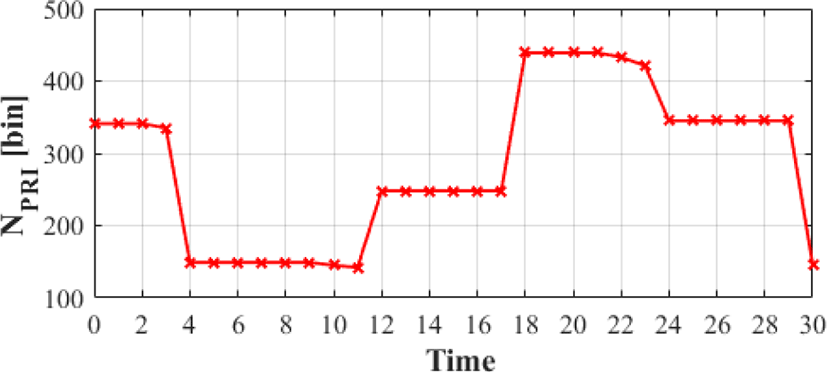
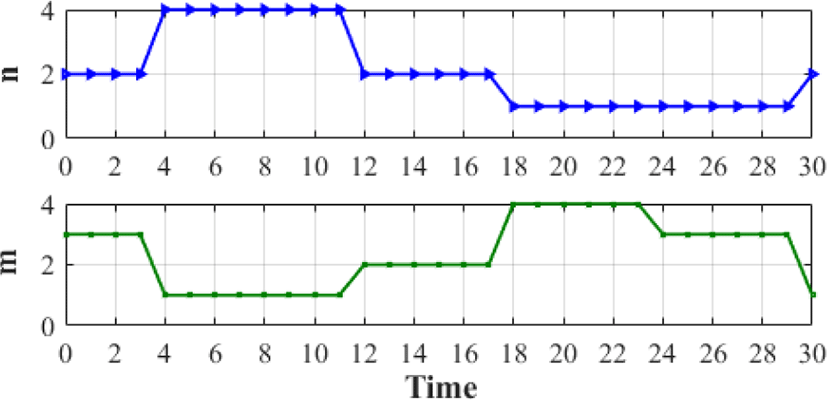
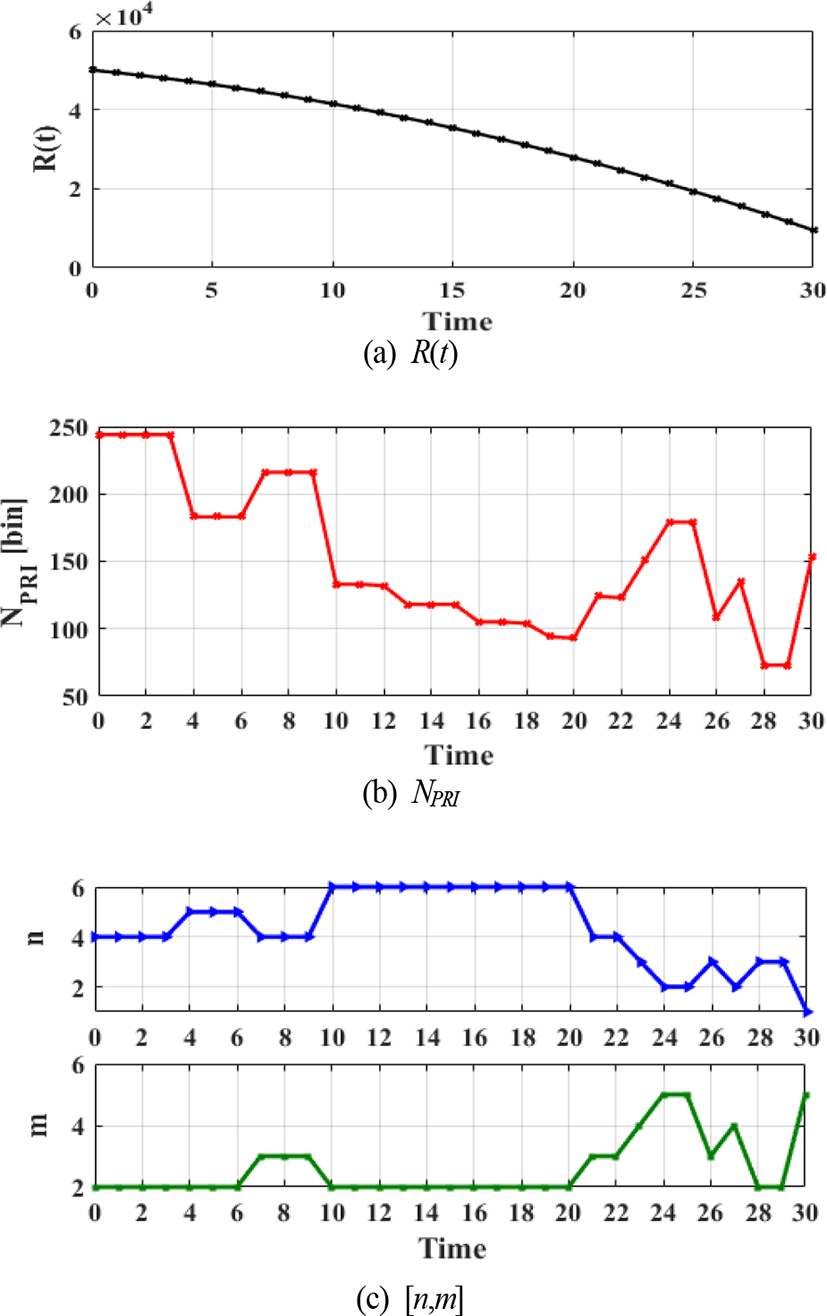
본 논문에서는 35 km에서 일정한 상대속도 600 m/s로 다가오고 있는 표적에 대해 30초간 추적을 실시하였다. 최소 탐지거리는 2 km, 항공기 고도는 5 km라고 가정하였다. R0가 현재 표적과 레이다 간 거리일 때, t초 후의 거리는 식 (9)와 같고 그림 6에 나타냈다. 상대속도가 일정해서 표적의 도플러 주파수는 변하지 않고, R(t)에 따라 표적의 거리 빈 Nt은 식 (10)과 같이 변하며, NPRI, [n, m] 선택 결과를 각각 그림 7과 그림 8에 나타냈다.
그림 8과 그림 9에 나타냈듯이, 3초까지는 준최적화 과정에 따라 동일한 [n, m]을 유지하고 있지만, 예측 표적의 위치가 허용구역의 왼쪽 경계에 도달하여, 4초에는 최적화 과정으로 [n, m]이 변경됐고, 허용 구역의 오른쪽에 위치하게 된다.
예측되는 표적의 위치와 최적 위치 사이 거리를 비용함수로 정의하여 그림 10에, PRF 선택 시간을 그림 11에 나타냈다. 비용함수가 작을수록 최적의 위치에 가까워 예측 표적을 클리어하게 볼 수 있고, 추적이 정확하다. 최적화 과정만 수행하였을 때는 매 추적 시 허용구역 중점과 가장 가까운 PRF를 선택하기 때문에 가장 최소한의 비용함수를 사용하지만, 그에 따른 계산량이 늘어난다. 준최적화 과정을 추가 시 비용함수는 더 늘어나지만, 선택 시간을 약 30 % 단축시킬 수 있다.
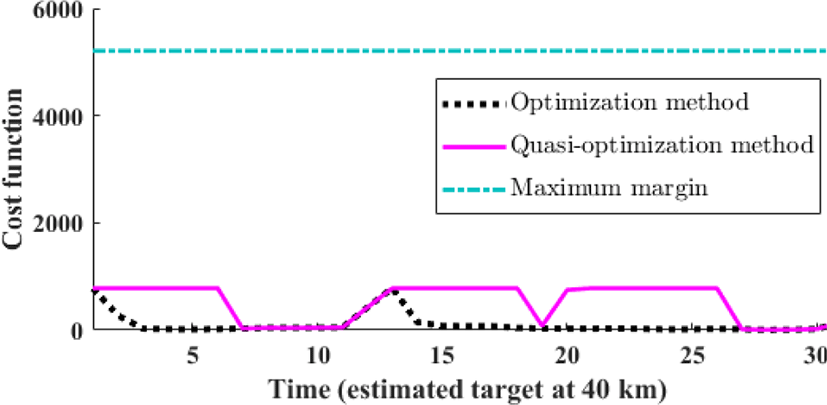
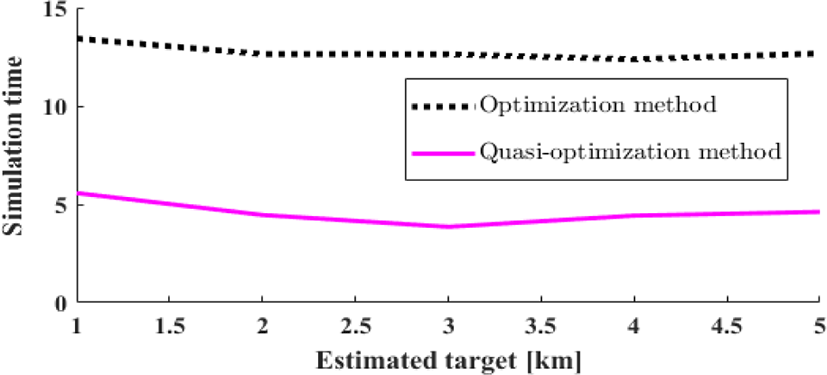
그림 12는 예측되는 표적의 가속도가 50 m/s2일 때이다. 이는 본 논문의 기법이 예측 표적에 대한 클리어 영역을 일반화하여 허용구역으로 정의하였기 때문에, 예측 표적의 도플러 주파수가 변화하는 상황에서도 적용이 가능함을 나타낸 것이다.
Ⅴ. 결 론
본 논문에서는 항공기용 레이다에서 표적을 추적하는 경우에 대하여, 예측되는 표적을 탐지하기 위한 PRF 선택 방법을 제안하였다. 제안된 방법은 거리와 속도영역에서 지상 클러터 신호를 피할 수 있는 허용구역을 정의하여 PRF 후보군을 계산하고, 표적의 거리와 속도 예측치의 불확실성을 고려하여 허용구역의 중심에 가까운 PRF 를 선택하는 최적화 기법과 실시간성을 높이기 위한 기법이 합쳐진 방식이다.
본 논문의 기법은 클러터가 없는 구역을 일반화하여 PRF 후보군을 선택하는 기법이기 때문에, 항상 최적의 PRF를 선택할 수 있다. 본 논문에서 실시간성을 고려하여 제안한 준최적화 과정의 성능은 최적화 과정의 성능과 비교함으로써 입증하였다. 항공기 레이다의 추적모드에서 이러한 기법을 사용하면, 추적 계산량을 크게 줄이고 클러터 환경에서 표적을 효과적으로 추적할 수 있을 것으로 기대된다.