Ⅰ. 서 론
항공기, 차량 등에 탑재되는 소형 레이다는 진동환경에서 동작하므로 기준발진기를 포함한 주파수합성기 출력신호의 위상잡음이 기존의 발진기보다 악화된다[1],[2]. 소형 레이다에서 송신신호 TX와 국부발진신호 LO의 위상잡음은 수신신호의 신호 대 잡음비(SNR, signal-to- noise ratio)의 성능에 영향을 미치는 요인 중 하나이므로[3]~[7] 진동에 의해 악화된 위상잡음이 레이다에 미치는 영향성을 분석해야 한다. 특히, 진동 중 위상잡음 성능이 우수한 발진기는 가격이 높고, 수급에 어려움이 있으므로 레이다 성능에 미치는 위상잡음 영향성을 최소화하면서 부품수급이 용이한 기준발진기 선정을 위해 위상잡음 규격 검토가 필요하다.
참고문헌 [6]에서는 신호처리 시 위상잡음 영향을 최소화할 수 있는 TX와 LO 위상잡음 규격 선정방안에 대해 제안한 바 있다. 단, 참고문헌 [6]에서는 W대역 레이다에 관한 내용으로 높은 주파수의 TX와 LO의 전력손실을 최소화하기 위해 송신기의 입력단과 수신기의 LO 입력단에 X대역 신호를 W대역으로 상향 변환하기 위한 각각 체배기를 배치하여 두 신호의 경로가 분리되도록 설계하였다. 그에 따라 TX와 LO의 위상이 결맞지 않으므로(incoherent), 수신기에서 위상잡음 감쇄(phase noise cancellation) 효과가 매우 적다고 가정하고 FMICW(frequency modulated interrupted continuous waveform) 파형에서 위상잡음 규격을 검토하였다.
그러나, 일반적으로 W 대역보다 주파수가 낮은 Ku, Ka 대역의 소형 레이다에서는 TX와 LO의 위상이 최대한 결맞도록 두 신호의 경로를 공통으로 유지되도록 설계한다[8],[9]. 공통 경로를 통해 주신호를 생성하며, LO 혹은 TX 최종단에서 IF 주파수만큼 신호를 하향 또는 상향 변환하여 수신기 출력신호의 주파수가 IF가 되도록 한다. 본 눈문에서는 그림 1과 같이 TX를 IF만큼 하향 변환하여 LO를 생성하는 소형 레이다의 송수신기 구조를 제시하였다.
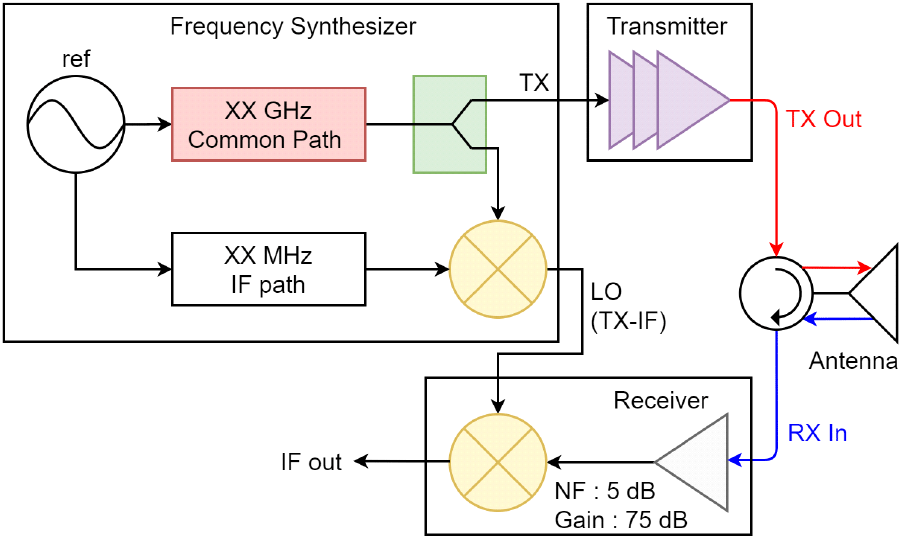
본 논문의 소형 레이다에서는 수십 GHz의 TX와 LO를 생성하기 위해 10 MHz를 기준신호를 사용하며, IF 역시 10 MHz가 되도록 설계하였다. 주파수가 기준신호 대비 N배 증가하면 위상잡음은 20 log10(N)만큼 높아지므로, LO의 위상잡음은 TX 위상잡음과 거의 같다. 다만, TX와 LO는 결맞음(coherent) 관계에 있으므로, TX가 LO에 의해 IF로 주파수 하향변환되면 IF의 위상잡음은 20 log10 (IF/ref)로 낮아진다.
한편, 그림 1에서 보이는 바와 같이 수신신호 RX는 TX가 표적에 의해 반사된 신호이므로, RX와 TX의 위상잡음 전력은 같다. 단, RX에는 표적거리 R에 따른 지연시간 Δt(=2 R/c)가 포함되므로, RX와 LO 사이에는 위상차가 발생한다. 특히, 위상잡음에 포함되는 위상차에 따라 주파수 하향변환 후 신호인 IF 신호의 위상잡음 전력은 아래식의 K(θ)와 같이 감쇄된다[10],[11].
식 (1)은 지연시간과 중심주파수에 대한 offset 주파수 foff에 따른 위상잡음 감쇄량을 나타내는 식으로 θ는 2πfoffΔt 이다. 식 (1)에 따라 Δt가 길수록, foff가 클수록 위상잡음 감쇄량은 감소한다. 그에 따라 참고문헌 [12]에서는 TX와 LO가 결맞는 FMCW(frequency modulated continuous wave) 파형의 레이다 시스템에서 위상잡음 영향성을 검토하였다.
유사한 방법으로 본 논문에서는 위상잡음이 결맞는 레이다 시스템에서 R에 따른 IF 신호의 위상잡음을 확인하기 위해 그림 1의 구조에서 Δt에 따른 수신기 출력신호 IF의 스펙트럼을 예측하였다. 파형에 따른 위상잡음 영향성에 검토하기 위해 FMICW 파형과 MPRF 파형에서 신호처리 결과를 분석하였다. 또한, 각 파형에서 위상잡음과 수신기의 열잡음 비교하여 레이다 성능에 위상잡음 영향을 최소화할 수 있는 위상잡음 규격 설정방안을 제안하였다.
Ⅱ. FMICW 파형에서 위상잡음 영향
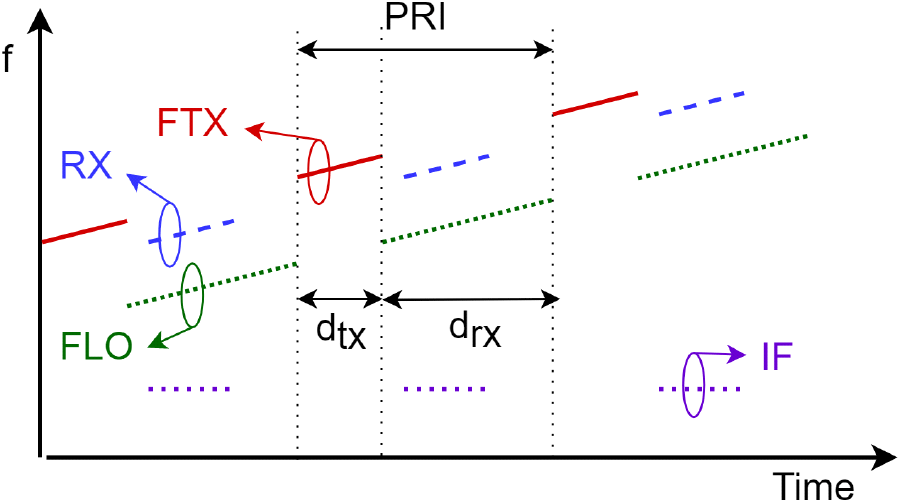
그림 2의 FMICW 파형에서는 LFM(linear frequency modulation) 파형의 RX가 LFM 파형의 LO에 의해 하향 변환하므로, IF는 단일 주파수로 출력된다. 단, 레이다에서는 펄스 주기인 PRI(pulse repetition interval) 중 송신듀티 dtx, 수신듀티 drx동안 각각 송신, 수신을 수행하므로 IF 신호는 펄스로 출력된다. 본 논문에서는 계산을 간단히 하기 위해 TX와 LO가 각각의 고정 주파수로 출력될 때, 출력되는 단일 주파수의 IF 성능을 확인하였다. 각 신호의 기준신호인 ref, ref’는 식 (2) 및 식 (3)과 같이 정의하였다[7].
fo는 기준신호의 중심주파수이며, ϕn(t)은 시간에 따라 변화하는 위상 즉, 위상잡음이다. 위의 식에 따라서 ref는 fo를 중심주파수로 하는 정현파와 중심주파수가 0 Hz이고 위상잡음을 포함하는 신호인 ψphn(t)의 곱으로 표현할 수 있다. ref, ref’이 결맞으면 ψphn(t)=ψphn’(t), 결맞지 않으면ψphn(t)≠ψphn’(t)이며, 결맞음과 관계없이 ψphn(t)와 ψphn’(t)에 의한 위상잡음 전력은 같다.
TX와 LO의 결맞음에 따라 IF를 분석하기 위해 각 신호의 기준신호를 ref, ref’로 분리하였으며, 각 기준신호를 a, a-1 체배하여 TX와 LO를 계산하였다. TX는 ref a에 비례하며 LO는 (ref’)a-1에 비례하므로 R에 따른 지연시간을 포함하는 IF는 식 (4)와 같이 나타낼 수 있다.
본 장에서는 계산 시간을 고려하여 ref와 IF 주파수는 10 MHz, a를 300로 가정하고, TX와 LO의 결맞음에 따라 식(4)의 계산결과를 그림 2에 나타내었다. 각 신호에 반영된 위상잡음은 표 1과 같다. 참고로 표 1에서는 진동 환경에서 발생하는 기준신호의 위상잡음을 반영하였다.
(unit: dBc/Hz)
| Offset Freq (Hz) | 100 | 1 k | 10 k | 100 k | 1 M |
| ref (=IF) (10 MHz) |
−100 | −110 | −120 | −130 | −140 |
| TX (3 GHz) |
−50.5 | −60.5 | −70.5 | −80.5 | −90.5 |
| LO (2.99 GHz) |
−50.5 | −60.5 | −70.5 | −80.5 | −90.5 |
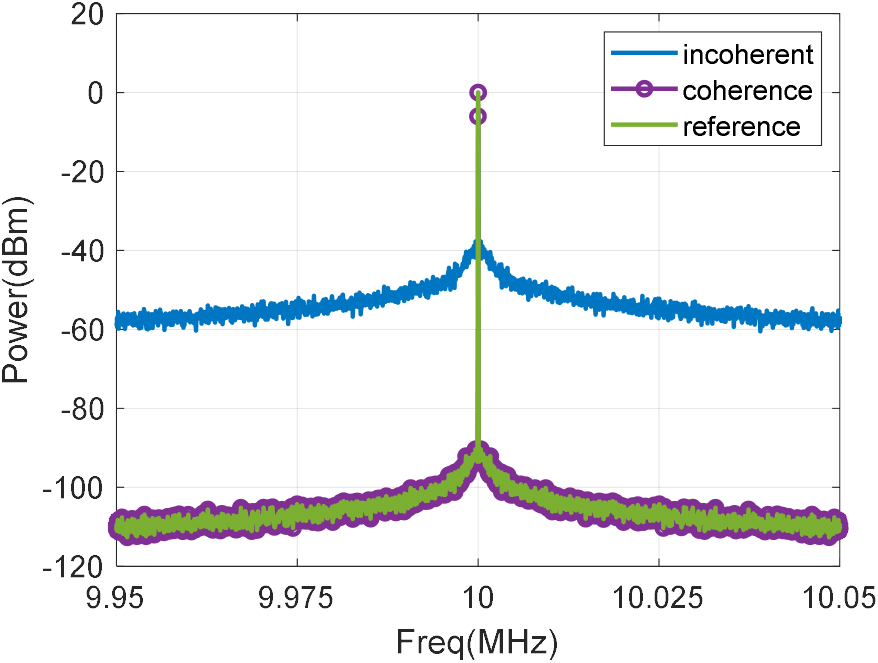
그림 3의 계산에 사용된 샘플링 주파수는 21 MHz, 스펙트럼의 RBW는 50 Hz이며, FFT 중 hann window를 적용하여 FMICW 파형의 IF 대역폭 100 kHz 이내의 IF를 분석하였다. 결맞음 유무에 따른 IF 결과만 확인하기 위해 RX의 Δt는 0이며, IF 출력전력인 0 dBm인 것으로 가정하여 비교하였다. 예상과 같이 결맞는 상태에서는 위상잡음이 상쇄되면서 IF 스펙트럼과 ref의 스펙트럼이 일치하였으나, 결맞지 않은 상태에서는 TX와 LO의 위상잡음이 서로 더해졌다. 10 kHz offset에서 ref와 결맞는 상태의 IF 위상잡음은 −119.5 dBc/Hz로 표 1의 ref 위상잡음과 거의 같다. 반면에 결맞지 않은 상태의 IF 위상잡음은 −68 dBc/Hz로 TX의 위상잡음의 약 2배(3 dB)만큼 높으며, 이는 결맞지 않은 상태에서 IF의 위상잡음은 TX와 LO 위상잡음의 합임을 의미한다. 본 결과를 통해 FMICW 파형에서 SNR 성능을 높이기 위해서는 TX와 LO가 결맞도록 주파수합성기를 설계하는 것이 중요함을 알 수 있다.
다음으로는 식 (1)을 검증하기 위해 TX와 LO가 결맞을 때, R에 따른 IF의 스펙트럼을 확인하였다. 그림 4와 같이 TX에서 R에 따른 Δt만큼 셀을 이동하여 RX를 구현하였다. 따라서 RX와 LO에는 Δt에 의한 위상차가 존재한다. R이 100 m일 때 IF 출력전력을 0 dBm으로 정의하고, R이 증가함에 따라 IF 출력전력이 R4에 반비례하여 감소함을 반영한 결과를 그림 5에 도식화하였다. 그 결과 고정된 R에서는 offset 주파수에 따라 위상잡음이 주기적으로 변화하였다. 이때, Δt 즉, R이 클수록 offset 주파수에 따른 위상잡음 변화 주기가 짧아지므로 IF 중심주파수 부근에서 위상잡음이 더 높아졌다.
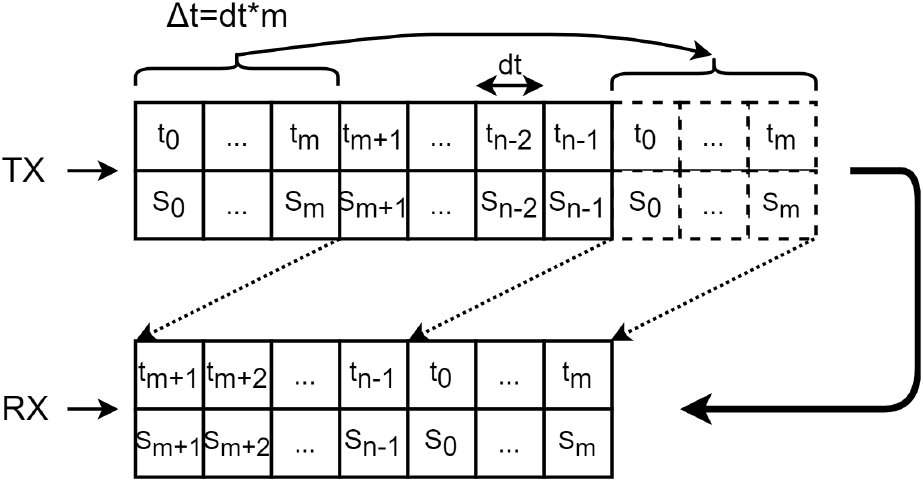
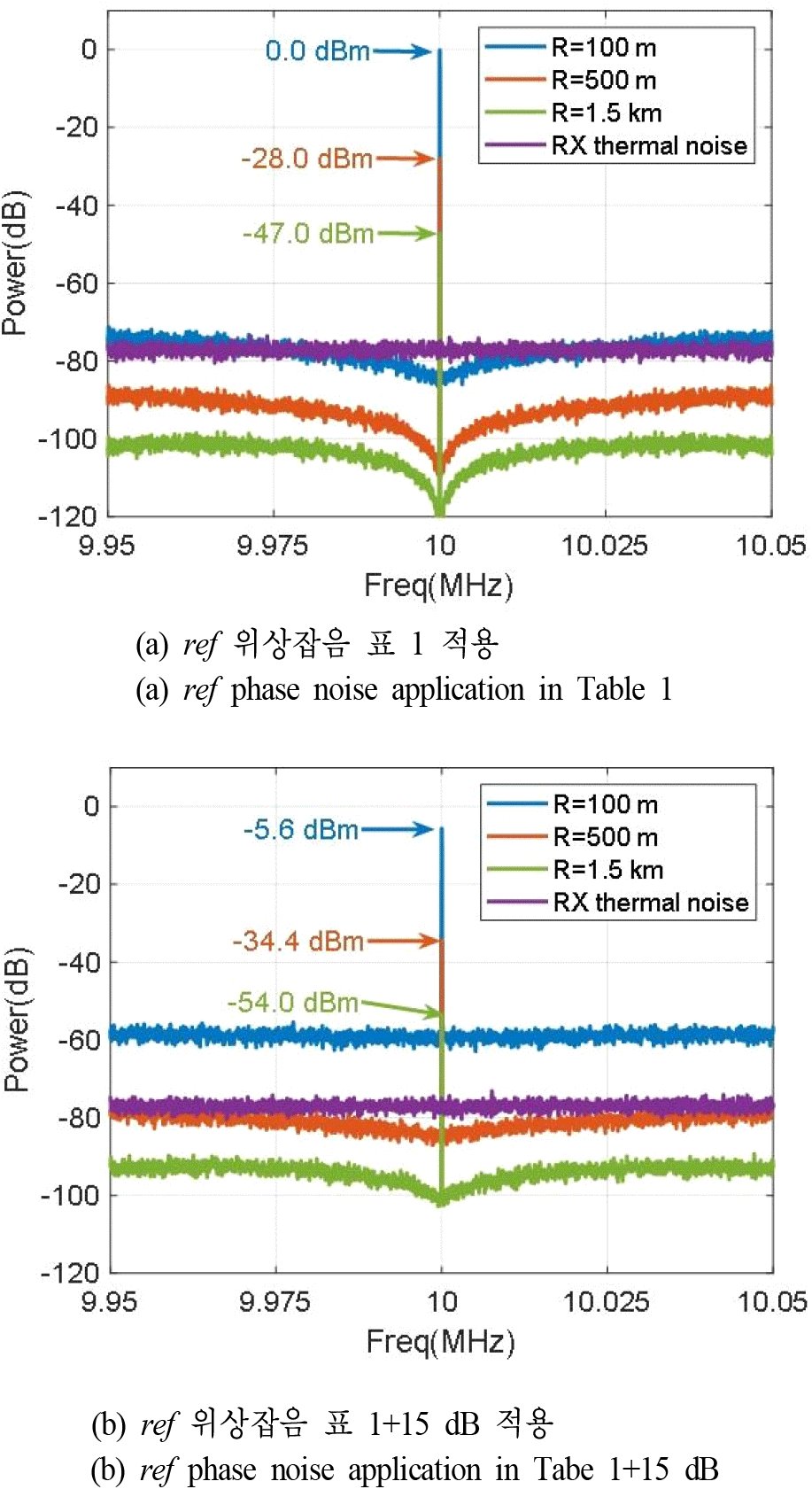
표 1의 ref 위상잡음을 적용한 그림 5(a)에서는 100 kHz IF 대역폭 이내에서 R이 100 m, 500 m, 1.5 km로 증가할수록 위상잡음에 대한 SNR은 73.5 dB, 60.5 dB, 53.5 dB로 감소하였다. 단, 일반적으로 레이다의 SNR은 수신기의 열잡음에 의해 결정된다. 본 논문에서는 그림 1의 잡음지수 5 dB, 이득 75 dB, FFT 1 cell의 열잡음이 −77 dBm인 수신기를 적용하였다. 그림 5의 위상잡음은 열잡음보다 낮거나 유사하므로 표 1의 위상잡음은 본 논문에서 검토하는 레이다의 SNR에 미치는 영향이 거의 없다고 판단할 수 있다. 단, R이 100 m일 때는 필터 대역 내 위상잡음과 열잡음에 의한 최대 잡음전력이 −72 dBm으로, 수신기 열잡음 전력보다 5 dB 높다. 그에 따라 위상잡음으로 인해 SNR이 악화되지만, 해당 조건에서는 주엽의 첨두전력이 높고 총 SNR이 70 dB 이상이므로 레이다 성능에 미치는 영향은 거의 없다.
참고로, 본 논문에서 적용된 수신기의 이득과 잡음지수는 표적 RCS 및 안테나 이득, 신호처리기의 잡음지수 등을 반영하여 본 레이다 시스템이 목표로 하는 최대탐지거리에서 열잡음보다 신호 전력이 최소 SNR이상을 만족하도록 설계되었다. 따라서 위상잡음에 의해 IF 신호의 잡음이 수신기 열잡음보다 높아지면, 시스템 성능이 악화될 수 있다.
한편, 하드웨어의 한계로 혹은 환경적 요인으로 위상잡음이 높아지는 상황을 가정하여 IF 스펙트럼을 그림 5(b)에 나타냈다. ref 위상잡음이 표 1보다 15 dB 높아지면서 필터 대역 내에서 스펙트럼 잡음이 10~15 dB 높아졌다. 특히, ref 위상잡음이 악화되면 근접한 표적의 잡음은 수신기 열잡음이 아닌 위상잡음이 지배적임을 확인할 수 있었다. 또한, 높은 위상잡음에 의해 전력이 여러 주파수로 분산되면서 각 스펙트럼의 첨두전력이 5.6~7 dB 더 낮아졌다. 이 결과는 ref 위상잡음이 악화되면 스펙트럼 잡음이 수신기 열잡음보다 낮은 원거리 신호의 SNR 성능도 열화시킴을 보여준다. 그리고 위상잡음에 의해 최대탐지거리 조건에서 최소 SNR을 만족하지 못하여 표적탐지가 불가능해질 수 있다.
따라서 FMICW 파형에서는 그림 5와 같은 검토를 통해 위상잡음이 수신기 열잡음보다 낮고, 스펙트럼 첨두전력을 유지할 수 있는 ref, TX와 LO의 위상잡음 규격 분석이 필요하다.
Ⅲ. MPRF 파형에서 위상잡음 영향
IF가 단일 주파수로 출력되는 FMICW와 달리 MPRF (medium pulse repetition frequency) 파형에서는 IF가 광대역 LFM 파형으로 출력된다. 각 LFM 형태의 펄스를 신호처리 중 펄스압축 한 뒤, N개의 펄스압축 결과를 모아서 RD Map(range Doppler map)으로 나타내면 표적 정보를 얻을 수 있다. 따라서 MPRF 파형에서 TX는 송신 펄스 한 주기 동안 특정 대역폭을 가지는 LFM 파형으로 출력되며, LO는 수신된 RX의 중심주파수를 IF 대역으로 하향 변환시켜주는 역할을 하기 위해 한 펄스 내에서 일정한 주파수로 출력된다.
본 장에서는 시작주파수 fLFM은 −5 MHz, 대역폭 BW는 10 MHz, 펄스폭 τ는 100 μsec로 하는 LFM 파형 ψLFM(t)에 식 (4)와 유사하게 위상잡음을 적용하여 IFLFM을 식 (5) 및 식 (6)과 같이 정의하였다.
FMICW 파형에서와 마찬가지로 TX와 LO가 결맞을 때(ψphn(t)=ψphn’(t) )와 결맞지 않을 때(ψphn(t) ≠ ψphn’(t) )로 나누어 식 (6)의 계산 결과를 그림 6에 나타내었다. 계산을 위해 사용한 샘플링 주파수는 40 MHz이며, 결맞음 효과만을 확인하기 위해 R=0 m 일 때, RX를 가정하여 계산하였다. 그 결과, 결맞지 않을 때는 결맞을 때보다 LFM 신호의 대역 내, 외에서 모두 잡음이 크게 확인되었다.
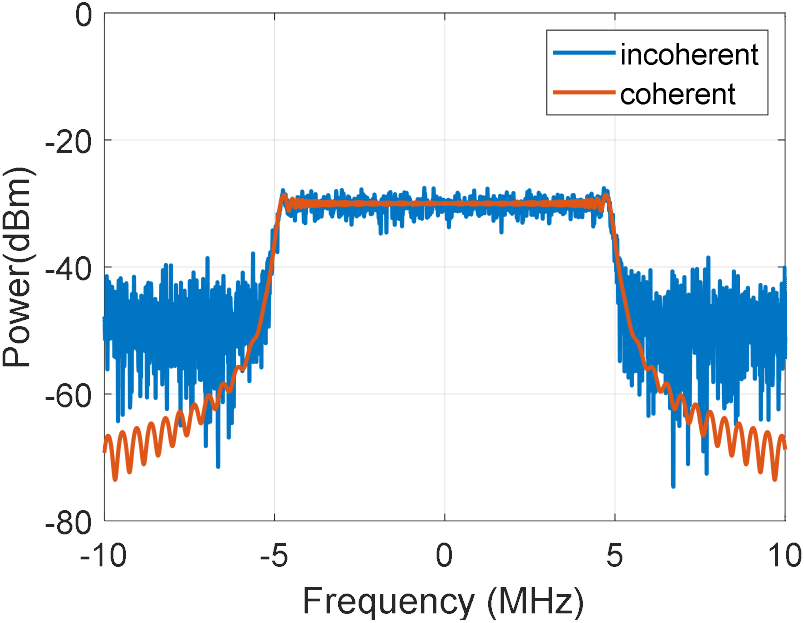
그림 6의 IFLFM을 이용하여 펄스압축을 수행한 결과는 그림 7과 같다. 그림 7에는 각 신호당 320개의 데이터를 도식화하였다. 각 신호의 지연시간은 서로 다르나, 비교가 쉽도록 주엽의 중심을 t=0 sec 위치로 일치시켰다. IFLFM에 잡음지수 5 dB, 이득 75 dB의 수신기 열잡음을 추가하여 펄스압축 과정에서 수신기 열잡음의 영향성을 확인하였다. 또한, TX와 LO가 결맞을 때, R에 의한 효과를 확인하기 위해 R이 해당 레이다의 최소거리 Rmin이 100 m일 때 수신기에서 IFLFM 전력을 0 dBm으로 정의하고, R이 Rmax인 1.5 km로 증가하면서 전력이 감소하도록 계산하였다. 참고로, 펄스압축 후에는 FFT 중 적용된 chebyshev 80 dB 윈도우에 의해 주엽 전력이 8 dB 감소하였다.
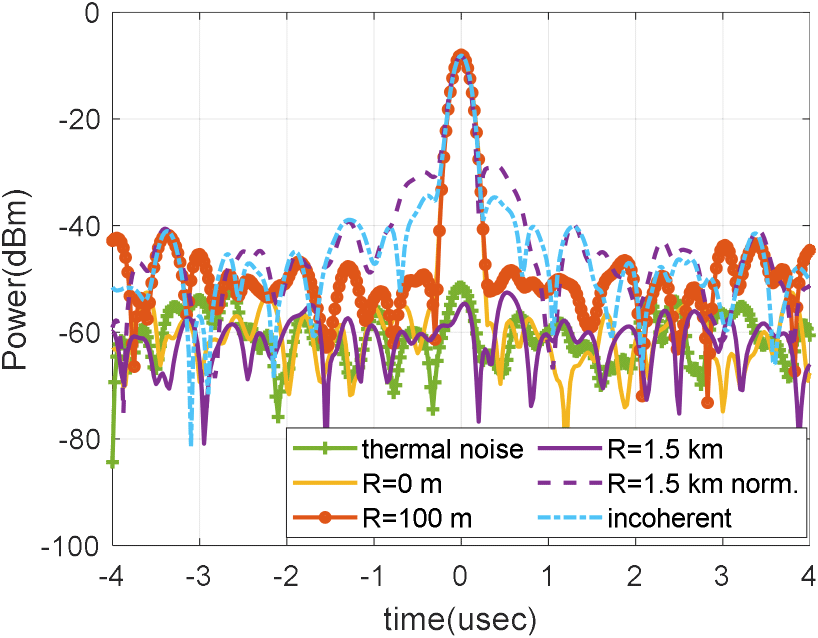
그림 7의 결과 펄스압축 파형에서도 FMICW 파형과 유사하게 R이 증가할수록 위상잡음 감쇄량이 줄어들고 부엽 전력이 높아졌다. 그에 따라 Rmin일 때는 위상잡음이 감쇄되어 주엽 부근의 약 ±1.5 usec 이내 범위에서는 위상잡음이 결맞지 않을 때보다 최소 8 dB 더 낮다. 그러나, 위상잡음에 의한 부엽이 열잡음보다 약 6 dB 높아져 SNR은 46 dB에서 40 dB로 낮아졌다.
Rmax일 때는 R의 변화에 따른 위상잡음 감쇄량을 확인하기 위해 주엽의 전력을 R이 100 m일 때와 같도록 정규화하여 비교하였다. 그 결과, 주엽 부근에서도 위상잡음이 거의 감쇄되지 않았으며, 높은 위상잡음에 의해 주엽폭이 넓어졌다. 거리가 증가함에 따라 감소한 신호의 주엽 전력은 R이 100 m일 때보다 47 dB 낮은 −55 dBm이므로, 펄스 압축 후 열잡음 −54 dBm과 비교했을 때 신호의 첨두전력 위치를 구분하기 어려웠다. 단, 이는 광대역 신호를 펄스 압축하면서 FFT 중 주파수 해상도가 FMICW 파형보다 크기 때문에 나타난 현상으로, N개의 펄스압축 결과를 이용하여 RD Map을 도출하면 열잡음이 낮아져 표적 식별이 가능해진다. 참고로 그림 7에서 FFT 1cell의 대역폭은 10 kHz이다.
다음으로 위상잡음과 열잡음 포함된 MPRF 파형의 RD Map를 분석하였다. 적용한 LFM 파형의 대역폭은 10 MHz, PRI는 0.2 msec, 펄스폭τ는 100 usec, 펄스 갯수 N은 101일 때, 표적거리는 Rmin, 표적 속도는 0 m/s 조건에서 수신기 열잡음을 포함하는 RD Map을 계산하여 그림 8에 나타냈다. 그림 8의 RD Map에서 x축인 fd는 표적의 속도 정보를 포함하는 도플러 주파수를 의미하며, y축인 t는 표적의 거리에 따른 지연시간으로 거리정보를 포함한다.
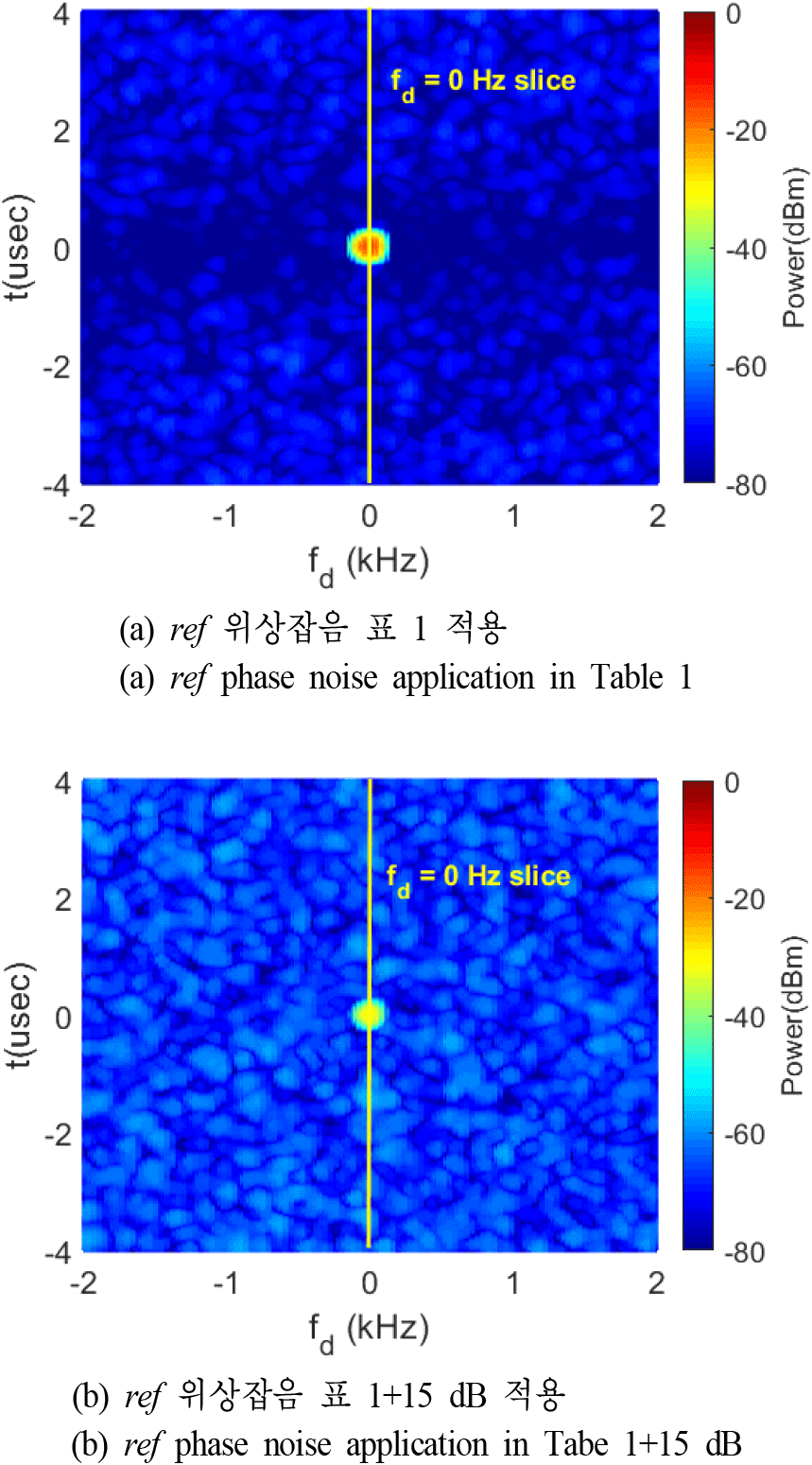
RD Map 결과, 그림 7 결과와 유사하게 잡음전력은 위상잡음이 지배적임을 알 수 있다. 좀 더 자세히 분석하기 위해 표적 속도가 0 m/s 인 위치(fd=0 Hz slice)에서 R 및 위상잡음에 따른 신호를 모아 그림 9에 도식화하였다.
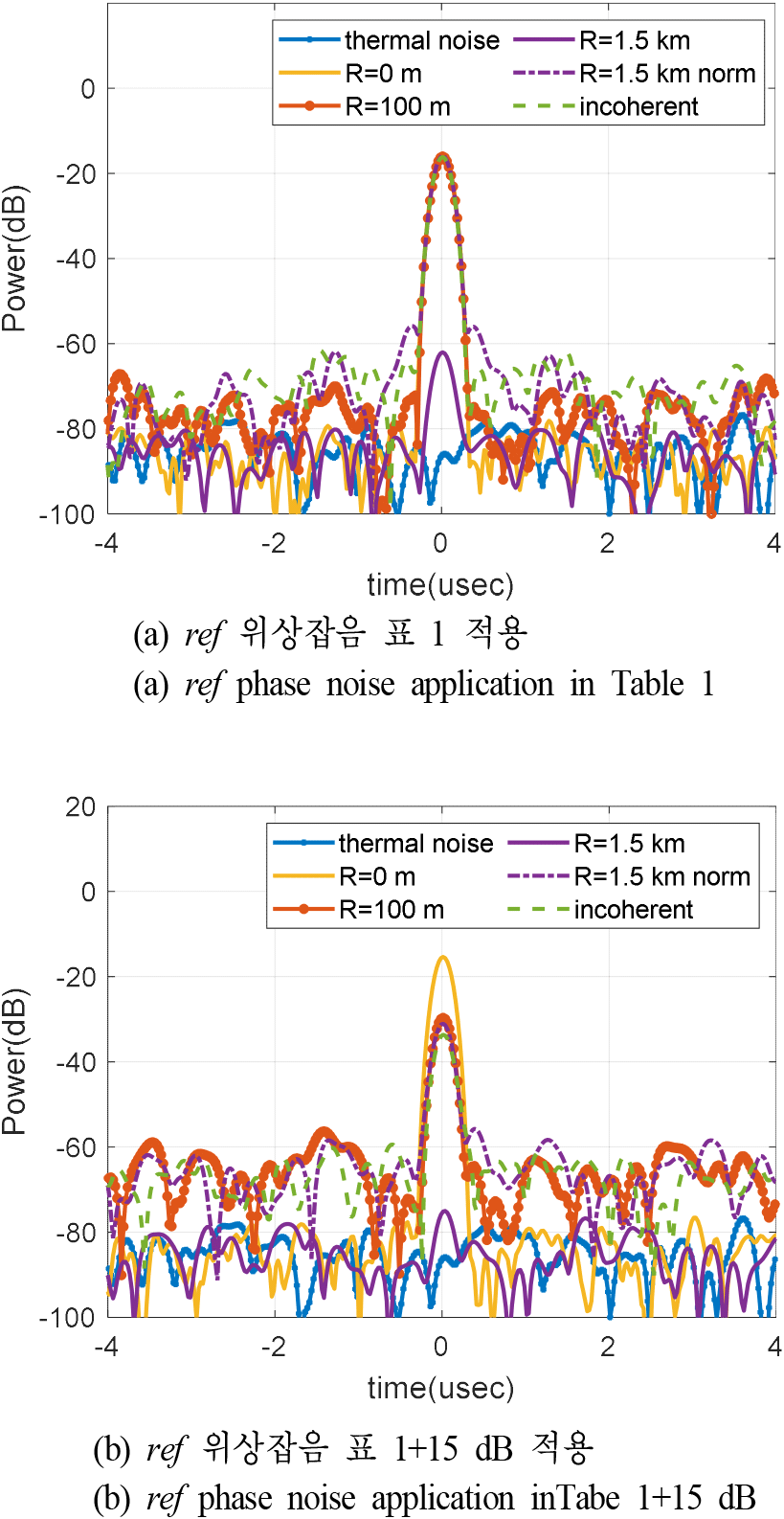
동일한 위상잡음을 적용한 그림 9(a) 및 그림 7을 비교하면 스펙트럼 형태가 유사하나, RD Map 신호처리를 통해 주파수 해상도가 높아지면서 부엽 전력이 전체적으로 감소하였다. RD Map에서는 도플러 주파수 해상도 Δfd가 1/(PRI×N)이므로 수신기 열잡음 및 위상잡음이 그림 8보다 23 dB 낮아졌다. 단, 펄스압축 결과를 FFT 하면서 적용한 chebyshev 80 dB 윈도우에 의해 주엽 전력도 추가로 8 dB 더 낮아지면서 그림 8 및 그림 9에서 SNR은 열잡음 및 위상잡음에 의한 SNR은 그림 7보다 15 dB 향상되었다. 그림 9에서 R이 Rmin, Rmax 일 때 SNR은 각각 54 dB, 14 dB이다. 그에 따라 그림 7에서는 구분되지 않았던 Rmax에서의 표적신호가 그림 9에서는 구분이 된다. 따라서 시스템에서 요구하는 최소 SNR이 14 dB 미만이면 Rmax에서도 표적탐지가 가능하다.
한편, ref 위상잡음이 표 1보다 15 dB 높아지면 그림 9(b)와 같이 Rmin 신호의 잡음전력은 15 dB 높아지며, 첨두전력은 14.3 dB 낮아져 SNR이 29.3 dB 열화된다. Rmax 신호의 잡음전력은 열잡음에 의해 유지되나, 위상잡음이 악화되었으므로 첨두전력이 13 dB 더 낮아진 −75 dBm이 되어 열잡음 전력 −77 dBm과 구분이 어려워졌다. 즉, FMICW 파형에서와 마찬가지로 위상잡음이 악화되면 MPRF 파형에서도 최대탐지거리 조건에서 최소 SNR을 만족하지 못하여 표적탐지가 불가능해질 수 있다.
Ⅳ. 결 론
본 논문에서는 소형 레이다에서 운용파형에 따른 위상잡음 영향성에 대해 분석하였다. 일반적으로 레이다용 신호는 위상잡음이 매우 낮은 기준발진기를 적용하므로, 위상잡음에 의한 성능악화 가능성이 낮다. 그러나, 기준발진기의 위상잡음은 진동환경에서 그 성능이 악화되므로, 레이다 시스템에서 요구하는 잡음전력과 최소 SNR을 확보할 수 있는 위상잡음 규격 검토가 반드시 필요하다.
따라서 본 논문에서는 TX와 LO의 위상이 결맞는 송수신 시스템에서 표적의 거리에 따른 지연시간을 RX에 포함하여, 소형 레이다의 출력신호를 확인하였다. 시뮬레이션 결과 파형에 관계없이 IF신호의 위상잡음은 표적거리가 멀수록, offset 주파수가 클수록 그 감쇄량이 줄어드는 것을 확인하였다.
100 kHz 협대역 IF 신호를 확인하는 FMICW 파형에서는 offset 주파수가 낮으므로 주파수에 의한 위상잡음 감쇄가 크다. 따라서 표적거리가 증가할수록 위상잡음 감쇄량이 줄어들어 SNR 성능이 떨어지는 현상이 두드러지가 나타났다. MPRF 파형에서도 표적거리가 멀어질수록 위상잡음이 높아지면서 부엽전력이 높아지는 것을 확인하였다. 단, 단일 주파수의 IF 신호를 생성하는 FMICW 파형과 달리 IF 신호가 수십 MHz의 광대역 LFM 파형인 MPRF 파형에서는 offset 주파수 범위가 수십 MHz이므로, 이미 IF 신호의 위상잡음이 높아 원거리 표적뿐만 아니라 근거리 표적의 위상잡음도 크게 감쇄되지는 않았다.
두 파형 모두에서 최소거리 부근에서는 높은 수신전력으로 인해 위상잡음도 높아지므로 열잡음 대비 SNR이 악화되는 현상을 확인하였다. 그러나, 본 논문에서 제시한 위상잡음에서는 시스템 성능을 만족하는 높은 SNR을 확보하고 있으므로 그림 1의 레이다 성능에는 영향성이 적을 것으로 판단된다. 한편, 표적의 거리가 멀어질수록 표적신호의 전력이 감소하여 위상잡음의 절대값은 줄어들었다. 따라서 특정거리 이상으로 표적이 멀어지면 IF 신호의 위상잡음보다 수신기의 열잡음이 높아져서 IF 신호의 SNR은 수신기 열잡음에 의해 결정되었다.
본 논문에서 위상잡음이 악화되면 신호의 잡음전력이 높아질 뿐만 아니라 전력이 여러 주파수로 분산되면서 첨두전력이 낮아져 SNR 악화가 더 크게 일어나는 것을 확인하였다. 이런 현상이 발생하면 최대탐지거리 상황에서 최소 SNR을 만족하지 못하고 표적탐지가 불가능해질 수 있다.
따라서 레이다 운용파형에 따라 본 논문에서 제시한 방법으로 표적거리에 따른 수신 출력신호의 위상잡음을 판단하고, 시스템 성능을 유지할 수 있는 적절한 위상잡음 규격을 설정하는 것이 중요하다. 추가로, 운용파형에 관계없이 RX와 LO의 위상이 결맞지 않은 시스템에서는 IF 위상잡음이 RX와 LO 위상잡음의 합으로 나타나 잡음전력을 높이고, IF 신호의 SNR을 악화시키는 영향을 미침을 확인하였다.











