논문/REGULAR PAPERS
공간 영역 및 고유 영역 기반 딥러닝 SAR 표적 식별 성능 비교
채승병
,
강민석†
Comparison of Spatial- and Eigenspace-Domain-Based Deep Learning SAR Target Classification Performances
Seung-Byung Chae
,
Min-Seok Kang†
Author Information & Copyright ▼
Division of Electrical, Electronic & Control Engineering, Kongju National University
© Copyright 2025 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the
Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits
unrestricted non-commercial use, distribution, and reproduction in any
medium, provided the original work is properly cited.
Received: May 28, 2025; Revised: May 31, 2025; Accepted: Jun 08, 2025
Published Online: Jun 30, 2025
요 약
본 연구는 합성개구레이다(SAR, synthetic aperture radar) 표적 식별을 위한 고유공간(eigenspace) 기반 접근법을 제안한다. 공간 영역 SAR 영상에 고유공간 변환을 적용한 후, 주요 정보를 보존하는 상위 고유벡터를 추출한 고유공간 영역 영상의 분류 성능을 평가하였다. MSTAR(moving and stationary target acquisition and recognition) 데이터셋을 대상으로, 다양한 합성곱 신경망을 사용하여 공간 영역 및 고유공간 영역 SAR 영상의 분류 정확도를 비교하였다. 실험을 통해 신호 대 잡음비(signal to noise ratio)가 낮은 조건에서 고유공간 영역이 공간 영역 대비 우수한 분류 성능을 나타냄을 확인하였다.
Abstract
This study proposes an eigenspace-based method for synthetic aperture radar (SAR) target classification. The classification performance of the eigenspace-domain image extracted from the upper eigenvectors that preserve the main information was evaluated post application of the eigenspace transformation to the spatial-domain SAR image. The classification accuracy of spatial- and eigenspace-domain SAR images was compared on Moving and Stationary Target Acquisition and Recognition datasets using various convolutional neural network architectures. The experiment confirmed that the eigenspace domain achieved a better classification performance than the spatial domain under low signal-to-noise ratio conditions.
Keywords: Deep Learning; Eigen Decomposition; Eigenspace; SAR Target Classification; Signal to Noise Ratio
I. 서 론
레이다 이미징(radar imaging)은 송신하는 전자기파가 관측 대상에서 반사되어 돌아온 신호를 수신 및 처리하여 영상을 재구성하는 기술로, 대표적으로 다음과 같은 기법이 있다. 합성 개구면 레이다(SAR, synthetic aperture radar)는 플랫폼의 이동을 통해 가상 안테나 길이를 확장함으로써 고해상도의 레이다 영상을 생성한다[1]~[7]. 역합성 개구면 레이다(inverse SAR)는 고정된 관측 레이다가 이동 표적으로부터 수신한 반사 신호를 고해상도로 재현하는 기술이다[8]~[10]. 간섭계 SAR(interferometric SAR)는 동일 지역을 약간의 서로 다른 관측 위치에서 취득한 두 SAR 영상의 위상 차이를 분석하여 지표면의 변화를 탐지한다[11]. 이러한 레이다 이미징 기술 중에서 SAR 영상은 지표면의 형상을 주‧야간 및 기상 조건과 무관하게 안정적으로 획득할 수 있는 특성을 지니므로, 현대 감시 및 정찰 체계의 핵심적인 관측 자료로 활용된다. 따라서 SAR 영상을 활용한 지상 및 해상 표적 자동 식별 기술의 필요성이 강조되고 있다.
SAR 표적 식별 연구는 공간 영역 SAR 영상에 대해 분류 성능을 발전시켜왔다. SAR 표적 식별은 전통적 특징 기반 방법과 딥러닝 기반 방법으로 양분된다. 초기에는 영상 기반 특징을 추출한 뒤 SVM(support vector machine)과 같은 분류기를 적용하여 정확도를 높여 왔으며[12], 딥러닝이 등장한 이후 높은 수준의 식별률을 달성하여 성능 향상을 주도하고 있다[13],[14].
그러나 SAR 영상은 일반적으로 클러터(clutter)나 스펙클 잡음(speckle noise)이 포함되어 있다[15]. 클러터는 관심 표적 이외의 산란체로부터 반사된 신호가 표적 신호와 중첩되어 나타나는 불규칙한 배경 잡음이다. 분류기는 이러한 잡음을 학습하면서 표적에 대한 분류 정확도가 저하되는 문제가 나타난다. 기존 연구에서는 SAR 영상에 불가피하게 포함되는 잡음을 완화하기 위해 전처리를 수행하거나, 잡음 특성을 학습하여 모델의 잡음 강건성을 높이는 등 다양한 기법이 제안되고 있다[16],[17].
SAR 영상의 표적 식별을 위한 방안으로 영상 변환 기법에 대한 연구가 시도되고 있다. 최신 연구에서는 푸리에 변환을 선형변환으로 해석하고, 이를 통해 공간 영역을 주파수 영역으로 변환하여 SAR 표적 식별을 수행하였다[18]. 기존 연구와 달리 본 연구에서는 공간 영역의 SAR 영상을 고유공간으로 변환하는 SAR 표적 식별 기법을 제안한다. 공간 영역과 고유공간 영역 간의 변환은 선형변환이므로 일대일 대응을 이룬다. 따라서 공간 영역에서 도시된 각 표적 정보의 특성은 고유공간 영역에서 일대일로 대응되어 재해석된다. 또한, 큰 고윳값에 대응하는 상위 고유벡터를 추출하여 표적의 주요 정보만을 다룬 고유공간 영상의 표적 분류 성능을 확인한다. 추가적으로 공간 영역에서 잡음에 해당하는 신호를 포함한 하위 고유벡터들을 제거함으로써 고유공간 영역 기반 표적 식별이 잡음에 강인함을 확인한다. 본 실험에서는 합성곱 신경망(CNN, convolutional neural network)을 분류기로 채택하여 MSTAR(moving and stationary target acquisition and recognition) 데이터셋에 대해 두 가지 실험을 수행하였다. 먼저, 고유공간 영역 기반 SAR 영상의 상위 고유벡터 추출 비율을 조정하여 공간 영역 영상과의 분류 성능을 비교하였다. 다음으로 동일 데이터셋에 가우시안 잡음을 주입하여 신호 대 잡음비(SNR, signal to noise ratio)가 낮은 환경을 구성한 실험에서 상위 고유벡터로 구성한 고유공간 영역 SAR 영상이 공간 영역 SAR 영상보다 잡음에 강인한 표적 식별 성능을 보임을 확인하였다.
II. 본 론
2-1 고유공간 영역에서의 SAR 영상
SAR 영상에서 표적을 효과적으로 분석하기 위해 다양한 변환 기법을 활용할 수 있다. 본 논문에서는 공간 영역 영상을 고유공간으로 변환한 후, 변환된 영상에 대한 식별 성능을 확인한다.
공간 영역의 영상에 대한 고유공간 변환이 여전히 유의미한 식별 정보를 보존하는 이유는, 공간 영역에서의 영상과 고유공간의 영상이 선형변환을 통한 일대일 대응 관계로 해석할 수 있기 때문이다. 이 두 공간을 각각 벡터 공간으로 간주하면, 선형변환을 통해 일대일 대응이 되며 기존 공간에서의 고유한 특징이 변환된 공간에서도 유일하게 표현된다. 이를 수식으로 정리하면 다음과 같이 표현할 수 있다.
식 (1)에서 행렬 A는 m×n 차원의 공간 영역 영상, 행렬 U는 m×m 차원의 고유공간 영역 영상이다. m과 n은 각각 A의 행(row)과 열(column)의 개수를 의미한다. H는 n×m차원의 선형 변환 행렬을 나타내며, 공간 영역 영상 A를 고유공간 영역 영상 U로 변환하는 역할을 한다. 식 (1)을 통해 공간 영역에서 표적의 주요 특징점들은 변환된 고유공간에서도 일대일 대응으로 유일하게 표현된다.
일반적인 SAR 영상 A는 행과 열의 개수가 서로 다른 비정방행렬이다. 고유공간 영상 U를 얻기 위해 SAR 영상 A를 식 (2)와 같이 분해한다[19].
식 (2)는 일반적인 m×n차원의 비정방행렬 A에 대해 특이값 분해(singular value decomposition)로 나타낸 것이다. U는 좌측 특이벡터들로 이루어진 m×m 행렬이고, V는 우측 특이벡터들로 이루어진 n×n 행렬이며, {·}T는 행과 열의 위치를 바꾸는 전치 연산자(transpose operator)이다. Σ는 A의 특이값으로 이루어진 m×n 대각행렬이다. 식 (2)를 기반으로, AAT에 고윳값 분해(eigen decomposition)를 적용하면 식 (3)과 같이 표현된다.
AAT는 m×m 정방행렬이며 고유공간 영상을 얻기 위한 행렬이다. Λ는 AAT의 고윳값 λi (i=1,…,m)로 구성된 m×m 대각행렬로 대각 성분에는 고윳값이 가장 큰 값부터 내림차순으로 배치된다. U는 AAT의 고유벡터 qi (i=1,…,m)로 이루어진 m×m 행렬이며, 각 열벡터는 Λ의 대각 성분에 대응하는 고유벡터를 나타낸다. 식 (3)을 통해, 일반적인 SAR 영상으로부터 고유공간 영상 U를 얻을 수 있다.
2-2 고유공간 영상의 고유벡터 추출
2-1 절에서 일반적인 공간 영역 SAR 영상 A로부터 고유공간 영상 U를 얻는 과정을 유도하였다. 고유공간으로 변환된 SAR 영상은 모든 고유벡터를 포함할 경우 원본 영상의 정보를 완전히 보존할 수 있으나, 유의미한 정보는 주로 큰 고윳값에 대응하는 상위 고유벡터에 집중된다. 상위 고유벡터는 식 (3)에서 Λ; 행렬의 대각 성분 중 큰 고윳값에 대응되는 고유벡터를 의미한다.
본 연구에서는 유의미한 정보를 주로 포함하고 있는 상위 고유벡터의 추출 비율을 조절하여 표적 분류 성능을 평가한다. Λ; 대각 성분인 고윳값 λi를 내림차순으로 정렬하고, 상위 k개의 고윳값이 전체 m개의 고윳값에 차지하는 비율 Ek를 식 (4)와 같이 정의한다[20].
Ek를 통해 상위고유벡터로 이루어진 고유공간 Uk는 설정한 임계값 η 이상을 만족하는 최소 k값으로 결정되며, 식 (5)와 같이 나타낸다[20].
고유공간 영상 U로부터 고유벡터 m개 중 상위 고유벡터 k개를 추출한 m×k 차원의 Uk로 구성하여, 표적의 주요 정보가 집약된 고유공간 영상을 효과적으로 확보할 수 있다. 상위 고유벡터로 구성된 Uk는 다음의 수식으로 나타낼 수 있다.
q1~qk는 각각 고윳값 λ1~λk에 대응하는 m×1의 고유벡터이며, 영상의 주요 정보를 반영한 고유공간 영상 Uk가 구성된다.
그림 1은 공간 영역의 SAR 영상을 고유공간 영역의 영상으로 변환한 후, 주요 정보를 담고 있는 상위 고유벡터를 추출하여 얻은 Uk를 설명하기 위한 예시이다. 그림 1의 (a)는 SSDD(SAR ship detection dataset)[21]에서 제공하는 SAR 영상이며, 그림 1(b)는 그림 1(a)로부터 획득한 고유공간 영상이다. 그림 1의 (b)에서 적색 사각형으로 표시한 영역은 상위 고유벡터로 구성된 고유공간의 영상 Uk를 나타내며, 표적의 주요 정보가 포함되어 있다.
그림 1. | Fig. 1.
SAR 공간 영상 및 고유공간으로 변환한 영상 | SAR spatial domain image and its corresponding eigenspace domain representation.
Download Original Figure
2-3 딥러닝 기반 CNN 구조
인공지능 분야에서는 대규모 데이터를 기반으로 특징을 자동 학습하는 딥러닝 기법이 다양한 분야에 폭넓게 적용되고 있다. 특히 CNN은 영상 데이터의 공간적 특징을 효과적으로 추출하고 분류하는 대표적인 신경망 모델이며, 합성곱(convolutional)과 풀링(pooling) 계층을 반복하며 데이터의 특징을 계층적으로 학습한다. 초기 계층에서는 주로 경계선과 같은 단순한 저수준(low-level) 특징을 감지하고, 깊은 계층으로 진행할수록 점차 복잡한 고수준(high-level) 패턴을 포착한다. 본 논문에서는 ResNet[22], DenseNet[23], EfficientNetV2[24]를 기반으로 한 CNN 모델을 활용하여 공간 영역과 고유공간 영역에 대해 SAR 표적 식별 성능을 평가하였다. 또한, 고유공간 영상에서 상위 고유벡터를 추출하여 얻은 고유공간 영상의 식별 성능도 비교하였다.
2-3-1 ResNet
ResNet은 딥러닝 모델이 깊어질수록 학습 성능이 정체되거나 오히려 하락하는 문제를 해결하기 위해 제안된 구조이다. ResNet은 신경망이 입력과 출력 간의 잔차(residual)만을 학습하도록 설계되었으며, 이를 통해 네트워크의 깊이가 증가하더라도 효과적인 학습이 가능하다. 이러한 잔차 학습 구조는 깊은 신경망의 최적화를 용이하게 한다.
2-3-2 DenseNet
DenseNet은 네트워크 내의 모든 계층을 직접 연결(concatenation)하는 밀집 연결(dense connectivity) 구조를 특징으로 한다. 네트워크는 여러 개의 밀집 블록(dense block)으로 구성되어, 각 계층이 선행 계층에서 추출한 특징을 효율적으로 재사용(feature reuse)할 수 있다. 이를 통해 파라미터 수를 감소시키면서도 다양한 특징을 학습할 수 있다.
2-3-3 EfficientNetV2
EfficientNetV2는 기존 EfficientNet 계열에서 학습 속도와 연산 효율을 향상하도록 설계된 모델이다. 초반 단계와 같이 채널 수가 적은 구간에서는 깊이별 합성곱(depthwise convolution)의 연산 이득이 크지 않다는 점을 고려해, 해당 구간을 단일 3×3 표준 합성곱으로 구성된 Fused-MBConv 블록으로 대체하여 병목을 제거한다. 이후 채널 수가 충분히 커지는 후반 단계에서는 기존의 MBConv 구조를 적용해 파라미터 수와 연산량을 최소화한다. 이러한 혼합 블록 전략은 모델 크기를 크게 늘리지 않고도 훈련 시간을 단축하고 정확도를 향상시키는 데 기여하였다.
III. 실험 및 평가
MSTAR 데이터셋은 SAR 기반 표적 식별 성능 평가를 위해 널리 사용되는 표준 데이터셋이며, 군사 감시 및 식별 목적으로 수집되었다. 총 10가지 군용 표적의 SAR 영상을 제공하며, 각 표적 영상은 다양한 경사각(depression angle) 조건에서 촬영되었다. 그림 2는 MSTAR 데이터셋에 포함된 표적 영상의 표본을 나타내며, 공간 영역과 고유공간 영역의 영상을 도시한다. 그림 2(a)~그림 2(c)는 원본 SAR 공간 영상이고 그림 2(d)~그림 2(f)는 동일 표적에 대해 고유공간으로 변환한 영상이다. 고유공간으로 변환된 영상은 고윳값 분해에서 얻은 고유벡터들을 열로 배열한 행렬로 나타낸다. 이 고유벡터들은 대응 고윳값의 크기에 따라 내림차순으로 정렬되어 가장 큰 고윳값에 대응하는 고유벡터가 행렬의 첫 번째 좌측 열에 위치한다. 그림 2(d)~(f)에서 적색 사각형으로 표시한 부분은 상위 고유벡터만을 추출한 고유공간의 영상을 나타낸다. 본 실험에서는 상위 고유벡터의 추출 비율을 조절하며 표적 식별 성능 평가를 수행하였다.
그림 2. | Fig. 2.
MSTAR 데이터셋의 SAR 공간 영상 및 고유공간 영상 표본 | Sample SAR images in the spatial and eigenspace domains from the MSTAR dataset.
Download Original Figure
표 1[18]은 본 연구에서 사용한 MSTAR 데이터셋의 표적 종류별 데이터 개수 및 영상의 크기를 나타낸 것이다. MSTAR 데이터셋의 영상 크기는 표적 종류에 따라 차이가 있다. 식 (3)을 통해, m×n 크기의 각 표적 SAR 영상 A로부터 m×m크기의 고유공간 SAR 영상 U를 획득한다. 각 표적의 고유공간의 영상 크기는 다음과 같다. BMP-2, T-72, BTR-60, BTR-70는 128×128, BRDM-2는 129×129, ZSU-23/4와 2S1은 158×158, T-62는 173×173, D7은 178×178, ZIL-131은 193×193이다. 고유공간의 영상은 상위 고유벡터의 추출 비율을 5 %, 10 %, 20 %, 50 %, 100 % 변화시켜서 분류 성능을 확인하였다. 각각의 고유벡터 추출 비율에 따른 실제 고유공간 영상의 크기는 표 2에 기입하였다.
표 1. | Table 1.
MSTAR 데이터셋의 학습 및 테스트 데이터셋 구성 | Training and test dataset configuration of MSTAR dataset.
| Target |
Train images |
Test images |
Image size |
| Depression angle (17°) |
Depression angle (15°) |
| BMP-2 |
233 |
195 |
128×128 |
| T-72 |
232 |
196 |
128×128 |
| BTR-60 |
256 |
195 |
128×128 |
| BTR-70 |
233 |
196 |
128×128 |
| BRDM-2 |
298 |
274 |
129×128 |
| ZSU-23/4 |
299 |
274 |
158×158 |
| 2S1 |
299 |
274 |
158×158 |
| T-62 |
299 |
273 |
173×172 |
| D7 |
299 |
274 |
178×177 |
| ZIL-131 |
299 |
274 |
193×192 |
| Total |
2,747 |
2,425 |
|
Download Excel Table
표 2. | Table 2.
고유벡터 추출 비율에 따른 고유공간 영상 크기 | Eigenspace image size according to eigenvector extraction ratio.
| Eigenspace image size |
5 % |
10 % |
20 % |
50 % |
100 % |
| 128×128 |
128×6 |
128×12 |
128×25 |
128×64 |
128×128 |
| 129×129 |
129×6 |
129×12 |
129×25 |
129×64 |
129×129 |
| 158×158 |
158×7 |
158×15 |
158×31 |
158×79 |
158×158 |
| 173×173 |
173×8 |
173×17 |
173×34 |
173×86 |
173×173 |
| 178×178 |
178×8 |
178×17 |
178×35 |
178×89 |
178×178 |
| 193×193 |
193×9 |
193×19 |
193×38 |
193×96 |
193×193 |
Download Excel Table
3-2 SAR 표적 식별 성능 평가
본 실험에서는 MSTAR 데이터셋을 이용하여 공간 영역과 고유공간 영역의 SAR 영상에 대해 딥러닝 기반의 표적 식별 성능을 평가하였다. 먼저 상위 고유벡터를 추출한 고유공간 영역의 SAR 영상과 공간 영역 SAR 영상의 분류 성능을 비교하였고, 추가로 낮은 SNR 실험 환경을 구축하여 두 영역의 표적 식별 성능 비교를 수행하였다.
성능 평가는 CNN 기반 ResNet-34, DenseNet-121, EfficientNetV2-S 모델들을 이용하여 수행하였으며, Python 및 PyTorch 프레임워크를 활용하여 구현하였다. CNN 기반 모델에 입력되는 모든 영상의 크기는 보간(interpolation)을 통해 128×128로 조정(resize)하였다. 공간영역 SAR 영상은 최소-최대 정규화를 적용하여 픽셀 값을 [0,1] 범위로 변환하였으며, 고유공간 영상은 픽셀 값에 대해 전처리 없이 분류 모델에 입력하였다. 학습 데이터는 17° 경사각 SAR 영상을 활용하여, 학습 및 검증 데이터 비율을 8:2로 분할하였다. 학습의 배치 크기는 32, 에폭(epoch) 수는 100으로 설정하였다. 31번째 에폭부터 매 에폭마다 검증 손실값(validation loss)을 모니터링하였고, 최저 검증 손실값을 기록할 때마다 해당 시점의 모델 가중치를 저장하였다. 손실 함수는 교차 엔트로피(cross entropy)를 사용하였으며, 평가 데이터는 15° 경사각 SAR 영상을 활용하여 분류 정확도를 측정하였다.
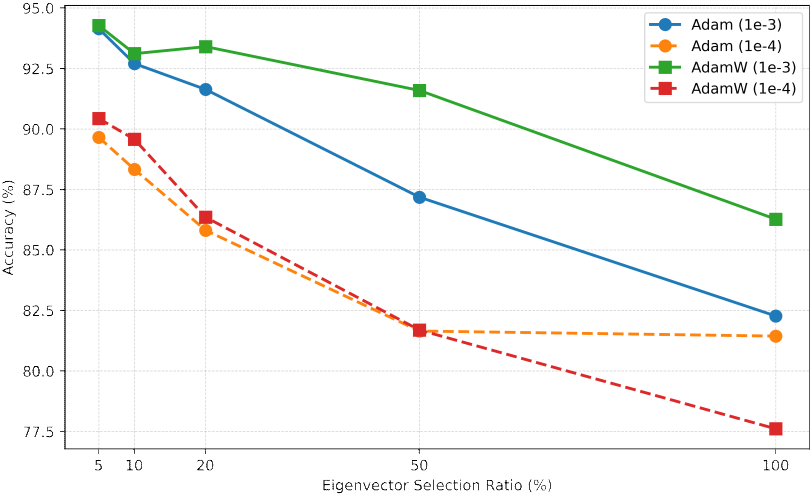
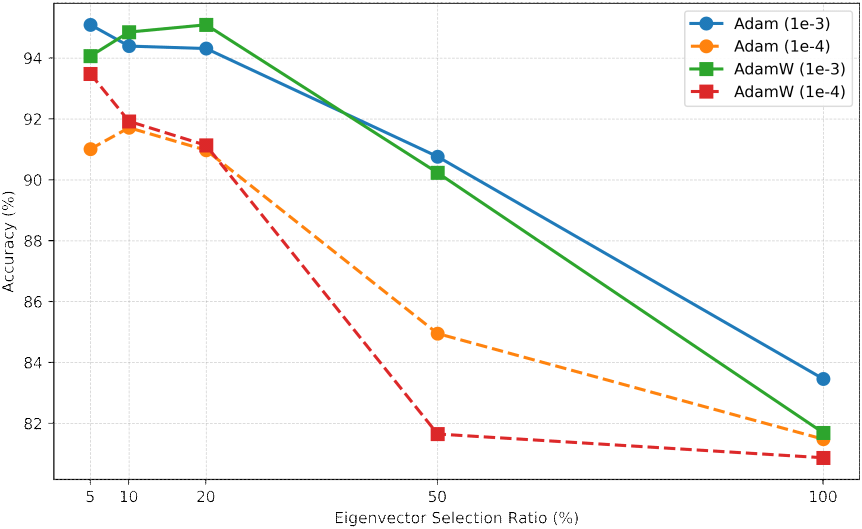
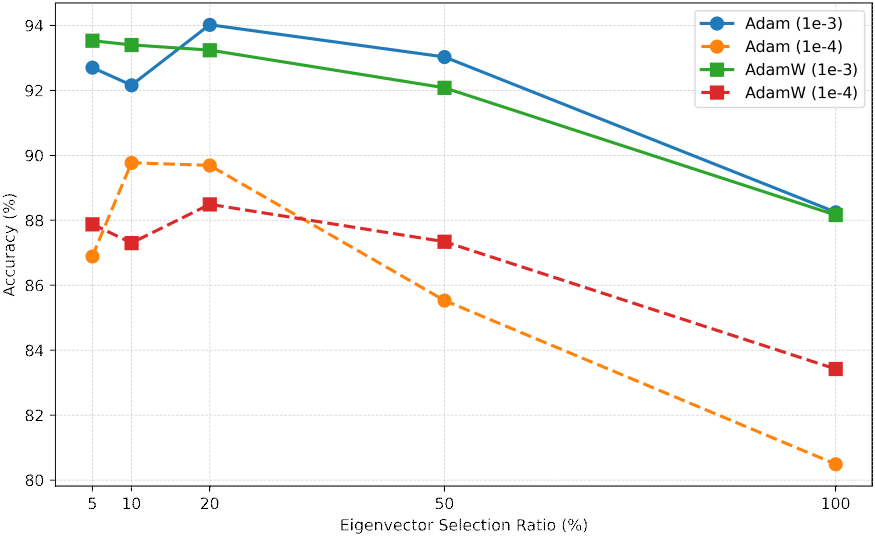
첫 번째 실험으로 딥러닝 하이퍼 파라미터 조정을 통해 주어진 MSTAR 데이터셋으로부터 고유공간 영역의 SAR 영상과 공간 영역의 SAR 영상과의 표적 분류 성능을 비교하였다. 최적화 알고리즘은 Adam과 AdamW, 각각에 대해 학습률은 10−3 및 10−4을 적용하였다. 공간 영역 SAR 영상에 대한 표적 분류 정확도는 표 3에 요약하였다. 실험 결과는 모든 시나리오에 대해서 90 % 이상의 분류 정확도를 나타내었으며, DenseNet-121이 가장 뛰어난 성능을 보였다. 또한, 학습률 10−3이 10−4보다 일관되게 우수한 결과를 보였다. 그림 3~그림 5는 각각의 CNN 기반 ResNet-34, DenseNet-121, EfficienctNetV2-S 모델에 따른 상위 고유벡터 추출 비율에 대한 고유공간 영역 SAR 영상의 분류 정확도를 도시한 것이다. 가로축에 상위 고유벡터 추출 비율을 나타내어 분류 정확도의 추세 비교가 용이하도록 구성하였다. 그래프에서 학습률 10−3은 실선, 10−4은 점선으로 나타내었으며, 최적화 알고리즘 Adam과 AdamW는 각각 원형과 사각형 마커로 표시하였다. 모든 CNN 기반 모델에서 학습률이 10−3인 경우 분류 성능이 높게 나타나는 경향을 보였다. 특히, 고유공간의 전체 고유벡터들을 모두 사용하였을 때보다 상위 고유벡터의 추출 비율을 줄일수록 표적 식별 성능이 개선됨을 확인하였다. ResNet-34 모델에서는 상위 고유벡터를 5 %만 추출하였을 때 학습률이 10−3인 조건에서 94 %의 분류 정확도를 기록하여 공간 영역의 분류 성능인 98 %에 근접한 수준을 달성하였다. DenseNet-121 및 EfficientNetV2-S에서는 상위 고유벡터 추출 비율이 5~20 %, 학습률이 10−3일 때 분류 성능이 92~95 %로 나타났으며, 공간 영역의 분류 성능인 97~99 %에 근접한 수준을 달성하였다. 이를 통해 고유공간의 상위 고유벡터에는 표적을 변별할 수 있는 주요 정보를 포함하는 것을 알 수 있다.
표 3. | Table 3.
공간 영역 SAR 영상의 표적 식별 정확도 | Target classification accuracy in spatial domain SAR images.
| Optimizer, Learning rate |
ResNet-34 (%) |
DenseNet-121 (%) |
EfficientNetV2-S (%) |
| Adam, 10−3 |
98.27 |
99.09 |
97.90 |
| Adam, 10−4 |
94.85 |
98.02 |
90.43 |
| AdamW, 10−3 |
97.40 |
98.93 |
97.03 |
| AdamW, 10−4 |
97.36 |
98.06 |
93.73 |
Download Excel Table
그림 3. | Fig. 3.
상위 고유벡터 추출 비율에 따른 고유공간 영역 SAR 영상의 표적 식별 정확도(ResNet-34) | Target classification accuracy of eigenspace-domain SAR images according to the proportion of extracted top eigenvectors (ResNet-34).
Download Original Figure
그림 4. | Fig. 4.
상위 고유벡터 추출 비율에 따른 고유공간 영역 SAR 영상의 표적 식별 정확도(DenseNet-121) | Target classification accuracy of eigenspace-domain SAR images according to the proportion of extracted top eigenvectors (DenseNet-121).
Download Original Figure
그림 5. | Fig. 5.
상위 고유벡터 추출 비율에 따른 고유공간 영역 SAR 영상의 표적 식별 정확도(EfficientNetV2-S) | Target classification accuracy of eigenspace-domain SAR images according to the proportion of extracted top eigenvectors (EfficientNetV2-S).
Download Original Figure
두 번째 실험에서는 SNR이 낮은 환경에서 공간 영역 및 고유공간 영역의 분류 성능을 비교하였다. 최적화 알고리즘은 Adam, 학습률은 10−3을 적용하였다. MSTAR 데이터셋에 인위적인 잡음을 삽입하여−15 dB 수준의 SNR 환경을 구축하였고, 잡음 환경에서 공간 및 고유공간 영역의 SAR 영상에 대한 표적 식별 성능을 비교한 결과는 표 4와 같다. 표 4를 통해 SNR이−15 dB일 때 공간 영역의 분류 성능이 63~70 % 정확도로 크게 하락한 것을 확인하였다. 고유공간 영역 전체를 활용하였을 때 67~69 %로 표적 분류 정확도가 관측되었다. 반면, 상위 고유벡터 추출 비율을 50 %로 설정하였을 경우 공간 영역의 분류 성능보다 높은 것을 확인하였다. 또한, 상위 고유벡터 5~20 %를 추출한 경우 분류 정확도는 75~79 %로 공간 영역보다 월등한 성능을 보였다. 이를 통해 표적 식별에 쓰인 상위 고유벡터들은 표적에 주요 특징들을 포함한 반면, 제외된 하위 고유벡터들에는 잡음 성분만을 포함한 것을 확인할 수 있다.
표 4. | Table 4.
고유공간 영역 및 공간 영역에 대한 SAR 영상의 표적 식별 정확도(SNR: −15 dB) | Target classification accuracy of SAR images for eigenspace and spatial domains (SNR: −15 dB).
| Domain |
Eigenvector extraction ratio (%) |
ResNet-34 Accuracy (%) |
DenseNet-121 Accuracy (%) |
EfficientNetV2-S Accuracy (%) |
| Eigenspace |
100 |
69.07 |
67.3 |
69.11 |
| Eigenspace |
50 |
75.13 |
72.37 |
74.10 |
| Eigenspace |
20 |
75.67 |
77.81 |
76.74 |
| Eigenspace |
10 |
76.78 |
77.28 |
77.90 |
| Eigenspace |
5 |
78.14 |
75.59 |
79.67 |
| Spatial |
|
70.80 |
63.71 |
68.66 |
Download Excel Table
IV. 결 론
본 연구에서는 SAR 표적 식별에서 고유공간으로 변환된 영상을 활용하는 접근법을 제시하였다. 공간 영역을 선형변환하면 표적의 특징이 보존 가능하며 일대일로 대응되는 새로운 신호로 해석될 수 있다. 따라서 이 선형변환을 고유공간 변환으로 선택하면 고유공간 영역에서도 SAR 표적식별이 가능하다.
두 가지 실험을 통해 공간 영역과 고유공간 영역의 SAR 표적 식별 성능을 비교하였다. 먼저, MSTAR 데이터셋 원본 영상에 대해 상위 고유벡터 추출 비율을 단계적으로 조정하여 공간 영역과 고유공간 영역의 분류 정확도를 평가하였다. 그 결과, 상위 고유벡터 5~20 %를 추출한 고유공간 영역의 분류 정확도가 전체 고유벡터를 이용하였을 때보다 높은 표적 식별 성능을 달성한 것을 확인하였다. 이를 통해 표적의 주요 정보가 상위 고유벡터에 집중되어 있음을 확인할 수 있다. 다음으로 SNR이 −15 dB인 고잡음 환경을 조성한 실험에서는 상위 고유벡터로 구성한 고유공간 영상이 공간 영역 영상보다 최대 14 %의 높은 표적 분류 정확도를 기록하였다. 이는 잡음 정보가 집중된 하위 고유벡터를 제거함으로써 얻은 결과이며 제안한 방법의 잡음 강건성을 실험적으로 입증하였다.
본 연구를 통해 기존에 공간 영역에서 수행되었던 SAR 표적 식별이 고유공간이라는 새로운 도메인에서도 효과적인 표적 식별 성능을 보임을 확인할 수 있다.
Acknowledgements
이 논문은 2025년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임(No. 2021R1I1A3043152).
References
I. G. Cumming, F. H. Wong,
Digital Processing of Synthetic Aperture Radar Data, Norwood, MA, Artech house, 2005.

M. S. Kang, J. M. Baek, “Compressive sensing-based Omega-K algorithm for SAR focusing,”
IEEE Geoscience and Remote Sensing Letters, vol. 22, p. 4003405, Jan. 2025.


M. S. Kang, J. M. Baek, “SAR image reconstruction via incremental imaging with compressive sensing,”
IEEE Transactions on Aerospace and Electronic Systems, vol. 59, no. 4, pp. 4450-4463, Aug. 2023.


M. S. Kang, J. M. Baek, “Efficient SAR imaging integrated with autofocus via compressive sensing,”
IEEE Geoscience and Remote Sensing Letters, vol. 19, p. 4514905, Oct. 2022.


M. S. Kang, K. T. Kim, “Automatic SAR image registration via tsallis entropy and iterative search process,”
IEEE Sensors Journal, vol. 20, no. 14, pp. 7711-7720, Jul. 2020.


M. S. Kang, K. T. Kim, “Ground moving target imaging based on compressive sensing framework with single-channel SAR,”
IEEE Sensors Journal, vol. 20, no. 3, pp. 1238-1250, Feb. 2020.


M. S. Kang, K. T. Kim, “Compressive sensing based SAR imaging and autofocus using improved Tikhonov regularization,”
IEEE Sensors Journal, vol. 19, no. 14, pp. 5529-5540, Jul. 2019.


M. S. Kang, J. H. Bae, B. S. Kang, and K. T. Kim, “ISAR cross-range scaling using iterative processing via principal component analysis and bisection algorithm,”
IEEE Transactions on Signal Processing, vol. 64, no. 15, pp. 3909-3918, Aug. 2016.


M. S. Kang, J. H. Bae, S. H. Lee, and K. T. Kim, “Efficient ISAR autofocus via minimization of Tsallis entropy,”
IEEE Transactions on Aerospace and Electronic Systems, vol. 52, no. 6, pp. 2950-2960, Dec. 2016.


M. S. Kang, S. J. Lee, S. H. Lee, and K. T. Kim, “ISAR imaging of high-speed maneuvering target using gapped stepped-frequency waveform and compressive sensing,”
IEEE Transactions on Image Processing, vol. 26, no. 10, pp. 5043-5056, Oct. 2017.



M. S. Kang, J. M. Baek, “Effective denoising of InSAR phase images via compressive sensing,”
IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, vol. 17, pp. 17772-17779, May. 2024.


M. Amoon, G. Rezai-rad, “Automatic target recognition of synthetic aperture radar (SAR) images based on optimal selection of Zernike moments features,”
IET Computer Vision, vol. 8, no. 2, pp. 77-85, Apr. 2014.


S. Chen, H. Wang, F. Xu, and Y. Q. Jin, “Target Classification Using the Deep Convolutional Networks for SAR Images,”
IEEE Transactions on Geoscience and Remote Sensing, vol. 54, no. 8, pp. 4806-4817, Aug. 2016.


J. Ding, B. Chen, H. Liu, and M. Huang, “Convolutional neural network with data augmentation for SAR target recognition,”
IEEE Geoscience and remote sensing letters, vol. 13, no. 3, pp. 364-368, Mar. 2016.

J. Martín-de-Nicolás, M. P. Jarabo-Amores, D. Mata-Moya, N. Del-Rey-Maestre, and J. L. Bárcena-Humanes, “Statistical analysis of SAR sea clutter for classification purposes,”
Remote Sensing, vol. 6, no. 10, pp. 9379-9411, Sep. 2014.


A. Passah, K. Amitab, and D. Kandar, “SAR image despeckling using deep CNN,”
IET Image Processing, vol. 15, no. 6, pp. 1285-1297, Jan. 2021.


Y. Kwak, W. J. Song, and S. E. Kim, “Speckle-noise-invariant convolutional neural network for SAR target recognition,”
IEEE Geoscience and Remote Sensing Letters, vol. 16, no. 4, pp. 549-553, Apr. 2019.


S. B. Chae, M. S. Kang, “Comparison of spatial- and frequency-domain-based SAR target classification performance,”
The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 36, no. 5, pp. 533-539, May 2025.


G. H. Golub, C. F. van Loan,
Matrix Computations, 4th ed. Baltimore, MD, The Johns Hopkins University Press, pp. 76-80, 2013.

S. H. Lee, J. H. Bae, M. S. Kang, and K. T. Kim, “Efficient ISAR autofocus technique using eigenimages,”
IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, vol. 10, no. 2, pp. 605-616, Feb. 2017.


T. Zhang, X. Zhang, J. Li, X. Xu, B. Wang, and X. Zhan, et al., “SAR ship detection dataset (SSDD): Official release and comprehensive data analysis,”
Remote Sensing, vol. 13, no. 18, p. 3690, Sep. 2021.


K. He, X. Zhang, S. Ren, and J. Sun, “Deep residual learning for image recognition,” in
Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition(CVPR), Las Vegas, NV, Jun. 2016, pp. 770-778.



G. Huang, Z. Liu, L. van der Maaten, and K. Q. Weinberger, “Densely connected convolutional networks,” in
2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, Jul. 2017, pp. 4700-4708.



M. Tan, Q. V. Le, “Efficientnetv2: Smaller models and faster training,” in
2021 International Conference on Machine Learning(ICML), Vienna, Jul. 2021, pp. 10096-10106.