High-Accuracy R-DML Angle Estimation for FMCW Radar

Lee, Jae-Won; Choi, Hyun-Hwan; Han, Ye-Ju; Lee, Si-Jun; Moon, Kwan-Woo; Song, Reem; Kim, Byung-Sung

doi:10.5515/KJKIEES.2025.36.5.509

J. Korean Inst. Electromagn. Eng. Sci. 2025; 36(5):509-517

pISSN: 1226-3133, eISSN: 2288-226X

DOI: https://doi.org/10.5515/KJKIEES.2025.36.5.509

논문/REGULAR PAPERS

FMCW 레이다용 고정밀 R-DML 각도 추정 기법

이재원

, 최현환

, 한예주

, 이시준

, 문관우

, 송림^*

, 김병성^*^,^†

High-Accuracy R-DML Angle Estimation for FMCW Radar

Jae-Won Lee

, Hyun-Hwan Choi

, Ye-Ju Han

, Si-Jun Lee

, Kwan-Woo Moon

, Reem Song^*

, Byung-Sung Kim^*^,^†

Author Information & Copyright ▼

^{성균관대학교 반도체융합공학과}

^*성균관대학교 정보통신대학

^{Department of Semiconductor Convergence Engineering, Sungkyunkwan University}

^*College of Information and Communication Engineering, Sungkyunkwan University

^†Corresponding Author: Byung-Sung Kim (e-mail: bskimice@skku.edu)

© Copyright 2025 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Feb 03, 2025; Revised: Feb 18, 2025; Accepted: Jan 10, 2025

Published Online: May 31, 2025

요 약

본 논문은 레이다의 각도 해상도, 정확도와 연산 속도에 대해 장점을 가진 각도 추정 기법 R-DML을 제안한다. 기존의 각도 추정 기법인 RELAX와 DML(deterministic maximum likelihood)을 결합한 각도 추정 기법으로 몬테카를로 방법을 통한 시뮬레이션과 W-대역 레이다 시스템을 통한 측정을 통해 검증하였다. 레이다 시스템 측정에서는 FFT(fast fourier transform)와 비교해 두 개의 물체에 대한 방위각 추정 결과를 비교하였다. 시뮬레이션 결과, SNR 20 dB 이하의 신호에 대해 ACRB(asymptotic cramer-rao bound)와 비교해도 RMSE(root mean square error) 상 거의 차이가 없음을 확인하였다. 다만, 낮은 SNR의 신호에 대한 부정확성이 존재했으며 이에 따른 한계도 확인하였다. 또한, DML과 비교해 동일한 각도 정확도를 16.8 %만의 연산 시간으로 R-DML 기법을 통해 획기적으로 줄일 수 있음을 확인하였다.

Abstract

This paper proposes an angle estimation technique that has advantages over conventional algorithms in terms of angular resolution, accuracy, and computational speed. This technique, named R-DML, combines the RELAX and deterministic maximum likelihood (DML) algorithms. Its performance was verified through Monte Carlo simulations and measurements using a W-band radar system. In the measurement, the azimuth DOA estimation results for two objects were compared using fast Fourier transform. In the simulation, the root mean square error was compared with the asymptotic Cramer-Rao bound, and was confirmed to be almost at the same level for a signal with an signal-to-noise ratio (SNR) of 20 dB. However, there was an inaccuracy in the angle estimate for signals with a low SNR, and the limitations were also confirmed. In addition, the same angular accuracy as that obtained using DML was achieved with a processing time of only 16.8 % compared with DML.

Keywords: FMCW Radar; DoA Estimation; Single Snapshot; W-Band; Thinned Array

I. 서 론

현재 레이다 시스템은 비행체와 선박 탐지와 같은 군사적 목적과 자율 주행 및 보안 감시 시스템과 같은 다양한 분야에 활용되고 있다^[1],[2]. 레이다는 카메라와 달리 물체의 거리를 식별할 수 있고, 라이다와 비교하여 악천후 조건에서 동작이 가능하다^[3]. 따라서, 넓은 범용성과 적은 제작 비용을 강점으로 차세대 센서로 주목받고 있으며, 최근에는 물체를 이미지의 형태로 표현하는 이미징 레이다 기술이 주목받고 있다. 이를 위해서는 높은 각도 추정 성능이 요구된다^[4]. 하지만, 이를 하드웨어로 구현하는 방식에는 많은 어려움이 있다^[5]. 대표적으로 각도 해상도를 높이기 위해 채널 수를 늘리는 방법이 있지만 다채널 패키징의 복잡성, 안테나 급전의 어려움 및 데이터 처리 속도의 부담과 같은 다양한 문제점을 수반한다. 따라서, 여러 각도 추정 기법을 이용하여 적은 수의 채널을 가진 레이다로도 높은 각도 해상도 및 정확도를 가지는 물체 탐지 방법이 연구되고 있다. 그 중에서 RELAX는 bias 오차를 반복을 통해 각도 해상도 및 정확도를 높이는 각도 추정 기법이다^[6]. 또한, DML(deterministic maximum likelihood)은 각도에 대한 likelihood를 구하고 그리드 서치 방식을 통해 각도 해상도 및 정확도를 높이는 각도 추정 기법이다^[7].

본 논문에서는 높은 각도 해상도와 정확도, 낮은 연산 시간에 목적을 두고 위의 RELAX와 DML을 결합하여 두 각도 추정 기법을 상호 보완한 각도 추정 기법을 제안한다. 또한, 기존의 RELAX와 DML의 단점을 극복하고, NMM(nelder-mead method)과 추정 범위 제한 방법을 사용해 연산 속도를 높인다. 그리고 RELAX를 변형해 물체 개수 추정을 가능하게 하였다. 또한, 시뮬레이션을 통해 낮은 SNR의 신호에 대한 각도 정확도 부정확성을 확인했으며 이에 따른 한계도 확인하였다.

본 논문은 다음과 같이 구성된다. Ⅱ장에서는 FMCW 레이다의 신호 모델과 기존의 각도 추정 기법 RELAX와 DML에 대해 기술한다. Ⅲ장에서는 본 논문에서 제안하는 R-DML 각도 추정 기법에 대해 설명하며 Ⅳ장에서는 실험에 사용되는 W-대역 FMCW 레이다를 소개한다. 마지막으로 Ⅴ장에서는 R-DML에 대한 시뮬레이션과 측정 결과를 제시한다.

Ⅱ. FMCW 레이다 신호 모델 및 각도 추정 기법

FMCW 레이다로 물체의 방위각을 추정하기 위해서는 방위각의 방향으로 나열된 다수의 수신 채널이 필수적으로 필요하다. 수신되는 신호를 원거리장(far-field)으로 가정할 경우, 특정한 간격으로 배치된 수신기 배열은 동일한 물체에 대해 각자 다른 위상을 가진 신호를 수신한다.

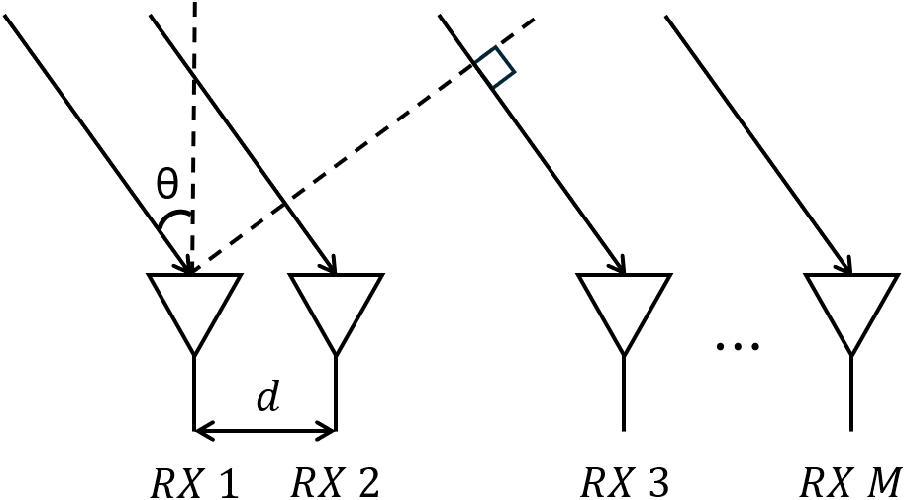
그림 1은 d(=αλ)의 간격으로 배치된 thinned array의 M개의 수신기가 원거리장을 수신하는 예시이다. 여기서, thinned array는 ULA(uniform linear array)에서 일부의 안테나를 제거한 정수배 간격을 가진 안테나 배열을 의미한다. 이 경우, θ의 방향에 대한 신호를 수신한다고 가정한다. 따라서 각 안테나에 수신된 신호를 다음과 같은 벡터로 나타낼 수 있다.

a (θ) = 1, e 2 π α r 2 sin (θ), e 2 π α r 3 sin (θ), ⋯, e 2 π α r M sin (θ) T

(1)

그림 1. | Fig. 1. Thinned array 수신 안테나 배열에 대한 예시 | Example of thinned array receiving antenna array.

Download Original Figure

위의 식에서 a(θ)는 steering 벡터라고 정의하고, r=[r₁,r₂,···,r_M]^T는 안테나의 정수 위치 벡터이다. α는 파장 단위로 표현된 안테나의 간격을 의미한다. 또한, steering 벡터는 물체가 한 개인 경우를 의미하며 물체가 여러 개일 경우 다음과 같이 표현한다.

A (θ) = a θ 1, a θ 2, ⋯, a θ K

(2)

이 식을 steering 행렬이라고 정의하고 K는 신호의 개수를 의미한다. 여기서 신호의 개수를 알고 있다고 가정한다. 이에 따라 FMCW 레이다 신호는 다음과 같이 정의할 수 있다.

y = A (θ) s + w

(3)

y는 측정된 데이터에 대한 벡터, s는 각 안테나에 수신된 신호의 진폭 벡터이고, w은 각 안테나에 수신된 신호에 추가된 N(0,σ²Ι)으로 정의되는 백색 잡음 벡터이다.

다음은 본 논문에서 제안한 각도 추정 기법의 기본 바탕인 RELAX와 DML을 기술한다. RELAX는 FFT를 사용해 신호의 각도와 진폭을 추정하는 각도 추정 기법이다. 또한, 반복을 통해 bias 오차를 줄여 정확도를 높이는 것이 가능하다. RELAX의 기본 설명은 다음과 같다. 반복의 이전 단계에서 추정된 각도와 진폭을 사용하여 k번째 신호의 새로운 각도 추정을 위해 자신을 제외한 나머지 신호를 제거한 y_k를 구한다. k번째 신호의 각도를 $θ k^$ 라고 할 경우, 다음과 같은 식을 정의할 수 있다.

y k = y − ∑ j = 1, j ≠ k K a θ j^s k^

(4)

이후, $y k^$ 에 FFT를 적용해 각도를 추정할 수 있다.

θ k^= arg max a H θ k y k 2

(5)

그리고 $S k^$ 는 최대 우도 추정(maximum likelihood)을 통해, 다음과 같이 추정할 수 있다.

s^k = a H θ k^y k M

(6)

여기서 M은 안테나의 개수를 의미한다. 이를 신호의 개수만큼 반복한다면 모든 신호에 대한 각도 벡터 $θ^$ 를 추정할 수 있다. 이후 다음과 같은 에러 지수 F 를 구할 수 있다.

F = ‖ y − A (θ^) s^‖ 2

(7)

반복을 통해 F의 전후 차이가 0.001 이하가 된다면 반복을 종료하고 $θ^f i n a l$ 를 확정한다. RELAX의 연산 복잡도를 빅오 표기법으로 나타내면 O(QK[NlogN])으로 표현된다. Q는 F의 차이가 0.001 이하가 되기까지 반복되는 수, K는 신호의 개수, N은 제로 패딩(zero padding) 개수를 포함한 데이터의 개수이다. RELAX의 경우, FFT를 사용하기에 제로 패딩의 개수에 의해 유한한 간격이 정해지기 때문에 각도 정확도가 제한된다. CRB(cramer-rao bound)에 의해 높은 SNR 신호일수록 정확도가 높아지고, 제로 패딩의 개수 또한 높아져야 한다^[8],[9]. 따라서 다음과 같은 공식이 성립해야 한다.

1 8 α 2 π 2 ρ M V a r (r) ≥ 1 12 N 2 α 2

(8)

ρ는 신호의 SNR을 의미한다. 그리고 Var(r)는 다음과 같은 공식으로 계산된다.

V a r (r) = 1 M ∑ i = 1 N r i − μ 2

(9)

이 식에서 μ는 r_i의 평균을 의미한다. 이 수식에 의하면, 신호의 SNR에 따라 제로 패딩의 개수가 늘어나야 한다는 단점이 존재한다. 다음은 DML에 대해 설명한다. y를 가우시안 분포를 따른 y ~ CN(A[θ]s,σ²I)라는 확률 분포로 표현할 수 있다. 이에 따라 측정 데이터에 대해 likelihood를 구하면 다음과 같다.

L θ, s, σ 2 = 1 π σ 2 M exp − (y − A (θ) s) H (y − A (θ) s) σ 2

(10)

이 공식에서 L(θ,s,σ²)가 최대가 되는 θ를 구하는 것이 DML의 목적이다. θ가 deterministic하다는 가정하에 해를 최적화하는 공식은 다음과 같이 나타낼 수 있다.

∂ (y − A (θ) s) H (y − A (θ) s) ∂ s = 0

(11)

위의 공식을 통해 최적의 $s^(θ)$ 를 찾는다면 다음과 같은 수식을 얻을 수 있다.

θ^D M L = arg min t r I − A A H A − 1 A H y y H

(12)

이 식을 그리드 서치(grid search) 방법을 통해 최솟값을 찾아낼 수 있다. 또한, 빅오 표기법으로 나타낼 경우, O(M³P^K)라고 표현할 수 있다. P는 그리드 서치의 간격 개수를 나타낸다. DML은 높은 각도 정확도를 가지는 장점이 있지만 연산 속도가 느리다는 단점이 존재한다.

Ⅲ. R-DML 각도 추정 기법

기존의 각도 추정 기법은 여러 장점이 있지만 한계 또한 존재한다. RELAX의 경우 FFT를 기반한 각도 추정 기법이기에 제로 패딩의 개수에 따라 각도 정확도의 제한이 생긴다는 단점이 존재한다. DML의 경우, 그리드 서치를 사용해 각도를 추정한다면 높은 연산 시간을 수반한다는 단점이 존재한다. 이러한 단점을 극복하기 위해 기존의 각도 추정 기법을 변형하고 결합한 R-DML 각도 추정 기법을 제안한다. R-DML은 기존의 RELAX 알고리즘이 가진 단점인 제로 패딩에 대한 의존도를 줄일 수 있다는 장점이 있다. 그리고 DML 알고리즘의 단점인 연산 속도를 NMM을 사용해 단축할 수 있다.

R-DML을 사용하기 이전, 물체의 개수를 추정하는 기법이 필요하다. 따라서 $∥ y − ∑ k = 1 K y k ∥$ 을 FFT를 사용한 값에서 최댓값이 일정한 레벨을 넘지 못한다면 반복을 종료하고 물체의 개수를 K 개로 추정하는 방식으로 물체의 개수를 추정한다^[10].

그림 2는 R-DML의 순서도를 나타낸다. 첫 번째는 y를 입력으로 RELAX를 사용해 각도 추정한다. 기존의 RELAX는 FFT의 제로 패딩의 개수를 식 (8)에서 계산되는 N 보다 높은 값으로 설정해야 한다. 하지만 R-DML 알고리즘에서 제로 패딩의 개수는 N 보다 작은 개수로 설정할 수 있다. 그 이유는 RELAX 알고리즘을 사용하는 목적은 coarse 추정이기 때문이다. 각도 정확도가 낮더라도 대략적인 각도 추정을 통해 해를 구하고 DML 알고리즘의 초기값으로 설정해 fine 추정을 하기 위한 이유이다.

그림 2. | Fig. 2. R-DML 각도 추정 기법 순서도 | Flow chart of R-DML angle estimation techniques.

Download Original Figure

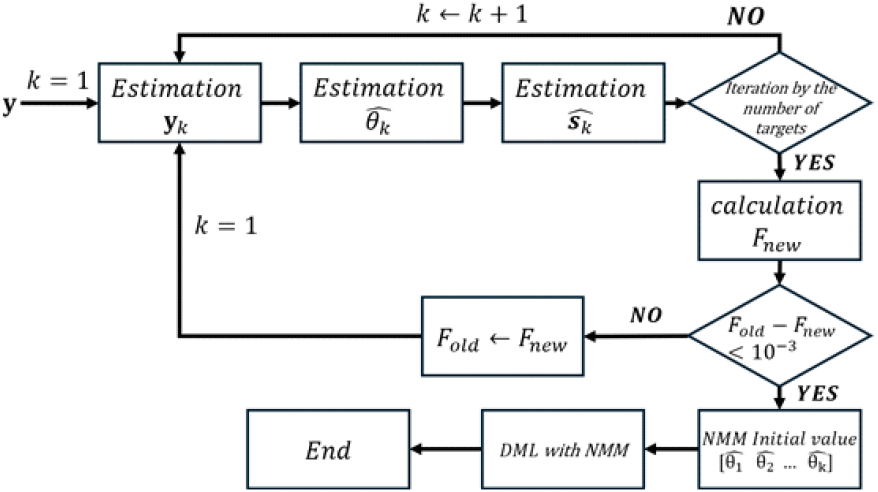
RELAX를 사용해 각도를 추정한 이후, NMM의 초기값으로 설정해 DML 알고리즘을 수행한다. NMM은 다차원 함수의 최댓값과 최솟값의 해를 구하는 방법이다. NMM을 사용하면 미분을 구할 필요가 없기 때문에 그리드 서치 방식보다 연산 시간이 짧다는 장점이 있다^[11].

또한, NMM이 수행되는 과정에서 연산 속도를 낮추기 위해 추정 범위 제한 방법을 적용한다. 추정 범위 제한 방법은 NMM의 모든 해가 다음과 같은 범위를 갖도록 제한하도록 설정하는 방식이다.

− δ 2 < Δ θ ⌢ k < δ 2, k = 1, 2, ⋯, K

(13)

$θ k^$ 는 k번째 초기값을 의미한다. δ는 제로 패딩으로 정해진 간격을 의미한다. NMM으로 구한 해가 식 (13)의 최솟값보다 작다면 최솟값으로 설정하고, 최댓값보다 크다면 최댓값으로 변경한다. 이와 같은 방식으로 각도 정확도를 높일 수 있다. 최종적으로 NMM을 사용한 DML으로 fine 추정을 하게 된다. 마지막으로 DML으로 추정한 각도를 최종 각도로 확정한다. R-DML 알고리즘의 빅오 표기법은 O(QK[NlogN]+HM³)이다. H는 NMM의 반복 수이다. 이 경우, R-DML은 RELAX 알고리즘과 비교해 N 의 개수를 낮추고, NMM을 사용해 연산 시간을 줄일 수 있다.

Ⅳ. W-대역 FMCW 레이다 시스템

본 논문의 검증에 사용한 W-대역 FMCW 레이다 시스템은 송신 1 채널 수신 16 채널로 구성되어 있다^[12]. 1채널 송신 칩과 4채널 수신 칩은 28 nm CMOS 공정으로 제작되었다. 1 채널 송신 칩은 97 GHz 기준, 출력 전력은 13 dBm이고, 4채널 수신 칩은 97 GHz 기준, 33 dB의 변환 이득을 가지고 있다.

본 논문에서는 SIW(substrate integrated waveguide) 안테나를 설계해 제작되었으며 그림 3은 안테나의 전면과 후면이다. 칩과 직접 급전을 통해 급전 손실을 최소화하였다. 송신 안테나의 경우, 안테나의 이득은 97 GHz 기준, 15.5 dBi이고 수신 안테나의 이득은 97 GHz 기준, 8.7 dBi이다. 수신 안테나 16 채널은 thinned 배열로 구성되어 있으며 동일한 수신 칩을 기준으로 각 안테나의 간격은 1.3 mm로 설계되었으며 97 GHz 기준, 0.61 λ의 간격으로 설계되었다.

그림 3. | Fig. 3. SIW 송수신 안테나 및 수신 안테나 배열 | Photographs of SIW Tx, Rx antennas and array.

Download Original Figure

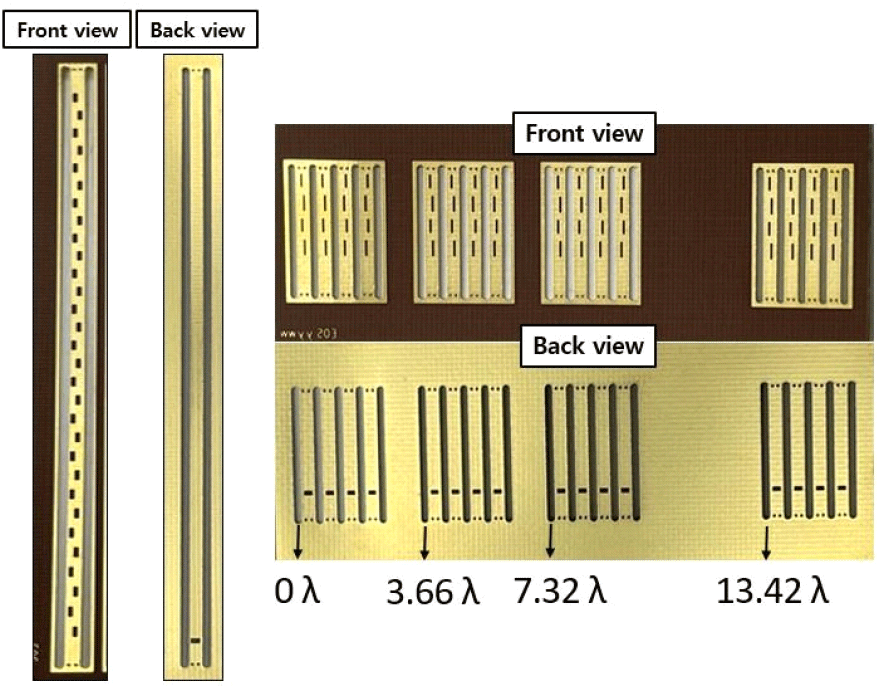
수신 안테나의 배열의 경우 유전 알고리즘을 통해 방위각 3 dB 빔폭 3.02°, SLL 8.024 dB로 최적화하였다. 각각의 수신 칩은 첫 번째 수신 칩의 위치를 0 λ라고 할 경우, 나머지 수신 칩은 3.66 λ, 7.32 λ, 13.42 λ에 위치한다.

그림 4은 W-대역 FMCW 레이다 시스템의 구조도를 나타낸 그림이다. 레이다 시스템의 하드웨어는 총 3개의 영역으로 나뉜다. PLL 보드는 송수신에 필요한 chirp 신호를 만들어내는 역할을 한다. 본 논문에서는 96.5~98.5 GHz의 2 GHz의 대역폭의 1 ms의 길이를 가지는 톱니파 chirp을 사용한다.

그림 4. | Fig. 4. W-대역 FMCW 레이다 시스템 구조도 | W-Band FMCW Radar system block diagram.

Download Original Figure

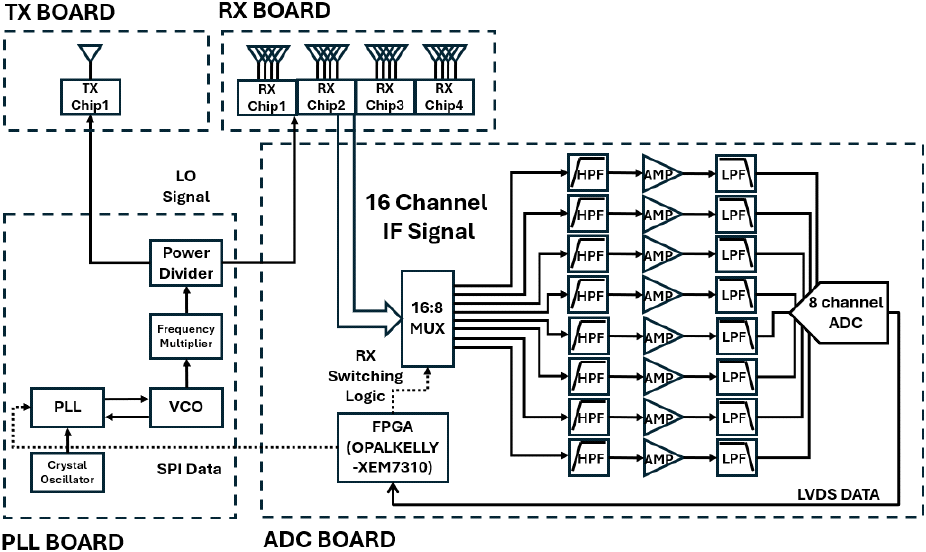
VCO와 PLL에서 2.01~2.05 GHz의 대역폭을 가진 chirp을 생성한 이후, frequency multiplier를 사용해 4.02~4.10 GHz의 신호로 만든다. 최종적으로 PLL 보드에서 생성된 chirp은 power divider를 사용해 송수신 칩에 전달된다.

송신 보드와 수신 보드는 각각 1채널 송신 칩과 송신 안테나, 4채널 수신 칩과 수신 안테나로 이루어져 있으며 PLL 보드에서 전달된 chirp 신호를 받아 송수신한다. 이후, 수신 보드에서 생성된 IF(intermediate frequency) 신호를 ADC 보드로 전달한다. ADC 보드는 수신 보드에서 생성한 IF 신호를 ADC를 통해 디지털 신호로 변환한 이후, FPGA로 전달하는 역할을 한다. 16 채널의 IF 신호는 multiplexer를 구성해 한 개의 chirp의 간격으로 8 채널 ADC로 데이터를 받을 수 있도록 하였다. 이후, 시간에 의한 위상 차이는 신호처리를 통해 보정하였다. 그림 5는 레이다 모듈의 정면 및 측면 사진이다. 최종 모듈의 크기는 92×130×87 mm이다.

그림 5. | Fig. 5. W-대역 FMCW 레이다의 정면 및 측면 사진 | Front view and side view of the entire module.

Download Original Figure

Ⅴ. 시뮬레이션 및 측정 결과 분석

R-DML 각도 추정 기법의 각도 정확도와 연산 시간을 검증하기 위해 몬테카를로 방법으로 시뮬레이션을 진행하였다. 시뮬레이션의 파라미터 설정은 다음과 같다. 방위각 기준, −2.1495°에 위치하고 진폭을 1로 설정한 물체 1과 방위각 2.6681°에 위치하고, 진폭을 0.7로 설정한 물체 2에 대한 신호를 생성하였다. R-DML에서 사용하는 RELAX의 제로 패딩의 개수는 240개를 사용했으며, 이는 SNR 20 dB 기준으로 식 (8)보다 적은 수이다. 이후, 식 (13)을 통해 추정 범위 제한 방법을 적용했으며, NMM은 매트랩의 fminsearch 함수를 사용하였다. 비교를 위해 사용된 각도 추정 기법은 FFT, RELAX, DML이다. FFT의 제로 패딩 개수는 1,024개로 설정했으며 findpeaks 함수를 사용해 물체의 각도를 추정하였다. RELAX의 제로 패딩 개수는 R-DML과 동일한 240개로 설정하였다. DML의 경우, R-DML과 동일한 fminsearch 함수를 사용해 구현하였다. 몬테카를로 방법은 총 10,000번을 수행했으며 신호의 SNR에 따른 RMSE 결과는 그림 6와 같다.

그림 6. | Fig. 6. 각도 추정 기법의 RMSE 비교 시뮬레이션 결과 | RMSE comparison simulation results of angle estimation techniques.

Download Original Figure

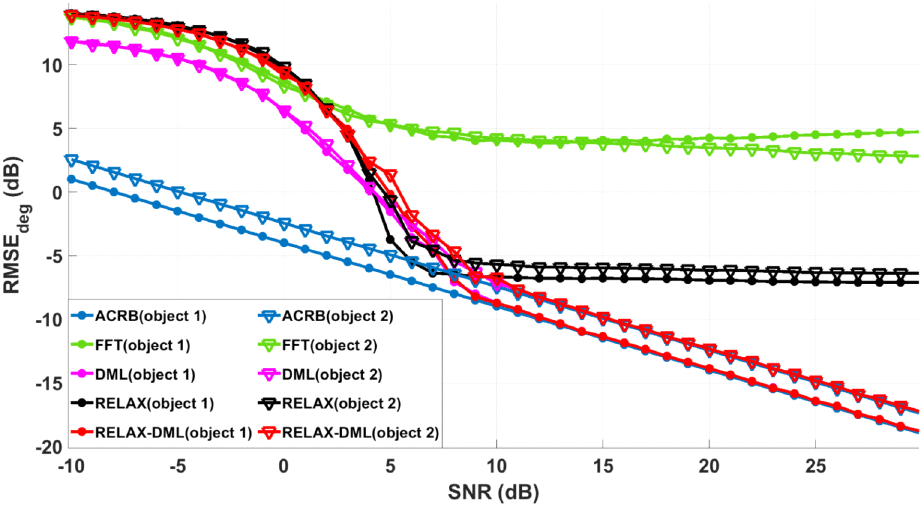
시뮬레이션 결과, 물체 1의 20 dB 신호를 기준으로 FFT의 RMSE는 4.254 dB, RELAX의 RMSE는 −6.950 dB, R-DML과 DML의 RMSE는 −13.863 dB로 측정된다. 따라서, R-DML은 RELAX와 비교해 RMSE가 6.913 dB만큼 개선된 수치를 확인할 수 있었다. ACRB(asymptotic cramar-rao bound)와 비교해도 R-DML은 거의 차이가 없음을 확인하였다. 다만, SNR 5 dB 이하에서는 RELAX로 구한 해의 오차로 인해 추정 범위 제한 방식의 범위에 실제 각도에 벗어나 추정이 부정확해지는 한계를 확인하였다. 물체 1의 SNR 5 dB 신호를 기준으로 R-DML과 DML의 RMSE는 0.9508 dB 만큼 차이를 보였다. 이는 RELAX를 사용한 각도 추정의 결과가 bias를 가져 부정확한 값을 추정하기 때문이라 사료된다.

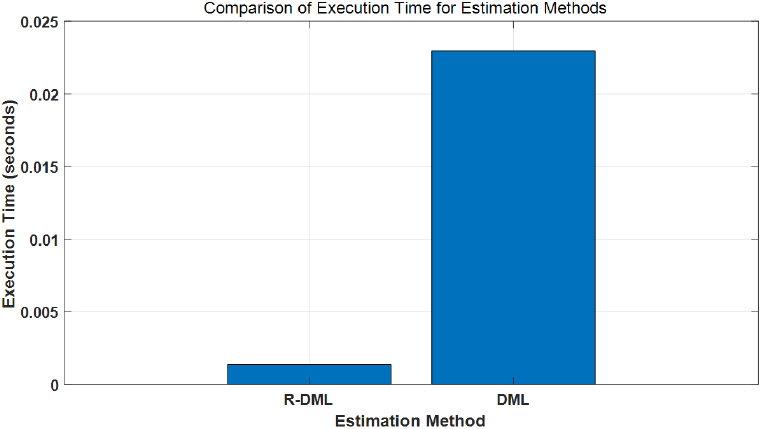
그림 7은 R-DML과 DML의 연산 시간 비교를 위한 막대그래프이다. 시뮬레이션 결과, R-DML의 연산 시간은 1.367 ms가 나왔으며 DML의 경우, 22.971 ms로 측정되었다. 이를 통해 R-DML은 DML보다 대략 16.8 %의 연산 시간으로 동일한 정확도를 가질 수 있음을 확인하였다.

그림 7. | Fig. 7. R-DML과 DML의 연산 시간 비교 시뮬레이션 결과 | Simulation results of R-DML and DML computational time comparison.

Download Original Figure

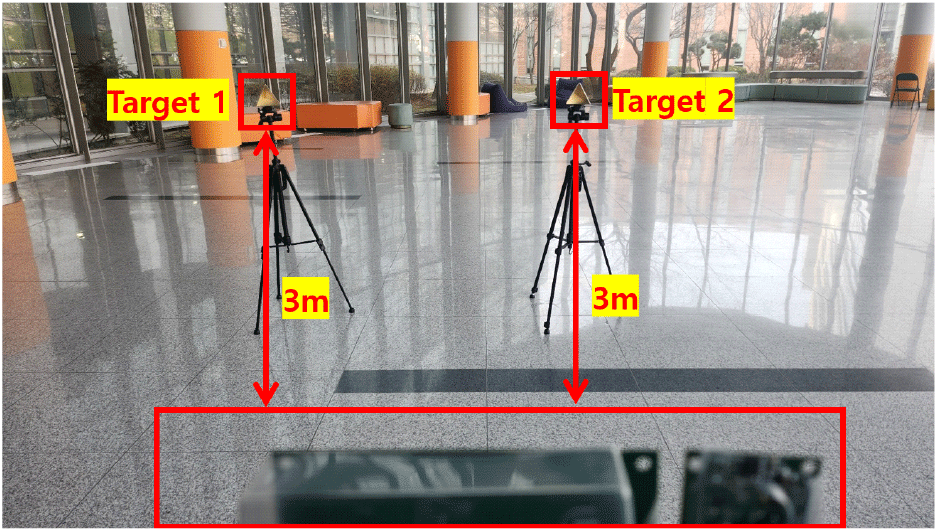
다음은 R-DML의 각도 해상도와 표적 탐지 성능을 검증하기 위해 W-대역 FMCW 레이다를 사용해 측정한 결과이다. 측정 표적으로는 동일한 RCS를 가진 두 개의 코너 반사경을 사용하였다. 그리고 레이더와의 거리는 두 개의 타겟 모두 3 m로 동일하다. 측정 결과에 대해 R-DML의 물체 개수 추정 성능을 검증했으며 각도 해상도의 성능은 FFT와 R-DML을 각각 적용해 비교하는 방식으로 성능을 검증하였다. FFT와 비교한 각도 해상도 성능을 비교하였다. 측정은 총 두 번 진행했으며 첫 번째 측정은 두 개의 코너 반사경 간 거리가 비교적 멀리 떨어진 환경에서 진행하였다. 그림 8은 첫 번째 측정 환경이다.

그림 8. | Fig. 8. 첫 번째 측정 환경 | First measurement environment.

Download Original Figure

그림 9는 FFT와 R-DML을 사용한 방위각 측정 그래프이다. FFT와 매트랩 함수 findpeaks를 사용해 각도 추정한 결과, 표적 1의 방위각은 −9.125°로, 표적 2의 방위각은 3.978°로 추정되었다. R-DML의 경우 표적의 개수를 2개임을 추정하고 표적 1의 방위각은 −9.162°, 표적 2의 방위각은 4.033°로 추정하였다. 이로써 두 방법 모두 각도 정확도 면에서 비슷한 성능을 보임을 확인하였다.

그림 9. | Fig. 9. 물체 두 개의 신호 방위각 첫 번째 측정 결과 | The first measurement result of the first measurement result.

Download Original Figure

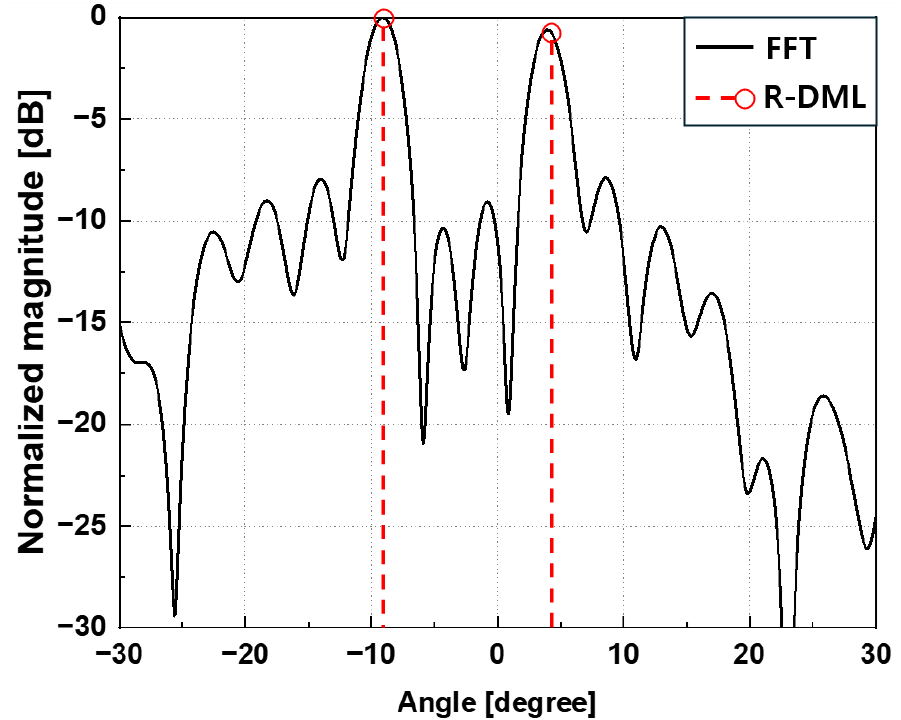
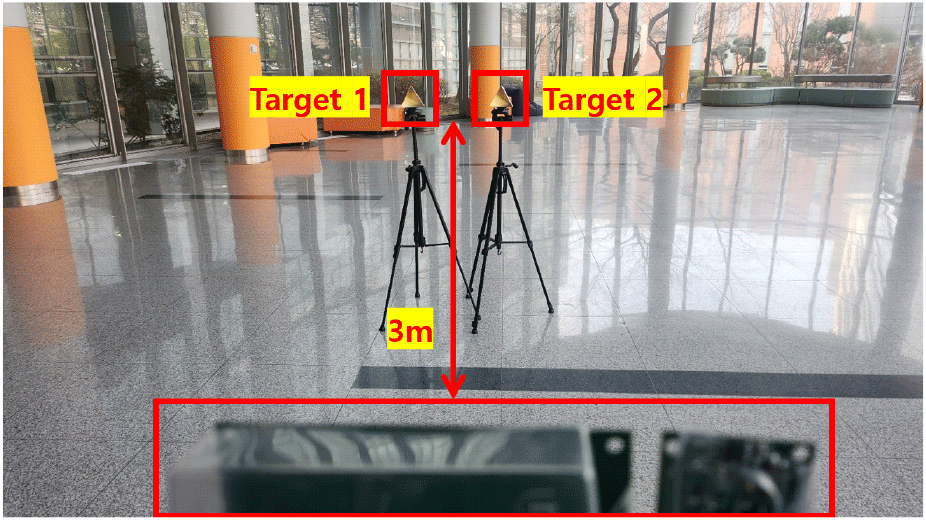
다음으로는 각도 해상도 비교를 위한 실험을 진행하였다. 그림 10은 두 번째 측정 환경으로 두 개의 코너 반사경의 거리가 비교적 가까운 경우이다.

그림 10. | Fig. 10. 두 번째 측정 환경 | Second measurement environment.

Download Original Figure

그림 11은 FFT와 R-DML을 사용한 방위각 측정 그래프이다. 측정 결과, FFT의 피크 서치 방식으로는 두 개 표적의 메인 빔을 구분할 수 없었다. 하지만 R-DML의 경우, 표적의 개수가 2개임을 추정한 이후, 표적 1의 방위각은 −3.013°, 표적 2는 1.039°로 두 물체가 뚜렷이 구별됨을 확인하였다. 이를 통해 FFT와 비교해 R-DML 방식이 높은 각도 해상도를 보임을 확인하였다.

그림 11. | Fig. 11. 물체 두 개의 신호 방위각 두 번째 측정 결과 | Second measurement of the azimuth of two objects.

Download Original Figure

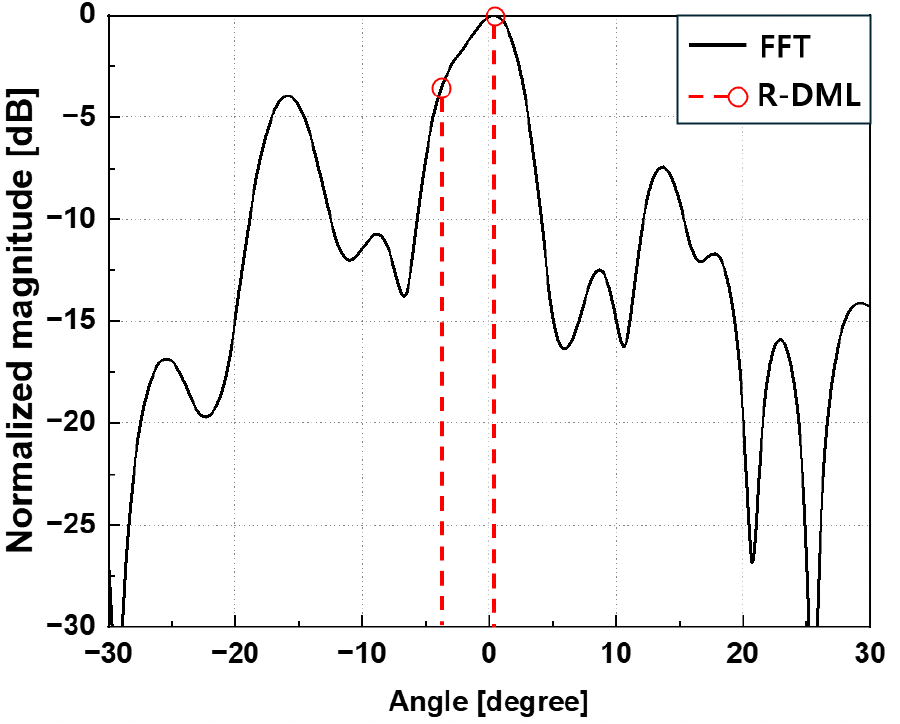
Ⅵ. 결 론

본 논문은 높은 각도 해상도와 정확도, 낮은 연산 시간을 목적으로 하는 R-DML을 제안하였다. 해당 각도 추정 기법은 몬테카를로 시뮬레이션을 통해 다른 각도 추정 기법과 비교해 높은 정확도와 빠른 연산 시간을 확인하였다. 또한, W-대역 FMCW 레이다를 사용해 FFT와 비교해 높은 각도 해상도와 물체 개수 판별이 가능함을 검증하였다. 더불어 낮은 SNR의 신호에 대해 정확도를 높이기 위한 추가 연구가 필요함을 확인하였다. 해당 각도 추정 기법이 고해상도 레이다 및 이미징 레이다의 물체 탐지 알고리즘에 적용된다면 높은 업데이트 속도와 더불어 물체 탐지 성능 향상에 기여할 것으로 기대된다.

Acknowledgements

이 논문은 산업통상자원부 ‘산업혁신인재성장지원사업’의 재원으로 한국산업기술진흥원(KIAT)의 지원을 받아 수행된 연구임(2024년 반도체특성화대 학원지원사업(성균관대학교), 과제번호: P0023704).

References

[1].

B. Gao, F. Zhang, G. Sun, and S. Pan, “High-resolution 3D imaging with a photonics-based broadband MIMO radar,” in 2021 International Conference on Microwave and Millimeter Wave Technology(ICMMT), Nanjing, May 2021.

[2].

F. Rutz, R. Rasshofer, and E. Biebl, “Radar cross section analysis for road debris in automotive FMCW radar,” in 2024 IEEE International Conference on Microwaves, Communications, Antennas, Biomedical Engineering and Electronic Systems(COMCAS), Tel Aviv, Jul. 2024. pp. 143-146.

[3].

D. Schwarz, T. Grebner, and C. Waldschmidt, “Imaging performance of 79 GHz MIMO radars: High-resolution 4D snapshots, grid maps, and SAR,” in 2023 20th European Radar Conference(EuRAD), Berlin, Sep. 2023, pp. 254-257.

[4].

H. Iqbal, A. Löffler, M. N. Mejdoub, and F. Gruson “Realistic SAR implementation for automotive applications,” in 2020 17th European Radar Conference(EuRAD), Utrecht, Jan. 2021, pp. 306-309.

[5].

L. Ren, D. Wu, “Resolution enhancement for forward-looking imaging of airborne multichannel radar via space-time reiterative superresolution,” IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, vol. 17, pp. 15288-15300, Aug. 2024.

[6].

J. Li, D. Zheng, and P. Stoica, “Angle and waveform estimation via RELAX,” IEEE Transactions on Aerospace and Electronic Systems, vol. 33, no. 3, pp. 1077-1087, Jul. 1997.

[7].

S. Theodoridis, R. Chellappa, M. Viberg, and A. Zoubir, Academic Press Library in Signal Processing Volume 3: Array and Statistical Signal Processing, 1st ed. New York, NY, Academic Press, 2013.

[8].

E. Aboutanios, A. Hassanien, M. G. Amin, and A. M. Zoubir, “Fast iterative interpolated beamforming for accurate single-snapshot DOA estimation,” IEEE Geoscience and Remote Sensing Letters, vol. 14, no. 4, pp. 574-578, Apr. 2017.

[9].

O. Lange, B. Yang, “Antenna geometry optimization for 2D direction-of-arrival estimation for radar imaging,” in Proceedings of the 2011 International ITG Workshop on Smart Antennas, Aachen, Feb. 2011, pp. 1-8.

[10].

T. Yu, E. Kim, J. H. Park, B. S. Kim, and S. Nam, “W-band co-prime array FMCW MIMO radar with IPCE algorithm for high-angular resolution,” IEEE Access, vol. 11, pp. 109899-109910, Oct. 2023.

[11].

J. C. Lagarias, J. A. Reeds, M. H. Wright, and P. E. Wright, “Convergence properties of the Nelder--Mead simplex method in low dimensions,” SIAM Journal on Optimization, vol. 9, no. 1, pp. 112-147, Dec. 1998.

[12].

Y. J. Han, S. W. Kang, J. B. Yoon, D. Y. Yang, H. H. Choi, and J. W. Lee, et al., “A W-band thinned array FMCW radar system,” The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 35, no. 9, pp. 754-761, Sep. 2024.