논문/REGULAR PAPERS
메쉬 반사판 안테나의 전자기적 시뮬레이션 분석을 위한 유효 손실 도체 표면 도출
황민수
,
임창현
,
서원구*
,
박슬기*
,
김기훈*
,
박성균*
,
추호성†
Effective Lossy Conducting Surface for Electromagnetic Simulation Analyses of Mesh Reflector Antennas for Satellite Application
Minsu Hwang
,
Changhyeon Im
,
Wongu Seo*
,
Seulgi Park*
,
Kihun Kim*
,
Sungkyun Park*
,
Hosung Choo†
Author Information & Copyright ▼
Department of Electronic and Electrical Engineering, Hongik University
*Hanwha Systems Company Ltd.
© Copyright 2025 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received: Jul 22, 2024; Revised: Aug 22, 2024; Accepted: Feb 28, 2025
Published Online: Apr 30, 2025
요 약
본 논문에서는 신호 정보 수집(SIGINT) 위성 탑재용 메쉬 반사판 안테나의 효율적인 전자기적 시뮬레이션 분석을 위한 유효 손실 도체 표면(ELCS, effective lossy conducting surface)을 제안한다. 복잡한 구조를 갖는 메쉬를 간단한 ELCS로 변환하기 위해 메쉬 형상을 평면 패치 형상으로 근사 모델링하여 유닛셀을 설계하고 무한 주기 구조 시뮬레이션 환경에서 반사도를 확인하였다. 주파수별 반사도를 확인하고 ELCS의 전도도를 변화시키며 각 표본 주파수에서 메쉬와 동일한 반사도를 가지는 전도도를 도출하였다. ELCS의 성능 검증을 위해 측정된 실제 메쉬의 반사도와 비교한 결과 평균 오차 0.4 % 이내로 잘 일치하는 것을 확인하였으며, 금속 포물형 반사판 안테나와 ELCS를 적용한 전개형 반사판 안테나의 방사 패턴을 비교한 결과 전면 방향 이득이 각각 36.6 dBi 와 34.2 dBi로 나타나는 것을 확인하였다.
Abstract
In this paper, we propose an effective lossy conducting surface (ELCS) for the efficient analysis of mesh reflector antennas for signal intelligence (SIGINT) satellite applications. To convert the complex real mesh structure into a simple ELCS, a unit cell was designed by modeling the mesh as a surface patch. Subsequently, the reflectivity was examined in an infinite periodic structure simulation environment. The conductivity with the same reflectivity as that of the mesh was derived at each sample frequency by varying the conductivity of the ELCS, and the reflectivity of the actual mesh was compared with that of the proposed ELCS. The results showed good agreement with an average error of less than 0.4 %. The radiation patterns of a metallic parabolic reflector antenna was then compared with those of a deployable reflector antenna with the ELCS, revealing bore-sight gains of 36.6 dBi and 34.2 dBi, respectively.
Keywords: Mesh Reflector Antenna; Deployable Reflector Antenna; Mesh Equivalent Model; Non-linear Regression
I. 서 론
최근 우주 산업이 발전하면서 인공위성을 활용한 통신, 방송, 감시, 정찰과 같은 다양한 위성 전파 기술에 관심을 받고 있다. 위성 전파 기술을 활용하기 위해서는 위성과 지상 간 전파 송수신이 원활하게 이루어져야 하는데, 높은 위성 운용 고도(수백 km~수만 km)로 인해 경로 손실이 발생한다. 또한 대기 중의 수증기 및 먼지 등으로 인해 전파 흡수 및 산란이 발생하여 추가적인 전파 손실이 발생한다. 이러한 전파 손실을 극복하기 위해 위성에서는 고이득 특성을 갖는 반사판 안테나를 주로 사용한다[1]~[5]. 일반적으로 반사판 안테나는 직경을 크게하여 사용함으로써 더 높은 이득 특성을 가질 수 있지만, 그에 따라 부피가 커지고 무게 또한 증가한다. 이로인해 위성을 운용 궤도까지 운반하기 위해 제한된 발사체 공간에 탑재할 때 어려움이 있다. 이를 극복하기 위해서 탑재 형상의 부피 및 무게를 줄일 수 있는 전개형 메쉬 반사판 안테나가 많이 사용된다[6]~[8]. 전개형 메쉬 반사판 안테나는 고정형 금속 반사판 안테나와 달리 특정 형상을 갖지 않는 전도성 메쉬를 반사판으로 활용하기 때문에 반사판 형상을 유지하기 위해 리브, 관절, 당김줄과 같은 형상 유지 장치를 사용한다. 이와 같은 형상 유지 장치에 메쉬를 고정하면 유지 장치 간 메쉬를 서로 다른 방향으로 당기는 힘이 발생하고, 그 결과 반사판 표면에 평평한 면이 발생한다. 따라서 형상 유지 장치를 많이 사용할수록 평평한 면의 면적이 작아지면서 이상적인 반사판의 곡면과 유사한 형상을 형성하고, 적게 사용하면 평평한 면의 면적이 커져서 이상적인 곡면 형상과 멀어지게된다. 형상 유지 장치를 많이 사용할수록 반사판 안테나의 성능은 개선되지만, 기계적 복잡성이 증가하고 전개 오차를 발생시킬 확률이 증가한다는 단점이 있다. 이는 반사판 제작 비용을 증가시키고, 우주에서 운용된다는 점을 고려했을 때 전개 오차 보정을 어렵게 한다. 이러한 이유로 전개형 메쉬 반사판 안테나 설계 시 성능 열화를 최소화하면서 형상 유지 장치의 적정 개수 및 위치를 도출하기 위해서, 메쉬 반사판 안테나의 전자기적 시뮬레이션을 통한 성능 분석이 필요하다[9],[10]. 이를 위해 메쉬 반사판 모델링을 진행해야하지만, 반사판 직경(수 m~수백 m)대비 메쉬 유닛셀의 크기(수백 μm)가 매우 작기 때문에, 실제 메쉬 짜임새 구조와 동일하게 모델링하면 성능 분석 시간 증가와 컴퓨팅 리소스의 부족으로 해석에 어려움이 있다. 이러한 문제점을 해결하기 위해 복잡한 메쉬 형상을 보다 간단한 형상의 등가 모델로 변환하고 무한 주기 구조 환경을 이용하여 반사도를 분석하는 방법에 대한 연구들[11]~[13]이 진행되었다. 이러한 방법들을 활용해 메쉬 반사도 및 소형 메쉬 반사판 성능 분석은 가능하지만, 대형 반사판 또는 높은 주파수 조건에서 성능을 분석할 때 앞에서 언급한 문제가 동일하게 발생한다. 따라서 반사판의 크기와 주파수 대역에 대한 제약이 적으면서 메쉬 반사판 안테나 성능을 분석할 수 있는 방법에 대한 추가적인 연구가 반드시 필요한 실정이다.
본 논문에서는 신호 정보 수집(SIGINT) 위성 탑재용 전개형 메쉬 반사판 안테나의 전자기적 시뮬레이션 분석을 위해 메쉬와 동일한 반사도를 갖는 유효 손실 도체 표면(ELCS, effective lossy conducting surface)을 제안한다. 복잡한 구조를 갖는 메쉬 반사판 표면을 단순한 도체 표면인 ELCS로 변환하기 위해, 먼저 직조 구조의 금속 와이어 메쉬를 보다 단순한 평면형 금속 stripline으로 등가 모델링하였다. 간략화된 등가 모델의 유닛셀을 설계하고 무한 주기 구조 환경에서 반사도를 확인하였다. 이때 메쉬의 제직 밀도 단위인 OPI(openings per inch)가 고정되어 있는 경우 주파수별로 서로 다른 반사도를 갖기 때문에 먼저 일정 간격의 표본 주파수를 선정하여 주파수별 반사도를 관찰하였다. 다음으로 ELCS에 활용할 평면 도체의 전도도를 변화시키면서, 앞서 등가 스트립 모델과 동일한 반사도를 갖는 전도도를 주파수별로 도출하였다. 선정된 특정 주파수뿐만 아니라 다양한 주파수에서 ELCS를 활용하기 위해 주파수와 전도도의 관계를 비선형 회귀모델을 활용하여 수식화하였다. 이렇게 도출 ELCS의 성능 검증을 위해서 실제 메쉬의 반사도를 측정하고 ELCS의 반사도와 비교하였다. 평균 오차를 계산한 결과 0.4 % 이내로 매우 잘 일치하는 것을 확인하였으며, ELCS를 활용하면 복잡한 형상을 갖는 메쉬 반사판의 시뮬레이션 분석을 보다 효율적이고 정확하게 수행할 수 있음을 확인하였다.
Ⅱ. ELCS 도출 및 메쉬 측정
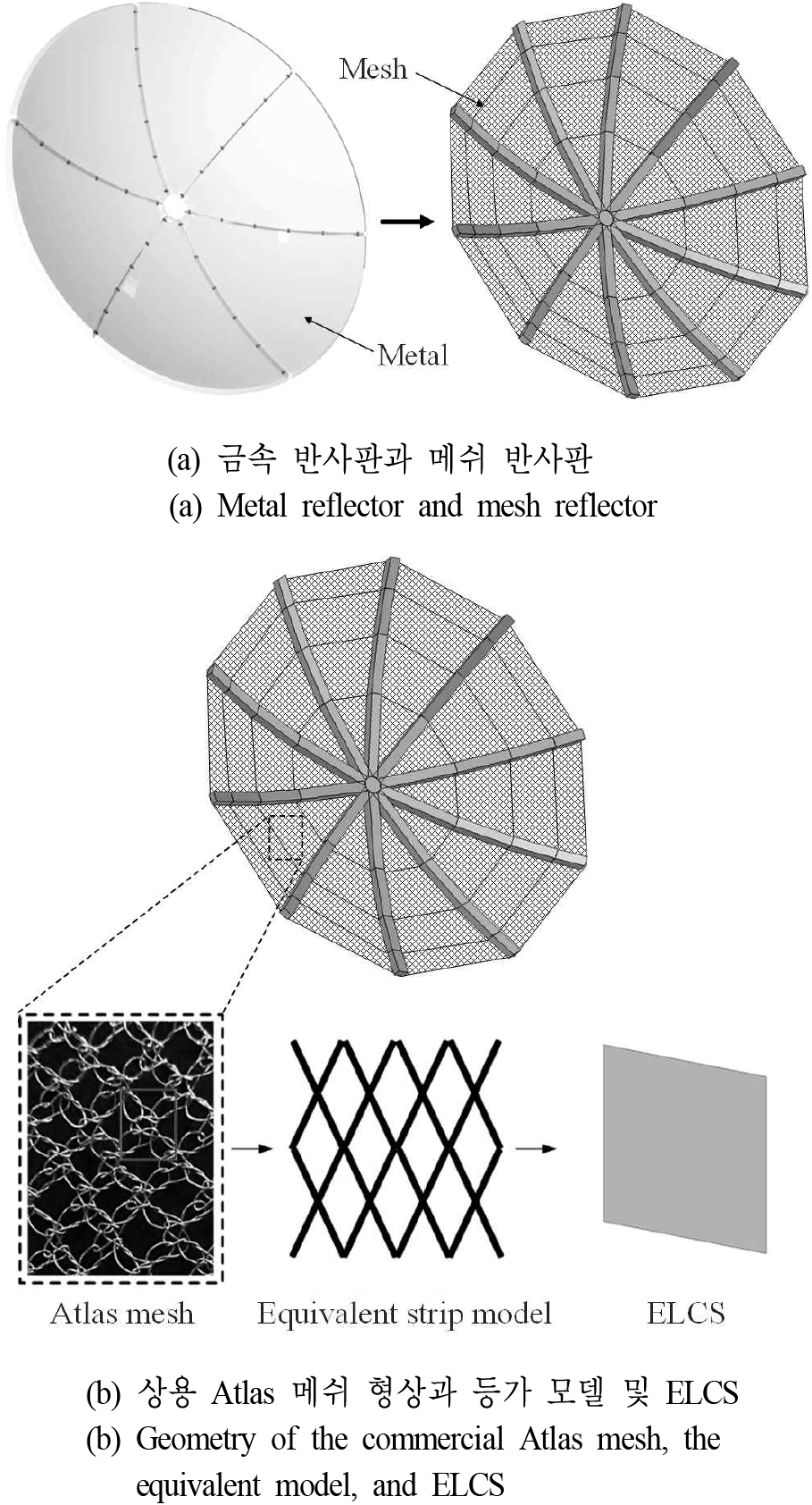
그림 1에서는 메쉬 반사판의 형상과 ELCS 도출 과정을 보여준다. 그림 1(a)는 금속 반사판과 메쉬 반사판의 예시를 보여주며, 일반적인 금속 반사판 안테나는 직경이 클수록 더 높은 이득 특성을 가질 수 있지만 그에 따라 부피가 커지고 무게 또한 크게 증가한다. 이러한 금속 반사판을 운용 궤도까지 운반하기 위해 발사체에 탑재 시 큰 부피와 무게 등으로 인해 제약이 있기 때문에 위성 탑재용 반사판으로는 적합하지 않다. 따라서 우주에서 사용되는 SIGINT용 대형 반사판은 기존 금속 반사판을 형태 변형이 자유롭고 무게가 가벼운 메쉬 반사판으로 대체하여 사용되고 있다. 그림 1(b)에서 볼 수 있듯이 실제 메쉬 형상은 복잡한 그물망 형상을 가지고 있다. 이러한 복잡한 구조를 가진 메쉬 반사판의 전자기 해석을 위해서는 반사판 형상을 보다 간단한 등가 모델로 대체하는 것이 필요하다. 먼저 복잡한 그물망 구조의 금속 와이서 메쉬를 보다 단순한 평면형 금속 stripline으로 근사 모델링하였다. 다음으로 반복되는 형상을 유닛셀로 선정하여 무한 주기 구조 시뮬레이션 환경에서 메쉬의 반사도를 확인했다. 이때, 입사되는 전파가 무한 주기 구조 내 모든 유닛셀에 균일하게 분포하도록 평면파를 입사파로 설정했다. 메쉬의 OPI가 고정되어 있는 경우 주파수 별로 서로 다른 반사도를 가지기 때문에 일정 간격의 주파수를 선정하여주파수별 반사도를 확인하였다. 다음으로 평면 도체의 전도도를 변화시키면서, 등가 스트립 모델과 동일한 반사도를 갖는 전도도를 주파수별로 도출하였다. 이 과정에서 복잡한 메쉬 반사판을 동일한 반사도를 가지는 도체 표면으로 대체하였으며, 이를 ELCS로 명명하였다. 제안된 ELCS는 메쉬 반사판과 넓은 대역에서 동일한 반사도를 가지도록 주파수별로 다른 전도도가 적용되었다. 표 1은 메쉬의 OPI가 20일 때 동일한 반사도를 가지는 ELCS의 전도도를 주파수별로 나타내었고, 실제 도체(금, 은, 구리)의 반사도 및 전도도와 상대적 비교를 위해 해당 도체들의 특성을 함께 기재하였다.
그림 1. | Fig. 1.
메쉬 반사판의 형상과 메쉬 등가 모델 및 ELCS | Geometry of the mesh reflector, mesh equivalent model, and ELCS.
Download Original Figure
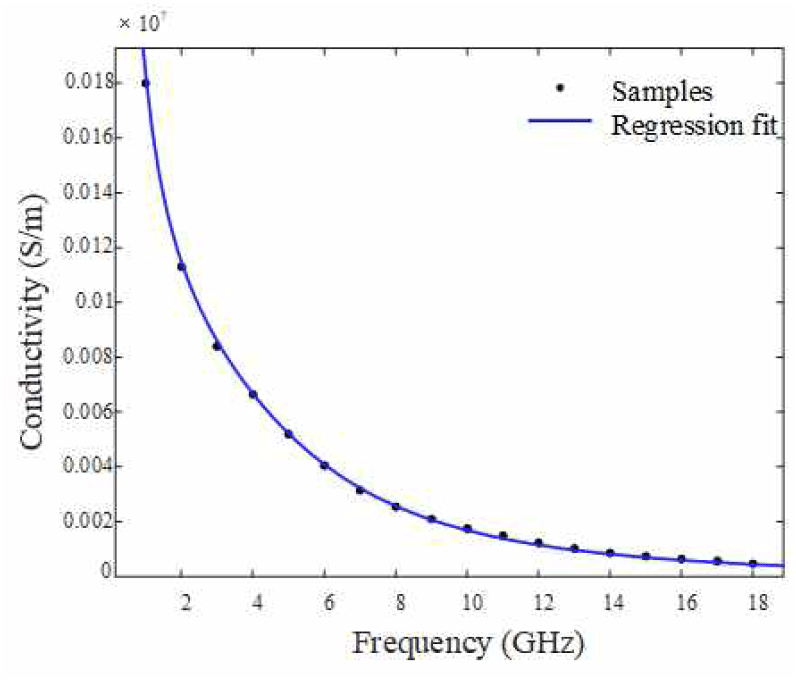
그림 2는 주파수에 따라 변화하는 메쉬와 동일한 반사도를 가지는 ELCS 전도도의 비선형 회귀분석을 나타냈다. 표 1에서 볼 수 있듯이 각 표본 주파수에서 메쉬와 동일한 반사도를 가지도록 ELCS의 전도도를 도출하였으며, 도출된 표본 값들을 그래프 상에 점으로 표시하였다. 선정된 표본 주파수뿐만 아니라 다양한 주파수에서 ELCS를 활용하기 위해 주파수와 ELCS의 전도도 관계를 비선형 회귀모델을 활용하여 수식화하였다. 이때 사용된 회귀 모델 함수는 도출된 전도도 표본값들의 추세에 가장 적합한 두 항의 지수 함수로 설정하였으며, 이를 통해 도출된 수식을 식 (1)에 나타내었다.
표 1. | Table 1.
메쉬와 동일한 반사도를 가지는 ELCS 전도도 | Conductivity of ELCS with the same reflectivity as the mesh.
| Material |
Frequency (GHz) |
Reflectivity (%) |
Conductivity (S/m) |
| ELCS |
1 |
99.9 |
0.018 × 107 |
| 2 |
99.8 |
0.006 × 107 |
| 3 |
99.6 |
0.0022 × 107 |
| 4 |
99.5 |
0.0015 × 107 |
| 5 |
99.3 |
0.0011 × 107 |
| 6 |
99.1 |
0.0009 × 107 |
| 7 |
98.9 |
0.0007 × 107 |
| 8 |
98.7 |
0.0005 × 107 |
| 9 |
98.4 |
0.0004 × 107 |
| 10 |
98.1 |
0.00035 × 107 |
| 11 |
97.8 |
0.0003 × 107 |
| 12 |
97.5 |
0.00026 × 107 |
| 13 |
97.1 |
0.0002 × 107 |
| 14 |
96.7 |
0.00016 × 107 |
| 15 |
96.3 |
0.0001 × 107 |
| 16 |
95.9 |
0.000094 × 107 |
| 17 |
95.4 |
0.00009 × 107 |
| 18 |
94.9 |
0.00008 × 107 |
| Gold |
DC~18 |
≥ 99.98 |
4.10 × 107 |
| Silver |
DC~18 |
≥ 99.98 |
6.30 × 107 |
| Copper |
DC~18 |
≥ 99.98 |
5.96 × 107 |
Download Excel Table
여기서 독립변수 x는 주파수를 의미하며 단위는 GHz이고, C(x)는 전도도를 의미한다. 위의 수식에 분석하고자 하는 운용 주파수를 대입하여 전도도를 도출하고, 그 값을 도체 표면의 전도도 값으로 활용하면 실제 메쉬의 반사도와 유사하며 형상이 간단한 등가 모델이 완성된다.
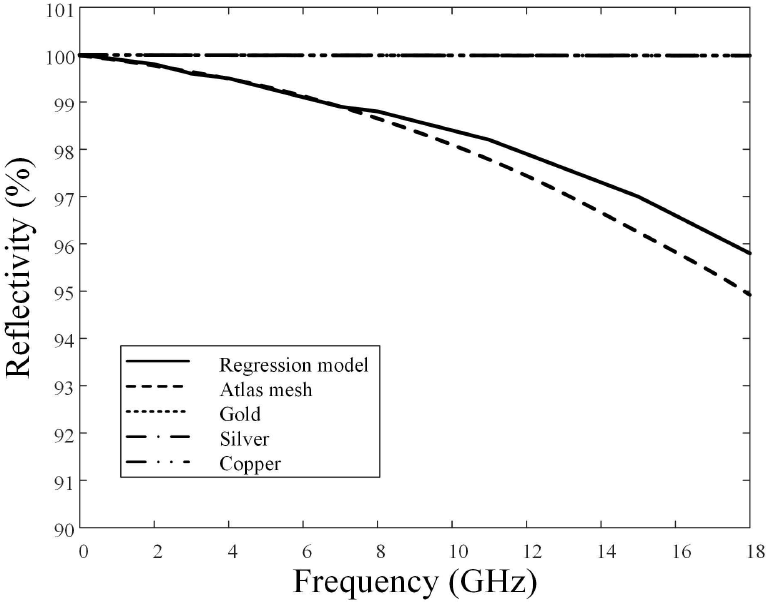
그림 3은 비선형 회귀분석을 통해 수식화된 전도도를 적용하여 도출된 ELCS의 반사도와 주기적 경계조건 시뮬레이션으로 도출된 메쉬의 반사도를 비교하여 나타내었다. 정확한 비교를 위해 무한 주기 구조를 활용한 금, 은, 구리판의 반사도를 분석했고, 그림과 같이 금, 은, 구리판의 반사도는 주파수에 상관없이 100 %에 인접한 반사도를 갖는 것을 확인했다. 모든 주파수 대역에서 회귀 분석을 통해 도출한 ELCS의 반사도와 실제 Atlas 메쉬 구조의 반사도 평균 오차를 계산한 결과 0.1 % 이내로 매우 유사함을 확인하였다.
그림 3. | Fig. 3.
회귀분석을 적용한 ELCS의 반사도와 무한 주기 구조 시뮬레이션으로 도출된 Atlas 메쉬의 반사도 | Reflectivity of the ELCS using a regression model and the reflectivity simulation of the periodic Atlas mesh structure.
Download Original Figure
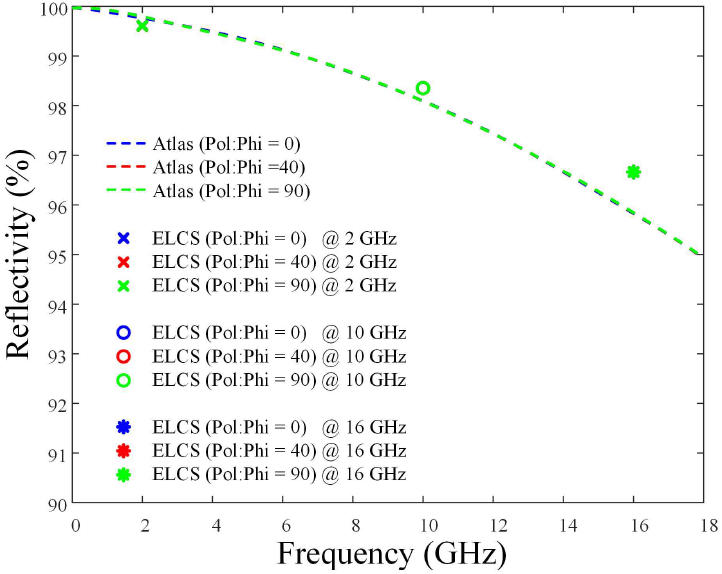
그림 4는 실제 atlas mesh의 짜임 패턴에 따라 입사파의 편파에 따른 atlas mesh와 ELCS의 반사도 특성을 분석하기 위해, 입사되는 편파를 0도에서 90도까지 변화하면서 반사도를 확인했다. 그림에서 확인할 수 있듯이 무한 주기 구조를 이용한 atlas mesh에 입사파의 편파(0도, 40도, 90도)를 변경하면서 반사도를 확인했을 때 편차에 관계없이 동일한 반사 특성이 나타나는 것을 확인했고, 제안하는 유효 손실 도체(ELCS)에서도 편파에 관계없이 동일한 반사도가 나타나는 것을 확인했다.
그림 4. | Fig. 4.
입사파의 편파에 따른 Atlas mesh와 ELCS의 반사도 | Reflectivity of Altlas mesh and ELCS according to incident wave polarization.
Download Original Figure
추가적으로 시뮬레이션 분석을 통해 얻은 결과들을 검증하기 위해 은도금 테플론으로 제작된 메쉬의 반사도를측정하였으며 측정을 위한 셋업은 그림 5와 같이 구성하였다. 고지향성 특성을 갖는 두 개의 렌즈 혼 안테나를 활용하여, 메쉬가 차지하는 면적을 제외한 외부로 방사되는 전파를 줄여 회절 성분을 최소화했다. 이러한 특성을 갖는 두 개의 혼 안테나를 서로 마주 보도록 배치하고, 두 안테나 사이에 측정하고자 하는 메쉬를 위치시킨 후 네트워크 분석기를 이용하여 반사계수 값을 측정했다. 메쉬의 반사도(|R|)는 메쉬와 금속 도체를 위치시켜 반사계수()를 측정하고 자유공간인 경우의 반사계수()를 측정한 후 식 (2)에 적용하여 계산한다. 하지만 이렇게 측정된 반사도는 여전히 측정 환경에 의한 불필요한 다중반사의 영향을 포함하고 있어 타임게이팅을 통해 필터링할 필요가 있다. 주파수 영역에서 측정된 신호를 역푸리에 변환을 통해 시간 영역에서 게이트 함수를 이용하여 불필요한 신호를 제거한다. 이는 특정 시료의 물성을 분석하기 위해 일반적으로 사용하는 비접촉식 측정 방법으로, 메쉬의 반사도를 측정할 때 통상적으로 활용하는 방법 중 하나이다[14]. 이렇게 각 시료들에서 측정된 반사계수 값들을 모두 타임게이팅을 진행한 후 식 (2)에 적용하여 최종적인 메쉬의 반사도를 구할 수 있다.
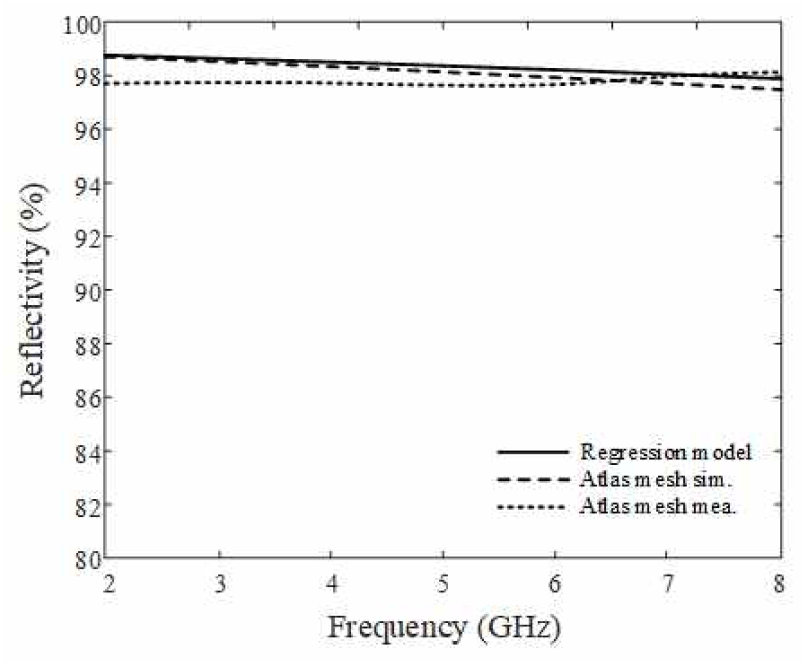
그림 6은 측정된 은도금 테플론 메쉬의 반사도를 나타낸다. 주기적 경계조건 시뮬레이션을 통해 도출된 메쉬의 반사도와 회귀분석을 통해 도출된 ELCS의 반사도와 비교하였다. ELCS의 반사도와 측정을 통해 얻은 상용 메쉬의 반사도를 비교했을 때 X 대역에서 반사도 차이는 평균 0.4 %로 나타나는 것을 확인하였다. 따라서 제안된 ELCS의 반사도와 실제 측정된 메쉬의 반사도가 잘 일치하는 것을 확인하였다.
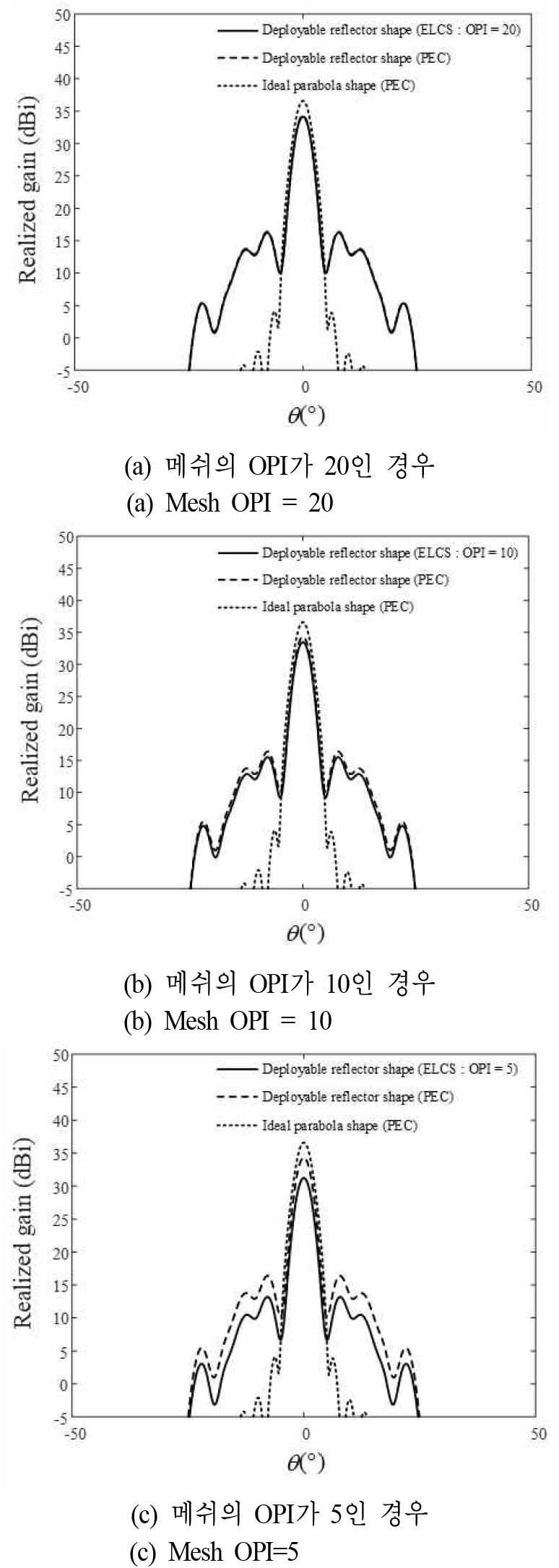
그림 7은 ELCS를 적용한 전개형 반사판 안테나의 시뮬레이션 방사 패턴(10 GHz)을 나타낸다. ELCS의 성능 유효성을 검증하기 위해 직경 1 m의 전개형 반사판을 설계하고, 메쉬 OPI(20, 10, 5)에 따른 서로 다른 세 가지 ELCS를 반사판에 안테나에 적용하여 패턴을 도출하였다. 다음으로 이와 동일한 전개형 반사판 표면에 PEC를적용한 경우와 이상적인 포물형 금속 반사판 안테나의 패턴을 도출하여 서로 다른 ELCS를 적용한 반사판 안테나의 패턴과 비교하였다. 그림 7(a)는 메쉬의 OPI가 20일 때의 ELCS가 적용된 전개형 반사판 안테나의 방사 패턴을 나타낸다. PEC를 적용한 전개형 반사판 안테나의 전면 방향 이득은 34.3 dBi로 이상적인 포물형 금속 반사판 안테나의 전면 방향 이득인 36.6 dBi 대비 2.3 dB 감소하였으며 ELCS가 적용된 전개형 반사판 안테나의 전면 방향 이득은 34.2 dBi로 PEC를 적용한 전개형 반사판 안테나의 전면 방향 이득 대비 0.1 dB 감소한 결과를 나타낸다. 그림 7(b)는 메쉬의 OPI가 10일 때의 ELCS가 적용된 전개형 반사판 안테나의 방사 패턴을 나타내며 전면 방향 이득은 33.3 dBi로 PEC가 적용된 전개형 반사판 안테나의 전면 방향 이득 대비 0.9 dB 감소한 결과를 나타낸다. 그림 7(c)에서는 메쉬의 OPI가 5인 경우의 ELCS가 적용된 전개형 반사판 안테나의 방사 패턴을 나타내며 PEC가 적용된 전개형 반사판 안테나 대비 3.1 dB 감소한 31.2 dBi의 전면 방향 이득을 확인하였다. 이러한 메쉬의 OPI에 따른 전면 방향 이득 차이는 OPI에 따라 반사도가 각각 98.1 %(−0.15 dB), 91.2 %(−0.8 dB), 70 %(−3.1 dB)로 감소하기 때문에 발생하는 것임을 확인하였다. 이를 통해 반사판 표면 형상 및 메쉬 특성에 따라 반사판 안테나의 이득 및 패턴 형상이 변하는 것을 확인하였다. 따라서 전개형 메쉬 반사판 설계 시 정확한 안테나 성능을 분석하기 위해 EM 시뮬레이션 분석을 진행하는 것이 필수적이고, ELCS를 활용하면 효율적으로 진행할 수 있다는 것을 확인하였다.
그림 7. | Fig. 7.
ELCS를 적용한 반사판 안테나의 시뮬레이션 방 사 패턴(10 GHz) | Radiation patterns of the mesh reflector antenna using ELCS at 10 GHz.
Download Original Figure
Ⅲ. 결론
본 논문에서는 신호 정보 수집(SIGINT) 위성 탑재용 전개형 메쉬 반사판 안테나의 효율적인 전자기적 시뮬레이션 분석을 위한 유효 손실 도체 표면(ELCS)을 제안하였다. 복잡한 메쉬 구조를 간단한 ELCS로 변환하여 주파수별 반사도를 확인하고, 이를 비선형 회귀모델을 통해 수식화하였다. ELCS와 실제 측정된 메쉬의 반사도와 비교한 결과 평균 오차 0.4 % 이내로 잘 일치함을 확인하였으며, ELCS를 적용한 전개형 전면 방향 반사판 안테나의 전면 방향 이득은 메쉬의 OPI가 20일때 34.2 dBi로 나타났다. 이를 통해 ELCS를 활용하여 복잡한 메쉬 반사판 시뮬레이션을 효율적으로 수행할 수 있음을 검증하였다.
Acknowledgements
이 논문은 2022년도 한화시스템(주)의 재원을 지원 받아 수행된 연구임.
References
N. Chahat, R. E. Hodges, J. Sauder, M. Thomson, E. Peral, and Y. Rahmat-Samii, “CubeSat deployable Ka-band mesh reflector antenna development for Earth science missions,”
IEEE Transactions on Antennas and Propagation, vol. 64, no. 5, pp. 2083-2093, Jun. 2016.


J. Wan, S. Lu, X. D. Wang, and Y. Q. Ai, “A steerable spot beam reflector antenna for geostationary satellites,”
IEEE Antennas and Wireless Propagation Letters, vol. 15, pp. 89-92, May 2015.


L. Jensen, R. Sekora, and N. Schröder, “Advanced reflector antennas for geostationary spacecraft,”
IETE Technical Review, vol. 16, no. 1, pp. 19-25, 1999.


J. H. Lim, J. W. Lee, and T. K. Lee, “Cross-pol pattern effects of parabolic reflector antennas on the performance of spaceborne quad-pol SAR systems,”
Journal of Electromagnetic Engineering and Science, vol. 21, no. 3, pp. 218-227, Jul. 2021.


S. A. Lee, S. J. Jo, S. J. Kim, T. K. Lee, and J. W. Lee, “Analysis of cross-polarized field by panel misalignment errors in a deployable reflector antenna,”
Journal of Electromagnetic Engineering and Science, vol. 23, no. 1, pp. 18-26, Jan. 2023.


Y. Rahmat-Samii, J. Wang, J. Zamora, G. Freebury, R. E. Hodges, and S. J. Horst, “A 7 m×1.5 m aperture parabolic cylinder deployable mesh reflector antenna for next-generation satellite synthetic aperture radar,”
IEEE Transactions on Antennas and Propagation, vol. 71, no. 8, pp. 6378-6389, Aug. 2023.


F. Zheng, M. Chen, “New conceptual structure design for affordable space large deployable antenna,”
IEEE Transactions on Antennas and Propagation, vol. 63, no. 4, pp. 1351-1358, Apr. 2015.


N. Chahat, J. Sauder, M. Mitchell, N. Beidleman, and G. Freebury, “One-meter deployable mesh reflector for deep-space network telecommunication at X-band and Ka-band,”
IEEE Transactions on Antennas and Propagation, vol. 68, no. 2, pp. 727-735, Feb. 2020.


C. Im, W. Seo, S. Park, K. Kim, S. Park, and H. Choo, “Design of a deployable broadband mesh reflector antenna for a SIGINT satellite system considering surface shape deformation,”
Sensors, vol. 24, no. 2, p. 384, Jan. 2024.




S. J. Jo, J. Y. Lee, S. S. Yoon, T. K. Lee, and J. W. Lee, “Panel misalignment effects on the radiation pattern from a solid surface deployable antenna,” Journal of Electromagnetic Engineering and Science, vol. 19, no. 4, pp. 253-258, Oct. 2019.


A. Miura, Y. Rahmat-Samii, “Spaceborne mesh reflector antennas with complex weaves: Extended PO/periodic-MoM analysis,”
IEEE Transactions on Antennas and Propagation, vol. 55, no. 4, pp. 1022-1029, Apr. 2007.


H. Rajagopalan, A. Miura, and Y. Rahmat-Samii, “Equivalent strip width for cylindrical wire for mesh reflector antennas: Experiments, waveguide, and plane-wave simulations,”
IEEE Transactions on Antennas and Propagation, vol. 54, no. 10, pp. 2845-2853, Oct. 2006.


T. Li, J. Su, “Electrical properties analysis of wire mesh for mesh reflectors,”
Acta Astronautica, vol. 69, no. 1-2, pp. 109-117, Jul.-Aug. 2011.


H. Ujihara, T. Bushimata. “Measurement of the antenna mesh: Characteeristics for VSOP-2/ASTRO-G,”
Approaching Micro-Arcsecond Resolution with VSOP-2: Astrophysics and Technologies ASP Conference Series, vol. 402, p. 66, Dec. 2007.