Integrated Compressive Sensing and Autofocus for SAR Imaging

Jo, Chanhee; Byeon, Jeong-Il; Lee, Wookyung; Choi, Jihoon

doi:10.5515/KJKIEES.2025.36.12.1224

J. Korean Inst. Electromagn. Eng. Sci. 2025; 36(12):1224-1236

pISSN: 1226-3133, eISSN: 2288-226X

DOI: https://doi.org/10.5515/KJKIEES.2025.36.12.1224

논문/REGULAR PAPERS

SAR 영상 형성을 위한 압축센싱과 자동초점 결합 기법

조찬희

, 변정일^*

, 이우경

, 최지훈^†

Integrated Compressive Sensing and Autofocus for SAR Imaging

Chanhee Jo

, Jeong-Il Byeon^*

, Wookyung Lee

, Jihoon Choi^†

Author Information & Copyright ▼

^{한국항공대학교 항공전자정보공학부}

^*LIG넥스원 레이다연구소 3팀

^{School of Electronics and Information Engineering, Korea Aerospace University}

^*Radar Research Institute Team 3, LIG Nex1

^†Corresponding Author: Jihoon Choi (e-mail: jihoon@kau.ac.kr)

© Copyright 2025 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Oct 17, 2025; Revised: Oct 27, 2025; Accepted: Nov 03, 2025

Published Online: Dec 31, 2025

요 약

고해상도 SAR(syhthetic aperture radar) 영상 획득을 위해서는 큰 대역폭과 저장 용량이 필요하며, 항공기나 무인기를 플랫폼으로 사용하는 경우 기체의 요동으로 인해 영상 품질 저하가 발생할 수 있다. 이를 해결하기 위해 압축센싱으로 SAR 원시 데이터 용량을 줄이고, 압축센싱 복원과 자동초점 기법의 결합을 통해 SAR 영상을 형성하는 방안을 새롭게 제안한다. 압축센싱 복원을 위해 거리-도플러 알고리즘에 기반한 수정 저 랭크 희소 분해 기법을 도입하고, 요동보상 후 잔여 위상에 의한 영상 품질 저하를 완화하기 위해 자동초점 알고리즘을 적용한다. SAR 모델링 데이터를 이용해서 압축센싱 복원 기법과 결합된 자동초점 알고리즘의 수렴 특성을 확인하고, 복원된 영상의 품질을 비교한다. 이를 통해 제안된 기법에 사용되는 자동초점 알고리즘을 선정한다. 차량 탑재 SAR 실측 데이터에 제안된 기법을 적용하여 원시 데이터의 일부만을 이용해서 SAR 영상을 복원과 자동초점 동작을 수행한다. 이를 통해 제안된 기법으로 복원한 SAR 영상의 품질이 기존 기법으로 획득한 영상에 비해 우수함을 보인다.

Abstract

High-resolution synthetic aperture radar (SAR) imaging requires large bandwidth and storage capacity, and trajectory errors caused by the motion of airborne or unmanned aerial vehicle platforms can degrade image quality. To address these challenges, compressive sensing (CS) is introduced to reduce the SAR raw data volume, and a novel method is proposed for SAR image formation that combines CS-based recovery with an autofocus technique. For CS-based reconstruction, a modified low-rank and sparse decomposition (MLRSD) scheme is employed based on the range-Doppler algorithm, and an autofocus algorithm is subsequently applied to mitigate image quality degradation caused by residual phase errors after motion compensation. Through simulations using SAR modeling data, we present the convergence characteristics of several autofocus algorithms combined with the MLRSD-based reconstruction technique. The quality of the recovered SAR images was compared, and the best autofocus algorithm was selected for the proposed method. Finally, the proposed method was applied to real vehicular SAR measurement data to perform SAR image reconstruction and autofocus operations using only a part of the raw data. The experimental results demonstrate that the SAR image reconstructed using the proposed method exhibits superior quality compared with those obtained using conventional techniques.

Keywords: Synthetic Aperture Radar (SAR); Compressive Sensing; Autofocus; Modified Low-Rank and Sparse Decomposition

Ⅰ. 서 론

SAR(synthetic aperture radar)는 움직이는 플랫폼을 통해 표적 지역에 레이다 신호를 송신한 후 반사파를 이용하여 고해상도의 영상을 얻는다. 광학 영상과 비교하여 기상이나 환경적인 영향을 적게 받아 안정적으로 이미지를 얻을 수 있으므로 장기적인 지형 변화 관측, 지진, 화산, 홍수와 같은 재난 감시, 이동 표적 탐지 등 다양한 분야에 사용된다. 하지만 SAR 시스템이 고도화됨에 따라 영상의 해상도가 높아지고 표적 영역 범위가 넓어지는 추세이며, 이로 인해 관측 데이터 저장 용량이 증가하는 문제가 발생한다. 이를 완화하기 위한 방안으로 압축센싱을 활용하는 연구가 진행되고 있다^[1]. 압축센싱은 특정 영역에서 신호의 희소성을 활용하여 압축된 데이터로부터 원래 신호를 복원하는 알고리즘으로 관측된 원시 데이터의 용량을 줄이면서 복원 신호의 손실을 최소화할 수 있다^[2]~[3]. 압축센싱 이론에 기반한 신호 복원을 위해 l₁-norm 기반 최적화 기법을 사용하는 BPDN(basis pursuit denoising) 알고리즘^[4], 수신 신호와 센싱 벡터의 상관 관계를 이용하여 가장 지배적인 신호 성분을 반복적으로 찾는 OMP (orthogonal matching pursuit) 기법을 개발하였다^[5]. 그리고 그래프 이론을 이용하여 반복적인 임계 처리를 통해 원 신호를 복원하는 AMP(approximate message passing) 알고리즘이 제안되었다^[6].

압축센싱을 SAR 영상 압축에 적용하는 경우 표적 영역의 희소성에 따라 복원 영상의 품질에 편차가 발생한다. 이미지의 방향 정보를 효율적으로 표현하기 위한 방안으로 DCWT(dual-tree complex wavelet transform)가 개발되었고^[7], 이를 이용하여 SAR 영상을 블록 단위로 압축하고 복원하는 블록 압축센싱 기법이 제안되었다^[8]. 일반적으로 고해상도 SAR 영상은 희소성이 높지 않지만 전체 영상을 배경 영역과 표적 영역으로 분할해서 희소 신호로 표현할 수 있다. 이를 이용하여 2차원 압축된 신호에 LRSD(low-rank and sparse decomposition)^[9]와 MLRSD (modified lrsd)^[10] 등의 복원 알고리즘을 적용하여 SAR 영상을 생성하는 방안이 제안되었다. 두 알고리즘은 배경 영상에 대한 표현 방식에 차이가 있는데 LRSD에서는 특이값 분해를 통해 배경 영상을 희소 신호 성분으로 표현하고, MLRSD에서는 DCWT를 이용해서 희소 웨이블릿 계수로 표현한다. 또한, 두 방식 모두 강한 표적 영상은 이미지 영역에서 희소 신호로 표현한다.

최근 항공기와 무인기를 SAR 플랫폼으로 사용하는 연구가 활발히 진행되고 있다. 이러한 플랫폼에서 좋은 품질의 영상을 획득하기 위해서는 GPS(global positioning system)와 IMU(inertial measurement unit) 기반 요동보상과 자동초점 기법이 필요하다^[11],[12]. GPS-IMU를 이용하여 요동에 의해 발생하는 센서 이동 경로 오차를 1차적으로 보상하고, 잔여 위상 오차를 자동초점 기법으로 보정한다. 대표적인 자동초점 알고리즘으로 인접 대역 간의 위상 기울기를 추정하는 PGA(phase gradient autofocus)^[13], 엔트로피를 최소화하는 MEA(minimum entropy autofocus)^[14], 최소자승오차에 기반해서 유도된 FPA(feature preserving autofocus)^[15]가 사용된다.

압축센싱이 적용된 원시 데이터를 이용해서 SAR 영상을 복원하면서 자동초점 기법을 적용하는 경우 다음과 같은 문제가 발생할 수 있다. 첫째, 압축센싱은 특정 영역에서 데이터의 희소성을 활용하는데, 요동으로 인해 해당 영역의 희소성이 저하되면서 복원 품질이 저하된다. 둘째, 압축센싱 과정에서 불완전하게 복원된 이미지에 자동초점 기법을 적용하는 경우 위상 오차 추정 정확도 저하로 인해 영상의 복원 성능이 제한된다. 이러한 문제는 희소성이 낮은 이미지에 압축센싱 복원 기법 적용 시 더욱 두드러지게 나타나며 심각한 SAR 영상 품질 저하를 유발한다^[16].

이를 극복하기 위해 본 논문에서는 압축된 원시 데이터에 MLRSD 기반 압축센싱 복원 기법과 자동초점 알고리즘을 동시에 적용하여 SAR 영상을 형성하는 기법을 새롭게 제안한다. MLRSD는 DCWT 변환과 SPL(smoothed projected landweber) 임계처리를 통해 SAR 이미지의 배경 영역을 복원하고, 소프트 임계처리를 통해 표적 영역을 복원하므로 전체 SAR 영상의 희소성이 낮은 경우에도 복원 성능이 우수하다. 제안된 기법에서는 RDA(range Doppler algorithm)를 이용해서 이미지화 함수(imaging function)와 관측 함수(observation function)를 정의한다. 또한, 잔여 위상 오차 보상 함수와 부여 함수를 정의하고, 압축센싱 기반 영상 복원 시에는 잔여 위상 오차 보상 함수를 적용하며, 원시 데이터와 복원된 SAR 영상에 대응되는 원시 데이터 추정값의 차이를 계산할 때는 잔여 위상 오차 부여 함수를 적용한다. 이를 통해 압축센싱 복원 알고리즘과 자동초점 알고리즘을 결합한다. 항공기 SAR 모델링 데이터에 제안된 기법과 자동초점을 위한 PGA, MEA, FPA 알고리즘을 각각 결합해서 적용하고, 모의실험을 통해 제안된 기법의 수렴 특성과 영상 품질을 비교한다. 또한, 제안된 압축센싱 기반 복원 기법을 차량 탑재 SAR 실측 데이터에 적용한다. 이를 통해 원시 데이터의 일부만을 이용해서 SAR 영상 복원이 가능하고, 자동초점 알고리즘과의 결합을 통해 기존 기법에 비해 SAR 영상의 품질이 향상됨을 보인다.

Ⅱ. 시스템 모델 및 기존 연구내용

2-1 시스템 모델

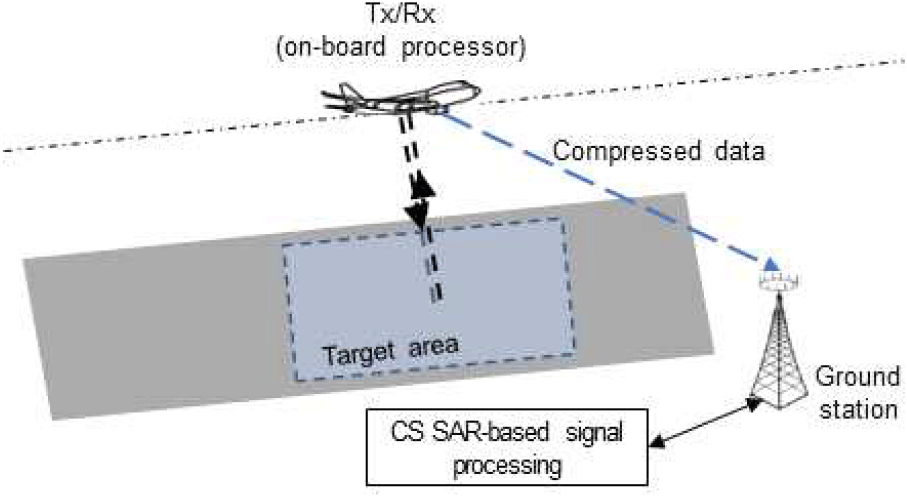
SAR 시스템은 위성, 항공기, 드론, 차량과 같은 다양한 플랫폼에 장착될 수 있다. 예를 들어 항공기를 이용해서 압축센싱 기반 모노스태틱 SAR 시스템을 구축하는 경우 그림 1과 같이 표현된다. 항공기 내에 레이다 송수신기를 부착하고 표적 지역을 일정 속도로 이동하며 주기적으로 LFM(linear frequency modulated) 펄스를 송신하고 반사 신호를 수신하여 저장한다. 표적의 방위 및 거리방향 픽셀 수를 각각 N_a와 N_r로 정의하면 표적 이미지는X∈ $X ∈ C N a × N r$ 로 표현된다. 또한, 관측 영역에 대한 2차원 좌표를 r =(x,y), 관측 지점 r에 대응되는 레이다 반사 단면적(RCS, radar cross section)을 σ(r)로 나타낸다. 이때 수신된 반사 신호를 방위 및 거리방향으로 샘플링한 신호를 식 (1)과 같이 표현할 수 있다.

Y (η, τ) = ∬ x, y σ (r) ϕ (η, τ; r) d x d y

(1)

그림 1. | Fig. 1. 압축센싱 기반 모노스태틱 SAR 시스템 | CS-based monostatic SAR system.

Download Original Figure

이때 $Y ∈ C L a × L r$ 는 반사 신호를 저장한 원시 데이터 행렬이고, L_a와 L_r은 각각 방위 및 거리방향 샘플 수를 나타내며, 신호에 대한 방위, 거리 샘플의 크기를 나타낸다. ϕ(η,τ;r)은 관측 지점 r에서 반사된 η번째 LFM 펄스, τ번째 거리방향 샘플링 신호를 의미하며 식 (2)와 같이 표현된다.

ϕ (η, τ; r) = ω r τ − 2 R (η; r) c w a η − η c × exp j 2 π f 0 τ − 2 R (η; r) c + j π K r τ − 2 R (η; r) c 2 + ψ (r)

(2)

여기서 w_a(·)와 w_r (·)은 방위 및 거리방향 윈도우 함수이고, R(η; r)은 방위 시간 η에서 플랫폼과 r지점 사이의 거리를 나타낸다. 또한, K_r은 거리방향 주파수 변조율, f₀는 중심 주파수, c는 빛의 속도, ψ(r)은 관측 지점 r에서 위상 변화, η_c는 빔 중앙을 지나가는 방위방향 시간을 의미한다. 이후 논문에서는 간결한 수식 표기를 위해 L_a=N_a, L_r=N_r을 가정한다.

스퀸트 각도가 크지 않을 때 RDA를 이용하여 SAR 데이터 Y를 통해 X를 얻는 이미지화 함수는 식 (3)과 같이 표현된다 ^[17].

X ≈ M (Y) = F a H {{P a ∘ C F a P r ∘ YF r F r H)

(3)

이때 $F a ∈ C N a × N a$ 와 $F r ∈ C N r × N r$ 은 각각 방위 및 거리방향 DFT(discrete fourier transform) 행렬이고, A ○ B는 행렬 A와 B의 아다마르 곱(Hadamard product)을 의미하며, C(·)는 RCMC(range cell migration correction)를 위한 보간함수를 나타낸다. $P a ∈ C N a × N r$ 와 $P r ∈ C N a × N r$ 은 방위 및 거리방향 주파수 영역 정합 필터로 식 (4)와 같이 주어진다.

P a f η, τ = exp − j π f η 2 K a, P r η, f τ = exp − j π f τ 2 K r

(4)

여기서 f_η는 도플러 주파수, f_τ는 거리방향 주파수이고, V_r이 센서의 이동 속도일 때 $K a = 2 f 0 V r 2 / c R 0$ 는 방위방향 주파수 변조율을 나타낸다. SAR 이미지 X에 대응되는 원시 데이터 행렬 Y는 식 (3)에서 정의한 이미지화 함수의 역함수로 계산할 수 있고, 식 (5)와 같이 관측 함수 G(·)로 정의한다 ^[17].

Y ≈ G (X) = {P r * ∘ F a H C − 1 P a * ∘ F a X F r) F r H

(5)

2-2 MLRSD 압축센싱 복원 기법

본 논문에서는 다양한 압축센싱 복원 알고리즘 중 이미지화 함수 M(·)과 관측 함수 G(·)를 사용하여 ITA(iterative thresholding algorithm)에 기반한 복원 기법을 고려한다^[18]. 우선 방위 및 거리방향 2차원 원시 데이터 압축 과정은 식 (6)과 같이 표현된다.

Y s = Θ a Y Θ r

(6)

이때 $Θ a ∈ R r a N a × N a, Θ r ∈ R N r × r r N r$ 은 각각 방위 및 거리방향 압축을 위한 랜덤 샘플링 행렬을 의미한다. X가 특정 영역에서 희소 신호로 표현 가능할 때, 압축센싱 이론을 이용해서 압축된 원시 데이터 Y_s로부터 SAR 이미지 X를 복원하는 문제는 식 (7)과 같이 정의할 수 있다.

min ‖ X ‖ 1, s . t . ‖ Y s − Θ a G (X) Θ r ‖ F < ϵ

(7)

이때 ∥·∥_F는 프로베니우스 놈(Frobenius norm)이고, ϵ은 허용 가능한 오차를 나타내는 0보다 큰 실수이다. MLRSD에서는 전체 SAR 영상을 식 (8)과 같이 배경 영상과 주요 표적 영상의 합으로 표현한다.

X = L + S

(8)

이때 배경 영상 $L ∈ C N × N r$ 은 웨이블릿 변환 영역에서 희소 계수로 나타낼 수 있고, 표적 영상 $S ∈ C N a × N r$ 는 이미지 영역에서 희소 행렬로 표현된다. 이와 같은 특성을 활용하여 식 (7)을 L과 S를 찾는 문제로 변형할 수 있다^[10].

L o, S o = arg min L,S ‖ Ψ (L) ‖ 1 + ‖ S ‖ 1 s . t . ‖ Y s − Θ a G (L + S) Θ r ‖ F < ϵ

(9)

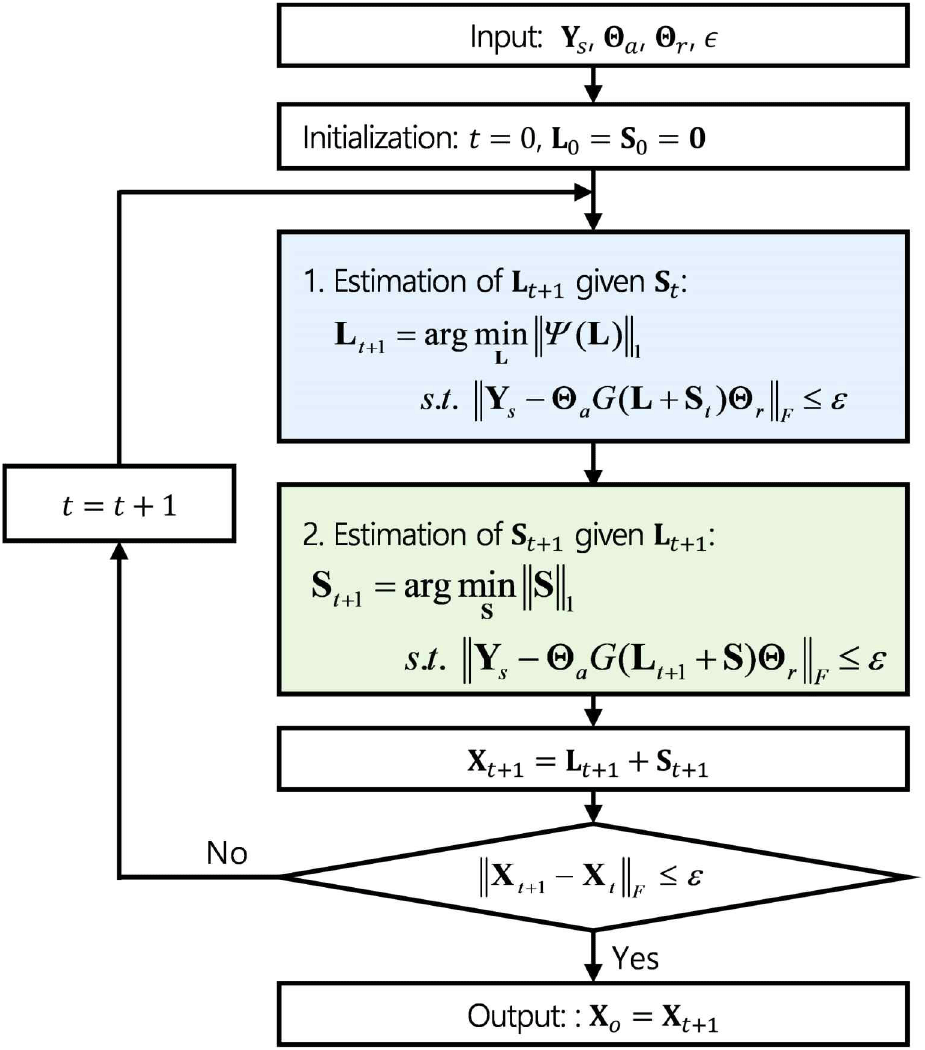
이때 Ψ(·)는 DCWT를 통해 얻어지는 복소 웨이블릿 계수 행렬을 의미한다. 행렬 S가 고정된 경우 원시 데이터 오차를 고려한 행렬 갱신과 웨이블릿 영역에서의 SPL 임계화 및 IDCWT(inverse DCWT)를 통해 배경 영상 L을 구할 수 있고, 행렬 L이 주어진 경우 원시 데이터 오차를 고려한 행렬 갱신과 소프트 임계화를 통해 주요 표적 행렬 S를 계산할 수 있다. 이와 같이 L과 S를 반복 갱신하는 방법으로 SAR 이미지 X를 복원할 수 있으며, 이 과정을 그림 2와 같이 나타낼 수 있다.

그림 2. | Fig. 2. MLRSD 기반 압축센싱 복원 기법 | CS reconstruction based on MLRSD.

Download Original Figure

MLRSD의 경우 배경 영상과 주요 표적 영상을 분리해서 복원할 때 요동에 의한 정합 성능 저하를 고려하지 않는다. 따라서 항공기 혹은 드론 SAR의 경우 기존 MLRSD 기법을 적용할 경우 희소성 저하로 인한 배경 영상과 표적 영상의 불완전한 분리, 표적 영상의 불완전한 정합 등으로 영상 품질 저하가 발생할 수 있다.

2-3 자동초점 알고리즘

기체의 요동과 같은 다양한 요인으로 인해 SAR 영상 정합에 적용한 센서 궤적과 실제 센서 궤적 사이에 오차가 발생할 수 있고, 통상적으로 GPS-IMU 정보를 이용해서 궤적 오차를 최소화한다. 자동초점 기법은 요동 보상 후 잔여 위상 오차를 최소화해서 SAR 영상의 품질을 개선하기 위해 사용된다. 자동초점 기법은 통상적으로 SAR 영상 형성을 위한 신호처리의 마지막 단계에서 방위 주파수 영역의 위상 오차를 추정하고, 이를 보간해서 보상하는 과정으로 구성된다.

거리방향 잔여 위상 오차 변화를 무시할 수 있는 경우 자동초점 행렬은 식 (10)과 같이 표현된다^[13].

D = diag e j ϕ

(10)

이때 $ϕ = θ 1, θ 2, ⋯, θ N a T$ 이고, θ_η는 방위방향 η번째 샘플의 잔여 위상 오차를 의미한다. 잔여 위상 오차 벡터 ϕ는 일정 주기마다 자동초점 알고리즘 수행을 통해 추정되며, 이를 이용해서 D를 정의한다. 자동초점 적용 전 SAR 이미지 X에서 잔여 위상 오차를 보정해서 자동초점 적용 후 이미지 X_f를 계산하는 과정과 그 역과정은 각각 식 (11) 및 식 (12)와 같이 나타낼 수 있다.

X f = f (X) = F a H DF a X

(11)

X = f − 1 X f = F a H D * F a X f

(12)

본 논문에서는 잔여 위상 오차 추정을 위한 자동초점 알고리즘으로 PGA, MEA, FPA를 고려한다. PGA는 이미지 영역에서 주요 표적 신호 추출 후 방위 주파수 영역에서 위상 경사 추정과 보간 기반 위상 오차 보상을 수행한다. 연산 복잡도가 낮고 구현이 용이하지만, 성능이 파라미터 변화에 민감하고 두드러진 주요 표적이 불명확한 경우 위상 추정 성능이 저하된다^[13]. MEA는 SAR 영상의 엔트로피가 감소하는 방향으로 방위 주파수 영역의 위상을 반복적으로 갱신하는 기법이다. 연산 복잡도가 높지만, 파라미터 변화에 둔감해서 안정적인 영상 품질 개선이 가능하다^[14]. FPA는 소프트 임계처리 전후 이미지의 최소자승오차가 최소가 되는 방향으로 방위 주파수 영역의 위상을 반복적으로 갱신하는 기법이다. 복잡도가 낮고 압축센싱 복원 기법과 결합이 용이하지만, 임계처리를 위한 기준값에 따라 수렴속도와 성능이 변화하므로 적절한 파라미터 설정이 중요하다^[15].

Ⅲ. 제안된 SAR 영상 복원 기법

이 절에서는 압축된 SAR 원시 데이터 Y_s에 MLRSD 기반 압축센싱 복원 기법과 자동초점 알고리즘을 결합한 기법을 적용하여 SAR 영상을 복원하는 형성하는 기법을 새롭게 제안한다. 제안된 기법의 경우 SAR 영상의 희소성이 낮거나 불완전한 요동 보상으로 인해 잔여 위상 오차가 포함된 경우에도 적용할 수 있다.

압축된 SAR 원시 데이터에 잔여 위상 오차가 포함된 경우 MLRSD에 기반한 압축센싱 복원 문제는 식 (13)과 같이 정의할 수 있다.

L o, S o = arg min L,S ‖ Ψ (L) ‖ 1 + ‖ S ‖ 1 s . t . ‖ Y s − Θ a G f − 1 (L + S) Θ r ‖ F 2 < ϵ 2

(13)

이때 L_o와 S_o는 자동초점 적용 후 최적 배경 이미지와 표적 이미지이고, 잔여 위상 오차 추정을 통해 자동초점 행렬 D가 정해지면 f⁻¹ (·)는 식 (12)와 같이 계산된다. 식 (13)에서 정의한 최적화 문제는 라그랑주 함수를 이용해서 식 (14)와 같이 변형할 수 있다.

L o, S o = arg min L,S L (L, S, λ)

(14)

이때 라그랑주 함수 $L (L, S, λ) = ‖ Y s − Θ a G f − 1 (L + S) Θ r ‖ F 2 + λ ‖ Ψ (L) ‖ 1 + ‖ S ‖ 1$ 이고, λ는 0 이상의 실수값을 갖는 라그랑주 파라미터이다.

최적화 문제 식 (14)에서 L은 웨이블릿 영역에서 희소성을 가지고, S는 이미지 영역에서 희소 신호로 표현되므로 최적해 L_o와 S_o를 동시에 찾는 것은 매우 어렵다. 따라서 ITA를 이용해서 배경 이미지와 표적 이미지를 반복적으로 갱신하는 방법으로 최적해를 구한다. t번째 갱신을 통해 표적 이미지 S_t를 얻었다고 가정하면, 배경 이미지를 구하기 위한 부분 최적화 문제는 식 (15)와 같이 정의된다.

L t + 1 = argmin L {‖ Y L, t − Θ a G f − 1 (L) Θ r) ‖ F 2 + λ ‖ Ψ (L) ‖ 1}

(15)

여기서 Y_L,t=Y_s-Θ_aG(f⁻¹ (S_t))Θ_r이다. DCWT 영역에서 계수 행렬을 Z=Ψ(L)로 정의하고, 자동초점 역과정과 관측 함수를 결합해서 Φ(Z)=G(f⁻¹ (Ψ⁻¹ (Z)))로 정의한다. 이를 통해 식 (15)를 식 (16)과 같이 행렬 Z에 대한 압축센싱 최적화 문제로 변경할 수 있다.

Z t + 1 = arg min Z Y L, t − Θ c Φ (Z) Θ r F 2 + λ ‖ Z ‖ 1

(16)

위 최적화 문제의 경우 닫힌 형태 해를 구하기 힘들므로 반복적인 갱신 과정을 통해 최적해를 구하는 방법을 유도한다. 이를 위해 식 (17)과 같이 식 (16)의 목적 함수에 대응되는 대리 함수(surrogate function)를 정의한다.

g L Z; Z t = Y L, t − Θ a Φ (Z) Θ r F 2 + λ ‖ Zvert 1 + c L Z − Z t F 2 − Θ a Φ Z − Z t Θ r F 2

(17)

이때 c_L은 대리 함수가 볼록 조건(convexity)을 만족하도록 하는 0보다 큰 상수이다. 위 대리 함수를 최소로 하는 최적해는 다음 1차 최적 조건을 만족한다.

∂ g L Z; Z t ∂ Z * = c L Z + λ sign (Z) − c L Z t − Φ − 1 Θ a T Y L, t − Θ a Φ Z t Θ r Θ r T = 0

(18)

이때 sign(·)은 부호 함수이다. 위 조건을 만족하는 (t+1)번째 반복 연산의 해는 식 (19)와 같이 계산된다.

Z t + 1 = T S P L Z t + μ L Ψ f A t, τ L

(19)

여기서 $μ L = c L − 1$ 은 배경 이미지 갱신을 위한 스텝 크기이고, τ_L는 DCWT 계수 임계값이며, T_SPL (Z,τ_L)은 참고문헌 [19]의 BSF(bivariate shrinkage function)를 이용한 SPL 임계화 과정을 의미한다. 행렬 A_t에 대한 정의를 포함해서 식 (19)의 연산을 단계별로 정리하면 식 (20)~식 (22)와 같이 배경 이미지 행렬을 갱신하기 위한 식을 얻을 수 있다.

A t = M Θ a T Y L, t − Θ a G f − 1 L t Θ r Θ r T

(20)

L ˜ t + 1 = L t + μ L f A t

(21)

L t + 1 = Ψ − 1 T S P L Ψ L ˜ t + 1, τ L

(22)

이 식은 기존 MLRSD 기반 SAR 영상 복원 기법과 식 (11) 및 식 (12)에서 정의한 자동초점을 위한 잔여 위상 오차 보상 과정과 그 역과정이 결합된 형태이다.

다음으로 배경 행렬 L_t+1이 주어졌을 때 표적 이미지를 갱신하기 위한 부분 최적화 문제는 식 (23)과 같이 정의할 수 있다.

S t + 1 = arg min S Y S, t − Θ c G f − 1 (S) Θ r F 2 + λ ‖ S ‖ 1

(23)

여기서 Y_S,t=Y_s-Θ_aG(f⁻¹(L_t+1))Θ_r이다. 위의 최적화 문제는 식 (16)과 유사한 형태이므로 배경 이미지에 대한 최적해를 구하는 과정을 적용한다. t번째 갱신 과정에서 구한 S_t를 중심으로 식 (23)에 대응되는 대리 함수를 식 (24)와 같이 정의한다.

g S S; S t = Y S, t − Θ a G f − 1 (S) Θ r F 2 + λ ‖ S ‖ 1 + c S S − S t F 2 − Θ a G f − 1 S − S t Θ r F 2

(24)

이때 c_S > 0는 대리 함수가 볼록 조건을 만족하도록 하는 상수이고, 위 대리 함수를 최소로 하는 최적해는 다음 1차 최적 조건을 만족한다.

∂ g S S; S t ∂ S * = c S S + λ sign (S) − c S S t − f M Θ a T Y S, t − Θ a G S t Θ r Θ r T = 0

(25)

위 조건을 만족하는 (t+1)번째 표적 이미지의 해는 식 (26)과 같이 표현된다.

S t + 1 = T S t + μ S f B t, τ S

(26)

여기서 $T (x, τ) = x | x | (| x | − τ) +$ 는 소프트 임계화 함수이고, x₊=max(x,0)이며, $μ S = c S − 1$ 은 표적 이미지 갱신을 위한 스텝 크기, τ_S는 소프트 임계화 기준값이다. 행렬 B_t에 대한 정의를 포함해서 식 (26)의 연산을 단계별로 정리하면 식 (27) 및 식 (28)과 같이 표적 이미지 갱신식이 얻어진다.

B t = M Θ a T Y S, t − Θ a G f − 1 S t Θ r Θ r T

(27)

S t + 1 = T S t + μ S f B t, τ S

(28)

식 (20)~식 (22)와 식 (27) 및 식 (28)에서 구한 배경 및 표적 이미지를 이용해서 (t+1)번째 갱신 과정의 SAR 영상은 X_t+1=L_t+1+S_t+1로 주어진다. 이를 이용해서 일정 주기마다 잔여 위상 오차 Δϕ를 추정하고, 식 (29) 및 식 (30)과 같이 자동초점 행렬 D를 갱신한다.

Δ ϕ = A F X t + 1

(29)

D t + 1 = diag e j ϕ t + 1, ϕ t + 1 = ϕ t + Δ ϕ

(30)

이때 AF(·)는 자동초점 알고리즘을 이용한 방위 주파수 위상 오차 추정 함수를 의미하고, PGA, MEA, FPA 등을 적용할 수 있다.

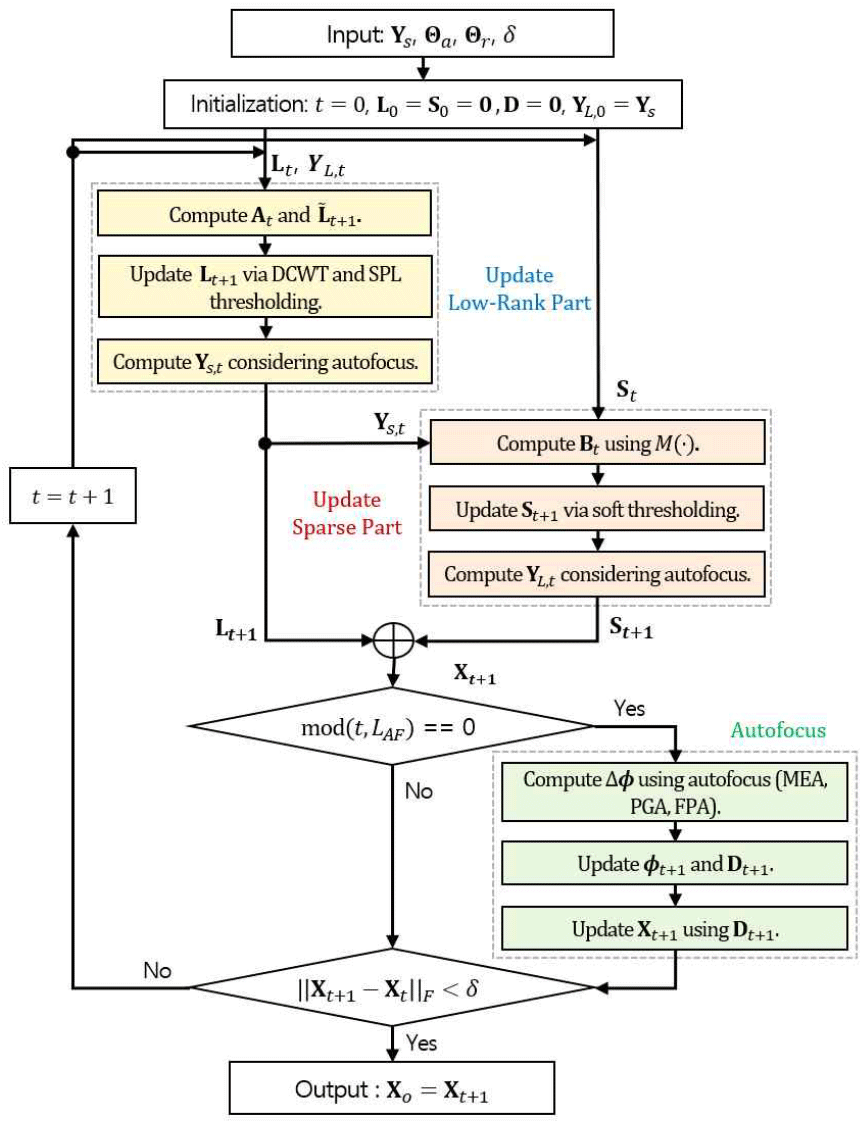
전체적으로 배경 이미지, 표적 이미지, 자동초점 행렬의 초기값을 0으로 설정한 후 식 (20)~식 (22), 식 (27)~식 (30)의 과정을 반복적으로 수행하여 자동초점이 적용된 SAR 영상을 복원한다. 제안된 기법의 전체 동작 절차는 그림 3으로 표현할 수 있다. 이때 L_AF는 자동초점 알고리즘 수행 주기를 나타내고, δ는 반복 알고리즘 종료를 위한 SAR 영상 변화량 기준값을 의미한다.

그림 3. | Fig. 3. 제안된 ITA 기반 SAR 영상 복원 기법 | Proposed ITA-based method for SAR image reconstruction.

Download Original Figure

Ⅳ. 모의실험 결과

4-1 SAR 모델링 데이터를 이용한 모의실험

이 절에서는 SAR 모델링 데이터를 이용한 모의실험을 통해 제안된 알고리즘의 수렴 특성과 유효성을 검증한다. 그림 1의 모노스태틱 항공기 SAR 기하 구조와 표 1에서 제시한 파라미터를 이용해서 SAR 모델링 원시 데이터를 생성하였다. 이때 표적 지역의 반사 계수는 그림 4와 같이 Sandia 레이다 연구실의 고해상도 SAR 이미지 2가지(naval air station, solar tower)를 이용해서 설정하였다^[20]. 2차원 압축센싱을 위한 방위 및 거리방향 관측률은 r_a=r_g=0.7로 설정하고 (압축률 51%), 식 (6)에서 정의한 방위 및 거리방향 랜덤 샘플링 행렬은 랜덤 가우시안 행렬의 특이값 분해를 통해 생성하였다. 이미지화 함수 G(·)와 관측 함수 M(·)는 표 1의 파라미터를 적용하여 각각 식 (3) 및 식 (5)로 정의한다. MLRSD에서 DCWT 레벨 수는 4, 스텝 크기는 μ_L=μ_S=0.33, τ_L=1.5, τ_S는 이미지 신호의 99.5 %가 포함되도록 설정한다. 잔여 위상 오차는 방위방향 2차 함수로 가정했고, 자동초점 수행 주기는 L_AF=75이며, PGA의 초기 윈도우 크기는 16, 윈도우 크기 조절을 위한 임계값은 13 dB, 위상 오차 갱신을 위한 최대 반복횟수는 80으로 설정한다. MEA에서 거리방향 셀 선택을 위한 임계치는 13 dB이며 위상 오차 갱신을 위한 최대 반복횟수는 50이고, FPA에서 초기 소프트 임계값은 0.6, 임계값 조절을 위한 망각계수(forgetting factor)는 0.98, 위상 오차 갱신을 위한 최대 반복횟수는 50으로 설정한다.

표 1. | Table 1. 항공기 SAR 모델링 파라미터 | Airborne SAR modeling parameters.

SAR mode	Spotlight monostatic
Carrier frequency (f₀)	9.6 GHz
Slant range to scene center (R₀)	20 km
Range FM rate (K_r)	0.25 × 10¹² Hz/s
Velocity (V_r)	120 m/s
Sampling rate (f_r)	7.5 MHz
PRF	100 Hz
Antenna length	3.3 m
Target image size (N_a × N_r)	256 × 256 pixels

Download Excel Table

그림 4. | Fig. 4. 반사 계수 모델링을 위한 표적 이미지 | Target image for modeling of reflection coefficients.

Download Original Figure

그림 5에서는 naval air station 반사 계수를 이용해서 모델링 데이터를 생성하고, MLRSD에 PGA, MEA, FPA를 결합해서 제안된 SAR 영상 복원 기법을 구현했을 때 수렴 특성을 비교한다. PSNR(peak signal-to-noise ratio)과NMSE(normalized mean square error)는 원본 SAR 이미지의 반사 계수를 기준으로 계산하였다. 3가지 자동초점 알고리즘 모두 정상 상태로 안정적으로 수렴하며, MEA와 FPA의 PSNR은 유사하고 PGA의 PSNR은 다소 낮게 나타난다. 엔트로피와 영상 대비(contrast)의 경우 MEA와 FPA는 안정적으로 수렴하고, PGA의 경우 t=75에서 자동초점 행렬 갱신 후 다소 불안정한 구간을 지나서 수렴하는 형태를 보인다. 전체적으로 3가지 자동초점 알고리즘 모두 제안된 영상 복원 기법을 150회 이상 반복하면 안정적으로 수렴함을 확인할 수 있다.

그림 5. | Fig. 5. 자동초점 알고리즘에 따른 제안된 복원 기법 수 렴 특성 비교(Naval air station) | Convergence characteristics of proposed reconstruction method according to autofocus algorithms (Naval air station).

Download Original Figure

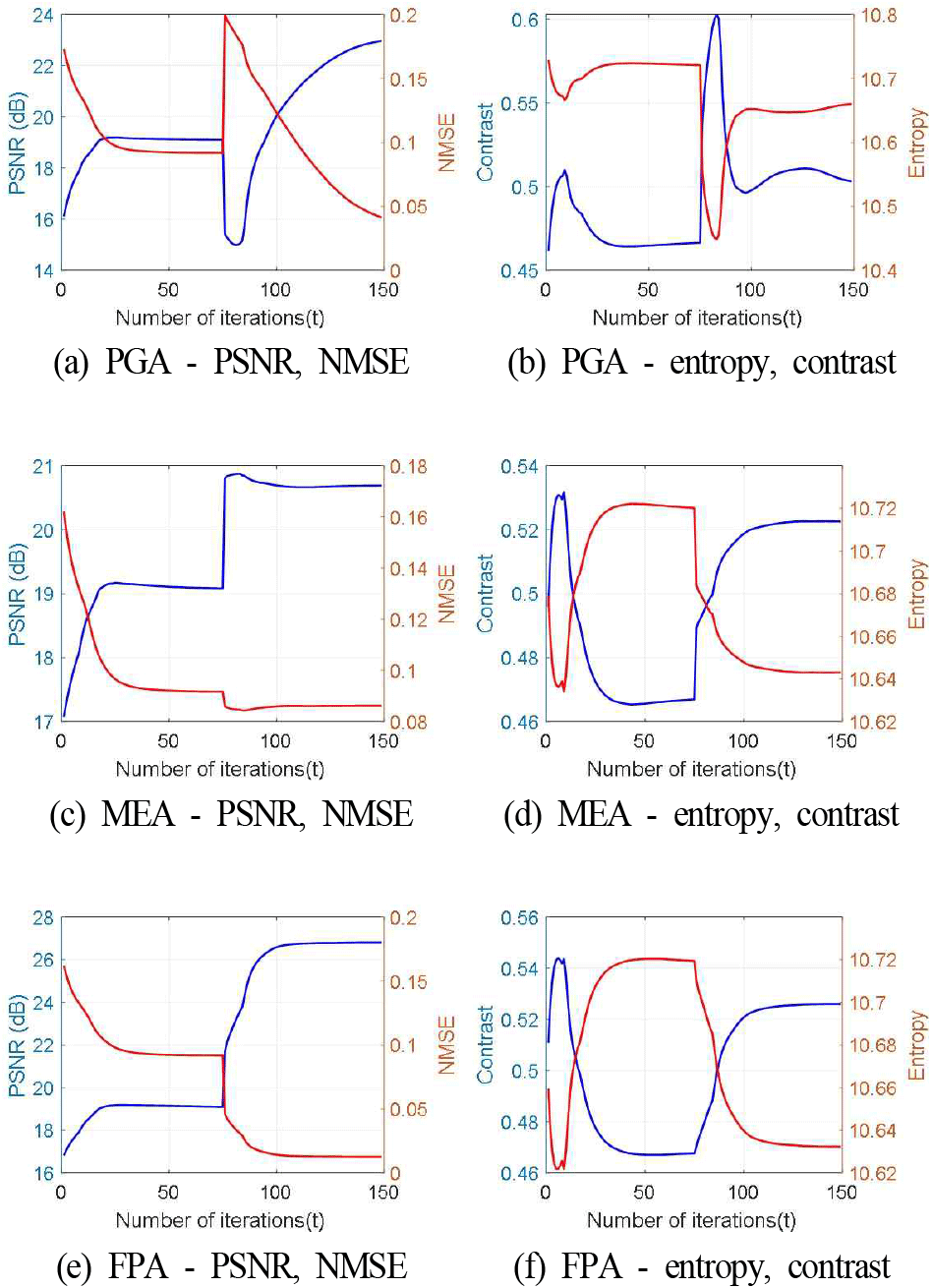
그림 6은 Solar Tower 반사 계수를 적용해서 모델링된 원시 데이터를 생성하고, RDA, MLRSD, 제안된 기법을 적용했을 때 복원된 SAR 영상을 비교한다. 그림 6(a)는 원시 데이터에 압축센싱을 적용하지 않고 위상 오차가 없는 경우 RDA를 이용해서 획득한 영상이고, 그림 6(b)는 압축센싱을 적용하지 않고 요동에 의한 잔여 위상 오차가 있을 때 RDA를 이용해서 획득한 영상이다. 그림 6(c)~그림 6(f)는 2차원 압축센싱을 적용한 원시 데이터를 이용해서 복원한 영상이다. 구체적으로 그림 6(c)는 자동초점을 고려하지 않고 기존 MLRSD를 이용해서 복원한 결과이고, 그림 6(d)~그림 6(f)는 제안된 복원 기법에 각각 PGA, MEA, FPA 자동초점 알고리즘을 결합해서 얻은 영상이다. 잔여 위상 오차가 있을 때 기존 RDA 혹은 MLRSD로 복원하는 경우 SAR 영상의 품질이 현저히 저하됨을 볼 수 있다. 반면에 제안된 기법을 적용하면, 그림 6(d)~그림 6(f)에 보인 바와 같이 3가지 자동초점 알고리즘 모두 잔여 위상 오차가 없는 RDA에 근접한 우수한 SAR 영상을 획득할 수 있음을 확인할 수 있다.

그림 6. | Fig. 6. 모델링 데이터를 이용한 SAR 복원 영상 비교 | Comparison of reconstructed SAR images using modeling data.

Download Original Figure

표 2는 모델링 원시 데이터에 RDA, MLRSD, 제안된 복원 기법을 적용해서 복원한 SAR 영상의 PSNR, NMSE, 엔트로피, 영상 대비 성능을 정량적으로 비교한다. RDA 영상의 경우 압축센싱을 적용하지 않은 원시 데이터를 이용해서 획득했고, MLRSD와 제안된 기법의 경우 압축센싱을 적용한 원시 데이터를 사용하였다. 또한, MLRSD와 제안된 기법의 경우 랜덤 샘플링 행렬 형태에 따라 성능이 변화되므로 5번 모의실험한 결과를 평균해서 정량 지표를 구하였다.

표 2. | Table 2. 모델링 데이터를 이용해서 복원한 SAR 영상의 품질 비교 | Comparison of reconstructed SAR image quality using modeling data.

Target	Imaging method	PSNR (dB)	NMSE	Entropy	Contrast
Naval air station	RDA without phase error	28.36	0.0089	10.63	0.530
	RDA with phase error	17.46	0.0930	10.72	0.459
	MLRSD without autofocus^[10]	19.11	0.0917	10.72	0.467
	Proposed method with PGA	23.10	0.4430	10.66	0.508
	Proposed method with MEA	25.39	0.0845	10.64	0.525
	Proposed method with FPA	26.92	0.0122	10.64	0.527
Solar tower	RDA without phase error	24.01	0.0311	10.11	0.864
	RDA with phase error	13.77	0.2407	10.50	0.636
	MLRSD without autofocus^[10]	14.46	0.2377	10.50	0.637
	Proposed method with PGA	17.00	0.2297	10.18	0.797
	Proposed method with MEA	17.86	0.1229	10.10	0.842
	Proposed method with FPA	21.47	0.0573	10.11	0.845

Download Excel Table

표 2에서 잔여 위상 오차가 없을 때 RDA는 성능 지표의 상한값을 나타내고, 잔여 위상 오차를 보상하지 않은 RDA는 모든 지표에서 가장 나쁜 성능을 보인다. 제안된 기법은 자동초점 알고리즘을 사용하므로 자동초점을 고려하지 않은 기존 MLRSD에 비해 모든 지표가 우수한 성능을 보인다. 예를 들면 제안된 기법 적용시 MLRSD 대비 PSNR이 2.54~7.81 dB 개선되고, 엔트로피의 경우 Naval Air Station에서 0.06~0.08, Solar Tower에서 0.32~0.40 감소한다. PSNR, NMSE, 영상 대비의 경우 제안된 기법을 FPA와 결합해서 사용하는 경우 가장 우수한 성능을 보이고(MEA 혹은 PGA와 결합한 경우 FPA 대비 각각 1.53~3.61 dB, 3.82~4.47 dB의 PSNR 손실 발생), 엔트로피는 MEA와 FPA를 결합한 기법이 유사한 성능을 나타내고 PGA와 결합한 기법의 경우 0.02~0.08의 손실이 발생한다. 전체적으로 제안된 기법을 FPA와 결합 시 가장 우수한 성능을 보인다.

4-2 SAR 실측 데이터를 이용한 모의실험

이 절에서는 차량 탑재 SAR 실측 데이터를 이용해서 제안된 압축센싱 기반 SAR 영상 복원 기법을 검증한다. 차량 SAR 실측 데이터는 그림 7과 같이 대전-당신 고속도로의 예산대교 부근에서 상행 방향으로 주행하면서 획득하였다. 그림 7은 표적 지역의 광학 영상과 주행 경로를 보여주고, 표 3은 실측 실험에 사용된 SAR 플랫폼의 주요 파라미터를 나타낸다.

그림 7. | Fig. 7. 표적 지역 광학 영상 및 레이다 이동 경로 | Target area optical image and radar path.

Download Original Figure

표 3. | Table 3. 실측 SAR 플랫폼 파라미터 | Parameters for experimental SAR platform.

SAR mode	Stripmap monostatic
Waveform	Pulse
Carrier frequency (f₀)	9.66 GHz
Bandwidth	600 MHz
Sampling rate (f_r)	800 MHz
PRF	1 kHz
Velocity (V_r)	21.72 m/s
Altitude	25 m
Slant range to scene center (R₀)	563 m
Target image size (N_a × N_r)	8,192 × 1,024 pixels

Download Excel Table

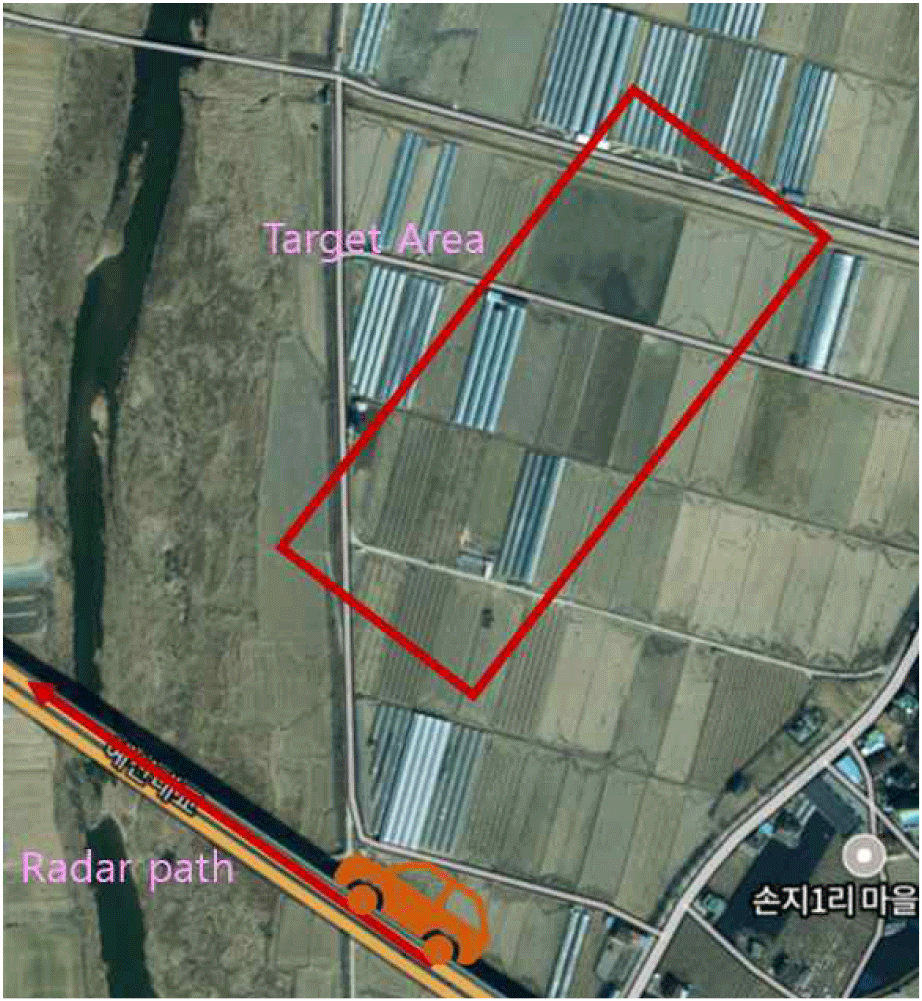
그림 8은 차량 탑재 SAR 실측 데이터를 이용해서 복원한 SAR 영상을 나타낸다. 그림 8(a)는 요동에 의한 위상 오차가 없는 원시 데이터에 압축센싱을 적용하지 않고 획득한 RDA 영상이다. 그림 8(b)~그림 8(d)에서는 레이다 속도 추정 오차에 의해 방위 주파수 방향으로 2차 함수 형태의 위상 오차가 포함된 원시 데이터를 사용한다. 그림 8(b)는 압축센싱과 자동초점 알고리즘을 적용하지 않고 획득한 RDA 영상이다. 그림 8(c)와 그림 8(d)는 원시 데이터에 압축센싱을 적용해서 용량을 49 %로 줄이고, MLRSD와 제안된 기법을 각각 사용해서 복원한 SAR 영상이다. 제안된 기법에서는 거리방향으로 256 픽셀 단위로 전체 이미지를 분할하고, 각 분할된 영상에 FPA를 적용해서 자동초점을 수행하였다. 그림 8(b)의 경우 잔여 위상 오차에 의해 RDA 영상의 품질이 저하됨을 볼 수 있고, 그림 8(c)의 경우 자동초점을 수행하지 않고 MLRSD를 이용해서 복원하므로 영상 품질이 현저히 저하된다. 제안된 기법의 경우 압축센싱과 자동초점 알고리즘을 동시에 적용하므로 그림 8(d)와 같이 전체적으로 정합 특성이 개선되어 영상 품질이 향상된다. 다만, 제안된 기법의 경우에도 이미지 분할 경계에서의 이미지 왜곡 등으로 인해 그림 8(a)의 위상 오차가 없는 RDA 이미지 대비 부분적인 영상 품질 저하가 나타난다.

그림 8. | Fig. 8. 차량 SAR 실측 데이터를 이용한 영상 복원 | Image reconstruction using real vehicular SAR data.

Download Original Figure

표 4는 그림 8에서 복원한 SAR 영상의 엔트로피와 영상 대비를 정량적으로 비교한다. 참고문헌 [10]의 MLRSD 기법과 제안된 기법의 경우 랜덤 샘플링 행렬에 따른 성능 편차를 고려해서 5번 반복 모의실험한 결과를 평균해서 구하였다. 제안된 기법 적용시 잔여 위상 오차를 갖는 RDA와 참고문헌 [10]의 MLRSD 기법에 비해 영상 품질 지표가 개선됨을 확인할 수 있다. 제안된 기법은 위상 오차가 없는 RDA 대비 엔트로피 0.50, 영상 대비 0.07의 손실을 보이고, 전체적으로 RDA에 근접한 영상 품질을 보인다. 이를 통해 제안된 기법을 잔여 위상 오차가 포함된 SAR 실측 데이터에 적용 가능함을 확인하였다.

표 4. | Table 4. 차량 실측 데이터를 이용해서 획득한 영상 품질 | Reconstructed SAR image quality using vehicular SAR real data.

Imaging method	Entropy	Contrast
RDA without phase error	14.40	1.04
RDA with phase error	15.54	0.71
MLRSD without autofocus^[10]	15.76	0.70
Proposed method with FPA	14.90	0.97

Download Excel Table

Ⅴ. 결 론

본 논문에서는 용량 저감 등을 위해 압축센싱을 수행한 원시 데이터에 요동에 의한 잔여 위상 오차가 포함된 경우 MLRSD 기반 압축센싱 복원 기법과 자동초점 알고리즘을 결합하여 SAR 영상을 획득하는 기법을 제안하였다. SAR 모델링 데이터를 통해 제안된 기법의 수렴 특성을 보이고, 영상 복원 성능 비교를 통해 제안된 기법을 FPA와 결합 시 성능이 가장 우수함을 확인하였다. 또한, 차량 탑재 SAR 실측 데이터에 FPA와 결합된 제안된 기법을 적용하여 기존 기법 대비 영상 품질이 향상됨을 확인하였다. 항공기 혹은 무인기 SAR에서 관측 데이터 용량을 줄이고 무선 전송 링크의 부하를 줄이기 위해 압축센싱된 원시 데이터를 전송하고, 이를 지상국에서 수신하여 SAR 영상을 생성하는 경우 제안된 SAR 영상 복원 기법을 활용하여 영상 품질을 개선할 수 있다.

Acknowledgements

이 논문은 행정안전부 급경사지 안전관리를 위한 드론 기반 SAR 모니터링 시스템 개발 사업(RS-2025-02633421)과 정부(과학기술정보통신부)의 재원으로 정보통신기획평가원-학․석사연계ICT핵심인재양성 사업(IITP-2024-RS-2024-00437857) 지원을 받아 수행된 연구임.

References

[1].

M. Çetin, I. Stojanović, N. Ö. Önhon, K. Varshney, S. Samadi, and W. C. Karl, et al., “Sparsity-driven synthetic aperture radar imaging: Reconstruction, autofocusing, moving targets, and compressed sensing,” IEEE Signal Processing Magazine, vol. 31, no. 4, pp. 27-40, Jul. 2014.

[2].

D. L. Donoho, “Compressed sensing,” IEEE Transactions on Information Theory, vol. 52, no. 4, pp. 1289-1306, Apr. 2006.

[3].

E. J. Candes, J. Romberg, and T. Tao, “Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information,” IEEE Transactions on Information Theory, vol. 52, no. 2, pp. 489-509, Feb. 2006.

[4].

J. Haupt, R. Nowak, “Signal reconstruction from noisy random projections,” IEEE Transactions on Information Theory, vol. 52, no. 9, pp. 4036-4048, Sep. 2006.

[5].

T. T. Cai, L. Wang, “Orthogonal matching pursuit for sparse signal recovery with noise,” IEEE Transactions on Information Theory, vol. 57, no. 7, pp. 4680-4688, Jul. 2011.

[6].

D. L. Donoho, A. Maleki, and A. Montanari, “Message passing algorithms for compressed sensing: I. Motivation and construction,” in 2010 IEEE Information Theory Workshop on Information Theory(ITW 2010, Cairo), Cairo, Jan. 2010, pp. 1-5.

[7].

I. W. Selesnick, R. G. Baraniuk, and N. C. Kingsbury, “The dual-tree complex wavelet transform,” IEEE Signal Processing Magazine, vol. 22, no. 6, pp. 123-151, Nov. 2005.

[8].

S. Mun, J. E. Fowler, “Block compressed sensing of images using directional transforms,” in 2009 16th IEEE International Conference on Image Processing(ICIP), Cairo, Nov. 2009, pp. 3021-3024.

[9].

H. R. Hashempour, M. Moradikia, H. Bastami, A. Abdelhadi, and M. Soltanalian, “Fast and robust LRSD-based SAR/ ISAR imaging and decomposition,” IEEE Transactions on Geoscience and Remote Sensing, vol. 60, pp. 1-13, May 2022.

[10].

J. I. Byeon, W. Lee, and J. Choi, “Compressive SAR imaging based on modified low-rank and sparse decomposition,” IEEE Access, vol. 13, pp. 1663-1679, Dec. 2024.

[11].

O. Frey, C. Magnard, M. Ruegg, and E. Meier, “Focusing of airborne synthetic aperture radar data from highly nonlinear flight tracks,” IEEE Transactions on Geoscience and Remote Sensing, vol. 47, no. 6, pp. 1844-1858, Jun. 2009.

[12].

M. Lort, A. Aguasca, C. López-Martinez, and T. M. Marin, “Initial evaluation of SAR capabilities in UAV multicopter platforms,” IEEE Journal on Selected Topics in Applied Earth Observations and Remote Sensing, vol. 11, no. 1, pp. 127-140, Jan. 2018.

[13].

W. L. Van Rossum, M. P. G. Otten, and R. J. P. Van Bree, “Extended PGA for range migration algorithms,” IEEE Transactions on Aerospace and Electronic Systems, vol. 42, no. 2, pp. 478-488, Apr. 2006.

[14].

T. Xiong, M. Xing, Y. Wang, S. Wang, J. Sheng, and L. Guo, “Minimum-entropy-based autofocus algorithm for SAR data using Chebyshev approximation and method of series reversion, and its implementation in a data processor,” IEEE Transactions on Geoscience and Remote Sensing, vol. 52, no. 3, pp. 1719-1728, Mar. 2014.

[15].

H. Lee, C. S. Jung, and K. W. Kim, “Feature preserving autofocus algorithm for phase error correction of SAR images,” Sensors, vol. 21, no. 7, p. 2370, Mar. 2021.

[16].

T. Jin, “Autofocus compressed sensing imaging based on nonlinear conjugate gradient,” in 2017 XXXIInd General Assembly and Scientific Symposium of the International Union of Radio Science, Montreal, QC, Aug. 2017, pp. 1-4,

[17].

J. Fang, Z. Xu, B. Zhang, W. Hong, and Y. Wu, “Fast compressed sensing SAR imaging based on approximated observation,” IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, vol. 7, no. 1, pp. 352-363, Jan. 2014.

[18].

Y. Wang, J. Zeng, Z. Peng, X. Chang, and Z. Xu, “Linear convergence of adaptively iterative thresholding algorithms for compressed sensing,” IEEE Transactions on Signal Processing, vol. 63, no. 11, pp. 2957-2971, Jun. 2015.

[19].

L. Sendur, I. W. Selesnick, “Bivariate shrinkage functions for wavelet-based denoising exploiting interscale dependency,” IEEE Transactions on Signal Processing, vol. 50, no. 11, pp. 2744-2756, Nov. 2002.

[20].

Sandia National Laboratories (SNL), “Pathfinder radar ISR & SAR systems: Modes & frequency bands of operation,” Available: https://www.sandia.gov/radar/pathfinder-airborne-isr-systems-modes-frequency-bands-of-operation/