제약 최적화와 Unscented Transform 기반의 강인한 우주물체 추적 개시 방법

제안하는 방법의 목적은 두 시점 t₁, t₂에서 측정된 불확실한 위치 벡터 p₁,p₂가 주어졌을 때, 물리적 제약 조건을 만족하면서 원 측정치와의 마할라노비스 거리를 최소화하는 새로운 상태 벡터 [p^′₂;v^′]와 그에 대응하는 초기 오차 공분산 행렬 p₂를 추정하는 것이다.

이 기법은 저궤도 영역의 다수 우주물체들이 낮은 이심률을 갖는다는 관찰에 기반하여, 이들의 운동 특성이 준원궤도에 가깝다는 점을 활용한다. 즉, 추적 개시 시점인 t₂에서의 상태가 원궤도에 가까운 형태일 것이라는 가정을 적용한다. 이 가정은 다음의 두 가지 제약 조건으로 구체화된다:

이러한 제약 조건은 측정치가 희소하고 불확실성이 큰 상황에서 속도 정보를 보완할 수 있는 물리적 정보를 제공하며, 특히 측정 오차가 클 때 초기 상태 추정의 안정성을 향상시킨다.

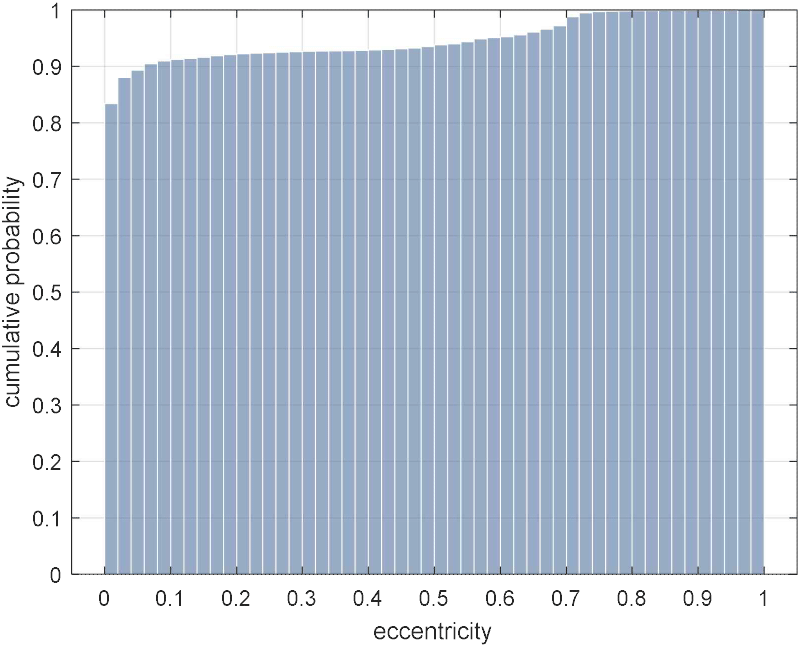
본 논문에서는 대상 레이다 시스템이 측정하는 표적을 저궤도 우주물체로 한정한다. 2025년 5월 13일자로 공개된 TLEs(two-line element sets)^[7] 데이터를 기반으로 분석한 결과, 근지점을 기준으로 고도 2,000 km 이하의 우주물체의 이심률 누적확률 히스토그램은 그림 1과 같이 나타난다. 전체의 90 % 이상이 이심률 0.1 이하의 낮은 값을 가지며, 이는 준 원궤도 가정이 대부분의 LEO 물체에 대해 유효한 초기 근사임을 보여준다.

제안하는 기법은 보정된 위치 벡터 p^′₁,p^′₂를 변수로 하여, 식 (1)과 같은 비용 함수와 제약 조건을 갖는 최적화 문제로 정의된다:

subject to:

여기서 C₁,C₂∈ℝ^3×3는 각각 t₁, t₂ 시점에서의 위치 측정치에 대한 오차 공분산 행렬로, 측정치의 불확실성의 크기와 방향 정보를 포함한다. n₂∈ℝ³는 t₂ 시점의 측정치의 위치 벡터를 단위 벡터로 정규화한 방향 벡터 (n₂=p₂/∥p₂∥)이며, 방향 제약의 기준으로 사용된다. 한편, V_abs는 t₂ 시점의 고도에서 준원궤도 조건을 만족하는 기준 속력으로, 식 (4)과 같이 계산된다^[3]:

여기서 μ는 지구 중력상수이다.

이 최적화 문제의 목적은, 측정된 위치 벡터 p₁,p₂에 대한 최소한의 통계적 보정을 통해, 준 원궤도 특성을 만족하는 새로운 위치 벡터 p^′₁,p^′₂를 추정하는 데 있다. 식 (1)은 보정된 위치와 원래 측정치 간의 마할라노비스 거리의 제곱합을 최소화하도록 설계되었다. 마할라노비스 거리는 단순한 유클리드 거리와 달리, 공분산을 반영하여 변수들의 상관관계(correlation)와 척도(scale) 차이를 보정한다^[4]. 따라서 마할라노비스 거리를 활용함으로써, 신뢰도가 높은 방향에는 작은 보정을, 신뢰도가 낮은 방향에는 더 큰 보정을 허용하는 통계적 가중치를 적용하는 효과를 얻는다.

제약 조건은 각각 다음과 같은 의미를 갖는다. 첫째, 식 (2)는 방향 제약 조건으로, 원궤도에서 속도 벡터는 위치 벡터에 수직이라는 물리적 특성을 수학적으로 표현한 것이다. 즉, 평균 속도 방향을 나타내는 변위 벡터 (p^′₁ − p^′₂)가 t₂ 시점의 위치 단위 벡터 n₂와 직교해야 함을 나타낸다. 둘째, 식 (3)은 속력 크기 제약으로, 두 시점 간 평균 속력(∥p^′₂−p^′₁∥/Δt)이 V_abs와 같아야 함을 의미한다. 이 두 제약은 시간 간격 Δt가 충분히 짧아 평균 속도 벡터가 순간 속도 벡터를 근사할 수 있다는 전제 하에 유효하며, 궤도상의 물리적 운동 특성을 t₂ 시점에 적용한다.

비용 함수는 변수에 대해 이차(quadratic) 형태이고, 제약 조건 중 식 (2)는 선형(linear)이지만 식 (3)은 벡터 놈(norm)을 포함한 비선형(nonlinear) 제약이기 때문에, 전체 최적화 문제는 해석적으로 직접 해를 구하기 어렵다. 따라서 본 논문에서는 각 제약 조건을 분리하여 두 단계의 최적화 문제로 근사함으로써 해석적 해를 구하였다. 이러한 방식은 실시간 추적 개시 시나리오에 적합한 빠른 계산 속도를 보장한다.

우선, 방향 제약 조건만을 고려한 상태에서 마할라노비스 거리를 최소화하는 중간 위치 추정값 ${\tilde{p}}_1,{\tilde{p}}_2$를 계산한다. 1단계 문제 정의는 식 (5) 및 식 (6)과 같다.

subject to:

이 문제의 해석적 해를 구하기 위해 라그랑주 승수법을 이용한다. 식 (5)의 목표 함수를 J₁이라고 할 때, 라그랑지안 L₁=J₁-λg의 그래디언트를 0으로 두어 식 (7) 및 식 (8)과 같이 해를 구한다.

이 결과를 식 (6) 대입하여 λ를 구하면 식 (9)와 같다:

1단계에서 계산된 중간추정값으로 구한 변위 벡터 $\tilde{d}={\tilde{p}}_2-{\tilde{p}}_1$는 방향 제약은 만족하지만, 속력 제약은 반영하지 않은 상태이다. 따라서, 방향은 유지한 채 크기만 조정하여 목표 변위 벡터 d’을 생성한다.

이제 문제는 p^′₁,p^′₂ 사이의 변위가 d’이 되도록 하는 선형 제약 조건하에서, 측정치와의 마할라노비스 거리를 최소화하는 문제로 정리된다:

subject to:

식 (11)의 목표 함수를 J₂라고 할 때, 라그랑지안 L₂=J₂-η^Th의 그래디언트를 0으로 두고 해를 구한다.

위 결과를 식 (12)에 대입하여 η를 계산하면 식 (15)와 같다.

다음으로, 추정된 초기 속도 벡터는 v’=d’/Δt로 계산된다.

추적 개시를 위해서는 초기 상태 벡터뿐만 아니라, 그 불확실성을 나타내는 초기 오차 공분산 행렬 p₂의 정확한 설정이 필수적이다. 앞서 유도한 상태 벡터 [p^′₂;v’]는 입력 위치 p^′₁,p^′₂에 대해 복잡한 비선형 변환 과정을 거쳐 얻어진 결과이다. 이와 같은 비선형 시스템에서의 정확한 공분산 추정을 위해 본 논문에서는 UT^[5]를 적용한다. UT는 자코비안 계산 없이, 입력 확률 분포를 대표하는 시그마 포인트(sigma point)를 이용하여 비선형 함수에 대한 확률적 효과를 근사하는 기법이다. 또한 이 과정에서 시그마 포인트들의 가중 평균으로 초기 상태 벡터를 추정한다.

제약 조건 자체가 갖는 물리적 불확실성까지 포함하기 위해 증강 상태 벡터(augmented state vector)를 적용한다. 이를 통해 제약 조건에 사용된 모델 파라미터의 오차를 확률 변수로 간주하여 상태 벡터에 포함하고, 전체 불확실성을 함께 고려한다.

증강 상태 벡터 및 오차 공분산 모델링은 다음과 같이 수행된다. 먼저 입력 벡터 x=[p₁;p₂]에 제약 조건의 불확실성을 나타내는 오차 항 w=[w_dir;w_spd]을 추가하여 8차원의 증강 상태 벡터를 정의한다:

이때 증강 상태의 평균 θ_a와 공분산 P_a는 식 (17) 및 식 (18)과 같이 정의된다:

여기서 σ_dir와 σ_spd는 예상 최대 이심률 e_max로부터 유도된 제약 조건의 표준편차이며, 3-6절에서 상세히 기술한다.

UT는 다음과 같은 시그마 포인트 생성, 비선형 함수 변환, 평균 및 공분산 계산의 3단계로 수행된다^[5]. 먼저 증강 상태 벡터와 공분산으로부터 2n+1=17개의 시그마 포인트 χ_i를 생성한다(n=8).

여기서 λ=α² (n+κ)는 스케일링 계수이며, 시그마 포인트의 분산을 조절한다. α와 κ는 각각 1, 0으로 설정하였다.

다음으로 비선형 함수 변환 단계는 다음과 같이 수행된다. 함수 H(·)를 앞서 기술한 p₁,p₂로부터 [p^′₂;v’]를 계산하는 알고리즘에서 w의 영향을 반영하기 위해 $V_{abs}=\sqrt{\mu /‖p_2‖}+w_{spd}$로 계산하고, 추정 속도 벡터 v’에 w_dirn₂만큼의 반경 방향 속도를 추가한 것으로 정의하고, 각 시그마 포인트에 대해 보정된 상태 벡터 y_i=H(χ)를 계산한다.

마지막으로 평균과 공분산 계산 과정에서는 최종 상태 벡터 x₂와 오차 공분산 p₂는 다음과 같이 시그마 포인트들의 가중 평균 및 가중 분산으로 계산된다:

여기서 W_m,i, W_c,i는 각각 평균 및 공분산 계산에 사용되는 가중치이다^[5]. 이 과정을 통해 제약 조건의 불확실성까지 포함한, 통계적으로 일관성 있는 초기 상태 오차 공분산 p₂를 도출할 수 있다. 또한 시그마 포인트들의 가중 평균인 x₂로 초기 상태 벡터를 초기화한다.

방향 제약은 속도 벡터가 위치 벡터에 수직함을 가정하므로, 실제 궤도에서의 반경 성분 속도 v_r는 이 제약 위반의 정도를 반영한다. 먼저, 타원 궤도에서 물체와 중심체 간 거리 r은 식 (22)와 같다^[3].

여기서 ν는 true anomaly이고, a는 장반경(semi-major axis)이다. 식 (22)를 시간에 대해 미분하면, 반경 성분 속도는 식 (23)과 같이 유도된다.

여기서 ν=±90°일 때 v_r이 최대가 되며, 이때 r=∥p₂∥를 가정하여 식 (22) 및 식 (23)으로부터 다음과 같이 근사할 수 있다:

여기에 최대 이심률 e_max를 적용하고, v_r의 최대 변동 폭(±e_maxV_abs)이 정규분포의 약 95 % 신뢰구간(±2σ_dir)에 해당한다고 가정하면^[8], 방향 제약의 표준편차는 식 (25)과 같이 근사할 수 있다.

다음으로, 속력 제약의 불확실성을 표현하는 표준편차 σ_spd는 아래과 같은 과정으로 추정한다. 이심률 e를 갖는 타원 궤도에서 근지점(perigee)과 원지점(apogee)에서의 속력은 vis-viva 방정식 v²=μ(2/r-1/a)^[3]에 따라 식 (26)과 같이 주어진다.

p₂가 근지점에 해당할 때(∥p₂∥=a(1-e_max)) 속력이 최대, 원지점에 해당할 때(∥p₂∥=a(1+e_max)) 속력이 최소가 된다. 이때 속력의 변동폭은 식 (27)과 같다:

이 변동폭이 정규분포의 약 95 % 신뢰구간(±2σ_spd)에 해당한다고 가정하면^[8], 식 (28)과 같이 표준편차를 근사할 수 있다.

우주물체와 레이다 측정치를 모의하고, 제안하는 알고리즘과 일반적인 2-point 초기화 방법의 성능을 동일한 환경에서 비교 분석하였다. 우주물체의 궤도는 2025년 5월 13일자 TLEs를 기반으로 SGP4(simplified general perturbations 4)^[9] 모델을 통해 생성하였다.

레이다 모델은 다음과 같이 설정하였다. 레이다는 대한민국 내 특정 위치(위도 36° N, 경도 128° E, 고도 0 m)에 위치하며, 안테나는 천정(zenith) 방향을 지향한다고 가정하였다. 최대 탐지 고도는 2,000 km로 설정하였다. 측정 오차는 평균이 0인 정규분포를 따르며, 표준편차는 거리 방향으로 10 m, 안테나 기준의 u,v 방향으로 각각 0.001으로 설정하였다.

제안하는 기법의 성능은 추적 소실률과 추적 정확도 두 가지 지표로 평가한다. 추적 소실률은 전체 트랙 중 추적 유효 영역(게이트)을 이탈하여 소실된 트랙의 비율을 의미한다. 여기서 게이트는 마할라노비스 거리의 제곱으로 결정되는 영역^[2]을 의미하고, 99.9 %의 포함 확률에 해당하는 임계값(16.2662)으로 설정하였다. 추적 정확도는 추정값과 참값의 차이를 나타내는 RMSE(root mean square error)로 계산한다.

각 시나리오에서 도출된 초기 상태 벡터와 오차 공분산은 확장 칼만 필터(extended Kalman filter)의 초기값으로 사용되며, 모든 시뮬레이션에서 총 30초 동안 0.5초의 추적 주기로 추적을 수행하였다.

전반적인 성능 분석을 위해, TLEs 데이터에 포함된 모든 우주물체 중, 24시간 이내에 특정 탐색 영역을 통과하는 물체에 대해 추적 실험을 수행하였다. 탐색 영역은 레이다 천정 기준 동서 방향으로 ±20°의 부채꼴 형태로 설정하였다. 표 1은 해당 시뮬레이션의 추적 소실률 결과를 요약한 것이다. 총 8,459개의 우주물체가 탐색 영역을 통과하였으며, 그중 500~1,000km 고도 범위의 물체가 5,569개로 가장 많았다. 제안하는 방법의 추적 소실률은 2.08 %로, 기존 방법의 4.73 %에 비해 절반 이하로 감소하였다. 특히 1,500~2,000 km의 고고도 구간에서 성능 차이(1.45 % vs 10.14 %)가 가장 크게 나타났다. 이는 시선거리가 멀어질수록 동일한 각도 오차가 더 큰 위치 오차로 변환되어 초기 속도 추정이 어려워지기 때문에 추적 소실률이 커질 수 있으나, 제안하는 기법이 이러한 환경에서 더 강인한 성능을 가진다는 것을 보여준다.

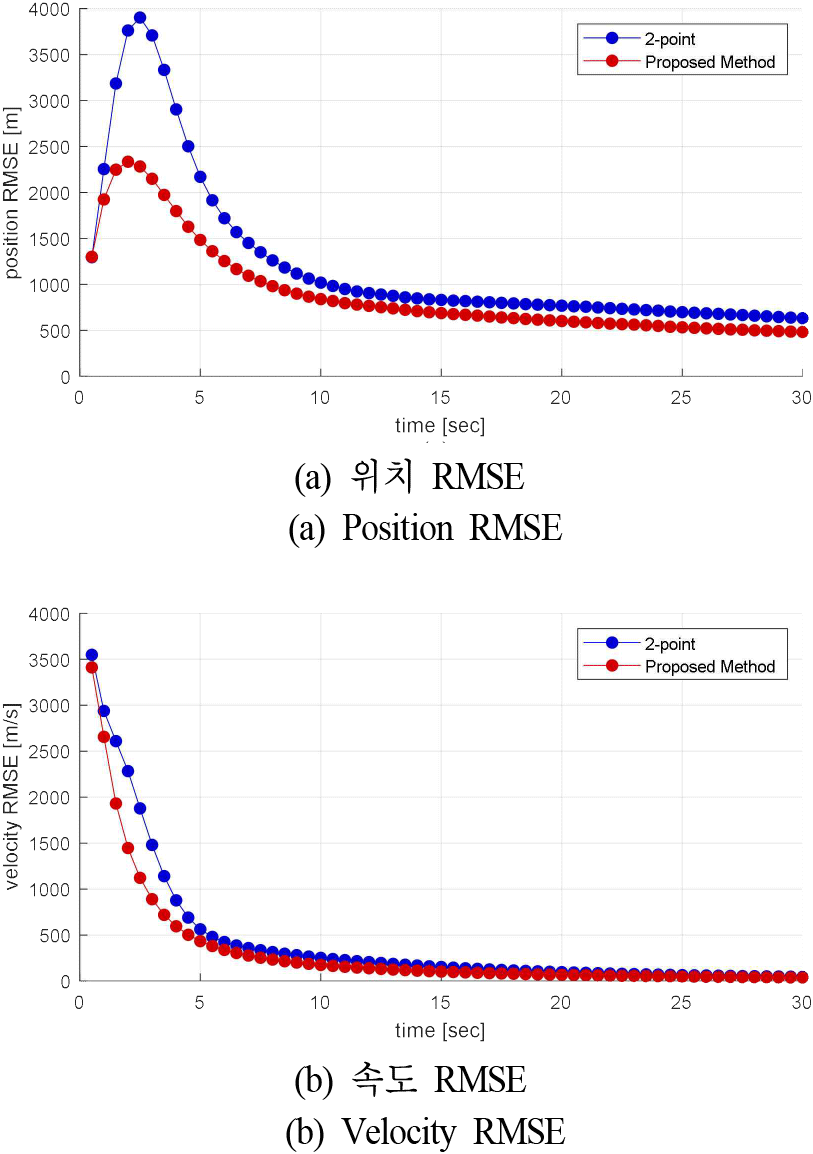
그림 2는 동일한 실험에서 모든 우주물체에 대한 추적 오차를 시간별 RMSE로 나타낸 것이다. 제안하는 방법이 기존 방법에 비해 전반적으로 낮은 위치 및 속도 오차를 보이며, 더 빠르게 수렴하는 것을 확인할 수 있다. 이는 정확한 초기 상태 추정이 후속 추적 필터의 전체 성능에 큰 영향을 미침을 보여준다.

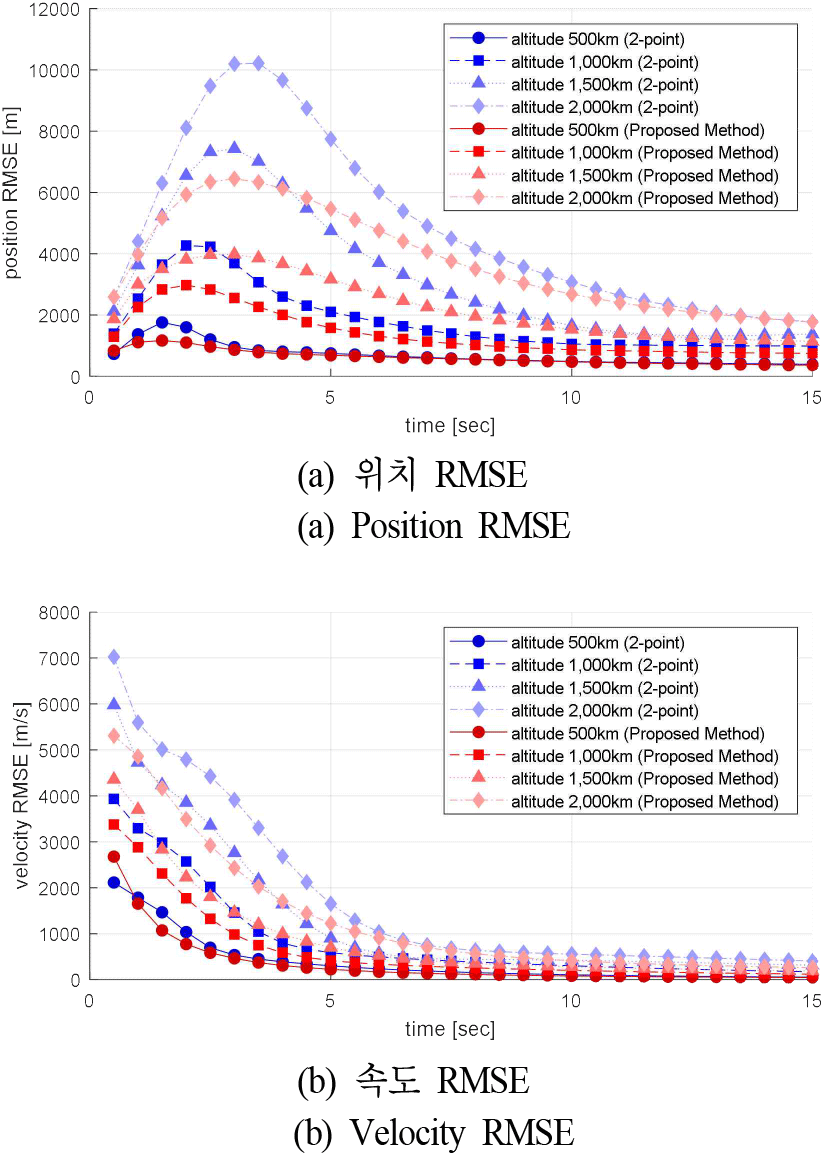
다음으로 고도 변화에 따른 성능을 확인하기 위해, 다양한 고도(500, 1,000, 1,500, 2,000 km)를 가지며, 이심률은 0.003을 가지는 가상의 우주물체의 TLEs를 생성하고, 이를 대상으로 각각 1,000회의 몬테카를로 시뮬레이션을 수행하였다. 그 결과는 그림 3에 나타내었으며, 시각적으로 비교를 용이하게 하기 위해 최초 15초 구간만 표시하였다. 두 방법 모두 고도가 높아질수록 RMSE가 증가하는 경향을 보였으나, 모든 고도에서 제안하는 방식이 더 낮은 오차를 가짐을 확인할 수 있다. 고도가 높아질수록 오차가 증가하는 것은 레이다의 각도 오차가 시선거리 증가에 따라 더 큰 위치 오차를 유발하기 때문이다. 또한, 동일한 시뮬레이션에서의 추적 소실률에 대한 결과는 표 2와 같다. 기존 2-point 초기화 방식은 고도 500, 1,000, 1,500 2,000 km의 우주물체에 대해 추적 소실 횟수가 1, 39, 62, 153회 나타난 반면, 제안하는 방법은 단 한 번의 소실도 발생하지 않았다. 이는 제안하는 방법이 고도가 높아짐에 따라 초기 추정 오차 증가에 의한 추적 실패 가능성이 증가함에도 불구하고, 물리적 제약을 통해 비교적 정확한 초기 속도 추정이 가능하여 우수한 성능을 유지할 수 있음을 보여준다.

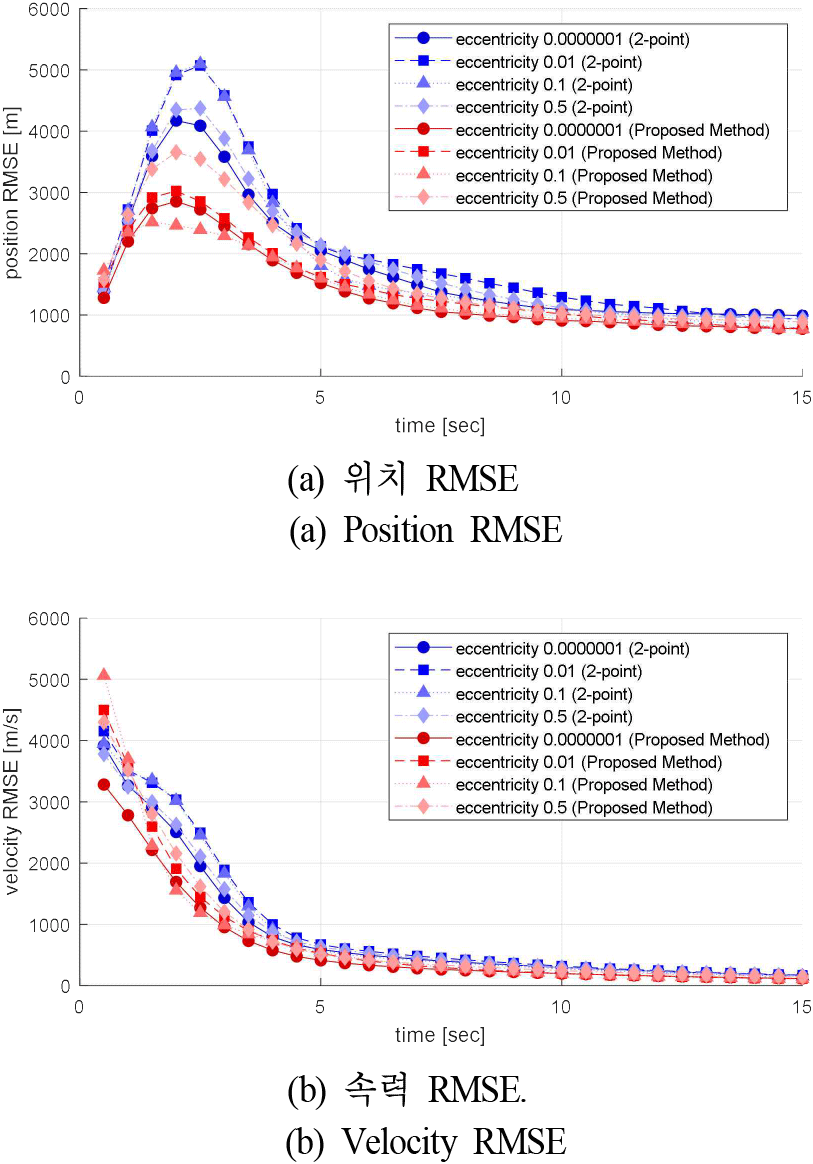
마지막으로 이심률 변화에 따른 성능을 확인하기 위해, 다양한 이심률(0.0000001, 0.01, 0.1, 0.5)을 갖는 가상 우주물체의 TLEs를 생성하고, 이를 대상으로 시뮬레이션을 수행하였다. 이심률 변화의 효과를 명확히 비교하기 위해, 모든 표적이 동일하게 1,000 km의 근지점 고도를 갖도록 설정하였다. 각 이심률에 대해 1,000회의 몬테카를로 시뮬레이션을 수행한 결과는 그림 4와 같다. 이전 결과들과 마찬가지로 제안하는 방식이 전반적으로 뛰어난 성능을 보였으며, 이심률이 커질수록 RMSE가 증가하는 경향을 보였다. 이는 이심률이 클수록 준원궤도라는 제안 기법의 기본 가정에서 벗어나기 때문으로 해석할 수 있다. 또한 해당 시뮬레이션에서 추적 소실률에 대한 결과는 표 3과 같다. 기존 2-point 초기화 방식은 이심률 0.0000001, 0.01, 0.1, 0.5에 대해 각각 추적 소실 횟수가 28, 63, 78, 49회로 나타난 반면, 제안하는 방법은 0, 0, 0, 1회의 추적 소실만이 발생하였다. 이는 제안하는 방법이 추적 소실률 관점에 있어, 이심률 변화에도 안정적인 추적이 가능함을 보여주고, 이는 이심률의 불확실성에 대한 영향을 UT를 통해 효과적으로 반영하였기 때문으로 해석할 수 있다.