J. Korean Inst. Electromagn. Eng. Sci. 2025; 36(12):1153-1164

pISSN: 1226-3133, eISSN: 2288-226X

DOI: https://doi.org/10.5515/KJKIEES.2025.36.12.1153

논문/REGULAR PAPERS

광대역 노이즈 입력에 대한 MOSFET 스위칭 회로의 출력 특성 예측

권태욱https://orcid.org/0009-0003-1971-3991, 최경륜https://orcid.org/0000-0002-3649-0000, 이한양https://orcid.org/0009-0007-7810-604X, 한준희https://orcid.org/0000-0002-7759-6717, 나완수†https://orcid.org/0000-0002-0315-3294
Prediction of the Output Characteristic of a MOSFET Switching Circuit with Broadband Noise Excitation
Taewook Kwonhttps://orcid.org/0009-0003-1971-3991, GyeongRyun Choihttps://orcid.org/0000-0002-3649-0000, Hanyang Lihttps://orcid.org/0009-0007-7810-604X, Junhee Hanhttps://orcid.org/0000-0002-7759-6717, Wansoo Nah†https://orcid.org/0000-0002-0315-3294
Author Information & Copyright ▼
성균관대학교 전자전기컴퓨터공학과
Department of Electrical and Computer Engineering, Sungkyunkwan University
†Corresponding Author: Wansoo Nah (e-mail: wsnah@skku.edu)

© Copyright 2025 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Aug 28, 2025; Revised: Oct 01, 2025; Accepted: Oct 02, 2025

Published Online: Dec 31, 2025

요 약

본 논문은 복잡한 전파 환경에 노출된 MOSFET 스위칭 회로의 특성을 회로 시뮬레이션을 통해 예측하고자 하였다. 외부 노이즈 신호원으로는 방사 내성 표준 IEC 61000-4-3, ISO 11452-1에 준하는 CW, AM, PM 신호를 사용하였으며, 광대역 노이즈 신호원으로는 20 MHz 대역폭의 OFDM 신호를 사용하였다. Dambrine의 방법을 적용하여 소자 내부 및 외부 성분 추출하였으며, 시뮬레이션에 반영함으로써 예측 정확도를 증가시켰다. 노이즈 신호는 DPI 방법으로 인가하였으며, 각 신호원에 대한 회로의 영향을 비교하였다. 그 결과, CW와 PM 신호보다 AM과 OFDM 신호가 스위칭 회로의 오동작을 일으킬 가능성이 높다는 것을 확인하였다. 또한, 시뮬레이션에서 그 결과를 예측할 수 있었다.

Abstract

This study aimed to predict the input and output characteristics of MOSFET switching circuits exposed to complex electromagnetic environments through circuit simulations. CW, AM, and PM signals compliant with the radiated immunity standards IEC 61000-4-3 and ISO 11452-1 were used as external noise sources, and a 20 MHz bandwidth OFDM signal was used as a broadband noise source. Dambrine’s extraction method was applied to extract the intrinsic and extrinsic components of the device, which were incorporated into the simulation model, resulting in improved prediction accuracy. The noise signals were applied using the DPI method, and the effects of each signal source on the circuit were compared. The results showed that AM and OFDM excitations are more likely to induce malfunctions than CW or PM excitations. Furthermore, the proposed simulations accurately predicted these outcomes.

Keywords: MOSFET Switching Circuit; OFDM; Extrinsic and Intrinsic Parameters Extraction; Direct Power Injection; EMC

Ⅰ. 서 론

최근 빠르게 증가하는 무선기기 데이터를 처리하기 위한 방법으로 광대역 디지털 통신이 응용되고 있다[1]. 일반적으로 OFDM(orthogonal frequency division multiplexing) 신호가 사용되고 있으며, 이러한 무선 통신 기술 발달로 인해 전자파 공간 복잡도가 증가하고 있다[2]. 이에 따라, 전자파 간섭(EMI, electromagnetic interference) 문제로 인한 전자기기의 오동작 사례가 발생하고 있다[3]. 오동작 원인 중 하나는 외부 노이즈 신호가 전자기기 내부 소자에 결합되는 경우이다[4]. 내부 소자 중 비선형 소자에 직접 결합되는 경우, 비선형 특성으로 인한 고조파(harmonics)와 상호 변조 효과(intermodulation effect)로 인해 전자기기 시스템에 치명적인 문제가 발생할 수 있다[5],[6]. 본 논문에서는 외부 노이즈 신호가 전자기기 내부의 비선형 소자에 직접 결합되는 경우를 모사하기 위해 단일 MOSFET(metal oxide semiconductor field effect transistor) 스위칭 회로를 사용하였으며, 외부 노이즈는 DPI(direct power injection) 방식으로 회로의 gate 단에 CE(conducted emission) 형태로 인가하였다. 외부 노이즈 신호원으로는 방사 내성 표준 IEC 61000-4-3, ISO 11452-1에 준하는 CW(continuous wave), AM(amplitude modulation), PM(pulse modulation) 신호를 사용하였으며, 광대역 신호원으로는 20 MHz 대역폭을 가지는 OFDM 신호를 사용하였다.

회로 시뮬레이션 모델은 제작사에서 제공되는 경우가 많다. 하지만, 일반적으로 대표적인 동작 기준에 맞춰 파라미터가 설정되어 있으며, 소자 자체의 특성만 반영되어 있다. 따라서, DUT(device under test)의 동작 조건이 다르거나 PCB(printed circuit board) 위에 탑재할 경우에는 시뮬레이션 결과가 부정확할 수 있다[7]~[9]. 이러한 모델을 여러 주파수 성분이 포함된 광대역 시뮬레이션에 사용할 시 정확도가 매우 떨어질 수 있다. 본 논문에서는 광대역 노이즈 시뮬레이션의 정확도를 증가시키기 위해, Dambrine의 추출 모델을 이용하여, 소자 및 PCB의 내부와 외부 성분을 측정 기반으로 추출하고, 이를 반영한 확장 모델을 구현하였다[10]. 외부 노이즈 신호에 의한 스위칭 회로의 출력 특성 변화를 측정하였으며, 그 결과를 확장 모델과 비교하였다. 기존 모델 대비 전자파 간섭 예측 정확도가 상승하였음을 보였다.

Ⅱ. 내부 및 외부 성분 추출 이론

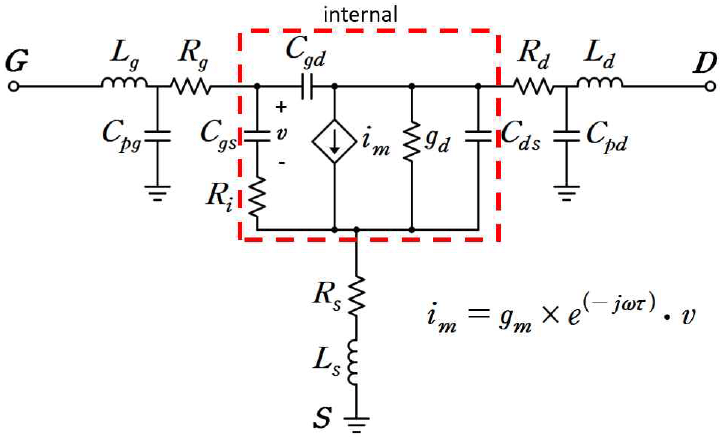
그림 1은 보편적인 FET 소신호 등가회로 모델이다. 이 소신호 등가회로 모델에서 내부와 외부 성분으로 나눌 수 있다. 내부 성분은 전압 레벨에 종속된 성분으로 Cgs,Cgd,Cds,gd,gm,τ이다[11]. 이때, gd는 채널에 대한 컨덕턴스, gm은 트랜스컨덕턴스, Ri는 Cgs의 채널 저항, τ는 위상 지연을 나타낸다. 외부 성분은 전압 레벨과 독립적인 성분으로 Cpg,Lg,Rg,Rs,Ls,Rd,Ld,Cpd이다. 이때, Lg,Rg,Rs,Ls,Rd,Ld는 PCB의 마이크로스트립 라인(microstrip line)을 포함한 기생 저항과 기생 인덕턴스이다. Cpg와 Cpd는 패드와 접지면 사이의 커패시턴스이다[10],[12].

jkiees-36-12-1153-g1
그림 1. | Fig. 1. FET 소신호 등가회로 모델 | Small-signal equivalent circuit model of a FET.
Download Original Figure

내부 및 외부 성분은 Y 파라미터와 Z 파라미터를 이용하여 단계적으로 추출된다. 자세한 추출 과정 및 값은 Ⅲ장에서 기술하며, 내부 성분 추출 과정은 과정 (a)~(e)를 따른다[10]:

  1. DUT의 2 포트 S 파라미터를 측정한다;

  2. S 파라미터를 Z 파라미터로 변환하여, 외부 직렬성분 Lg와 Ld를 제거한다;

  3. Z 파라미터를 Y 파라미터로 변환하여, 외부 병렬성분 Cpg와 Cpd를 제거한다;

  4. Y 파라미터를 Z 파라미터로 변환하여, 나머지 외부 성분 Rg,Rs,Rd,Ls를 제거한다;

  5. Z 파라미터를 Y 파라미터로 변환하여, 내부 성분Cgs,Cgd,Cds,im,gd,Ri를 추출한다.

과정 (a)~(d)를 통해 외부 성분을 제거할 수 있다. 그러므로 과정 (e)를 통해 내부 성분의 Y 파라미터를 얻을 수 있으며, 식 (1)~식 (4)와 같이 표현할 수 있다[11].

y 11 = R i C g s 2 ω 2 D + j ω C g s D + C g d
(1)
y 12 = − j ω C g d
(2)
y 21 = g m e ( − j ω τ ) 1 + j R i C g s ω − j ω C g d
(3)
y 22 = g d + j ω C d s + C g d w i t h   D = 1 + ω 2 C g s 2 R i 2
(4)

일반적인 저잡음 소자의 경우 ω2Cgs2Ri2이 0.01보다 작으므로 D=1이다. 또한, ωτ≪1에서 식 (1)~식 (4)은 식 (5)~식 (8)과 같이 근사화할 수 있다[10].

y 11 = R i C g s 2 ω 2 + j ω C g s + C g d
(5)
y 12 = − j ω C g d
(6)
y 21 = g m − j ω C g d + g m R i C g s + τ
(7)
y 22 = g d + j ω C d s + C g d
(8)

Ⅲ. 측정 기반 내부 및 외부 성분 추출

본 논문에서는 제작사에서 제공한 ADS(advanced design system) 회로 모델을 기반으로 하였으며, gd,gm,τ,Ri는 데이터 시트를 참고하였다. 그 외 성분들은 과정 (a)~(e)를 단계적으로 진행하여 추출하였다. 추출된 기생 성분을 기존 회로 모델에 반영하여 모델을 확장하였으며, 기존 모델과의 비교 결과는 Ⅳ장에서 보이겠다.

3-1 외부 기생 저항 및 기생 인덕턴스 추출

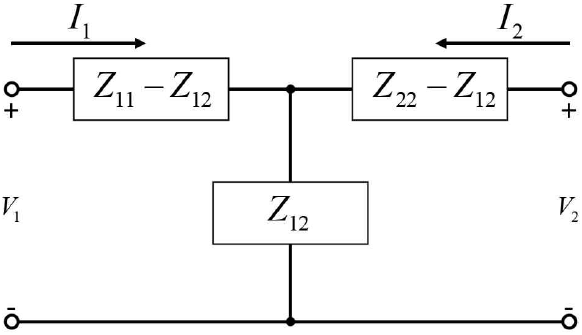
Rg, Rs, Rd, Lg, Ls, Ld를 추출하기 위해 Vgs>Vth,Vdd=0 V조건에서 S 파라미터를 측정하였다. 위 조건에서는 채널이 충분히 형성되기 때문에 Cds의 영향을 무시할 수 있다[10]. Cgs, Cgd의 경우 Cg로 등가하였다. Cpg, Cpd의 경우 본 단계에서는 무시하였으며, 이 값은 3-2장에서 확인할 수 있다. 또한, 출력 컨덕턴스 gm은 채널 저항과 역수 관계이며, 채널 저항은 여러 개의 분포 저항으로 분리할 수 있다[10]. 따라서, 그림 2와 같이 소신호 등가회로로 표현할 수 있다. Cg는 gate 단자와 채널 사이의 절연층으로 인한 커패시턴스이다. Rcs, Rcd는 채널 저항 성분이며, 서로 같다고 가정한다.

jkiees-36-12-1153-g2
그림 2. | Fig. 2. Vgs>0 V, Vdd=0 V에서 DUT의 소신호 등가회로 모델 | Small-signal equivalent circuit model of the DUT under Vgs>0 V, Vdd=0 V.
Download Original Figure

그림 3은 DUT가 2 포트일 때의 Z 파라미터이다. 따라서 그림 2의 gate, source, drain 단 Z 파라미터 Zg, Zs, Zd를 식 (9)~식 (11)과 같이 표현할 수 있다.

Z g = Z 11 − Z 12 = R g + j ω L g + 1 j ω C g
(9)
Z s = Z 12 = Z 21 = R s + R c s + j ω L s
(10)
Z d = Z 22 − Z 12 = R d + R c d + j ω L d
(11)
jkiees-36-12-1153-g3
그림 3. | Fig. 3. DUT가 2 포트일 때, Z 파라미터 | Z-parameters for a two-port DUT.
Download Original Figure

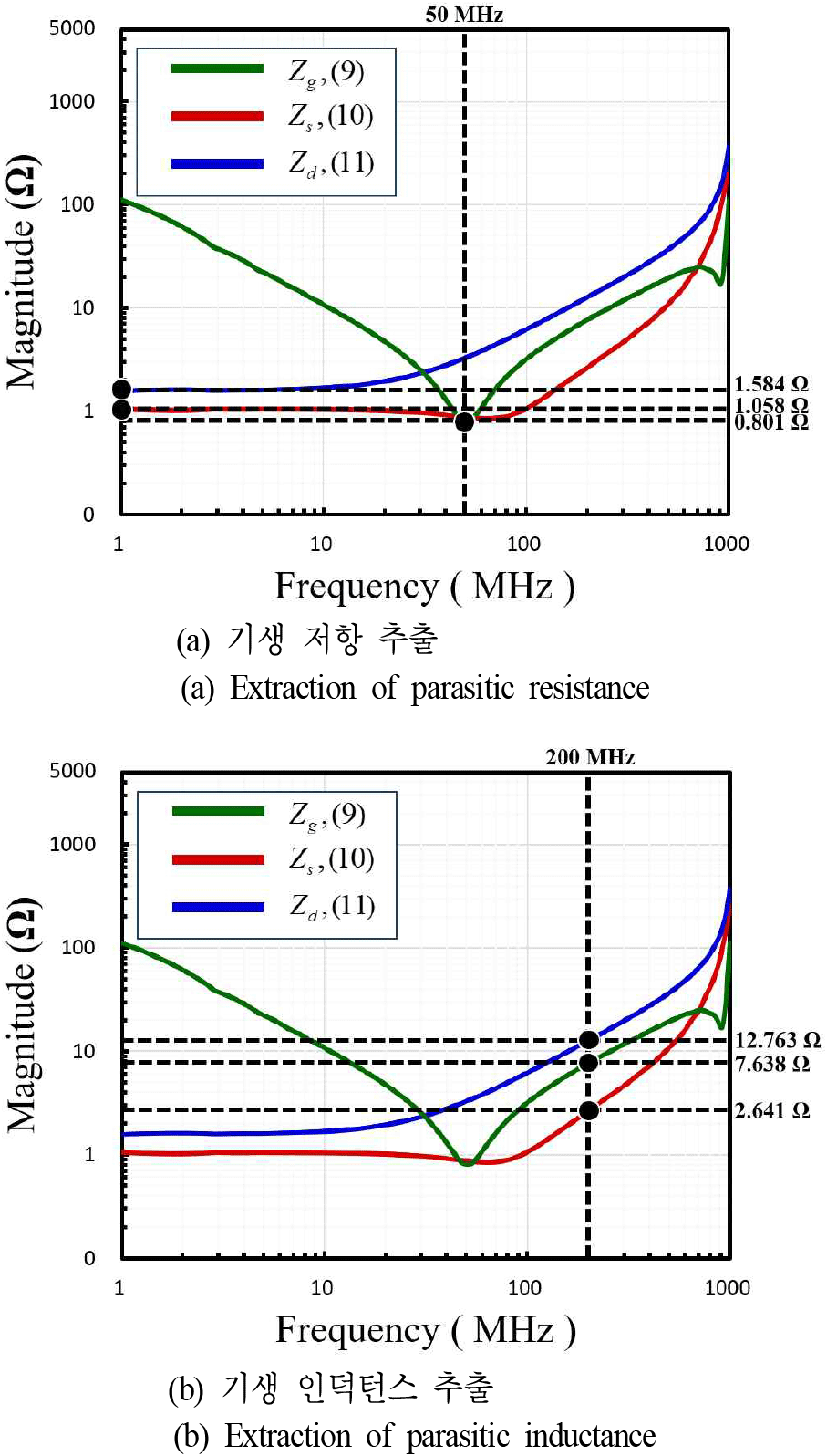
측정된 ~Zg~, ~Zs~, ~Zd~는 그림 4와 같다. 그림 4(a) 및 그림 4(b)는 같은 그림이며, 그림 4(a)에서는 기생 저항을, 그림 4(b)에서는 기생 인덕턴스를 추출하였다. ~Zg~는 식 (9)에 의해 Rg,Lg,Cg 성분이 있으며, 공진 주파수 50 MHz를 기준으로 Rg,Lg,Cg 성분이 잘 나타났음을 확인할 수 있다. ~Zs~와 ~Zd~는 식 (10) 및 식 (11)에 의해 저항 Rs,Rcs,Rd,Rcd와 인덕턴스 Ls,Ld 성분만 존재하는데 이 또한 잘 나타났음을 확인할 수 있다. 기생 저항의 경우, 1 MHz에서 추출하였으며 채널 저항은 데이터 시트를 참고하여 Rcs=Rcd=0.0125 Ω을 사용하였다. 기생 인덕턴스의 경우, 200 MHz에서 추출하였다. 추출된 값은 표 1과 같다.

jkiees-36-12-1153-g4
그림 4. | Fig. 4. Zg, Zs, Zd의 크기 | Magnitude of Zg, Zs and Zd.
Download Original Figure
표 1. | Table 1. 추출된 기생 저항과 기생 인덕턴스 | The extracted parasitic resistance and parasitic inductance values.
Parameters Extracted values
Parasitic resistance Rg 0.801 Ω
Rs 1.0455 Ω
Rd 1.5715 Ω
Parasitic inductance Lg 6.0781 nH
Ls 2.1016 nH
Ld 10.156 nH
Download Excel Table
3-2 외부 기생 커패시턴스 Cpg,Cpd 추출

기생 커패시턴스 Cpg는 gate 패드와 접지면 사이의 커패시턴스이며, Cpd는 drain 패드와 접지면 사이의 커패시턴스이다. 측정 기반으로 Cpg,Cpd를 추출한 다른 연구들에서는 온 웨이퍼(on-wafer) 상태에서 추출했기 때문에 Cpg, Cpd가 fF 정도로 매우 작다[13]~[15]. 하지만, 본 논문에서는 PCB를 포함하기 때문에 PCB에 의한 Cpg,Cpd가 지배적이다. 따라서 본 논문에서는 MOSFET 자체의 Cpg,  Cpd보다 PCB에 의한 Cpg, Cpd가 매우 크다고 가정하였다. 이때 Cpg,Cpd를 식 (12) 및 식 (13)과 같이 근사화할 수 있다.

C p g = C p g − M O S F E T + C p g − P C B ≃ C p g − P C B
(12)
C p d = C p d − M O S F E T + C p d − P C B ≃ C p d − P C B
(13)

Cpg-PCB와 Cpd-PCB는 MOSFET을 포함하지 않은 상태의 PCB를 측정함으로써 추출할 수 있다. 그때의 소신호 등가회로 모델은 그림 5와 같다. 여기서 Cbgd는 gate와 drain 단 마이크로스트립 라인의 상호 커패시턴스이다. Source 단의 경우, ground이기 때문에 등가회로에서 제외하였다.

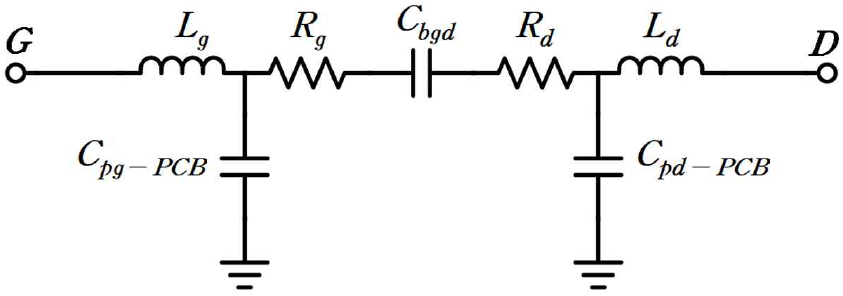
jkiees-36-12-1153-g5
그림 5. | Fig. 5. MOSFET이 탑재되지 않은 PCB의 소신호 등가회로 모델 | Small—signal equivalent circuit model of PCB without the MOSFET.
Download Original Figure

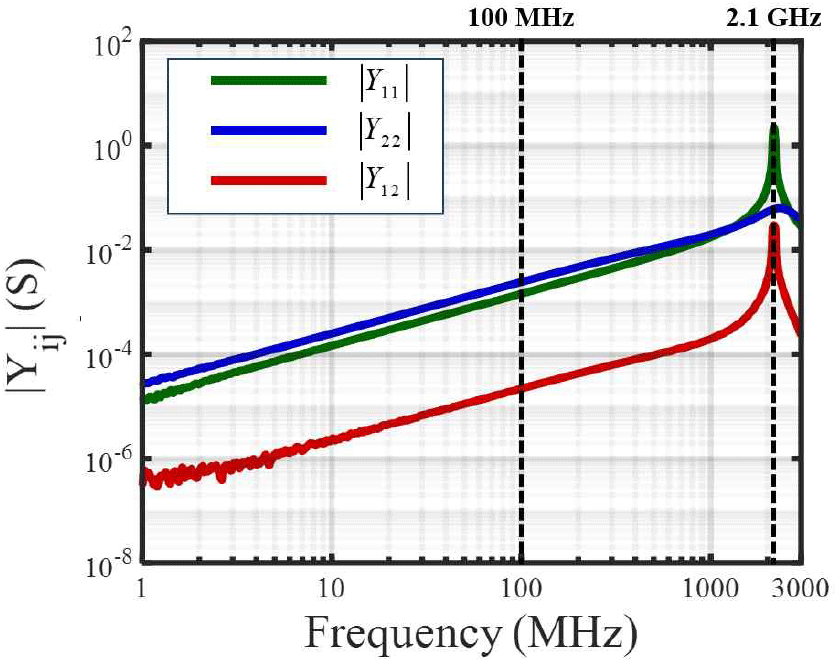
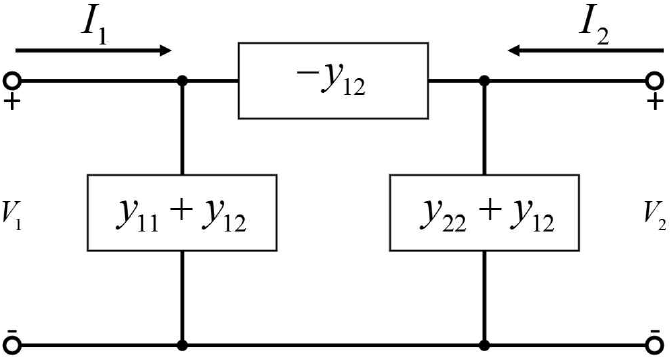
그림 6은 측정된 Y11,Y12,Y22의 크기이다. 약 2 GHz에서 공진이 발생한 것을 볼 수 있으며, 100 MHz 이하 주파수 대역에서 저항 성분과 인덕턴스 성분은 무시되고 커패시턴스 성분만 있음을 확인할 수 있다. 따라서 100 MHz 이하 주파수 대역에서의 커패시턴스는 식 (14)~식 (19)와 같다.

I m Y 11 = j ω C p g − P C B + C b g d
(14)
I m Y 12 = I m Y 21 = − j ω C bgd 
(15)
I m Y 22 = j ω C p d − P C B + C b g d
(16)
C p g − P C B = I m Y 11 − I m Y 12 ω
(17)
C b g d = − I m Y 12 ω = − I m Y 21 ω
(18)
C p d − P C B = I m Y 22 − I m Y 12 ω
(19)
jkiees-36-12-1153-g6
그림 6. | Fig. 6. Y11,Y12,Y22의 크기 | Magnitude of Y11,Y12, and Y22.
Download Original Figure

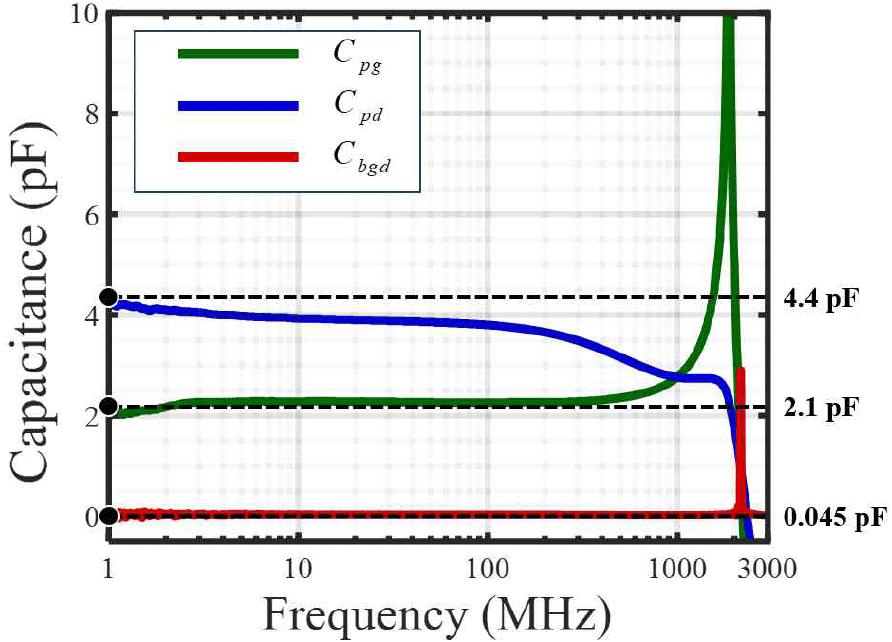
식 (14)~식 (19)에 의해 Cpg-PCB, Cpd-PCB, Cbgd를 추출하였으며, 주파수별 값은 그림 7과 같다. 이때, 1 MHz일 때의 커패시턴스 값을 추출하였으며, 표 2와 같다.

jkiees-36-12-1153-g7
그림 7. | Fig. 7. 추출된 Cpg,Cpd,Cbgd | The extracted Cpg,Cpd, and Cbgd.
Download Original Figure
표 2. | Table 2. 추출된 Cpg, Cpd, Cbgd | The extracted Cpg, Cpd and Cbgd.
Parameters Extracted values (pF)
Parasitic capacitance Cpg 4.4
Cpd 2.1
Cbgd 0.045
Download Excel Table
3-3 내부 기생 커패시턴스 Cgs,Cgd,Cds 추출

추출된 Rg,Rs,Rd,Lg,Ls,Ld,Cpg,Cpd를 제거하고 Y 파라미터로 변환하여, 기생 커패시턴스 Cgs,Cgd,Cds를 추출하였다. 외부 성분을 모두 제거한 상태이기 때문에 그림 1에서 내부 성분만 남아있다. 따라서, 그림 8과 같이 DUT가 2 포트일 때 Y 파라미터로 변환할 수 있다. 따라서, Cgs,Cgd,Cds를 식 (5) 및 식 (6) 그리고 식 (8)을 이용하여 식 (20)~식 (22)와 같이 표현할 수 있다.

I m y 11 + y 12 = ω C g s
(20)
I m y 12 = − ω C g d
(21)
Im y 22 + y 12 = ω C d s
(22)
jkiees-36-12-1153-g8
그림 8. | Fig. 8. DUT가 2 포트일 때, Y 파라미터 | Y-parameters for a two-port DUT.
Download Original Figure

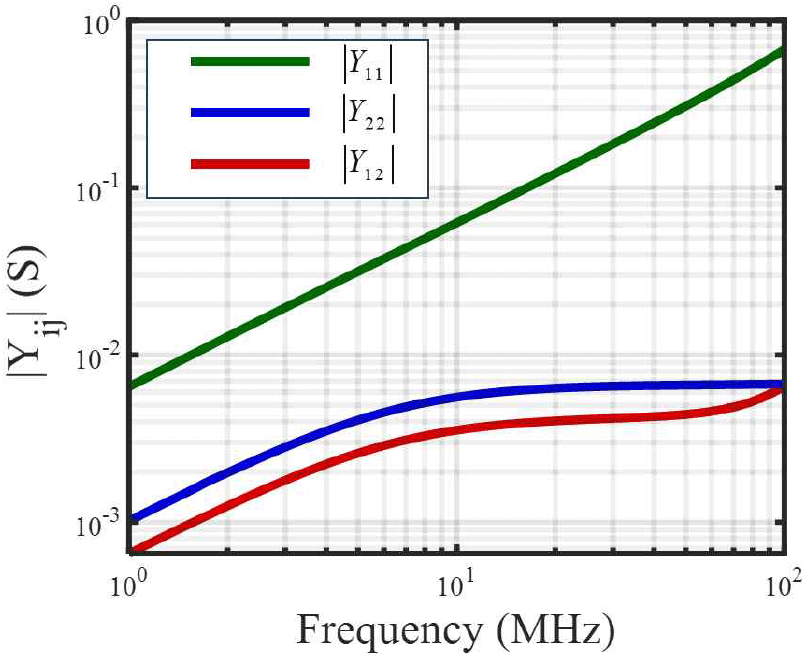
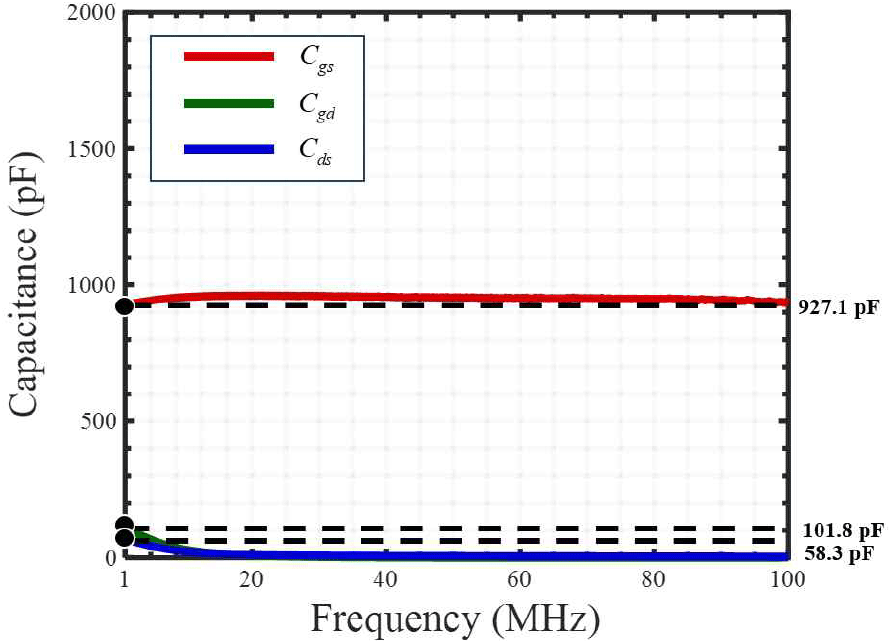
그림 9는 Vgs=0,Vdd=5 V일 때, |Y11|,|Y12|,|Y22|이며 그때의 Cgs,Cgd,Cds는 그림 10과 같다. Cgs,Cgd,Cds는 MOSFET의 스위칭 주파수가 1 MHz인 것을 고려하여, 1 MHz에서 추출하였다. Cgs,Cgd,Cds의 경우, 전압에 따라 변하는 파라미터이다. 따라서 Vgs=0, Vdd를 0~5 V까지 1 V 간격으로 추출하였으며, 그 결과는 표 3과 같다.

jkiees-36-12-1153-g9
그림 9. | Fig. 9. Vgs=0, Vdd=5 V일 때 |Y11|, |Y12|, |Y22| | |Y11|, |Y12| and |Y22| at Vgs=0 and Vdd=5 V.
Download Original Figure
jkiees-36-12-1153-g10
그림 10. | Fig. 10. Vgs=0 and Vdd=5 V일 때 Cgs,Cgd,Cds | Cgs,Cgd, and Cds at Vgs=0 and Vdd=5 V.
Download Original Figure
표 3. | Table 3. 추출된 Cgs, Cgd, Cds | The extracted Cgs, Cgd, and Cds.
Parameters
Bias Extracted values
Vdd Cgs (pF) Cgd (pF) Cds (pF)
0 937.1 221.1 169.9
1 939.4 150.9 106.1
2 936.1 130.5 84.8
3 932.7 117.8 73.1
4 929.7 108.8 64.1
5 927.1 101.8 58.3
Download Excel Table

Ⅳ. 시뮬레이션 및 측정 결과

Ⅲ장에서 추출한 내부 및 외부 성분들을 회로 시뮬레이션에 적용하여, 확장 모델을 구축하였다. Ⅳ장에서는 기존 모델과 확장 모델을 측정과 비교하여 확장 모델을 검증하였다. 확장 모델의 경우, 전압에 따라 기생 커패시턴스 값이 자동으로 바뀌도록 구현하지는 않았으며, Ⅳ장에서 보인 모든 결과는 Vdd=5 V를 기준으로 하였으므로, 표 3을 참고하여 그에 해당하는 기생 커패시턴스 값 Cgs=927.1 pF, Cgd=101.8 pF, Cds=58.3 pF을 고정하여 사용하였다.

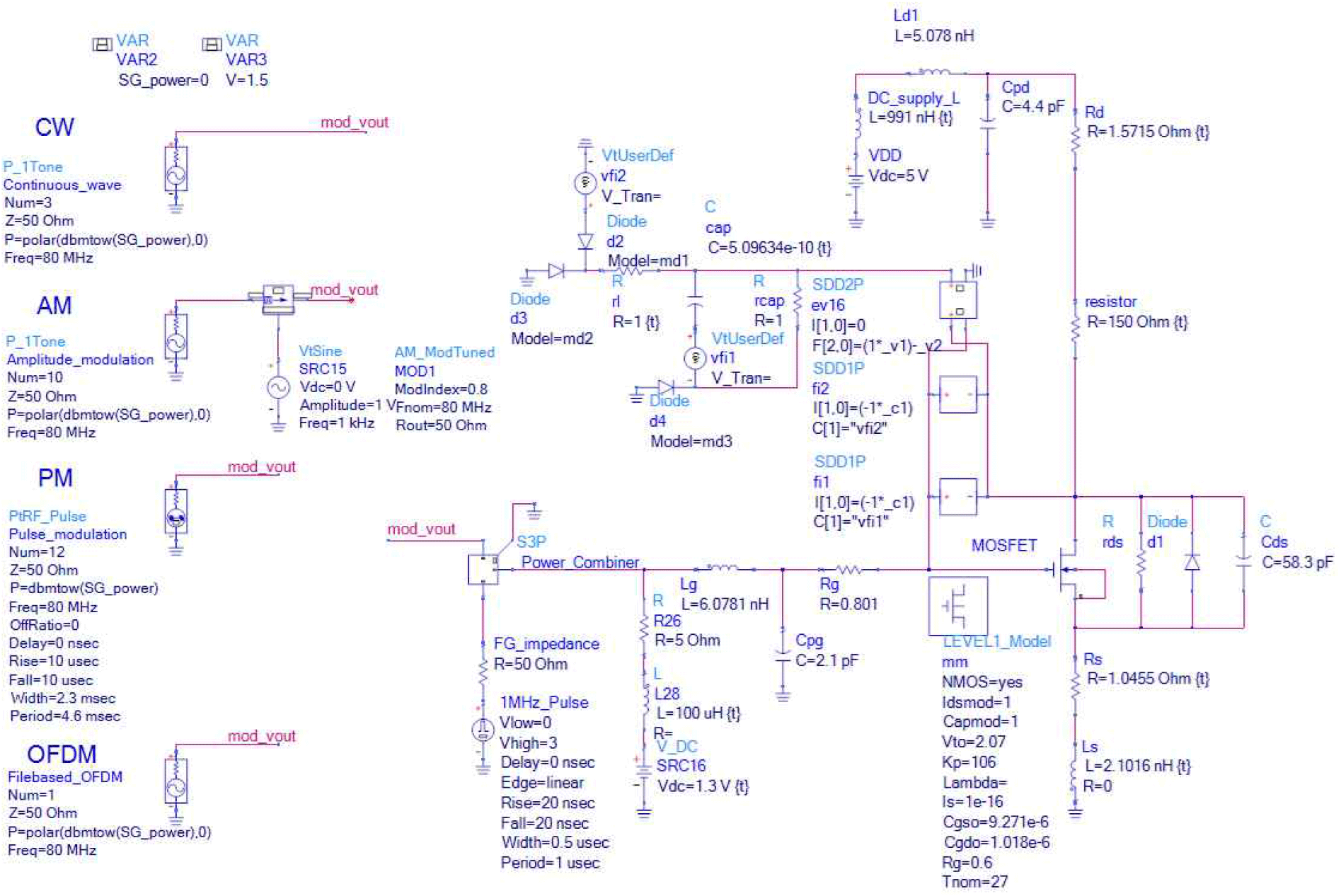
그림 11은 내부 및 외부 성분들을 모두 반영한 확장 모델이다. Gate 단에 노이즈를 인가하기 위해 사용한 전력 결합기(power combiner), 바이어스 티(bias tee), 함수 발생기(function generator), 벡터 신호 발생기(vector signal generator), DC supply를 모두 반영하였다. 또한, 외부 노이즈 신호 CW, AM, PM 그리고 OFDM 신호를 실제 발생 파형과 동일한 파형을 발생시킬 수 있도록 설정하였다. 이때 CW, AM 그리고 PM 신호 같은 경우, ADS 자체 기능을 사용하여 발생시켰다. OFDM 신호는 MA-TLAB의 무선 파형 생성 기능을 사용하여 적절한 OFDM 파라미터를 선정하였으며, 그 파라미터를 파형 생성 MATLAB 코드에 적용하였다. 생성된 데이터 기반 파일을 ADS에 적용하여 OFDM 신호를 발생시켰다.

jkiees-36-12-1153-g11
그림 11. | Fig. 11. 확장 모델 | Extended model.
Download Original Figure
4-1 확장 모델 검증

확장 모델을 검증하기 위해 노이즈가 없을 때 스위칭 회로의 입력/출력과 노이즈 신호가 인가된 스위칭 회의 입력/ 출력을 측정과 비교하였다. 측정 셋업은 그림 12와 같으며, 측정 장비 설정은 표 4와 같다.

jkiees-36-12-1153-g12
그림 12. | Fig. 12. 측정 셋업 | Measurement setup.
Download Original Figure
표 4. | Table 4. 측정 장비 설정 | Measurement instruments and settings.
Instrument Parameter Setting
DC supply Drain voltage 5 V
Gate voltage 1.3 V
Function generator Signal Pulse wave
Frequency 1 MHz
Duty cycle 50 %
Rise / fall time 20 ns
Vp-p 3 V
DC offset 0 V
Vector signal generator Signal Continuous wave
Frequency 10 MHz
Power 0 dBm
Download Excel Table

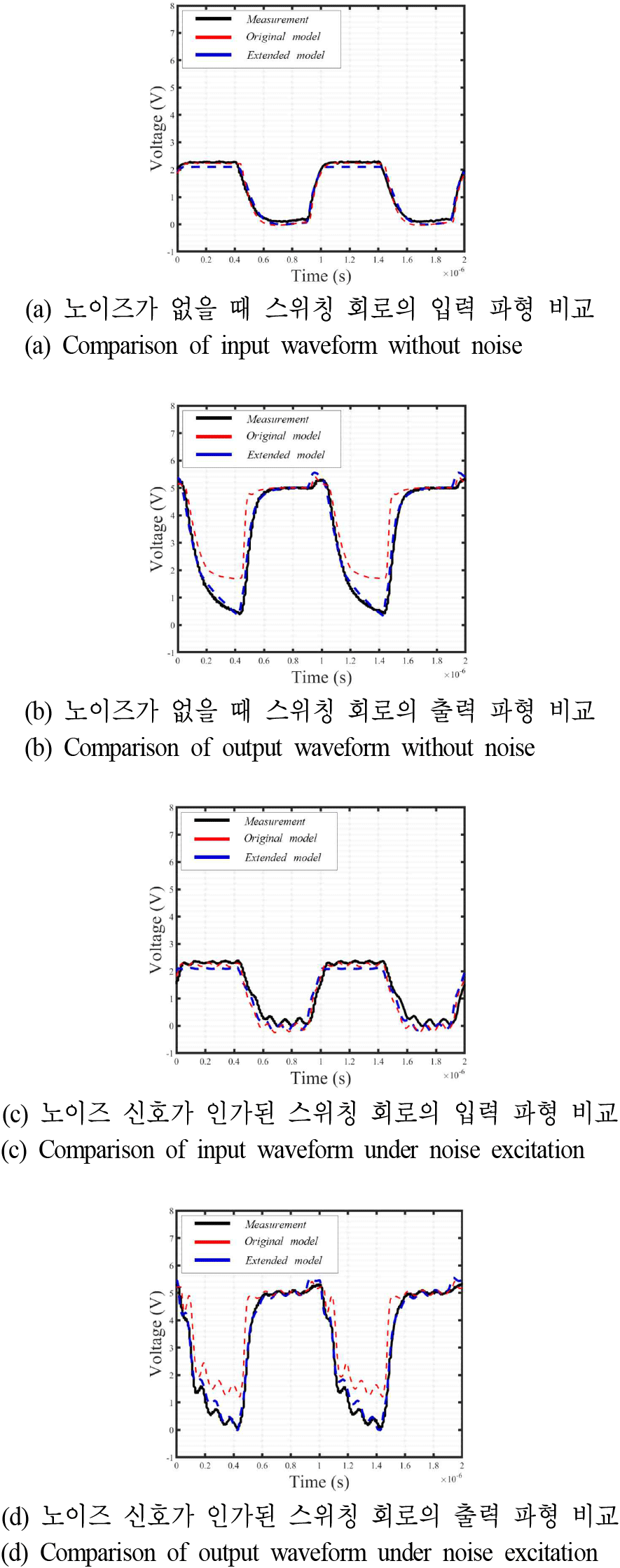
그림 13은 제작사에서 제공한 기존 모델, 본 논문에서 제시한 확장 모델 그리고 측정의 입력/ 출력 파형을 비교한 결과이다. 그림 13(a) 및 그림 13(b)는 노이즈가 없을 때 스위칭 회로의 입력/출력 파형이다. 입력 파형의 경우, 두 모델 모두 측정과 매우 유사한 것을 확인할 수 있다. 출력 파형의 경우, 기존 모델이 측정에 비해 1 V 이상 차이가 나는 것을 확인할 수 있다. 그림 13의 (c)와 (d)는 전력이 0 dBm이고, 주파수가 10 MHz인 CW 노이즈 신호가 인가된 스위칭 회로의 입력/출력 파형이다. 그림 13(a) 및 그림 13(b) 결과와 마찬가지로 입력 파형은 두 모델 모두 측정과 매우 유사하며, 출력 파형에서 기존 모델의 오차가 발생했다. 따라서, 확장 모델이 기존 모델보다 정확도가 높은 것을 알 수 있다. 결론적으로 Ⅲ장에서 추출된 내부 및 외부 성분들은 적절한 과정으로 추출되었다고 볼 수 있다. 또한, 전력 결합기, bias tee, 함수 발생기, 벡터 신호 발생기의 영향들이 시뮬레이션에 잘 반영되었음을 확인할 수 있다.

jkiees-36-12-1153-g13
그림 13. | Fig. 13. 스위칭 회로의 입력/출력 파형 비교 | Comparison of input and output waveforms of the switching circuit.
Download Original Figure
4-2 노이즈 신호 인가 시뮬레이션 및 측정 결과

다양한 노이즈 시뮬레이션을 통해 확장 모델을 검증하고, 각 노이즈원에 대한 DUT의 출력을 비교하였다. 협대역 노이즈 신호원으로는 방사 내성 표준 IEC 61000-4-3, ISO 11452-1에 준하는 CW, AM, PM 신호를 사용하였다. 광대역 신호원으로는 OFDM 신호를 사용하였으며, 보편적으로 사용되는 20 MHz 대역폭의 16-QAM 변조를 적용하였다. 모든 신호의 전력은 0 dBm으로 하였으며, 주파수 대역은 DUT의 특성 및 방사 내성 표준을 고려하여 80 MHz로 하였다. 인가한 노이즈 신호의 특성은 표 5와 같다.

표 5. | Table 5. 노이즈 신호원 특성 | Specification of noise signals.
Signal Parameter Setting
CW Frequency 80 MHz
AM Carrier frequency 80 MHz
Modulation frequency 1 kHZ
Modulation depth 80 %
PM Carrier frequency 80 MHz
Repitition period 4.6 ms (=217 Hz)
Duty cycle 50 %
OFDM Carrier frequency 80 MHz
Number of carriers 1,334
Sub-carrier spacing 15 kHz
Bandwidth 20 MHz
Modulation 16 QAM
Download Excel Table

그림 14는 노이즈 신호원별 스위칭 회로의 출력 파형이다. 정상적인 스위칭 회로의 출력 파형과 비교했을 때, CW 신호와 PM 신호는 출력 파형에 미치는 영향이 적었다. 하지만, AM 신호와 OFDM 신호의 경우, 출력 파형의 최솟값을 약 2 V 증가시켰으며, 최대 0.4 V 정도의 노이즈가 전달된 것을 확인할 수 있다. 따라서, 같은 전력 조건에서 AM 신호와 OFDM 신호는 CW 신호와 PM 신호보다 스위칭 회로에 오동작을 일으킬 가능성이 높다는 것을 확인하였다. OFDM 신호를 포함한 방사 내성 시험에 대한 논문[16]에서도 유사한 결과를 확인할 수 있다.

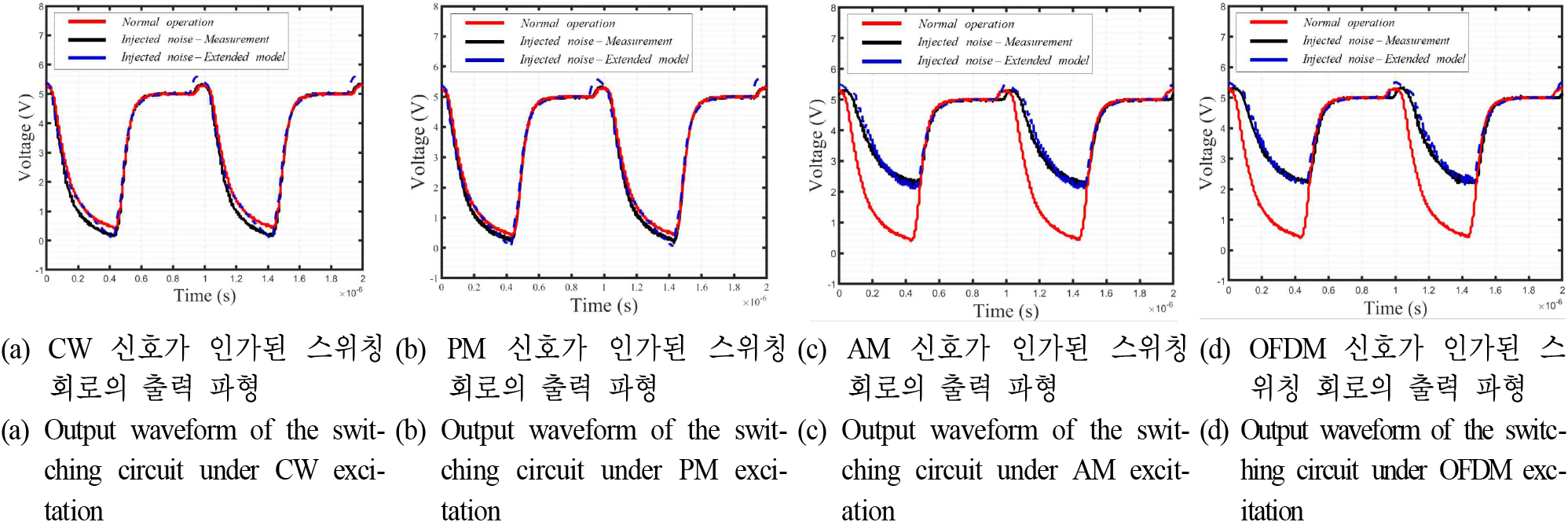
jkiees-36-12-1153-g14
그림 14. | Fig. 14. 노이즈 신호가 인가된 스위칭 회로 출력 파형 | Output waveforms of the switching circuit under noise excitation.
Download Original Figure

그림 15는 각 신호원을 벡터 신호 발생기로 발생시켰을 때를 가정한 그림이다. 동일 전력, 동일 캐리어 주파수로 발생시켰을 때, 첨두 전력이 신호원마다 다름을 확인할 수 있다. 따라서, PAPR(peak to average power ratio)이 신호마다 다름을 알 수 있으며, OFDM, AM, PM, CW 신호 순으로 큼을 확인할 수 있다. 이때, PM과 CW 신호의 첨두 전력은 같지만 PM 신호의 경우 신호가 꺼지는 순간을 포함하여 평균 전력을 계산하기 때문에 결과적으로 PM 신호가 CW 신호보다 PAPR이 높다.

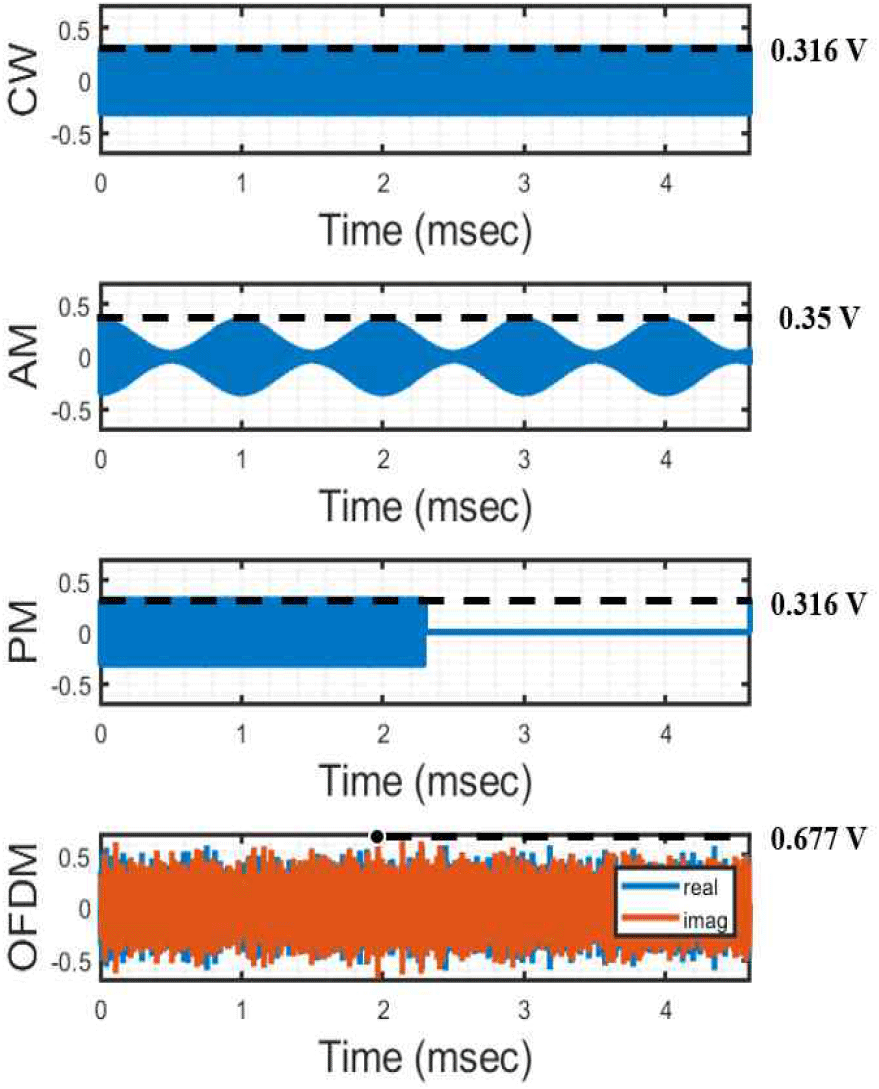
jkiees-36-12-1153-g15
그림 15. | Fig. 15. 노이즈 신호원의 첨두 전력 비교 | Peak power comparision of noise sources.
Download Original Figure

그림 16은 전체 신호에 대해서 평균 전력보다 높은 전력이 얼마나 분포하는지 나타낸 그림이다. CCDF(complementary cumulative distribution function)는 보통 기저 대역에서 사용하는 분포 함수이지만, 본 논문에서는 각 신호원이 스위칭 회로 출력에 미치는 영향 정도가 다른 원인을 분석하기 위해 사용하였다. CCDF/PAPR 그래프를 봤을 때, 그림 15와 같이 PAPR이 OFDM, AM, PM, CW 순으로 큼을 확인할 수 있다.

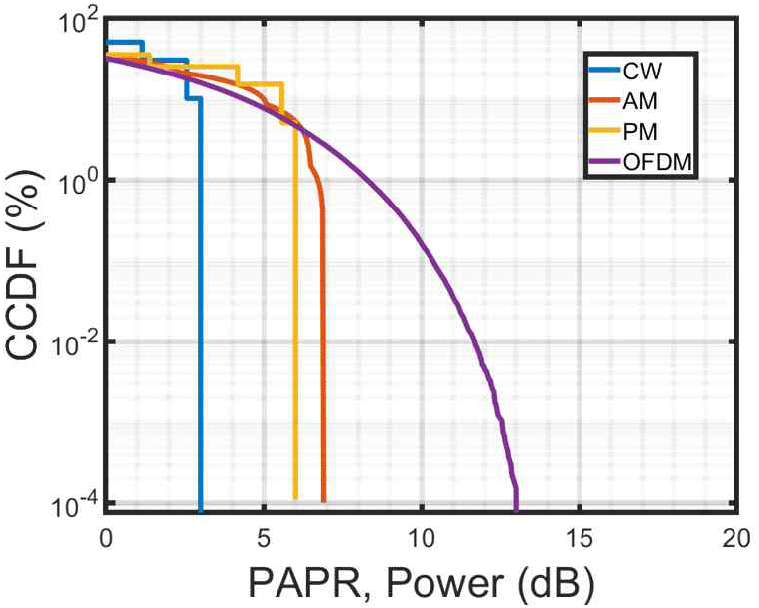
jkiees-36-12-1153-g16
그림 16. | Fig. 16. 노이즈 신호원의 CCDF/PAPR 비교 | CCDF/PAPR comparision of noise sources.
Download Original Figure

따라서, 오동작의 원인은 높은 첨두 전력이 스위칭 회로의 입력단에 유기된 것으로 예상할 수 있고, 각 신호원이 스위칭 회로 출력에 미치는 영향 정도가 다른 원인은 PAPR이 다르기 때문이라고 유추할 수 있다. 이때, OFDM 신호의 경우 매우 큰 PAPR이 존재하지만 매우 작은 확률임을 확인할 수 있으며, 이 구간을 제외하고 AM 신호와 비교했을 때, 전력의 분포가 유사함을 확인할 수 있다. 결과적으로, OFDM 신호는 AM 신호와 유사하며, PM 신호는 CW 신호와 유사하기 때문에 그림 14와 같은 결과가 나온 것으로 볼 수 있다.

Ⅴ. 결 론

본 논문에서는 복잡한 전파 환경에 노출된 MOSFET 스위칭 회로의 특성을 회로 시뮬레이션을 통해 예측하고자 하였다. 예측 정확도를 증가시키기 위해 소자의 내부 및 외부 성분을 측정 기반으로 추출하였으며, 그 결과를 시뮬레이션 모델에 반영하였다. 확장 모델을 검증하기 위해 정상적인 스위칭 회로의 입력/출력 파형과 노이즈 신호가 인가된 스위칭 회로의 입력/출력 파형을 측정과 비교하였다. 그 결과, 기존 모델보다 확장 모델의 예측 정확도가 높음을 확인하였다. 또한, 방사 내성 표준 IEC 61000-4-3과 ISO 11452-1에 준하는 CW, AM, PM 신호와 대역폭이 20 MHz인 광대역 신호 OFDM을 이용하여 노이즈 인가 실험을 수행하였다. 그 결과, CW 신호와 PM 신호는 스위칭 회로의 출력에 미치는 영향이 적었으나, AM 신호와 OFDM 신호는 출력 파형의 최솟값을 약 2 V 정도 증가시켰으며, 최대 0.4 V 정도의 노이즈가 출력에 전달됨을 확인할 수 있었다. 따라서, 동일 전력 대비 AM 신호와 OFDM 신호가 CW 신호와 PM 신호보다 스위칭 회로의 오동작을 일으킬 가능성이 높다는 것을 유추할 수 있으며, 이를 CCDF/PAPR 그래프를 통해 그 가능성을 뒷받침하였다.

향후 연구에서는 본 논문의 결과를 기반으로 주파수를 확장하여 진행하였을 때, 어떤 신호원이 스위칭 회로에 치명적인지 정확히 분석할 수 있을 것으로 기대된다. 또한, 공간상의 전달함수를 통해 실제 방사 내성 시험 결과를 시뮬레이션으로 예측할 수 있도록 노력하고자 한다.

Acknowledgements

이 연구는 2023학년도 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. 2023R1A2C2008116).

References

[1].

Cisco, “IEEE 802.11ax: The sixth generation of Wi-Fi white paper,” 2020. Available: https://www.cisco.com/c/en/us/products/collateral/wireless/white-paper-c11-740788.html

[2].

M. Li, G. Wei, “A review of quantitative evaluation of electromagnetic environmental effects: Research progress and trend analysis,” Sensors, vol. 23, no. 9, p. 4257, Apr. 2023.

[3].

Ftoday, “Why is the screen malfunctioning? It’s the fault of the mobile carrier’s 5G repeater,” 2022. Available: https://www.ftoday.co.kr/news/articleView.html?idxno=241795

[4].

F. Fan, Z. Zhao, P. Tu, H. Jie, M. Dong, and K. Y. See, “Electromagnetic interference attacks on GaN half-bridge module,” in 2022 Asia-Pacific International Symposium on Electromagnetic Compatibility(APEMC), Beijing, Sep. 2022, pp. 225-227.

[5].

T. Dörlemann, A. Bendicks, C. Krause, and S. Frei, “Noise reduction in periodically switching MOSFET circuits using iteratively found synthesized control signals,” in 2019 International Symposium on Electromagnetic Compatibility - EMC EUROPE, Barcelona, Sep. 2019, pp. 848-853.

[6].

M. T. Abuelma’atti, A. M. T. Abuelmaatti, “Effect of electromagnetic interference (EMI) on the DC shift, harmonic, and intermodulation performance of NMOSFET mirror eith a capacitor between the mirror node and the ground,” IEEE Transactions on Electromagnetic Compatibility, vol. 55, no. 5, pp. 849-854, Oct. 2013.

[7].

W. J. de Paula, G. H. M. Tavares, G. M. Soares, P. S. Almeida, and H. A. C. Braga, “Switching losses prediction methods oriented to power MOSFETs: A review,” IET Power Electronics, vol. 13, no. 14, pp. 2960-2970, Jun. 2020.

[8].

S. Havanur, V. Siliconix, “Dealing with nonlinear MOSFET capacitances,” 2017. Available: https://www.how2power.com/pdf_view.php?url=/newsletters/1703/articles/H2PToday1702_design_VishaySiliconix.pdf

[9].

B. Khvitia, A. Gheonjian, Z. Kutchadze, and R. Jobava. "A SPICE model for IGBTs and power MOSFETs focusing on EMI/EMC in high-voltage systems,” Electronics, vol. 10, no. 22, p. 2822, Nov. 2021.

[10].

G. Dambrine, A. Cappy, F. Heliodore, and E. Playez, “A new method for determining the FET small-signal equivalent circuit,” IEEE Transactions on Microwave Theory and Techniques, vol. 36, no. 7, pp. 1151-1159, Jul. 1988.

[11].

R. A. Minasian, “Simplified GaAs m.e.s.f.e.t. model to 10 GHz,” Electronics Letters, vol. 13, no. 18, pp. 549-551, Sep. 1977.

[12].

F. Giannini, F. Graglia, G. Leuzzi, and A. Serino, “Accurate microwave characterisation of power LD-MOSFETs,” in 2000 Gallium Arsenide Applications Symposium(GAAS), Paris, Oct. 2000, pp. 165-168.

[13].

J. Kim, “A new GaN HEMT small-signal model considering source via effects for 5G millimeter-wave power amplifier design,” Applied Sciences, vol. 11, no. 19, p. 9120, Sep. 2021.

[14].

P. Yan, P. Lei, W. Liang, C. Xiaojuan, L. Chengzhan, and L. Xinyu, “Improvements to the extraction of an AlGaN/GaN HEMT small-signal model,” Journal of Semiconductors, vol. 30, no. 12. p. 124003, Dec. 2009.

[15].

S. Chakraborty, W. Amir, H. M. Kwon, and T. W. Kim, “New methodology for parasitic resistance extraction and capacitance correction in RF AlGaN/GaN high electron mobility transistors,” Electronics, vol. 12, no. 14, p. 3044, Jul. 2023.

[16].

G. R. Choi, Y. G. Hong, T. Kwon, H. Keum, S. Park, and W. Nah, “Experimental study on radiated immunity comparison between broad-band and conventional test signals on the equipment under test,” The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 35, no. 1, pp. 47-58, Jan. 2024.

Notes

권 태 욱 [성균관대학교/석사과정]

jkiees-36-12-1153-i1

  • https://orcid.org/0009-0003-1971-3991

  • 2022년 2월: 한서대학교 항공전자공학과 (공학사)

  • 2024년 3월~현재: 성균관대학교 전자전기컴퓨터공학과 석사과정

  • [주 관심분야] EMI/EMC

최 경 륜 [성균관대학교/박사과정]

jkiees-36-12-1153-i2

  • https://orcid.org/0000-0002-3649-0000

  • 2021년 2월: 수원대학교 전자공학과 (공학사)

  • 2023년 2월: 성균관대학교 전자전기컴퓨터공학과 (공학석사)

  • 2023년 3월~현재: 성균관대학교 전자전기컴퓨터공학과 박사과정

  • [주 관심분야] EMI/EMC, SI/PI, EMS

이 한 양 [성균관대학교/석사과정]

jkiees-36-12-1153-i3

  • https://orcid.org/0009-0007-7810-604X

  • 2024년 8월: 성균관대학교 전자전기공학부 (공학사)

  • 2024년 9월~현재: 성균관대학교 전자전기컴퓨터공학과 석사과정

  • [주 관심분야] EMI/EMC

한 준 희 [성균관대학교/석·박사통합과정]

jkiees-36-12-1153-i4

  • https://orcid.org/0000-0002-7759-6717

  • 2018년 2월: 성균관대학교 전자전기컴퓨터공학과 (공학사)

  • 2018년 3월~현재: 성균관대학교 전자전기컴퓨터공학과 석·박사통합과정

  • [주 관심분야] EMI/EMC, SI/PI

나 완 수 [성균관대학교/교수]

jkiees-36-12-1153-i5

  • https://orcid.org/0000-0002-0315-3294

  • 1984년 2월: 서울대학교 전기공학과 (공학사)

  • 1986년 2월: 서울대학교 전기공학과 (공학석사)

  • 1991년 2월: 서울대학교 전기공학과 (공학박사)

  • 1991년~1993년: SSCL Guest Collaborator

  • 1993년~1995년: 한국전기연구원 선임연구원

  • 1995년~현재: 성균관대학교 전자전기컴퓨터공학과 교수

  • [주 관심분야] EMC, SI/PI, EMS


The Journal of Korean Institute of Electromagnetic Engineering and Science
101-1101 Lotte Castle President, 109 Mapo-daero, Mapo-gu, Seoul 04146, Republic of Korea
Tel : +82-2-337-9666 | Fax : +82-2-711-7550 | kees@kiees.or.kr

Copyright © The Korean Institute of Electromagnetic Engineering and Science. 2026. Powered by Guhmok