Ⅰ. 서 론
레이돔(radome)이란, radar와 dome의 합성어로서 항공기 및 유도무기 등 비행체의 선단에 장착되어 낙뢰, 강우, 침식과 같은 외부 환경으로부터 탐색기 안테나를 보호하는 장치를 말한다. 레이돔은 비행 중 발생하는 공력 하중에 견딜 수 있도록 유선형 구조로 제작되어야 할 뿐만 아니라, 물리적으로 충분한 강도를 가져야 한다[1]. 이러한 레이돔의 형상 및 물질 특성으로 인해 보어사이트 오차(BSE, boresight error), 투과 손실(TL, transmission loss)과 같은 탐색기 안테나의 성능 저하가 발생하게 된다. BSE란, 탐색기 안테나에서 송, 수신되는 전자파가 레이돔에 의해 굴절되는 안테나의 지향 각도 오차를 의미하며 TL은 레이돔에 입사하는 전자파에 대한 투과 전자파의 비율로서, 탐색기 안테나로부터 송수신되는 전자파 에너지가 레이돔에 의해 반사, 흡수되어 레이돔을 투과하는 전자파의 전력이 감소, 최대탐지거리 성능에 영향을 미치는 현상을 의미한다[2]. 이러한 요소들은 유도무기의 목표물(target) 추적 성능의 저하로 이어지기 때문에, 제작 과정에 앞서 레이돔의 영향성을 고려한 안테나의 성능을 미리 파악하여 가능한 작은 BSE와 TL을 갖도록 레이돔을 설계해야 한다.
레이돔의 전자파 특성 해석 방법으로는 full-wave EM 시뮬레이션을 활용할 수 있으나[3], 안테나의 동작 주파수에 비해 전기적으로 큰 구조를 해석할 경우 해석 시간과 메모리 사용량이 급격히 증가하는 단점이 있다. 이에 반해, 물리 광학(PO, physical optics) 기반의 광선 추적법(ray tracing)은 full-wave EM 시뮬레이션 대비 계산 효율이 높고 메모리 요구량이 적어, 레이돔의 전자파 특성을 보다 효율적으로 분석할 수 있다[4],[5]. 본 논문에서는 효율적인 레이돔 전자파 특성 분석을 위해 ray tracing 기법과 상용 시뮬레이션 도구인 CST MWS를 이용한 전자파 특성 분석을 수행하였으며, 실제 측정 결과와의 비교를 통해 효율적인 레이돔 성능 분석 방법에 대해 소개한다.
Ⅱ. 본 문
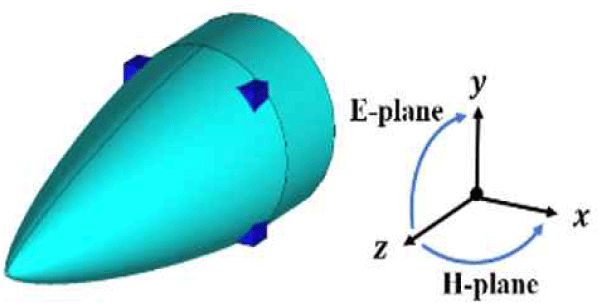
레이돔 성능 분석에 앞서, 실제 측정 환경을 모사하기 위해 안테나의 근거리장 source를 추출하여 그림 1에 나타낸 바와 같이 레이돔 내부 특정 위치(z, xy-plane)에 위치시켜 시뮬레이션을 수행하였다. 해석에 사용된 안테나는 합, 차 패턴을 형성할 수 있는 SWA(slotted waveguide array) 모노 펄스 안테나로, 김발(gimbal) 회전을 통해 빔 조향이 이루어진다. 레이돔은 본 칼만(Von Karman)[4] 형상으로 길이 400 mm 이상, 지름 약 150 mm이상의 크기를 갖는 레이돔이다.
그림 2는 BSE 및 TL 계산을 위한 설정을 나타내며, 레이돔 회전 각도에 따른 BSE 및 TL을 살펴보기 위해 레이돔을 안테나의 E-plane (ϕ=90°, θ-sweep) 및 H-plane (ϕ=0°, θ-sweep) 방향으로 각각 ±9° 회전시킴에 따라 발생하는 BSE 및 TL을 확인하였다. 각도 분석 범위를 이와 같이 설정한 이유는, 레이돔 내부에 위치한 안테나 위치로 인해 물리적인 김발 회전 각도가 ±9°로 제한되기 때문에 해당 범위 내에서 BSE 및 TL을 확인하였다.
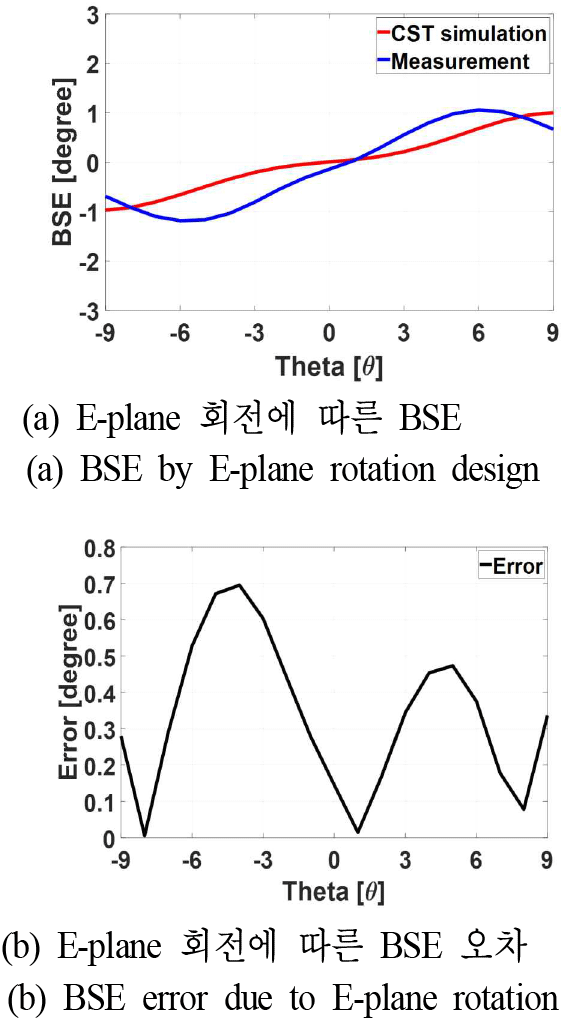
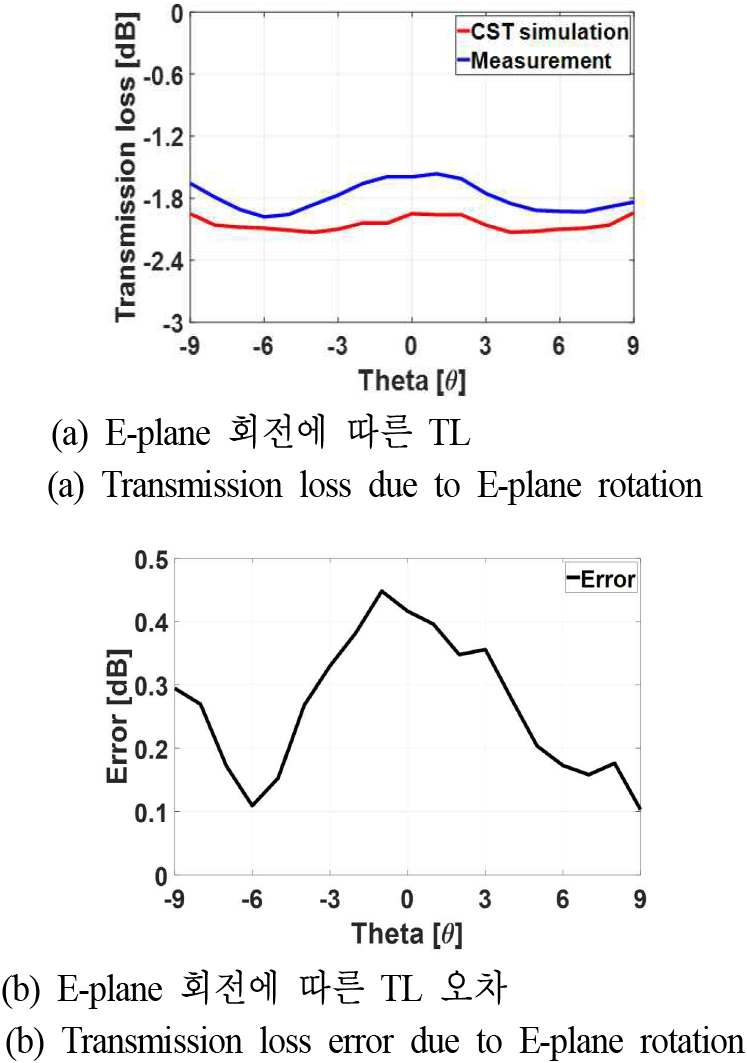
그림 3(a) 및 그림 4(a)는 각각 E-plane상 고각 방향(θ)으로 레이돔을 회전시킴에 따라 측정된 BSE 및 TL을 CST MWS 시뮬레이션을 통해 계산된 결과와 비교한 그래프이며, 그림 3(b) 및 그림 4(b)는 측정된 BSE 및 TL과 CST MWS 시뮬레이션을 통해 계산된 BSE 및 TL 간의 오차를 나타낸 그래프이다. 측정과 CST MWS 시뮬레이션 사이의 BSE 최대 오차는 θ=−4°에서 0.7° 발생하였으며, TL의 경우, θ=−1°에서 0.45 dB 발생했음을 확인할 수 있다.
마찬가지로, 그림 5(a) 및 그림 6(a)는 각각 H-plane 상고각(θ) 방향으로 레이돔을 회전시킴에 따라 측정된 BSE 및 TL을 CST MWS 시뮬레이션 결과와 비교한 그래프이며, 그림 5(b) 및 그림 6(b)는 측정 결과와 CST MWS 시뮬레이션 결과 사이의 오차를 나타낸 그래프이다. BSE의 경우, θ=−6°에서 최대 오차 0.4°가 발생하였고, TL은 θ=−9°에서 최대 0.4dB의 오차가 발생했음을 확인할 수 있다.
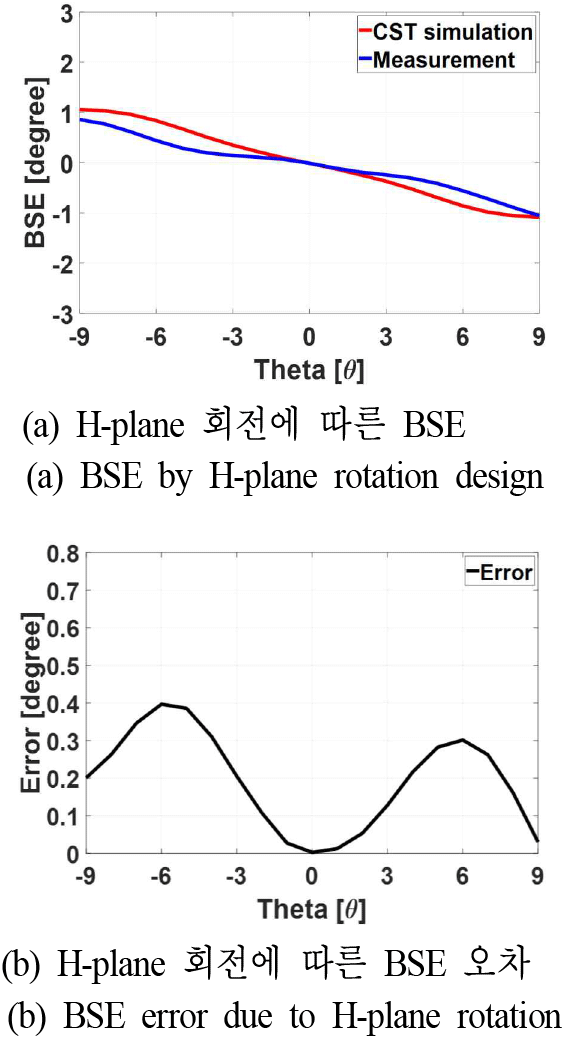
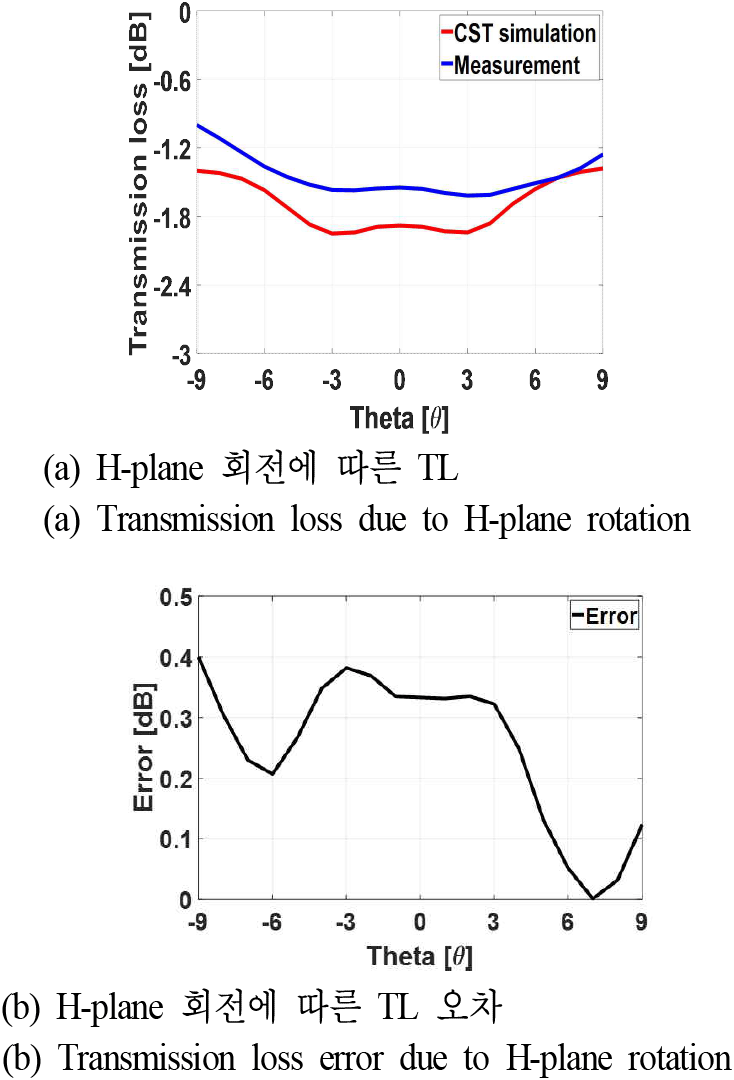
E-plane 및 H-plane 회전에 따른 BSE와 TL의 결과를 살펴보면, 전반적으로 E-plane의 오차가 H-plane의 오차보다 더 큰 경향성을 확인할 수 있으며, E-plane, H-plane오차 모두 −9°≤θ≤0° 범위에 집중되는 경향을 보였다. 이러한 오차의 원인을 보다 면밀하게 분석하기 위해, 해당 각도 범위에서 안테나의 방사 패턴을 비교, 분석하였다. 이를 위해 CST MWS 시뮬레이션을 통해 계산된 SWA 안테나의 방사 패턴과 측정된 패턴을 비교하였으며, 그 결과는 그림 7 및 그림 8에 각각 제시하였다. 그림 7은 레이돔이 없는 단일 안테나의 방사 패턴 비교 결과로, −9°≤θ≤0° 범위에서 시뮬레이션과 측정 간의 패턴 불일치가 0°≤θ≤9°에 비해 최대 1 dB만큼 크게 발생했음을 보여준다. 또한, 그림 8의 레이돔이 포함된 안테나 방사 패턴의 경우, 레이돔이 없는 경우의 단일 안테나 방사 패턴과 비교하였을 때, 동일한 범위에서 패턴 불일치가 최대 2 dB 나타났다. 이는 3D 프린팅을 통해 제작된 SWA 안테나의 E-plane 방향의 슬롯 길이가 H-plane 방향보다 상대적으로 짧아, 동일한 절대 오차가 발생하더라도 E-plane에서 상대적인 제작 오차 비율이 더 크게 나타났기 때문인 것으로 판단된다.
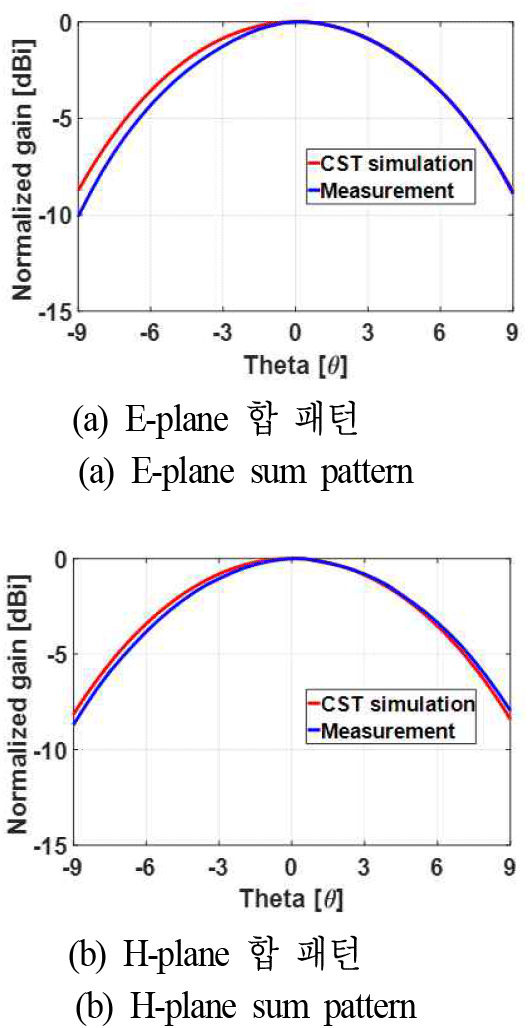
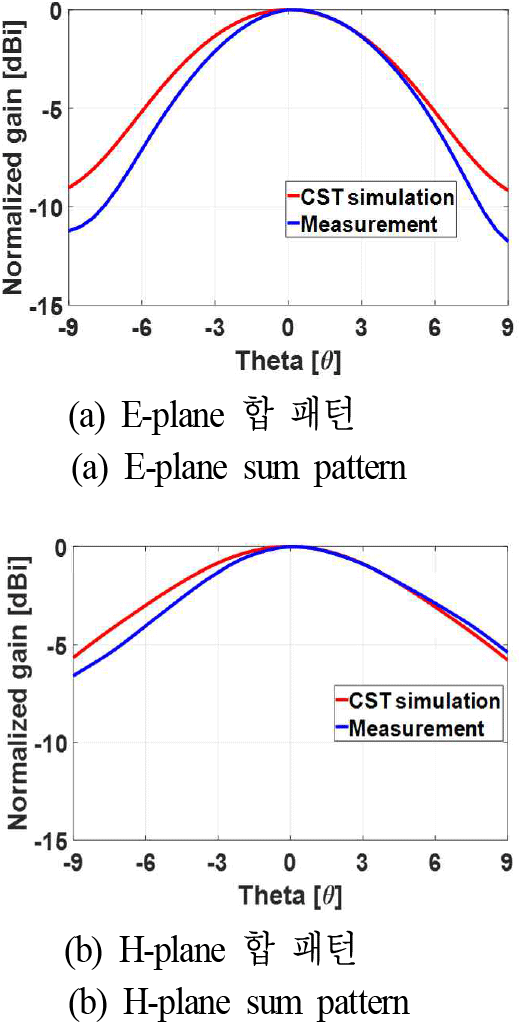
한편, CST MWS 시뮬레이션을 통해 레이돔 회전 각도별 BSE 및 TL을 계산하는 데 총 43시간이 소요되었으며, 사용된 워크스테이션의 사양은 표 1에 제시하였다. 분석 대상인 레이돔이 안테나의 운용 주파수에 비해 전기적으로 큰 부피를 가지므로, 시뮬레이션 과정에서 많은 메모리와 긴 해석 시간이 요구된 것을 알 수 있다. 본 절에서는 CST MWS 시뮬레이션을 통해 도출된 BSE, TL, 방사 패턴을 측정 결과와 비교․분석함으로써, 안테나 제작 오차가 레이돔의 전자파 성능 해석에 미치는 영향을 정량적으로 확인하였다. 이를 통해 레이돔 설계에 앞서 정밀한 안테나 제작과 정확한 모델링이 필수적으로 선행되어야 함을 검증하였다. 또한, 본 연구에서 측정에 사용된 레이돔은 가변 두께를 가지며 노즈팁(nose tip)이 포함된 형상인 반면, CST MWS 시뮬레이션에서는 균일한 두께를 가지며, 노즈팁이 생략된 단순화된 레이돔 형상을 사용하였다. 이와 같은 형상 차이가 시뮬레이션과 측정 결과 간의 불일치를 유발한 주요 요인 중 하나로 판단되며, 향후에는 가변 두께 및 노즈팁이 반영된 정밀한 모델링을 통해 보다 정확한 해석 결과를 도출할 수 있을 것으로 기대된다.
| Processor | Intel Xeon gold 6226R |
|---|---|
| O/S | Windows 10 pro (×64) |
| CPU | 2.90 GHz |
| RAM | 512 GB |
| GPU | RTX A-6000 |
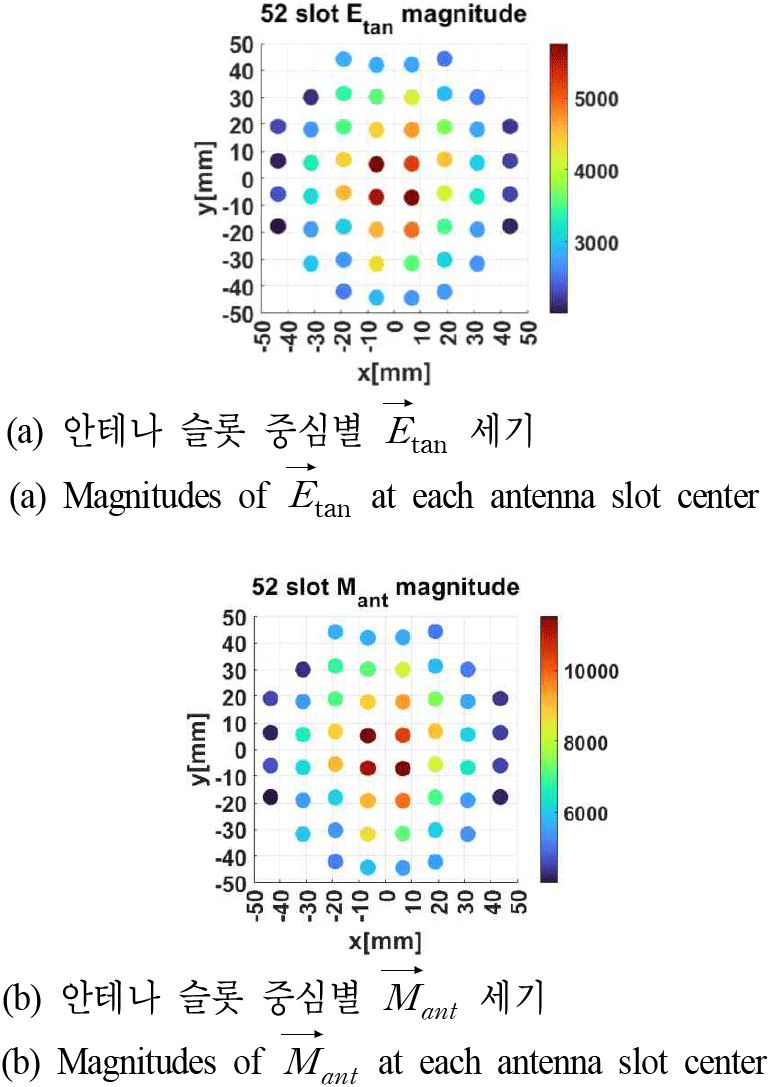
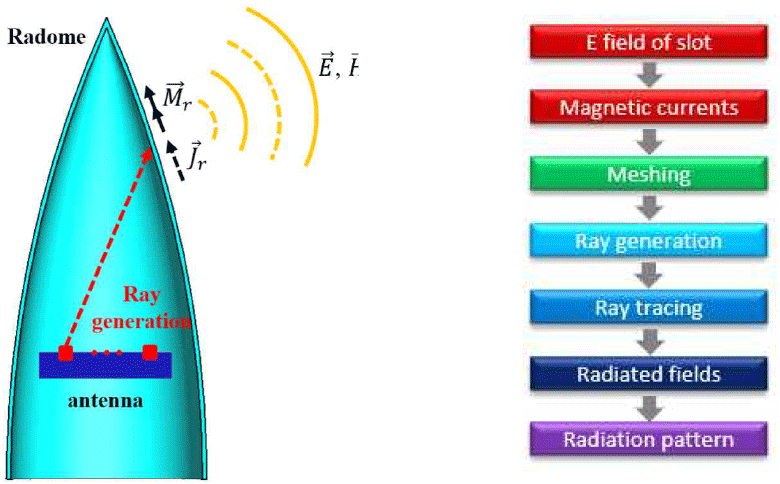
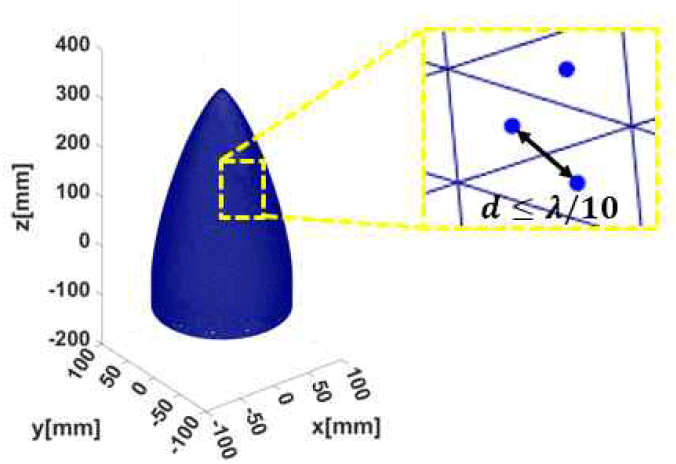
그림 9는 PO(physical optics) 기반 ray tracing 알고리즘 개념을 나타낸다[6]. Ray tracing은 source 안테나로부터 외부 관측 지점까지 도달하는 광선(ray)의 경로를 추적함으로써 원거리장 방사 패턴을 계산하는 고주파 근사기법으로, 전기적으로 큰 구조체에 대해 full-wave EM 시뮬레이터 대비 적은 메모리와 계산 시간으로 효율적인 해석이 가능하다는 장점이 있다. 본 해석에 사용된 레이돔은 안테나의 운용 주파수 파장의 약 25 λ의 해당하는 전기적으로 큰 구조체이다. 이에 따라 본 절에서는 PO를 기반으로 하는 ray tracing 알고리즘을 활용하여 레이돔 성능을 분석하였으며, 알고리즘 구현은 MATLAB 상에서 수행하였다.한편, 본 연구에서 실제 측정에 사용된 레이돔은 가변 두께를 갖는 레이돔이며, 해석에 사용된 레이돔은 균일한 두께를 갖는 레이돔이다. 이처럼 해석 모델과 실제 측정 대상간에 차이가 있음에도 비교 분석을 진행한 이유는 레이돔 내부 다중 반사를 고려하는 IPO(iterative physical optics)가 아닌 단순 PO 기반 ray tracing만으로도 균일 두께 레이돔 성능의 정량적 예측 가능성을 확인하고자 하였기 때문이다. Ray tracing의 source 정의를 위해, 먼저 SWA안테나 각 슬롯 중심에서의 자기 전류 ()를 계산하였다. 그림 10(a)는 CST MWS 시뮬레이션을 통해 획득한 안테나 각 슬롯 중심의 전기장의 세기를 나타내며, 해당 전기장의 세기와 위상을 기반으로 식 (1)의 표면 등가 원리를 적용하여 그림 10(b)와 같이 자기 전류()를 도출하였다[6]. SWA 안테나의 구조적 특성상, 각 슬롯 중심에는 전기장만 인가되므로 이는 자기 전류로 근사하여 해석이 가능하다. 광선의 출발 지점은 SWA 안테나의 슬롯 중심으로 정의하였으며, 도착 지점은 레이돔 내부 벽면 분할 메쉬의 중심점으로 설정하였다. 해당 중심점은 그림 11에 나타난 바와 같이, 레이돔 내부 표면을 삼각형 메쉬로 분할 후, 각 메쉬의 무게 중심으로 설정하였다. 해석 정확도 확보를 위해 중심점간의 거리는 λ/10 이하가 되도록 설정하였다[7].
레이돔 내부 요격 지점과 탐색기 안테나의 각 슬롯 중심 간의 거리를 계산한 결과, 레이돔 내부 벽면은 모두 근거리장 영역에 해당하는 것으로 확인되었다. 이에 따라, 각 요격 지점에서의 전기장 및 자기장을 계산하기 위해 슬롯 중심의 을 기반으로 근거리장 영역에서 산란 되는 전기장 및 자기장을 식 (2)~식 (9)을 통해 계산하였다[8]. 식 (2)~식 (9)에서 x,y,z는 레이돔 내부 중심점의 좌표를 나타내며 x',y',z'는 탐색기 안테나 각 슬롯 중심의 위치 좌표를 나타낸다. 또한 R은 레이돔 내부 중심점과 각 슬롯 중심 간의 거리를 나타내며 β,η는 각각 공기의 전파상수, 임피던스를 나타낸다.
Ray tracing의 최종 목적은 레이돔 외부 원거리장 영역에서의 방사 패턴을 계산하는 것으로, 이를 위해 레이돔 외부 표면에서의 magnetic current()와 electric current() 계산이 필요하다. 레이돔 외부 표면의 은 식 (10) 및 식 (11)과 같이 PO 기법을 기반으로 하며, 레이돔 외부 표면의 각 중심점에서 투과된 전기장 및 자기장은 레이돔 외부 중심점에서의 단위 법선 벡터의 외적을 통해 계산하였으며, 분할 메쉬 중심점 간의 거리는 λ/10 이하이며, 삼각형 메쉬의 등가 표면 내에서 모두 같은 값으로 근사될 수 있다. 적분 계산을 통해 등가 표면의 방사 전기장 및 자기장을 계산하였으며 레이돔 전체 면적에서 방사된 전기장 및 자기장을 중첩하여 원거리장 방사 패턴을 계산하였다. 최종적으로 등가 표면에서 방사되는 전기장 및 자기장의 위상차를 고려하여 원거리장에서의 방사 패턴을 계산하였다.
그림 12는 최종적으로 계산된 원거리장 영역에서 방사 패턴을 CST MWS 시뮬레이션 패턴과 비교한 그림으로, 그림 12(a)의 E-plane 방사 패턴은 전반적으로 일치하는 경향성을 보이는 반면, 그림 12(b)의 H-plane 방사 패턴은 CST MWS 시뮬레이션 결과와 일치하지 않는 것을 확인할 수 있다. H-plane의 방사 패턴 불일치 원인을 분석하고자 CST MWS의 floquet port 시뮬레이션을 추가로 수행하였으며 그림 13은 해당 시뮬레이션 설정을 나타낸다. 이때, unit cell의 길이는 레이돔의 두께인 6 mm로 설정하였으며 밑면의 가로세로의 길이는 레이돔 중심점 간의 거리를 고려하여 λ/10(1.71 mm)로 설정하였다. 한편, 그림 14는 탐색기 안테나의 52개 슬롯 중심에서 발생한 광선이 레이돔 내부 중심점에 인가될 때, 각 중심점별 입사각도의 크기를 나타낸 것으로, 해당 각도의 크기는 한 중심점에 인가된 52개 광선의 단위 방향 벡터를 모두 합산한 뒤, 해당 벡터의 크기로 나눈 방향 벡터를 이용하여 계산하였다. 이를 통해 고이득 탐색기 안테나의 방사 특성상 대부분의 전력이 특정 입사각도인 약 60°~70° 부근에 집중됨을 확인할 수 있었으며, 해당 각도에서의 반사 및 투과계수를 특성을 중점적으로 분석할 필요가 있음을 알 수 있다.
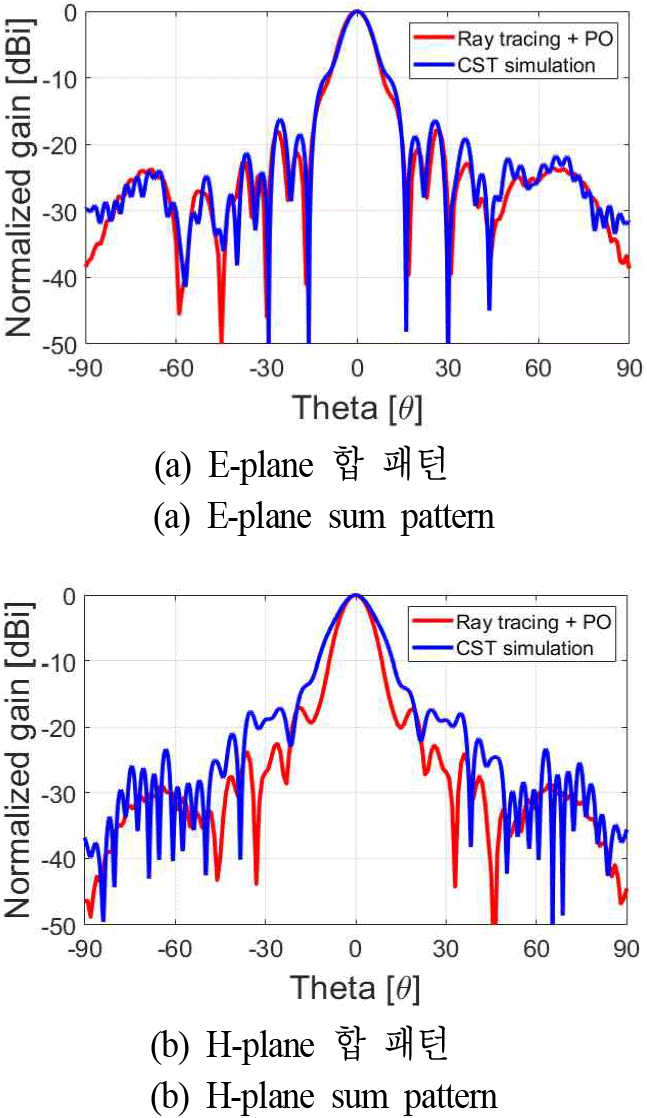
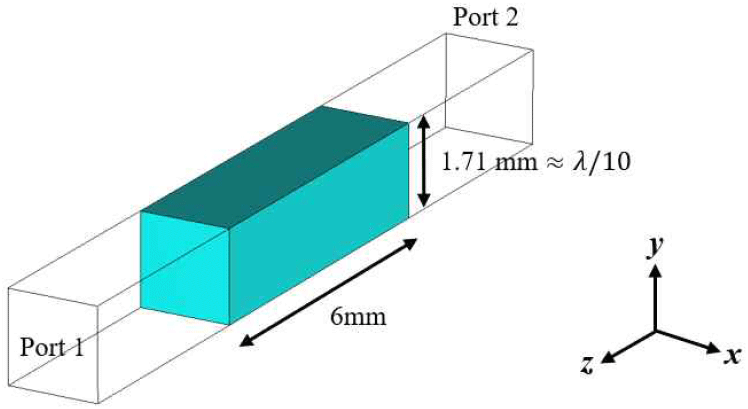
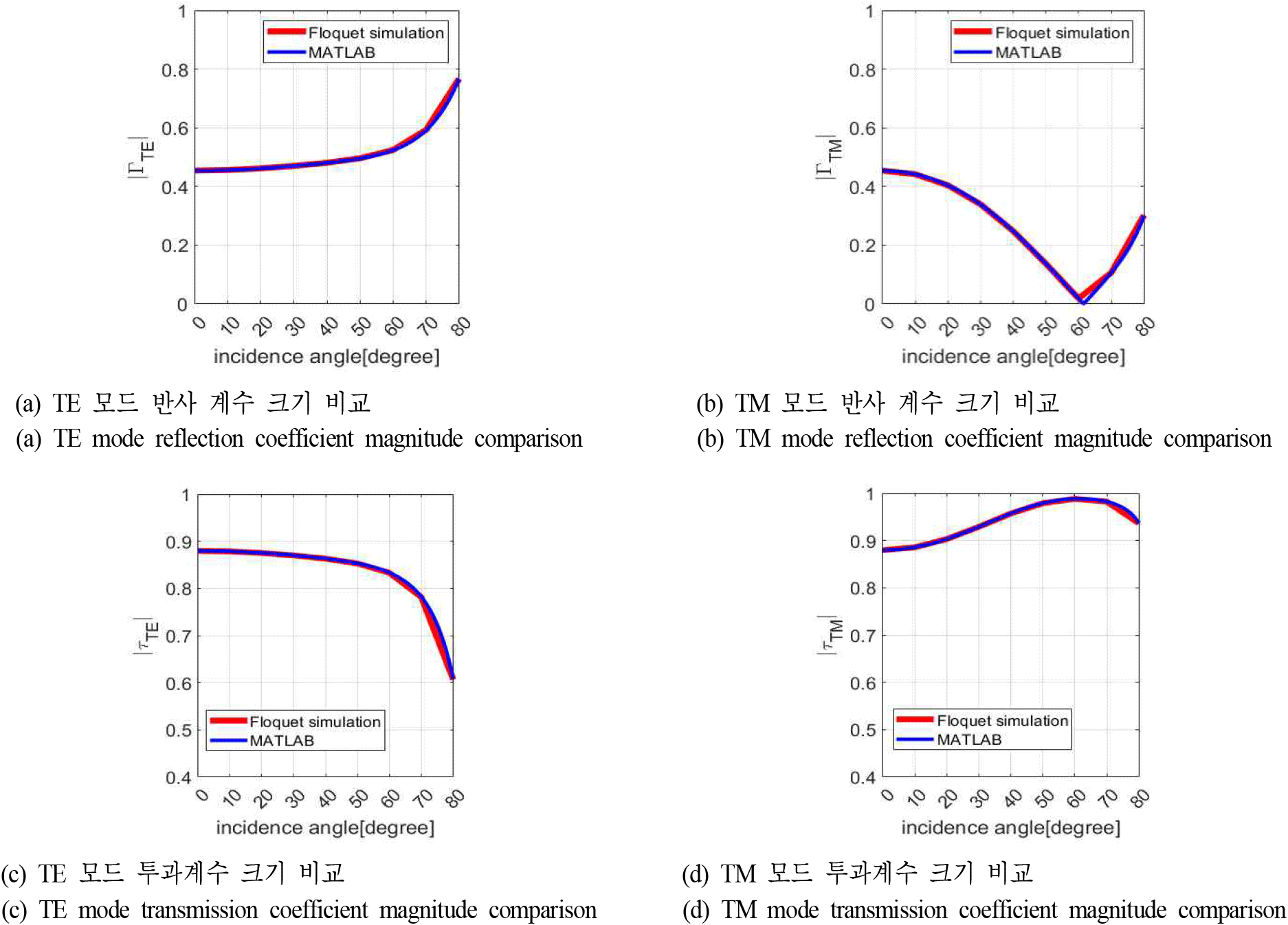
그림 15는 CST MWS의 floquet port 시뮬레이션을 통해 계산된 반사 및 투과계수를 MATLAB을 통해 계산된 반사 및 투과계수와 비교한 그림으로, CST MWS의 floquet port 시뮬레이션과 MATLAB 계산 결과가 일치함을 확인하였다. 그림 15(a) 및 그림 15(b)의 그래프를 통해 광선의 입사각 60°~70° 구간에서는 반사 계수의 크기가 TE 모드 대비 TM 모드에서 낮음을 확인할 수 있다. 반면, 그림 15(c) 및 그림 15(d) 그래프에서는 입사각 60°~70° 구간에서 투과계수의 크기가 TE 모드 대비 TM 모드에서 높음을 확인할 수 있다.
또한, 레이돔 내부에 배치된 탐색기 안테나의 전기장 성분은 슬롯의 모양과 배치로 인해 Ey 성분이 지배적이며 그림 16에서 보이듯, E-plane상의 레이돔 내부 중심점에서 의 성분을 확인해 볼 때 Ey의 크기는 TE 모드 보다 TM 성분이 더 우세한 것을 확인할 수 있다. 즉, 레이돔의 전력 집중 구간인 입사각 60°~70°에서 TE 모드 대비 TM 성분이 반사 및 투과계수 측면에서 임피던스 매칭이 우수하므로 그림 12과 같이 E-plane 합 패턴이 H-plane 합 패턴보다 시뮬레이션 결과와 더 잘 일치함을 확인할 수 있다. 그림 17은 레이돔의 전력 집중 구간인 60°~70°에서 최적 유전율을 적용하였을 때의 TE, TM 모드별 반사 계수를 계산한 그래프이다. 계산된 레이돔의 최적 유전율은 ϵr=2.87이며 그림에서 보이듯 60°~70° 구간에서 두 모드의 반사 계수가 ϵr=3.4일 때에 비해 현저히 낮음을 확인할 수 있다.
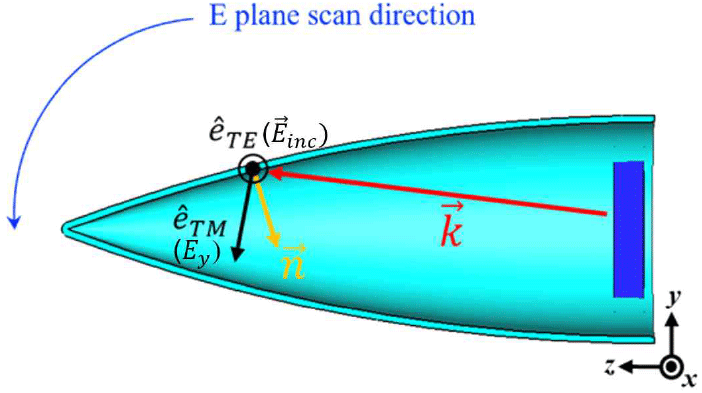
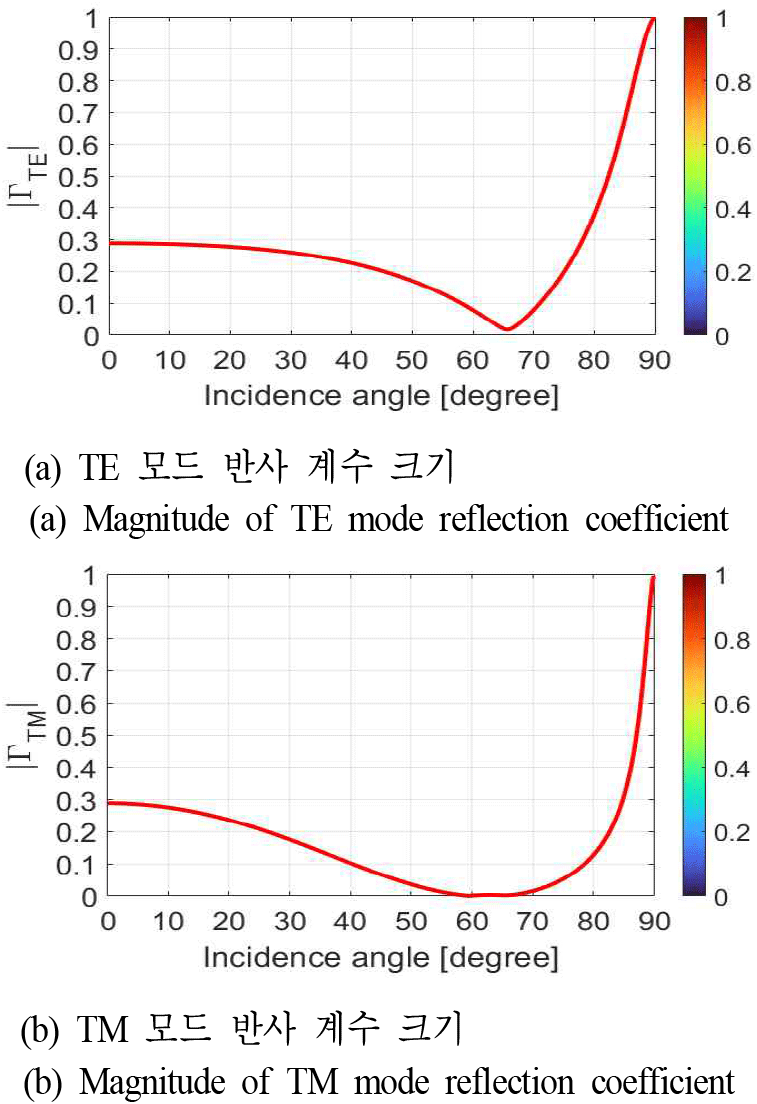
그림 18은 레이돔의 유전율을 2.87로 변경했을 때의 방사 패턴을 나타내며, H-plane 합 패턴이 main lobe 측면에서 그림 12에 나타낸 레이돔 유전율이 3.4일 경우보다 ray tracing 결과가 CST MWS 시뮬레이션 결과와 더 잘 일치함을 확인할 수 있다. 이를 통해 레이돔의 최적 유전율 값을 도출하여 설계가 이루어져야 한다는 것을 알 수 있으며 추후 입사 각도에 따른 레이돔의 최적 두께를 도출, 가변 두께 설계 방향성을 제시할 수 있을 것이라 기대된다. 또한, 본 연구에서 사용된 PO 기반 ray tracing 기법은 임피던스 매칭이 되지 않은 radome, 즉, 균일한 두께를 갖는 radome에 대해서 CST MWS 시뮬레이션 결과와 비교했을 때 방사 패턴에서 다소 차이가 발생한 것을 보였다. 이는 레이돔 내부의 다중반사를 고려하지 않는 PO의 특성으로 인한 결과이며, 레이돔 내부 다중반사를 고려한 IPO(iterative physical optics)를 사용하여 균일 두께를 가진 레이돔 분석 시 정확한 계산이 가능할 것으로 판단된다[9],[10].

표 2는 CST MWS 시뮬레이션과 ray tracing 기법을 이용한 레이돔 해석 소요 시간을 비교한 것으로, T-solver를 이용한 CST MWS 시뮬레이션에는 34분 35초가 소요된 반면, ray tracing은 4분 18초로 약 87.5 %의 해석 시간 단축 효과를 보였다. 본 절에서는 PO 기반 ray tracing 해석을 통해 주요 입사각 영역에서의 전력 집중 특성을 고려한 반사 및 투과 계수를 분석하였으며, 이를 바탕으로 레이돔의 최적 유전율 및 두께에 대한 설계 방향성을 제시하였다. 또한, ray tracing을 이용한 단순한 해석 시간 절감과 더불어 CST MWS 시뮬레이션 결과와 ray tracing 결과 간의 방사 패턴 경향성이 전반적으로 잘 일치하는 것으로 나타났다. 이는 제안된 ray tracing 기법의 신뢰성과 정확성을 뒷받침한다. 이러한 결과는, 설계 초기 단계에서 CST 기반의 full-wave 해석보다 훨씬 빠르고 적은 자원을 소모하면서도, 레이돔의 성능을 정량적으로 예측하고 최적 설계 파라미터를 도출할 수 있는 실용적인 분석 도구로써의 가능성을 보여준다. 특히, 실제 제작 과정 이전에 레이돔 성능을 빠르게 예측하고, 이후 제작 오차 검증까지 연계할 수 있다는 점에서, 제안된 기법은 실질적인 설계 효율을 크게 향상시킬 수 있다. 이는 ray tracing을 활용해 레이돔 성능을 설계 초기 단계에서 효율적으로 예측하고, 설계에 직접 적용할 수 있음을 의미한다.
| Tools | Mesh cells | Intercept point | Analysis time |
|---|---|---|---|
| CST MWS | 293,464,584 | 34m 35s | |
| Ray tracing @MATLAB | 38,734 | 4m 18s | |
Ⅲ. 결 론
본 연구에서는 CST MWS 기반의 full-wave EM 시뮬레이션, PO 기반 ray tracing 기법, 그리고 실제 측정 데이터를 유기적으로 연계하여 레이돔의 전파 특성을 종합적으로 분석하였다. CST MWS 시뮬레이션과 실측된 안테나 방사 패턴을 비교함으로써, 3D 프린팅으로 제작된 안테나의 제작 오차를 정량적으로 검증하고, 해당 오차가 BSE 및 TL과 같은 레이돔 전자파 성능지표에 미치는 영향을 분석하였다. 이를 통해 정밀한 안테나 제작 및 모델링이 레이돔 해석의 정확도에 큰 영향을 미침을 확인하였다. 또한, ray tracing 기법을 활용하여 단순한 방사 패턴 예측을 넘어 주요 입사각에서의 전력 분포를 반영한 투과 및 반사 특성 해석을 수행하였으며, 이를 바탕으로 레이돔의 최적 유전율과 두께 설계 방향성을 도출하였다. 특히 BSE는 look-up table 기반의 보정이 가능하나, TL을 최소화하기 위해서는 입사각에 따른 최적 두께 산정이 필요하며, 이는 가변 두께 레이돔 설계의 필요성을 뒷받침한다. 이러한 분석을 통해 full-wave 해석에 대한 의존도를 줄이면서도 설계 초기 단계에서 정밀한 성능 예측이 가능함을 입증하였다. 아울러, CST MWS, ray tracing, 측정 결과를 통합한 다단계 해석 및 검증 체계를 구축함으로써 레이돔 해석의 신뢰성을 높이고, 성능 저하 요인의 정량적 분석과 구조 최적화를 위한 실질적인 설계 피드백을 제공할 수 있는 기반을 마련하였다. 결론적으로, 본 연구는 레이돔 설계 이전 초기 성능 예측부터 제작 후 성능 검증에 이르기까지 폭넓게 활용 가능한 통합 해석 프로세스와 설계 가이드를 제시하며, 향후 고정밀 레이돔 개발에 실질적인 기여를 할 수 있을 것으로 기대된다. 특히, 본 연구는 균일한 두께 레이돔의 해석 조건에서도 PO 기반 ray tracing 해석이 일정 수준 이상의 정합도를 보임을 확인함으로써, 균일 두께 레이돔을 대상으로 한 설계 초기 단계에서 PO 기반 ray tracing의 실효성을 검증하였다. 이러한 비교 분석은 향후 IPO 기반 ray tracing 해석으로의 확장을 위한 사전 검증 과정으로도 기능할 수 있다.