특집단편논문/SPECLAL SHORT PAPERS
SAR 영상에서의 소형 선박 감시정찰을 위한 2단계 탐지 기법
박기배
,
김정배
,
정윤하
,
아나톨리코노노프
,
가민호†
Two-Step Detection Strategy for Small Ships in SAR Images
Kibae Park
,
Jeongbae Kim
,
Yunha Jung
,
Anatolii A. Kononov
,
Min-Ho Ka†
Author Information & Copyright ▼
School of Integrated Technolohy, Yonsei University
© Copyright 2025 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the
Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits
unrestricted non-commercial use, distribution, and reproduction in any
medium, provided the original work is properly cited.
Received: Jun 20, 2025; Revised: Jul 24, 2025; Accepted: Aug 28, 2025
Published Online: Oct 31, 2025
요 약
본 논문에서는 합성개구레이다(SAR, synthetic aperture radar) 영상에서 RCS가 낮아 검출이 어려운 소형 선박을 효과적으로 탐지하기 위해, CFAR에 기반한 2단계의 탐지 기법을 제시한다. 본 논문에서 제시하는 탐지 기법은 CA-CFAR (cell-averaging constant false alarm rate)로 1차 표적 후보를 확보하며, 2단계로 현실적 선박의 형상에 대응하는 윈도우 단위에서의 BI(binary integration) 스크리닝을 수행하여, 탐지 확률과 오경보율에서 큰 이득을 가져간다. 본 논문에서 제안된 기법의 성능을 평가하기 위해, 복소 정규 분포를 이용한 해수면 클러터를 모사한 가상 영상을 생성하고, 로그 정규 분포를 따르는 실제 선박 모사 표적을 모델링, 해상 클러터에 삽입하였다. 이어 표적 형상을 고려한 target window를 구현, 해당 윈도우에 기반하여 BI 알고리즘을 적용하였다. 이후, Monte Carlo 시뮬레이션을 통해 다양한 SNR 조건에서의 표적 탐지 확률을 ROC(receiver operating characteristic) 곡선으로 분석하였다. 마지막으로 제안된 기법과 CA-CFAR 탐지기의 탐지 결과를 비교하여 제안 기법이 낮은 SNR수준 탐지 환경에서 효과적인 탐지 성능을 보임을 확인하였다.
Abstract
This paper proposes a two-step detection strategy for small ship detection in synthetic aperture radar (SAR) images under low radar cross section (RCS) conditions. First, a cell-averaging constant false alarm rate (CA-CFAR) algorithm is applied to extract preliminary target candidates. Second, a window-level binary integration (BI) screening is performed using a log-normal block target model that approximates actual ship dimensions. To evaluate performance, a simulated sea surface clutter map is generated using a complex Gaussian distribution, with block targets inserted based on a log-normal distribution. A matching target window is used for BI, and Monte Carlo simulations across various scenarios yield receiver operating characteristic curves for both the proposed method and standalone CA-CFAR. The results show that integrating window-level BI with conventional CA-CFAR significantly improves small ship detection performance in low signal-to-noise ratio (SNR) SAR conditions.
Keywords: Ship Detection; CFAR; Binary Integration; Monte Carlo Simulation
Ⅰ. 서 론
최근 해양 감시 및 불법 어업 대응 분야에서 합성개구레이다(SAR, synthetic aperture radar) 영상의 활용이 활발히 논의되고 있다. 합성개구레이다는 기상, 주야간의 제약이 없어 광학 영상에서는 어려운 선박 탐지와 해양 감시에 효과적으로 사용될 수 있다. 전통적으로 레이다를 활용한 선박 탐지에는 CFAR(constant false alarm rate)기법이 널리 사용되어 왔다. CFAR 탐지기는 배경 클러터를 기반으로, 탐지 임계값을 동적으로 설정하는 알고리듬이다[1]. 그러나 CFAR 탐지기는 소형 선박과 같이 레이다 단면적(RCS, radar cross section)이 낮은 경우, CFAR 탐지기만으로는 탐지 확률이 낮고 오경보가 자주 발생한다는 한계가 있다[2]. 본 논문에서는 이를 보완하기 위해, CA-CFAR(Cell-averaging CFAR) 1차 표적 후보를 생성한 뒤, 표적 크기를 반영한 target window 기반의 binary integration 스크리닝을 결합한 2단계 탐지 기법을 제안한다. 본 연구에서는 18톤급 어선을 표적으로 설정, 해당 표적 탐지에 최적화된 target window를 고정하여 사용하였다. 본 논문에서 다양한 표적 크기나 방향성 등 복잡한 표적 특성은 고려하지 않았으며, 이상적인 조건 아래에서 제안하는 기법의 성능 평가에 초점을 두어 실험을 진행하였다.
Ⅱ. 가상 해상 환경 모델링
본 논문은 해상 클러터 환경에서 RCS가 낮은 소형 선박 탐지를 위해 두 단계로 구성된 탐지 기법을 제안한다. 1단계에서는 CA-CFAR 탐지기로 1차 표적 후보를 획득, 2단계에서는 실제 선박 크기에 기반하는 target window를 적용 후, binary integration을 수행하여 최종 표적을 탐지한다. 이를 평가하기 위해 복소 정규 분포 기반 해상 클러터 환경과 로그 정규 분포 블록 표적을 모델링한 후, 탐지 실험을 진행하였다.
2-1 해수면 클러터 모델링
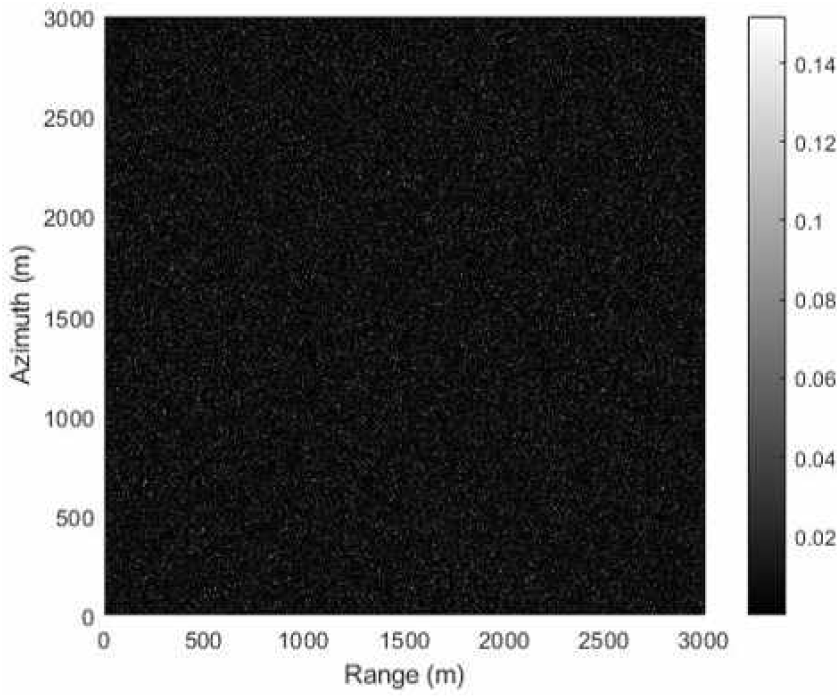
시뮬레이션 SAR 영상에서 해수면 클러터를 IQ 도메인에서 복소 정규 분포(complex gaussian distribution)를 이용하여 생성하고, 전력 도메인에서 지수 분포로 모델링하였다. 본 모델은 가장 기본적인 해수면 클러터 특성을 모의할 수 있다[3]. 본 논문에서는 공간해상도 3 m의 1,000×1,000 픽셀 영상으로 실험을 진행하였다(그림 1).
그림 1. | Fig. 1.
복소 정규 분포로 해상 클러터 환경을 시뮬레이션한 모의 영상 | Simulated sea clutter map using complex Gaussian distribution.
Download Original Figure
2-2 선박 표적 모델링
SAR 영상의 공간 해상도를 3 m로 가정하였을 때, 실제 18톤급 어선의 크기(폭 5 m×길이 20 m)는 2×7 픽셀 블록으로 계산되며, 픽셀의 개수 N은 식 (1)과 같다[4].
여기서 Lship 과 Wship 은 목표 선박의 길이와 폭, δaz 와 δra 는 각각 방위(azimuth) 방향, 거리(range) 방향의 공간해상도이다. 선박의 RCS 분포는 로그 정규 분포(log-normal distribution)로 근사화할 수 있음이 알려져 있으며[4], 본 논문에서는 선박 블록의 전력이 로그 정규 분포를 따르도록 설정하였다. 로그 정규 분포의 확률 밀도 함수는 식 (2)와 같다[5].
여기서, α와 β는 각각 평균과 표준편차를 의미하며, I 는 픽셀 강도로 나타난다. 선박의 로그 정규 분포 표준편차(β)는 선박의 픽셀 수와 관계없이 2 dB로 추정되며[4], 평균(α)은 표적의 정규화된 후방 산란 계수 와 β로부터 식 (3)과 같이 계산된다[4].
이에 따라 2×7 픽셀 크기의 총 150개 블록 표적(2,100 픽셀/1,000,000 픽셀)을 그림 2와 같이 시뮬레이션 영상 임의 위치에 삽입하였다.
그림 2. | Fig. 2.
모의 영상 임의 위치에 로그 정규 분포에 기반한 블록 표적을 삽입한 모습 | The simulation map with log-normal distribution block target at random location.
Download Original Figure
Ⅲ. 제안된 탐지 기법
3-1 CA-CFAR 탐지기 구현
본 논문에서는 Pfa=3×10−5를 목표 오경보율로 설정하고, 참조 셀 수 Nref=840, 블록 표적이 참조 셀 계산에 주는 영향을 최소화하기 위해 가드 셀 수 Nguard=120으로 설정하였다. CA-CFAR의 임계값 T=KZ은 식 (4)와 같다[1]. K는 임계값 계수, Nref는 참조 셀 개수, Z는 참조 셀 평균이다.
3-2 Target Window 정의
기존의 픽셀 단위 탐지를 넘어, 표적의 크기․형상을 반영한 target window를 정의하였다[4]. 윈도우 형태는 길이가 긴 선박의 형상을 고려하여, 목표 선박의 길이가 긴 변을 참고하는 형태로 설정하였으며, 윈도우 내 픽셀 수 NTW 은 식 (5)와 같이 계산된다. Lship 은 목표 선박의 폭과 길이 중 더 큰 값을 의미한다.
영상 내 윈도우의 개수 NTWs 는 식 (6)과 같이 산출된다. Nra 와 Naz 는 각각 거리, 방위 방향으로의 TW 개수이며, LAOI 와 WAOI 는 탐지할 영역의 거리, 방위 방향 거리이다.
3-3 Binary Integration 적용
CFAR의 탐지에서는 소형 선박과 같이 낮은 RCS의 표적에 대하여, 일정한 오경보율 유지가 어려워, 탐지 확률을 향상하기 힘들다. BI는 이를 보완하기에 효과적인 방법이다[6],[7]. 원리는 전체 영상을 NTWs 개 윈도우로 분할한 후, 개별 윈도우에서 CFAR 탐지기로 탐지된 픽셀 수가 사전에 설정한 최소 탐지 개수 Mpixel 이상일 경우, 해당 윈도우 전체를 최종 ‘표적 블록’으로 판단하는 것이다. 이는 아래 식 (7)과 같이 M-out-of-N 규칙으로 나타낼 수 있다.
이 과정을 통해 일정 면적 이상에서 신호가 누적된 경우에만 표적으로 판정된다. CFAR는 낮은 SNR 환경에서 표적 신호가 배경 잡음에 묻히는 경우가 많아 탐지 확률이 감소하고 오경보율은 증가할 수 있다. 제안 기법은 다수 픽셀의 누적 신호를 고려하므로, 개별 픽셀의 낮은 SNR이 전체 탐지 결과에 미치는 영향을 억제할 수 있다.
Ⅳ. Monte Carlo 시뮬레이션 결과 및 분석
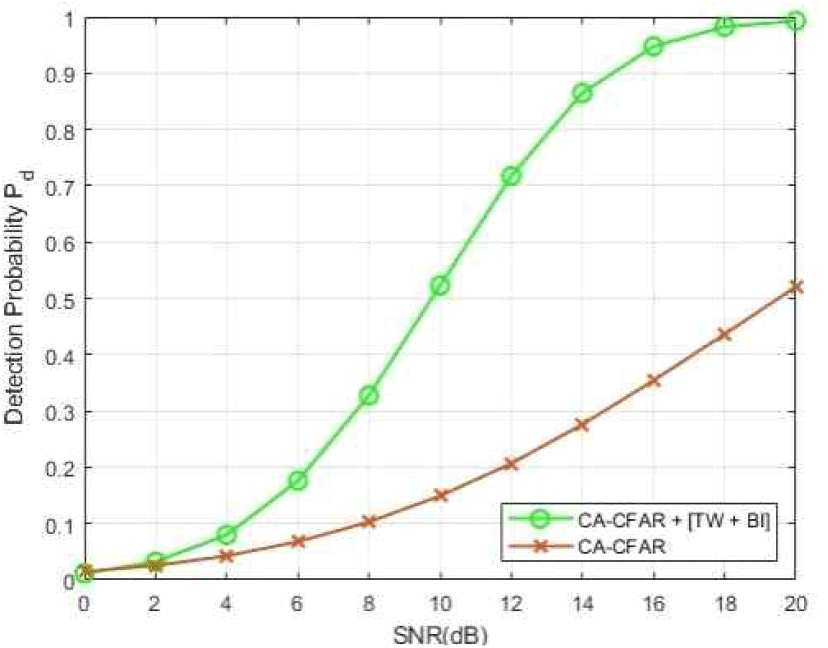
그림 3은 Monte Carlo 시뮬레이션을 통해 생성한 제안 기법과 단독 CA-CFAR 탐지기의 ROC 곡선을 비교한 결과이다. BI의 최소 탐지 픽셀은 2 픽셀로 설정하였으며, SNR 0~20 dB 구간에서 105회의 시뮬레이션을 진행하였다. 이는 낮은 신호 대비 잡음비 상황부터 상대적으로 양호한 조건까지 포함하여, 다양한 클러터 및 표적 탐지 성능을 현실적으로 모사하기 위함이다. 단독 CA-CFAR는 전체 SNR 구간에서 탐지 확률이 Pd≤0.52인 반면, 제안 기법은 CA-CFAR 대비 2배가량 높은 탐지 성능을 보여준다. 특히, 제안 기법에서는 Pd=0.95를 달성하기 위해 16 dB만의 SNR이 요구됨을 확인할 수 있다.
그림 3. | Fig. 3.
Monte Carlo 시뮬레이션으로 생성한 제안 기법과 CA-CFAR 단일 적용 탐지기의 ROC 곡선 | ROC curves of the proposed detector and CA-CFAR detector generated with Monte Carlo simultion.
Download Original Figure
Ⅴ. 결 론
본 논문에서는 전통적 CA-CFAR 탐지에 이어 target window 및 binary integration 적용 단계를 추가한 2단계의 탐지 기법을 제시하였다. 이를 검증하기 위해 해상 클러터 환경과 선박의 반사도를 모사하는 모의 SAR 영상을 생성하였다. 본 논문에서 제시하는 2단계 탐지 기법은 CA-CFAR을 적용한 후, target window 단위 binary integration을 추가 적용한다. Monte Carlo 시뮬레이션 결과, 동일한 오경보율 조건에서 기존의 CA-CFAR 대비 탐지 확률이 크게 개선됨을 확인하였다. 본 논문에서 제안한 2단계 탐지 기법은 단일 단계 기법이 가지는 성능 한계를 극복하고, 해상 환경에서 안정적이고 효과적인 소형 선박 탐지를 가능하게 하는 대안을 제공한다.
Acknowledgements
이 성과는 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(2021R1A2C2006025).
References
M. I. Skolnik,
Introduction to Radar, Columbus, OH, McGraw-Hill, pp. 5-6, 1962.

A. A. Kononov, M. H. Ka, “Rapid adaptive matched filter for detecting radar targets with unknown velocity,”
IEEE Access, vol. 12, pp. 25411-25428, 2024.


K. D. Ward, S. Watts, and R. J. A. Tough,
Sea Clutter: Scattering, the K Distribution and Radar Performance, vol. 20. London, IET, pp. 121-122, 2006.


J. Krecke, M. Villano, N. Ustalli, A. C. M. Austin, J. E. Cater, and G. Krieger, “Detecting ships in the New Zealand exclusive economic zone: Requirements for a dedicated SmallSat SAR mission,”
IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, vol. 14, pp. 3162-3169, 2021.


J. J. Shynk,
Probability, Random Variables, and Random Processes, Hoboken, NJ, John Wiley & Sons, 2012.

D. A. Shnidman, “Binary integration for swerling target fluctuations,”
IEEE Transactions on Aerospace and Electronic Systems, vol. 34, no. 3, pp. 1043-1053, Jul. 1998.


H. Lim, D. Yoon. ”Refinements of binary integration for Swerling target fluctuations,”
IEEE Transactions on Aerospace and Electronic Systems, vol. 55, no. 2, pp. 1032-1036, Apr. 2019.