해면 저고도 및 고기동 표적의 추적 정확도 향상을 위한 이중대역 다기능 레이다 시스템 활용

Ⅰ. 서 론

해상용 다기능 레이다(MFR, multi-functional radar)는 위상배열안테나를 바탕으로 표적 탐지, 추적 등의 다양한 임무들을 효과적으로 수행한다. 반면, 함정을 향해 다가오는 적군 유도미사일은 최신 해상용 MFR의 감시에서 벗어나기 위하여, 1) 고기동 움직임 및 2) 해수면 저고도 움직임을 가진다. 이때, 적군 유도미사일의 1) 고기동 특성은 MFR의 모노펄스 추적 빔 폭 내에 적 표적이 갑자기 사라져버려, MFR이 적 표적을 순간적으로 놓치게 만든다^[1]. 이러한 적 표적의 고기동 영향은 MFR이 모노펄스 추적 과정에서 매우 짧은 반복 주기로 추적 빔을 조사하게 만든다. 다음으로, 적군 유도미사일의 2) 해수면 저고도 특성은 해수면 다중경로 레이다 반사 신호를 만들게 되고, 직접 경로 레이다 반사 신호 내 심각한 간섭 영향을 준다^[2]. 이러한 다중경로 레이다 반사 신호 간섭 영향은 모노펄스 추적 과정에서 심각한 적 표적 고각 추정 문제를 야기한다^[3]. 따라서 고기동 및 해수면 저고도 움직임을 가지는 적 표적의 보다 안정적인 MFR 모노펄스 추적을 위해서는 다양한 연구가 반드시 요구된다.

최근, 고기동 움직임에 따른 표적 추적 정확도를 향상하기 위한 연구들이 활발히 수행되어 왔다^[4]~[6]. 먼저, 참고문헌 [4]에서는 고기동 표적 측정치가 추적할 실제 대상인지 결정하는 추적 초기화 알고리즘을 제안하여 오탐지된 결과들에 대한 불필요한 추적 임무를 완화한다. 참고문헌 [5]는 표적의 기동 정도에 따른 단계별 잡음 분산을 인공 신경망으로 학습시켜 추적하는 능동형 칼만 필터를 제안한다. 참고문헌 [6]은 표적 측정치를 딥러닝 기반으로 학습시켜 다양한 기동 특성을 예측하고, 최적 가중치를 적용하는 칼만 필터를 제안한다. 이와 동시에, 해수면 저고도 움직임에 따른 표적 고각 추정 문제를 극복하기 위한 연구들이 수행되어 왔다^[7],[8]. 그중 참고문헌 [7]은 이동평균 기법을 활용해 고각 측정치의 잡음 영향을 최소화하고, 다중경로 반사 신호 방향으로 안테나 빔이 조사되는 것을 억제하는 부엽 제어 제한조건을 제안한다. 참고문헌 [8]에서는 모노펄스 오차 복소 신호의 허수부에서 나타나는 특징적 곡선에서 유도된 식을 반복계산하여 수렴하는 표적 고각을 구하고, 필터링을 통해 해상 환경 영향을 극복하는 알고리즘을 제안한다. 하지만, 기존 연구들에도 불구하고, 단일대역 MFR 구조 기반의 교전 상황에서 해수면 저고도 및 고기동하는 적 표적들의 추적 과정에 많은 어려움이 존재한다. 특히, 고기동 표적의 추적 정확도 향상을 위해서는 추적 빔을 자주 조사해야 하는 자원 할당 문제가 발생하고, 저고도 표적의 고각 추정 향상을 위해서는 복잡한 알고리즘^[7],[8]을 활용해야 한다. 최근, 두 개의 운용 주파수를 이용하여 해수면 저고도 표적의 고각 추정 문제를 해결하기 위한 연구^[9]가 개발되어 왔다. 이는 모노펄스 채널 수신신호에 포함된 적 표적 고각과 다중경로 반사각을 각각 해석적으로 추정하는 방식이며, 두 개 운용 주파수로 두 개 방정식을 유도하여 두 개의 미지수(i.e., 적 표적 고각 및 다중경로 반사각)를 자명하게 추정하는 알고리즘이다. 따라서, 두 개 운용 주파수를 활용할 경우 심플한 알고리즘^[9]을 통해 고각 추정이 가능하다.

최신 함정 사업에서는 이중대역(i.e., S-대역 및 X-대역) MFR을 개발하고 있다. 여기서, 이중대역의 활용은 다양한 공학적 문제를 단일대역보다 효율적으로 해결할 수 있게 한다^[10],[11]. 본 논문에서는 고기동 및 해수면 저고도 움직임을 가지는 적 표적의 보다 정확한 모노펄스 크기 비교 추적을 수행하기 위하여, 최근 개발되어 오고 있는 이중대역 MFR 시스템을 활용한다. 먼저, 적 표적이 높은 고도에서 고기동 움직임을 가질 경우, 이중대역 MFR 수신 신호들을 교차 활용하여 보다 많은 측정치를 확보하고, 적 표적이 추적 빔 내를 벗어나지 못하게 한다. 그리고 적 표적이 낮은 고도에서 해수면 저고도 움직임을 가질 경우, 이중대역 MFR 수신 신호를 동시 활용하여 참고문헌 [9]의 방식으로 표적 고각 추정을 수행한다. 교전 상황을 고려한 시뮬레이션 결과, 제안된 기법을 통하여 고기동 및 해수면 저고도 움직임을 가지는 적 표적의 보다 안정적인 추적이 가능함을 확인할 수 있었다.

Ⅱ. 해수면 저고도 및 고기동 표적의 반사 신호 모델 및 기존 모노펄스 추적 성능 분석

2-1 다중경로 환경 레이다 반사 신호 모델

본 논문은 해수면 다중경로 환경에서 적 표적의 레이다 반사 신호를 모델링하기 위하여 지구의 곡률을 고려한다. 그림 1의 A는 MFR의 위치, B는 해수면의 다중경로 반사 지점, C는 적 표적의 위치라 가정한다. 이때, h_R은 해수면으로부터 MFR의 높이, h_T는 해수면으로부터 적 표적의 높이, α_E는 지구의 실효 반지름이다. 지구 곡률을 고려한 적 표적과 MFR의 직접경로 거리 R은 식 (1)과 같이 정의된다.

그림 1. | Fig. 1. 해수면 다중경로 환경에서 모노펄스 크기비교 추적을 위한 지구 곡률 모델링^[7] | Earth curvature modeling for monopulse amplitude comparison tracking in a sea-surface multipath environment^[7].

Download Original Figure

$$R=\sqrt{\begin{array}{l}{\left(h_R+a_E\right)}^2+{\left(h_T+a_E\right)}^2,\hfill \\ -2\left(h_R+a_E\right)\left(h_T+a_E\right)\cos \left(\frac{r}{a_E}\right)\hfill \end{array}}$$

(1)

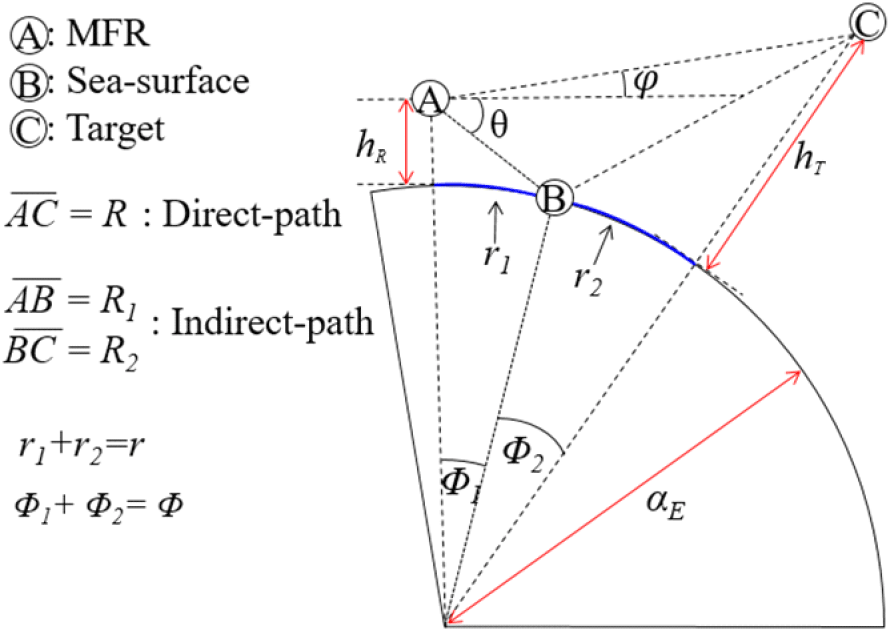
여기서, r₁, r₂는 표적의 움직임에 따른 지표면에 투영된 다중경로 거리이고, Φ₁, Φ₂는 r₁, r₂에 대응되는 지구 중심에서의 각도이다. 또한, Φ₁ + Φ₂ = Φ, r = r₁ + r₂이며, 이는 식 (2)와 같은 관계를 갖는다.

$$r_1=\frac{r}{2}-\frac{1}{\sqrt{3}}\sqrt{4{\alpha }_E\left(h_R+h_T\right)+r^2}\times \sin \left(\frac{\Phi }{3}\right).$$

(2)

지구 곡률을 고려한 해수면에서 반사되는 다중경로 거리 R₁, R₂는 식 (3)과 같이 정의된다^[7].

$$R_1=\sqrt{{\left(h_R+{\alpha }_E\right)}^2+{\alpha }_E^2-2\left(h_R+{\alpha }_E\right){\alpha }_E\cos \left(\frac{r_1}{{\alpha }_E}\right)},$$

(3)

$$R_2=\sqrt{{\left(h_T+{\alpha }_E\right)}^2+{\alpha }_E^2-2\left(h_T+{\alpha }_E\right){\alpha }_E\cos \left(\frac{r_2}{{\alpha }_E}\right)}.$$

(4)

다음으로, 다중경로 환경에서 적 표적에 반사된 레이다 기저 대역 수신신호 S_r(t)는 식 (5)와 같이 정의한다.

$$S_r\left(t\right)=\sqrt{P_r}\times \exp \left(j\frac{4\pi }{{\lambda }_c}R\right)+\sqrt{P_0}\times \exp \left(j\frac{4\pi }{{\lambda }_c}\left(R_1+R_2\right)\right),$$

(5)

여기서, 식 (5)의 첫 줄은 직접경로 신호, 두 번째 줄은 다중경로 반사 신호이다. 특히, 다중경로 반사 신호는 그림 2와 같이 전파 경로의 증대와 해수면의 반사 특성에 따라 크기와 위상이 직접 경로 신호와 다르게 변조되어 나타난다. 그리고, 식 (5)에서 λ_c는 파장, P_r은 직접경로 수신전력, P₀는 다중경로 수신전력이며, 식 (6)과 같다.

그림 2. | Fig. 2. 해수면의 다중경로 반사 현상 예시 | Example of multipath reflection phenomenon for sea-surface.

Download Original Figure

$$\begin{array}{l}{P}_r=\frac{P_t{G}_t{G}_r{\lambda }_c^2\sigma }{{\left(4\pi \right)}^3{R}^4},\hfill \\ P_0=\frac{P_t{G}_t{G}_r{\lambda }_c^2\sigma \Gamma D{\rho }_s}{{\left(4\pi \right)}^3{\left(R_1+R_2\right)}^4}.\hfill \end{array}$$

(6)

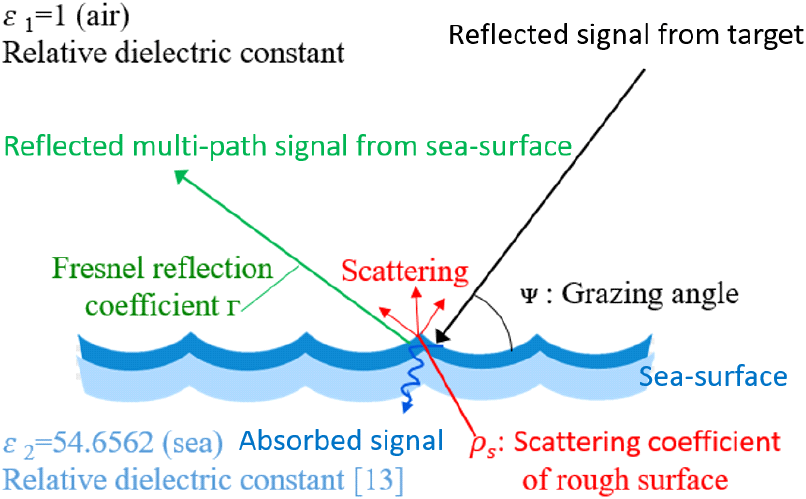
식 (6)에서 P_t는 송신전력, G_t, G_r은 각각 송신 및 수신 안테나 이득, σ는 표적의 레이다 반사 단면적, 그리고 Γ는 유전율 및 해수면 입사각(grazing angle)에 따른 해수면의 반사 계수로 식 (7)과 같이 나타낸다^[12].

$$\Gamma =\frac{\sin \psi -\sqrt{\epsilon -{\cos }^2\psi }}{\sin \psi +\sqrt{\epsilon -{\cos }^2\psi }}.$$

(7)

여기서, Ψ는 그림 2과 같이 해수면으로 입사하는 grazing angle, ε는 해수면 복소 유전율이다^[13]. 그리고, 식 (6)의 D는 지구 곡률에 따른 해수면의 divergence factor로 식 (8)과 같이 근사할 수 있다^[14].

$$D\approx {\left(1+\frac{2r_1{r}_2}{{\alpha }_E\times r\sin \psi }\right)}^{-\frac{1}{2}},$$

(8)

그리고, 식 (6)의 ρ_s는 해수면의 랜덤한 파고(sea spike)에 의한 산란 계수(scattering coefficient)이며, 식 (9)로 나타낼 수 있다.

$${\rho }_s=\left\{\begin{array}{l}{e}^{-8{\left(\pi k\right)}^2},0\le k\le 0.1\hfill \\ \frac{0.812537}{1+8{\left(\pi k\right)}^2},0.1\le k\le 0.3\hfill \end{array}\right.,$$

(9)

여기서, l는 roughness factor이다^[15].

2-2 해수면 저고도 및 고기동 표적의 기존 모노펄스 추적 성능 분석

해수면 저고도 표적의 추적 과정에서 다중경로 반사 신호는 표적의 고각 추정 문제를 야기한다. 이 문제를 해석하기 위하여, 그림 3과 같이 2개의 모노펄스 안테나 수신 빔이 고각을 추정하는 기하 구조를 가정한다. 이때, 모노펄스 안테나 Rx 1, Rx 2의 수신신호 S_r1(t), S_r2(t)는 식 (5)로부터 식 (10)과 같이 나타낼 수 있다.

그림 3. | Fig. 3. 해수면 환경에서 고각 추정을 위한 모노펄스 추적 기하 구조 예시 | Example of monopulse tracking geometry for elevation estimation in a sea-surface environment.

Download Original Figure

$$\begin{array}{c}{S}_{r1}\left(t\right)=\sqrt{P_{r1}}\times \exp \left(j\frac{4\pi }{{\lambda }_c}R\left(1+\frac{d}{2R}\sin \phi \right)\right)+I_1\left(t\right),\\ S_{r2}\left(t\right)=\sqrt{P_{r2}}\times \exp \left(j\frac{4\pi }{{\lambda }_c}R\left(1-\frac{d}{2R}\sin \phi \right)\right)+I_2\left(t\right),\end{array}$$

(10)

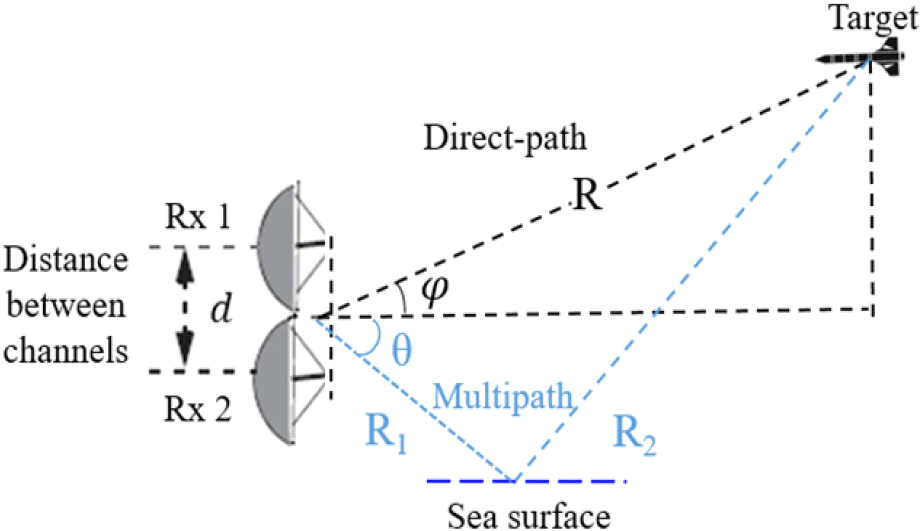
여기서, P_r1, P_r2는 각 모노펄스 안테나에 수신되는 직접경로 신호의 전력이고 I₁(t), I₂(t)는 각 안테나에 수신된 다중경로 반사 신호로 식 (11)과 같이 나타낼 수 있다.

$$\begin{array}{c}{I}_1\left(t\right)=\sqrt{P_{01}}\times \exp \left(j\frac{4\pi }{{\lambda }_c}{R}_1\left(1+\frac{d}{2R_1}\sin \theta \right)\right)\times \exp \left(j\frac{4\pi }{{\lambda }_c}{R}_2\right),\\ I_2\left(t\right)=\sqrt{P_{02}}\times \exp \left(j\frac{4\pi }{{\lambda }_c}{R}_1\left(1-\frac{d}{2R_1}\sin \theta \right)\right)\times \exp \left(j\frac{4\pi }{{\lambda }_c}{R}_2\right).\end{array}$$

(11)

여기서 P₀₁, P₀₂는 각 안테나에 수신된 다중경로 반사 신호의 전력이다. 모노펄스 크기 비교 기반의 각도 추정을 위하여 식 (10)을 활용하여 합 신호(Σ)와 차 신호(Δ)를 식 (12)와 같이 정의한다.

$$\begin{array}{c}\sum =S_{r1}\left(t\right)+S_{r2}\left(t\right)\\ ={\sum }_{direct}\left(\phi \right)+\left|\rho \right|e^{j\alpha }{\sum }_{indirect}\left(\theta \right),\\ \Delta =S_{r1}\left(t\right)-S_{r2}\left(t\right)\\ ={\Delta }_{direct}\left(\phi \right)+\left|\rho \right|e^{j\alpha }{\Delta }_{indirect}\left(\theta \right),\end{array}$$

(12)

여기서 ρ는 직접경로 신호와 다중경로 신호의 크기 변조 차이, α = (4π/λ_c) R₂, Σ_direct(φ) 및 Δ_direct(φ)는 직접경로 고각 φ을 매개변수로 하는 각 안테나에서 수신된 직접경로 신호의 합과 차 신호, 그리고 Σ_indirect(θ) 및 Δ_indirect(θ)는 다중경로 반사각 θ을 매개변수로 하는 각안테나에 수신된 다중경로 신호의 합과 차 신호이다. 최종적으로 모노펄스 크기 비교에서는 식 (12)의 합과 차 신호비를 통해 식 (13)과 같은 각도 오차를 검출한다.

$$ϵ=\frac{\left|\Delta \right|}{|\sum |}.$$

(13)

여기서, 기존 모노펄스 크기 비교 방식은 다중경로 영향이 없을 때, 직접경로 고각 φ의 추정이 가능하다. 하지만, 식 (13)에는 다중경로 영향이 존재하기 때문에, 합과 차 신호비 방정식 1개에 미지수 2개(φ, θ) 존재하는 과소결정계 문제로 해석되고, 직접경로 고각 추정 문제는 자명하지 않다.

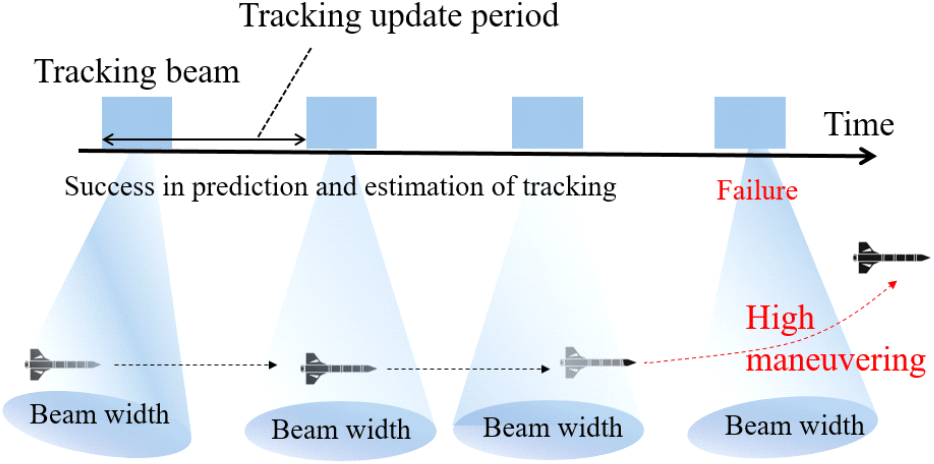
다음으로 고기동 표적의 추적 과정에서 고기동 움직임은 적 표적이 MFR의 추적 빔을 이탈하여 추적 실패 문제를 야기한다. 이 문제를 직관적으로 분석하기 위하여, 그림 4와 같은 시나리오를 가정한다. 이때, MFR이 다른 임무를 수행하는 동안 적 표적이 급격하게 고기동하여 예측된 추적 빔 영역을 벗어날 수 있다. 이러한 문제를 해결하기 위하여 MFR은 매우 짧은 주기로 추적 빔을 조사해야 하나, 다수의 임무를 수행해야 하는 MFR 입장에서 자원 부족 문제가 생길 수 있다.

그림 4. | Fig. 4. 표적 측정치 획득 실패 예시 | Example of fail to obtain target measurements.

Download Original Figure

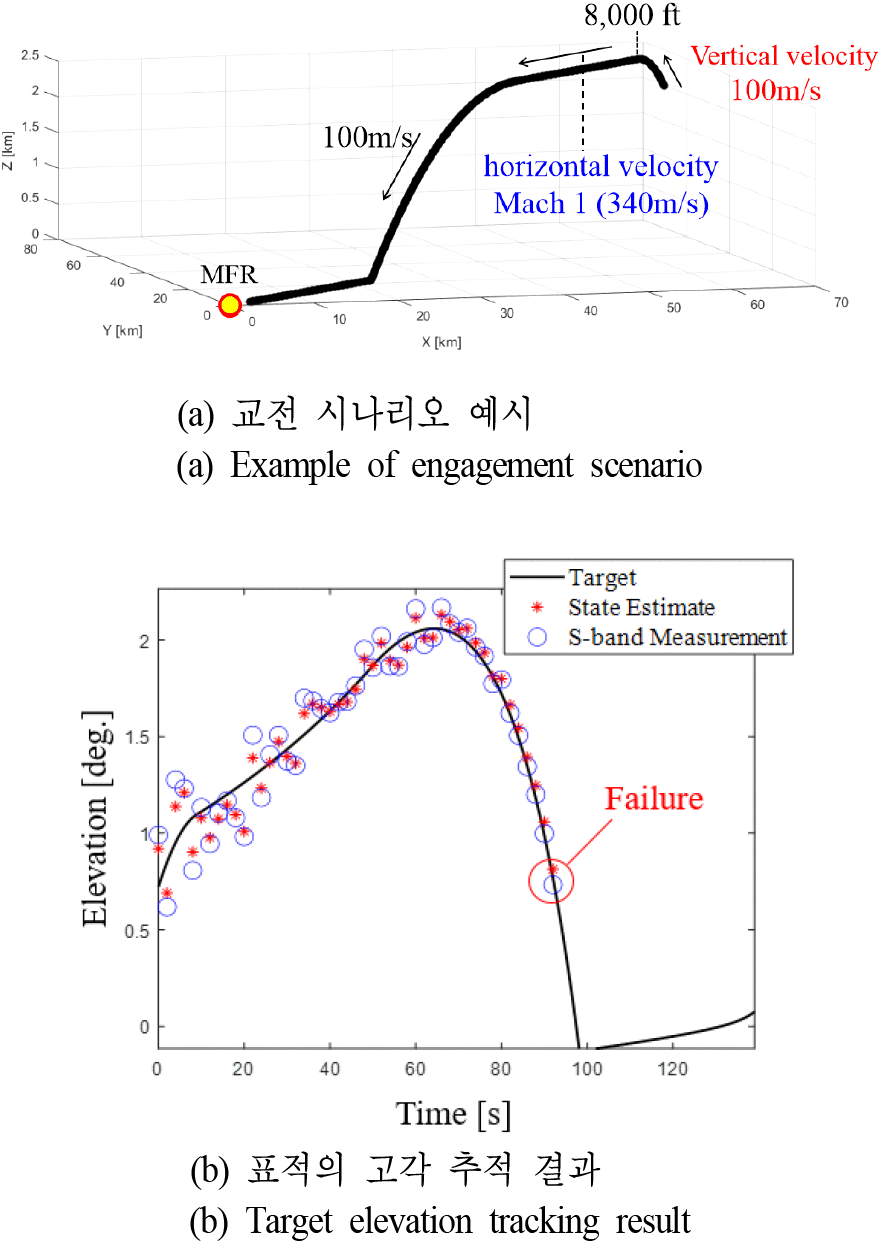
앞서 언급한 문제를 보다 직관적으로 분석하기 위하여, 그림 5(a)와 같은 시나리오에서 기존 추적 기법의 시뮬레이션을 수행하였다. 이때 실시간 성능 검증을 위하여 AMD Ryzen 5기반의 Window 10 운영체제에서 MATLAB R2024a버전을 활용하였다. 고기동 표적의 추적을 위하여 S-대역 추적 빔을 1.5초 주기로 반복하여 조사하였고, 이외 다중경로 모델링 변수는 표 1, MFR 시스템 변수는 표 2와 같다. 그림 5(b)는 모노 펄스 크기 비교 기반 고각 추정 결과이며, 저고도에서 고각의 오차가 크게 발생함과 동시에 급하강 구간에서 추적에 실패함을 볼 수 있다. 이는 고각의 급격한 변화로 추적 빔 영역 안에 표적이 벗어나기 때문이다. 따라서, 해수면 저고도 및 고기동 표적의정확한 추적을 위해서는 위 두 가지 공학적 문제를 보다 효율적으로 해결하기 위한 새로운 알고리즘이 필요하다.

그림 5. | Fig. 5. 해수면 저고도 및 고기동 표적의 기존 추적 결과 | Simulation results of conventional tracking method for sea skimming and high maneuvering target.

Download Original Figure

표 1. | Table 1. 다중경로 모델링 변수들 | Parameters for multipath modeling.

Effective earth radius αE	6,500 km
Temperature of sea surface	25°C
Salinity	50 %
Complex dielectric constant ε	63.97+56.08i V/m
Roughness factor k	0.05
Scattering coefficient of rough coefficient ρs	0.8209

Download Excel Table

표 2. | Table 2. S-대역 MFR 시스템 변수들 | Parameters for S-band MFR system.

Carrier frequency fc	3 GHz	Wave length λc	0.1 m
Effective aperture area	4.9 m2	Beam width	4.09°
Thermal noise power	4 × 10−18 W	Transmit power	50 kW

Download Excel Table

Ⅲ. 제안된 기법

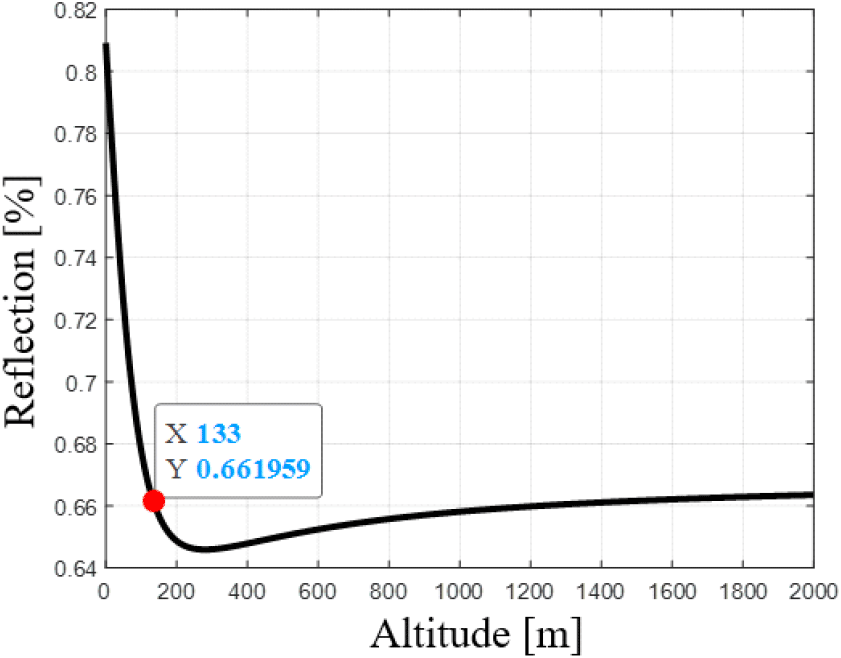
본 논문에서는 해수면 저고도 및 고기동 특성을 가진 표적의 추적 정확도를 향상하기 위하여 이중대역(i.e. S-대역, X-대역) MFR 시스템을 활용한다. 이때, MFR은 모노펄스 크기 비교를 통해 적 표적 정보(i.e., 거리, 방위각, 고각)를 측정한 후, 확장형 칼만 필터(extended Kalman filter)를 활용하여 3차원 좌표(i.e., [X, Y, Z])를 추정할 수 있다. 여기서, Z 값은 적 표적 고도를 의미하며, 고도 Z가 일정 임곗값보다 높으면 고고도 고기동, 낮으면 해수면 저고도 기동으로 적 표적 비행 특성을 판단할 수 있다. 여기서, 일정 임곗값은 표 1의 조건에서 다중경로 반사 신호가 약 66.2 % 이상 정반사되어서 직접경로 고각추정에 영향을 줄 수 있는 고도로 정의되며, 대략 0.133 km로 추정된다(그림 6). 만약 해수면 저고도에서 적 표적이 기동할 경우(i.e. Z<0.133 km), 이중대역 추적 빔을 동시 활용하여 직접 경로 고각을 자명하게 추정한다. 반면에, 만약 고고도에서 적 표적이 고기동할 경우(i.e. Z≧ 0.133 km), 이중대역 추적 빔을 교차 할당하여 추적 실패율을 낮추고, 추적 오차 표준 편차를 보다 빠르게 감소시킨다. 본 논문의 전반적인 알고리즘 구조는 그림 7과 같다.

그림 6. | Fig. 6. 고도에 따른 해수면 반사 | Reflection at sea-surface along altitude.

Download Original Figure

그림 7. | Fig. 7. 제안된 이중대역 추적 알고리즘의 구조 | Framework of proposed dual-band tracking algorithm.

Download Original Figure

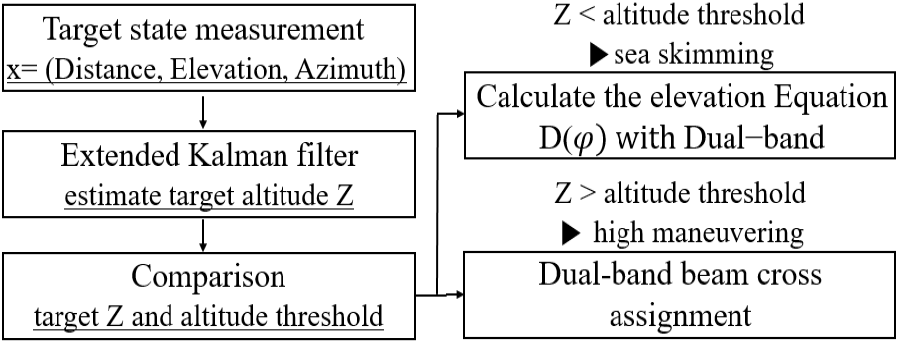
먼저, 해수면 저고도에서 적 표적이 기동할 경우(i.e. Z <0.133 km), 이중대역의 합 및 차 신호를 다음과 같이 2개 방정식으로 유도한다^[9].

여기서, Σ_S 및 Δ_S는 각각 S-대역의 모노펄스 합 신호와 차 신호이고 Σ_S 및 Δ_S는 각각 X-대역의 모노펄스 합 신호와 차 신호이다. ${\alpha }_S=\frac{4\pi }{{\lambda }_S}{R}_2$, ${\alpha }_X=\frac{4\pi }{{\lambda }_X}{R}_2$이며, 여기서 λ_S 및 λ_S는 각각 S-대역 파장 및 X-대역 파장이다. 그리고 D(φ)는 적 표적 고각(φ)을 매개변수로 하는 방정식, I(θ)는 다중경로 반사각(θ)을 매개변수로 하는 방정식이다. 다음으로 D(φ)에 대하여 T₁, T₂을 정리하면 최종적으로 식 (16)과 같은 직접경로 고각 φ을 자명하게 추정하기 위한 방정식이 정의된다.

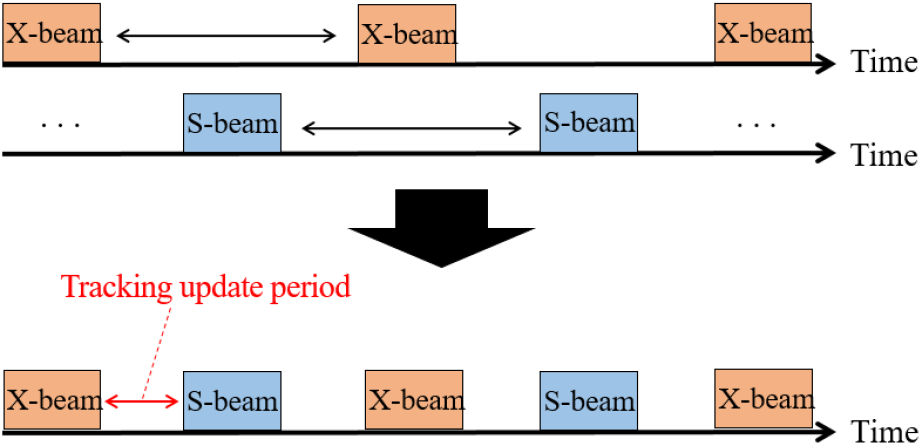
다음으로 고고도에서 적 표적이 고기동할 경우(i.e., Z ≧0.133 km), 고기동 표적의 추적 실패율을 낮추기 위하여 이중대역 추적 빔을 교차 할당한다. 이는 한 주파수 대역이 표적에 추적 빔을 조사한 후 다른 임무를 수행하는 동안, 나머지 주파수 대역이 이 표적에 추적 빔을 조사하는 방식이다(그림 8). 이는 MFR이 다양한 임무들을 수행하는 와중에, 고기동 표적을 추적 빔 내에 벗어나지 않게 할 수 있다. 그리고, 단일대역과 달리 이중대역에서 다수의 측정치를 보다 많이 확보함으로써 고기동 표적의 추적 오차 통계적 값인 표준 편차가 보다 빨리 줄어들 수 있다. 또한, 운용 주파수를 다양하게 활용할 경우 표적의 레이다 반사 단면적이 수치 해석적으로 보다 다양하게 나타난다는 점에서 추적 정확도를 높일 수 있다. 마지막으로, X-대역은 파장이 상대적으로 짧아 좁은 빔 폭을 가지기에 각도 해상도가 뛰어나나, 추적 빔 영역이 좁아 고기동 표적이 사라질 수 있는 단점이 있다. 이와 반대로 S-대역은 상대적으로 긴 파장으로 넓은 빔 폭을 가지기에, 추적 빔 영역이 상대적으로 넓다. 따라서, X-대역과 S-대역을 교차하여 추적 빔을 조사할 경우, 단일대역을 운용하는 것보다 다양한 이점을 가질 수 있다.

그림 8. | Fig. 8. 이중대역 추적 빔 교차 할당 예시 | Example of dual-band tracking beam cross allocation.

Download Original Figure

Ⅳ. 시뮬레이션 결과

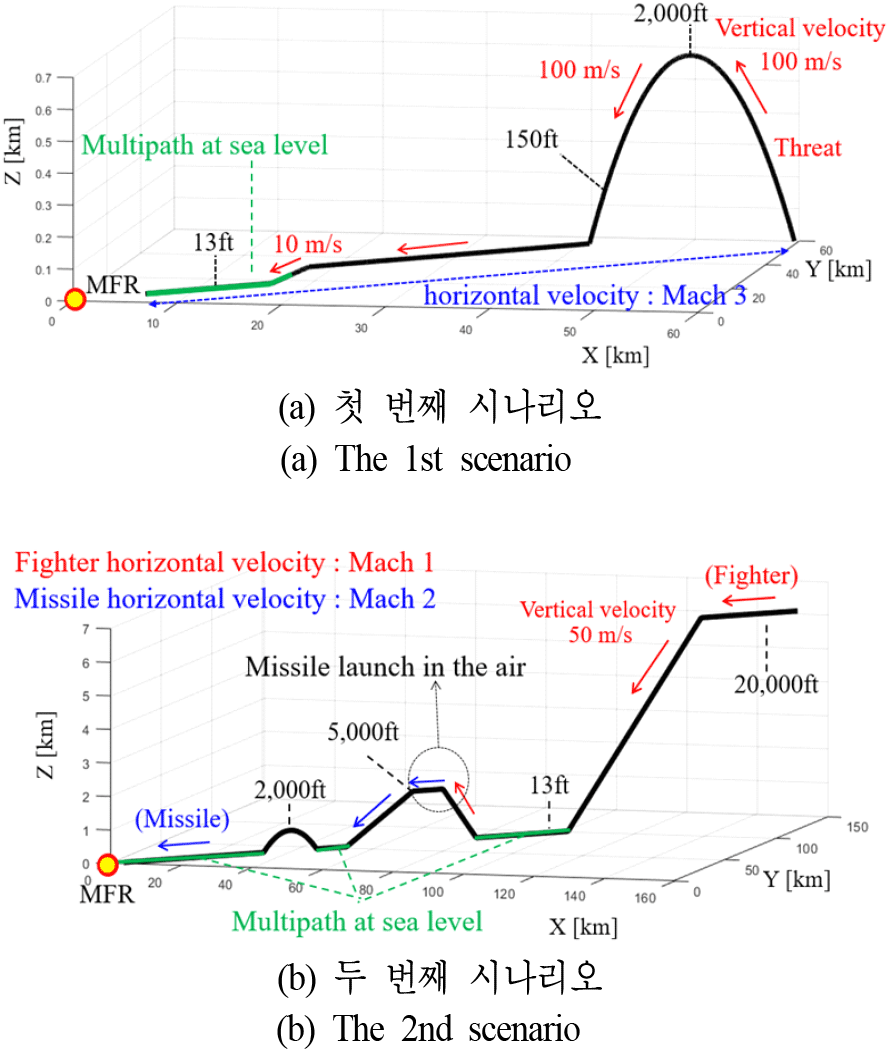
본 절에서는 제안된 이중대역 MFR 기반 추적 알고리즘을 기존 단일대역 MFR 기반 추적 알고리즘과 비교한다. 여기서, 제안된 알고리즘은 확장 칼만 필터의 등속도 모델을 사용하였고, 기존 기법은 등속도 모델과 고기동 표적 추적에 더욱 용이한 등가속도 모델을 각각 사용하였다. 또한, 두 가지 시나리오에서 MFR로 다가오는 해수면 저고도 및 고고도 고기동 적 표적을 가정하였다 (그림 9). 여기서, 두 시나리오의 다중경로 모델링 변수는 표 1, S-대역 MFR 시스템 변수는 표 2, X-대역 MFR 시스템 변수는 표 3과 같으며, 1 ft=0.3048 m, 마하 1=340 m/s이다.

그림 9. | Fig. 9. 제안된 기법을 검증하기 위한 교전 시나리오 예시 | Example of engagement scenario to verify the proposed method.

Download Original Figure

4-1 첫 번째 시나리오 시뮬레이션 결과

그림 9(a)의 첫 번째 시나리오에서 제안된 이중대역 MFR 기반 추적 알고리즘은 각 대역의 추적 빔을 1초 주기로 반복하여 교차 조사하였고, 확장 칼만 필터를 활용하는 기존 단일대역 추적 기법은 S-대역 추적 빔을 1초 주기로 조사하였다.

먼저, 그림 10(a)는 표적 좌표 추적 결과를 보여주며, 지구 곡률을 고려함에 따라 적 표적 고도가 음수로 나타났다. 기존 기법은 해수면 저고도 기동 구간에서 다중경로 반사 신호 영향에 의해 극심한 오차를 보였으며, 적 표적이 급격하게 기동하는 구간에서 추적 빔 폭을 벗어남에 따라 추적이 실패하였다. 반면에, 제안된 알고리즘은 적 표적을 안정적으로 추적할 수 있었다.

그림 10. | Fig. 10. 그림 9(a)의 첫 번째 시나리오 표적 추적 시뮬레이션 결과 | Simulation results for target tracking at the 1st scenario in Fig. 9(a).

Download Original Figure

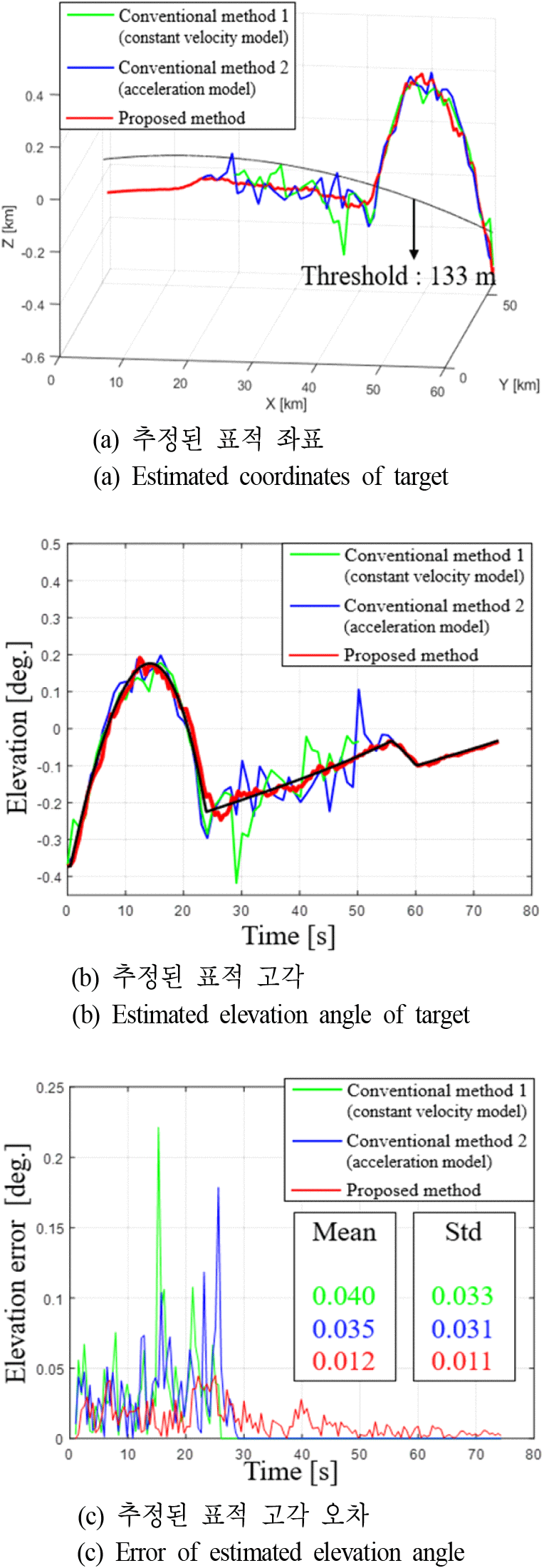
다음으로 그림 10(b) 및 그림 10(c)는 추정된 적 표적 고각 및 고각 오차를 보여준다. 특히, 해수면의 영향을 받는 저고도 구간에서 큰 고각 오차 (i.e. 등속 모델 기반 기존 기법의 평균 오차=0.040°, 가속 모델 기반 기존 기법의 평균 오차=0.035°)를 가지는 기존 기법과 달리, 제안된 알고리즘은 0.012°의 평균 오차로 보다 안정적인 추적이 가능하였고, 고각 오차 표준편차도 0.011°로 보다 안정적으로 줄어드는 것을 확인할 수 있었다.

4-2 두 번째 시나리오 시뮬레이션 결과

그림 9(b)의 두 번째 시나리오에서는 첫 번째 시나리오 시뮬레이션과 달리, 제안된 이중대역 MFR 기반 추적 알고리즘은 각 대역이 추적 빔을 1초 주기로 반복하여 교차 조사하였고, 기존 단일대역 추적 기법은 S-대역 추적 빔을 0.5초 주기로 조사하였다.

먼저, 그림 11(a)은 적 표적의 좌표 추정 결과를 보여준다. 이때, 기존 기법은 해수면 저고도 기동 구간에서 심한 고각 추정 오차로 인해 추적 빔 폭에서 표적이 벗어남에 따라 추적이 실패하였다. 반면에, 제안된 알고리즘은 고기동 및 해수면 저고도 기동 구간에서 적 표적을 성공적으로 추적하였다.

그림 11. | Fig. 11. 그림 9(b)의 두 번째 시나리오 표적 추적 시뮬레이션 결과 | Simulation results for target tracking at the 2nd scenario in Fig. 9(b).

Download Original Figure

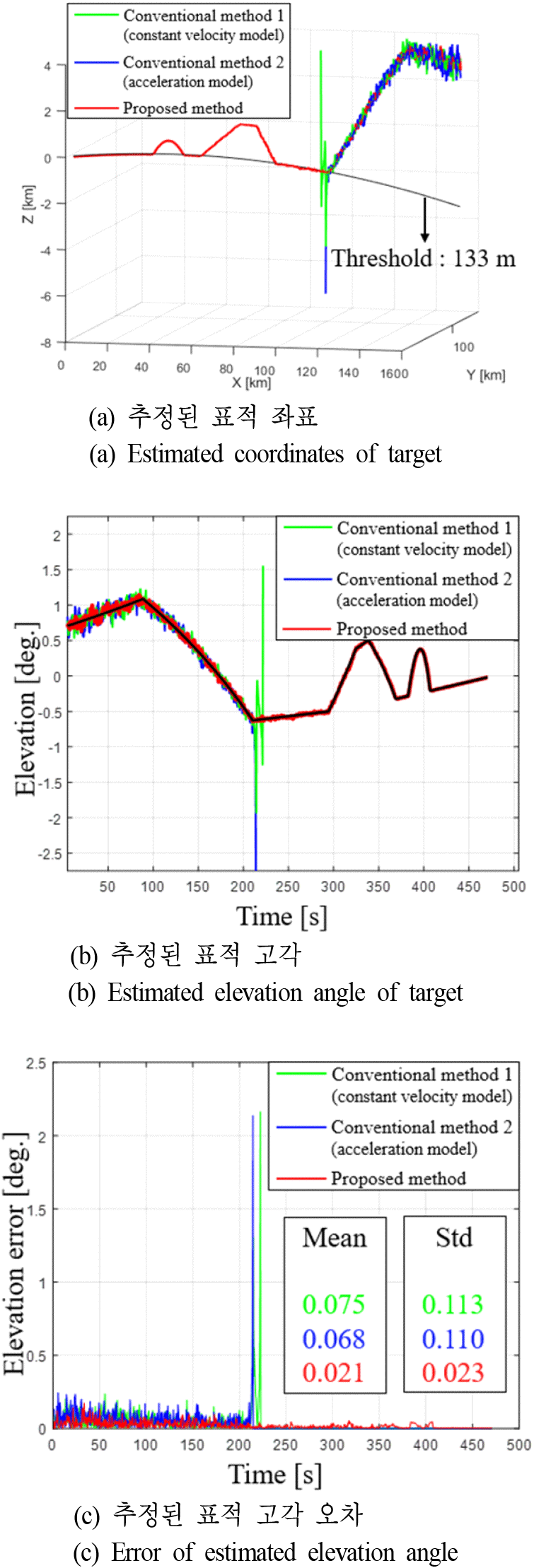
다음으로 그림 11(b) 및 그림 11(c)는 추정된 적 표적 고각 및 고각 오차를 보여준다. 이때, 다중경로 간섭 영향으로 기존 기법의 고각 오차가 급증한 것을 볼 수 있고, 제안된 알고리즘은 표준편차가 약 0.021°로 고각 오차가 안정적으로 줄어드는 것을 확인할 수 있었다. 그리고, 첫 번째 시나리오에 비하여 보다 급격한 기동 특성을 가지는 두 번째 시나리오에서 두 기존 기법의 고각 오차 평균은 0.075° 및 0.068°인 반면, 제안된 알고리즘은 평균 0.023°의 고각 오차로 표적을 추적할 수 있었다.

Ⅴ. 결 론

본 논문에서는 고기동 및 해수면 저고도 비행하는 적 표적을 보다 정학히 추적하기 위하여, 1) 적 표적이 해수면 저고도 기동할 때, 이중대역 수신 신호를 활용하여 직접경로 고각을 자명하게 추정하고, 2) 고고도 고기동 할 때, 이중대역 추적 빔을 교차 할당하는 이중대역 MFR 기반의 알고리즘을 제안하였다. 제안된 알고리즘의 성능을 검증하기 위하여 시뮬레이션을 수행한 결과, 제안된 알고리즘은 해수면 저고도에 의한 다중경로 간섭을 효과적으로 보상할 수 있었고, 고기동 표적을 보다 안정적으로 추적할 수 있었다.