Ⅰ. 서 론
도플러 레이다는 수신 신호의 주파수 편이로부터 표적의 위치 및 속도 정보를 추정한다[1]. 도플러 신호로부터 표적의 속도 변화와 기동 특성을 알 수 있어 도플러 레이다는 표적 분류나 표적의 움직임 특성 분석에 널리 활용되고 있다[2]~[4]. 특히 무기 체계 성능 시험 분야에서는 도플러 레이다를 활용하여 부스터 분리나 신관 작동에 따른 자탄 방출과 같은 이벤트 현상을 계측하고 표적의 움직임을 분석한다[5],[6].
도플러 레이다의 계측 자료로부터 이벤트 현상 및 움직임 특성을 가시화하기 위해서는 시간 대 도플러 맵, 즉 DTI(Doppler time intensity)가 활용된다. DTI는 각 시간대에서 도플러 속도별 신호 세기의 변화를 나타낸 2차원의 이미지로 FFT(fast Fourier transform)이나 STFT(short time Fourier transform)을 통해서 얻을 수 있다[3],[4].
모노펄스 계측 레이다는 진폭 비교 방식으로 표적의 각도를 추정하여 각도 정확도가 높아 표적의 정확한 위치 정보를 획득할 수 있어 무기 체계 시험장에서 널리 운용되고 있다[7]. 모노펄스 계측 레이다는 단일 표적 추적 레이다로 이벤트 현상 계측보다는 한 번에 한 개의 표적을 정확히 추적하는 데에 활용되고 있다. 코히런트 모노펄스 계측 레이다는 일정 구간, 즉 드웰 동안 수신된 다수의 펄스를 중첩하여 표적을 탐지하여 펄스 중첩을 수행하지 않는 일반적인 모노펄스 계측 레이다 대비 신호 대 잡음 비가 높다[1].
수신 신호로부터 직접적으로 속도를 추정할 수 없는 일반적인 모노펄스 계측 레이다와 달리, 코히런트 모노펄스 계측 레이다는 드웰 내 펄스 간 주파수 편이로부터 도플러 주파수를 추정할 수 있다. 코히런트 모노펄스 계측 레이다는 펄스 반복 주파수(PRF, pulse repetition frequency)의 제한으로 일반적인 도플러 레이다에 비해 낮은 속도 분해능을 가지나 도플러 신호로부터 표적의 속도를 직접적으로 계측할 수 있다.
코히런트 모노펄스 레이다는 속도 모호성을 해결하고, 추적 성공률을 높이기 위해서 드웰마다 PRF를 비주기적으로 변경한다는 특징을 가진다. 이러한 특징으로 인해 기존 도플러 레이다에서 사용되는 SFTF나 FFT를 활용하여 DTI를 얻을 수 없다.
일반적인 펄스 도플러 레이다는 속도 모호성을 해결하기 위해서 다중 PRF나 스태거드(staggered) PRF 방식을 적용하여 DTI를 생성한다[8],[9]. 다중 또는 스태거드 PRF 적용은 정확한 속도 추정을 가능하게 하지만, 연산량을 증가시키고 주엽 성분이 증폭된다는 문제점이 있다[9],[10]. 단일 표적의 정확한 위치 추정에 중점을 두는 코히런트 모노펄스 계측 레이다는 다중 또는 스태거드 PRF를 사용하지 않으며, 한 드웰에서 PRF를 변경하지 않는다. 따라서 코히런트 모노펄스 계측 레이다의 DTI 생성에는 기존 다중 및 스태거드 PRF 방식의 코히런트 펄스 도플러 레이다 DTI 생성 방법을 적용할 수 없다.
본 논문에서는 코히런트 모노펄스 계측 레이다 신호로부터 DTI를 얻는 방법을 제안한다. 제안하는 방법을 통해 계측 레이다에서 추적이 된 표적의 기동 특성을 가시화하여 DTI를 얻을 수 있다. 제안하는 방법은 비주기적 PRF 변경을 고려하여 주기도 파워 스펙트럼 밀도 추정값으로부터 DTI를 산출하였으며, 속도 모호성 해결을 위해서는 추적 결과를 활용하였다.
제안하는 방법으로 산출된 DTI를 통해 코히런트 모노펄스 계측 레이다의 계측 자료로부터 부스터 분리와 자탄 방출과 같은 이벤트 현상 발생 여부를 계측할 수 있다. 또한 제안하는 방법은 실시간으로 DTI를 산출할 수 있어 레이다 장비 운용 중에 운용자가 신호 및 추적 상태를 확인하는 데에 활용될 수 있다.
Ⅱ장에서는 코히런트 모노펄스 계측 레이다의 신호 모델 및 PRF 변경 방법에 대해 요약한다. Ⅲ장에서는 제안 방법을 기술한다. Ⅳ장에서는 모의실험을 통해 코히런트 모노펄스 계측 레이다의 계측 자료로부터 얻은 DTI가 표적 움직임을 가시화할 수 있음을 검증하였다.
Ⅱ. 코히런트 모노펄스 계측 레이다
본 절에서는 코히런트 모노펄스 계측 레이다의 수신 신호 모델을 정의한다. 그림 1은 코히런트 모노펄스 계측 레이다의 송신 펄스를 나타낸다. 드웰 시간(Dwell time)은 드웰 간 시간 간격을 나타낸다. 드웰 시간 동안 다수의 펄스를 일정한 시간 간격으로 송신한 후 휴지 시간을 갖는다. 드웰 내 펄스 간에는 동기화가 되어 있다. PRF의 역수인 펄스 반복 주기(PRI, pulse repetition interval)는 인접한 펄스 간 시간 간격이며, 같은 드웰 내에서는 PRI가 변경되지 않는다.
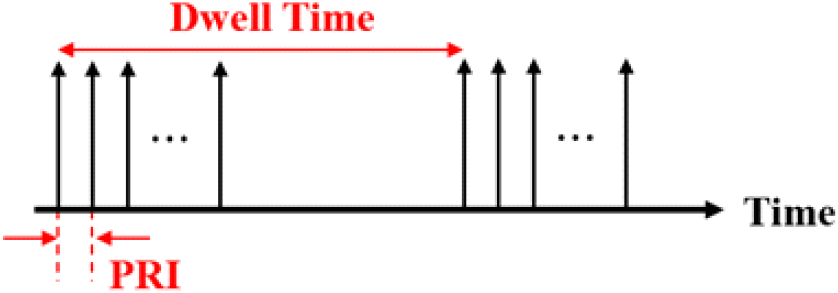
코히런트 모노펄스 계측 레이다의 수신 신호는 표적이 검출된 거리 게이트 내의 신호만이 구저 믹서(quadrature mixer)와 ADC(analog digital converter)를 거쳐 IQ 신호로 저장된다. 이동하는 표적을 추적할 때 드웰 내 펄스 간의 수신 신호의 위상이 표적의 도플러 속도 즉 레이다 기준 시선 속도와 PRI에 따라 일정하게 변화할 것이다.
이동하는 표적을 추적 중일 때 드웰 내 펄스의 개수 N에 대해, n번째 (n=0,1,···,N-1) 펄스에 해당하는 수신 신호는 식 (1)과 같이 나타낼 수 있다.
식 (1)에서 펄스 계수 a는 표적의 신호 진폭 값과 초기 위상값에 대한 정보를 나타내며, wn은 가산성 백색 가우시안 잡음(AWGN, additive white Gaussin noise)을 나타낸다. 도플러 주파수 fD는 표적의 도플러 속도 Vr과 레이다의 송수신 주파수 ft로부터 식 (2)와 같이 정의될 수 있다.
식 (2)에서 c는 광속을 나타낸다.
식 (2)의 신호로부터 도플러 속도를 추정하는 것은 PRI의 시간 간격으로 샘플된 N개의 신호로부터 도플러 주파수를 추정하는 문제로 이해할 수 있다. 계측할 수 있는 최대 속도는 PRF로부터 나이키스트 샘플링 이론에 따라 정해질 것이며, 이보다 더 큰 도플러 속도를 갖는 표적에 대해서는 앨리어싱이 일어나 속도 모호성이 발생할 것이다. 식 (2)로부터 속도 모호성 없이 계측할 수 있는 도플러 속도의 범위는 −cPRF/4ft부터 cPRF/4ft 사이임을 알 수 있다. 이러한 속도 모호성을 고려하면 도플러 주파수는 아래와 같이 나타낼 수 있다.
식 (3)에서 fr은 축소된 도플러 주파수로 0에서 PRF사이의 값을 가진다. M은 도플러 정수로 fD/PRF에 버림 연산을 적용하여 구할 수 있다.
속도 모호성으로 인해 한 드웰 신호만을 가지고는 fD을 구할 수 없으며, 축소된 도플러 주파수 fr만을 알 수 있다. 추적 중인 표적에 대해서는 추적 필터에서 예측되는 속도 값으로부터 도플러 정수를 구할 수 있으므로, 한 드웰 신호만을 가지고도 도플러 속도를 구할 수 있다. 추적을 시작 직후에 사전 정보가 없는 표적에 대해서는 도플러 모호성을 해결해야 한다.
이를 위해서 코히런트 모노펄스 레이다는 fr은 PRF에 따라 변화한다는 점을 활용하여 인접한 드웰 간에 PRF를 변경하고 PRF가 다른 다수의 드웰 신호를 종합하여 도플러 속도를 추정함으로써 속도 모호성을 해결한다.
거리가 R에 해당하는 표적에 대한 송수신 신호 간 지연 시간은 2R/c이다. 이 지연 시간이 PRI보다 크면 거리 모호성이 발생하게 된다. 거리 모호성이 발생하여 축소된 지연 시간 td는 식 (4)와 같이 정의할 수 있다.
식 (4)에서 축소된 지연 시간 td는 0에서 PRI 사이의 값을 가진다. 거리 정수 N은 2R/cPRI의 버림 값에 해당한다. 거리 모호성은 속도 모호성과 마찬가지로 펄스 반복 주파수를 변경에 따른 td값 차이로부터 해결할 수 있다.
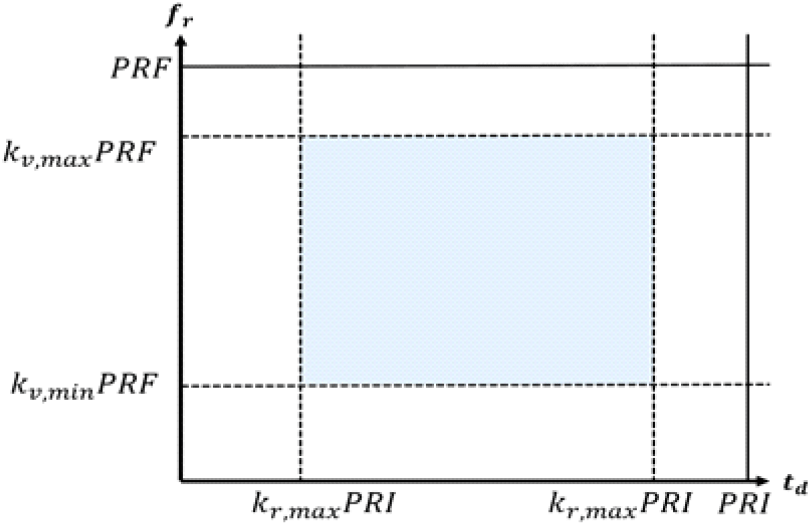
앞 절에서는 코히런트 모노펄스 계측 레이다는 추적 초기에 거리 및 속도 모호성을 해결하기 위해 PRF를 변경함을 기술하였다. 이 외에도 추적 중으로 거리 및 속도를 알고 있는 표적에 대해서도 클러터가 있는 환경에서 탐지율을 높이기 위해서 PRF를 변경한다. 축소된 도플러 주파수가 0 또는 PRF에 가깝다면 클러터 간섭 신호의 영향을 받을 수 있다. 마찬가지로 축소된 지연 시간이 0 또는 PRI에 가까울 때도 클러터 신호의 영향을 받을 수 있다. 따라서 코히런트 모노펄스 계측 레이다는 표적의 거리와 속도에 따라 fr과 td가 각각 0과 PRF, 0과 PRI에 가까워지지 않도록 PRF를 변경한다.
그림 2는 코히런트 모노펄스 계측 레이다의 PRF 설정 영역을 나타낸다. 속도와 거리를 알고 있는 표적은 PRF에 따라 td 대 fr의 2차원상에서 위치가 결정된다. 코히런트 모노펄스 계측 레이다는 클러터 잡음 신호의 영향을 최소화하기 위해서 표적이 음영 영역 이내에 위치하도록 PRF를 변경한다. 그림 2에서 kr,min,kr,max와 kv,min,kv,max는 각각 속도와 거리에 대한 하한 계수와 상한 계수이다.
Ⅲ. 도플러 신호 처리 방법
일반적으로 도플러 레이다 신호로부터 DTI를 얻기 위해서 FFT를 활용한다. 드웰 신호 yn에 대해 N 포인트 FFT는 식 (5)와 같이 정의될 수 있다.
식 (5)에서 주파수 인덱스 k는 0에서 N-1사이의 정수이며, X(k)는 FFT 주파수 스펙트럼이다. 인덱스 k에 대응하는 도플러 주파수는 PRF(N−k)/k로, PRF에 종속된다. 즉 PRF가 변경되면 FFT 인덱스 k에 대응하는 도플러 속도가 변화하게 된다. 따라서 코히런트 펄스 레이다에 FFT를 적용한다면 PRF가 변경되는 구간에서 DTI가 불연속적으로 나타날 것이다.
파워 스펙트럼 밀도 추정을 이용하여 특정 축소된 도플러 주파수에서의 파워 스펙트럼 밀도를 구하면 분해능을 유지하여 DTI를 정의할 수 있다. 드웰 신호 yn에 대해 주파수 f에서 파워 스펙트럼 밀도는 식 (6)~식 (8)과 같이 정의할 수 있다.
식 (6)에서 P(f)는 주파수 f의 파워 스펙트럼 밀도를 나타내며, f는 0에서 PRF사이의 값을 가진다.
식 (6)은 PRF가 다른 드웰에서도 동일하게 적용될 수 있어 축소된 도플러 주파수 신호의 성분을 구할 수 있다. 하지만 축소된 도플러 주파수는 PRF가 변경되는 지점과 도플러 정수가 변경되는 지점에서 불연속적인 값을 가지게 된다.
따라서 식 (6)으로부터 구한 축소된 도플러 주파수의 파워 스펙트럼 밀도는 불연속적인 값을 가지므로, DTI 상에서 표적의 움직임을 자연스럽게 가시화할 수 없다.
코히런트 모노펄스 계측 레이다의 자료로부터 DTI를 얻기 위해서는 PRF의 비주기적인 변화와 이로 인한 폴딩 정수의 변화를 고려하여야 하며, 이를 위해서는 속도 모호성이 해결되어야 한다.
제안하는 방법은 레이다에서 추적이 된 표적의 신호를 가시화하는 것을 목표로 하며, 추적 필터로부터 얻은 속도 예측값을 사전 정보로 활용하여 도플러 모호성을 해결한다.
코히런트 모노펄스 계측 레이다는 확장형 칼만 필터(extended Kalman filter)를 사용하여 계측 자료로부터 직교 좌표계 상의 위치를 추적한다[11]. 추적 필터는 이전 스캔의 계측값으로부터 현재 스캔의 상태를 추정하게 하며, 이로부터 페데스탈과 거리 게이트 및 PRF를 조정할 수 있다[7].
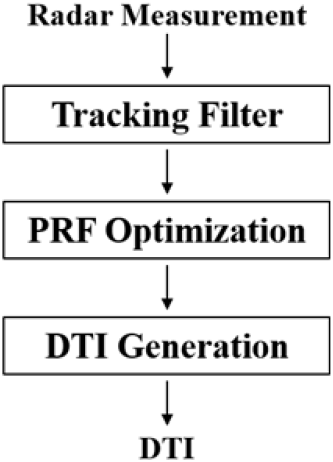
그림 3은 코히런트 모노펄스 계측 레이다의 도플러 신호 처리 방법의 흐름도를 나타낸다. 추적 필터로부터 예측된 k번째 스캔에서의 속도 값 와 거리 값 에 따라 최적의 PRF인 PRFk가 결정되며, 로부터 도플러 정수 Mk을 구할 수 있다. 제안하는 방법은 PRFk와 Mk를 고려하여 DTI를 생성하여 속도 모호성을 해결한다.
식 (6)의 주파수 밀도 스펙트럼 추정 정의로부터 도플러 속도 v에 해당하는 도플러 스펙트럼 신호 크기는 도플러 정수 사전 정보를 활용하여 식 (7)과 같이 정의 할 수 있다. 식 (7)에서 D(v,k)는 시간 k에서 속도 v에 해당하는 주파수 밀도 성분의 크기를 나타낸다. 식 (7)에서 yk,n은 k번째 스캔에서 n번째 신호를 나타낸다. 식 (7)은 v의 도플러 정수가 Mk인 구간, 즉 제한된 속도 구간인 에서 정의된다. 해당 구간 밖의 속도에 대해서는 앨리어싱 표적의 신호가 있을 것이다.
도플러 정수가 일정한 구간에서는 제한된 속도 구간에서 식 (7)로부터 도플러 신호 성분 크기를 구하여 DTI를 얻을 수 있다. PRF의 변화를 고려하여 속도의 하한선은 최대 PRF 기준으로, 상한선은 최소 PRF를 기준으로 설정하여야 앨리어싱 표적에 해당하는 신호가 DTI 상에서 가시화되지 않는다.
식 (7)은 PRF의 영향도 고려하였으므로, 식 (7)을 활용하면 PRF가 변화하는 구간에서도 연속적인 DTI 맵을 얻을 수 있다.
도플러 정수가 변화하는 구간에서 DTI를 가시화하기 위해서는 전체 DTI의 최소 및 최대 속도를 정의하여야 한다. 시간대별 도플러 정수와 PRF로부터 앨리어싱 표적의 영향 없이 구할 수 있는 속도 범위를 구한 후 해당 범위 밖의 값은 0으로 채워 넣음으로써 DTI를 가시화하는 방법을 고려할 수 있다.
또한 DTI 상의 인공물(artifact)을 제거하기 위하여 필터링을 적용하는 것을 고려할 수 있다. 필터링을 통해 링잉 인공물(artifact)이나 유령 인공(ghost artifact)과 같이 주엽(side lobe) 신호의 영향을 억제할 수 있다. 표적의 특성에 따라서 체비세브(Chebyshev) 필터나 해닝(Hanning) 필터의 활용이 고려될 수 있다[12].
종합하면, PRF의 변경과 도플러 정수와 이에 따라 결정되는 제한된 속도 구간을 고려하여 산출되는 DTI는 식 (8)과 같이 정의될 수 있다. 식 (8)은 계측하고자 하는 속도의 최솟값 v1과 최댓값 v2 사이에서 L 포인트의 속도 빈(Bin)에 대해서 DTI를 산출하며, l은 0에서 L−1 사이의 정수이다. 식 (8)은 각 시간대에서 제한된 속도 구간 밖의 값은 0으로 채워 전 구간에서 연속성을 갖게 한다.
식 (8)에서 wn은 커널 길이가 N인 윈도우 필터 w에 대해, 필터의 n번째 값을 나타낸다. 필터의 이득(filter gain)은 1로 조정되어야지 파워 스펙트럼의 전체적인 크기가 변화하지 않는다.
앞서 기술한 바와 같이 제안 방법은 이미 추적이 되어 추적 필터로부터 도플러 정수의 사전 정보를 얻은 상황에서, 속도 값에 대응하는 도플러 정수가 Mk에 해당하는 제한된 속도 구간에서 DTI를 구한다. 제한된 속도 구간 밖에 있는 표적에 대해서는 도플러 모호성이 해결될 수 없으며, DTI 상에 앨리어싱 표적이 나타나게 된다. 특히 속도 오차값, 즉 예측한 속도와 실제 표적의 속도의 차인 εv가 허용 속도 오차보다 크면 앨리어싱이 일어날 수 있다.
제한된 속도 범위로부터, εv이 −MPRFc/2ft 또는 −(M+1)PRFc/2ft보다 클 경우, 앨리어싱이 일어날 수 있음을 알 수 있다. 그림 2와 식 (2) 및 식 (3)으로부터 는 (M+kv,min)PRFc/2ft와 (M+kv,max)PRFc/2ft 두 값 사이이며, 가 이 두 값에 해당할 때 허용 속도 오차가 가장 작을 것이다. 이로부터 허용 속도 오차는 식 (9)와 같이 정의할 수 있다.
식 (9)는 도플러 모호성이 해결되는 조건을 정의한다. 추적 필터의 성능 저하로 속도 오차 εv가 커져 식 (9)가 만족되지 못하면 앨리어싱 표적이 DTI 상에 나타날 수 있으며, 도플러 모호성이 해결되지 않을 수 있다. 식 (9)가 만족되지 않더라도 예측된 속도 값과 실제 속도 값에 따라 앨리어싱이 일어나지 않을 수도 있다. 하지만, 속도 오차가 (1−kv,min)PRFc/2ft와 kv,maxPRFc/2ft보다 큰 경우에는 반드시 앨리어싱이 일어날 것이다.
Ⅳ. 실험 결과
모의실험의 계측 요구 조건은 현재 군에서 운용 중인 155 mm OOO탄 제원을 기준으로 설정하였다. Matlab R2020a 환경에서 자탄이 분리되는 시나리오를 가정하여 IQ 단계의 모의신호를 생성하였다. 제안 방법과 파워 스펙트럼 밀도 추정 방법을 적용하여 단일 및 다수 표적 환경에서의 도플러 신호 처리 결과를 비교 및 분석하였다.
신호 생성을 위해 6 자유도 탄도 방정식으로부터 모탄과 자탄의 궤적을 얻고, 이로부터 레이다 기준의 위치를 얻었다[13]. 위치별로 표 1의 파라미터로부터 모의 계측 데이터를 생성하였다. 계측 데이터 생성 시에는 탄의 RCS(radar cross section)와 거리 및 계측 레이다의 사양으로부터 산출된 시간별 SNR(signal noise ratio)에 맞는 잡음 신호를 더하였다.
| Parameter | Value | Unit |
|---|---|---|
| f | 5.0 | GHz |
| Min PRF | 2,000 | Hz |
| Max PRF | 2,500 | Hz |
| kv,min | 0.2 | - |
| kv,max | 0.8 | - |
| Number of pulses in dwell | 48 | - |
자탄 분리 이전 구간에서는 식 (1)을 활용하여 드웰 내 수신 신호를 산출하였다. 추적 필터로부터 예측된 표적의 현재 속도에 맞추어 PRF를 조정하였다. PRF는 예측된 속도에 대응하는 축소된 도플러 주파수가 허용 범위인 PRFkv,min과 PRFkv,min 사이에 있되, PRF가 최소 및 최댓값 사이의 값을 가지도록 조정하였다. 축소된 도플러 주파수가 허용 범위 밖에 있으면 PRF를 50 Hz씩 낮추었으며, 50 Hz 낮춘 값이 최소 PRF보다 작으면 최대 PRF로 설정하였다.
초기 포구 속도 및 발사 고각을 변경해가며 서로 다른 궤적 5개를 생성하여 실험을 반복 수행하였다. 첫 번째 실험에서 레이다 기준 최대 속도는 229 m/sec였으며, 자탄 분리 시점에 레이다 기준 거리는 47 km로 이에 대응하는 td는 0.31 m 초이다. 최소 PRI가 0.4 m 초로 도플러 모호성은 발생하지 않으며, kr,max를 0.9로 가정하면 클러터 신호 억제를 위한 PRF 변경은 일어나지 않는다. 따라서 시뮬레이션 전 구간에서 거릿값은 PRF 설정에 영향을 미치지 않는다.
모노펄스 계측 레이다는 단일 표적 추적 레이다이므로, 자탄이 분리되는 26초 이후에는 추적하지 않고 도플러 수신 신호만 관찰하는 상황을 고려하였다. 따라서 26초 이후에는 PRF를 변경하지 않고 안테나 및 거리 게이트는 이전 추적 자료를 활용하여 등속으로 제어하였다.
분리 이후 30초까지는 자탄과 모탄 간 레이다 기준 거리 차이 최대 400 m이다. 펄스폭이 일반적인 모노펄스 계측 레이다의 펄스폭인 2.5 u초[7]이고, 레인지 게이트의 폭이 펄스폭과 동일하게 설정된 환경에서는 모탄 궤적을 기준으로 거리 게이트가 제어되더라도 자탄의 신호도 가산될 것임을 가정하였다.
단일 표적 수신 신호 모델인 식 (1)로부터 각 표적별 속도 및 펄스 계수를 고려하여 표적별 신호 성분을 가산하여 다수 표적의 수신 신호를 얻었다.
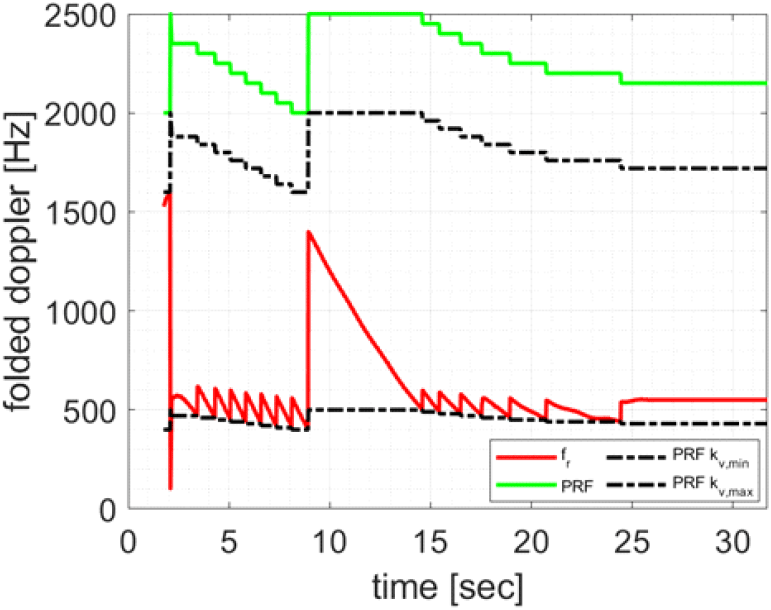
그림 4는 시간 대 축소된 도플러 주파수와 PRF를 나타낸다. 그림 4에서 적색 실선은 속도 추적 결과에 대응하는 축소된 도플러 주파수를 나타낸다. 녹색 실선은 축소된 도플러 주파수에 맞추어 조정된 PRF를 나타낸다. 두 흑색 점선은 각각 PRFkv,min과 PRFkv,min에 해당한다.
그림 4에서 축소된 도플러 주파수 값이 PRFkv,min과 PRFkv,min 사이의 값을 가질 수 있도록 PRF가 조정되었음을 확인할 수 있다. PRF는 표 1의 파라미터에 따라 2,000~2,500 Hz 사이로 설정되었으며, 분리 이후에는 PRF와 축소된 도플러 주파수가 변경되지 않았다.
표 1의 매개 변수의 최소 PRF 2,000 Hz 기준으로, 도플러 정수가 0이 되어 속도 모호성이 발생하지 않는 최대 속도 PRFc/2ft는 60 m/sec이다. 해당 실험에서 추적 시작 지점 기준 도플러 속도는 225 m/sec으로 이에 대응하는 도플러 정수는 3으로 도플러 모호성이 발생한다. 추적 필터의 사전 정보를 활용하지 않는 파워 스펙트럼 밀도 추정 방법은 도플러 모호성을 해결할 수 없다.
그림 5는 수신 신호에 식 (6)의 파워 스펙트럼 밀도 추정 방법을 적용하여 구한 DTI이다. 그림 5에서 PRF 2,500 Hz를 기준으로 128포인트에서 DTI를 산출하였다.
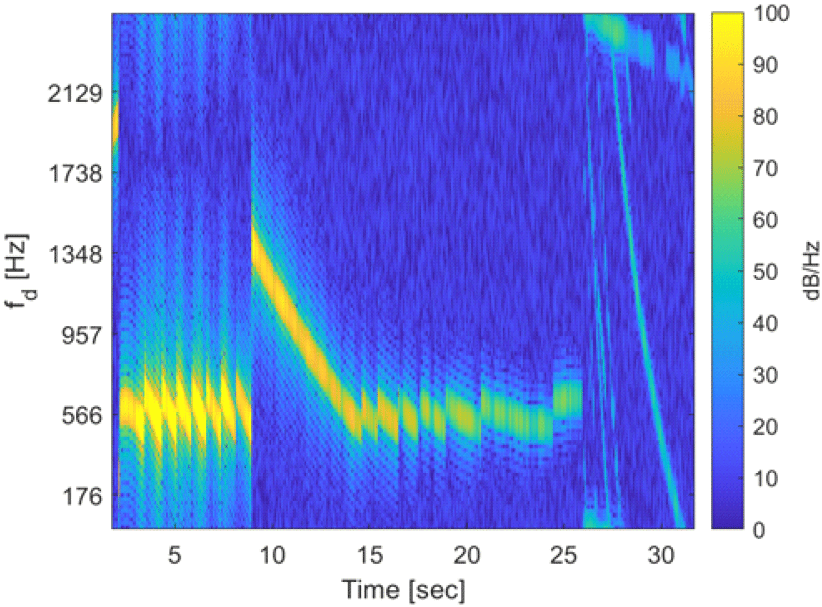
그림 5에서 자탄 분리 시점 이전에는 표적에 축소된 주파수에 따라 표적 신호가 나타난다. 그림 4에서 PRF가 변경되는 2~8초와 14~24초 구간에서 DTI가 불연속적임을 확인할 수 있다. 또한 도플러 정수가 변경되는 9초에서도 역시 DTI가 불연속적이다. 자탄 분리 이후 구간에서는 도플러 모호성이 해결되지 않아 다수 표적을 구분하거나 자탄 분리 이벤트 발생 여부를 확인하기 어렵다.
그림 5와 같이 파워 스펙트럼 밀도 추정 방법은 PRF 변경을 고려하지 않았기 때문에 PRF가 변경되는 구간에서 파워 스펙트럼 밀도가 불연속 값을 가지며, DTI가 부자연스럽게 나타난다. 또한 도플러 정수를 고려하지 않고 축소된 주파수에서 파워 스펙트럼 밀도를 추정하였기 때문에 도플러 모호성이 해결되지 않았다.
이러한 불연속성과 도플러 모호성으로 인해 파워 스펙트럼 밀도 추정 방법으로 획득한 DTI는 표적의 기동을 확인하거나 이벤트 현상을 계측하는 데에 적합하지 않다.
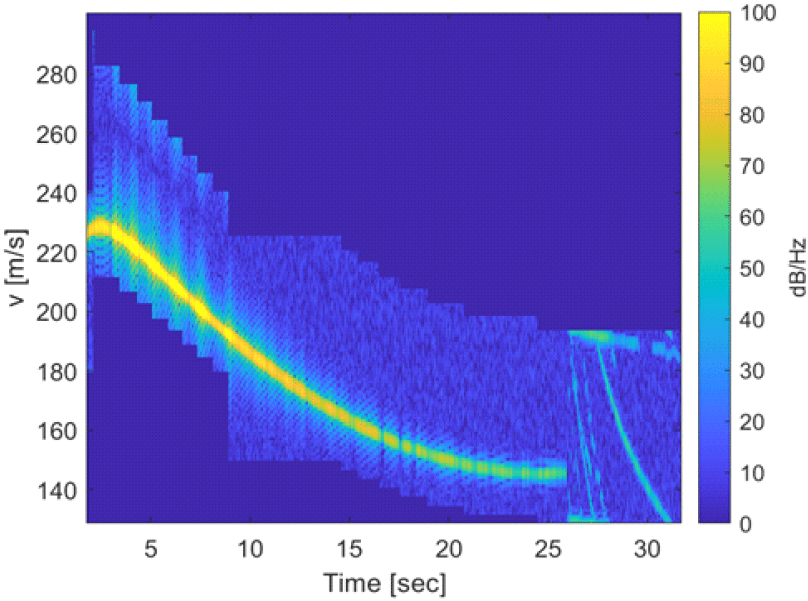
그림 6은 수신 신호에 제안하는 방법을 적용하여 산출한 DTI이다. 식 (8)에서 속도의 최솟값 v1과 최댓값 v2 및 속도 포인트 개수 L은 각각 129 m/sec, 300 m/sec, 172로 설정되었다. 추적 필터에서 추정된 속도 값에 대응하는 폴딩 정수를 사전 정보로써 활용하여 DTI를 얻었으며, 단 분리 시점인 26초 이후에는 폴딩 정수 역시 변경되지 않음을 가정하였다. 잡음 억제를 위해서 핸 윈도우를 적용하였다[8].
그림 6에서 각 시간대별로 폴딩 정수와 PRF에 따라 도플러 모호성 없이 DTI를 구할 수 있는 제한된 속도 범위에서 주파수 밀도 성분을 구하였으며, 제한된 속도 범위 밖의 값은 0으로 하였다.
그림 6에서 2~8초와 14~24초 구간에서 PRF가 변경되면서 제한된 속도 범위가 변경되는 것을 확인할 수 있다. 제한된 속도 범위가 변경되어도 PRF의 변경이 DTI 산출 시에 고려가 되어 표적의 해당하는 신호가 연속적으로 나타났다. 또한 폴딩 정수가 변경되는 9초에서도 DTI가 연속적으로 나타났다.
식 (9)의 는 표 1의 최소 PRF인 2,000 Hz를 기준으로 12 m/sec이다. 실험 1의 전 구간에서 예측된 속도 값의 오차는 12 m/sec보다 작았으며, 도플러 모호성이 해결된 DTI를 얻을 수 있었다.
제안하는 방법은 추적 결과를 사전 정보로 활용하여 도플러 모호성을 해결하였으며, 제안 방법으로 산출한 DTI는 자탄 분리 이후 구간에서도 다수 표적을 분리하여 가시화할 수 있다. DTI 상에서 26초에 표적이 다수 표적으로 분리되는 것을 확인할 수 있다.
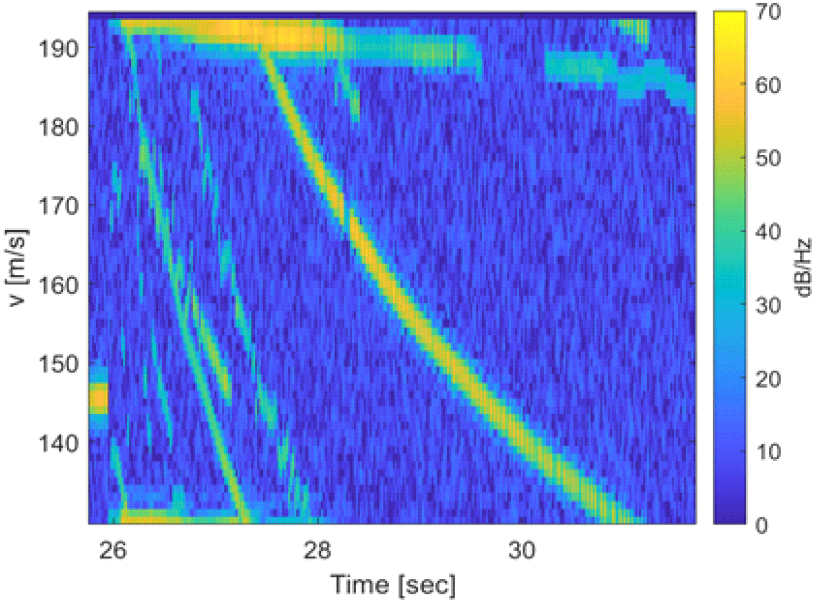
그림 7은 그림 6의 26초 이후 구간을 확대한 DTI를 나타낸다. 그림 7에서 가장 속도가 큰 신호 성분은 모탄에 해당한다. 26초 이후 PRF는 모탄의 분리 직전 속도에 맞추어 설정되어 모탄 신호는 앨리어싱 없이 나타난다.
일부 자탄은 분리 직전 모탄의 속도와 속도 차이가 벌어지면서 앨리어싱 신호가 제한된 속도 구간에 나타났다. 해당 구간의 PRF 2,150 Hz를 기준으로 와는 둘 다 51.6 m/sec이었다. 27.8초 이후에는 빔폭 내 모든 자탄의 속도가 모탄의 분리 전 속도와 속도 차이가 51.6 m/sec가 되며 앨리어싱 된 자탄의 신호만이 나타남을 확인할 수 있다. 27.8초 이후 나머지 자탄은 모탄 기준 빔 폭 내에 들어오지 않아 신호 확인이 불가하다.
실험 1을 통해 제안하는 방법으로 자탄 분리와 같은 이벤트 현상 발생 여부를 계측할 수 있음을 검증하였다. 본 실험에서 자탄 분리 이후 다수 표적이 존재하는 구간에서는 PRF가 최적화되지 않고, 분리 시점의 모탄 속도 기준에서 변경되지 않았다. 이에 따라 자탄 신호와 분리 직전 모탄 속도 차이가 벌어지는 구간에서는 DTI 상에 앨리어싱 신호가 나타났다.
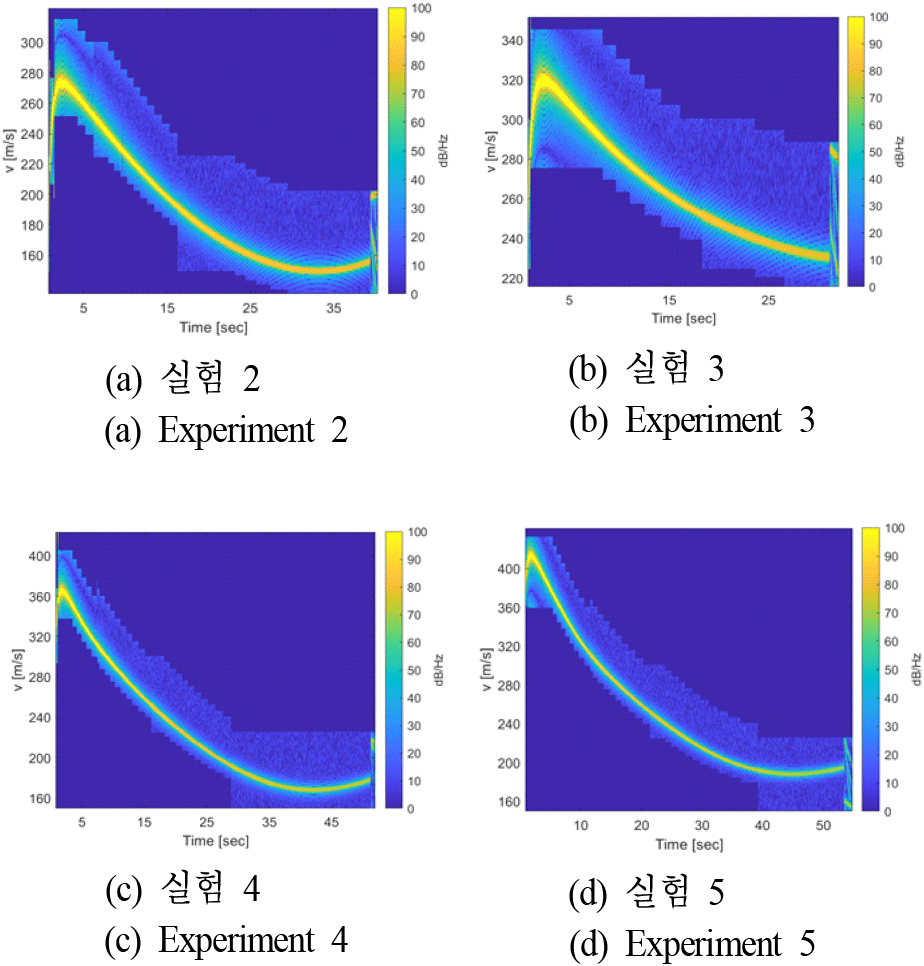
초기 포구 속도와 발사 고각을 변경하여 서로 다른 궤적을 생성하여 동일 실험을 총 5회 반복 수행하였다. 각 실험별로 식 (8)의 v1, v2 및 L은 궤적의 최대 및 최소 속도에 맞추어 조정되었으나, 속도 빈의 분해능은 1 m/sec로 동일하게 적용하였다. 그림 8은 실험 2~5의 제안 방법으로 생성된 DTI를 나타낸다.
5회 실험 결과에 대해 자탄 분리 이전 단일 표적만 존재하는 구간에서 DTI 속도 추정 정확성을 평가하였다. 각 스캔에 피크 검출기를 적용하여 표적을 검출하였다[14]. 정답 속도에 대응하는 속도 빈과 피크 검출기로부터 검출된 속도 빈이 같은 경우에는 정답으로, 다른 경우에는 오답으로 처리하였다. 정확도는 전체 스캔 수 중 정답 스캔의 비율을 나타낸다. 표 2로부터 제안하는 방법은 DTI 상에서 0.999 이상의 정확도로 OOO탄 단일 표적의 속도 정보를 가시화할 수 있음을 검증하였다.
모의실험을 통해서 제안 방법으로 생성된 DTI는 단일 표적의 속도 정보를 정확하게 가시화할 수 있으며 자탄 분리와 같은 이벤트 현상 발생 여부를 계측할 수 있음을 검증하였다. 실험 결과 파워 스펙트럼 밀도 추정 방법은 PRF 변경 및 도플러 모호성을 고려하지 않아 DTI가 불연속적으로 나타난다. 이에 반해 제안 방법은 속도 추적 결과를 사전 정보로 활용하여 도플러 모호성을 해결한다. 제안하는 방법으로 얻은 DTI는 PRF 변경 구간과 폴딩 정수가 변화하는 지점에서도 연속적으로 나타나 표적의 이동 및 추적 상태를 확인할 수 있다.
제안하는 방법은 단일 표적 추적을 목표로 하는 코히런트 모노펄스 계측 레이다의 신호로부터 DTI를 생성하는 것을 목표로 하여, 이벤트 시점 이후 다수 표적이 존재하는 구간에서는 도플러 모호성이 해결되지 않는다. 다수 표적의 DTI 생성을 위해서는 예상 궤적 활용을 통한 PRF 최적화와 같은 방법이 연구될 필요가 있다.
Ⅴ. 결 론
본 논문에서는 코히런트 모노펄스 계측 레이다의 계측 자료로부터 DTI를 얻을 수 있는 도플러 신호 처리 방법을 제안하였다. 제안하는 방법은 PRF 변경을 고려하고, 속도 추적 결과를 사전 정보로 활용하여 도플러 모호성을 해결하여 DTI를 산출한다. 모의실험 결과로부터 제안하는 방법을 적용하여 산출한 DTI는 불연속성 없이 표적의 움직임을 가시화할 수 있음을 검증하였다.
제안하는 방법은 무기 체계 성능 시험 시에 계측 자료로부터 단 분리 및 자탄 분리와 같은 이벤트 현상 발생 여부를 계측하는 데 활용할 수 있다. 또한 제안하는 방법은 레이다 장비 운용 중 실시간으로 DTI를 생성할 수 있어 운용자가 신호 및 추적 상태를 직관적으로 확인하게 하여 추적 성공률을 높이는 데에 활용될 수 있다.
제안하는 방법은 단일 표적 추적을 목적으로 하는 코히런트 모노펄스 계측 레이다를 위해 설계되었으며, 제안하는 방법이 다수 표적 추적에 응용되기 위해서는 PRF 최적화를 포함한 추가적인 연구가 필요하다.