논문/REGULAR PAPERS
적분방정식과 반사계수를 기반한 두 Iterative Physical Optics의 임피던스 및 유전체 물체 산란 해석 비교
유정운
,
고일석†
Comparative Analysis of Scattering by Impedance and Dielectric Objects Computed by Integral Equation- and Reflection-Based Iterative Physical Optics Algorithms
Jeong-Un Yoo
,
Il-Suek Koh†
Author Information & Copyright ▼
Department of Electronic Engineering, Inha University
© Copyright 2024 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the
Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits
unrestricted non-commercial use, distribution, and reproduction in any
medium, provided the original work is properly cited.
Received: Jan 04, 2024; Revised: Jan 17, 2024; Accepted: Feb 06, 2024
Published Online: Mar 31, 2024
요 약
IPO는 근사 방법으로 해석 속도가 빨라 전기적 대형 물체의 전자기 산란 해석에 이점이 있다. IPO는 적분방정식과 반사계수를 이용해 표면 전류를 계산하여 RCS를 예측하는 두 가지 방법이 있다. 적분 방정식 기반 IPO는 계산 복잡도가 낮고 완전도체 및 임피던스 매질의 해석이 가능하다. 반사계수 기반 IPO는 표면 전류의 흡수효과를 고려할 수 있어 유전체 매질의 해석 정확도가 높은 장점이 있다. 본 논문에서는 적분방정식과 반사계수 기반 IPO의 수식을 비교하고 장단점을 분석한다. 손실 금속과 유전체로 구성된 전투기, 무익항공기 및 거친 해양 표면 위 미사일과 같은 복합 매질 대상을 해석한다. 표면전류와 RCS를 각 IPO의 해석 결과를 FEKO 또는 자체개발한 full-wave simulation인 MLFMM과 비교하여 검증한다.
Abstract
Given their high analytical speed, iterative physical optics (IPO) algorithms present an advantageous approximation method for analyzing the electromagnetic scattering of electrically large objects. IPO approaches for radar cross-section (RCS) prediction are of two types-one based on integral equations, and the other based on reflection coefficients. Integral equation (IE)-based IPO approaches have remarkably low computational complexity and facilitates the analyses of conducting and impedance media. In contrast, reflection (R)-based IPO approaches can consider the absorption effects of surface currents, yielding a higher accuracy in analyzing dielectric media. This study compared and analyzed the formulas of IE-based and R-based IPO and examined their respective advantages and limitations. Complex media targets composed of lossy metals and dielectrics, such as fighters, tailless airplanes, and missiles, above rough ocean surfaces were examined. The surface currents and RCS obtained using each approach were verified by comparing the results with those from FEKO or an in-house full-wave simulation (MLFMM).
Keywords: Iterative Physical Optics; Integral Equation; Reflection Coefficient; Electromagnetic Scattering
Ⅰ. 서 론
반복적 물리 광학(IPO, iterative physical optics)은 전자기 산란을 계산하기 위한 고주파 근사방법으로 전기적 대형 물체의 해석에 널리 사용되고 있다. IPO는 저주파 해석 방법에 비해 속도가 빠르고, 필요한 메모리 사용량도 낮아 전기적 대형 물체의 해석에 장점이 있다. 초기 IPO는 완전도체(PEC, perfect electric conductor) 및 손실 매질(lossy material)로 구성된 open-end cavity를 해석하기 위해 개발되었다[1],[2]. 이후, open-end cavity 해석에서 벗어나 tank, 비행체 및 rough ocean surface 등 다양한 물체의 해석에 적용 되었다[3]~[6]. 자계 적분 방정식(MFIE, magnetic field integral equation)을 반복적으로 계산하여 이를 기반으로 레이다 단면적(RCS, radar cross section)을 예측하는 적분 방정식 기반(IE-based) IPO는 완전도체 및 임피던스 경계조건(IBC, impedance boundary condition)을 이용한다. 그에 따라, IE-based IPO는 매 반복 절차마다 반사계수를 계산할 필요가 없어, R-based IPO에 비해 상대적으로 해석 속도가 빠르다는 장점이 있다. 이는 특히 대규모 시뮬레이션 및 처리가 요구되는 경우에 유용하다. 그러나 IE-based IPO는 흡수 효과를 반영할 수 없어 전류가 강하게 반사하여 유전체 물체 해석에 정확도가 떨어지는 단점이 존재한다. 특히 군용 장비는 피탐지를 위해 RAM(radar absorbent material) 등의 특수 코팅을 한다. 이러한 코팅은 파장을 흡수하고 투과시키는 특수 유전체와 같은 재료로 구성되어 RCS 해석을 방해한다. 또한 안테나를 보호하기 위해 유전체로 이루어진 radome 해석은 중요한 이슈이다[7]. 반면 물체 표면 위 국소적으로 매질의 반사 계수(reflection coefficient)를 수평 및 수직 성분으로 나누어 표면 전류를 계산하는 반사 계수 기반(R-based) IPO는 매질의 흡수 성질을 고려할 수 있어 유전체 해석 정확도가 높은 장점이 있다[8],[9].
본 논문에서는 적분방정식 및 반사계수기반 IPO의 표면 전류를 구하는 수식에 대해 Ⅱ장에서 분석한다. 또한 Ⅲ장에서 단일 및 복합 손실매질 또는 유전체인 매질로 구성된 전기적 대형 물체의 시뮬레이션을 통해 표면 전류의 차이가 전자기 산란 특성에 미치는 영향을 조사하고 장단점을 비교한다.
II. IPO FORMULATION
2-1 적분 방정식 기반 IPO
IPO는 물체를 삼각형 메쉬로 나눈 후 메쉬의 표면 전류를 계산한다. 적분 방정식 기반 IPO의 표면 전류는 식 (1)과 같이 계산할 수 있다[1]. 은 n번째 갱신한 표면 전류이고, n−1 번째 전류에 의해 최신화 된다. 입사파에 의한 표면전류는 와 같이 정의한다. 으로 과 은 각각 소스와 관측점의 위치 벡터이다. Z0와 ZS는 각각 자유공간 임피던스(free-space impedance) 및 물체의 표면 임피던스이다. 또한 G는 자유공간 그린 함수(free-space green’s function)로 식 (2)와 같이 각각 표현 된다.
G1, G2, G3는 자유 공간에서의 전자기파 산란을 기술하는 자유공간 그린 함수로 이들은 각각 1/R,1/R3 및 1/R5거리에 따라 감소하는 전자기장의 강도를 나타낸다.
2-2 반사계수 기반 IPO
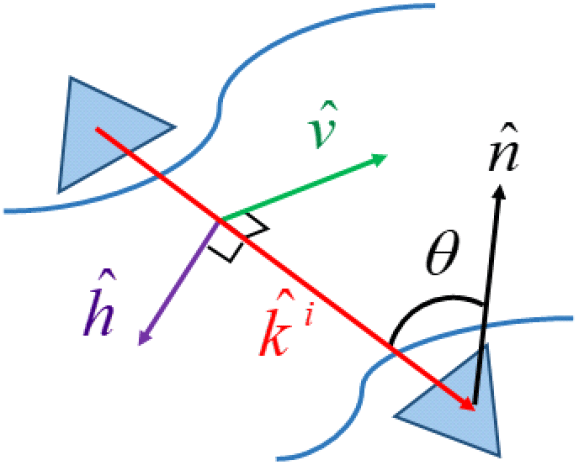
R-based IPO는 그림 1과 같이 물체 표면의 지역적 평면 근사화(local tangential approximation) 및 반사 계수를 고려하여 전자기 산란을 예측하는 근사화 방법이다. 는 입사파의 방향벡터이고 와 는 각각 수평(horizontal) 및 수직(vertical) 편파(polarization)로 식 (3)과 같이 표현된다.
유전체 표면의 반사 계수는 식 (4)와 같이 알려져 있다[10].식 (4)의 Rh와 Rv는 각각 수평 및 수직 편파에 대한 반사계수이고, θ는 삼각형 메쉬에 대한 입사 각도이다. 또한, ϵr은 유전체의 반사 유전률이다. 입사파를 지역적 수평 및 수직 편파의 성분으로 분해하고, 매질의 반사 계수와 입사파를 통해 R-based IPO의 표면 전류는 식 (5)와 같이 계산할 수 있다[11].
식 (5)에서 와 은 각각 전류 및 자류이다. R-based IPO는 식 (5)으로부터 구해진 표면 전류를 1차 PO전류로 반복적으로 계산해 갱신한다.
식 (1)의 IE-based IPO는 적분 방정식 내부의 표면전류와 매질의 임피던스를 이용해 계산한다. 반면 R-based는 식 (5)와 같이 전기장을 계산한 후, 편파와 물체의 유전률을 이용해 표면 전류를 갱신한다. IE-based와 R-based는 각각 임피던스와 유전률을 고려해 계산한다. 그러나 적분방정식으로 전류를 갱신하는 IE-based와 달리 R-based IPO의 경우 전기장과 편파 분해로 인해 계산 복잡도가 증가한다.
2-3 반복절차 중단 조건
IPO의 반복 절차는 전류의 크기가 발산하면 중단해야 한다. 본 연구에서 반복법은 가장 일반적인 Jacobi 반복법을 사용한다[12]. 반복절차를 멈추기 위해 잔여오차(ϵn, residual error)를 식 (6)과 같이 정의하고 허용오차(δ, tolerance)를 임계값으로 설정한다. 식 (6)에서 은 n번째 갱신된 IPO 표면전류로 와 같다.
식 (7)은 IPO의 stop criterion으로 ϵn < δ는 IPO의 표면 전류가 임계값 아래로 내려가 정확한 해에 충분히 근접했음을 의미하고 수렴(converging)으로 간주하여 계산을 중단한다. 본 연구에서는 IE-based와 R-based의 정확성 및 해석 속도 비교를 위해 δ=10−3으로 설정한다. 또한 ϵn-1 < ϵn는 n번째의 잔여오차가 n−1번째 잔여오차보다 큰 경우로 정확한 해에서 멀어짐을 의미하고 발산(diverging)으로 정의한다.
Ⅲ. 시뮬레이션 결과
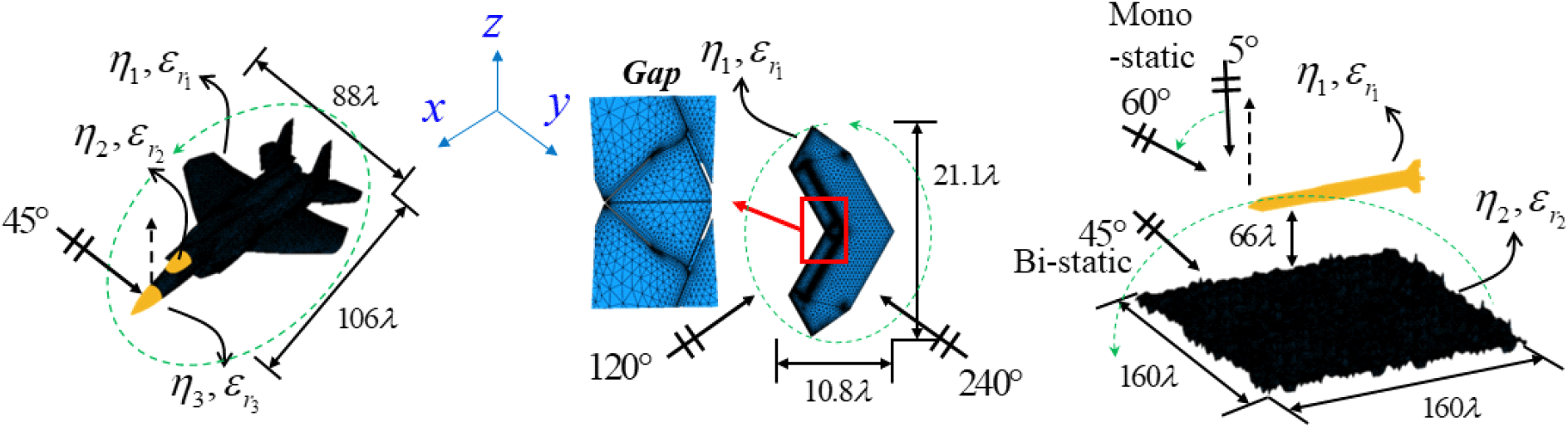
IE와 R-based IPO의 특성을 비교하기 위해 세 가지 산란체에 대한 시뮬레이션을 수행하고 결과를 FEKO 및 자체개발(inhouse) MLFMM(multi level fast multipole method)[13] 결과와 비교한다. 산란체는 각각 불균질 전투기, 단일 매질 무익항공기(tailless airplane) 및 해수면 위 미사일(missile above rough ocean surface)로 구성되고 그림 2에 나타낸다. 전투기는 몸체, canopy 및 radome으로 구성된 복합 매질 및 복잡 구조를 해석한다. 몸체는 임피던스 매질[14]로 구성되어 있으며 canopy[15]와 radome[14]은 유전체로 구성되어 있다. IE-based IPO 해석을 위해 canopy와 radome은 임피던스로 가정하고 정규화 임피던스(normalized impedance, ) 매질로 η=0.71 +j0.01및 η=0.53이다. R-based IPO는 몸체를 유전체 매질로 가정해 , μr=1로 해석한다. 자체개발 MLFMM의 경우 canopy와 radome을 임피던스 매질로 가정하고 해석했다. 무익항공기는 완전도체 위 코팅된 laminate RAS(radar absorbing structure)의 단일 매질로 구성되며, 두께는 t=0.02λ0, ϵr=6.6-j2.8 그리고 μr=1이다. IE기반 IPO의 경우 유전체를 임피던스 매질로 가정하여, 로 계산한다[16]. 마지막으로 복합 매질로 구성된 거대 물체의 시뮬레이션을 위한 해수면의 해석을 비교한다. 해수면은 open surface로 자체개발 코드의 해석이 불가능하여, FEKO의 impedance sheet model로 시뮬레이션 했다. 해수면의 RMS height 10.6λ, 온도와 염도는 각각 20°C 및 32.54 %0을 고려하여, IE-based는 η=0.0926-j0.0371, R-based IPO는 ϵr=72.64+j69.36,μr=1로 각각 해석한다[17]. λ0는 자유 공간 파장을 나타내고, 시뮬레이션 분석 주파수는 전투기와 무익항공기는 2GHz로, 해수면 위 미사일은 4GHz로 설정한다. 산란체의 삼각형 메쉬 개수, 치수(길이×폭×높이) 및 매질 정보는 표 1에 요약한다. 시뮬레이션의 입사파와 관측점은 각각 전역좌표계의 고도각과 방위각으로 정의되며, 이는 θ와 ϕ로 표기한다. 시뮬레이션의 허용오차는 10−3으로 설정한다.
그림 2. | Fig. 2.
해석 대상 기하학 정보 및 시뮬레이션 환경 | Geometry information of analyzed object and simulation environment.
Download Original Figure
표 1. | Table 1.
메쉬 및 매질 정보 | Mesh and material information.
| Objects |
# of mesh |
Dimension[λ0] |
η, ϵr |
| Fighter |
60,244 |
106.8×88×28 |
η1=0.38−j0.06
η2=0.71+j0.01
η3=0.53
ϵr1=6.19+j1.9
ϵr2=2.0−j0.08
ϵr3=3.5 |
| Tailless airplane |
50,376 |
10.8×21.1×0.9 |
η=0.39−j0.2
ϵr=6.6−j2.8 |
| Missile+ocean |
112,068 |
106×10.6
160×10.6 |
η1=0.38−j0.05
ϵr1=6.19+j1.9
η2=0.09+j0.04
ϵr2=72.6+j69.4 |
Download Excel Table
각 IPO와 MLFMM를 수치적으로 비교하기 위해, 식 (10)과 같이 정의된 정규화 평균 제곱근 오차(NRMSE, normalized root mean square error)로 검증한다.
식 (10)에서 N은 관측점의 개수이고, σMLFMM과 σIPO는 각각 MLFMM과 IPO의 RCS 해석 결과이다. 각 시뮬레이션 환경은 표 2에 요약한다.
표 2. | Table 2.
시뮬레이션 환경 | Simulation environment.
| Objects |
Incident wave |
Observation |
| Fighter bi-static |
θinc=45°, ϕ inc=0° |
θ=0°~360°, ϕ =0° |
| Tailless airplane bi-static |
θinc=120°, ϕ inc=0° |
θ=0°~360°, ϕ =0° |
| Tailless airplane mono-static |
θinc=120°~240°, ϕ inc=0° |
| Missile+ocean bi-static |
θinc=45°, ϕ inc=0° |
θ=90°~−90°, ϕ =0° |
| Missile+ocean mono-static |
θinc=5°~60°, ϕ inc=0° |
Download Excel Table
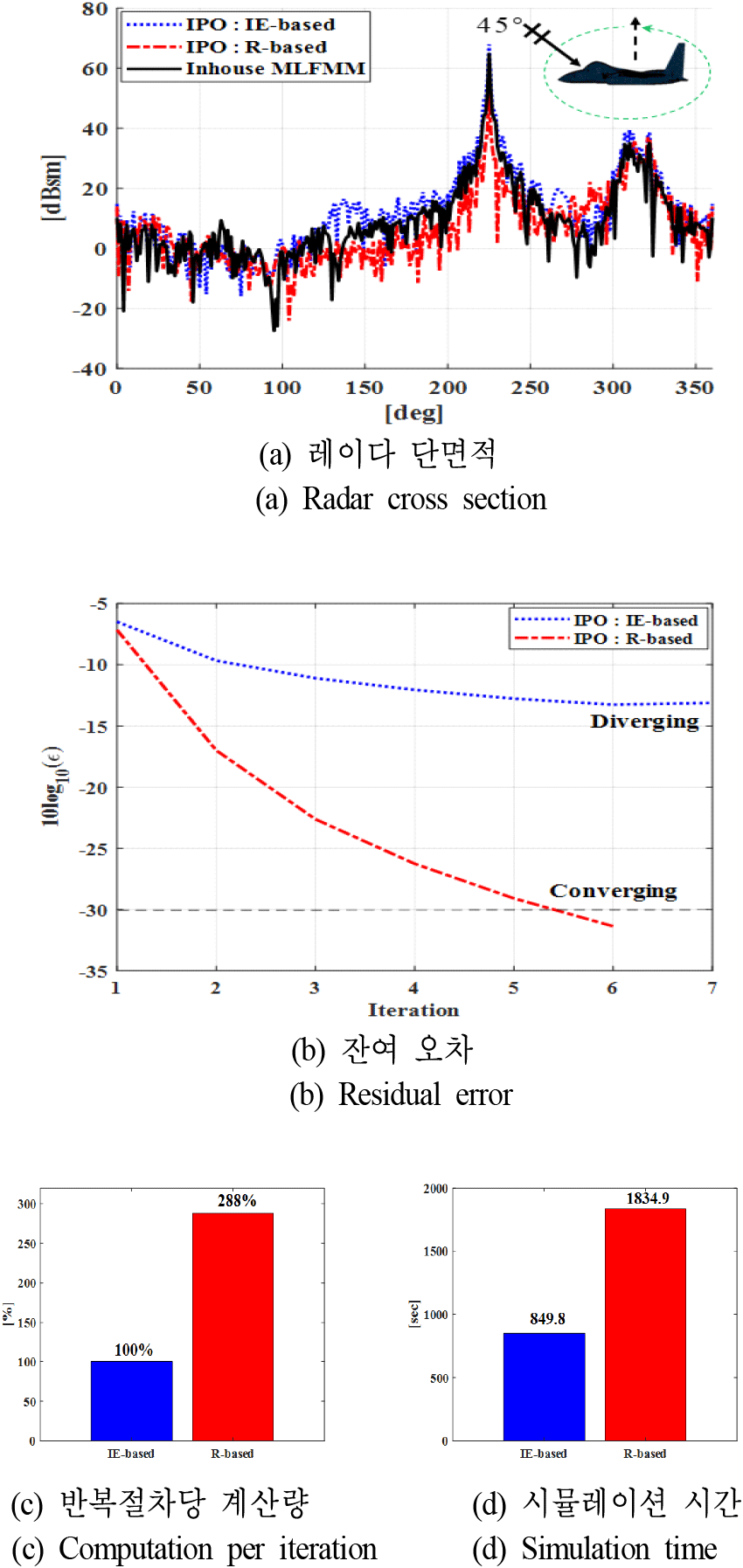
첫 번째 시뮬레이션은 복합매질 전투기의 bi-static 시뮬레이션 결과이다. 그림 3(a)는 각 IE와 R-based IPO 및 자체개발 MLFMM의 RCS해석 결과이다. MLFMM과 비교한 결과 IE기반 IPO의 RCS가 더 높게 나타나고, R-based IPO의 경우 상대적으로 정확하게 예측했다. NRMSE 는 IE와 R-based 각각 17.67 m2, 14.92 m2이다. 그림 3(b)는 residual error로 IE-based IPO의 경우 8번째 반복 절차에서 발산한데 반해 R-based IPO는 6번의 반복절차에서 잔여오차가 설정한 허용오차 10−3 아래로 내려가 수렴했다. 그림 3(c)는 각 IPO의 1번 반복 당 계산량을 IE-based 100 % 기준의 비율로 R-based는 IE대비 약 2.8배 많은 계산량을 보였다. 또한 그림 3(d)는 전체 시뮬레이션 시간으로 걸리는 시간은 반복 횟수를 고려해 각각 849.8초, 1,834.9초로 R-based가 약 2.15배 더 소요된다.
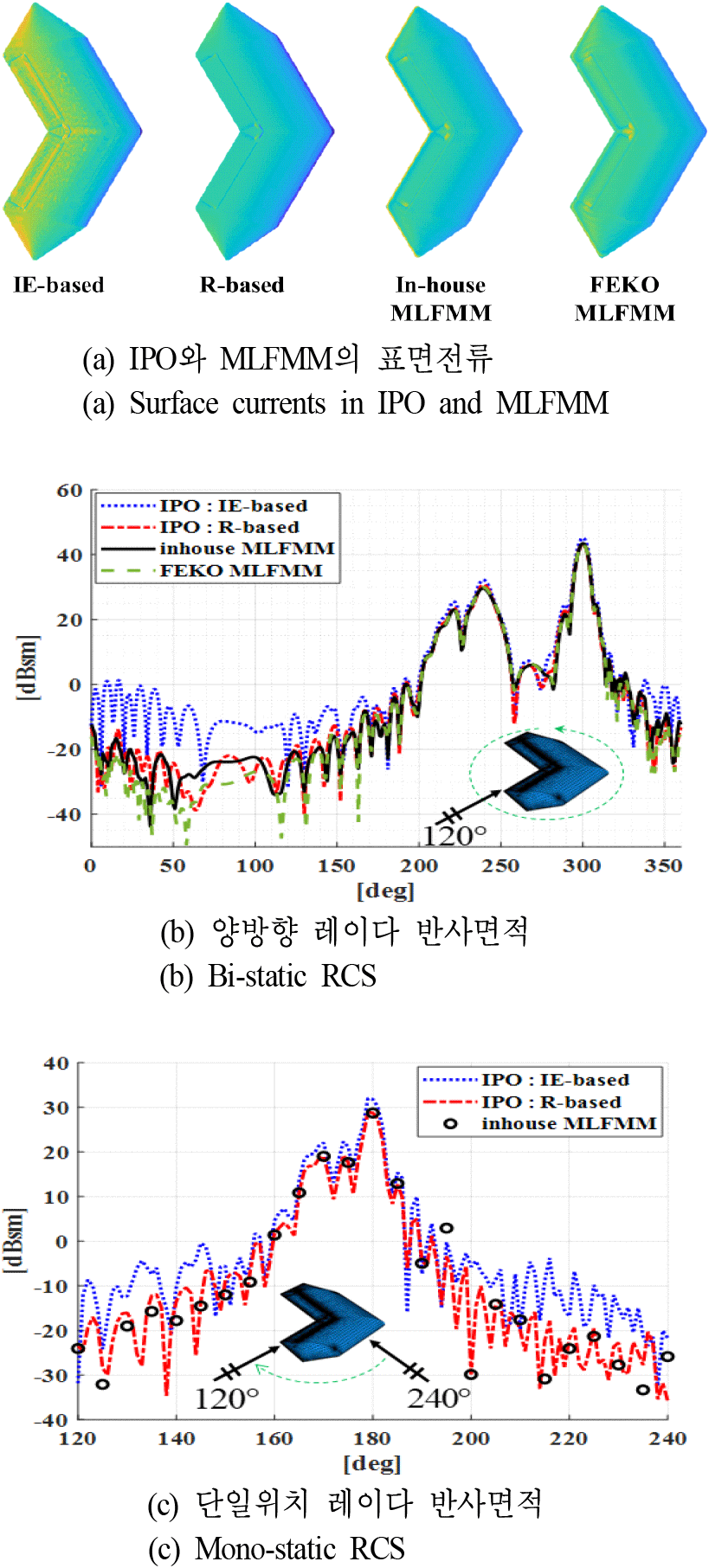
다음은 무익항공기로 bi-static과 mono-static의 시뮬레이션 결과이다. 그림 4(a)는 bi-static 시뮬레이션의 표면 전류로 IE-based와 자체개발 MLFMM은 임피던스 모델로, R-based와 FEKO는 유전체로 해석했다. 무익항공기 후면의 미세 gap으로 인해 표면 전류의 차이가 생기는 것을 볼 수 있다. IE-based IPO는 완만한 표면을 가진 전방에 비해 복잡하고 협소한 형태인 후미의 표면 전류가 특히 강하게 나타나는 것을 알 수 있다.
그림 4. | Fig. 4.
무익 항공기의 mono-static 시뮬레이션 결과 | Mono-static simulation results of tailless airplane.
Download Original Figure
그림 4(b) 및 그림 4(c)는 각각 IPO의 bi-static 및 mono-static RCS 결과이다. mono-static 시뮬레이션의 경우 IPO는 1도 간격, MLFMM은 5도 간격으로 해석했다. Bi-static의 시뮬레이션 결과 두 방법 모두 정확한 전방 산란에 비해 IE-based IPO의 후방 산란은 오차가 큰 것을 알 수 있다. 그림 2에서 볼 수 있듯, 무익항공기 형상은 전면의 매끄러운 구조와 후면의 복잡한 틈새가 특징적이다. IE-based 및 R-based IPO 방법은 전면부의 RCS를 정확히 예측하는 데 효과적이었으나, 후방부에 위치한 미세 틈새에 대해서는 IE-based IPO가 흡수 효과를 충분히 반영하지 못했다. 이는 그림 4(a)에서 보여지는 후방에 대한 강한 표면 전류 결과로 나타났으며, 그림 4(b)에 나타나듯이 0~160°의 범위에 걸쳐 미세 틈새의 영향으로 인해 증가된 RCS를 관찰할 수 있다. FEKO의 결과를 기준으로 삼았을 때, 0~160° 범위의 NRMSE는 IE-based와 R-based 방법에 대해 각각 0.32 m2, 0.16 m2로 산출되었다. 후방 산란만 계산한 mono-static은 가장 RCS가 강한 θ=180° 부근을 제외하고 IE-based IPO는 낮은 정확도를 보였다. 반면 R-based IPO의 결과 bi-static과 mono-static 모두 상대적으로 정확도가 높은 것을 알 수 있다.
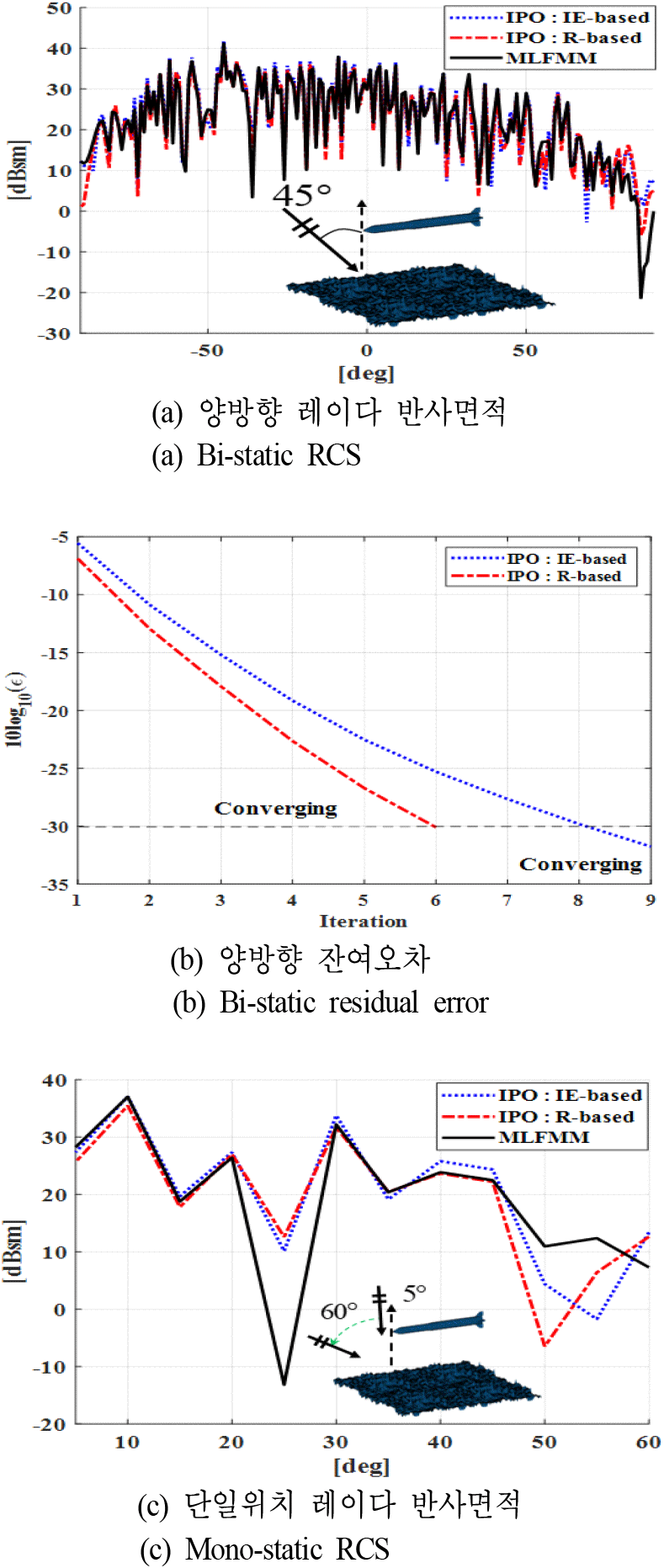
마지막으로, 복합 매질로 구성된 거친 해수면 위 미사일의 해석 결과이다. 앞선 물체대비 복잡도가 낮은 해수면은 두 IPO 모두 정확한 것을 그림 5(a)의 bi-static RCS 그래프에서 알 수 있다. 그림 5(b)는 bi-static의 residual error로 IE와 R-based IPO는 각각 9번째, 6번째 반복절차에서 수렴해 R-based IPO의 전체 계산량은 IE-based 대비 1.91배로 감소했다. 그림 5(c)는 mono-static 해석 결과로 IPO와 MLFMM 모두 5도 간격으로 진행했다.
그림 5. | Fig. 5.
거친 해수면 위 미사일 시뮬레이션 결과 | Simulation results of missile above rough ocean surface.
Download Original Figure
적분방정식과 반사계수 기반의 두 IPO에 대한 다섯 가지 시뮬레이션 결과의 시간, MLFMM과의 NRMSE 비교 및 각 IPO의 반복 횟수에 대해 표 3에 요약한다. Mono-static의 경우 전체 반복 횟수로 기록했다. 시뮬레이션 결과 IE-based가 R-based 대비 2.1배에서 최대 4.5배까지 빠르게 해석했다. 그러나 전반적으로 R-based가 정확하게 RCS를 예측했다. 또한 표면 전류의 흡수를 고려 하기 때문에 residual error가 수렴하는 경우 R-based가 IE-based 대비 빠르게 수렴하는 것으로 나타났다. 그러나 무익항공기의 mono-static에서 알 수 있듯 전류가 발산하는 경우 R-based의 반복 횟수는 증가했다. 두 방법의 필요 메모리는 메쉬 사이즈에 의해 결정되므로 유사하다.
표 3. | Table 3.
IE 및 R-based IPO의 해석 결과 요약 | Summary results of IE and R-based IPO.
| Objects |
IPO |
Time [sec] |
NRMSE [m2] |
Iterations |
| Fighter Bi-static |
IE |
849.8 |
17.67 |
8 |
| R |
1,834.9 |
14.92 |
6 |
| Tailless airplane Bi-static |
IE |
531.64 |
2.98 |
3 |
| R |
1,527.9 |
0.26 |
3 |
| Tailless airplane Mono-static |
IE |
60,858 |
4.33 |
360 |
| R |
274,801 |
0.69 |
402 |
| Missile+ocean Bi-static |
IE |
1,835.3 |
2.06 |
9 |
| R |
3,549.5 |
2.00 |
6 |
| Missile+ocean Mono-static |
IE |
25,503 |
2.21 |
114 |
| R |
54,291 |
2.20 |
80 |
Download Excel Table
Ⅳ. 결 론
본 논문에서는 적분방정식과 반사계수를 이용해 계산한 IPO의 해석 결과를 비교 분석했다. 단일 및 복합 임피던스 또는 유전체 매질로 구성된 물체를 두 IPO의 표면 전류 및 RCS를 통해 비교하고, FEKO 및 자체개발 MLFMM과 수치적으로 검증하였다. 유전체로 구성된 복잡한 구조인 전투기와 무익항공기의 경우 R-based에 비해 IE-based의 표면 전류가 강한 상호작용이 나타나고, 그에 따라 RCS의 오차가 큰 것을 알 수 있다. 그러나 상대적으로 복잡도가 낮은 해수면에서 두 IPO 모두 수렴하고 RCS 또한 잘 일치했다. 단일 반복 절차에서 R-based는 IE-based IPO 계산량에 약 2.8배 많고 수렴 특성을 고려하여 전체 해석 시간은 최대 4.5배까지 더 많이 소요 되었다. Residual error를 통해 IE-based와 R-based IPO의 세 물체에 대해 수렴 특성을 확인했다. 본 연구의 시뮬레이션 결과에 따르면, R-based IPO는 IE-based IPO에 비해 정확도 면에서 우수하지만, 전기장 및 자기장 두 필드 계산의 필요성으로 인해 해석에 소요되는 시간이 증가하는 단점을 지닌다.
Acknowledgements
본 연구는 방위사업청과 국방과학연구소가 지원하는 스텔스 대형 플랫폼 전파해석 특화연구실 사업의 일환으로 수행되었음(UD230016JD).
References
F. Obelleiro-Basteiro, J. Luis Rodriguez, and R. J. Burkholder, "An iterative physical optics approach for analyzing the electromagnetic scattering by large open-ended cavities,"
IEEE Transactions on Antennas and Propagation, vol. 43, no. 4, pp. 356-361, Apr. 1995.


F. Obelleiro, M. G. Araújo, and J. L. Rodríguez, "Iterative physical-optics formulation for analyzing large waveguides with lossy walls,"
Microwave and Optical Technology Letters, vol. 28, no. 1, pp. 21-26, Jan. 2000.


J. W. Rim, I. S. Koh, "Convergence and accuracy of near-field-corrected iterative physical optics for scattering by imperfectly conducting and dielectric objects,"
IET Microwaves, Antennas & Propagation, vol. 14, no. 10, pp. 999-1005, May 2020.


R. J. Burkholder, Ç. Tokgöz, C. J. Reddy, and W. O. Coburn, "Iterative physical optics for radar scattering predictions,"
The Applied Computational Electromagnetics Society Journal, vol. 24, no. 2, pp. 241-258, Apr. 2009.

R. Wang, L. Guo, and Z. Zhang, "Scattering from contaminated rough sea surface by iterative physical optics model,"
IEEE Geoscience and Remote Sensing Letters, vol. 13, no. 4, pp. 500-504, Apr. 2016.


J. Li, B. Wei, Q. He, L. X. Guo, and D. B. Ge, "Time-domain iterative physical optics method for analysis of EM scattering from the target half buried in rough surface: PEC case,"
Progress in Electromagnetics Research, vol. 121, 391-408, Nov. 2011.


S. Liao, N. Gopalsami, A. Venugopal, A. Heifetz, and A. C. Raptis, "An efficient iterative algorithm for computation of scattering from dielectric objects,"
Optics Express, vol. 19, no. 4, pp. 3304-3315, Feb. 2011.



J. G. Meana, J. Á. Martinez-Lorenzo, F. Las-Heras, and C. Rappaport, "Wave scattering by dielectric and lossy materials using the modified equivalent current approximation(MECA),"
IEEE Transactions on Antennas and Propagation, vol. 58, no. 11, pp. 3757-3761, Nov. 2010.


E. Rashidi-Ranjbar, M. Dehmollaian, "Target above random rough surface scattering using a parallelized IPO accelerated by MLFMM,"
IEEE Geoscience and Remote Sensing Letters, vol. 12, no. 7, pp. 1481-1485, Jul. 2015.


C. A. Balanis,
Advanced Engineering Electromagnetics, New York, NY, John Wiley & Sons, 1989.

I. S. Koh, C. H. Park, and W. Sun, "Analysis of radiation characteristics of Ka-band Von Karman radome based on IPO scheme,"
The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 22, no. 12, pp. 1148-1154, Dec. 2011.


J. U. Yoo, I. S. Koh, "Comparison of linear iteration schemes to improve the convergence of iterative physical optics for an impedance scatterer,"
Journal of Electromagnetic Engineering and Science, vol. 23, no. 1, pp. 78-80, Jan. 2023.


H. Lee, I. S. Koh, and J. H. Yoo, "Modified SDIE MLFMM method for inhomogeneous impedance material containing PEC or PMC region,"
The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 29, no. 10, pp. 805-810, Oct. 2018.


Y. Shao, Z. Peng, K. H. Lim, and J. F. Lee, "Non-conformal domain decomposition methods for time-harmonic maxwell equations,"
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, vol. 468, no. 2145, pp. 2433-2460, Sep. 2012.




L. W. Guo, Y. Chen, J. Hu, M. Jiang, J. L. W. Li, and Z. Nie, "A novel JMCFIE-DDM for analysis of EM scattering and radiation by composite objects,"
IEEE Antennas and Wireless Propagation Letters, vol. 16, pp. 389-392, Jun. 2016.


T. B. A. Senior, J. L. Volakis,
Approximate Boundary Conditions in Electromagnetics, London, IET, 1995.


C. Li, C. Tong, Y. Bai, and L. Qi, "Iterative physical optics model for electromagnetic scattering and Doppler analysis,"
Journal of Systems Engineering and Electronics, vol. 27, no. 3, pp. 581-589, Jun. 2016.