I. 서 론
레이다의 표적·탐지 성능 확보를 위해서는 표적 신호 이외의 불요파 및 고조파를 최소화하여 레이다 시스템의 신호 대 잡음비(signal-to-noise ratio: SNR)를 높이는 RF 송수신기 개발이 필수적이다. 따라서 레이다 운용에 필요한 다양한 신호의 불요파를 최소화하는 주파수합성기 개발이 필수적이다.
반면, 주파수합성기에서는 기준 발진 신호를 레이다에서 운용하는 송신신호(FTX), 수신기용 국부 발진 신호(FLO) 등의 밀리미터파대역 신호로 상향변환 및 증폭하기 위해 혼합기, 체배기 등 여러 능동소자를 활용한다. 능동소자는 비선형성에 의해 원신호 이외의 고조파, 혼변조 신호, 기생성분 신호 등을 생성하므로, 각 신호 주변의 불요파는 불가피하다[1],[2]. 또한 주파수합성기에서 운용파형을 생성하는 DDS(direct digital synthesizer)는 동작 특성에 의해 대역 내에 불요파를 생성한다[3].
일반적으로 라디오 주파수를 사용하는 무선 통신기기 및 레이다 등의 전파통신 장치에서는 송신신호의 대역 외에서 발생된 불요파가 타 채널 및 장비들의 신호 간섭을 일으키지 않도록 ITU-R[4],[5]의 권고에 따라 관리되고 있다. 이 내용에 따르면 본 논문과 같이 밀리미터파 대역을 적용하는 레이다에서는 운용 대역 밖 1 MHz 이상 떨어진 불요파파 FTX에 대해 43+10 log(첨두 전력(W)) dBc 혹은 60 dBc 중 더 작은 값으로 이상으로 격리도를 확보해야 한다.
밀리미터파 소자의 성능 한계로 인해 약 60 dBc의 불요파 규격 만족이 어려우므로, 기존의 레이다 시스템에서는 주파수합성기의 FTX 경로에 필터를 적용하여 대역 밖의 불요파 준위를 낮추도록 설계하고 있다[6],[7]. 또한, 수신기에서는 FLO와 함께 입력된 그 불요파가 표적신호 RX 및 RX의 불요파를 하향 변환시켜 IF 주변의 불요파를 생성하는 요인이되므로, FLO 경로의 불요파도 FTX에서와 마찬가지로 관리하고 있다[8].
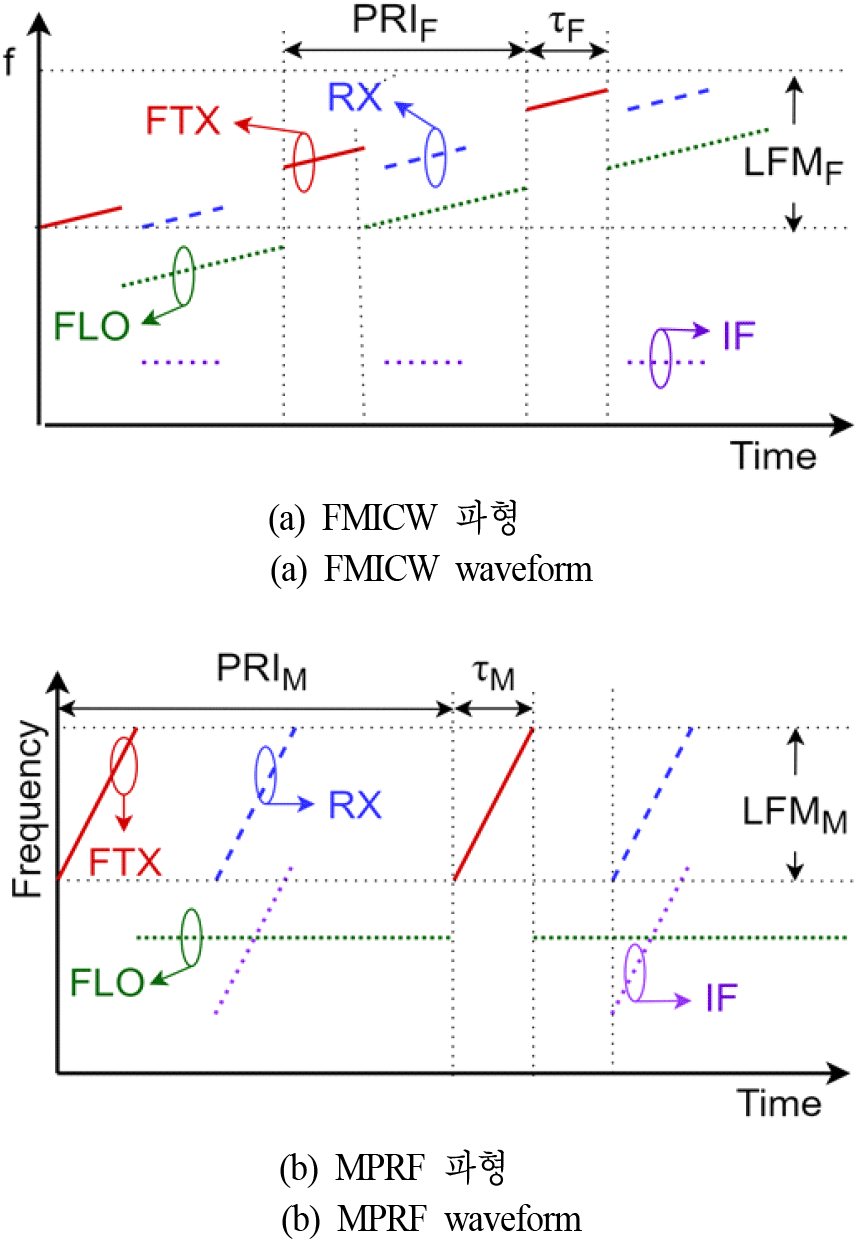
그러나 레이다가 적용되는 시스템들이 다양해지고 소형화됨에 따라 레이다 소형화/저가화 필요성이 높아지면서 필터를 적용하는 데에 공간상의 제약이 있다. 따라서 본 논문에서는 대역에 따른 FTX, FLO 불요파가 소형 레이다의 SNR에 미치는 영향성을 분석하고, 레이다의 SNR 성능을 유지하기 위해 시스템에서 허용 가능한 불요파 규격을 도출하였다. 개발 중인 소형 레이다는 단독으로 운용되며 단일 주파수 채널로만 동작하므로 타 레이다 신호에 의한 영향성은 상대적으로 낮다. 따라서 본 논문에서는 소형 레이다에서 사용하는 운용 파형인 FMICW 파형과 MPRF 파형(그림 1)에서 불요파가 레이다의 SNR 성능에 미치는 영향성을 최소화하는 규격을 도출하였다.
II. FMICW 파형에서 불요파 영향
그림 1(a)와 같은 FMICW 파형에서는 CPI(cohoeren preocession interval) 동안 펄스 파형의 IF를 여러 개 모아서 FFT한 뒤 표적정보를 얻어낸다. 이때, 주파수 도메인에서 IF의 FFT 결과는 식 (1) 및 식 (2)와 같다[9].
여기에서 fc가 carrier 신호의 중심주파수일 때, ω는 2 πf, ωc는 2 πfc, A는 펄스 파형의 진폭, N은 펄스 개수, PRI는 펄스반복주기, τ는 펄스폭, n은 PRF 주기로 복사된 신호의 차수이며, carrier 주파수에서 멀어질수록 그 값이 커진다. 식 (1)의 첫 번째 항은 carrier 신호의 FFT 결과가 sinc 함수임을 의미하며, 두 번째 항은 부엽을 의미한다. 부엽은 carrier 신호가 PRF 간격으로 복사된 신호로 구성되며, 그 크기는 PRF, 펄스폭, 신호의 차수에 따라 결정된다. 따라서 FMICW 파형을 사용하는 레이다에서는 수신기 최종단에서 IF 신호만을 수신하기 위해 협대역 필터를 적용하여 PRF 간격으로 복사된 신호들을 감쇄시킨다.
단, PRF 간격으로 복사되어 IF 중심주파수에서 n×PRF 만큼 멀어진 신호 주변에 불요파가 존재하면, 불요파 역시 PRF 간격만큼 역방향으로 복사되어 IF 대역 내로 들어올 수 있다. 여기서 IF의 n×PRF 근처에 생성된 불요파는 그림 2의 IF 스펙트럼에서 나타낸 바와 같이 FTX가 반사된 신호인 RX 혹은 FLO의 불요파가 수신기에서 하향 변환된 것으로, 원신호에서의 offset과 같은 곳에 있으며, 그 전력 차이도 그대로 유지된다.
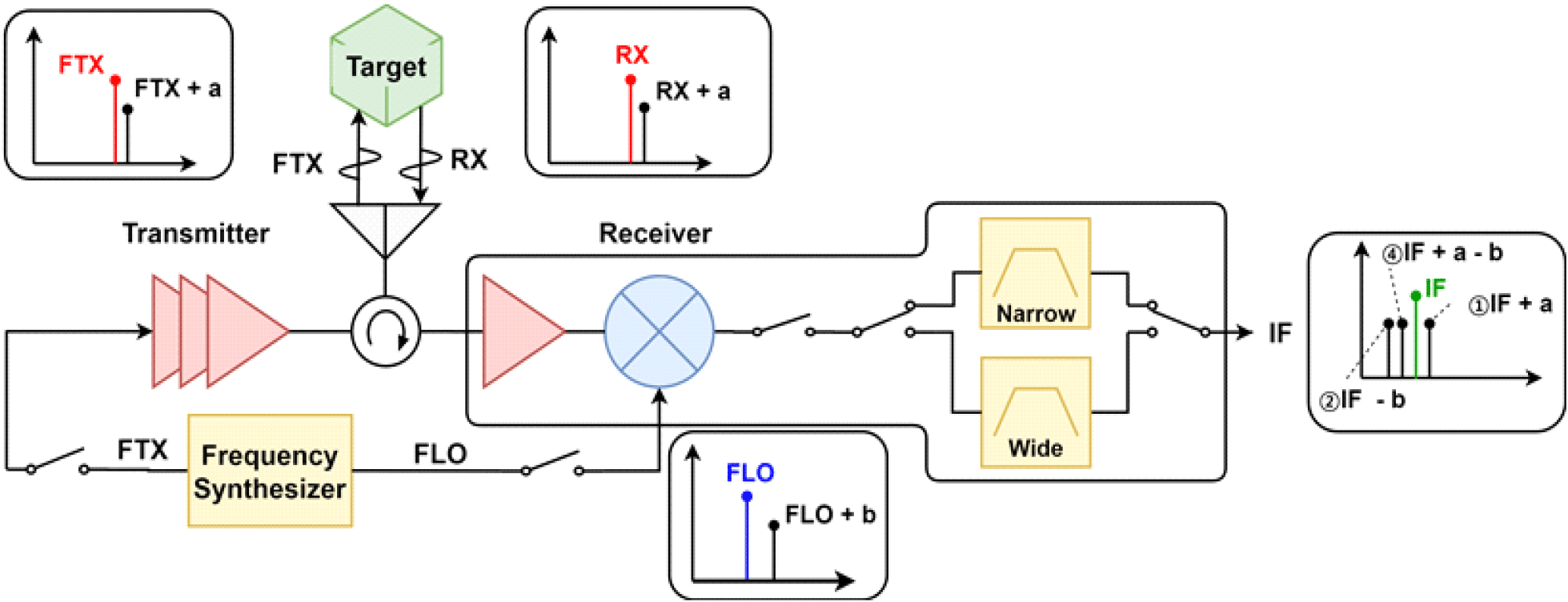
각 레이다에서 목표로 하는 SNR 및 그에 따른 threshold에 따라 IF 대역 내에 허용 가능한 불요파 준위는 달라질 수 있으며, 본 논문의 소형 레이다 시스템에서 신호처리 중 FMICW 파형의 SNR을 만족하기 위해 요구하는 IF 협대역 필터 대역 내의 불요파 준위는 −55 dBc 이하이다. 이를 참고하여, RX(FLO) 불요파의 복사된 성분이 IF 대역 내에서 시스템 요구사항을 만족하기 위한 RX (FLO)의 불요파의 준위를 계산하였다. 불요파의 offset은 PRF의 정수배(n)와 IF 필터의 반측 대역폭(BW/2) 이내 주파수의 합으로 아래와 같이 설정하였다. 즉, 불요파를 기준으로 n번 복사된 성분이 IF 신호 부근에 위치하도록 설정하였으므로, 정수배 n은 식 (1) 및 식 (2)의 n과 같은 의미로 사용할 수 있다.
식(1) 및 식 (2)을 이용하여 IF와 식 (3)의 offset만큼 떨어진 불요파의 스펙트럼을 그림 3과 같이 계산하였다. n을 변화시키며 불요파의 offset 주파수를 달리한 결과, 100 kHz PRF, 40 % 송신 듀티비 조건에서 n이 2인 불요파의 준위가 −45 dBc 이하이면, IF 대역 내로 들어오는 복사된 불요파 준위는 −55 dBc 이하였다. n이 26인 불요파는 그 준위가 −25 dBc 이하이면, IF 대역 내로 들어오는 복사된 불요파는 −55 dBc 이하를 만족함을 계산하였다.
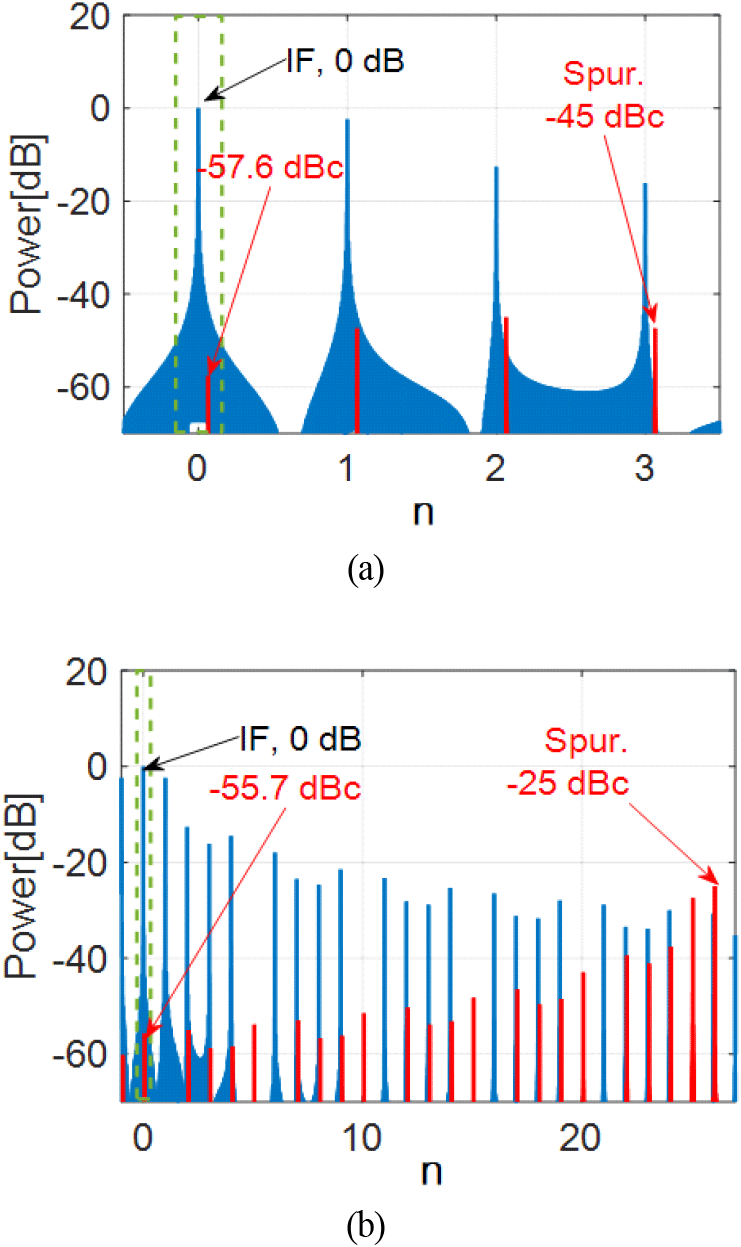
위와 같은 계산을 통해 IF 대역 내 불요파 준위가 −55 dBc를 넘지 않도록 하는 FTX 혹은 FLO의 불요파 조건을 계산하여 표 1에 나타내었다. 식 (3)을 이용하면 n에 대한 각 신호의 불요파 offset을 계산할 수 있다. 참고로, FMICW 파형에서 FTX, FLO 신호는 그림 2(a)와 같이 LFM 파형으로 생성되므로, 각 신호의 중심주파수를 기준으로 LFMF 대역 내의 모든 신호에 대해 표 1을 만족해야 한다. 따라서 FTX, FLO 신호의 최대, 최소 운용 주파수를 기준으로 표 1을 적용하여 불요파 규격을 정의하고, 성능을 확인해야 한다.
식 (1)의 두 번째 항에서 τ는 PRI×송신 듀티비로 바꿀 수 있으며, 그에 따라 복사된 신호의 크기는 식 (4)와 같다.
따라서, 송신 듀티비가 같으면 식 (1)의 n에 따른 부엽신호의 준위는 PRF에 관계없이 차수 n과 송신 듀티비에 의해 계산된다. 이를 반영하면 송신 듀티비가 작을수록 sinc 함수는 중심주파수에 대해 완만히 감소하므로 상대적으로 원신호 대비 먼 영역의 offset 주파수에서도 불요파 관리가 필요함을 알 수 있다.
앞선 계산 결과를 확인하기 위해 수신기를 이용하여 그림 1의 수신기 대역통과필터 전단에서 불요파 offset에 따라 변화하는 IF 대역 내의 주파수를 측정하였다. 수신기 입력단과 LO단에는 각각 두 개의 신호발생기를 사용하여 40 % 듀티비의 RX와 RX의 불요파, FLO와 FLO의 불요파를 모사하였다. 그림 4는 식 (3)에 따라 RX와 FLO의 불요파 offset이 n은 0, x는 각각 a, b이고, 그 준위는 각각 원신호에 대해 −35 dBc가 되도록 설정하여 측정한 수신 출력신호이다. 여기서 BW는 수신기의 협대역필터 대역폭이다. 측정된 offset a, b의 준위는 각각 −34.6 dBc(신호 ①), −39 dBc(신호 ②)로 입력된 불요파 준위와 유사하다. 신호 ②의 준위가 4 dB 가량 더 낮은 이유는 혼합기가 정상 동작하는 FLO 전력보다 FLO 불요파의 전력이 더 낮아서 변환 효율이 떨어졌기 때문으로 판단된다. 그림 1에서 나타낸 a-b offset 신호의 준위는 두 불요파 준위의 합과 같으므로 약 −70 dBc가 되며, 이는 그림 4의 잡음준위와 유사하거나 더 낮아 스펙트럼에서 측정되지 않았다. 참고로 수신 출력신호 측정 시 RBW(resolution bandwidth)는 50 Hz로 설정하였다. 반면에, 그림 1에서 예상하지 않았던 2a offset ③이 확인되었다. 해당 신호는 RX와 그 불요파인 RX+a 신호의 혼변조 신호인 RX+2a에 의한 결과로 불요파의 크기에 따라 그 준위가 변화하는 성분이다.
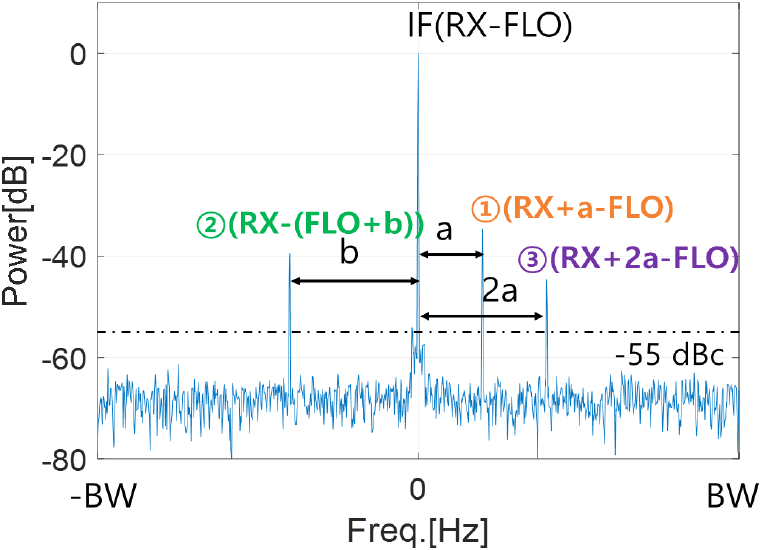
그림 5는 식 (3)을 참고하여 FTX, FLO의 불요파 offset이 n은 2, x는 각각 a, b이며, 그 준위는 −35 dBc일 때 측정한 IF 신호이다. 그림 5의 신호 ①, ②, ③은 그림 4의 각 신호와 같은 이유로 생성된 불요파이며, 각 불요파들은 PRF 간격으로 복사되어 IF 대역 내에 불요파를 생성하였다. 그림 5에서 사각형, 원, 삼각형으로 표시한 신호들은 각각 ①, ②, ③신호가 복사된 신호들이며, IF 대역 내로 복사된 각 신호의 크기는 −54.3 dBc, −53.7 dBc, −64.6 dBc이다. 송신 듀티비가 40 %, 불요파 준위가 −35 dBc 일 때, n=2인 offset에서는 필터 대역 내 불요파가 −55 dBc 이상으로 측정되므로, ①, ② offset의 불요파는 −35 dBc보다 그 준위가 더 낮아야 하며, 표 1에서 검토된 내용은 적절하다.
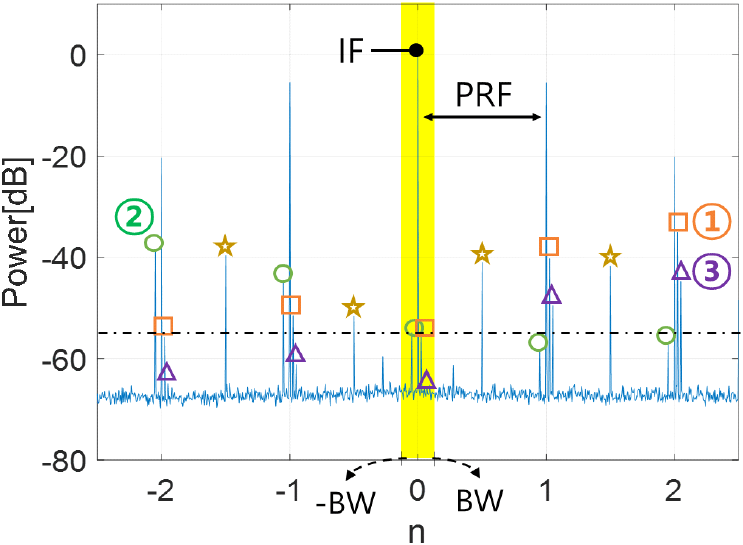
그림 6에서 별모양으로 표시한 신호는 펄스 동작을 위한 스위칭으로 DC 부근부터 생성된 PRF 하모닉 신호이다. 이외의 불요파 신호는 신호발생기에서 출력된 불요파로 확인되었다. IF 대역 이외의 불요파는 수신기 최종단의 대역통과필터에 의해 감쇄되므로 시스템에 미치는 영향은 거의 없다.
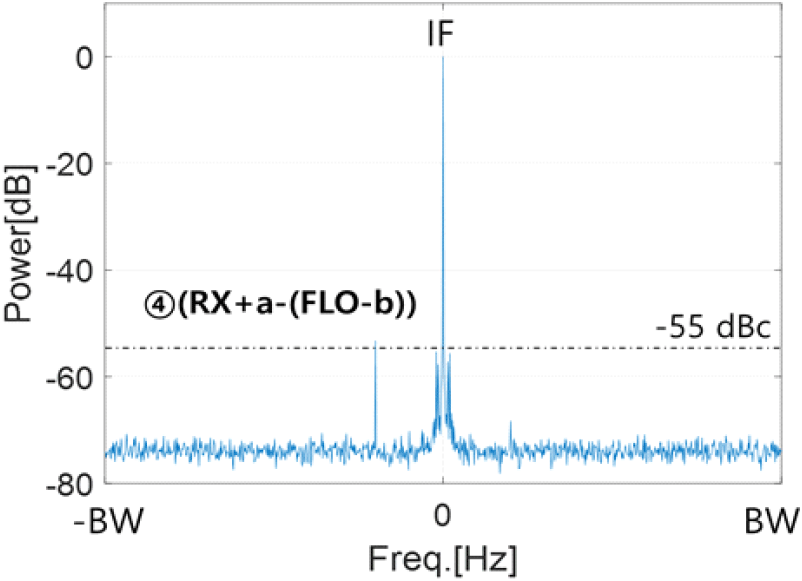
그림 7은 식 (3)을 참고하여 RX, FLO의 불요파 offset이 n은 188, x는 각각 a, b이며, 그 준위는 각각 −15 dBc, −35 dBc일 때 측정한 IF 신호이다. 표 1에서 분석한 바와 같이 불요파 offset이 IF 대역폭보다 월등히 크므로 신호 ①, ②, ③에 의한 불요파는 측정되지 않았다. 반면, RX의 불요파 준위가 그림 5 및 그림 6보다 20 dB 높아지면서 RX 불요파가 FLO 불요파에 의해 하향 변환된 신호 ④가 −53.2 dBc의 준위로 두 불요파의 준위의 합인 −50 dBc와 유사하게 측정되었다. 이 결과를 통해 신호 ④와 같은 요인으로 생성된 대역내 불요파 준위가 −55 dBc가 되기 위해서는 RX, FLO의 불요파 준위 합이 −55 dBc가 되도록 해야 함을 알 수 있다. 그에 따라 표 1에서 허용되는 FTX, FLO 불요파 준위가 각각−25 dBc 이하인 조건들은 모두 −28 dBc 이하가 되도록 수정 반영하였다.
추가로, 수신기 동작 주파수 이상으로 떨어진 불요파에 대해서는 혼합기의 변환 효율 및 증폭기의 이득이 감소하므로, 신호 ④의 준위가 두 불요파의 합보다 더 낮아짐을 실험적으로 확인하였다. 따라서 동작 주파수 대역 이상의 불요파에서는 수신기의 성능에 따라 더 높은 준위도 허용될 수 있다.
III. MPRF 파형에서 불요파 영향
본 논문에서는 펄스 압축을 사용하는 MPRF 파형에서 불요파의 영향성을 검토하였다. 펄스 형태의 IF 신호를 모아서 FFT를 수행하는 FMICW 파형과 달리 MPRF 파형에서는 한 펄스 동안 LFMM대역으로 선형변조된 표적신호를 수신기에서 단일 주파수의 FLO로 하향변환한 뒤, 신호처리 중 matched filter를 이용하여 펄스 압축하여 표적 정보를 얻어낸다(그림 1(b)). 따라서 MPRF 파형에서는 펄스 동작에 의한 불요파 복사는 발생하지 않는다. 다만, IF 신호의 LFMM 대역 내에 들어오는 불요파에 의해 펄스 압축 과정 중 표적 신호의 부엽준위가 상승하거나, 표적 정보와는 다른 위치에서 신호가 발생하여 오표적으로 인식될 가능성이 있다.
불요파는 앞서 검토한 바와 같이 RX, FLO의 불요파와 그에 의한 혼변조 신호에 의해 발생한다. 그중, 첫 번째로 FLO 불요파로 인해 IF 주변으로 생성되는 LFM 파형의 불요파를 가정하고, 펄스 압축에 미치는 영향을 검토하였다. 계산을 위해 IF 중심주파수는 10 MHz, LFM 대역폭 LFMM은 6 MHz, 펄스폭은 9 usec인 MPRF 파형을 설정하였다. FFT 과정에서 샘플링 주파수는 100 MHz를 사용하였고, Hamming 윈도우를 적용하였다.
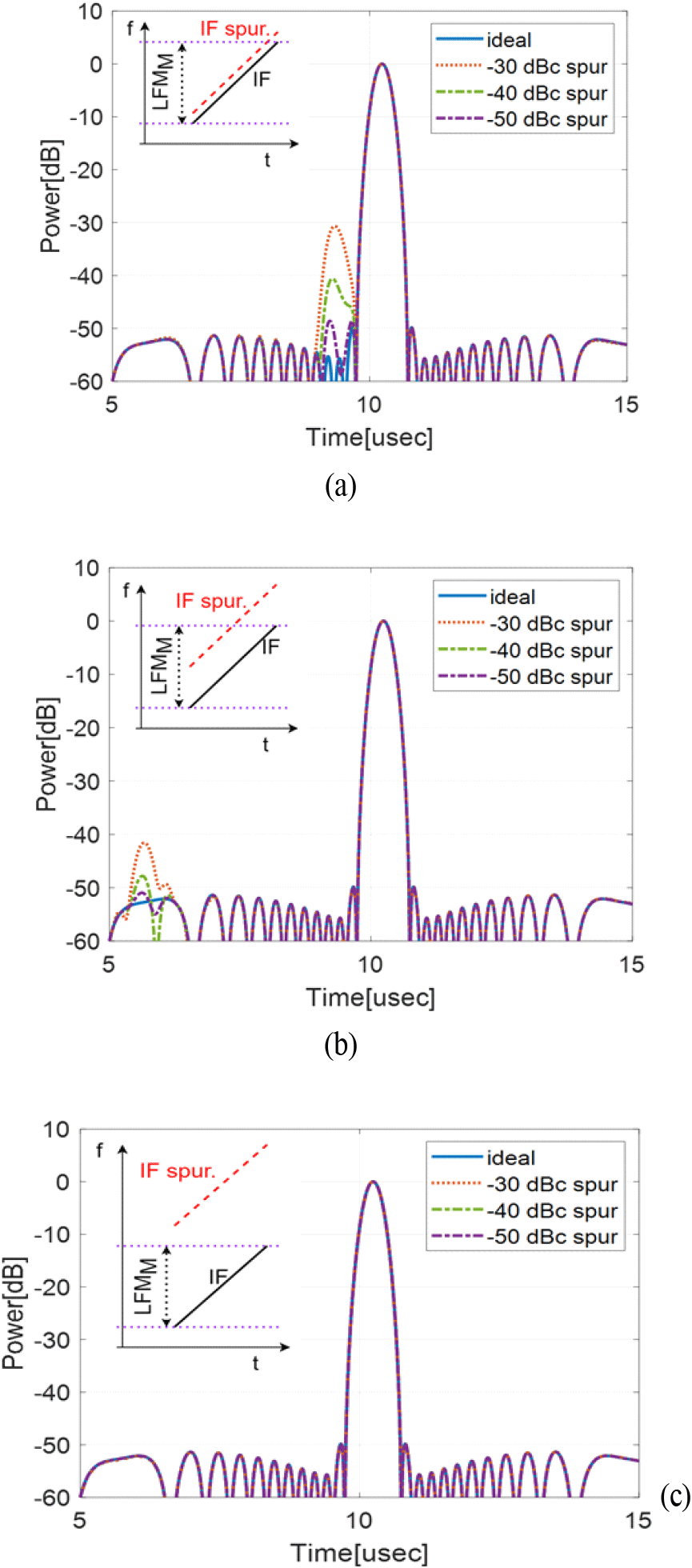
수신기 출력단의 LFM 파형 불요파는 그림 2의 광대역 필터에 의해 IF 대역의 신호만 신호처리부에 전달되므로, 그림 7의 각 그래프 상단에 나타낸 바와 같이 원신호보다 펄스폭 및 대역폭이 작다. 이때, 원신호에 대해 불요파의 offset이 증가할수록 불요파의 펄스폭 및 대역폭이 줄어듦으로 펄스폭 및 LFM 대역폭에 비례하는 펄스 압축 이득도 감소한다. IF와 matched filter에 적용된 Hamming 윈도우의 가중치를 추가 반영하면 불요파가 LFMM과 90 %, 50 %, 10 % 겹쳐질 때, 펄스 압축 후 전력은 원신호보다 0.48 dB, 12.6 dB, 50.8 dB 감소함을 계산으로 알 수 있다. 이를 반영하여 FLO 불요파의 offset을 −0.6 MHz, −3 MHz, −7 MHz로 설정하여, IF 불요파가 LFMM과 90 %, 50 %, 0 % 겹쳐질 때 펄스 압축 결과를 비교하였다. 원신호와 근접한 불요파는 펄스 압축 후에도 불요파 준위가 유지되었으나, 불요파 offset이 증가함에 따라 감쇄량이 커짐을 알 수 있다.
다만, 불요파 준위가 −40 dBc 이하로 낮아지면, 윈도우에 의한 부엽 영향성이 높아지면서 예상보다 불요파에 의해 부엽준위가 낮아지는 폭이 줄어들었다. 이상적인 조건에서 Hamming 윈도우에 의한 부엽은 약 −50 dBc이다. 또한, 그림 7(c)와 같이 불요파가 LFMM 밖에 있으면 펄스 압축 결과에 영향을 전혀 미치지 않았다.
따라서 이상적인 조건에서 펄스 압축 결과와 유사한 부엽 준위를 만족하기 위해서는 FLO 주파수를 기준으로 불요파 offset이 LFMM/2 이내면 −50 dBc 이하, LFMM/2 ~LFMM이면 −40 dBc 이하인 경우, 시스템에서 허용 가능하다. 적용되는 윈도우에 따라 불요파의 offset에 따른 펄스 압축 이득 감쇄량은 일부 차이가 있을 수 있으나, 제안된 규격으로 SNR을 50 dB 이상 확보할 수 있으므로 시스템 적용이 가능한 것으로 판단된다.
두 번째로, IF의 LFM 대역폭 내에 일정한 신호의 불요파가 존재할 때, 불요파 준위에 따른 펄스 압축 결과를 확인하였다. 해당 불요파는 FTX, FLO 신호뿐만 아니라, 수신기 출력단에서도 생성될 가능성이 있는 불요파이다.
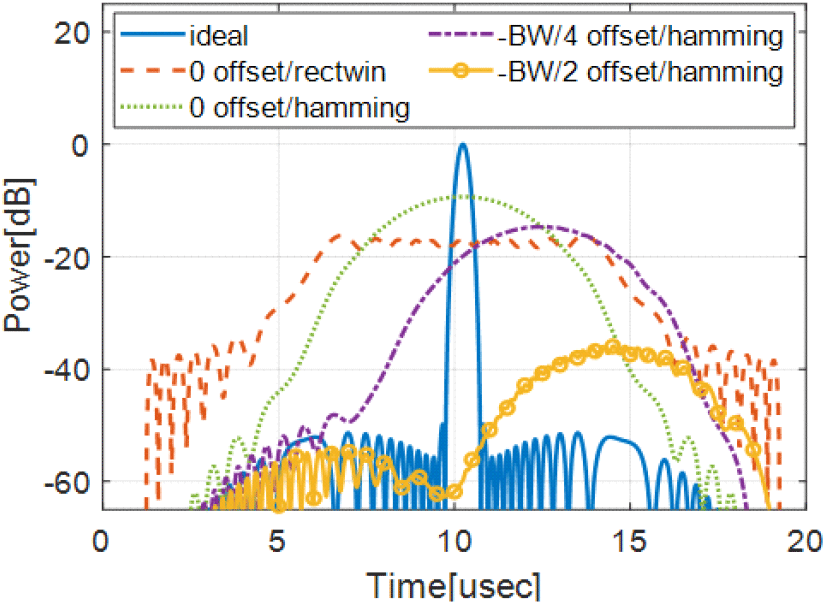
CW 신호로 펄스 압축을 수행하면, 신호가 하나의 짧은 펄스폭에 대해 모이지 않고 matched 필터의 윈도우 모양을 따라 넓게 퍼진다. 그림 8은 수신기 출력신호와 matched 필터에 사각 윈도우와 Hamming 윈도우를 적용했을 때 CW 신호의 펄스 압축 결과이다. 여기에서 이상적인 LFM 신호와 CW 신호의 전력은 같다. 그림 8에서 보면, FFT 중에 사각 윈도우를 적용했을 때에는 펄스 압축 후 CW 신호의 LFM 신호의 이득차이가 10log(펄스폭 ×LFMM)인 17.3 dB로 계산된다. 반면에 Hamming 윈도우가 적용되었을 때에는 윈도우의 가중치에 의해 불요파의 offset 주파수가 0, −LFMM/4, −LFMM/2로 변함에 따라 두 신호의 이득 차이값이 최소 9.3 dB, 14.7 dB, 36.9 dB로 증가하였다. 이 결과를 통해 불요파의 offset 주파수에 따라 허용되는 불요파 준위가 달라짐을 알 수 있다.
위의 내용을 반영하여 LFM 파형의 원신호와 CW 파형의 불요파가 펄스 압축된 후 결과를 계산하여 그림 9에 나타냈다. IF 중심주파수에 있는 불요파는 그림 9(a)와 같이 주엽과 가까운 영역의 부엽 준위를 높인다. 단, 펄스 압축 과정 중에 그 에너지가 넓게 퍼지면서 불요파 준위가 −30 dBc, −40 dBc, −50 dBc일 때, 부엽의 최대 준위는 −37.8 dBc, −44.5 dBc, −48.0 dBc로 계산된다. 불요파가 IF 중심주파수에서 −LFMM/4만큼 떨어져 있을 때는 그림 9(b)와 같이 주엽에서 벗어난 영역의 부엽 준위가 높아졌으며, 각 조건에서 최대 부엽준위는 각 조건에서 최대 −41.5 dBc, −47.2 dBc, −49.4 dBc로 계산되었다. 이상적인 조건에서도 부엽이 약 −50 dBc에 위치하므로, 불요파에 의한 잡음과 부엽이 더해져서 앞서 예상된 불요파 offset에 따른 부엽 감쇄량보다는 감쇄값이 더 작았다.
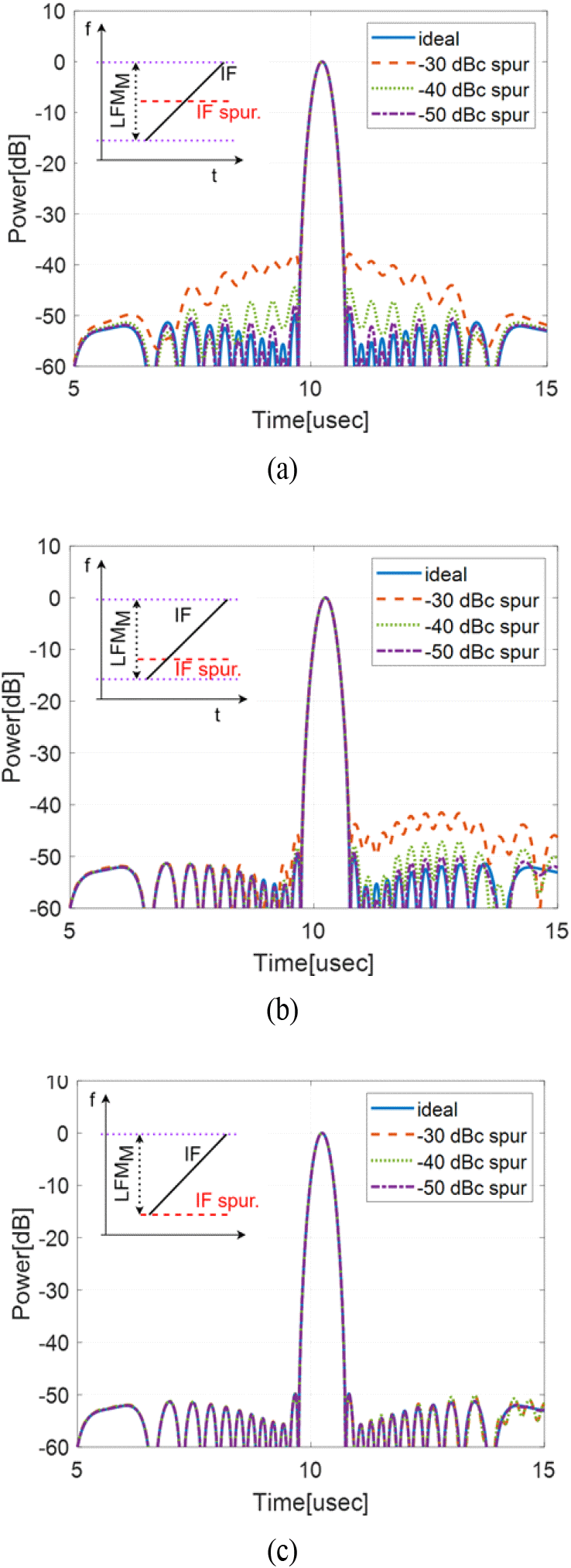
그림 9의 결과에 따라서 LFM 파형의 중심주파수에 대해 불요파가 펄스 시간 동안 같은 주파수로 존재할 때, offset이 LFMM/2 이내이면 불요파는 −50 dBc 이하가 되어야 하며, 이는 그림 8의 결과와 같다. 추가로, 그림 9(c) 결과와 같이 불요파 offset이 LFM 대역 밖에 있는 불요파는 펄스 압축에 영향을 미치지 않았다.
IV. 결 론
일반적으로 레이다의 FTX, FLO 신호는 채널 간의 간섭을 최소화하기 위해 −60 dBc 이하의 불요파를 만족해야 한다. 하지만 소형화/저가화된 레이다 시스템에서는 공간상의 제약으로 해당 규격 만족이 어려우므로 본 논문에서는 FTX(RX), FLO 신호의 불요파가 FMICW 파형 및 MPRF 파형에서 신호처리 중 미치는 영향성을 각각 분석하고, 허용 가능한 불요파 규격을 제안하였다. 단, 적용 레이다는 단독으로 운용되며, 단일 채널을 사용하므로 타 채널에 대한 간섭 영향성은 배제하였으며, 불요파가 존재하더라도 SNR 성능이 유지되도록 하는 규격을 도출하였다.
FMICW 파형에서는 펄스 파형의 IF 영향으로 FFT 처리 후 신호들이 PRF 간격으로 복사된다. 따라서 FTX, FLO의 불요파가 IF 대역폭보다 멀리 떨어져 있더라도 IF 대역폭 내의 불요파를 발생시킬 수 있다. 본 논문에서는 FMICW 수신 출력신호 범위인 협대역 IF 대역폭 내에 표적신호 이외의 불요파 준위가 본 레이다 시스템에서 요구하는 −55 dBc 이하가 되도록 각 불요파의 offset 주파수에 따른 허용 준위를 도출하였다. 또한 분석 내용을 반영하여 수신기에 불요파를 포함하는 RX와 FLO 신호를 인가하고, 계산적으로 검토된 내용이 하드웨어에서 재현되며, 도출된 불요파 규격이 실제 상황에서도 적절함을 확인하였다. 그 결과, FTX, FLO 신호의 최대, 최소 운용주파수에 대한 offset 주파수가 멀어질수록 높은 준위의 불요파도 허용이 가능하다. 따라서 주파수합성기에 적용되는 혼합기 선정 시 불요파 규격을 참고하면, 최종단 필터를 제거하고 공간상 여유를 확보할 수 있을 것으로 판단된다.
한편, FMICW 파형에서 LFMF 대역폭을 포함하는 FTX, FLO 운용주파수 범위의 불요파는 파형을 생성하는 DDS의 성능이 지배적이므로, DDS 선정 및 파형 설계 시 불요파 준위가 −55 dBc 이하가 되도록 반영해야 한다.
MPRF 파형에서는 LFMM 대역폭 내에 존재하는 불요파로 인해 펄스 압축 후 부엽 준위가 높아짐을 계산적으로 확인하였다. IF 중심주파수에 대해 불요파가 LFMM/2보다 가까울 때는 불요파가 −50 dBc 이하, 불요파가 LFMM/2~LFMM 범위에 있을 때에는 −40 dBc 이하이면, 이상적인 펄스 압축 결과와 유사한 결과를 얻을 수 있다. 또한, LFMM 이외의 불요파는 펄스 압축에 영향을 주지 않는다. 따라서 MPRF 파형에서는 최종단의 필터의 필요성이 낮은 것으로 판단되며, FMICW 파형에서와 마찬가지로 DDS를 통한 LFM 대역 내의 불요파 관리가 필수적이다.
본 논문의 결과는 신호처리 중 불요파의 영향성을 최소화하면서, 소형화/저가화된 주파수합성기를 설계하는데 이바지할 것으로 기대된다.