Ⅰ. 서 론
레이다(radar)는 전자기파를 공간상으로 방사하여 표적으로부터 산란된 신호를 이용하여 정보를 획득하는 센서이다[1]. 초기의 레이다는 안테나 개구면을 기계적으로 회전시킴으로써 빔을 형성하는 수동배열형태로 구현되었으나[2], 현재의 레이다 개발 추세는 안테나복사소자 각각의 위상값을 조절하여 빔을 원하는 위치로 형성하는 능동배열형태가 주목을 받고 있다[3],[4].
능동배열형태의 레이다는 크게 아날로그 빔형성 방식, 부배열디지털 빔형성 방식, 디지털 빔형성 방식으로 구분된다. 아날로그 빔형성 방식과 부배열 디지털 빔형성 방식은 RF 위상변위기와 급전기를 사용하여 빔조향의 정확도가 위상변위기에 종속되며, 다중 빔형성과 자유로운 방향으로의 빔형성이 제한된다. 디지털 빔형성 방식은 RF 위상변위기와 급전기 없이 디지털 위상가중기로 빔을 형성하며, 다수의 빔을 높은 정확도로 원하는 방향으로 조향할 수 있다[5]~[7]. 위와 같은 특징으로 디지털 빔형성 방식의 능동배열레이다는 단일 표적의 탐지 추적과 동시다발적인 위협으로부터 아군을 보호하기 위한 군사용 레이다 시스템에 적합하다[3]. 그러나, 디지털 빔형성 방식에서 빔조향의 정확도를 높이기 위해서는 많은 안테나복사소자가 필요하며, 이는 처리해야 할 데이터 양의 증가로 이어지게 된다[8].
군사용 레이다와 같이 실시간성을 요구하는 시스템에서는 연산의 가속화는 중요한 문제이며, 디지털 능동배열레이다의 연산을 가속하기 위하여 FPGA(field programmable gate array)를 활용하는 방법이 연구되고 있다[4],[9]. FPGA 기반 연산 가속기는 엄격한 타이밍 제약사항을 달성할 수 있어 실시간 시스템 운영에 적합하다. 또한 긴 수명과 높은 신뢰성을 가지며[10],[11], 부동소수점 수 체계로 연산되는 범용 시스템과 달리 고정소수점 수 체계를 활용할 수 있어 주어진 요구사항에 맞추어 리소스를 능동적으로 사용할 수 있다는 이점이 있다[12]. 위와 같은 이유로 본 논문에서는 Xilinx Kintex UltraScale FPGA를 이용하여 디지털 능동배열레이다의 빔형성을 위한 고정소수점 기반 빔형성 계수 연산기를 설계하고, 그 성능을 분석한다.
본 논문의 구성은 Ⅱ장에서는 디지털 능동배열레이다의 빔형성 기법과 2진 실수 표현 방식에 관해 설명하고, Ⅲ장에서 기존의 빔형성 계수 연산과 제안된 고정소수점 기반 연산의 성능을 분석한다. Ⅳ장에서는 제안된 고정소수점 기반 빔형성 계수 연산기의 구조와 설계 결과를 제시하며, 기존의 연구와의 비교를 진행한다. Ⅴ장에서는 본 논문을 요약하여 마무리한다.
Ⅱ. 배 경
레이다를 이용하여 표적의 정보를 획득하기 위해서는 표적이 존재하는 방향에 대하여 빔조향이 수행되어야 한다. 능동배열레이다인 경우, 안테나 개구면의 기계적 회전 없이, 안테나복사소자에서 방사하는 전자파의 위상값을 조절하여 빔을 조향할 수 있다. 능동배열레이다의 빔조향 방식은 아날로그 빔형성 방식, 부배열디지털빔형성 방식, 디지털 빔형성으로 구분할 수 있다. 디지털 빔형성 방식은 안테나복사소자 단위로 디지털 위상 계수를 소자의 신호에 곱하여 빔을 조향하며, 다른 두 방식에 비하여 빔의 감도와 정확도가 높다는 장점이 있다. 본 논문에 적용된 디지털 빔형성을 위한 시스템 구조는 그림 1과 같다.
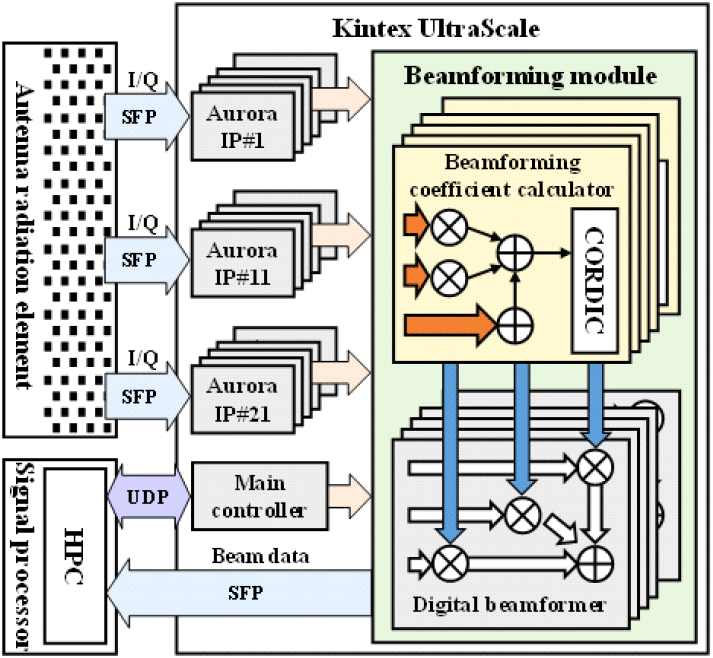
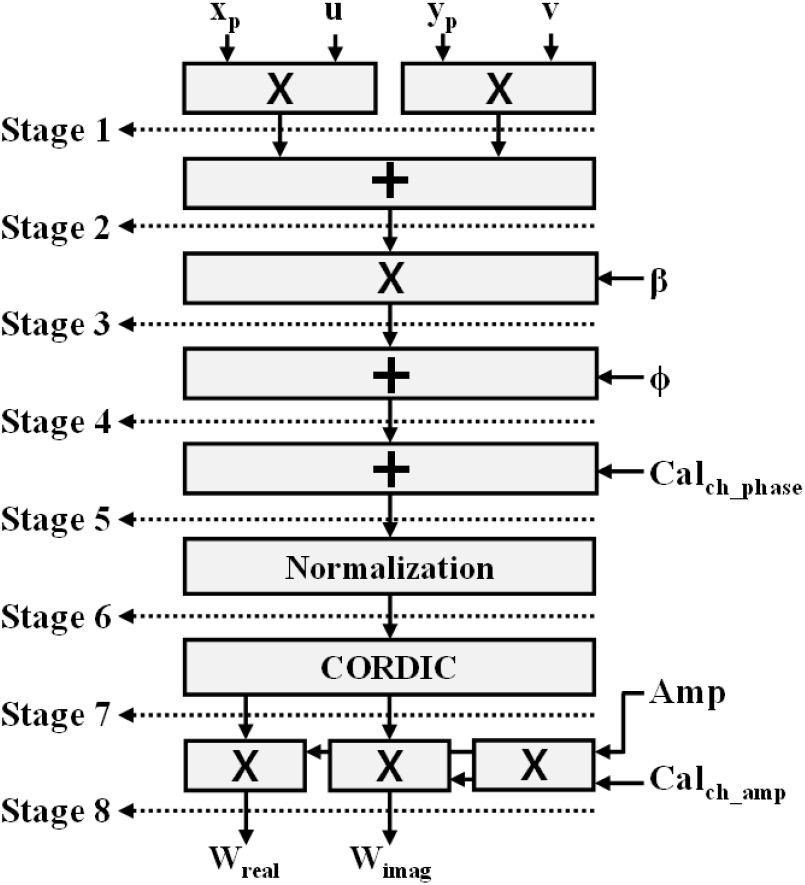
그림 1의 빔형성 계수 연산기(beamforming coefficient calculator)에서 수행하는 계수 연산은 식 (1)과 같다.
여기서 xp와 yp는 안테나 중앙으로부터의 안테나복사소자의 위치값이며, u와 v는 빔을 조향하고자 하는 방향의 방위각과 고각의 u=sin(θaz), v=cos(θel) 값이다. 2 π/λ는 레이다 주파수의 베타 값이며, ϕ는 안테나복사소자별 빔 스포일링 값이다. Calch phase와 Calch amp는 안테나복사소자의 배열면 정렬을 위한 위상값과 크기 값이며, Amp는 안테나복사소자별 Taylor-window 값이다.
디지털 빔형성 방식을 사용하기 위해서는 모든 안테나복사소자에 대하여 식 (1)의 계수를 연산하여야 한다. 정확한 빔을 얻기 위한 안테나복사소자의 증가는 처리하여야 하는 데이터양의 증가를 의미하며, 높은 데이터양의 입력에 대하여 실시간 빔형성을 위해서는 FPGA를 이용한 연산 가속의 필요성이 있다.
부동소수점 실수 표현 방식은 일반적으로 IEEE 754 표준을 따르는 표현법을 말한다. 부동소수점은 sign, mantissa, exponent의 3가지 필드로 표현되고, 필드 길이에 따라 double, single, half precision의 3가지 정밀도로 구분된다. 표 1은 각 정밀도에서 3가지 필드가 차지하는 길이를 나타낸 것이다.
| Precision | Total bit | Sign | Exponent | Mantissa |
|---|---|---|---|---|
| Half | 16 | 1 | 5 | 10 |
| Single | 32 | 1 | 8 | 23 |
| Double | 64 | 1 | 11 | 52 |
전체 길이가 16-비트인 half-precision 정밀도 부동소수점의 필드 구조는 그림 2와 같다.
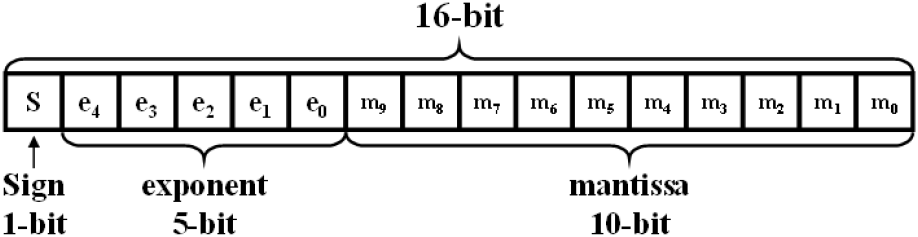
부동소수점은 식 (2)를 이용하여 sign, mantissa, exponent 값으로 실수를 표현한다. 식 (2)에서 x는 부동소수점 방식으로 표현하고자 하는 실수를 의미하며, bias는 사용하는 정밀도가 double일 때 1,023, single일 때 127, half일 때 15로 상수값을 사용한다.
부동소수점 방식은 표현할 수 있는 수의 범위가 넓고 정밀한 수 표현이 가능하다. 그러나 연산을 위해서는 작은 수의 exponent를 큰 수의 exponent로 맞추는 작업과 중복되는 bias의 제거 등의 추가 작업이 필요하며, 연산 후에는 연산 결과값을 부동소수점으로 표현하기 위하여 과학적 기수법에 맞추기 위한 정규화 과정이 필요하여 연산이 복잡하다는 단점이 있다.
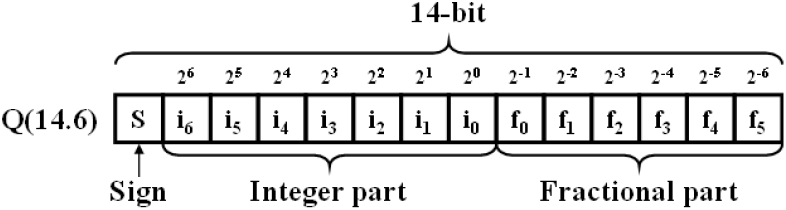
고정소수점 방식은 일반적인 2진수와 2의 보수 표현에서 사용자가 임의로 소수점의 위치를 설정하여 사용하는 방식을 말한다. 그림 3에서 고정소수점 포맷 Q(14.6)은 사용자가 전체 14-비트 숫자에서 소수를 나타내는 fractional part를 6-bit로 할당하였다는 것을 의미한다.
고정소수점 방식의 연산은 일반적인 2진수 연산기를 통하여 얻을 수 있어 부동소수점 방식에 비해 연산 회로의 복잡도를 줄일 수 있다. 그러나 부동소수점 방식의 연산과 비교하였을 때, 표현할 수 있는 수의 범위와 정밀도가 떨어져 전체 회로를 구성할 때, 성능의 열화가 없도록 적당한 길이의 비트를 찾는 과정이 필요하다.
Ⅲ. 고정소수점 빔형성 계수 연산
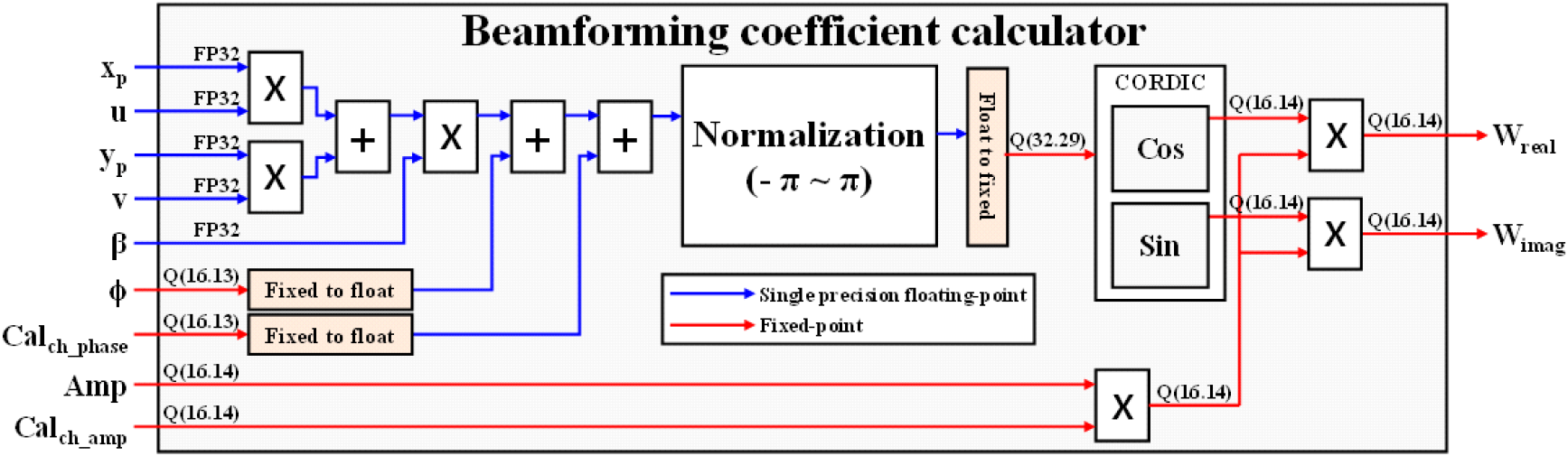
그림 4는 기존에 해상용 레이다 시스템에서 사용하고 있는 single-precision 부동소수점(이하 FP32로 표기) 기반 빔형성 계수 연산기 구조를 나타낸 것으로 그림의 normalization 블록은 Xilinx CORDIC[13] 입력을 위하여 입력값을 −π~π 사이로 정규화하는 블록이다. 기존의 빔형성 계수 연산기는 신호처리장치와 안테나복사소자에서 FP32 형태로 입력되는 u, v, β, xp, yp 값을 처리하기 위해 FP32 연산을 이용하여 식 (1)의 지수 함수 내부의 값을 계산한다. 위 FP32 연산을 맞추기 위하여 고정소수점으로 입력되는 ϕ과 Calch phase 값은 연산 전 FP32로 변경하는 과정을 거친다. 그러나, Xilinx CORDIC은 고정소수점 입력만을 지원함으로, 지수 함수의 연산을 위하여 FP32 연산 결과를 다시 고정소수점으로 변경하여야 한다. 위와 같이 기존의 연산기는 많은 FP32 연산과 잦은 수 체계의 변경으로 인하여 회로의 복잡도와 연산 지연시간이 높다는 단점이 있다.
본 논문은 기존의 빔형성 계수 연산기의 회로 복잡도와 연산 시간을 줄이기 위하여 FP32로 입력되는 u, v, β, xp, yp 값을 고정소수점으로 변경하여 연산을 수행하는 고정소수점 기반 빔형성 계수 연산기를 제안하였다.
성능의 열화가 없는 고정소수점 비트 길이를 찾기 위하여 입력 u, v, β, xp, yp 값을 18-비트, 16-비트 고정소수점으로 변환한 고정소수점 기반 연산과 기존의 FP32 기반 빔형성 계수 연산과의 SQNR(signal to quantization noise ratio) 비교와 형성된 빔의 조향 각도를 비교하였다.
비교를 위하여 FP32와 고정소수점 연산을 수행하는 MATLAB R2020b 환경을 구축하였고, 고정된 위치값을 가지는 xp, yp 값과 현재 시스템에서 정수 1의 값을 가지는 Calch amp를 제외한 나머지 변수인 u, v, β, ϕ, Calch phase, Amp 변수는 각 변수의 값의 범위 내에서 랜덤 변수를 생성하여 100,000회 시뮬레이션을 진행하였다.
표 2는 FP32로 입력되는 u, v, β, xp, yp를 18-비트 고정소수점으로 변환하였을 때 FP32 대비 평균 SQNR 값을 정리한 것이며, 표 3은 16-비트 고정소수점으로 변환하였을 때 FP32 대비 평균 SQNR 값을 정리한 것이다. yp인 경우 정수값으로 무한대의 SQNR을 가져 표에서 제외하였다.
| 18-bit | u | v | β | xp |
|---|---|---|---|---|
| Format | Q (18.16) | Q (18.16) | Q (18.17) | Q (18.6) |
| SQNR [dB] | 93.94 | 94.18 | 89.5 | 106.56 |
| 16-bit | u | v | β | xp |
|---|---|---|---|---|
| Format | Q (16.14) | Q (16.14) | Q (16.15) | Q (16.4) |
| SQNR [dB] | 81.99 | 82.21 | 77.38 | 94.52 |
표 4는 16-비트 고정소수점으로 입력되는 ϕ, Calch phase, Amp를 고정소수점으로 변경하기 전의 FP32 값과 비교하였을 때, 평균 SQNR 값을 정리한 것이며, 현재 Calch amp은 정수 1로 표현되어 무한대의 SQNR을 가지므로 표 5에서 생략하였다.
| 16-bit | ϕ | Calch phase | Amp |
|---|---|---|---|
| Format | Q(16.13) | Q(16.13) | Q(16.14) |
| SQNR[dB] | 94.15 | 94.23 | 90.25 |
그림 5는 고정소수점 기반 빔형성 계수 연산 중 변경되는 SQNR을 확인하기 위한 스테이지를 표시한 것이다. 각 스테이지는 연산 후 증가하는 비트 수를 억제하기 위하여 fractional part의 round 연산과 integer part의 MSB를 제거하는 clip 연산을 진행하였다.
표 5는 입력이 18-비트와 16-비트 고정소수점일 때, 그림 5의 각 스테이지 출력이 가지는 포맷과 평균 SQNR 값을 나타낸 것이다. 표에서 SQNR이 증가하는 경우는 출력 비트 수가 증가하거나, 높은 SQNR 값을 가지는 입력과의 연산 때문이다. 입력 고정소수점 값이 18-비트일 때와 16-비트일 때 모두 최종 출력의 SQNR이 50 dB 이상으로 높은 값을 가짐을 확인할 수 있다.
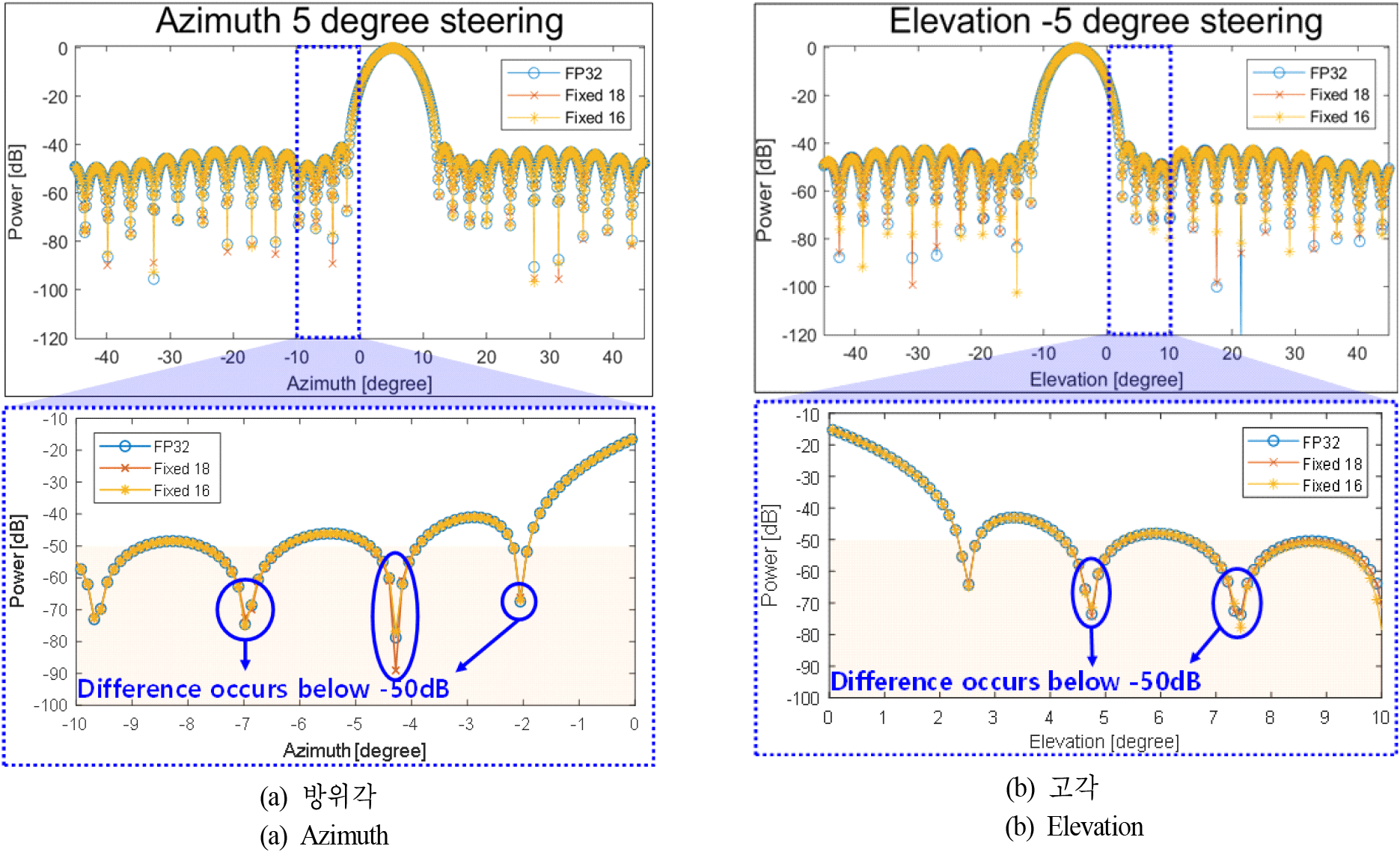
소수점일 때 고정소수점 기반 연산으로 구해진 빔형성 계수 값에 안테나복사소자의 값을 곱하여 생성된 빔 패턴을 비교하였다. 그림 6은 빔 조향 방향이 방위각 +5°와 고각 −5° 일 때, 만들어진 빔 패턴을 겹쳐 그린 것이다. 푸른색 선은 기존의 FP32 기반 방식으로 생성된 빔 패턴이며, 주황색과 노란색 선은 각각 입력이 18-비트와 16-비트 고정소수점일 때, 고정소수점 기반 연산으로 생성된 빔 패턴을 나타낸 것이다.
그림 6에서 기존의 FP32 기반 연산 방식과 고정소수점 기반 연산으로 생성된 빔 패턴은 빔의 파워가 강한 영역에서는 차이가 거의 없으나, 빔 패턴의 −50 dB 이하의 일부 null 영역에서는 차이가 발생함을 알 수 있다. 이는 고정소수점 빔형성 계수 연산 중 수행하는 round 연산으로 인하여 LSB 쪽의 소수점 자리의 정보가 소실되기 때문이다. 빔 패턴의 null 영역은 표적의 탐색, 추적에 영향을 주지 않음으로, 해당 차이는 무시할 수 있다.
빔 조향 각도의 정확도를 비교하기 위하여 빔을 여러 방향으로 조향하였을 때, 기존 방식과 고정소수점 기반연산으로 생성된 빔의 조향 각도를 비교하였다. 표 6 및 표 7은 빔을 10,000회 생성하였을 때, 기존 방식과 고정소수점 방식으로 생성되는 빔의 조향 각도 차이와 그 빈도값을 정리한 것이다.
| 18-bit | Difference of steering angle | ||||
|---|---|---|---|---|---|
| > | −0.05° | 0° | 0.05° | < | |
| Format | 0 | 157 | 9,690 | 153 | 0 |
| SQNR[dB] | 0 | 164 | 9,730 | 106 | 0 |
| 18-bit | Difference of steering angle | ||||
|---|---|---|---|---|---|
| > | −0.05° | 0° | 0.05° | < | |
| Format | 0 | 581 | 8,794 | 625 | 0 |
| SQNR[dB] | 0 | 494 | 8,994 | 512 | 0 |
표 6 및 표 7을 통하여 기존 방식과 고정소수점 기반 연산으로 형성한 빔의 조향 각도의 차이는 −0.05°~0.05° 사이로 발생함을 알 수 있다. 이는 본 논문이 적용되는 요구사항을 만족하는 것으로, 기존의 빔형성 계수 연산에서 고정소수점 기반의 빔형성 계수 연산으로 변경하더라도 성능의 열화가 발생하지 않음을 알 수 있다. 또한 18-비트 입력과 16-비트 입력의 고정소수점 기반의 빔형성 계수 연산 또한 성능의 큰 차이가 없음을 검증하였다.
Ⅳ. 제안된 고정소수점 기반 빔형성 계수 연산기
본 논문은 실험적으로 성능과 연산 복잡도 사이의 교환관계를 맞춘 16-비트 입력의 고정소수점 기반 빔형성 계수 연산기를 제안하고, 기존의 빔형성 계수 연산기와의 리소스 사용량 비교를 진행한다. 제안된 연산기는 Verilog-HDL(hardware description language)을 통하여 RTL(register-transfrer level) 설계 후, Xilinx의 Kintex UltraScale FPGA를 이용하여 구현과 검증을 진행하였다.
그림 7은 MATLAB 시뮬레이터 결과와 설계된 연산기의 testbench 시뮬레이션 결과를 비교한 것이며, 그림 8은 제안된 고정소수점 기반 빔형성계수 연산기의 하드웨어 구조도를 나타낸 것이다. 그림 8을 통하여 그림 9의 제안된 고정소수점 기반 빔형성계수 연산기의 모든 결과가 MATLAB 시뮬레이터와 같은 값을 가짐을 확인하였다.
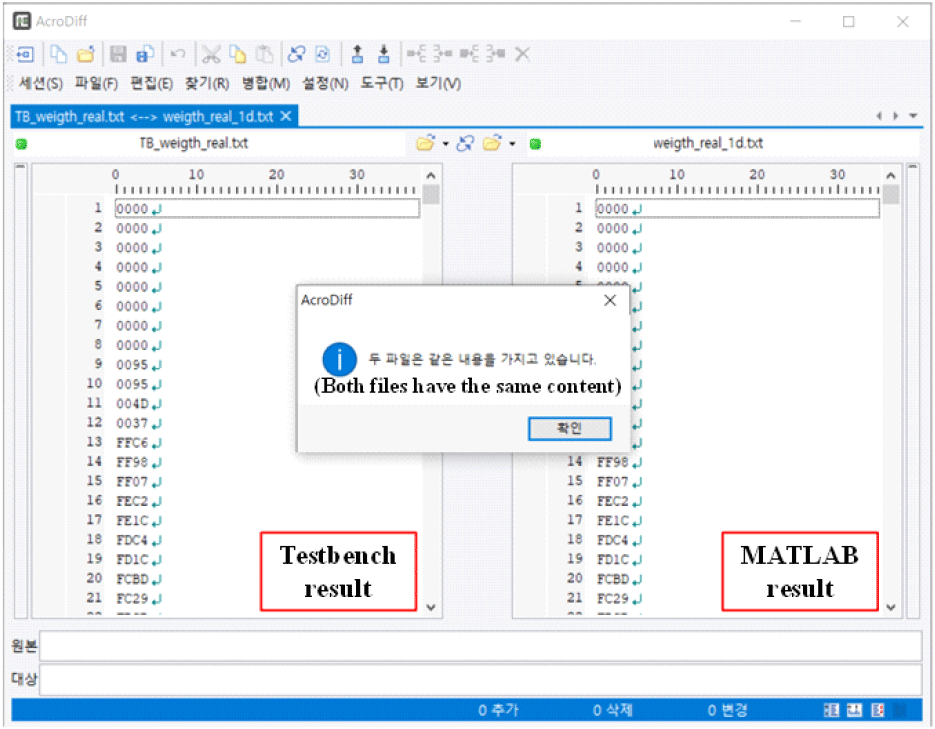
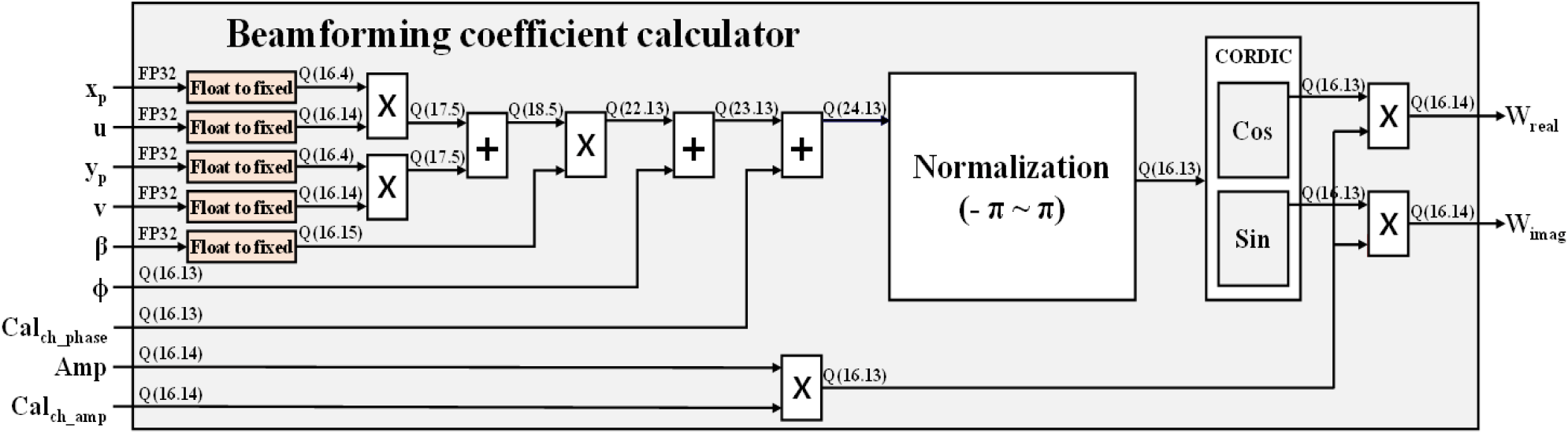
표 8은 제안된 고정소수점 기반 빔형성 계수 연산기의 리소스 사용량을 정리한 것이다. 제안된 연산기는 동작주파수 300 MHz 일 때, 기존의 FP32 기반 연산 방식보다 CLB register를 54.94 %, CLB LUT를 44.33 %, DSP를 60 % 적게 사용하며, 레이턴시가 −58.16 % 감소하였다.
| Resource | Conventional | Proposed | Resource comparison |
|---|---|---|---|
| CLB register | 58,860 | 26,520 | −54.95 % |
| CLB LUT | 39,410 | 21,940 | −44.33 % |
| DSP | 150 | 60 | −60 % |
| Latency[clock] | 141 | 59 | −58.16 % |
| Operating clock speed : 300 MHz | |||
표 9는 이전 연구의 연산기[5]와 제안된 빔형성 계수 연산기를 비교한 표이다. 이전 연구는 빔형성을 위하여 16-비트 고정소수점 연산과 FP32 연산을 혼용하는 구조이나, 제안된 연구는 16-비트 고정소수점 연산을 이용하여 빔을 형성한다. 제안된 빔형성 계수 연산기는 빔 패턴을 형성하였을 때, −50 dB 이하의 null 영역에서 차이가 발생하였으며, 이전의 연구는 −40 dB 이하에서 차이가 발생함을 확인하였다. 이를 통하여 제안된 빔형성 계수 연산기는 이전 연구의 연산기와 비교하였을 때, 더 작은 빔 패턴 파워에서도 연산의 성능 열화가 적음을 검증하였다.
| Work | [5] | This Work |
|---|---|---|
| Targer FPGA | Arria 10 | Kintex UltraScale |
| Number format | Fixed + FP32 | Fixed |
| Reliable beam pattern power | > −40 dB | > −50 dB |
| System clock speed | 192 MHz | 200 MHz |
Ⅴ. 결 론
본 논문에서는 디지털 능동배열레이다의 빔형성을 위한 고정소수점 기반 빔형성 계수 연산기가 제안되었다. 제안된 연산기는 기존의 부동소수점과 고정소수점의 연산이 혼합된 형태에서 부동소수점 연산부를 입력이 16-비트인 고정소수점 기반 연산으로 교체하였다. 제안된 고정소수점 기반 빔형성 계수 연산의 출력값은 평균 51.35 dB의 SQNR을 가지고, 형성된 빔의 조향 각도는 기존 방식과 비교하였을 때 −0.05°~0.05° 사이의 방위각과 고각의 위치 차이를 가진다. 설계된 연산기는 기존 연산기 대비 약 2배가량의 리소스를 절약할 수 있어, 연산기가 적용되는 시스템의 전체 리소스 사용량을 감소시킬 수 있었다. 또한 이전 연구의 연산기와 비교하여 더 작은 빔 패턴 파워에서도 연산의 성능 열화가 적음을 확인하였다.