Ⅰ. 서 론
무선전력전송(wireless power transfer, WPT) 시스템은 그 편리성으로 인해 많은 응용 분야에 적용되기 위해 연구되고 있다. 그 응용 분야로는 스마트폰이나 가전부터 전기자동차, AGV(automated guided vehicle), 드론 등까지 수많은 분야에서 기존의 유선 충전 방식을 대체하기 위한 연구가 많이 진행되었다[1]~[3]. 또한, 일부 애플리케이션의 경우에는 실제 상용화된 제품까지 등장하였다.
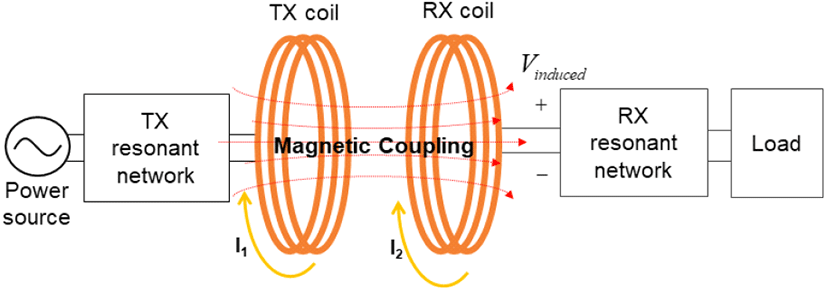
WPT 시스템의 송신(transmitter, TX)측과 수신(receiver, RX)측 사이에 도선 등의 물리적 결합 없이 자기적 결합으로 전력이 전달되는 원리이며[4], 이는 그림 1에서 나타내었다. 그림 1과 같이 TX 코일에 시변 정현파 전류(I1)가 흐름으로써 자기장이 발생하며, 이 자기장이 RX 측에 쇄교하여 패러데이의 법칙으로 인해 유도 전압이 발생되는 원리이다. 하지만 이는 물리적인 현상에 대한 설명이며, 실제 분석을 위해서는 모델링이 필요하다.
WPT 시스템 코일의 모델링 방법에는 전기회로 분석을 통한 방법들[5],[6], S 파라미터(scatterring parameters)를 이용하는 방법[7], coupled mode theory를 이용하는 방법[8] 등 다양한 방법이 존재한다. 각각의 모델링 방법들은 모두 장점과 단점이 존재하지만, WPT 시스템의 다른 핵심 구성요소인 전력전자 회로들과의 상호 분석을 위해서는 전기 회로적 분석 방법이 가장 유용하다[5],[6]. WPT 시스템의 코일을 전기회로 모델링을 통해 분석하는 방법에는 크게 자화 인덕턴스(magnetizing inductance) 모델링 방법[9]과 상호 인덕턴스(mutual inductance) 모델링 방법[5]으로 크게 나뉜다. 본 논문에서는 각 방법에 대한 자세한 분석을 수행하여 비교 및 서술한다.
또한, WPT 코일 시스템은 에너지를 자기장의 형태로 저장하는 동시에, TX 측에서 RX 측으로 에너지를 전달하기도 한다. 본 논문에서는, WPT 시스템에서의 정확한 전력 전달과 저장에너지에 대한 수식적, 물리적 분석을 통해서 어떤 조건에서 전력이 효과적으로 전달될 수 있는지를 분석하여 WPT 시스템과 가장 많이 비교되는 변압기(transformer) 와의 차이점에 대해 자세히 서술한다.
한편, 분석된 WPT 시스템의 코일 간 에너지 전달이 최대가 되는 조건을 달성하기 위한 공진 토폴로지(resonant topology)에 대한 자세한 분석을 수행한다. 공진 토폴로지는 매우 다양하며, 최대 전력전달뿐 아니라, WPT 시스템의 입, 출력 특성, soft switching[10], 전압, 전류 레귤레이션 등 다양한 특성을 나타낸다. 이와 관해서, 대표적인 몇 가지 토폴로지에 대해 분석하여 어떤 조건에서 어떤 토폴로지가 선정되어야 하는지를 분석하고, 실험을 통해 분석 내용을 증명한다.
Ⅱ. WPT 코일의 자화 인덕턴스 모델링과 상호 인덕턴스 모델링 분석
그림 2는 WPT 코일들의 두 가지 전기회로 모델링 방법인 상호 인덕턴스, 자화 인덕턴스 모델을 나타낸다. 본 논문에서는 두 모델에 대한 자세한 차이와 상호 변환 방법을 분석한다.
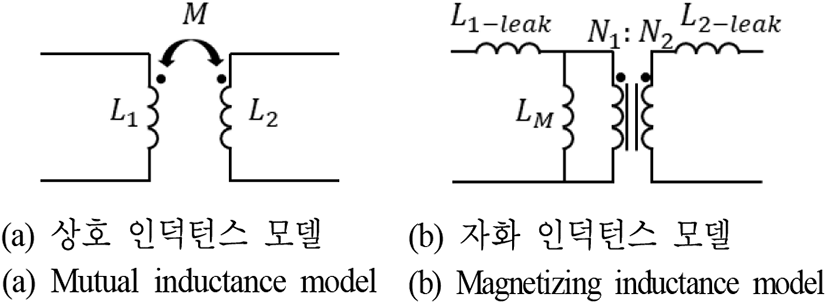
그림 2의 WPT 코일의 모델링 방법에 대한 비교 분석을 위해선, 우선 코일에서 발생하고 쇄교(interlinkage) 하는 자속(magnetic flux)에 대한 정확한 정의와 자세한 이해가 필요하다. 그림 3은 TX 코일에서 발생하는 자속을 나타낸다. 그림 3에서, Φ11은 TX 코일에서 발생하는 모든 자속, Φ12는 TX 코일에서 발생한 자속 중 RX 코일에 전달된 자속, Φ1-leak는 TX 코일에서 발생한 자속 중 RX 코일에 전달되지 못한 자속을 나타낸다. 특히, TX 코일에서 발생한 자속 중 RX 코일에 전달되지 못한 자속을 누설자속(leakage flux)이라고도 표현한다. TX 코일에서 발생하는 모든 자속은 반드시 다시 TX 코일로 다시 돌아오게 된다. 이는 자기장을 닫힌 체적에 대해서 면적분한 식 (1)에서 알 수 있다[11].
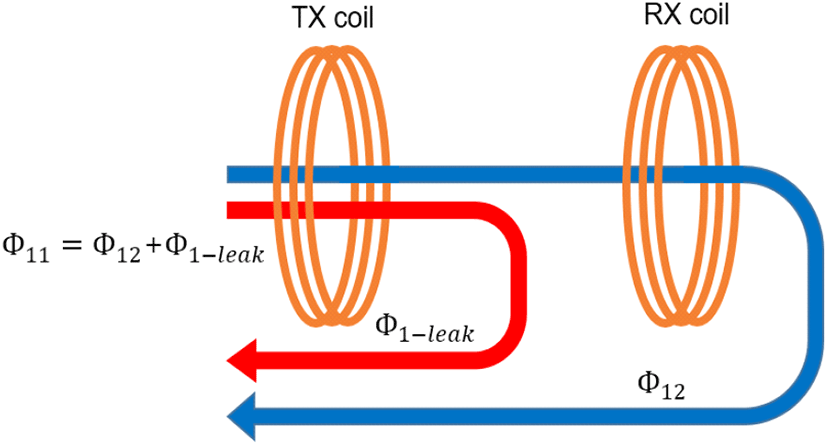
한편, TX 코일의 전체 생성 자속(Φ11), 누설 자속(Φ1-leak), RX 코일에 전달 자속 (Φ12)의 식은 각각 식 (2)~식 (4)와 같다.
식 (2)~식 (4)에서 P는 자속의 퍼미언스(perneance)로, 자기저항(reluctance)의 역수이며 단위는 H(Henry)이다. 퍼미언스는 코일 주변의 구조와 투자율에 관한 함수이다. 또한, N1과 I1은 TX 코일의 턴 수와 전류이다. TX 코일에서 발생한 총 자속(Φ11)은, TX 코일에서 RX 코일에 전달되는 자속(Φ12)과 전달되지 못한 자속(Φ1-leak)의 합이라는 것이 식 (5)를 통해 알 수 있다. 한편, 각 코일에 쇄교되는 자속은 식 (6)~식 (8)과 같다.
식 (6)은 TX 코일에서 발생한 전체 자속이 TX 코일에 자체 쇄교하는 자속이며, 식 (7)은 TX 코일에서 발생한 자속 중에서 누설 자속이 TX 코일에 쇄교하는 자속이다. 또한, 식 (8)은 TX 코일에 발생한 자속 중 RX 코일에 전달된 자속이 RX 코일에 쇄교한 자속을 의미한다. 즉, 식 (2)~식 (8)에서 알 수 있듯이, 전달 자속 혹은 발생 자속과 쇄교 자속은 반드시 구분되어야 한다.
한편, TX 코일에서 RX 코일로 전달된 자속이 TX 코일과 자체 쇄교하는 자속은 식 (9)와 같다.
식 (8)과 식 (9)의 차이점은, TX 코일에서 발생한 자속이 RX 코일에 전달된 자속 (Φ12)이 어느 코일에 쇄교되는가에 따라 쇄교 자속을 구분한다는 점이다. 즉, TX 코일에서 RX 코일로 전달된 자속을 RX 코일에 쇄교로 나타내면 식 (8)과 같고, 이 자속이 TX 코일과 쇄교한 자속은 식 (9)와 같다.
정의된 쇄교 자속들을 통해 각 WPT 코일의 인덕턴스를 나타낸다. 인덕턴스의 정의는 ‘A 회로의 단위 전류당 B 회로에 쇄교 자속 수’이다. 여기서 A는 B와 동일한 회로일 수도 있다. 이 정의에 맞게 쇄교 자속 식 (6)~식 (9)를 인덕턴스로 나타내면, 식 (10)~식 (13)과 같다.
식 (10)은 ‘TX 코일의 단위 전류당 발생한 총 자속이 TX 코일 스스로 쇄교되는 자속’을 나타내므로, 그림 2(a)의 L1, 즉 TX 코일의 자기 인덕턴스(self inductance)를 의미한다. 식 (11)은 그림 2(b)의 TX 코일의 누설 인덕턴스를 나타내며, 식 (12)는 ‘TX 코일의 단위 전류당 발생한 총 자속이 RX 코일에 쇄교되는 자속’이므로 그림 2(a)의 상호 인덕턴스(M)를 나타낸다. 마지막으로, 식 (13)은 ‘TX 코일의 단위 전류당 TX 코일에서 발생한 자속 중 RX 코일에 전달되는 자속의 TX 코일로의 쇄교 자속’을 나타내며, 이 정의가 바로 그림 2(b)의 자화 인덕턴스이다.
자화 인덕턴스 모델과 상호 인덕턴스 모델의 변환을 위해, 결합계수(coupling coefficient, k)의 물리적 정의를 내린다.
결합계수는 ‘TX 코일에서 생성된 총 자속에 대한 TX 코일에서 RX 코일로 전달된 자속의 비’이다. 따라서, 결합계수는 코일들의 턴 수와는 관련이 없다. 단지, ‘TX 코일에서 발생된 총 자속의 어떤 비율이 RX 코일로 전달되는가’이다. 반면, 상호 인덕턴스의 정의인 식 (12)에서는 TX 코일의 턴수와 RX 코일의 턴수가 증가하면 상호 인덕턴스가 증가함을 알 수 있다. 한편, 코일들의 자기 인덕턴스, 상호 인덕턴스, 그리고 결합계수와의 관계는 식 (15)와 같다.
앞서 분석된 내용을 토대로, 상호 인덕턴스의 모델인 자기 인덕턴스와 상호 인덕턴스들로 자화 인덕턴스와 누설 인덕턴스가 어떻게 상호 변환되는지를 분석한다.
먼저, 자화 인덕턴스를 나타내는 두 가지 방법은 식 (16) 및 식 (17)과 같다.
TX 누설 인덕턴스는 식 (18)과 같이 나타낼 수 있다.
한편, 자화 인덕턴스는 식 (16) 및 식 (17)과 같으므로, TX 측의 누설 인덕턴스는 식 (19)와 같다.
식 (19)와 같이, 상호 인덕턴스 모델들을 이용하여 TX 측의 누설자속을 나타낼 수 있다.
마찬가지로, RX 측의 누설자속은 식 (20)과 같다.
식 (16)~식 (20)을 통해 알 수 있듯이, WPT 코일에 두 가지 상호 인덕턴스 모델과 자화 인덕턴스 모델은 서로 변환이 가능하다. 코일이라는 하나의 현상을 모델링한 다른 방법일 뿐이므로, 결국 상호 변환이 가능하다.
Ⅲ. WPT 코일 시스템에서의 전력전달과 저장 에너지
본 절에서는, 앞서 모델링된 WPT 코일의 상호 인덕턴스 모델을 바탕으로, TX 코일에서 RX 코일로 전달되는 에너지와 코일에 저장되어 있는 에너지를 분석한다. 이는 이미 기존 연구들에서 분석이 되었지만[12], 본 논문을 통해서 보다 자세히 다시 한번 정리한다. 또한, 이를 바탕으로 WPT 코일과 변압기와의 차이를 설명하며, WPT 코일에서의 최대 전력 전달 조건을 분석한다.
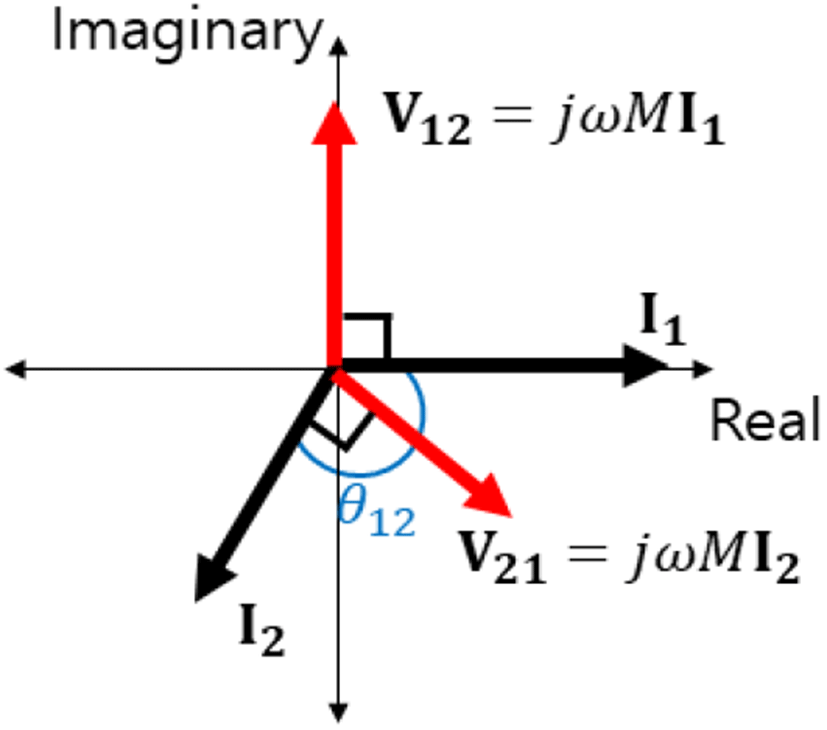
그림 4는 앞 절에서 설명한 WPT 코일의 모델링 방법 중, 상호 인덕턴스 모델링 방법에서 코일의 입, 출력 전압, 전류를 고려한 등가회로를 나타낸다. I1과 I2는 각각 TX, RX 코일에 흐르는 전류이며, V21과 V12는 각각 RX 코일 전류(I2)에 의해 TX 측에 유도된 전압과 TX 코일 전류(I1)에 의해 RX 측에 유도된 전압을 나타낸다. 각 코일의 전류와 유도전압에 대한 상대적인 페이저도를 그림 5에서 나타내었다.
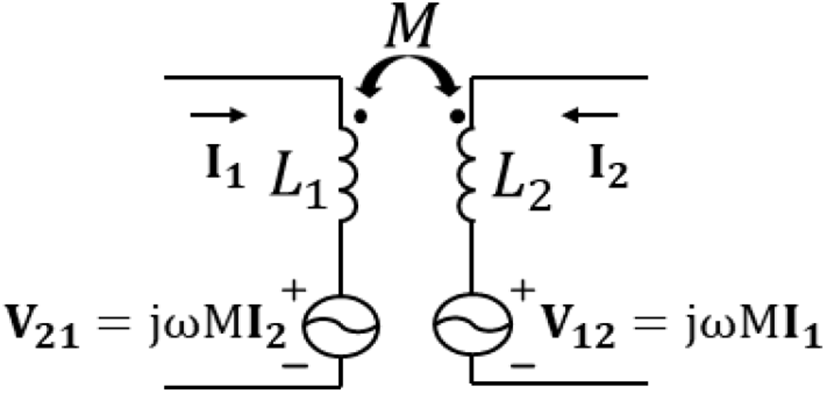
TX 측에서 RX 측으로 전달되는 피상전력(apparent power) S12는 TX 코일 전류에 의해 RX 측에 유도되는 전압에 의해 전달된다. 이는 식 (21)과 같다.
식 (21)에서, θ1과 θ2는 각각 TX 코일과 RX 코일의 위상이며, θ12는 TX 코일과 RX 코일 전류의 위상차다. θ12는 그림 5에서 보여준다. 한편, RX 코일에서 TX 코일로 전달되는 피상전력 S21은 식 (22)와 같다.
따라서, 식 (21)과 식 (22)에서 알 수 있듯이, TX에서 RX로 전달된 유효 전력(평균 전력)은 식 (23)과 같다.
코일 간에 전달되는 유효 전력에 대해 식 (21)~식 (23)에서 알 수 있는 것은, θ12가 0°에서 180° 사이라면(TX 코일 전류가 RX 코일 전류보다 0~180° 앞서면), P12는 양수가 되어 유효 전력은 TX 코일에서 RX 코일로 전달된다. 반대로, TX 코일의 전류가 RX 전류보다 0~180° 뒤지면, 반대로 RX 코일에서 TX 코일로 전력이 전달된다. 즉, 그림 5에서 TX 전류(I1)가 x축에 존재하여 기준이 되고, RX 전류(I2)가 1, 2분면에 존재하면 RX 측에서 TX 측으로 전력이 전달되고, 3, 4분면에 존재하면 TX 측에서 RX 측으로 전력이 전달된다. 하지만, RX 전류 I2는 TX 코일에 의한 RX 측의 유도전압 V12에 의해 발생하며, 그림 4와 그림 5에 의하면, I2는 반드시 3, 4분면 위에 존재하게 된다. 따라서, TX 측에서 전원이 공급되어 RX 측에 전압이 유도되면 반드시 TX 측에서 RX 측으로 전력이 전달된다.
한편, 코일들 각각 저장전력은 식 (24) 및 식 (25)와 같다.
또한, WPT 코일들에 입력되는 전력은 각 코일에서 출력 피상 전력을 나타내는 식 (21)과 식 (22)의 합에서 부호만 반대이다. 즉, 식 (26)과 같다.
따라서, WPT 코일에 저장되는 총 전력은 식 (27)과 같다.
식 (27)에서 알 수 있는 것은, WPT 코일에서는 각각의 자기 인덕턴스에 전력이 저장되며, 추가적으로 상호 자속에 의한 상호 인덕턴스에 의해서도 전력이 저장된다는 점이다. 식 (27)의 모든 성분은 피상전력에서 허수부분, 즉 무효전력이므로 에너지의 손실이 아니라 단지 자속으로 저장되는 에너지를 나타낸다.
WPT 코일 시스템은 변압기와 매우 유사하다. 하지만, 두 시스템의 결정적인 차이점이 존재하며, 이에 따른 영향이 기존 연구들에서도 많이 분석되었다[12]. 본 논문에서는 WPT 코일과 변압기와의 차이에 대해 분석하며, 각각의 경우에 따른 최대전력전달 위상 조건을 도출한다. 본 절에서 유도된 WPT 코일의 최대전력전달 위상조건은, 4절에서 소개할 WPT 시스템의 토폴로지의 필요조건이 된다.
변압기는 그림 2(b)와 같이 자화 인덕턴스로 주로 모델링되며, 전력전달 원리는 WPT 코일과 동일하다. 하지만 변압기와 WPT 코일과의 결정적인 차이점은 결합계수의 차이이다. 결합계수의 정의 식 (14)에서, WPT 코일은 그 결합계수가 대부분 약 0.1에 가까운 값을 갖는다[13]. 즉, TX 코일에서 발생한 자속 중 약 10 % 만이 RX 측으로 전달되는 것이다. 즉, TX 코일에서 발생한 자속의 약 90 %는 누설자속이 되어, 식 (1)에 의해 TX 코일로 다시 돌아간다. 따라서, WPT 시스템은 그림 2(b)에서 L1-leak와 L2-leak가 LM보다 매우 크다. 반면, 변압기의 경우 결합계수가 대부분 1에 가까운 값을 갖는다. 즉, 변압기는 TX 코일에서 발생한 자속이 대부분 RX 코일로 전달된다. 따라서, 변압기는 L1-leak와 L2-leak가 LM에 비해 매우 작다.
식 (23)에 의하면 코일 시스템에서 최대 유효전력전송을 위한 위상은, θ12가 90도 차이일 때 성립된다. 이는 변압기나 WPT 코일에서 모두 마찬가지이다. 하지만, 일반적으로 변압기와 WPT 코일 시스템에서는 자속을 원하는 방향으로 유도하기 위해 자성체를 사용한다. 자성체에서는 무효 전력에 의해서 core loss가 발생하는데, 따라서, 식 (27)의 코일의 무효전력도 고려해야 한다.
코일 시스템의 무효전력을 고려한 유효전력전달을 분석하기 위해서, 코일에 저장되어 있는 무효전력에 대한 유효전력의 비 f(θ12)를 식 (28)과 같이 정의할 수 있다[12].
식 (28)이 최대가 되는 θ12를 찾기 위해, 식 (29)와 같이 식 (28)의 위상차에 대한 도함수를 구하고, 도함수의 해를 구하면, 식(30) 및 식 (31)과 같다[12].
식 (29) 및 식 (30)을 WPT 코일과 변압기에 대해 각각 분석한다. 먼저, WPT 코일의 경우에는, 결합계수 k가 0에 가깝다. 따라서, 식 (30) 및 식(31)은 각각 0과 1의 값을 갖는다. 식 (30) 및 식(31)이 0과 1이 되는 위상차 θ12는 90 도일 때이다. 즉, WPT 시스템에서는 식 (23)의 TX 코일에서 RX 코일로의 전달 유효전력이 최대가 될 때, 무효전력에 대한 유효전력의 비가 가장 크다. 다시 말하면, WPT 시스템에서는 상호 자속이 매우 작으므로, 상호 자속에 의해 코일에 저장되어 있는 에너지가 매우 작다. 무효전력으로 인한 core loss를 의미하는 식 (27)이 최소가 되지 않아도 식 (23)의 유효전력이 최대가 될 때 전력이 가장 효과적으로 전달된다. 따라서, 일반적으로 WPT 시스템에서는 θ12가 90도가 설계한다.
반면, 변압기의 경우에는 자기 인덕턴스의 비와 전류의 비가 식 (32)와 같이 표현된다.
앞서 설명하였듯이, 변압기의 결합계수 k는 1에 근사되므로, 식 (32)를 이용하면, 식 (30)과 식 (31)은 각각 −1과 0이 된다. 따라서, 변압기의 경우에는 θ12가 180도일 때, 무효전력에 대한 유효전력의 비가 최대가 된다. 주목할 점은, 식 (23)에 의하면, θ12가 180도에 가까울 때는 TX 측에서 RX 측으로 전달되는 유효전력이 최대가 아니라는 것이다. 변압기는 결합계수가 거의 1에 가깝기 때문에 상호 인덕턴스가 매우 크므로, 식 (23)에서 sin(θ12)가 최대가 아니어도 충분한 전력이 TX 측에서 RX 측으로 전달된다. 따라서, 변압기에서는 유효전력 전달보다 무효전력의 최소화가 더 중요하다.
다시 한번 정리해 보면, WPT 코일에서는 θ12가 90도일 때, 무효전력에 대한 전달 유효전력의 비가 최대가 되어, 전력이 효과적으로 전달된다. 이는 그림 6(a)에서 보여준다. 그림 4의 등가회로와, 그림 6(a)의 전류 위상을 살펴보면, TX 전류 (I1)에 의해 유도되는 RX 측의 전압(V12)가 항상 I1보다 90도 앞선다. 이 전압에 의해 RX 코일 전류(I2)가 발생하는데, 만약 그림 4의 등가회로에서, RX 코일 뒷단의 저항성 부하에 연결되면 RX 코일 전류 I2는 V12보다 90도에 가깝게 앞설 것이다. 따라서, θ12는 180도에 가까울 것으로, 이는 WPT 코일에서의 효과적인 전력전달의 위상인 90도와 다르다. 따라서, WPT 코일에서 θ12가 90도가 되어 효과적인 전력전달을 위해서는, RX 코일의 전류 위상을 90도 빠르게 해줄 공진 네트워크가 반드시 필요하다.
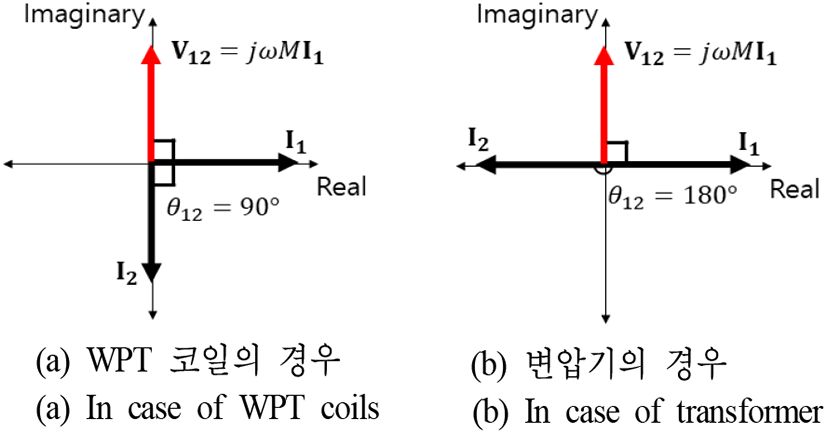
반면, 변압기의 경우에는 θ12가 180도일 때, 무효전력에 대한 전달 유효전력의 비가 최대가 되어, 전력이 효과적으로 전달된다. 이는 그림 6(b)와 같은데, 변압기의 경우에는 RX 측 이후에 보상회로가 없을 경우가 오히려 θ12 가 180도가 되어 효율적으로 전력전달이 가능하다. 따라서, 변압기에서는 공진 네트워크가 별도로 필요하지 않다.
Ⅳ. WPT 시스템 공진 토폴로지의 특성과 선택 방법
Ⅲ장에서 살펴본대로, WPT 시스템에서는 θ12가 90도 일 때 가장 효율적으로 전력이 전달된다. 따라서, 그림 6과 같이, RX 코일의 전류(I2)를 RX 코일의 유도 전압(V12)과 180도 차이로 만들어 주기 위한 회로가 필요한데, 이 역할을 하는 것이 RX 측의 공진 회로이다.
그림 7은 입력 인버터(inverter), TX 및 RX 공진 회로들 (TX Comp, RX Comp), 그리고 부하(Load)를 포함한 전체 WPT 시스템을 나타낸다. 또한, 전체 시스템을 나타내기 위하여, TX 및 RX 코일의 직렬 등가 저항(equivalent series resistance, ESR)을 R1과 R2로 나타내었다. 앞서 설명하였듯이, I2와 V12가 180도 위상차를 가지기 위해서는, RX 코일의 유도 전압에서 바라본 RX 측의 입력 임피던스 (Zin−RX)가 반드시 저항 성분만 가져야 한다[14]. 이를 만족한다면 그림 6(a)와 같이 I2와 V12의 위상차가 180도가 되고, θ12가 90도에 가까워져 전력이 최대로 전달될 수 있다. RX 측의 입력 임피던스를 수식으로 나타내면 식 (33)과 같다.
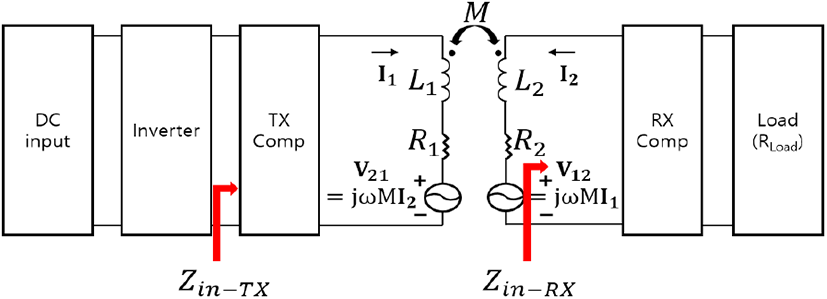
식 (33)에서 RX 측의 보상회로 임피던스(ZRX−Comp)는 RX 코일의 자기 리액턴스(jωL2)를 보상(compensation) 해주어야 한다.
보상회로의 필요성은 코일 간의(coil to coil) 전력전달 효율에서도 나타나는데, 코일 간의 전력전달 효율은 ηcoil−coil로 나타낼 수 있으며, 식 (34)와 같다[14].
식 (34)에서, Pcoil−loss는 TX, RX 코일의 ESR에 의한 손실이다. 식 (34)에서도 알 수 있듯이, 코일 간의 전력 효율에서, TX와 RX의 전류(I1, I2)는 입력 전압, 출력 부하에 따라 결정되므로 코일의 손실은 정해지고, 결국 전달된 전력(Ptransfer)이 최대가 될 때 효율이 가장 높다. Ptransfer가 가장 높을 때가 바로, θ12가 90도일 때이며, 이는 식 (33)에서, 전력전달 관점에서의 공진 토폴로지 필요성과 같이 RX 공진 토폴로지가 RX 코일의 자기 리액턴스 (jωL2)를 보상해줘야 한다는 의미가 된다.
한편, TX 코일의 공진회로(TX Comp)는 WPT 코일 앞단에 존재하기 때문에, 코일 간의 전력전달이나 효율과는 관련이 없다. 하지만, 그림 7에서 인버터에서 바라본 WPT 시스템 전체 입력 임피던스는 식 (35)와 같다.
식 (35)에서, RX 측의 임피던스는 RX 공진회로를 통해 리액턴스 성분이 모두 상쇄되고 순수 저항성분만이 존재한다고 가정하였다. 따라서, RX 측의 임피던스가 TX 측으로 반사된 리액턴스 (Z2−reflect)는 식 (35)과 같이 ω2M2/ ZRX(ω2M2/RRX)로 나타낼 수 있다. RX 측과 마찬가지로, 인버터에서 바라본 WPT 시스템의 전체 임피던스에서는 반드시 리액턴스 성분이 제거되어야 한다. 그 이유는, WPT 시스템의 입력 리액턴스가 존재하면, 인버터 출력에 무효전력이 증가하여, 인버터의 VA(voltage-ampere) rating이 증가하게 되고, 이로 인해 결국 WPT 시스템의 전체 효율을 감소시키기 때문이다.
마지막으로, WPT 시스템의 공진 토폴로지는 부하에 정전압(constant voltage, CV), 또는 정전류(constant current, CC)를 제공해야 한다[15]. 이를 위한 다양한 토폴로지들이 존재하며, 이는 다음 절에서 자세히 소개한다. 각 토폴로지들은 CV와 CC 출력 특성 중 적어도 하나의 특성을 갖는다.
앞서 분석한 대로 WPT 시스템의 공진 토폴로지의 필요조건을 정리하면 다음과 같다.
1) TX와 RX 측의 각각의 입력에서 바라본 리액턴스 값이 0이 되어야 한다.
2) 정전압, 또는 정전류 출력을 가져야 한다.
이외에도, 부하 및 상호 인덕턴스 변화에도 인버터의 소프트 스위칭[10], 혹은 영전압 스위칭(zero voltage switching)이 가능해야 하거나[15], 주파수 스플릿 현상(frequency split phenomenon)에 강인해야 한다는 등[16],[17]의 특성 등이 추가로 필요하지만, 이는 토폴로지마다 그 특성이 상이하다.
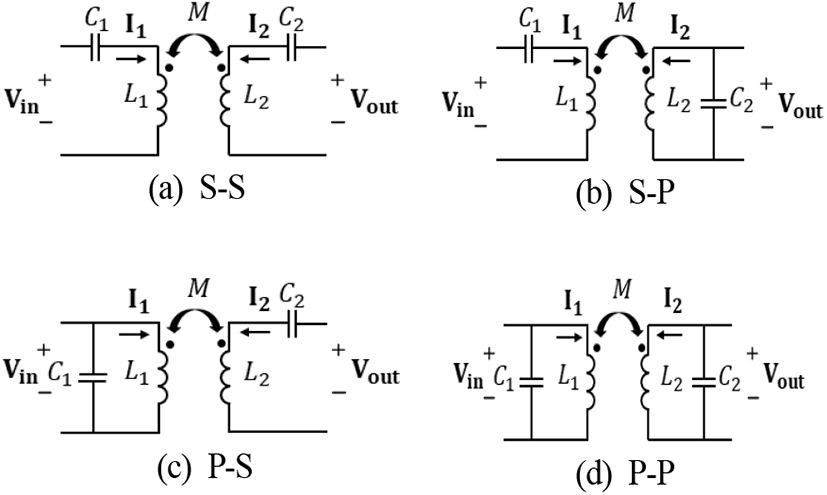
WPT 시스템의 가장 기본적인 공진 토폴로지 4종류를 그림 8에서 보여준다. 그림 8에서, S는 직렬(series)을 뜻하며, P는 병렬(parallel)을 뜻한다. 각 토폴로지는 앞서 설명한 대로, θ12가 90도에 가깝게 하거나, 부하에 관계없이 정전압, 또는 정전류 출력을 부하에 전달할 수 있다. 표 1은 그림 8의 기본적인 공진 토폴로지 각각의 공진 커패시턴스 값과 해당 토폴로지의 출력 특성을 나타낸다[16]. 표 1에서, RL은 출력의 등가 저항, ωo는 인버터의 동작주파수이며, 이는 TX 측과 RX 측의 공진주파수와 같아야 한다. 또한, 일정한 구형파를 가지는 인버터를 입력으로 사용하였다고 가정한다. 표 1에서 알 수 있듯이, P-S와 P-P 토폴로지는 TX 측의 공진 커패시턴스값(C1)이 부하 (RL)에 의존하는 것을 알 수 있다. 실제 WPT 시스템에서, TX측에서 부하의 특성을 알기란 현실적으로 매우 어려우므로, TX 측에 병렬 공진 토폴로지를 사용하는 경우는 매우 드물다. 따라서 본 논문에서는 먼저 S-S와 S-P 토폴로지의 특성을 분석한다.
| Type | TX capacitance (C1) | RX capacitance (C2) | Output characteristics |
|---|---|---|---|
| S-S | Constant current | ||
| S-P | Constant voltage | ||
| P-S | Constant voltage | ||
| P-P | Constant current |
S-S 토폴로지에서 표 1과 같은 공진 조건을 만족할 때, 그림 7과 같이 RX 코일의 유도 전압에서 바라본 입력 임피던스 (Zin−RX)는 식 (36)과 같다.
식 (36)에서 알 수 있듯이, RX 유도전압에서 바라본 입력 임피던스는 저항성분만이 존재한다. 따라서, 그림 6(a)와 같이 RX 코일의 유도전압(V12)과 RX 전류(I2)는 동상이며, θ12는 90도에 가깝다. 따라서, S-S 토폴로지는 TX 코일에서 RX 코일로 전력이 효율적으로 전달된다.
한편, S-S 토폴로지에서, 식 (35)와 같이 RX 측의 임피던스를 TX 측으로 환산한 임피던스는 식 (37)과 같으며, 이를 통해 계산되는 RX 측 부하에 전달되는 전류(I2)는 식 (38)과 같다.
식 (38)에서 Vin과 θin은 각각 인버터의 출력 전압 (WPT 시스템의 입력 저압)의 기본파(fundamental)의 크기와 위상을 나타낸다. 식 (37)에서 알 수 있듯이, S-S 토폴로지에서 TX 측과 RX 측의 공진주파수들이 시스템의 동작주파수 ωo와 일치하면, 식 (37)과 같이 반사임피던스는 순수 저항성이다. 또한, 식 (38)에서 알 수 있는 점은, WPT 시스템의 입력 전압(Vin)이 일정하면, S-S 토폴로지는 부하에 관계없이 정전류 출력을 갖는다는 것이다. 하지만, 식 (37)에서 알 수 있듯이, 만약 WPT 시스템의 무부하인 경우(RL=ᔕ), 식 (38)이 0이 되어 TX 측 코일에 과도한 전류가 흐를 수 있다는 단점을 가진다.
다음으로, S-P 토폴로지에서 그림 7과 같이 RX 코일의 유도전압에서 바라본 입력 임피던스는 식 (39)와 같다.
만약, S-P 토폴로지에서 그림 6(a)와 같이 θ12가 90도 차이에 가깝게 하기 위해, 식 (39)의 리액턴스 성분이 0이 되게 하는 RX 측 공진 커패시턴스는 식 (40)과 같다.
식 (40)에서 알 수 있듯이, 식 (39)의 모든 리액턴스 성분이 0이 되게 하는 C2값에는 부하 저항(RL)이 포함된다. 이는 WPT 시스템의 동작에서 부하가 변함에 따라 RX 측의 공진 커패시턴스 C2를 바꿔줘야 한다는 의미인데, 이것은 현실적으로 매우 어렵다. 따라서, S-P 토폴로지에서는 θ12가 90 도가 되는 조건은 포기하여, 표 1과 같이 정전압 출력만을 가지도록 공진 조건을 선정한다. 이를 위한 S-P 토폴로지의 실제 RX 측의 공진 커패시턴스 값 (C2)은 표 1에서 보여주며, 이때의 RX 유도전압에서 바라본 RX 측의 등가 입력 임피던스와, RX의 임피던스를 TX 측으로 환산한 임피던스는 각각 식 (41) 및 식 (42)와 같다.
식 (41)의 S-P 토폴로지의 반사 임피던스는 허수부를 포함하게 된다. 따라서, 식 (35)에서 TX 측의 공진 커패시턴스(C1)를 통해서 TX 코일의 리액턴스(jωL1)뿐 아니라, RX 측에서 TX 측으로 환산된 허수부를 함께 보상해줘야 한다. 이를 통해 구해진 S-P 토폴로지의 TX의 공진 커패시턴스(C1)값을 표 1에서 보여준다. 하지만, S-P 토폴로지의 문제점이 있는데, S-P 토폴로지가 무부하(RL=ᔕ) 출력을 가지는 경우, 식 (41)의 RX 유도전압에서 바라본 입력 임피던스가 0이 되어 RX측 L-C 병렬 루프에 과전류가 발생할 수 있다.
한편, S-P 토폴로지에서 표 1의 공진 조건을 모두 만족할 때, 출력 부하 전압(Vout)은 식 (43)과 같다.
따라서 S-P 토폴로지는 부하에 관계없이, 항상 부하에 정전압 출력을 전달한다는 것을 알 수 있다.
S-P 토폴로지는 앞서 분석한 WPT 시스템의 두 가지 요구 조건 중 하나인 정전압 출력 조건만 만족한다. 따라서, S-P 토폴로지는 식 (23)의 TX 코일에서 RX 측으로 효율적인 전력전달의 조건을 만족하지 못한다. 실제로, S-P 토폴로지는 상호 인덕턴스가 상대적으로 높은 경우에만 사용되며, 이 경우에는 θ12가 90 도에 가깝지 못한 단점을 극복할 수 있지만, 이는 매우 제한적이다. 또한, 표 1의 S-P 토폴로지의 TX 공진 커패시턴스(C1)에서 알 수 있듯이, 상호 인덕턴스가 변하면 그에 따라 반드시 C1이 함께 변하여야 한다. 따라서, 실제 S-P 토폴로지는 상호 인덕턴스가 변하지 않는 조건을 요구하는 또 다른 제약을 갖는다.
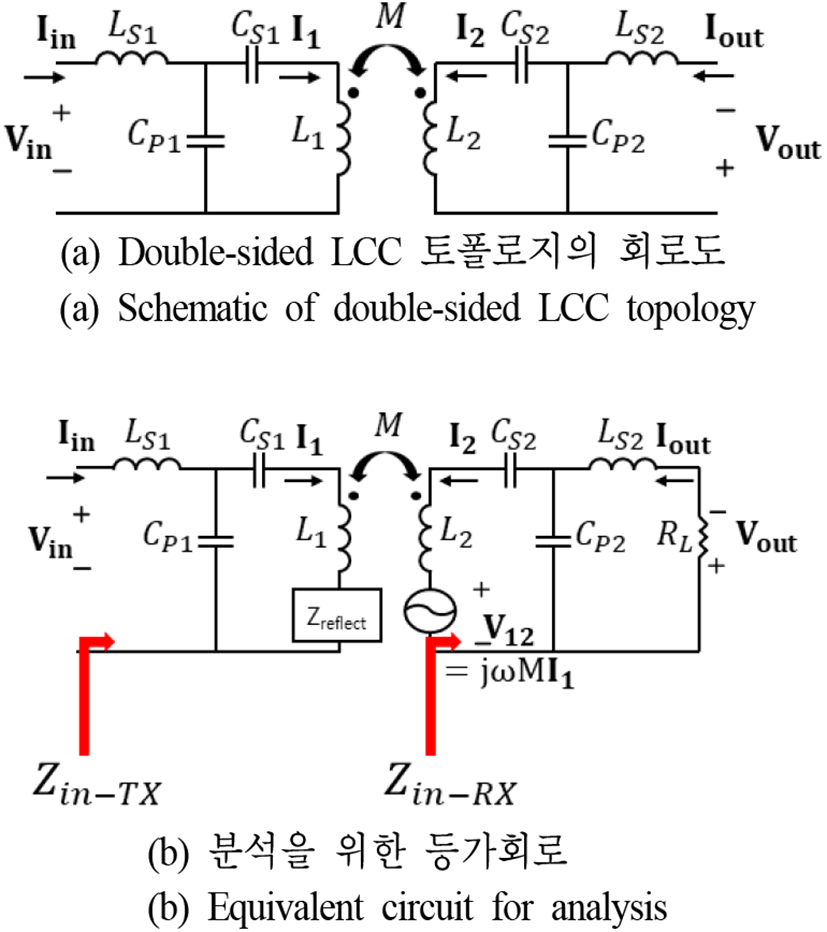
최근, 국제자동차기술자협회(Society of Automotive Engineers, SAE)에서 배포한 전기자동차 무선충전 표준인 SAE J2954[18] 등에서 double-sided LCC 토폴로지를 채택하였고, 또한 해당 토폴로지가 다른 애플리케이션에도 많이 사용되고 있다[19]~[21]. Double-sided LCC 토폴로지는 그림 9(a)와 같은데, 기존의 한 개의 커패시터가 아닌 TX, RX 각각 3개의 소자들을 통해 보상을 해주는 형태이다.
Double-sided LCC 토폴로지의 분석을 위한 등가회로는 그림 9(b)와 같다. Double-sided LCC 토폴로지의 특징은, 입력 전압(Vin)이 일정하면 TX 코일의 전류(I1)와 출력 전류(Iout)가 부하에 관계없이 정현파 정전류를 출력을 갖는다는 점이다. 먼저, RX 측부터 분석하기 위해, RX 측의 2개의 루프(I2, Iout)에 KVL을 적용하면 식 (44)와 같다.
만약, RX 측이 공진 조건 식 (45)를 만족하면, 출력 전류(Iout)와 RX 코일의 유도전압 (V12)에서 바라본 입력 임피던스는 식 (46) 및 식 (47)과 같다.
식 (46)에서 알 수 있듯이, TX 전류(I1)가 일정하면, 부하에 관계없이 부하에 전달되는 전류는 정현파 정전류가 된다. 또한, RX코일의 유도전압에서 바라본 입력 임피던스가 저항성이므로, 그림 6(a)와 같이 θ12가 90도에 가깝게 된다. 따라서, double-sided LCC 토폴로지는 효율적인 전력전달을 위한 위상차 조건과 정전류 출력의 요구조건을 모두 만족한다.
한편, double-sided LCC 토폴로지의 TX 측의 두 루프 (Iin, I1)의 KVL은 식 (48)과 같고, TX 측의 공진 조건 식 (49)를 만족하면 TX 코일의 전류(I1)와 TX 측 전원(Vin)에서 바라본 전체 입력 임피던스는 각각 식 (50)과 식 (51)과 같다.
식 (48)과 식 (51)에서, Zrelfect는 RX 측의 임피던스를 TX 측으로 환산한 등가 임피던스이다. 식 (50)에서 알 수 있듯이, TX 측에 LCC 토폴로지를 채택하면, TX 코일의 전류(I1)는 RX 측과 부하에 관계없이 항상 정현파 정전류가 된다. 또한, 식 (51)에서 알 수 있듯이, double-sided LCC 토폴로지는 TX 전원(Vin)에서 바라본 입력 임피던스가 순수 저항성이기 때문에 피상전력이 최소화되어 손실이 최소화된다.
Double-sided LCC 토폴로지는 이외에도, 다양한 장점을 가진다. 특히, 앞서 설명한 S-S, S-P 토폴로지에서는 부하나 TX 측과 RX 측의 결합계수가 변할 경우, 인버터의 소프트 스위칭 (zero voltage switching, ZVS)가 확보가 되지 않는다[22]. 이 경우 인버터의 손실이 크며, 인버터가 파괴될 수도 있다. 하지만, double-sided LCC 토폴로지의 경우, 넓은 부하, 넓은 결합계수 범위에도 ZVS가 확보되어, 매우 강인하다는 것이 여러 연구를 통해 확인되었다[22]. 또한, double-sided LCC 토폴로지는 부하가 변함에 따라서도 정현파 정전류 출력을 부하에 전달하는데, WPT 시스템의 출력 전류가 정전류이기 때문에, RX 측 AC 전류를 DC 전류로 변환해주는 정류기(rectifier) 앞단의 역률(power factor)이 상대적으로 높은 장점을 가진다[19]. 또한, double-sided LCC 토폴로지는 양방향 무선전력전송 (bi-directional WPT)이 가능하다는 장점을 가진다[23]. 하지만, double-sided LCC 토폴로지는 기존의 S-S, S-P 토폴로지에 비해 많은 소자들이 필요한데, 이는 각 소자들에 가격 및 부피 면에서 불리하고, 각 소자의 ESR에 의한 손실이 증가하는 단점을 가진다.
본 논문에서는, WPT 시스템에서 가장 많이 사용되는 S-S, S-P, double-sided LCC 토폴로지를 분석하였고, 각각의 장단점을 언급하였다. 이는 표 2에서 정리하였다. 우선, S-S 토폴로지의 경우 많은 장점을 가지지만, 부하와 결합계수 변화에 따라 ZVS가 불가능하다는 단점을 가지는데, 이로 인해 주로 저전력에만 사용된다. 특히, 스마트폰 무선충전 표준인 Qi 스탠다드에는 S-S 토폴로지가 주로 사용된다[24]. S-P 토폴로지의 경우, 많은 단점에도 불구하고, 식 (42)에서와 같이 S-S 토폴로지에 비해 작은 RX 자기 인덕턴스에도 전력전송이 가능하다는 장점을 가지고, 정전압 공급이 가능하다는 장점도 가져서 작은 코일이 필수인 인체 삽입형 무선전력전송 등의 인체 관련 애플리케이션에 중점적으로 사용되고 있다[25]. 마지막으로, double-sided LCC 토폴로지의 경우 많은 장점, 그중에서도 부하와 상호 인덕턴스 변화에 강인하다는 장점 때문에 전기자동차 무선충전 표준에 채택되고 있다[18]. 각 토폴로지의 장, 단점을 통해서 애플리케이션에 필요한 토폴로지를 채택할 수 있으며, 또한, LCC-S, LCC-P 등의 혼합된 토폴로지도 채택할 수 있다[5].
앞서 4-2에서 중점적으로 설명한 S-S, S-P, double-sided LCC 토폴로지를 실제 구성하여, 실험을 통해 부하에 따른 입, 출력 특성을 살펴본다. 그림 10은 실험을 위해 실제 제작된 코일들을 보여준다. 코일은 Litz wire의 도선으로 제작하였고, 실제 상황에 맞게 자기장 차폐 및 전력전송 효율 증가를 위한 페라이트를 추가로 구성하였다. 그림 10의 코일의 자세한 설계 사양과 전기적 회로 소자값들은 표 3에서 정리하였다.

그림 11은 실험을 위해 제작된 S-S, S-P, double-sided LCC 토폴로지 공진회로들을 보여준다. 그림 11(a)는 그림 8(a)와 같은 직렬 커패시터들을 보여주며, 그림 11(b)는 그림 8(b)와 같이 송신측 직렬과 수신측 병렬 커패시터들을 보여준다. 또한, 그림 11(c)는 그림 9와 같이 double-sided LCC 토폴로지의 직렬 인덕터들, 병렬 커패시터들, 그리고 직렬 커패시터들을 보여준다. 각 회로 소자들의 값들은 표 4에서 정리하였다.
그림 12는 실제 무선전력전송 실험 환경을 보여준다. 그림 7과 같이, 입력 전원은 DC 파워 서플라이에서 공급해 주었으며, 출력 부하(RLoad)는 정류기와 전자부하를 통해 구성하였다. 그림 12의 실험 셋업을 통해 S-S, S-P, double-sided LCC 토폴로지 각각의 경우 50~200 W의 부하에서 입력과 출력의 전압, 전류, 그리고 전력을 분석한다.


표 5~표 7은 각각 S-S, S-P, double-sided LCC 토폴로지에서 50 W에서 부터 200 W까지 전력을 부하에 전달했을 때의 입력과 출력 특성을 나타낸다. 표 5에서 알 수 있듯이, S-S 토폴로지에서는 출력 전력이 변화하여도, 부하에 전달되는 출력 전류는 비교적 일정하게 유지되는 것을 알 수 있다. 이는 S-S 토폴로지의 정전류 특성이다. 또한, 표 6에서 알 수 있듯이, S-P 토폴로지는 부하가 변화하여도 출력 전압은 비교적 일정하게 유지되는 것을 알 수 있다. 마지막으로 표 7은 double-sided LCC 토폴로지를 적용하였을 때인데, 부하가 변함에 따라 출력 전류가 거의 변화하지 않고, 출력 전압이 변화하는 정전류 출력 특성을 갖는 것을 알 수 있다. 위 세 가지 실험을 통해서, 앞서 분석한 대로, S-S, S-P, double-sided LCC 토폴로지에서의 출력 정전압 혹은 정전류 특성이 실제로 구현 가능함을 보였다.
Ⅴ. 결 론
본 논문에서는 WPT 시스템 코일의 전기적 회로 모델링 두 가지를 분석하고, 효율적인 전력전달을 위한 조건과 토폴로지의 필요조건과 각 특성에 대해 분석하였다. WPT 시스템 코일의 전기적 회로 모델링 방법에는 자화 인덕턴스 모델과 상호 인덕턴스 모델이 있으며, 이 둘은 쇄교 자속의 관점 차이로 인해 표현이 다르지만 상호 변환될 수 있다는 것을 분석하였다.
또한, 코일 간의 전력전달이 효율적인 조건을 분석하였으며, 특히 WPT 시스템이 가장 많이 비교되는 변압기와의 차이점을 TX 코일 전류와 RX 코일 전류의 위상 차이 관점에서 분석하였다. 변압기는 core loss가 최소가 되기 위해 TX 코일 전류와 RX 코일 전류의 위상차(θ12)가 180도 일 때 가장 효율적으로 전력전달이 가능하여 별도의 보상회로가 필요하지 않다. 하지만, WPT 코일에서는 TX와 RX 전류의 위상차(θ12)가 90도일 때 가장 효율적이기 때문에, 위상차를 90도가 되게 하는 공진 회로가 필요하다는 것을 분석하였다.
한편, WPT 시스템의 공진 토폴로지의 요구 조건에는, TX 코일 전류와 RX 코일 전류의 위상차가 90도가 되게 하는 것 이외에도, 정전류 혹은 정전압 출력 특성을 가져야 한다는 것을 분석하였으며, 이 조건을 만족하는 다양한 토폴로지의 특성에 대해 분석하였다. 본 논문에서 분석한 S-S, S-P, double-sided LCC 토폴로지는 각각의 특성과 장, 단점이 매우 뚜렷하여, 해당 토폴로지들의 각 특성을 요구하는 해당 애플리케이션들이 존재한다는 것을 분석하였다. 또한, S-S, S-P, double-sided LCC 토폴로지의 전력전송 실험을 통해, 실제 각 토폴로지의 정전압, 혹은 정전류 특성이 실제로 구현 가능함을 알 수 있었다.