Ⅰ. 서 론
능동위상배열 안테나는 수백 개 혹은 수천 개의 복사소자로 구성되어 있으며, 각각의 복사소자에 부착된 TRM(transmitter and receiver module)을 통하여 급전 신호의 크기 및 위상을 제어하며, analog to digital convertoer (ADC)를 활용하여 디지털 빔포밍 및 신호처리가 수행된다. 그러나, 수백 개 혹은 수천 개의 복사소자로부터 송/수신된 신호량의 증가는 신호처리의 계산속도를 느리게 하고, 많은 TRM의 개수로 인하여 가격이 증가된다는 단점이 있다[1]. 이러한 단점을 극복하기 위하여 복사소자를 grouping하는 부배열 설계 기법이 적용되어 왔다.
부배열 구조를 설계하기 위해서는 최적화 알고리즘이 필요하다. 복사소자를 주기적으로 묶어 부배열을 형성하게 되면 작은 각도라도 빔 조향 시 grating lobe가 발생되기 때문이다[2]. 이러한 이유로 부배열은 빔 조향 각도내에 grating lobe가 발생하지 않도록 임의의 복사소자를 비주기적인 형태로 grouping함으로써 빔 조향 범위 내에서 grating lobe가 발생하지 않는 최적의 부배열 구조를 찾아야 한다. 최적화 알고리즘을 활용함으로써, 부배열을 비주기적인 형태로 grouping 하여 빔 조향 범위 이내 grating lobe가 발생되지 않도록 하기 위한 다양한 연구가 수행되어 왔다[3]∼[6]. 참고문헌 [3]과 참고문헌 [4]는 GA(genetic algorithm)을 활용하여 빔 조향 범위 내에 grating lobe가 발생되지 부배열 최적 설계 방법을 소개한다. 참고문헌 [5]에서는 PSO(particle swarm optimization)을 활용하여 부배열을 설계하는 방법에 대해 설명하고 있다. 참고문헌 [6]은 GA와 PSO를 결합한 GSO(genetic swarm optimization)와 K-means를 결합한 hybrid 알고리즘을 활용하여 부배열에 속한 복사소자를 동일하게 한 조건하에 부배열 최적 설계 방법을 소개한다. 그러나, 참고문헌 [3]∼참고문헌 [6]은 부배열을 디지털 단에서 형성한 것으로 모든 복사소자에 TRM이 부착된 형태이다. 그러므로, 급전신호 최적화는 Taylor 또는 체비세프 tapering을 활용하여 낮은 부엽준위 달성이 가능하다.
본 논문에서는 최적 설계된 부배열 각각에 한 개의 TRM을 부착한 안테나 시스템을 제안한다. 그러므로, Taylor 또는 체비세프 tapering을 통한 낮은 부엽준위 달성이 불가능하며 추가적인 amplitude tapering 최적화 과정이 필요하다. 참고문헌 [7]∼참고문헌 [12]는 부배열 기반의 amplitude tapering을 소개하고 있다. 참고문헌 [7]에서는 Hybrid GA를 활용하여 각 부배열마다 낮은 부엽준위를 달성하였다. 그러나 빔 조향에 따른 부엽 또는 HPBW의 변화가 제시되어 있지 않다. 참고문헌 [8]은 quadaratic programming을 활용하여 부배열 기반의 능동위상배열 안테나의 amplitude tapering을 최적화하였으나, 작은 빔 조향 각도에 대한 빔 특성만 제시하고 있다. 참고문헌 [9]는 부배열의 모양을 변화시킴으로써 낮은 부엽준위를 달성하였으나, 구현하기 위해서는 부배열 구조가 실시간으로 변동 가능해야 된다는 제한사항이 있다. 참고문헌 [10]은 overlapped subarray를 활용하여 부배열이 적용된 위상배열안테나의 낮은 부엽준위를 확보하였으나, overlapped sub_array의 경우, 조향손실이 매우 크다는 단점이 있다. 이외로도 부배열 기반 또는 비주기적인 배열안테나에서 낮은 부엽준위를 달성하기 위한 다양한 급전신호 최적화 연구가 수행되었다[11],[12]. 그러나 빔 조향 방향에 따른 amplitude tapering 기법 또는 빔 특성에 대한 결과는 제시되어 있지 않는 상황이다.
본 논문에서는 참고문헌 [13]에서 소개한 GLPSO(genetic learning particle swarm optimization)를 활용하여 부배열 구조 및 빔 조향 방향별로 급전 신호 크기를 최적화하여 빔 조향 범위에 따른 부배열 TRM이 적용된 능동위상배열 안테나의 FoV(field of view)를 분석하였다. GLPSO 알고리즘은 기계학습 기반의 최적화 알고리즘으로 빠른 수렴속도와 정밀하게 해를 찾는 능력을 가진 알고리즘으로 GA와 PSO 알고리즘보다 높은 성능을 보인다[13]. 본 논문의 구성은 다음과 같다: Chapter Ⅱ에서는 부배열 TRM이 적용된 능동위상배열 안테나에 대한 array factor에 대한 수식적 정의에 대해 소개하며 부배열 구조 및 급전신호 크기 최적화 알고리즘 흐름도에 대해 소개한다. Chapter Ⅲ에서는 부배열 개수, 복사소자 간격 따른 빔 특성에 대한 분석이 수행된다. 복사소자 간격은 0.525 λ, 0.6 λ, 0.7 λ 변화에 따른 분석, 그리고 부배열 개수는 48개, 64개, 96개 변화에 따른 분석이 각각 수행되었다. Chapter Ⅳ 16.8 λ2의 동일한 개구면 크기 및 동일한 96개의 부배열 개수 조건하에 복사소자 간격 변화에 따른 빔 특성 분석이 수행되었다. Chapter Ⅴ에는 결론이 제시된다.
Ⅱ. 부배열 TRM이 적용된 능동위상배열 안테나의 Array Pattern 및 최적화 알고리즘 흐름도 소개
그림 1은 본 논문에서 제안하는 부배열이 적용된 능동위상배열 안테나 시스템이다. 각 부배열마다 하나의 TRM이 위치하여 동일한 부배열에 속한 복사소자의 급전신호의 크기 및 위상은 서로 동일한 값을 가진다. 그림 1에 대하여 수식적으로 표현하면 식 (1)∼식 (5)와 같다. 식 (1)은 부배열이 적용된 능동위상배열 안테나의 AP(array pattern)이며, fk와 fs으로 결정된다. 식 (2)는 단일 부배열에 대한 array factor이며 fk라고 정의하였으며, k번째 단일 부배열에 속한 복사소자의 위치(xk,n, yk,n)에 의하여 결정된다. 식 (3)은 단일 부배열이 K개만큼 배열되었을 때의 array factor이며, fs라고 정의하였다. fs는 k번째의 위상중심(ρk,x, ρk,y)과 TRM으로부터 제어된 급전신호의 크기(ak), 위상 값(uk,0,vk,0)에 의해 결정된다[2]. 여기서, u, v, uk,0,vk,0는 식 (4)와 같이 θ, ϕ, θk,0,ϕk,0에 결정되며, θ, ϕ는 R, θ, ϕ 구좌표계의 축을 의미하며, θk,0, ϕk,0는 빔 조향을 위해 복사소자에 인가된 위상지연 값을 의미한다. 식 (5)는 각 부배열의 위상중심의 위치를 정의하며, 부배열에 속한 복사소자의 위치, TRM으로부터 제어된 급전신호의 크기에 의해 결정된다.
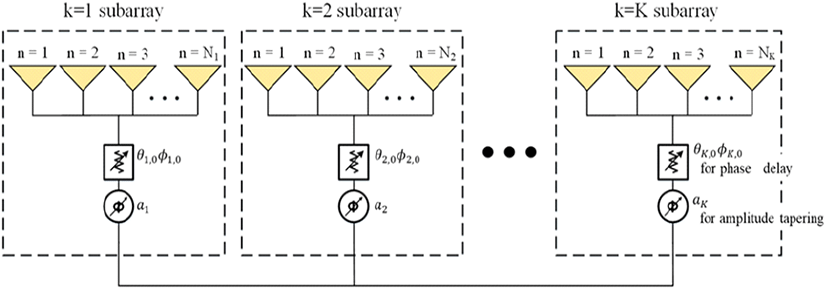
그림 2는 부배열의 모양 및 낮은 부엽준위 달성을 위한 최적화 알고리즘 흐름도이다. 최적화 알고리즘 흐름도는 부배열 구조 최적화 부분과 부배열 급전신호 최적화 부분으로 나뉘어 수행된다. 부배열 구조에 대한 최적화를 수행하는 목적은 부배열을 주기적 형상으로 설계하게 되면 부배열 간 위상중심이 한파장 이상되므로 부배열을 비주기적으로 형성함으로써 빔 조향 범위 내의 grating lobe를 피하기 위함이다. 식 (6)은 grating lobe가 발생하는 위치(θGL)를 표현하는 식으로 grating lobe는 파장(λ), 복사소자 간격(d), 복사소자 개수(n), 빔 조향 각도(θ0)에 의해 결정되므로, 급전신호 최적화를 통하여 grating lobe는 줄일 수 없다[14]. 그러므로 부배열 구조에 대한 최적설계가 우선적으로 수행된다.
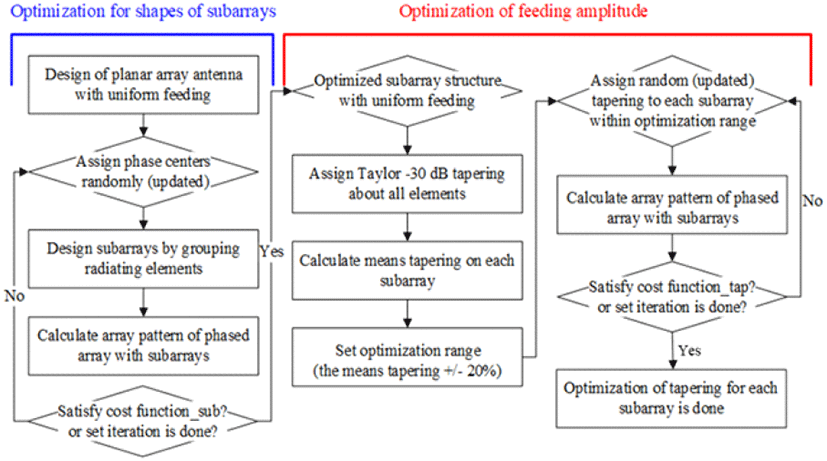
부배열 구조에 대한 최적 설계 과정은 다음과 같다.
-
(Step 1) 균일 급전신호를 가지는 평면 배열안테나의 임의의 지점에 위상중심을 할당한다.
-
(Step 2) 할당된 위상중심을 기준으로 복사소자를 grouping하여 임의의 부배열을 각각 형성한다.
-
(Step 3) 식 (1)을 활용하여 조향 각도에 따른 AP 계산을 통해 부엽준위를 확인한다.
-
(Step 4) 부엽준위 크기가 만족스럽지 못하거나 또는 설정한 iteration이 완료가 되지 않은 경우 위상중심을 update한다.
Step 5. Step 2∼Step 4를 반복함으로써 빔 조향시 낮은 부엽준위가 달성 가능한 부배열 구조를 획득한다.
식 (7)은 부배열 구조 최적화에 사용된 cost function으로 cost_function_sub로 정의되며, 그림 2에 제안된 최적화 알고리즘 흐름도의 부배열 구조 최적화 부분에 cost_fucntion_sub의 위치를 표기하였다.
여기서, PSL(azimuth scan)은 방위각 15° 조향 시 최대 부엽준위를 의미하며, PSL(elevation_scan)은 고각 15° 조향 시 최대 부엽준위를 의미한다. 방위각/고각 방향으로 각각 15° 조향한 경우, 최대 부엽준위 중 가장 높은 값을 cost_function_sub로 정의하며, 최적화는 cost_function_sub가 최솟값에 수렴되는 방향으로 iteration이 수행된다.
최적화 알고리즘 흐름도 상에서, Step 1의 균일 급전신호를 가진 평면배열을 기준으로 부배열 구조를 형성하였다. 그림 1의 제안된 능동위상배열 안테나의 구조를 보면 각 부배열당 한 개의 TRM이 할당되어 있으므로, 동일한 부배열에 속한 복사소자의 급전신호의 크기와 위상은 서로 같은 값을 가지게 된다. 동일한 부배열에 속한 복사소자의 급전신호가 같을 경우, 식 (5)의 분모와 분자에 위치한 급전신호가 약분됨으로써 식 (8)로 표현할 수 있다. 그러므로 동일한 부배열에 속한 복사소자의 급전신호가 같을 경우, 복사소자의 위치에 의해 부배열의 위상중심이 결정된다[8].
최적화가 완료된 부배열 구조에 대해 낮은 부엽준위 달성을 위해 급전신호에 대한 최적화가 수행된다. 최적화가 완료된 부배열의 위상중심은 비주기적 형태를 가지고 있으므로 Taylor 또는 체비세프 amplitude tapering이 적용될 수 없다. 이러한 이유로 다음과 같은 급전신호 최적화 절차를 통하여 낮은 부엽준위가 달성된다.
-
(Step 6) 평면배열 안테나의 복사소자에 Taylor amplitude tapering을 적용한다.
-
(Step 7) 각 부배열에 속한 복사소자의 amplitude tapering의 평균값을 계산하여 평균 급전신호를 구한다.
-
(Step 8) 각 부배열에 인가되는 급전신호의 최적화 범위를 설정한다(본 논문의 경우에는 최적화 범위를 각 부배열에 인가되는 평균 급전신호의 ±20 % 설정 시 ±30 % 설정한 경우와 동일한 결과를 빨리 도출하였으며, ±10 % 설정한 경우보다 우수한 결과를 도출하였으므로 최적화 범위를 ±20 %로 설정하였다.).
-
(Step 9) 임의의 급전신호를 각 부배열에 할당하여 AP를 계산하여 부엽준위를 확인한다.
-
(Step 10) 부엽준위의 크기가 만족스럽지 못하거나 설정한 iteration이 완료되지 않은 경우 급전신호를 update하여 각 부배열에 할당한다.
-
(Step 11) Step 9, Step 10을 반복함으로써 낮은 부엽준위 달성을 위한 각각의 급전신호 크기를 획득한다.
본 논문에서 제안하는 능동위상배열 안테나의 구조는 부배열단에 TRM이 장착되어 있으므로 실시간으로 급전신호를 변화시킬 수 있다. 그러므로, boresight, 방위각 조향, 고각 조향 시 낮은 부엽 준위 달성을 위한 급전신호를 각각 도출한다. Boresight 방향으로 낮은 부엽준위 달성을 위해 사용된 부배열 급전신호 최적화 cost function은 식 (9)이며, boresight 방향으로 빔이 조향될 때 부엽준위를 cost function값으로 정의하였으며 cost function은 최솟값에 수렴되는 방향으로 iteration이 수행된다. 식 (10)과 식 (11)은 방위각과 고각 15° 각각 조향 시 낮은 부엽준위 달성을 위해 사용된 부배열 급전신호 최적화 cost function이다. 여기서, 빔 조향 방향별 낮은 부엽준위 달성을 위한 급전신호 최적화는 독립적으로 수행되며, 그림 2의 제안된 최적화 알고리즘 흐름도의 급전신호 최적화 부분에 식 (9)∼식 (11)에서 사용된 cost _function_tap의 위치를 표기하였다.
Ⅲ. 복사소자 간격 및 부배열 개수 변화에 따른 빔 특성 분석
그림 3은 복사소자 간격이 0.7 λ이고, 24×24 배열안테나에 대하여 48개, 64개 그리고 96개의 최적화된 부배열 구조의 1 사분면을 각각 보여주고 있다. 부배열 구조는 모노펄스 운용방식을 고려하여 원점대칭 형태로 설계되었다. Bold 실선을 통하여 부배열 간의 경계를 표기하였으며, ‘●’은 복사소자를 의미한다.

그림 4와 그림 5 및 그림 6은 최적화가 완료된 부배열 구조에 대하여 boresight, +방위각, +고각 조향 방향에서 낮은 부엽준위를 가지기 위한 급전신호의 분포를 각각 보여주고 있다. –방향의 방위각/고각 조향 시 최적화된 급전신호는 부배열 구조가 원점 대칭 형태이므로 급전신호의 좌/우 또는 상/하 대칭을 통하여 추출할 수 있으며, 능동위상배열 안테나 특성상 TRM 제어를 통하여 실시간을 급전신호 tapering이 가능하기 때문이다.
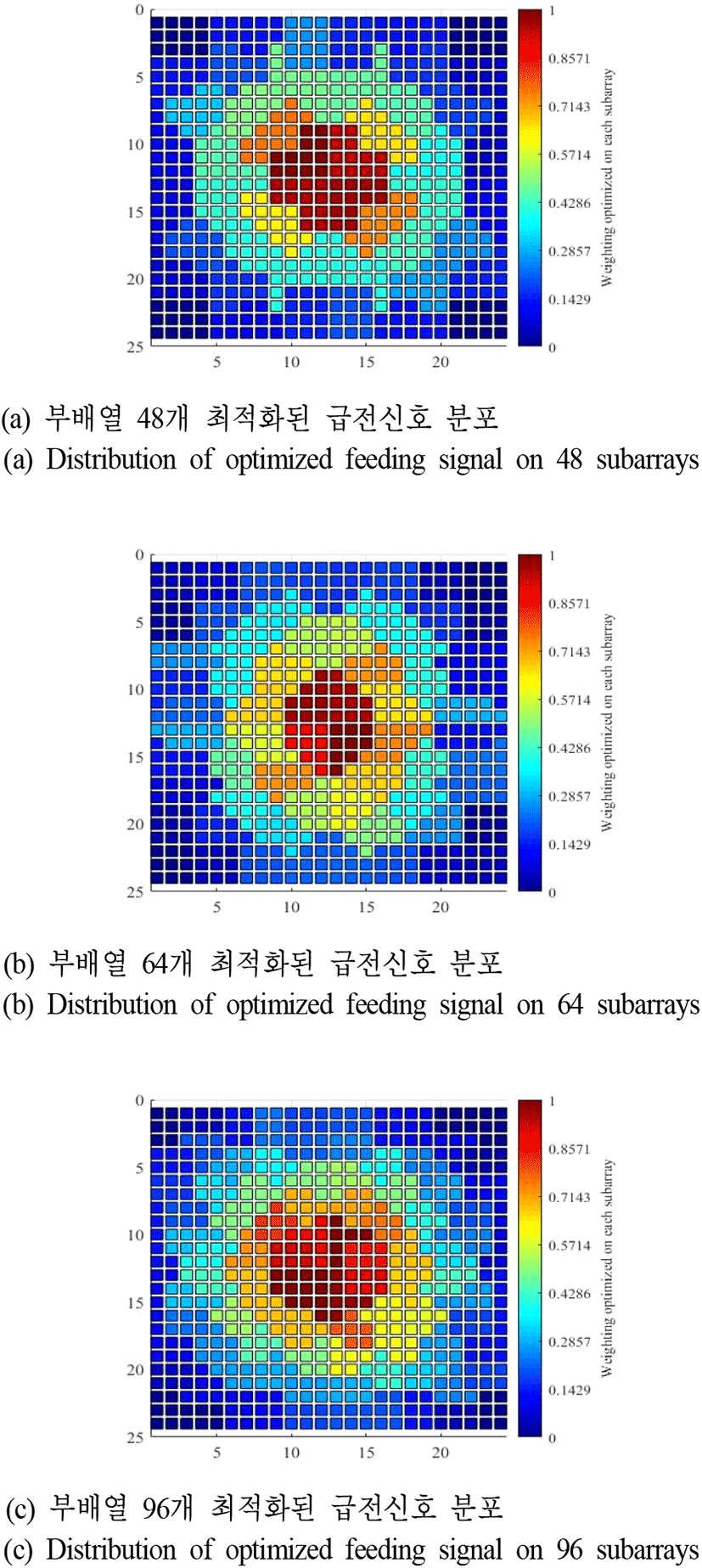
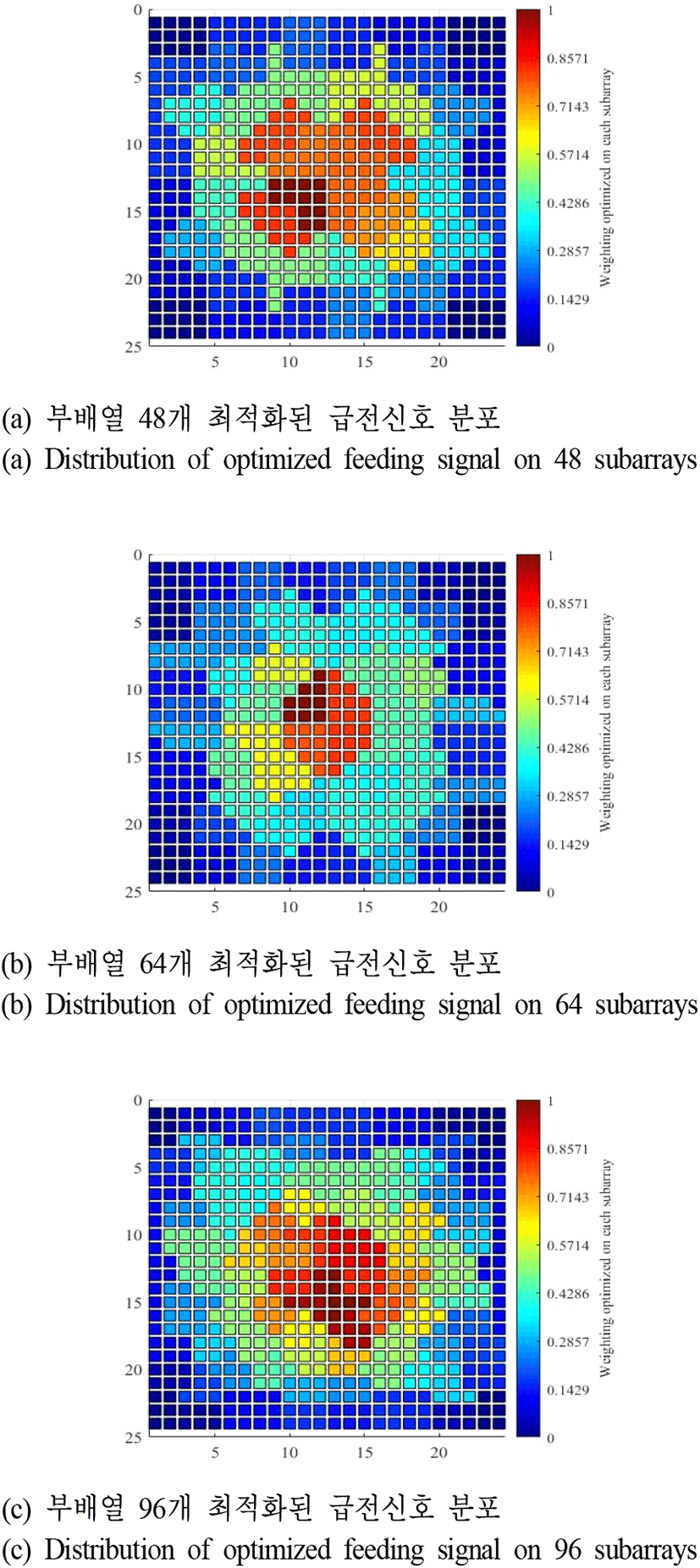
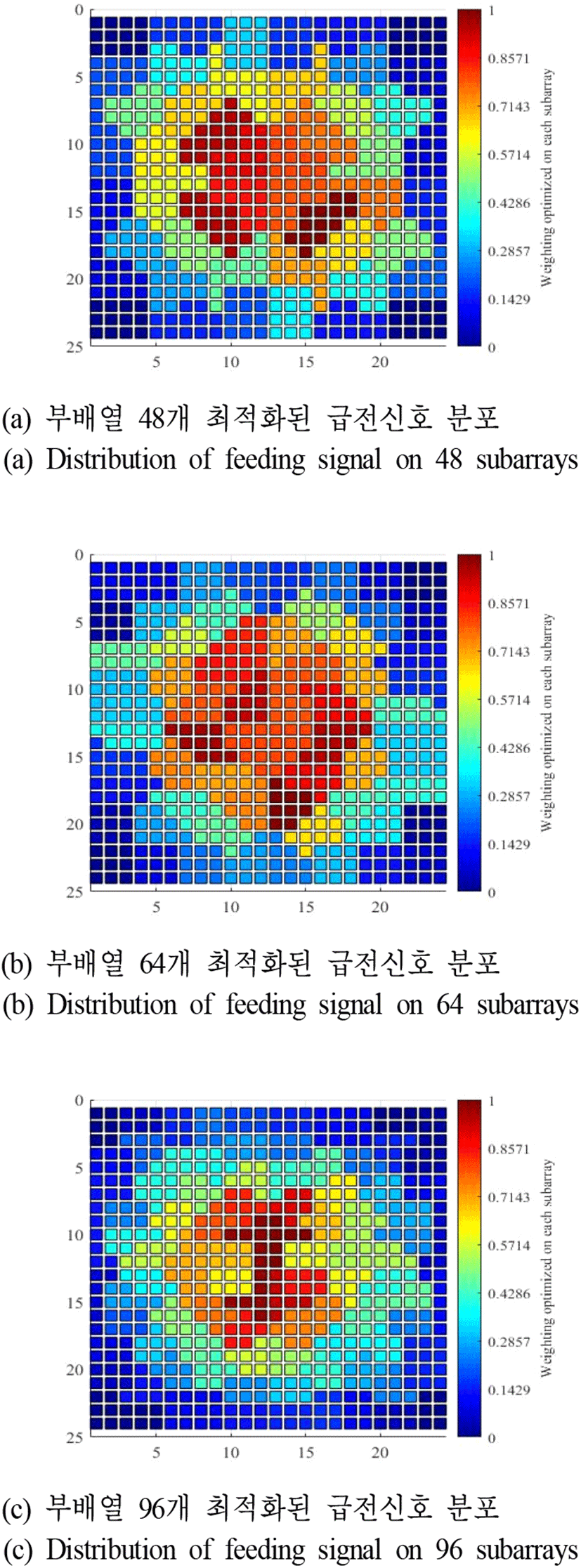
복사소자 간격 및 부배열 개수 변화에 따른 빔 특성의 변화를 분석하기 위해 모든 방사패턴에 적용된 단일소자 방사패턴은 cos1.5θ의 형태를 활용하였으며, 모든 배열 구조에는 상호간섭 조건이 없으며 식 (1)∼식 (5)를 Matlab을 통하여 계산함으로써 방사패턴을 추출하고, 부엽준위 및 반전력 빔폭의 변화를 분석하였다.
그림 7 및 그림 8은, 그림 4에서 그림 6의 최적화된 급전신호 분포를 그림 3의 최적화된 부배열 구조에 인가하였을 때 빔 조향 각도에 따른 빔 특성 변화를 보여주고 있다. 여기서, 복사소자의 좌/우 간격은 0.7 λ이다. Boresight 방향에서 모두 −29 dB 이하의 낮은 부엽준위가 달성되었다. 그러나, 조향 각도가 증가할수록 부배열 개수가 적을수록 부엽준위가 급격하게 증가한다. 각 부배열에 대한 급전신호 크기를 최적화하였음에도 부엽준위 크기가 증가하는 이유는 boresight 방향의 경우, grating lobe가 단일 부배열의 평균 방사패턴의 null에 위치하게 된다. 그러나, 빔 조향 시 grating lobe가 null 밖으로 이동하게 되면서 부엽준위가 증가하게 된다. 이를 grating effect라고 하며, grating effect에 의한 부엽준위 상승은 급전신호 크기 최적화를 통하여 감소가 불가능하다. 96개의 부배열이 적용된 위상배열안테나가 빔 조향시 낮은 부엽준위를 가지는 이유는 동일한 개구면적에서 부배열의 개수가 많으므로 부배열간의 위상중심간의 거리가 좁아져 main beam과 grating lobe와의 거리가 멀어지게 되어 grating effect의 영향이 작아지게 되어 빔 조향시 부배열의 개수가 적은 배열안테나보다 다소 낮은 부엽준위를 달성하게 된다[15](표 1, 표 2).
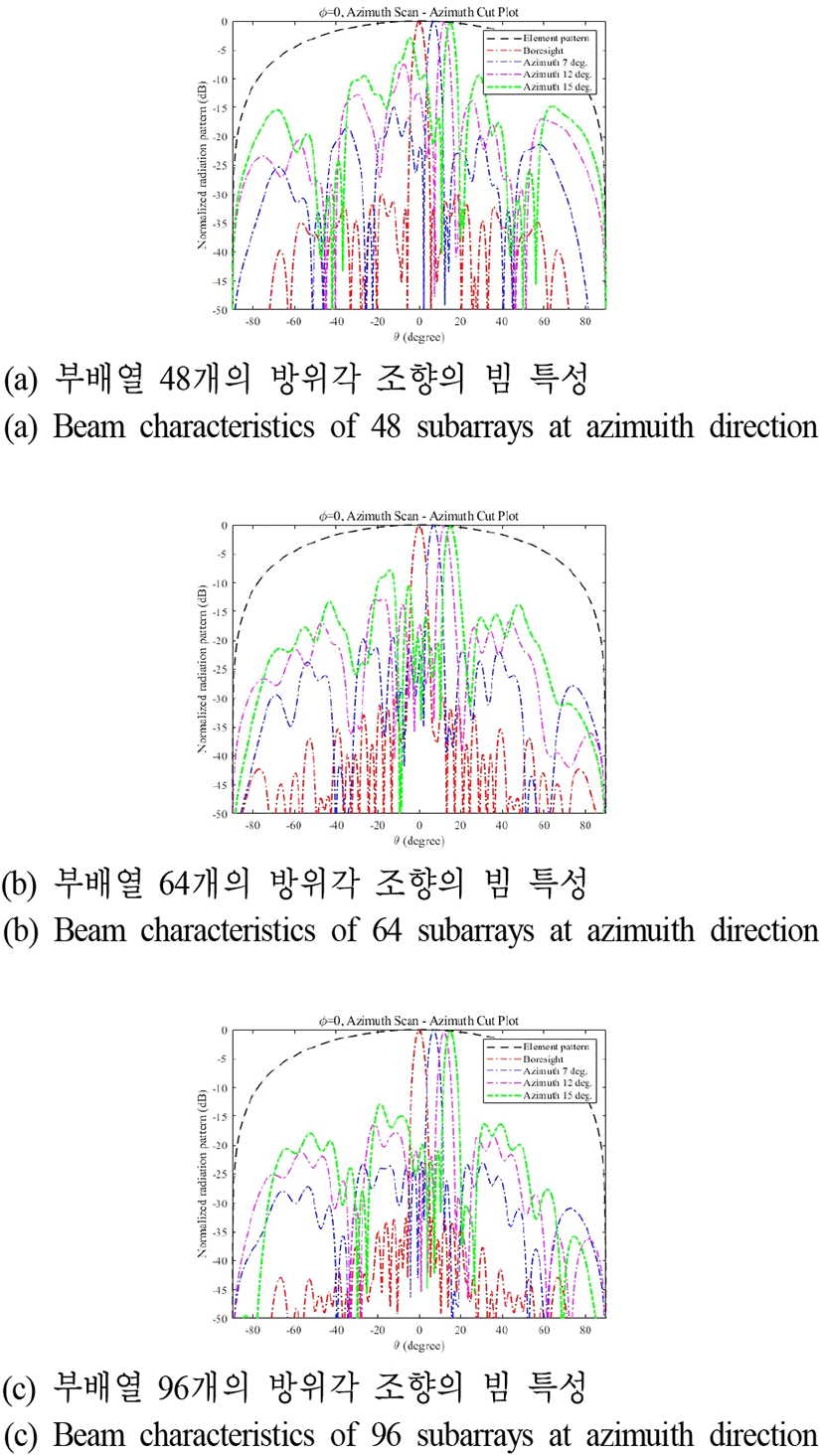
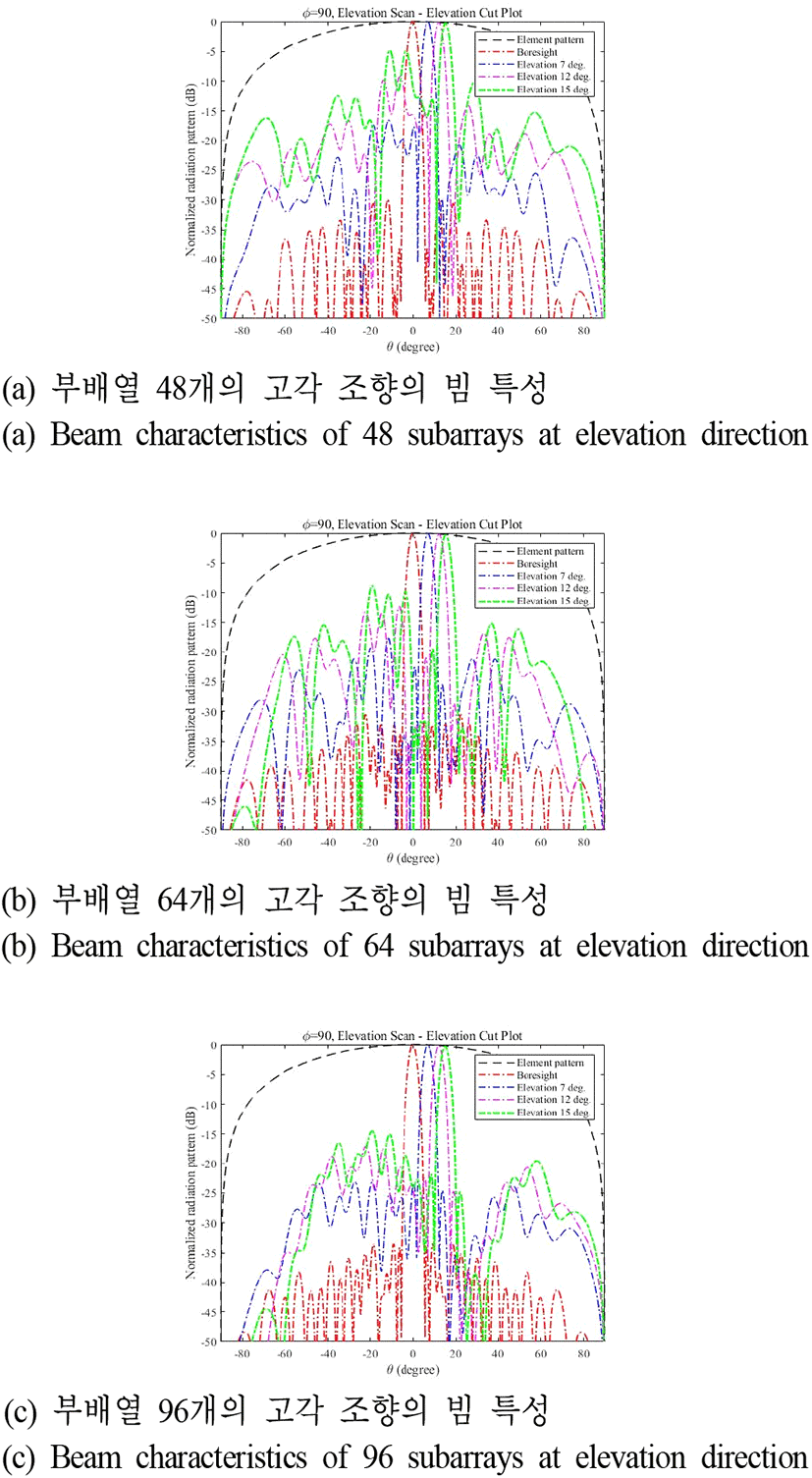
그림 9 및 그림 10은 복사소자 간격이 그림 3의 최적화된 부배열 구조의 복사소자 간격을 0.6 λ로 변경하고, 급전신호 분포틑 그림 4와 그림 5 및 그림 6을 적용하였을 때, 빔 조향 각도에 따른 빔 특성을 보여주고 있다. 복사소자 간격이 0.7 λ인 경우와 비교해 보면 boresight에서의 부엽준위는 서로 큰 차이가 없으나 빔 조향 시 부엽준위가 소폭 감소하는 형태를 볼 수 있다. 그 이유는 부배열의 위상중심 간의 거리가 0.7 λ인 경우보다 가까워져 grating lobe와 main lobe의 간격이 증가하기 때문이다. 그러나, 반전력 빔폭은 커지는 것을 확인할 수 있다. 표 3 및 표 4에, 그림 9 및 그림10에 대한 빔 특성의 정량적 수치를 제시한다.
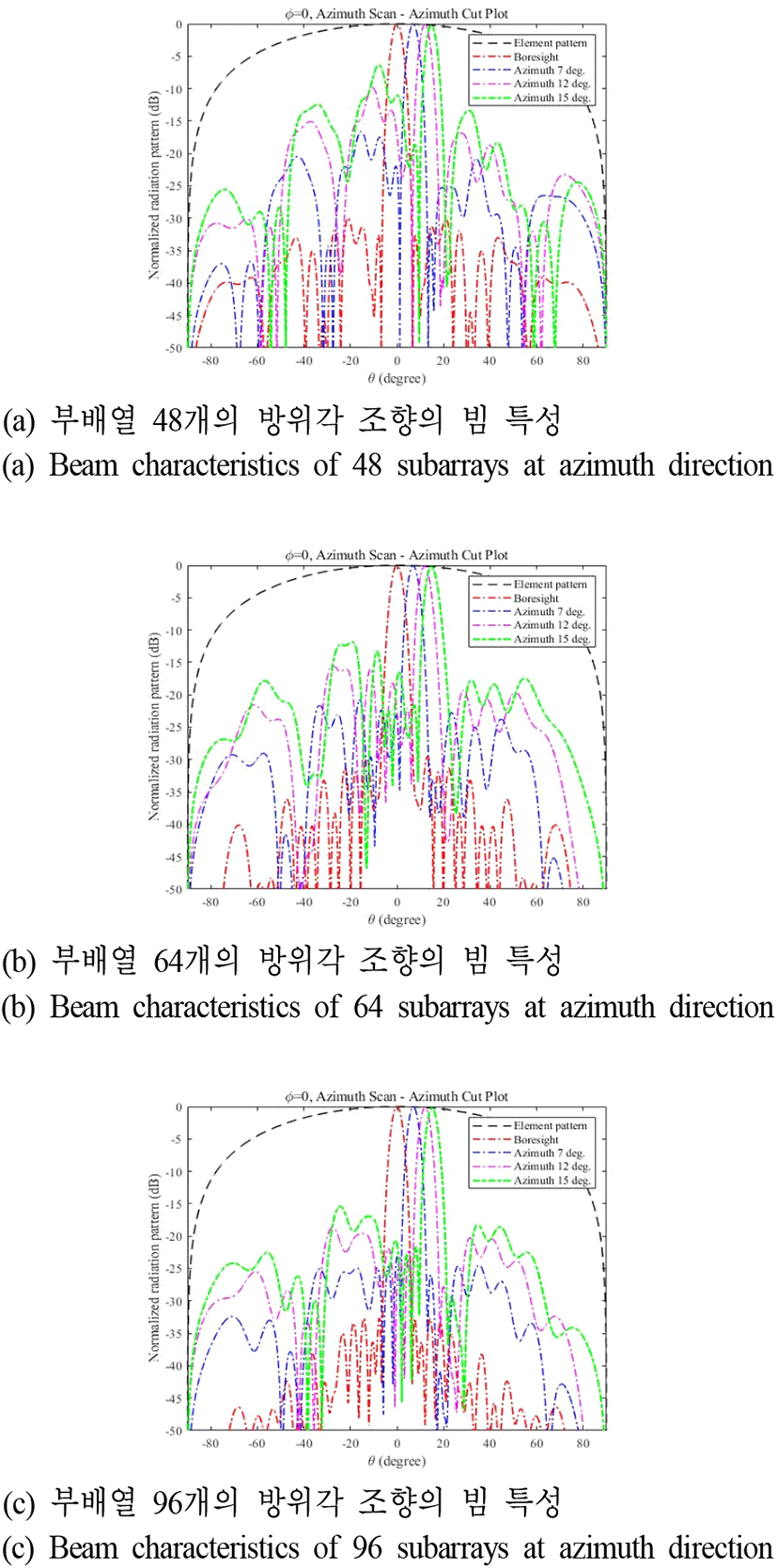
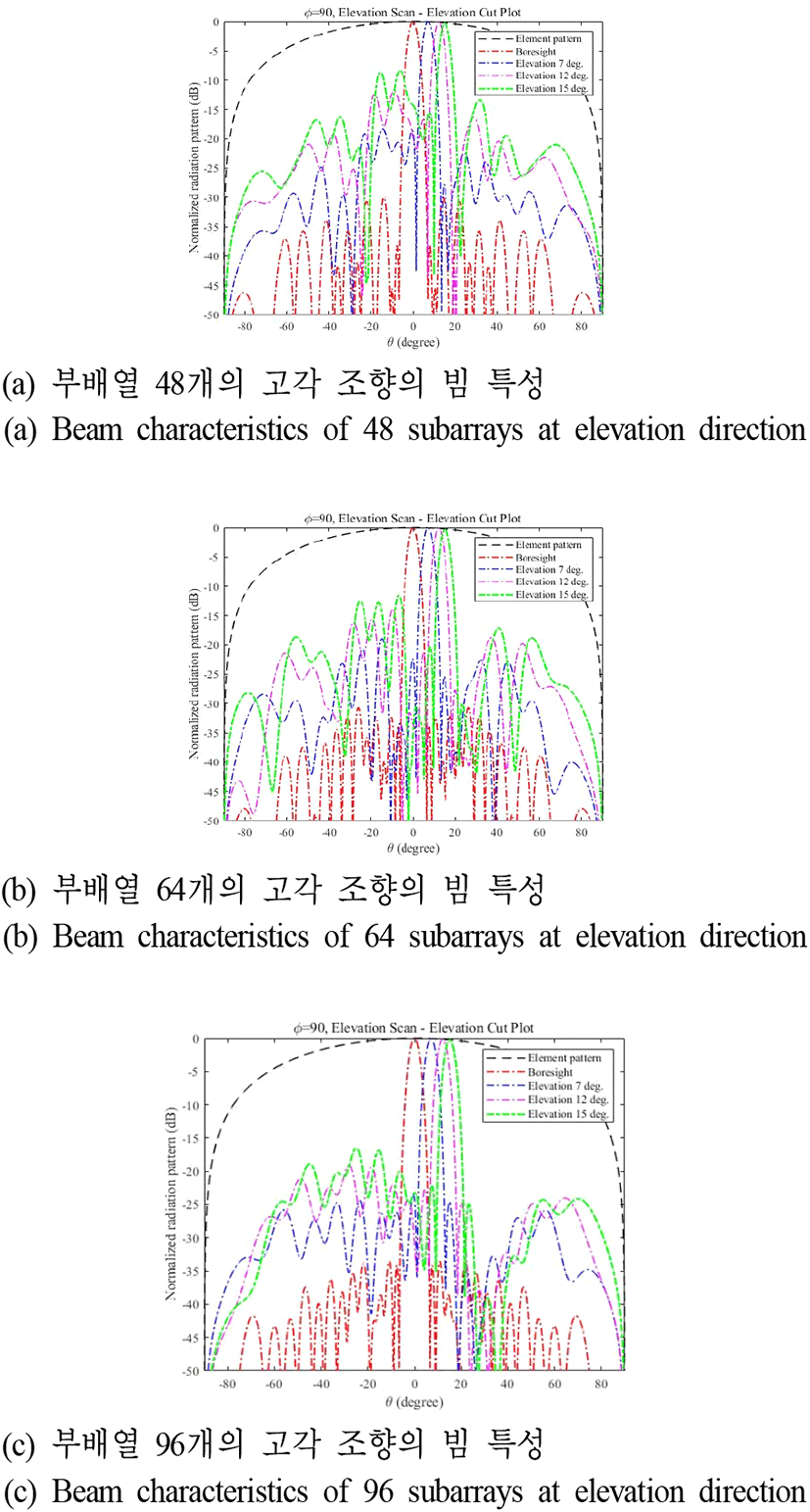
그림 11 및 그림 12는 복사소자 간격이 그림 3의 최적화된 부배열 구조의 복사소자 간격을 0.525 λ로 변경하고, 급전신호 분포를 그림 4와 그림 5 및 그림 6을 적용하였을 때, 빔 조향 각도에 따른 빔 특성을 보여주고 있다. 복사소자 간격이 0.525 λ인 경우가 부엽 준위는 가장 작지만, 빔폭이 가장 큰 것을 확인할 수 있다 (표 5, 표 6).
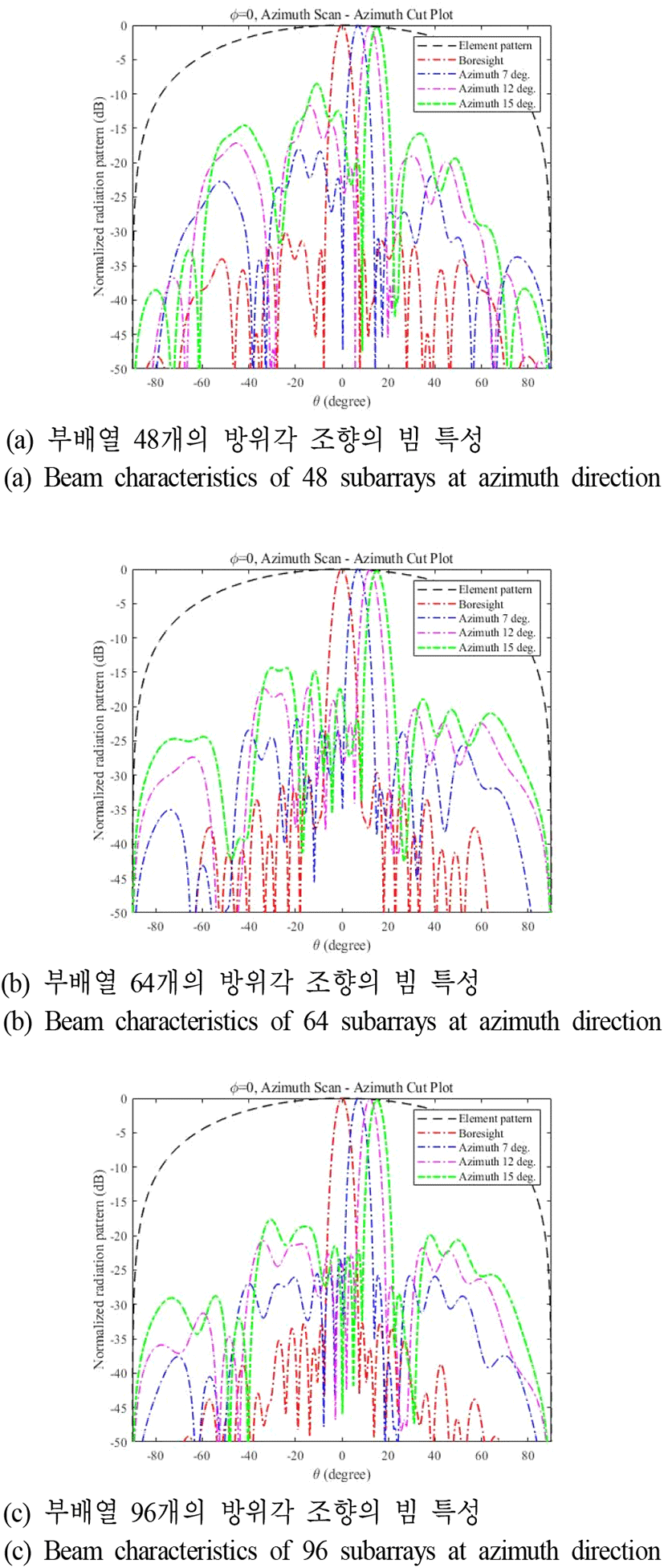
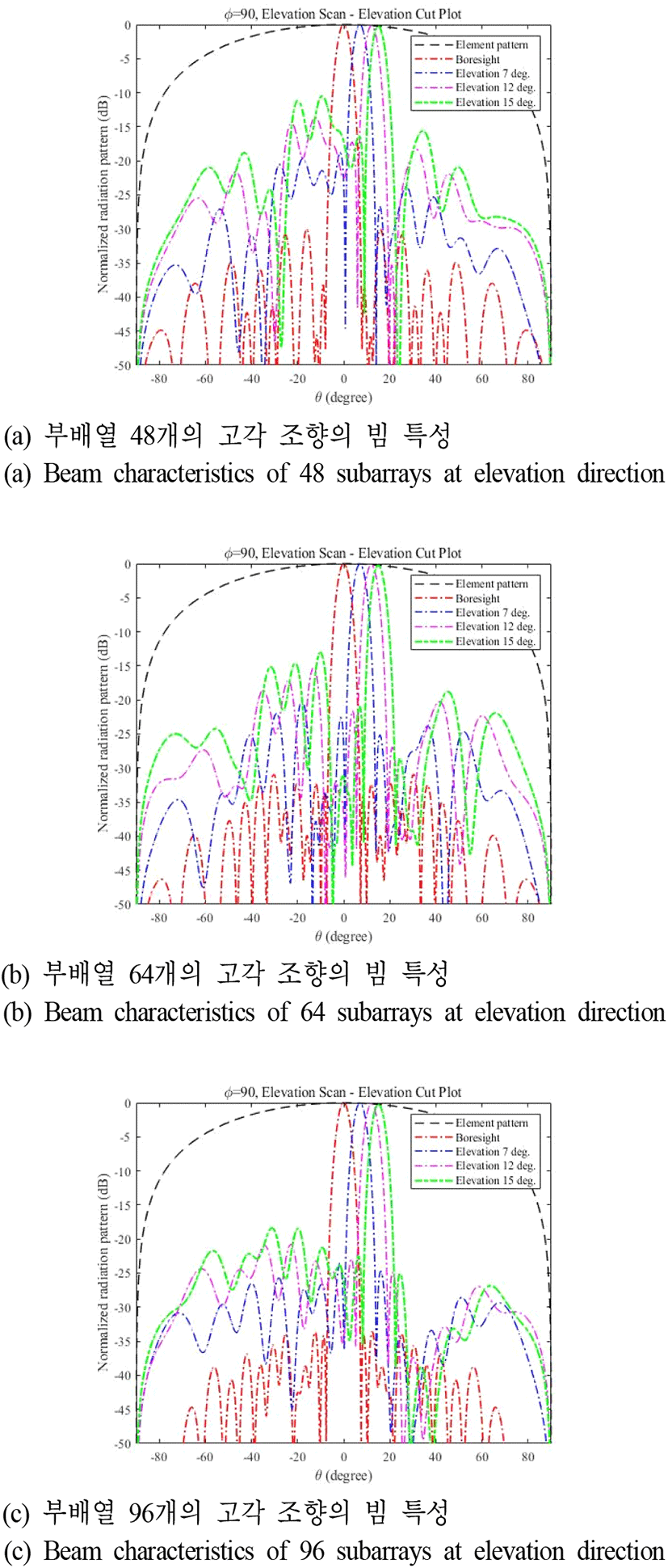
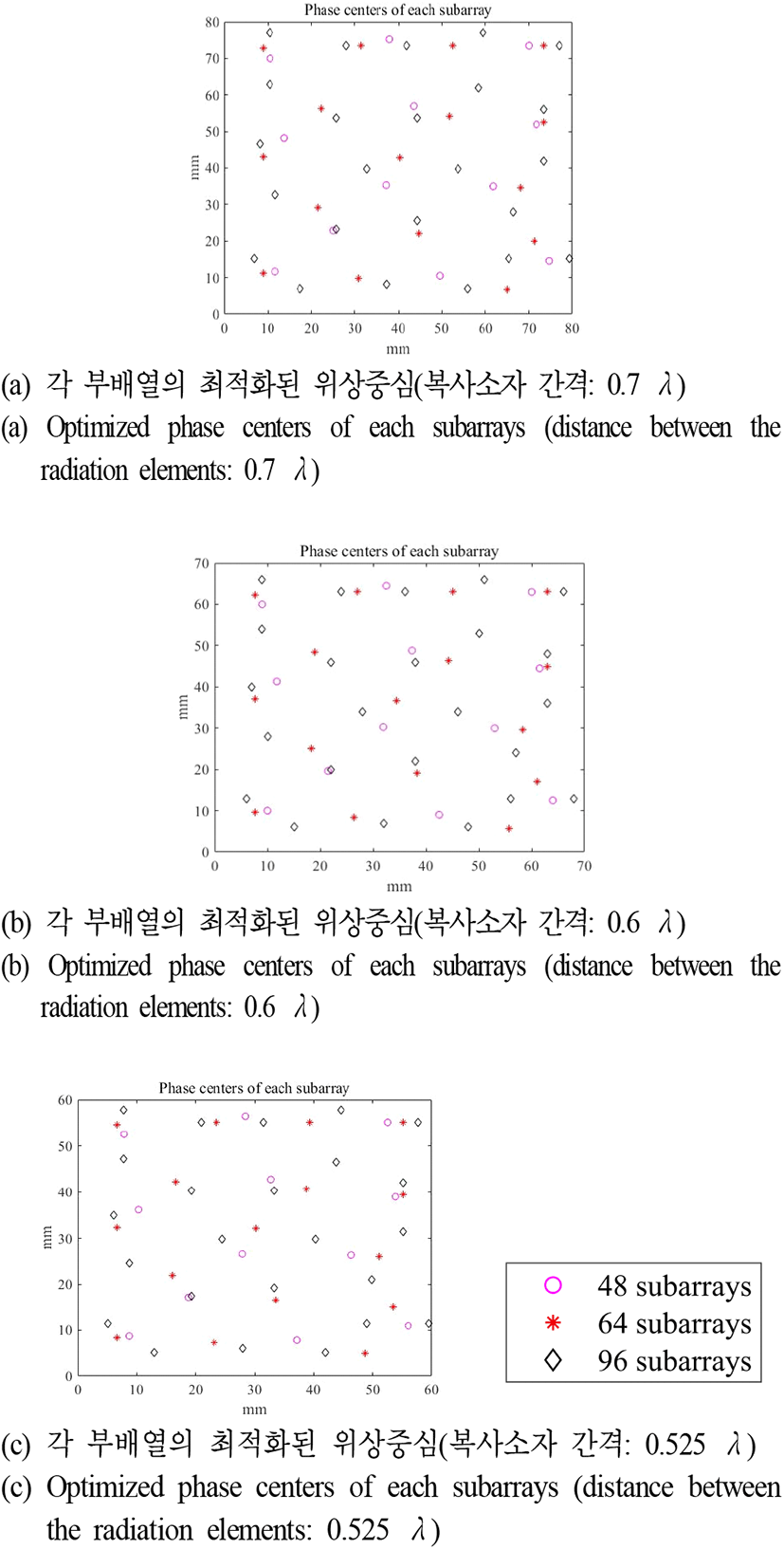
그림 13은 부배열의 개수 및 복사소자 간격 변화에 따른 각 부배열간 위상중심을 보여주고 있다. 부배열 개수가 적은 경우, 부배열 간의 간격이 큰 상태가 되므로 빔 조향 시 grating effect에 영향을 크게 받게 되어 빔 조향 시 높은 부엽준위가 나타나게 된다. 그러나 부배열의 개수를 증가시킨 경우, 부배열간 위상중심 간의 거리가 좁아지므로 grating effect의 영향이 작아져, 상대적으로 넓은 빔을 조향하더라도 적은 부배열 개수를 가진 배열안테나에 비해 작은 부엽준위를 가지게 된다. 마찬가지로 복사소자 간격을 줄인 경우, 부배열 간의 간격이 작아지는 상태가 되므로 grating effect의 영향을 적게 받게 되며 상대적으로 넓은 빔을 조향하더라도 소자 간격이 넓은 배열안테나보다 작은 부엽준위를 가지게 된다. 대신에 안테나 개구면적이 작아지게 되어 반전력 빔폭은 넓어지게 된다.
Ⅳ. 동일 부배열 개수 및 동일 개구 크기 조건 하에 복사소자 개수 변화에 따른 빔 특성 변화
Section Ⅲ의 분석에 따르면 부배열의 개수가 많을수록 복사소자 간격이 작을수록 빔 조향 시 상대적으로 낮은 부엽준위가 확보된다는 것을 확인할 수 있다. 이번 장에서는 복사소자 간격을 줄이고 복사소자 개수를 증가시킴으로써, 안테나 개구면적을 동일시하였고 부배열의 개수도 동일하게 하여 빔 조향에 따른 빔 특성을 분석하였다.
표 7은 비교 분석할 배열안테나의 configuration을 소개한다. Case 1의 경우 Section Ⅲ에서 빔 특성을 제시하였으므로 본 장에서는 case 2, 3의 경우에 대해 제시하고 이들의 빔 특성 분석을 수행한다.
| Radiation elements spacing | Aperture size | Number of radiation elements | Number of subarrays | |
|---|---|---|---|---|
| Case 1 | 0.7 λ | 16.8 λ2 | 24×24 | 96 |
| Case 2 | 0.6 λ | 16.8 λ2 | 28×28 | 96 |
| Case 3 | 0.525 λ | 16.8 λ2 | 32×32 | 96 |
그림 2에서 소개된 최적화 알고리즘을 활용하여 case 2, 3에 대하여 부배열 구조 및 급전신호 최적화를 수행하였으며, 최적화가 완료된 부배열 구조 및 급전신호 분포를 그림 14와 그림 15 및 그림 16 에 제시한다. 여기서 그림 14는 case 2와 case 3에 대하여 최적화가 완료된 부배열 구조의 1 사분면을 보여주고 있으며 최적화된 부배열 구조는 제시된 1 사분면의 원점대칭 형태이다. 그림 15와 그림 16은 방위각 및 고각 조향시 낮은 부엽준위를 확보하기 위한 급전신호 크기 분포도이다.

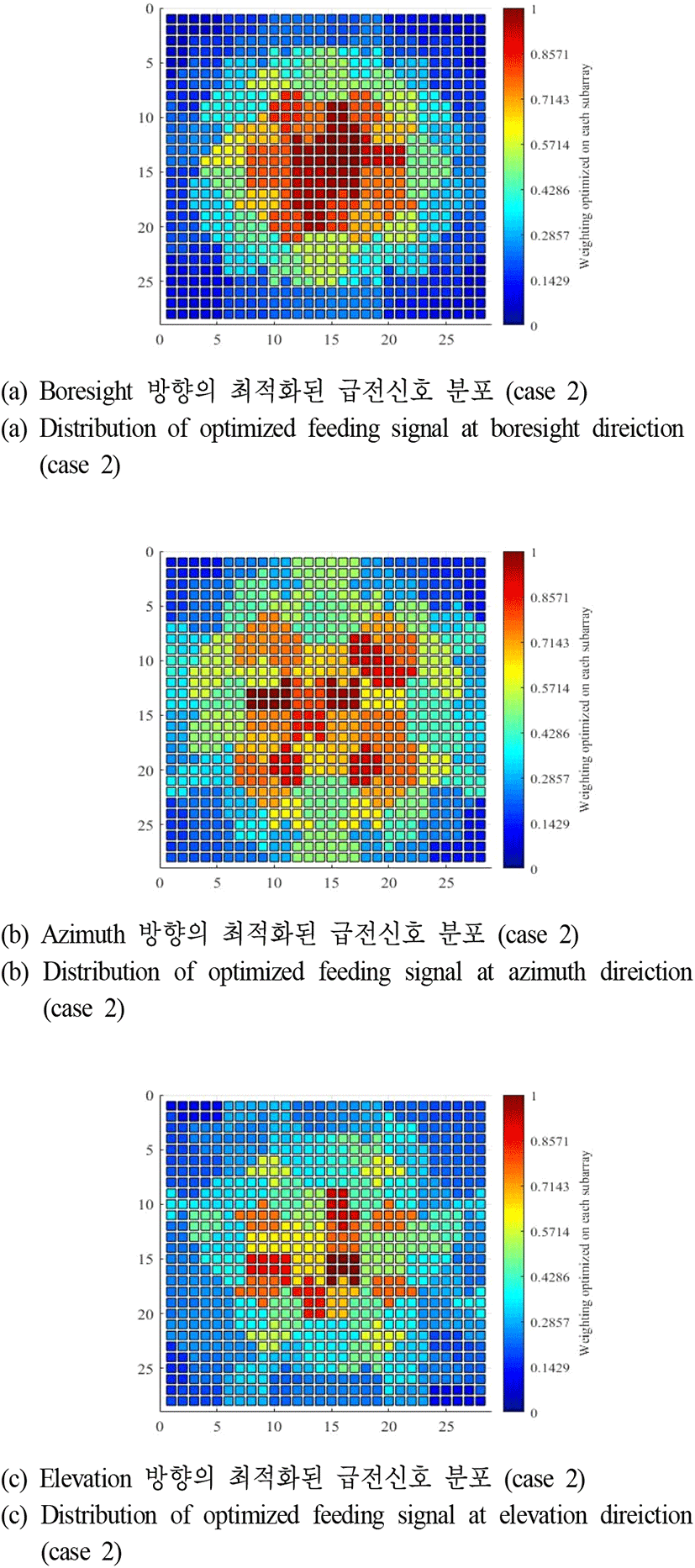
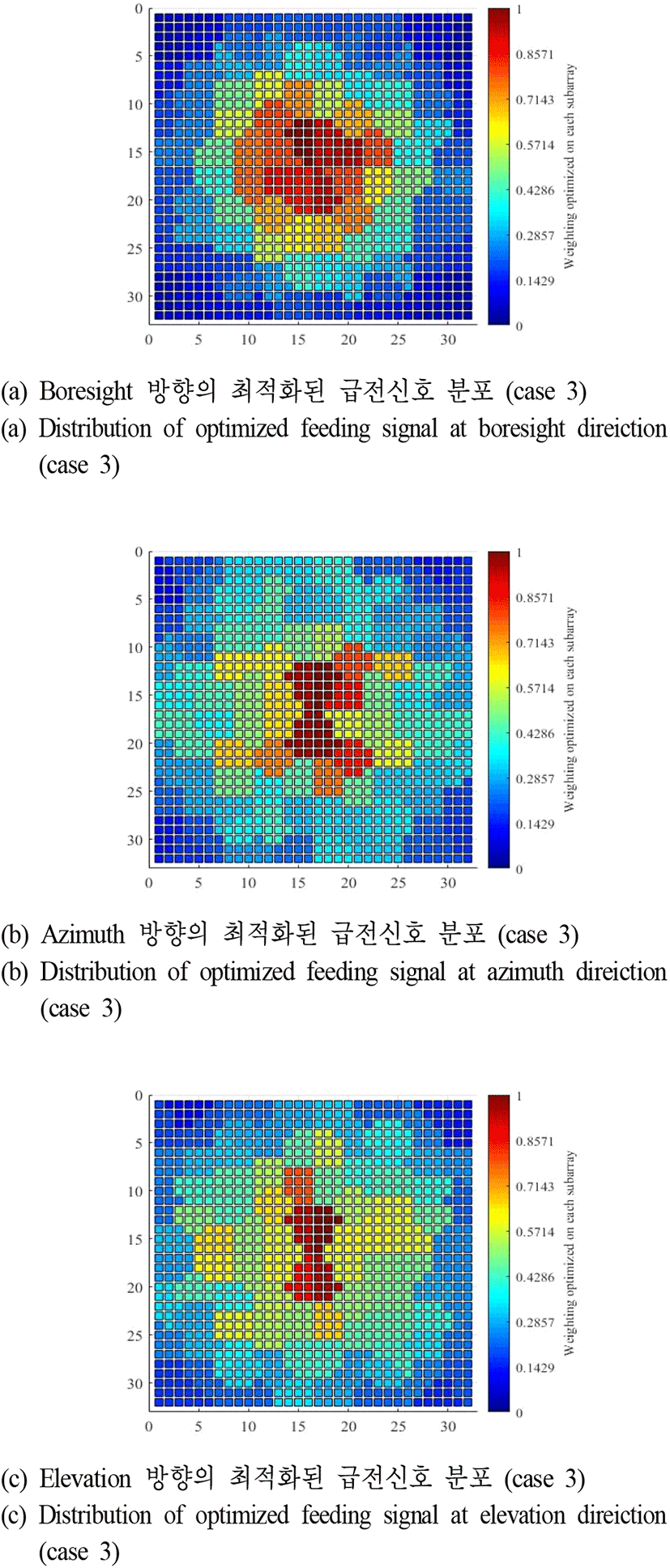
그림 17과 그림 18은 case 2, 3의 방위각, 고각 조향시 빔 특성을 보여주고 있으며, 이에 대하여 표 8 및 표 9에 정리하였다. 빔 조향 법위가 증가할수록 부엽준위가 증가하는 것을 확인할 수 있다. Case 2와 case 3는 case 1보다 복사소자 간격이 줄어 들었으나, boresight 및 빔 조향 시 부엽준위의 크기가 감소하지 않고 비슷한 수준을 유지하는 것을 확인할 수 있다. 표 8 및 표 9를 통하여 정량적으로 빔 조향에 따른 빔 특성 수치를 제시한다.
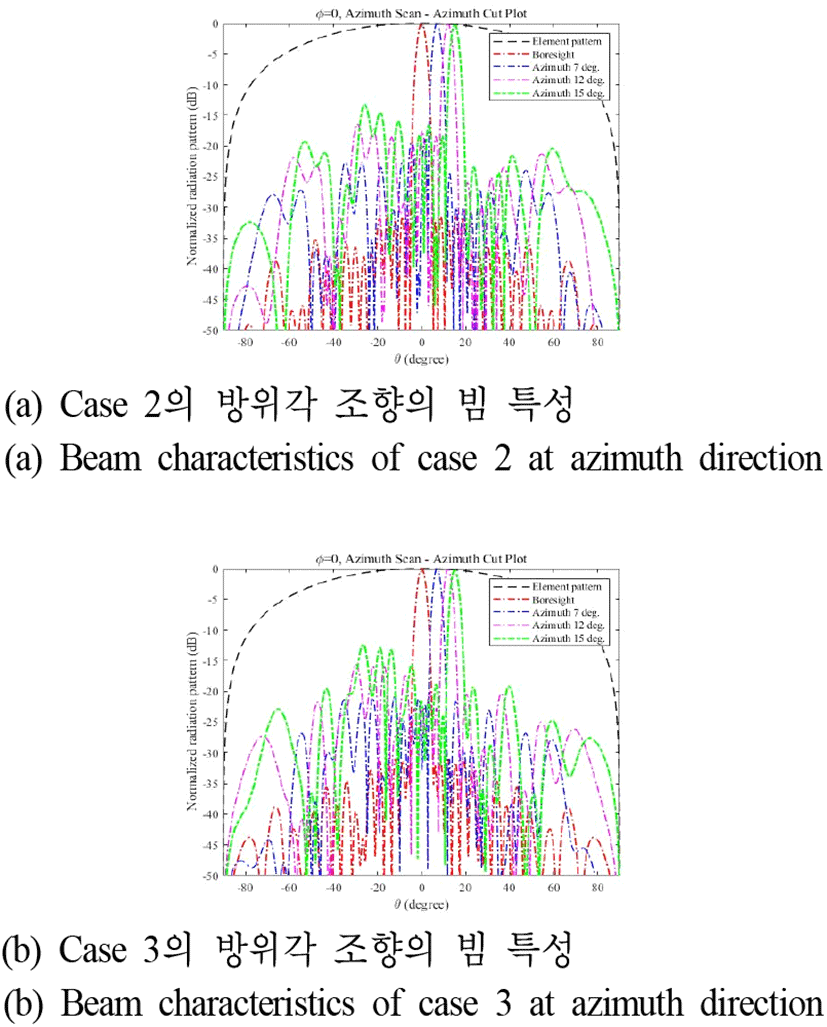
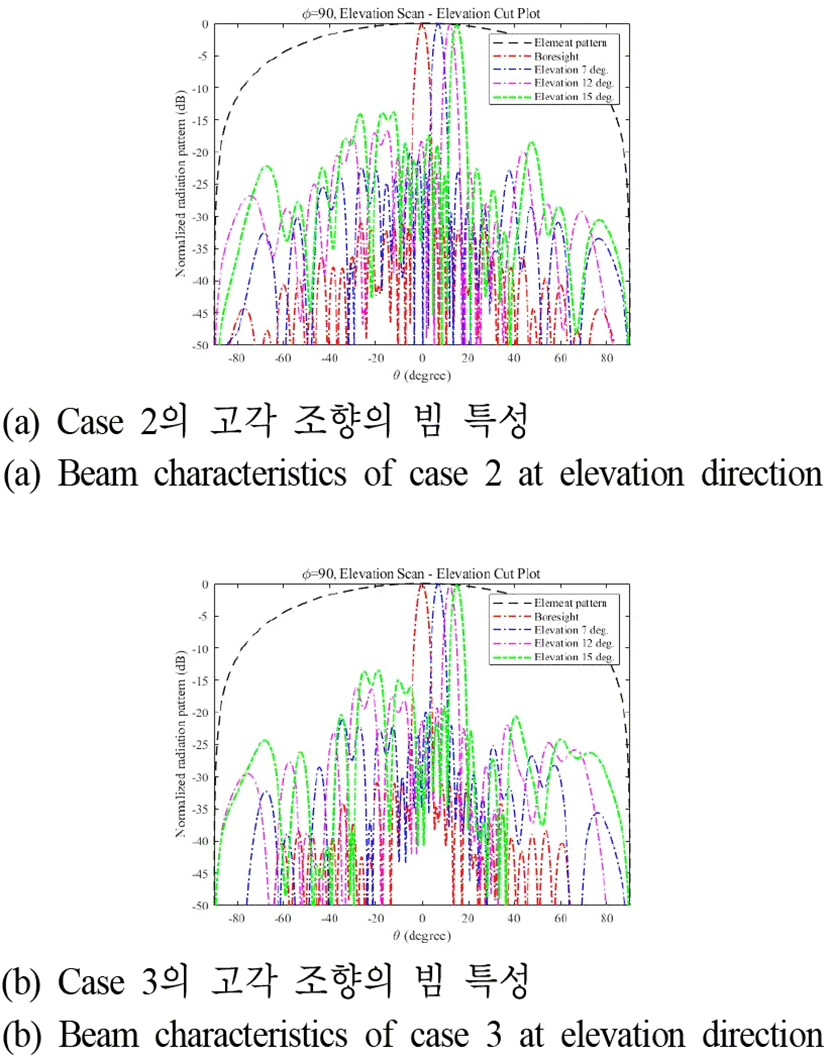
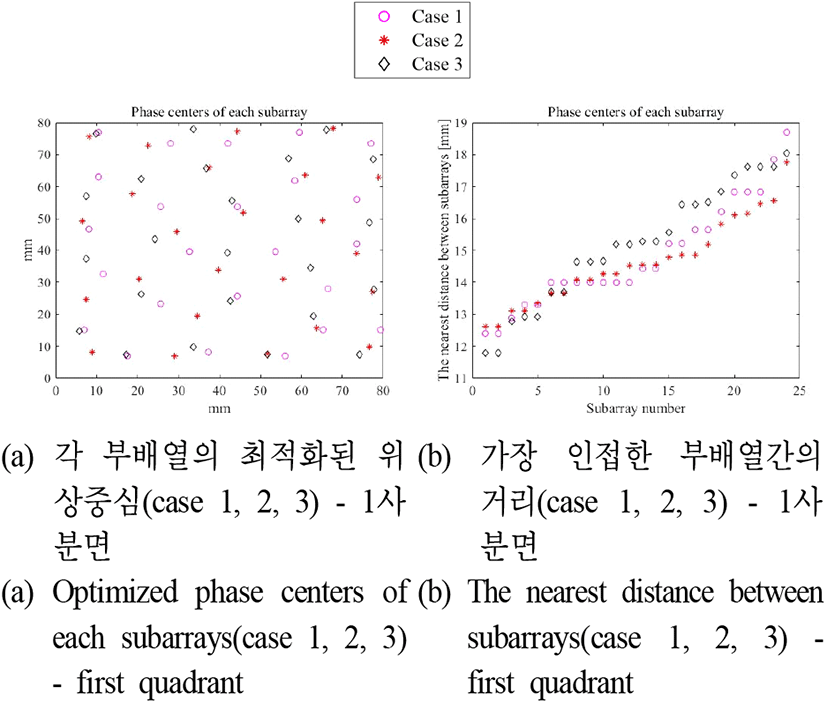
그림 19는 case 1, 2, 3에 대하여 1사분면에 대하여 각 부배열의 위상 분포와 각 부배열의 위상중심과 가장 인접한 부배열의 위상중심간의 거리를 보여주고 있다. Case 1의 복사소자 간격이 가장 크지만 case 1, 2, 3의 부배열 위상중심의 분포와 인접한 부배열과의 위상중심 사이 간격에는 큰 차이가 없는 것을 확인할 수 있다. 복사소자의 간격을 줄였으나 복사소자를 증가하여 안테나의 개구면을 동일하게 하였으며, 안테나의 개구면적에 할당되는 부배열의 개수도 동일하므로 각 부배열의 위상중심간의 거리는 좁혀지지 않아 case 1, 2, 3의 부엽준위 크기가 비슷한 수준을 가지게 된다.
Ⅴ. 결 론
본 논문에서는 위상배열안테나에 부배열을 적용하기 위한 부배열 설계 및 급전신호 크기 최적화 방법에 대하여 소개하였다. 부배열 구조 및 급전신호를 최적화하고, 복사소자 간격과 부배열 개수를 다르게 설정하였을 때 빔 특성을 비교 분석하였다. 또한, 동일한 개구면적 및 부배열 개수의 조건하에 복사소자 간격 변화에 따른 부엽준위 특성을 비교 분석하였다. 동일한 개구면적에서 부배열의 개수가 증가할수록 빔 조향 시 낮은 부엽준위를 달성하였으며, 복사소자 간격이 좁을수록 빔 조향 시 낮은 부엽준위가 달성되었다. 그러나 동일한 개구면적과 동일한 부배열 개수의 조건하에 복사소자 간격을 줄인 경우, 부엽준위의 변화가 없는 것이 확인되었다. 따라서, 빔 조향 시 낮은 부엽준위를 확보하기 위해서는 부배열 개수를 증가시키고 복사소자 간격을 좁은 상태로 배열함으로써 위상중심 간의 거리를 작게 형성하여 낮은 부엽준위를 달성할 수 있다. 본 논문은 부배열 TRM이 적용된 능동위상배열 안테나의 FoV 분석에 활용 가능할 것으로 기대된다.











