특집논문/SPECIAL EDITION
육각형 형상의 광대역 전자기파 메타물질 흡수체 단위 셀 최적 설계
Optimal Design of Broadband Hexagonal Electromagnetic Metamaterial Absorber Unit Cells
Yongjune Kim*
,
Sun-Gyu Lee1
,
Jeong-Hae Lee1,†
Author Information & Copyright ▼
*Metamaterial Electronic Device Research Center, Hongik University
1Department of Electronic and Electrical Engineering, Hongik University
© Copyright 2021 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the
Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits
unrestricted non-commercial use, distribution, and reproduction in any
medium, provided the original work is properly cited.
Received: Apr 12, 2021; Revised: May 06, 2021; Accepted: May 25, 2021
Published Online: Jun 30, 2021
요약
전자기파 메타물질 흡수체는 전도성 패턴을 기반으로 우수한 전자기파 흡수 성능을 구현할 수 있는 차세대 전자기파 흡수체이다. 메타물질 흡수체는 단위 셀이 주기적으로 배치되었을 때 우수한 흡수 성능이 구현되므로, 기존 사각형 테두리를 갖는 메타물질 흡수체를 주기적인 배치가 어려운 임의의 내각을 갖는 다각형 또는 입체의 모서리 부분에 적용할 경우 성능이 급격히 열화되는 문제점을 갖는다. 본 논문에서는 내각이 60° 또는 120°를 이루는 모서리 구조에 적용하여도 단위 셀이 연속적으로 연결될 수 있는 육각형 형상의 전자기파 메타물질 흡수체 단위 셀의 최적 설계 방법을 제시한다. 전도성 패턴을 최적 형상으로 설계하기 위해 적응형 유전 알고리즘을 이용한 타일링 방법이 제안되었으며, TE (transverse electric) 및 TM (transverse magnetic) 편파에 대해 동시에 최적화를 진행하여 두 편파 모두에 대해 X 밴드 전체에서 반사율이 –10 dB 이하로 감소된 시뮬레이션 결과를 확인하였다. 최적의 성능을 나타낸 축 대칭 형상의 패턴의 경우 최대 45°의 경사 입사에 대해 반사율이 –8 dB 이하로 감소되었다. 설계 결과의 정확도는 유한 요소 기법 기반의 서로 다른 수치 해석 툴을 이용한 해석 결과의 비교를 통해 검증하였다.
Abstract
Electromagnetic (EM) metamaterial absorbers are new types of EM absorbers that can absorb the EM waves via conductive patterns. The performances of the EM metamaterial absorbers can be guaranteed when the unit cells of them are connected periodically. Therefore, the absorbing performances based on square unit cells may be degraded significantly when they are applied to a polygonal area or a corner that do not allow the periodic connection. In this paper, an optimization method is proposed for hexagonal EM metamaterial absorber unit cells that can be connected periodically for the c orners of which the interior angles are 60° or 120°. To achieve optimal hexagonal patterns, a tiling method is proposed based on an adaptive genetic algorithm. By minimizing the reflectances for both the transverse electric (TE) and transverse magnetic (TM) polarizations, the −10 dB reflectances were confirmed in the X band for the two polarizations simultaneously. Based on the finalized axially symmetric pattern along six axes, the −8 dB reflectances were confirmed in the same band for the oblique incidence with the vertical angle up to 45°. By comparing simulation results calculated by two different commercialized simulators based on the finite element method, the accuracy of the design was verified.
Keywords: Electromagnetic Metamaterial Absorber; Broadband; Hexagonal Pixel; Tiling; Genetic Algorithm
Ⅰ. 서 론
전자기파 흡수체(electromagnetic absorber)는 페라이트 (ferrite)[1], 카본(carbon)[2] 등 복합재를 기반으로 전자기파 에너지를 열로 변환하여 전자기파를 흡수할 수 있는 소재이다. 전자기파 흡수체는 우수한 전자기파 흡수 성능을 바탕으로 아군 무기체계에서 반사되는 전자기파 신호를 감소시킬 수 있는 국방 스텔스[3] 및 무선 통신 단말기, 레이다 등에서 발생하는 전자기파 간섭 방지용 소재[4]로 광범위하게 응용되고 있다. 하지만 복합재 기반 전자기파 흡수체는 상대적으로 부피가 크고 무거운 단점을 갖는다.
최근 주목받고 있는 전자기파 메타물질 흡수체 (metamaterial absorber)는 전도성 패턴과 비교적 얇은 두께의 유전체, 그리고 금속 반사 층을 결합하여 공기와의 임피던스 정합뿐만 아니라, 패턴에서 발생하는 높은 저항 손실(ohmic loss)을 이용하여 전자기파 반사율을 획기적으로 낮출 수 있는 차세대 전자기파 흡수체이다[5]~[12]. 전자기파 메타물질 흡수체는 전도성 패턴 최적화를 바탕으로 광대역, 광각 흡수 성능을 구현할 수 있는 장점을 갖는다 [6]~[11]. 하지만 사각형 형상의 테두리를 갖는 기존 메타물질 흡수체의 경우, 배치 시 단위 셀 간의 엇갈림에 의해 주기적인 배치가 어려운 다각형 또는 입체의 모서리 구조에 적용이 어려운 한계를 갖는다. 본 논문에서는 내각이 60° 또는 120°를 이루는 모서리 구조에 적용하여도 단위 셀이 연속적으로 연결될 수 있는 육각형 형상의 전자기파 메타물질 흡수체 단위 셀의 최적 설계 방법을 제시한다.
Ⅱ. 설계 방법
육각형 경계면을 갖는 단위 셀 내부에 육각형 전도성 픽셀을 최적으로 배치하기 위해 유전 알고리즘[13] 기반의 타일링[14] 방법을 제안하였다. 이 때 육각형 단위 셀의 한 변의 길이는 12 mm로 설정하였고, 육각형 전도성 픽셀의 한 변의 길이는 0.5 mm로 설정하였다. 전도성 픽셀을 구성하는 물질은 높은 저항 손실을 갖는 카본 잉크를 가정하였다. 카본 잉크의 면 저항 Rs는 100 Ω/sq으로 설정하였으며[15], 패턴 두께 d 가 20 μm일 때 전도도 σ는 식 (1)을 이용하여 500 S/m로 계산된다[16].
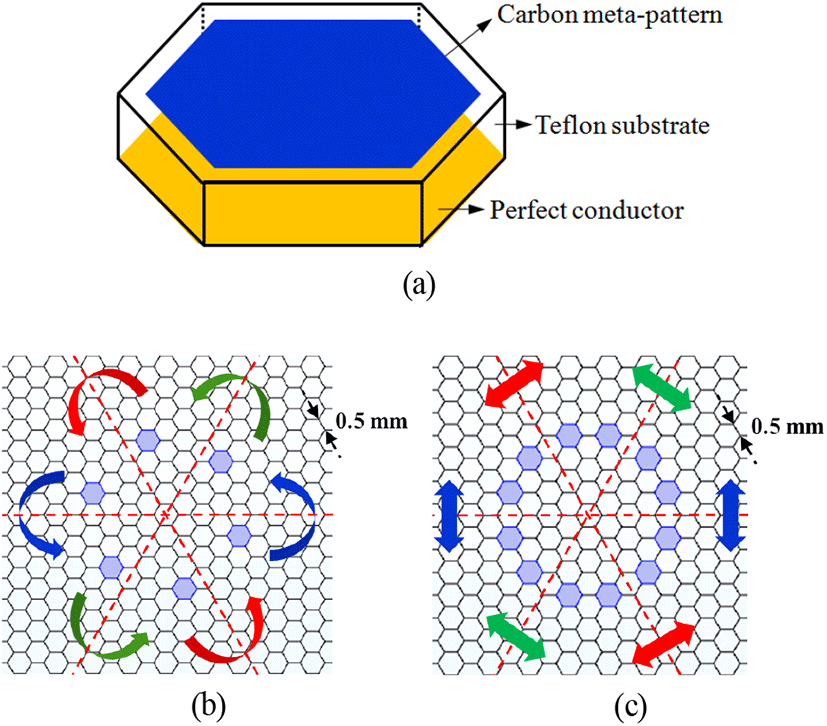
육각형 단위 셀 내부에 배치된 전도성 패턴은 그림 1(a)와 같이 바닥면을 완전 도체로 설정한 테플론 기판 상단에 결합되며, X 밴드 전체에서 반사율이 −10 dB 이하로 낮아지도록 설계를 진행하였다. X 밴드 중심 주파수인 10 GHz를 기준으로 테플론 기판의 유전율은 4.1-i0.014를 사용하였고, 카본 잉크의 상대 유전율의 실수부는 약 8.72이다[17]. 이때 카본 잉크는 폴리이미드 필름에 인쇄한 뒤 기판에 부착하는 것을 가정하였다[11]. 유전 손실(Dielectric loss)에 비해 전도성 손실(Conduction loss)이 매우 크다고 가정하였을 때, 카본 잉크의 유전율의 허수부 ϵ″는 식 (2)를 이용하여 주파수 f가 10 GHz일 때 근사적으로 898.76으로 계산된다[18]. 이때 ϵ0은 자유 공간에서의 유전율을 나타낸다.
그림 1. | Fig. 1.
육각형 형상의 전자기파 메타물질 흡수체 단위 셀 구성도 (a) 단위 셀 전체 모식도, 여섯 축에 대해 (b) 회전 대칭 및 (c) 축 대칭으로 묶인 육각형 픽셀 쌍 설정 예시. | Hexagonal electromagnetic metamaterial absorber unit cells. (a) An overall schematic. Examples of (b) Rotationally symmetric and (c) Axially symmetric groups of hexagonal pixels along the six axes.
Download Original Figure
육각형 전도성 픽셀은 그림 1(b), 그림 1(c)와 같이 육각형 경계면 내부의 여섯 축에 대해 회전 또는 축 대칭을 이루도록 배치하였다. 그림 1(b)와 같이 여섯 축에 대해 회전 대칭을 이루는 픽셀들을 하나의 쌍으로 묶고 카본이 채워지는 경우는 1, 공기가 채워지는 경우는 0에 해당되도록 설정하여 이를 1과 0으로 구성된 비트(Bit) 배열로 인코딩(encoding) 할 수 있다. 또한 그림 1(c)와 같이 여섯 축에 대해 축 대칭을 이루는 픽셀들을 쌍으로 묶은 뒤 카본 또는 공기로 채워지는 경우를 1과 0으로 지정할 수 있다. 그림 1(b)와 같이 회전 대칭을 이루도록 지정한 경우 인코딩된 비트 배열은 총 92개의 비트로 구성되며, 그림 1(c)와 같이 축 대칭을 이루도록 지정한 경우, 총 56개의 비트로 구성된다.
앞서 그룹으로 지정된 육각형 픽셀 쌍의 물성을 카본 또는 공기로 지정하기 위해 유사 난수(pseudo-random number) 발생 함수를 이용하여 회전 및 축 대칭 각각에 대해 92개와 56개의 비트로 구성된 랜덤 배열을 생성하였다. 이를 바탕으로 인코딩 과정과 반대로 육각형 픽셀 쌍에 랜덤 생성된 배열의 비트가 1인 경우 카본 물성을 설정하고, 0인 경우 공기 물성을 설정하는 디코딩 (decoding) 과정을 수행할 수 있다. 랜덤 배열 개수는 배열에 포함된 비트 개수만큼 회전 대칭의 경우 92개, 축 대칭의 경우 56개 생성하여 충분히 많은 개수의 조합이 탐색될 수 있도록 하였다[13].
디코딩된 육각형 픽셀 배열 기반 메타물질 흡수체는 유한 요소 기법 기반의 상용 수치해석 툴인 COMSOL Multiphysics를 이용하여 전파 해석(full-wave simulation)하였다. 시뮬레이션 시간 단축 및 메모리 절약을 위해 전파 해석 시 육각형 픽셀의 경우, 2차원 면 구조에 전도도와 두께를 지정하여 해석할 수 있는 transition boundary condition을 이용하여 설계를 진행하였다[19]. 또한 편파 변화에 따른 메타물질 흡수체의 성능 차이를 최소화하기 위해 입사 평면(plane of incidence)인 x-z 평면에 전기장이 수직인 TE 편파(transverse electric polarization)와 자기장이 수직인 TM 편파(transverse magnetic polarization) 모두에 대해 해석하였다. TE 및 TM 편파는 III 장에 포함된 그림 2~그림 4에 자세히 표시하였다. 해석 결과를 바탕으로 성능 지수(figure of merit)를 계산하여 최적의 성능 지수를 갖는 한 쌍의 배열을 선택하였다. 성능 지수는 X 밴드 내 세 개의 주파수 8, 10, 12 GHz에서 TE, TM 편파 모두에 대한 반사율의 합을 계산한 뒤 더해진 개수로 나눈 평균 값을 사용하였다.
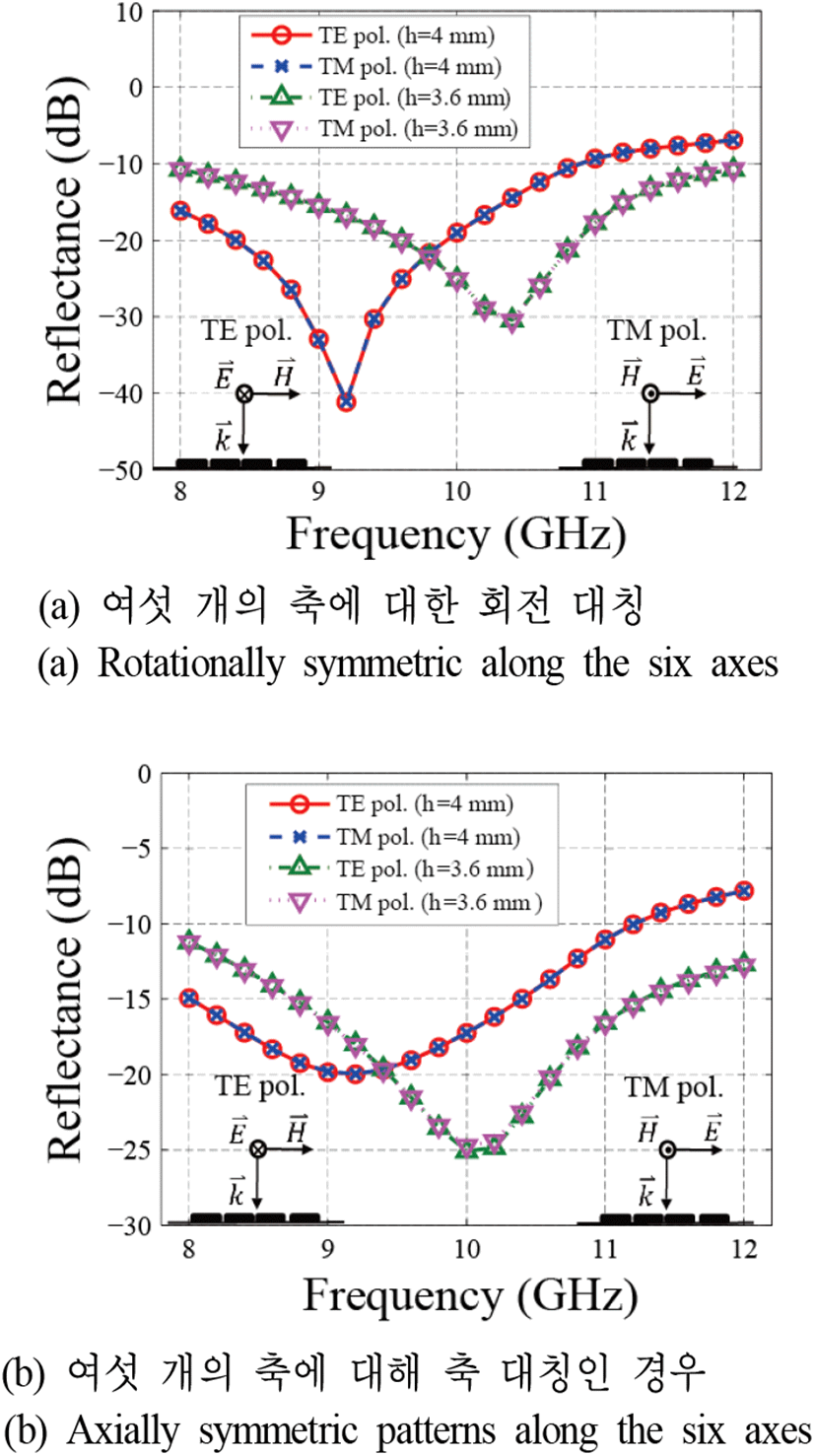
그림 2. | Fig. 2.
테플론 기판 두께 h를 4 mm에서 3.6 mm로 조정하기 전, 후 수직 입사 조건에서의 반사율 시뮬레이션 결과 | Reflectances for normal incidences with TE and TM polarizations before and after adjusting the thickness of the teflon substrate from 4 mm to 3.6 mm.
Download Original Figure
선택된 한 쌍의 배열에는 유전 알고리즘의 교차(cross), 변이(mutation) 연산을 적용하여 이전 조합 개수와 동일한 개수의 배열을 새로 생성하였다. 이때 교차 연산은 한 쌍의 배열을 구성하는 비트 중 임의의 비트를 선택한 뒤, 그 비트 이후에 위치한 비트 전체를 배열끼리 서로 맞바꾸는 방식으로 연산하였다. 교차 연산은 배열을 구성하는 비트 개수의 1/4에 해당하는 횟수만큼 회전 대칭의 경우 23번, 축 대칭의 경우 14번 적용하였다. 변이 연산은 회전과 축 대칭 모두 각각의 배열에 포함된 비트 중 임의로 5개의 비트를 선택하여 0과 1을 반전시키는 방법으로 연산을 수행하였다. 초기 랜덤으로 생성된 배열에서 최적의 한 쌍의 배열을 선택한 방법과 마찬가지로 유전 알고리즘으로 생성된 배열 중 성능 지수 비교를 통해 최적의 한 쌍의 배열을 다시 선택하였다. 이와 같은 과정을 반복하여 X 밴드 대역 내에서 −10 dB 반사율을 충족시키는 최적의 패턴을 도출하였다.
Ⅲ. 시뮬레이션 결과
육각형 픽셀이 여섯 축에 대해 회전 또는 축 대칭을 갖도록 배치된 메타물질 흡수체는 유전 알고리즘 연산 과정을 각각 17회, 12회 반복한 후 최적의 성능 지수가 확인되었다. 이때 확인된 성능 지수는 회전 및 축 대칭 각각에 대해 0.057과 0.075이다. 전파 해석 시 테플론 기판의 두께 h는 4 mm로 고정하여 설계를 진행하였으며, 회전 및 축 대칭 설계 결과, 모두 그림 2(a)와 같이 중심 주파수가 낮은 주파수 영역으로 이동된 결과를 확인하였다. 그림 2는 그림 내부에 포함시킨 모식도와 같이 TE 및 TM 편파를 메타물질 흡수체 상부 표면을 기준으로 수직 입사시켰을 때 계산된 반사율을 나타낸다.
설계 단계에서 기판의 두께를 이진법으로 표현한 뒤 유전 알고리즘에 포함시켜 최적화를 진행하거나 성능 지수 계산 시 주파수 성분 별로 가중치를 곱하여 설계하는 방법도 가능하지만, 본 논문에서는 기판 두께를 고정하여 설계한 뒤, 목표 성능에 맞게 두께를 재조정하는 적응형 유전 알고리즘[13] 방법을 적용하였다. 적응형 유전 알고리즘은 구체적으로 공진 주파수에 가장 큰 영향을 미치는 기판 두께의 조정을 통해 낮은 주파수 쪽으로 이동된 공진 주파수를 중심 주파수 근처에 위치시킨 뒤 패턴 최적화를 다시 진행하는 방법을 의미한다. 제안된 방법은 주파수 성분에 가중치를 적용하는 방법보다 단순하면서 직관적으로 최적화 방향을 설정할 수 있어 시행 착오를 최소화할 수 있고, 최적화 대상을 패턴으로 한정시켜 두께까지 유전 알고리즘을 통해 최적화하는 방법보다 설계 시간을 단축시킬 수 있는 장점을 갖는다.
적응형 방법으로 중심 주파수를 상향 이동시키기 위해 기판 두께 h를 3.6 mm로 조정하였으며, 그 결과 그림 2(b)와 같이 중심 주파수가 10 GHz 근처로 이동하고, X 밴드 대역 전체에서 반사율이 −10 dB 이하로 감소된 결과를 확인하였다. 기판 두께를 3.6 mm로 고정시킨 뒤 회전 및 축 대칭 패턴 각각에 대해 8회, 10회의 유전 알고리즘 연산을 다시 반복하여 추가 최적화를 진행하였다. 그 결과, 성능 지수는 회전 및 축 대칭 설계에 대해 각각 0.044와 0.042로 최종 확인되었다. 성능 지수는 반사율의 합으로 계산되므로 성능 지수가 낮을수록 흡수 성능이 향상된 것으로 판단할 수 있으며, 이는 중심 주파수가 10 GHz 근처로 이동하면서 X 밴드 내의 반사율이 전체적으로 낮아졌음을 의미한다.
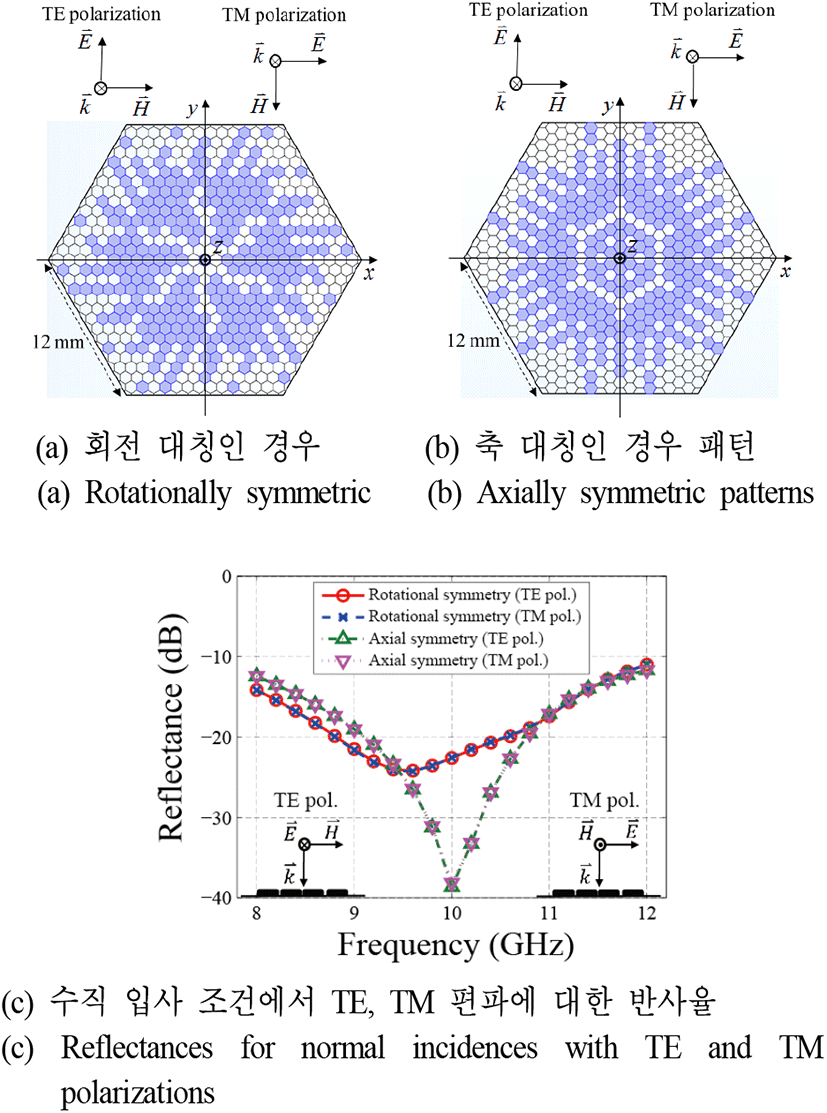
회전 및 축 대칭 형상을 갖는 최적화된 패턴은 각각 그림 3(a), 그림 3(b)와 같으며, TE 및 TM 편파를 이용한 수직 입사 시 계산된 반사율은 그림 3(c)와 같다. 그림 3(c)로부터 회전 및 축 대칭 형상의 패턴 모두 TE, TM 편파에 대해 X 밴드 전체에서 −10 dB 이하의 반사율을 만족함을 확인하였다. 두 결과 중 패턴을 회전 대칭으로 설계하였을 때보다 축 대칭으로 설계한 경우 X 밴드 내에서 반사율이 더 낮은 결과를 확인할 수 있다. 따라서 최종 패턴으로 축 대칭 형상을 나타내는 그림 3(b)를 선택하였다.
그림 3. | Fig. 3.
최종 설계된 메타물질 흡수체 패턴 및 시뮬레이션 결과 | Final patterns and simulation results of hexagonal metamaterial absorbers.
Download Original Figure
그림 4는 측정을 대신하여 comsol multiphysics를 이용하여 설계한 패턴의 정확도를 검증하기 위해 축 대칭으로 설계된 그림 3(b)를 유한 요소 기법 기반의 또 다른 상용 툴인 HFSS로 해석한 결과를 나타낸다. 그림 3(c)는 시뮬레이션 시간 단축을 위해 육각형 픽셀을 2D 구조로 근사적으로 해석하여 설계한 결과이므로, 보다 정확한 검증을 위해 Comsol Multiphysics와 HFSS 모두 육각형 픽셀을 3D 구조로 해석하였다. 또한 반사율의 감소와 흡수율의 연관성을 검증하기 위해 Comsol Multiphysics를 이용하여 1로 정규화된 전체 power와 흡수율의 차이를 계산한 뒤 반사율과 그 결과를 비교하였다[8]~[10]. 흡수율은 메타물질 흡수체를 구성하는 매질 내부에서 power dissipation density를 적분하여 계산한 전력 손실 총량[19]과 입사된 전체 power의 비로 계산하였다. 만약 전체 power 1에서 반사율을 뺀 결과가 반사율과 일치하지 않을 경우, 그 차이는 흡수되지 않고 산란된 power 비율로 간주할 수 있다[10].
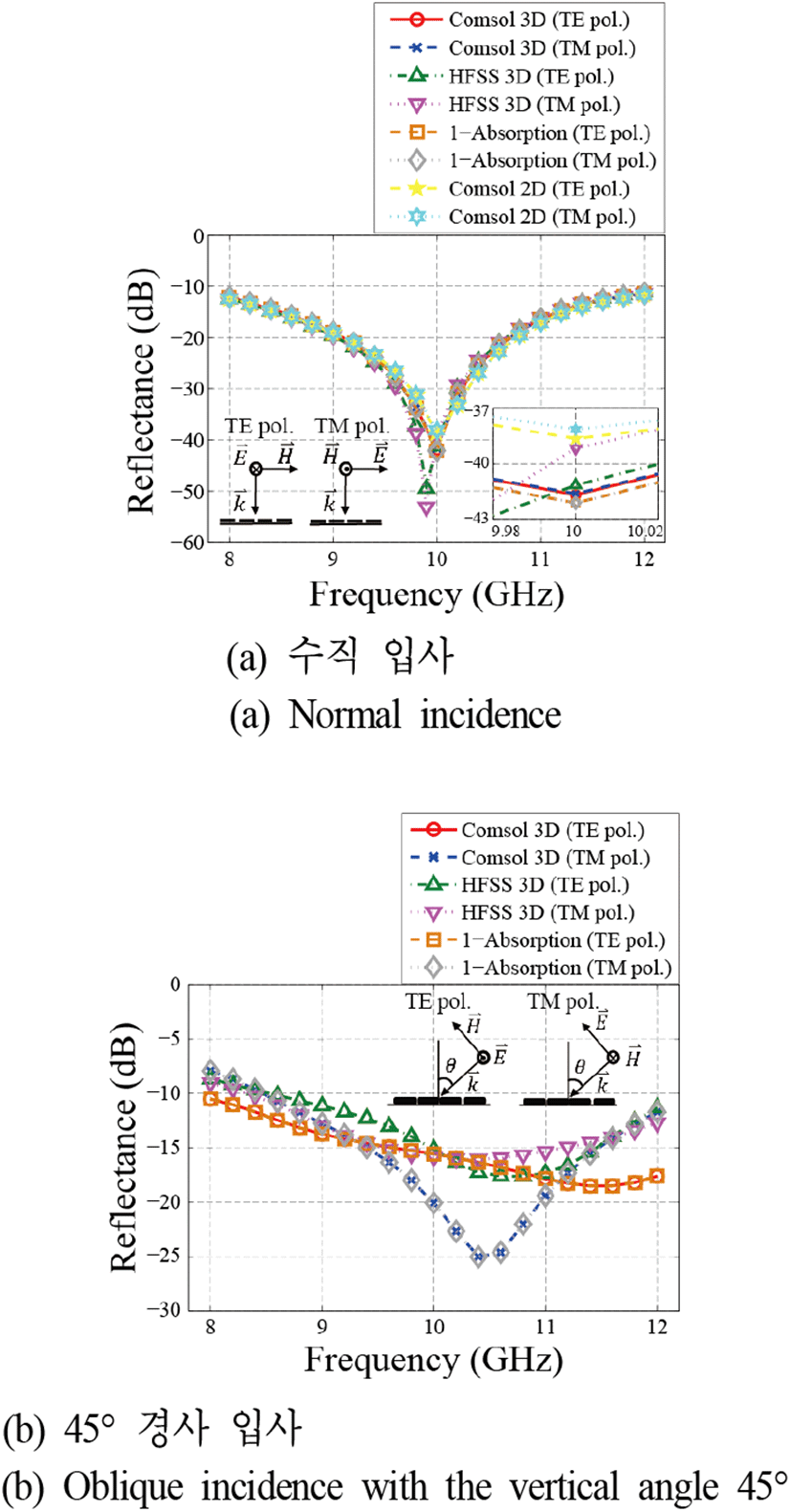
그림 4. | Fig. 4.
Comsol multiphysics와 HFSS 해석 결과 비교 | Comparison between simulation results of comsol multiphysics and HFSS.
Download Original Figure
그림 4(a)는 수직 입사에 대한 비교를 나타내며, 그림 4(b)는 45도 경사 입사 시 계산된 반사율을 비교한 결과이다. 그림 4(a)와 그림 4(b)로부터 수직 입사 및 45도 경사 입사 시 반사율이 X 밴드 전체에서 각각 −10 dB와 −8 dB 이하로 감소함을 확인하였다. 그림 4(a)로부터 Comsol Multiphysics와 HFSS 해석 결과 사이에 0.1 GHz의 주파수 차이가 확인되었으나, 전체적인 경향성과 반사율의 크기는 서로 잘 일치하는 결과를 확인하였다. 그림 4(a) 내부에 포함된 그래프는 10 GHz 부근을 확대한 그래프를 나타낸다. 1로 정규화된 전체 power에서 흡수율을 뺀 결과와 반사율이 잘 일치하는 결과를 확인할 수 있으며, 이로부터 반사율 감소는 전자기파의 흡수와 연관되어 있음을 검증하였다. 또한 3D 해석 결과와 2D 해석 결과의 비교를 통해 2D 구조 기반 설계의 신뢰도를 검증하였다. 45° 경사 입사의 경우, 그림 4(b)와 같이 해석 툴 사이에서 일부 차이가 확인되어 향후 측정을 통해 보다 정확한 검증이 필요한 상황이지만 모든 경우에서 X 밴드 전체에서 반사율이 −8 dB 이하로 감소한 결과를 통해 경사 입사에 대한 메타물질 흡수체의 성능을 검증하였다.
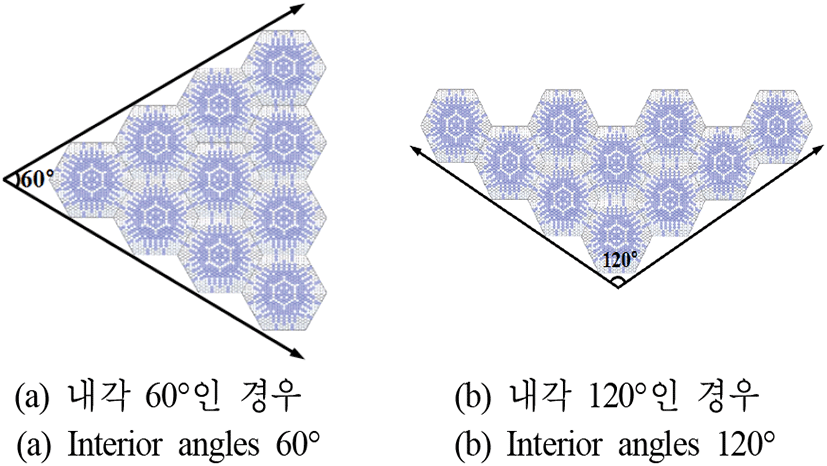
그림 5(a)와 그림 5(b)는 축 대칭으로 최적 설계된 육각형 형상 메타물질 흡수체 단위 셀을 내각이 60°, 120°인 모서리 구조에 적용한 예시를 나타낸다. 기존 사각형 메타물질 흡수체 단위 셀을 배치할 경우, 모서리 구조 내부에서 단위 셀 간 엇갈림이 발생하여 주기적인 배열 조건이 성립되지 못하는 반면, 제안된 구조는 인접 단위 셀과 주기적인 배치가 가능함을 알 수 있다. 이로부터 그림 5와 같은 모서리 구조에 제안된 육각형 형상의 메타물질 흡수체 단위 셀을 적용할 경우, 주기 경계 조건 하에 설계된 전자기파 흡수 성능을 기대할 수 있으며, 향후 연구를 통해 그 성능을 검증할 예정이다.
그림 5. | Fig. 5.
육각형 형상 전자기파 메타물질 흡수체 단위 셀의 모서리 구조에의 배치 예시인 경우 | Arrays of hexagonal electromagnetic metamaterial absorber unit cells for the corners.
Download Original Figure
Ⅳ. 결 론
육각형 단위 셀 내부에 카본이 채워진 육각형 픽셀이 최적으로 배치된 메타물질 흡수체 설계 방법을 제시하였다. 픽셀의 최적 배치를 위해 적응형 유전 알고리즘이 적용되었으며, 여섯 개의 축에 대해 회전 또는 축 대칭 형상을 갖는 패턴을 설계한 뒤 성능 지수 비교를 통해 최적 패턴을 도출하였다. 각각의 경우에 대해 최종 설계된 패턴을 기반으로 수직 입사 시 TE, TM 편파 모두에 대해 X 밴드 전체에서 반사율이 −10 dB 이하로 감소된 결과를 확인하였다. 성능 지수가 가장 우수한 축 대칭 형태의 패턴을 이용하여 45도 고각을 갖는 경사 입사에 대해서도 X 밴드 전체에서 −8 dB 이하로 반사율이 감소됨을 확인하였다. 또한 1로 정규화된 전체 파워에서 흡수율을 뺀 결과와 반사율이 잘 일치하는 결과를 확인하였으며, 이로부터 반사율 감소가 메타물질 흡수체의 흡수에 의한 결과임을 검증하였다. 최종 설계된 구조의 정확도는 유한 요소 기법 기반의 서로 다른 상용 수치 해석 툴인 Comsol Multiphysics와 HFSS로 해석한 시뮬레이션 결과의 비교를 통해 검증되었다.
Acknowledgements
이 논문은 2021년도 정부(과학기술정보통신부)의 재원으로 한국연구재단 기초연구사업 (2015R1A6A1A03031833)의 지원을 받아 수행된 연구임.
References
Y. Naito, K. Suetaki, “Application of ferrite to electromagnetic wave absorber and its characteristics,”
IEEE Transactions on Microwave Theory and Techniques, vol. 19, no. 1, pp. 65-72, 1971.


N. Dishovsky, M. Grigorova, “On the correlation between electromagnetic waves absorption and electrical conductivity of carbon black filled polyethylenes,”
Materials Research Bulletin, vol. 35, no. 3, pp. 403-409, 2000.


C. G. Jayalakshmi, A. Inamdar, A. Anand, and B. Kandasubramanian, “Polymer matrix composites as broadband radar absorbing structures for stealth aircrafts,”
Journal of Applied Polymer Science, vol. 136, no. 14, p. 47241, 2019.


A. Namai, S. Sakurai, M. Nakajima, T. Suemoto, K. Matsumoto, and M. Goto, et al., “Synthesis of an electromagnetic wave absorber for high-speed wireless communication,”
Journal of the American Chemical Society, vol. 131, no. 3, pp. 1170-1173, Jan. 2009.



N. I. Landy, S. Sajuyigbe, J. J. Mock, D. R. Smith, and W. J. Padilla, “Perfect metamaterial absorber,”
Physical Review Letters, vol. 100, no. 20, p. 207402, May. 2008.



J. Tak, Y. Lee, and J. Choi, “Design of a metamaterial absorber for ISM applications,”
Journal of Electromagnetic Engineering and Science, vol. 13, no. 1, pp. 1-7, 2013.


H. M. Lee, “Electromagnetic wave absorbers with metamaterial structure for RCS reduction,”
The Journal of Korean Institute of Electromagnetic Engineering and Science,vol. 26, no. 1, pp. 1-15, Jan. 2015.


H. K. Kim, S. Lim, “Flexible microfluidic metamaterial absorber for remote chemical sensor application,”
The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 27, no. 2, pp. 123-130, Feb. 2016.


H. Jeong, S. Lim, “Wideband frequency tunable metamaterial absorber using switchable ground plane,”
The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 29, no. 4, pp. 241-246, Apr. 2018.


T. Li, K. Chen, G. Ding, J. Zhao, T. Jiang, and Y. Feng, “Optically transparent metasurface salisbury screen with wideband microwave absorption,”
Optics Express, vol. 26, no. 26, pp. 34384-34395, 2018.



Y. E. Ra, Y. Kim, H. J. Jung, P. Park, J. Jo, and J. Lee, et al., “Verification of durability of electromagnetic metamaterial absorber in temperature varying environment for its application to integrated mast of next-generation destroyer,”
Journal of Institute of Korean Electrical and Electronics Engineers, vol. 24, no. 1, pp. 347-353, Mar. 2020.

Y. Kim, D. Kim, S. H. Lee, M. Seo, H. J. Jung, and B. Kang, et al., “Single-layer metamaterial bolometer for sensitive detection of low-power terahertz waves at room temperature,”
Optics Express, vol. 28, no. 12, pp. 17143-17152, Jun. 2020.



M. Baake, F. Gähler, and U. Grimm, “Hexagonal inflation tilings and planar monotiles,”
Symmetry, vol. 4, no. 4, pp. 581-602, 2012.


F. Costa, A. Monorchio, and G. Manara, “Analysis and design of ultra thin electromagnetic absorbers comprising resistively loaded high impedance surfaces,”
IEEE Transactions on Antennas and Propagation, vol. 58, no. 5, pp. 1551-1558, 2010.


G. Tomaszewski, T. Wałach, J. Potencki, and M. Pilecki, “The influence of sintering conditions on the inkjet printed paths resistance,”
International Journal of Electronics and Telecommunications, vol. 62, no. 2, pp. 135-140, 2016.


J. A. Reedijk, H. C. F. Martens, B. J. G. Smits, and H. B. Brom, “Measurement of the complex dielectric constant down to helium temperatures. II. Quasioptical technique from 0.03 to 1 THz,”
Review of Scientific Instruments, vol. 71, no. 2, pp. 478-481, 2000.


D. K. Cheng,
Field and Wave Electromagnetics, Reading, MA, Addison-Wesley, 1989.