Deep-Learning-Based Automatic Modulation Classification Using Imaging Algorithm

Park, Ji-Yeon; Seo, Dong-Ho; Nam, Hae-Woon

doi:10.5515/KJKIEES.2021.32.4.328

J. Korean Inst. Electromagn. Eng. Sci. 2021; 32(4):328-333

pISSN: 1226-3133, eISSN: 2288-226X

DOI: https://doi.org/10.5515/KJKIEES.2021.32.4.328

특집논문/SPECIAL EDITIONS

이미지화 알고리즘 및 딥러닝을 이용한 자동 변조 분류

박지연¹

, 서동호¹

, 남해운¹^,^*

Deep-Learning-Based Automatic Modulation Classification Using Imaging Algorithm

Ji-Yeon Park¹

, Dong-Ho Seo¹

, Hae-Woon Nam¹^,^*

Author Information & Copyright ▼

¹한양대학교 전자공학과

¹Department of Electronic Engineering, Hanyang University

^*Corresponding Author: Haewoon Nam (e-mail: hnam@hanyang.ac.kr)

© Copyright 2021 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Nov 20, 2020; Revised: Dec 15, 2020; Accepted: Mar 15, 2021

Published Online: Apr 30, 2021

요약

본 논문은 convolutional neural network (CNN) 모델에 이미지화 알고리즘을 적용한 자동 변조 분류 기법을 제안한다. 또한 다양한 이미지화 알고리즘을 이용하여 시계열 데이터의 이미지화 작업 후 이를 이용한 CNN 모델의 분류 성능을 비교 및 분석한다. 실험 결과, 원시 데이터를 Markov Transition Field (MTF)를 사용하여 이미지화한 후 CNN을 이용한 분류를 수행했을 시−6 dB 환경에서는 오차율이 34 %에서 30 %로 감소하였으며, 0 dB 환경에서는 오차율이 37 %에서 18 %로 감소하였다. 본 논문은 시계열 데이터의 이미지화가 CNN 기반 변조 분류 성능 개선으로 이어지는 것을 보여줌으로써 이미지화 알고리즘 적용의 유효성을 보여준다.

Abstract

This paper presents an automatic modulation classification method that involves the application of various imaging algorithms to a convolutional neural network (CNN). The effect of time-series data imaging on the performance of CNN-based modulation classification is analyzed. Our experiment suggests that converting raw signal data into image data using Markov transition field can reduce the error rate of CNN classification from 34 % to 30 % in case of −6 dB signal to noise ratio (SNR) and from 37 % to 18 % in case of 0 dB SNR. This study shows that time-series imaging is a viable preprocessing method for improving the performance of CNN-based modulation classification.

Keywords: Automatic Modulation Classification; CNN; Deep Learning; Imaging Algorithm

Ⅰ. 서 론

시계열 데이터란 일정 시간 간격으로 배치된 데이터들의 수열 형태를 의미하며, 예로 특정 센서에서 일정한 시간 간격으로 수집되는 RF 신호나 혹은 생체 신호 등 시간적 순서에 따른 데이터를 의미한다. 이러한 시계열 데이터는 송신되는 신호의 종류, 수신 환경 및 조건에 따라 신호의 세기 혹은 신호 파형 등 다양한 시각적 형태로 나타날 수 있다. 이러한 시계열 데이터의 특징 분석 및 시간적 변화를 기계학습에 적용한 데이터의 검출 및 분류 그리고 예측 알고리즘에 관한 많은 연구가 진행되고 있다^[1]~[3]. 특히 시계열 데이터를 이용한 딥러닝 연구가 많이 진행되고 있으며, 그중 시계열 데이터 변환(transform) 알고리즘을 이용해 데이터 전처리 및 변환을 진행한 후, 딥러닝을 적용한 방식이 주목받고 있다. 대표적으로 시계열 데이터 간의 상대적인 위치를 계산하여 1차원 시계열 데이터를 2차원 데이터로 변환하는 Relative Position Matrix 알고리즘을 CNN과 연계하는 방식이 있으며^[2], 또 다른 방법으로는 다변량 시계열 데이터를 차원 축소하여 2차원의 RGB 이미지로 인코딩하여 CNN 학습에 이용하는 방식이 연구되었다^[3].

본 논문에서는 시계열 데이터의 이미지화 알고리즘을 이용하여 I/Q 데이터에 이미지화를 적용한 자동 변조 분류(automatic modulation classification) 방식을 제안한다. 기존의 자동 변조 분류 연구는 원시 I/Q 데이터를 입력데이터로 활용한 반면, 본 논문에서 제안하는 방식은 시계열 이미지화 알고리즘을 통해 변조 신호의 특징을 효과적으로 시각화하였으며, 변환된 데이터를 입력 데이터로 이용하여 ResNet18 기반의 CNN 모델의 학습을 진행하였다. 더불어, 다양한 이미지화 알고리즘을 적용하여 분류 성능에 대해 시뮬레이션을 진행하였으며, 해당 결과를 토대로 모델 학습에 이미지화 알고리즘 적용의 유효성을 보인다.

Ⅱ. 이미지화 알고리즘

2-1 Recurrence Plot Algorithm

Recurrence Plot(RP) 알고리즘은 2차원에 데이터값의 회귀를 표현함으로써 m-차원 위상 공간 궤도를 탐색하는 것을 목표로 하는 시각화 알고리즘이다^{[4], [5]}. 시계열 데이터의 m-차원 공간 궤적을 구한 후, m-차원 궤적과 시간에 따른 거리의 차를 이용해서 거리 행렬을 구한다. 모든 조합의 거리 행렬을 기록한 것을 RP 행렬이라고 부른다.

본 논문에서 고려하는 시계열 데이터는 n개의 시간 인덱스에 따른 값으로 이루어진 집합으로 정의하며, 으로 표현할 수 있다. 이때 주어진 시계열 데이터의 공간 궤적 을 식 (1)과 같이 나타낼 수 있다.

x i → = [x i, x i + τ, ⋯, x i + (m − 1) τ]

(1)

이때, m은 궤적의 차원, τ는 지연시간, 그리고 i는 1부터 n−(m−1)τ까지의 인덱스 값이다. RP 행렬 R_i,j는 i와 j의 시간 쌍으로 이루어진 벡터이며, 식 (2)와 같이 정의할 수 있다.

R i, j = Θ (ϵ − ∥ x i → − x j → ∥)

(2)

이때, Θ는 단위 계단 함수이며, ε은 임계값을 의미한다.

RP는 궤적의 회귀를 이용하기 때문에 시계열 데이터의 주기성 혹은 순간적으로 값이 크게 변하는 데이터에 대해서도 특징 정보를 잘 추출한다. 또한, 궤적의 유사도에 따라 데이터 값 간의 연관성을 알 수 있고, 데이터의 종류에 따라 적절한 임계값을 설정함으로써 딥러닝의 학습 성능을 향상시킬 수 있다^[6].

2-2 Gramian Angular Field Algorithm

GAF(gramian angular field)는 각 시점 간의 시간적 상관관계를 극좌표를 기반으로 표현하는 알고리즘이다^[7]. 극좌표 기반 행렬은 시계열 데이터를 이미지로 변경할 때 시간 상관관계를 보존할 수 있다는 장점이 있다.

GAF는 먼저 주어진 시계열 데이터 값이 너무 크거나 작을 수 있으므로 [−1, 1] 혹은 [0, 1] 구간으로 정규화시킨다. 정규화된 신호 $x ˜ i$ 의 시간 인덱스 t_i를 반지름 r_i로 표현하며, 각도 ϕ와 함께 다음과 같이 극좌표로 변환한다.

{ϕ i = across (x ˜ i), − 1 ≤ x ˜ i ≤ 1, and x ˜ i ∈ X ˜ r i = t i N, t i ∈ N

(3)

여기서 N은 극좌표계의 범위에 대한 정규화 상수이다.

GAF는 각도의 합과 차에 따라 두 가지 방식으로 나뉜다. Garamian angular summation field (GASF)는 i와 j의 시간쌍으로 이루어진 극좌표계 시계열 데이터의 각도의 합으로 나타내며, 식 (6)과 같이 정의한다.

G A S F = [cos (ϕ i + ϕ j)] = x ′ ˜ ⋅ x ˜ − I − x ′ ˜ 2 ⋅ I − x ˜ 2

(4)

Gramian angular difference fIeld(GADF)는 GASF와 반대로 극좌표계의 각도의 차로 다음과 같이 정의한다.

G A D F = [sin (ϕ i − ϕ j)] = I − x ′ ˜ 2 ⋅ x ˜ − x ′ ˜ ⋅ I − x ˜ 2

(5)

GAF는 왼쪽 상단에서 오른쪽 하단으로 이동함에 따라 시간이 증가하기 때문에 시간 종속성을 보존한다. 주대각선은 원시 데이터의 값과 각도 정보를 포함하기 때문에 이를 이용하여 원시 데이터를 복구할 수 있다.

2-3 Markov Transition Field Algorithm

Markov Transition Field (MTF) 알고리즘은 이산화한 시계열 데이터의 전이 확률을 나타내는 알고리즘이다^[7].

MTF를 구성하기 위해 주어진 시계열 데이터 집합 X를 값에 따라 개의 Q구간으로 나눈 뒤, 시간 인덱스 t_i의 시계열 데이터 값 x_i에 맞는 구간 q_j (j∈[1,Q])에 배정한다. 시간 축을 따라 1차 마르코프 체인 방식으로 Q×Q 크기의 가중치 인접 행렬 W를 구성한다.

W = [w 11 ∣ P (x t ∈ q 1 ∣ x t − 1 ∈ q 1) ⋯ w 1 Q ∣ P (x t ∈ q 1 ∣ x t − 1 ∈ q Q) w 21 ∣ P (x t ∈ q 2 ∣ x t − 1 ∈ q 1) ⋯ w 2 Q ∣ P (x t ∈ q 2 ∣ x t − 1 ∈ q Q) ⋮ ⋱ ⋮ w Q 1 ∣ P (x t ∈ q Q ∣ x t − 1 ∈ q 1) ⋯ w Q Q ∣ P (x t ∈ q Q ∣ x t − 1 ∈ q Q)]

(6)

w_i,j는 q_i 구간에서 q_j 구간으로 전이하는 빈도를 나타낸다. W의 각 열의 합을 1로 정규화함으로써 마르코프 전이 매트릭스를 구성할 수 있다. 이 과정에서 W는 X의 분포와 시간 인덱스 t_i에 대한 시간 종속성이 제거된다. 이러한 W의 정보 손실을 극복하기 위해, 시간 순서를 따라 각 확률을 정렬하여 MTF를 다음과 같이 정의한다.

M = [M 11 M 12 ⋯ M 1 n M 21 M 22 ⋯ M 2 n ⋮ ⋱ ⋮ M n 1 M n 2 ⋯ M n n] = [w i j ∣ x 1 ∈ q i, x 1 ∈ q j ⋯ w i j ∣ x 1 ∈ q i, x n ∈ q j w i j ∣ x 2 ∈ q i, x 1 ∈ q j ⋯ w i j x 2 ∈ q i, x n ∈ q j ⋮ ⋱ ⋮ w i j ∣ x n ∈ q i, x 1 ∈ q j ⋯ w i j x n ∈ q i, x n ∈ q j]

(7)

MTF의 i행 j열 값인 M_{ij ∣ |i−j|=k}는 시간 인덱스 t_i일 때의 데이터 값이 속한 구간 q_i에서 시간 인덱스 t_j의 데이터 값이 속한 구간 q_j로 전이할 확률, 즉 두 시간의 차이가 k인 지점 간의 전이 확률을 나타낸다. 구간의 너비가 크면 대부분의 값을 평균에 가장 가까운 구간으로 집계하고, 구간의 너비가 작으면 극한 구간에서 집계되는 값이 적어진다^[7].

Ⅲ. 모의실험 및 결과

본 논문에서는 신호대잡음비(SNR)를 −6 dB부터 2 dB 단위로 0 dB까지의 통신환경을 고려하였으며, 본 연구에서는 RadioML 데이터^[8]를 사용하였으며, 이는 GNU Radio 를 사용하여 생성된 신호 데이터로 주파수 천이, 샘플 레이트 천이, 백색 가우시안 소음이 부가된 다중 경로 페이딩과 같은 실제 통신 채널의 불완전한 특징이 포함된 I/Q 데이터이다. 최대 도플러 주파수는 1 Hz, power delay profile이 [0.0, 0.9, 1.7]인 환경이 적용되었다. 변조 방식은 BPSK, QPSK, 16-QAM 그리고 64-QAM에 대해 고려하였으며, SNR에 따라 각 변조 신호를 1,000개씩 추출하여 전체 데이터 셋을 구성하였다. 전체 데이터 셋은 9:1의 비율로 학습과 테스트에 각각 사용하였으며, 이때 I/Q 데이터는 2×128 크기를 갖는 행렬이다.

모의실험을 통해 이미지화 알고리즘 적용 여부에 따른 성능을 비교하기 위해 알고리즘을 적용하지 않고 I/Q 데이터를 직접 학습하는 방식을 비교군으로 설정하였다. 제안하는 방식을 이용한 모의실험에서는 기존의 I/Q 데이터를 In-phase 성분과 Quadrature 성분을 분리하여 각각 이미지화 알고리즘을 적용하여 2×128×128의 3차원 입력 데이터로 학습을 진행하였다.

표 1은 본 논문에서 사용된 CNN 모델의 상세 구조를 나타낸다. 이때, 손실함수는 cross entropy error를 사용하였고, 확률적 경사 하강(stochastic gradient descent) 알고리즘을 이용하여 학습을 진행하였다.

표 1. | Table 1. 자동 변조 분류를 위한 합성곱 신경망 구조 | CNN structure for AMC.

Layer	Output dimension (image data)	Output dimension (IQ data)
Input	2×128×128	1×2×128
Conv1	64×64×64	64×1×64
Conv2	64×32×32	64×1×32
Conv3	128×16×16	128×1×16
Conv4	256×8×8	256×1×8
Conv5	512×4×4	512×1×4
Average pool	512×1×1	512×1×1
Fully connected	4	4
Softmax	4	4

Download Excel Table

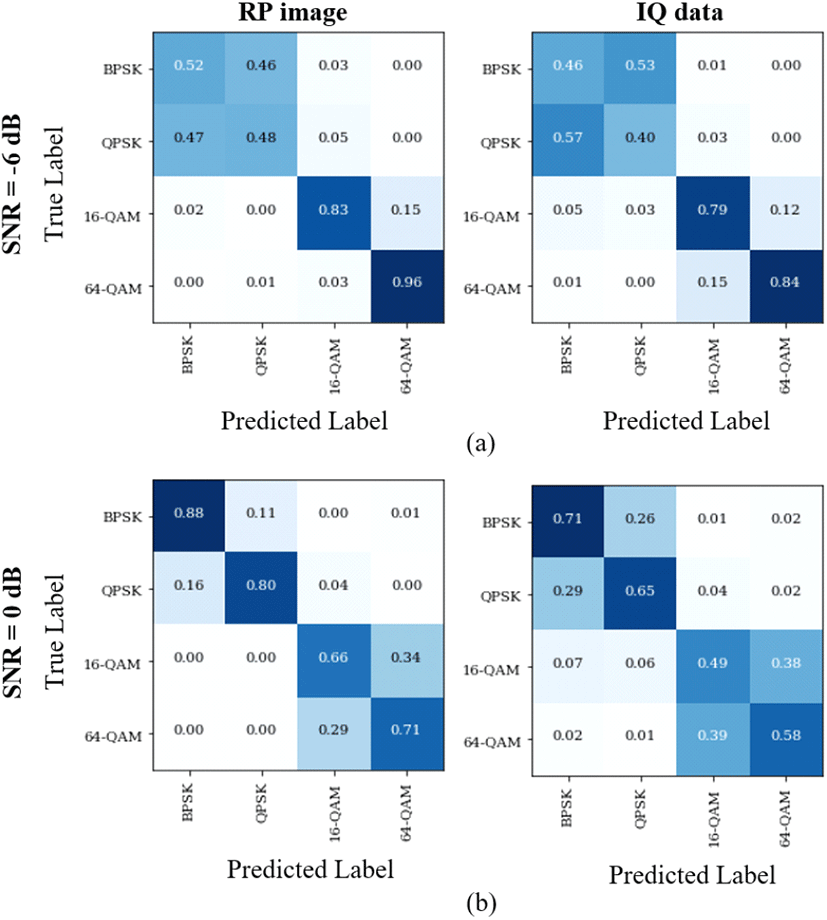
그림 1은 CNN 모델을 통해 학습한 자동 변조 분류 성능을 나타낸다. 그림 1(a)와 그림 1(b)는 각각 SNR이 −6 dB인 환경과 0 dB인 환경에서 RP 알고리즘을 이용한 이미지 데이터와 알고리즘을 사용하지 않고 I/Q 데이터만을 이용하여 학습했을 때의 성능을 나타낸다. 그림 1을 통해서 알 수 있듯이 −6 dB 환경에서는 이미지화 알고리즘의 적용 여부에 상관없이 양쪽 모두 BPSK와 QPSK 간의 분류 성능이 떨어짐을 알 수 있다. 반면에 16-QAM과 64-QAM 간의 분류 성능은 제안하는 방식의 성능이 약 4 % ~12 % 높게 나타남을 알 수 있다. 또한 0 dB 환경에서는 BPSK와 QPSK 간의 분류 성능은 좋아졌으나, 16-QAM과 64-QAM 간의 분류 성능은 떨어짐을 알 수 있다. 다만, RP 이미지를 이용한 CNN 모델의 분류 성능이 I/Q 데이터를 이용하여 학습한 모델보다 SNR에 상관없이 높게 나타남을 알 수 있다. 이는 수신되는 시계열 데이터를 이미지로 인코딩하는 방식은 시간의 흐름에 따라 진행되는 변조 방식의 패턴을 보다 효과적으로 나타냄으로써 원시 I/Q 데이터를 사용할 때보다 직관적인 해석을 제공하기에 분류 성능이 높아진 것으로 생각할 수 있다^[9].

그림 1. | Fig. 1. SNR에 따른 자동 변조 분류 성능: (좌) RP 이미지 데이터, (우) I/Q 데이터 | Automatic modulation classification performance under various SNR conditions: (left) RP image data, (right) I/Q data.

Download Original Figure

표 2는 RP, MTF 그리고 GAF 이미지화 알고리즘을 적용한 방식과 I/Q 데이터를 이용하여 학습한 모델들의 분류 error rate(오차율)를 나타낸 표이다. −6 dB 환경에서의 오차율을 보면 MTF를 이용하였을 경우, 다른 이미지화 알고리즘 대비 오차율이 최대 2.4 % 적으며, I/Q 데이터를 이용한 모델의 성능과 비교 시 오차율이 약 4.8 % 낮음을 알 수 있다. 더욱이 SNR이 높아질수록 그 차이가 크게 나타나며, 특히 0 dB 환경에서의 MTF 오차율은 I/Q 데이터 기반의 학습 모델의 오차율과 비교해 19 % 이상 낮음을 알 수 있다.

표 2. | Table 2. SNR에 따른 이미지화 기반 변조 신호 분류 성능 | Modulation classification performance using signal imaging and CNN under various SNR conditions.

Algorithm	Error rate
Algorithm	−6 dB	−4 dB	−2 dB	0 dB
RP	0.316	0.281	0.266	0.242
MTF	0.3	0.27	0.197	0.18
GASF	0.324	0.299	0.299	0.294
GADF	0.3	0.282	0.262	0.253
I/Q	0.348	0.362	0.374	0.375

Download Excel Table

실험 결과를 통해 이미지화 알고리즘 중 MTF를 이용한 자동 변조 분류 성능이 가장 우수함을 알 수 있다. 이는 MTF가 RP나 GAF에 비해 일정한 시간 구간의 세부적인 정보를 잡아내는 데 유용하기 때문이다.

Ⅳ. 결 론

본 논문은 이미지화 알고리즘을 이용한 CNN 기반의 자동 변조 신호 분류 방법을 제안하였다. 모의실험 결과를 통해 제안하는 이미지화 알고리즘을 이용한 이미지 데이터를 기반으로 학습한 CNN 모델의 분류 성능이 더 우수함을 확인하였다. 향후 연구과제로는 시계열 데이터를 이미지화하는 과정에서 발생할 수 있는 데이터의 특징 및 정보 손실을 줄이기 위한 전처리 방식 및 알고리즘과 시계열 데이터의 특징에 따른 최적의 하이퍼파라미터를 찾기 위한 연구가 필요하다.

Acknowledgements

이 논문은 2020년도 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(2019M3F6A1106108).

References

[1].

S. Barra, S. M. Carta, A. Corriga, A. S. Podda, and D. R. Recupero, "Deep learning and time series-to-image encoding for financial forecasting," IEEE/CAA Journal of Automatica Sinica, vol. 7, no. 3, pp. 683-692, May. 2020.

[2].

W. Chen, K. Shi, "A deep learning framework for time series classification using relative position matrix and convolutional neural network," Neurocomputing, vol. 359, pp. 384-394, Sep. 2019.

[3].

C. L. Yang, Z. X. Chen, and C. Y. Yang, "Sensor classification using convolutional neural network by encoding multivariate time series as two-dimensional colored images," Sensors, vol. 20, no. 1, p. 168, Dec. 2019.

[4].

J. P. Eckmann, S. O. Kamphorst, and D. Ruelle, "Recurrence plots of dynamical systems," Europhysics Leter, vol. 4, no. 9, p. 973, 1987.

[5].

H. Lee, J. Lee, and M. Shin, "Using wearable ECG/PPG sensors for driver drowsiness detection based on distinguishable pattern of recurrence plots," Electronics, vol. 8, no. 2, p. 192, Feb. 2019.

[6].

S. Schinkel, O. Dimigen, and N. Marwan, "Selection of recurrence threshold of signal detection," The European Physical Journal Special Topics, vol. 164, pp. 45-53, Oct. 2008.

[7].

Z. Wang, T. Oates, "Encoding time series as images for visual inspection and classification using tiled convolutional neural networks," in Workshops at the 29th AAAI Conference on Artificial Intelligence, Jan. 2015, vol. 1.

[8].

T. J. O’Shea, J. Corgan, and T. C. Clancy, "Convolutional radio modulation recognition networks," in International Conference on Engineering Applications of Neural Networks, Aberdeen, Aug. 2016, vol. 629, pp. 213-226.

[9].

G. R. Garcia, G. Michau, M. Ducoffe, J. S. Gupta, and O. Fink, "Time series to images: Monitoring the condition of industrial assets with deep learning image processing algorithms," 2020. Available: https://arxiv.org/abs/2005.07031v3

Author Information

박 지 연 [한양대학교/석사과정]

jkiees-32-4-328-i1

https://orcid.org/0000-0001-7620-1499
2021년 2월: 한양대학교 전자공학부 (공학사)
2021년 3월~현재: 한양대학교 전자공학과 석사과정
[주 관심분야] Deep Learning, AMC, Time-Series Processing

서 동 호 [한양대학교/박사과정]

jkiees-32-4-328-i2

https://orcid.org/0000-0002-3394-3422
2014년 2월: 한양대학교 전자공학과 (공학사)
2014년 3월~현재: 한양대학교 전자통신공학과 박사과정
[주 관심분야] Deep Learning, Spectrum Sensing, AMC 등

남 해 운 [한양대학교/교수]

jkiees-32-4-328-i3

https://orcid.org/0000-0001-9847-7023
1997년 2월: 한양대학교 전자통신학과 (공학사)
1999년 2월: 서울대학교 전기공학부 (공학석사)
2006년 12월: The University of Texas at Austin, 전자 및 컴퓨터공학과 (공학박사)
2011년 3월~현재: 한양대학교 전자공학부 교수
[주 관심분야] 통신 네트워크, 인지무선시스템, 임베디드 SW 시스템, 로보틱스 등