Ⅰ. 서 론
레이다를 이용하여 표적의 정보를 획득하기 위해서는 주변 환경 및 표적 정보 획득/추출에 적합한 파형을 설계해야 한다. 파형을 설계할 때 고려할 중요한 요소 중 한 가지는 PRF이다. PRF의 선택에 따라 관심 영역의 표적에 대한 거리/속도 정보의 모호성(ambiguity)이나 간섭에 대한 영향성 등이 결정되기 때문이다.
PRF는 거리와 속도의 모호성의 유무에 따라 LPRF(Low PRF), MPRF, HPRF로 분류[1]할 수 있으며, LPRF는 거리에 대한 모호성이 없는 PRF로서 SAR(Synthetic Aperture Radar)와 같은 레이다 모드의 설계에 사용하는 파형이다. LPRF는 거리 영역으로의 정보를 주로 이용하므로 LPRF를 설계할 때에는 정확한 거리 정보를 얻는 것이 중요하다. 상기의 목적을 달성하기 위해서 사용하는 방법 중 한 가지는 거리 영역으로의 간섭을 회피하여 PRF를 설계하는 것이다. 간섭이 예상되는 PRF를 제거하기 위한 기존의 기법[2]~[6]은 관측각 및 PRF의 변화에 따라 관심영역과의 송신 신호 간섭 및 직하방 신호와의 간섭을 고려하고 있다. 그러나 빔폭이 포함하는 거리 영역이 PRF보다 충분히 좁은 경우, 즉, PRI(Pulse Repetition Interval)보다 충분히 넓은 경우 인접한 PRI/PRF 구간에서, 이전 구간에서 송신한 신호에 의해 간섭이 발생(그림 4)할 수 있다. 상기의 간섭은 조향각에 따라 빔폭이 변화하는 ESA 레이다의 경우 특히 심각하게 발생할 것이다.
본 논문에서는 ESA 레이다를 사용하는 경우를 가정하여, 빔폭 및 지구 모델 등을 고려하여 간섭이 예상되는 PRF를 배제하여 적절한 PRF 설계하기 위한 파형 설계 기법을 제시하고 있다. 본 기법은 특히 거리 영역의 정보가 중요한 LPRF의 경우에 유용하게 사용될 수 있다.
Ⅱ. 간섭을 회피하는 파형 설계 기법
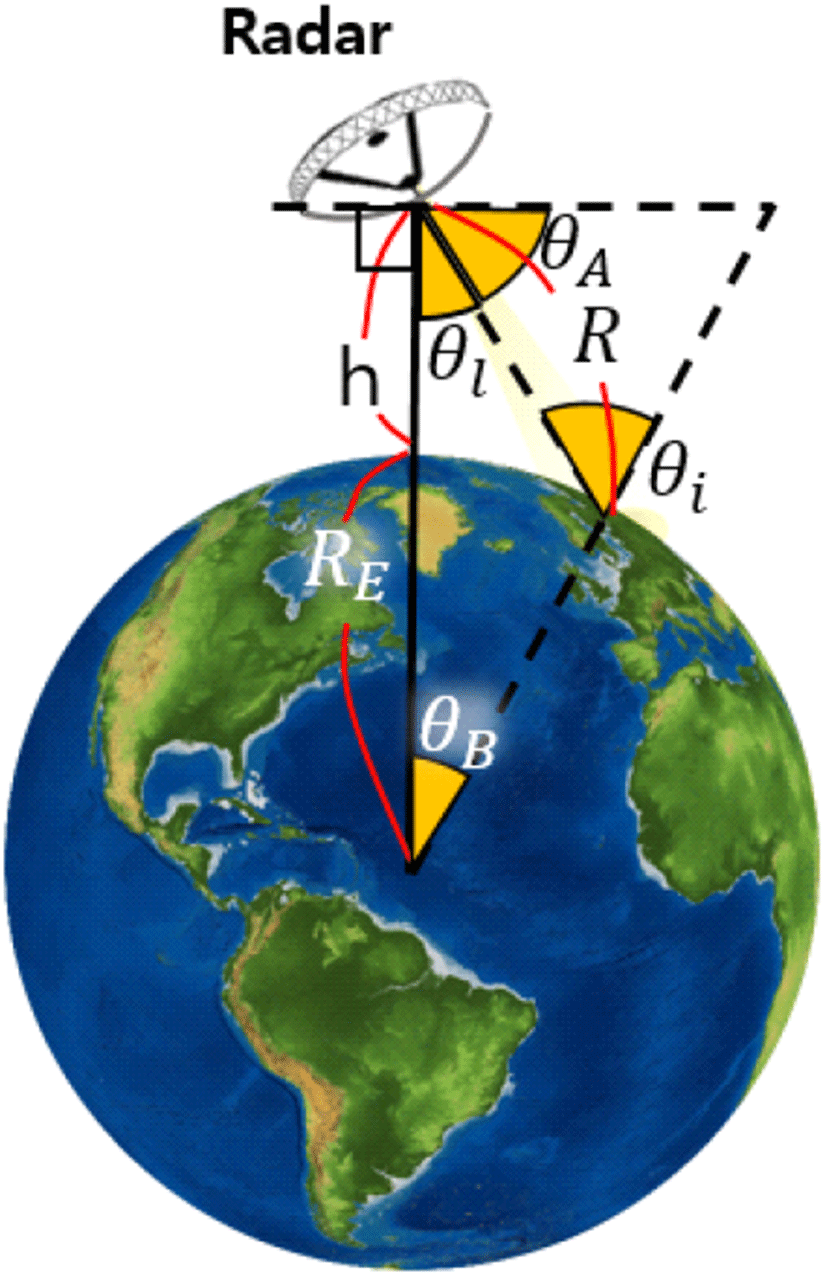
본 논문에서는 레이다와 표적 간의 지리적인 정보를 원형 지구 모델(그림 1)을 가정하고 있다. 원형 지구 모델은 지구를 원으로 가정하여 2차원 상에서 레이다의 기하 구조를 분석하는 모델로서, 지구, 지면을 평면으로 가정하는 모델이 비하여 정확하면서도 크게 복잡하지 않아서 SAR의 설계와 같은 경우에, 자주 쓰이는 방법이다.
그림 1에서 R, Re는 각각 표적(대상 위치)으로부터의 거리 및 지구의 반지름이며, h는 레이다 탑재체의 고도, θl, θi, θA, θB는 각각 관측각, 입사각, 각 A, 각 B이다.
관측각 θl과 표적과의 거리 R과의 관계를 구하기 위하여 그림 1에 대하여 sin법칙을 이용하여 변수들 간의 관계를 표현하면 식 (1)~식 (3)과 같다.
식 (3)에서 입사각 θi를 사용자가 미리 알고 있는 변수들(θl, h, Re)로 표현하기 위하여 다시 한 번 그림 1에서 sin 법칙으로 변수 간의 관계를 도출하면 식 (4) 및 식 (5)와 같다.
이때, 입사각 θi는 둔각이 될 수 없으므로 최종적으로 원형 지구 모델에서의 경사거리 R은 고도 h와 지구의 반지름 Re, 관측각 θl를 이용하여 아래와 같이 나타낼 수 있다.
최종적으로 원형 지구 모델에서의 경사거리 R은 고도 h와 지구의 반지름 Re, 관측각 θl를 이용하여 아래와 같이 나타낼 수 있다.
기존의 방법[2],[4]은 서론에서도 밝혔듯이 관측각 및 PRF의 변화에 따른 관심영역과 두 가지 간섭, 송신 신호 및 직하방 신호에 의한 간섭을 회피하여 PRF를 설계하는 것이 목적이다. 먼저 송신 신호에 의한 간섭을 회피하는 방법을 살펴보자. 본 방법은 표적 신호가 원거리에 있는 경우의 간섭을 회피할 수 있다. 이때의 원거리란 표적의 위치가 PRI보다 먼 거리를 의미하며, 위성 SAR의 경우 일반적으로 표적이 원거리에 있다.
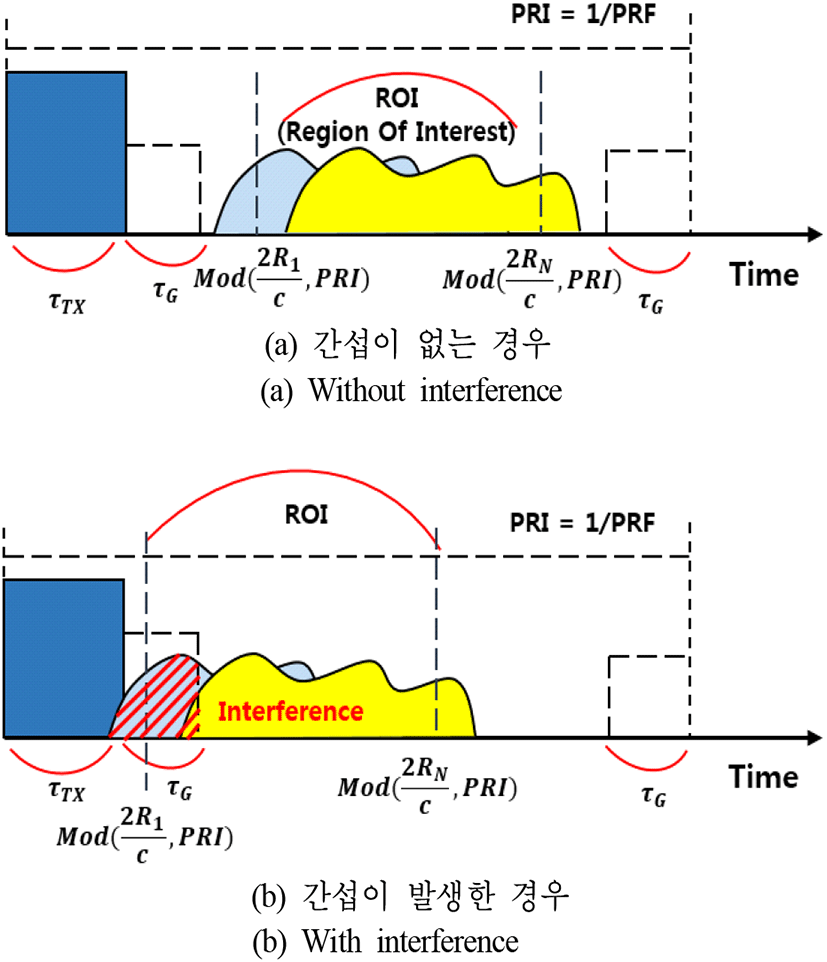
표적이 원거리에 있는 경우, 관심영역과 송신 신호와의 간섭을 회피하기 위해서는 관심 영역에 해당하는 거리 (R1~RN)의 신호가 시간 축에서 송신신 호의 송신구간 τTX 및 송신 전․후의 보호시간 τG와 겹치지 않게 PRF를 설계해야 한다. 편의를 위하여 A를 B로 나눈 나머지를 mod(A, B)로 정의(식 8)하면, 송신 간섭을 피하기 위한 조건은 식 (9) 및 식 (10)과 같이 표현할 수 있다.
그림 2(a)의 경우는 식 (9) 및 식 (10)에 따라 송신 신호의 간섭을 계산한 결과 설계한 PRF가 관심영역에서 송신신호와 간섭이 없는 경우이고, 그림 2(b)의 경우는 설계한 PRF가 관심영역에서 송신신호와 간섭이 생긴 경우로서, 송신 구간 및 송신 보호시간과 간섭이 일어난 것을 확인할 수 있다.
다음으로 직하방신호의 간섭을 회피하기 위한 방법을 살펴보자. 직하방신호는 관심영역의 신호보다 그 크기가 세기 때문에[4] 적절하게 회피하는 것이 매우 중요하다.
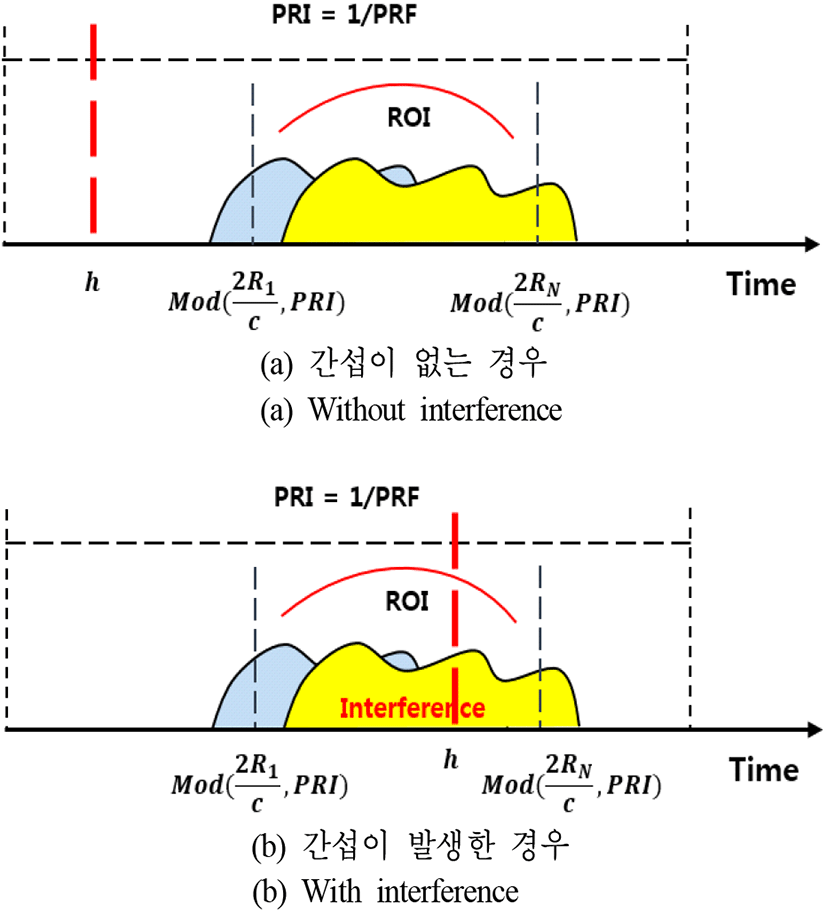
높이 h에 위치한 레이다 탑재체가 수신하는 직하방신호가 관심영역의 신호와 간섭(그림 3)을 일으키지 않으려면 아래와 같은 부등식[4]를 만족해야 한다.
Ⅲ. 제안하는 방법
직하방신호의 간섭의 경우, 식 (11) 및 식 (12)에서는 직하방신호의 펄스폭 τTX를 고려하지 않았으며[4], 교재[2]의 수식은 펄스폭 τ_TX를 고려하였으나 식 (15)의 경우만을 고려한 것으로 판단된다. 그러나 펄스폭이 유한하면 높이 h에 따라 직하방신호가 한 PRI 내에 존재하지 않고 인접한 PRI 간에 겹쳐서 나타날 수 있으며, 원거리의 경우에는 관심영역보다 높이 h가 더 가까움에도 직하방신호와의 간섭이 발생할 수 있으므로, 직하방신호와 관심 영역의 간섭을 회피하기 위해서는 아래의 부등식(식 13~식 15)을 모두 만족해야 한다.
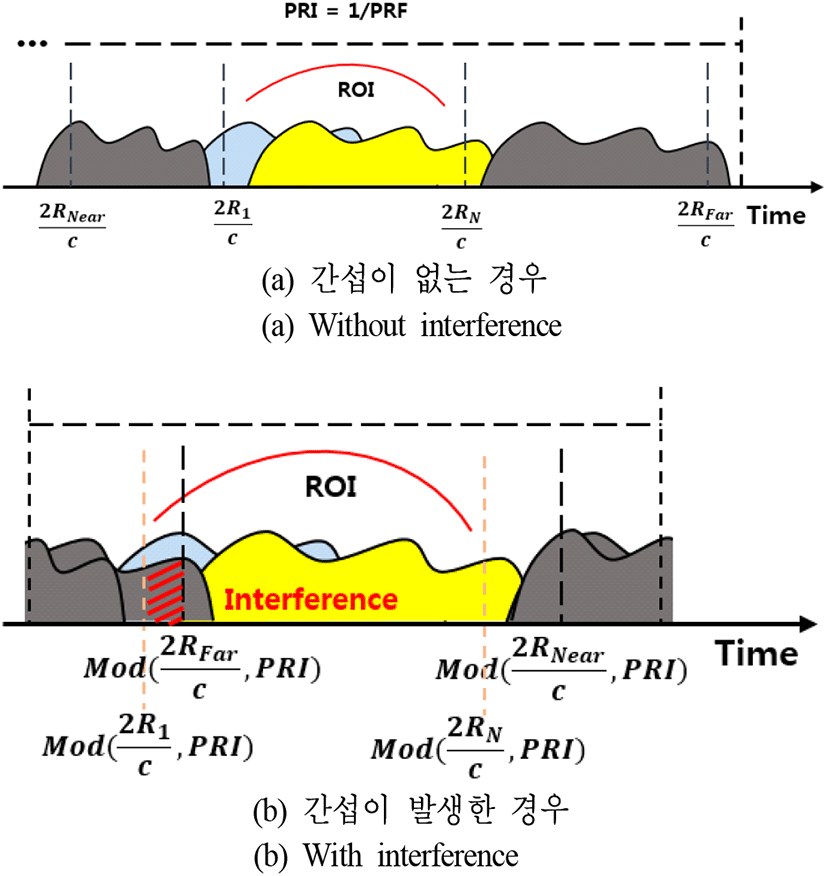
본 논문에서 제안하는 기법은 빔폭과의 간섭을 추가적으로 고려하고 있다. 레이다가 송신하는 전파는 운용자가 설정한 관심영역에 대해서만 수신이 이루어지는 것이 아니다. 실제로는 관심영역뿐만이 아니라, 송․수신 빔의 패턴에 따라 관심영역 밖의 신호도 수신이 될 수 있다. 본 논문에서는 실제로 의미있는 신호가 수신되는 기준을 3 dB 빔폭(이하 빔폭)으로 설정하여서, 식 (16)과 같이 빔폭에 해당하는 거리 영역(RNear~RFar)이 관심 영역(R1~RN)에 비하여 클 때, 발생할 수 있는 간섭인 빔폭과 관심영역 간의 간섭을 새롭게 고려하고 있다.
그림 4는 식 (16)의 조건에서 관심영역의 신호와 빔폭 내 신호와의 간섭이 발생한 경우를 나타내고 있다. 그림 4(a)는 PRF가 충분히 커서, (R1~RN) 및 (RNear~RFar)의 거리에 해당하는 신호가 겹치지 않는 경우이며, 그림 4(b)는 PRF가 낮아서 (R1~RN) 및 (RNear~RFar)의 거리에 해당하는 신호가 겹치는 경우를 나타내고 있다.
빔폭이 조향각과 무관하게 유지되는 MSA(Mechnically Steering Antenna)와 다르게 ESA(Electronically Steering Antenna)는 조향각 θs에 따라 빔폭이 변화한다. ESA의 빔폭 변화를 알아보기 위하여 ESA의 빔폭 θBW을 식[7]으로 표현하면 식 (17)과 같다.
이때, k는 빔폭 계수이며, k에 따라 빔폭의 기준이 변한다. 가령 1일 경우 θBW는 4 dB 빔폭이며, 0.886일 경우 θBW는 3 dB 빔폭이다. L은 개구면의 길이이며, λ는 파장의 길이이다. 식 (17)에서 볼 수 있듯이 다른 모든 변수들 이 고정되어 있을 경우, 조향각 θs에서의 빔폭은 조향각이 0° 때에 비하여 배 만큼 넓어지며, 식 (17)은 아래와 같이 표현이 가능하다.
θBW (θs)는 조향각 θs의 ESA의 빔폭이다. 즉, ESA는 조향각이 커짐에 따라 직하방신호 및 송신신호와의 간섭 구간이 MSA에 비하여 넓게 발생함을 예상할 수 있으며, 이를 고려하여 적정 PRF 범위를 설계해야 한다.
종합하여 보면, 제안하는 기법은 기존의 교재[2],[4]에서의 방법과 비교하여, 직하방신호의 간섭에 대한 부분을 더욱 정확하게 고려하였으며, 빔폭에 의한 간섭 및 ESA에 의한 빔폭의 퍼짐(broadening) 효과를 추가적으로 고려하고 있다.
Ⅳ. 시뮬레이션 결과
시험은 MATLAB 2015 프로그램에서 ESA 레이다를 가정하여 수행하였으며, 시험 파라미터는 표 1과 같으며 관련 논문[3],[5]들의 수치들을 일부 수정하여 차용하였다.
| Parameter | Value |
|---|---|
| PRF | 1,000~5,000 Hz |
| Look angle (θl) | 15~50 deg |
| Height (h) | 500 km |
| 3 dB beamwidth (θBW(0)) | 3, 5 deg |
| Pulse length (τTX) | 20 us |
| Guard time (τG) | 20 us |
| ROI(RN-R1, patch size) | 10 km |
시험은 아래의 세 가지 방법을 이용하여 수행하였다.
PRF 설계 방법 1(method 1): 기존의 방법(Ⅱ.2) + 직하 방신호의 간섭 보강(Ⅲ. 1)
PRF 설계 방법 2(method 2): 제안하는 방법(방법1+(Ⅲ. 2))
PRF 설계 방법 3(method 3): 제안하는 방법(방법2+(Ⅲ. 3))
방법 1은 기존의 방법에서 직하방신호의 간섭 계산을 개선한 방법으로서 기존의 방법이라고 보면 된다. 방법 2는 빔폭과의 간섭을 포함하였으나, ESA의 효과는 무시하였다. 즉, MSA의 경우로 보면 된다. 방법 3의 경우는 방법 2에서 ESA의 효과까지 포함하는 경우로서 본 논문에서 ESA의 PRF 설계를 위해 제안하는 방법이다.
방법 1~3에서 설계한 PRF에서 발생한 간섭의 평가는 다음의 세 가지 지표를 이용하여 평가하였다. 먼저 첫 번째로, 간섭이 예상되는 PRF를 회피하여 PRF를 설계한 것을 시각적으로 평가하였다. 해당 방법은 교재[2]에 최초로 제안된 것으로 파악하며, 공식적인 명칭은 없으나 diamond diagram[3],[6] 혹은 timing diagram[4],[5], zeebra graph 등으로 표현되고 있다.
두 번째 지표는 간섭이 발생한 범위를 평가하는 간섭율 η(식 19)이며, 마지막 지표는 간섭 신호의 세기를 나타내는 신호 대 간섭비 Ψ(식 20) 이다. 두 지표(식 19 및 식 20)는 본 논문에서 자체적으로 설정한 지표이다.
간섭율 η는 [0, 100]의 값을 가지며, 100에 가까울수록 관심 영역에 대비하여 간섭이 넓게 발생하였음을 나타낸다. 다음으로 신호 대 간섭비 Ψ의 정의는 다음과 같다.
E(R, θl)는 거리 R 및 관측각 θl에서의 레이다가 수신하는 에너지[8]이며, Pt, τ, G(θl), λ, σ는 각각 송신 피크 파워, 펄스폭, 관측각에서의 안테나 이득, 레이다 운용 파장, RCS이다.
EBW(R, θl)는 거리 R과 apparent range[9]이 동일한 거리에서 빔폭과의 간섭(그림 4)으로 인해 수신하는 간섭신호의 수신 에너지이다. 이때, c는 빛의 상수이며, k는 안테나 주엽(mainlobe) 파워의 피크값에 대비한 감쇠값이다. 가령 3 dB 빔폭에 해당하는 지점에서의 k값은 2가 된다. n은 정수이다.
신호 대 간섭비 Ψ를 식 (21)과 식 (22)를 이용하여 정리하면 식 (23)과 같다.
이때, 식 (23)은 클러터의 특성이 동일한 지역에서 3 dB 빔폭으로 인한 간섭이 반드시 발생한 경우를 가정하였다. Ψ는 [0, 3] dB 범위의 값을 가지며, 값이 클수록 간섭이 심하게 발생하였음을 나타낸다. 0 dB의 경우는 EBW (R, θl)이 0인 경우로서 간섭이 발생하지 않은 경우를 나타낸다.
ESA 레이다에 대한 방법 1~3의 PRF 설계 결과를 시각적으로 평가한 결과는 그림 5와 같다.
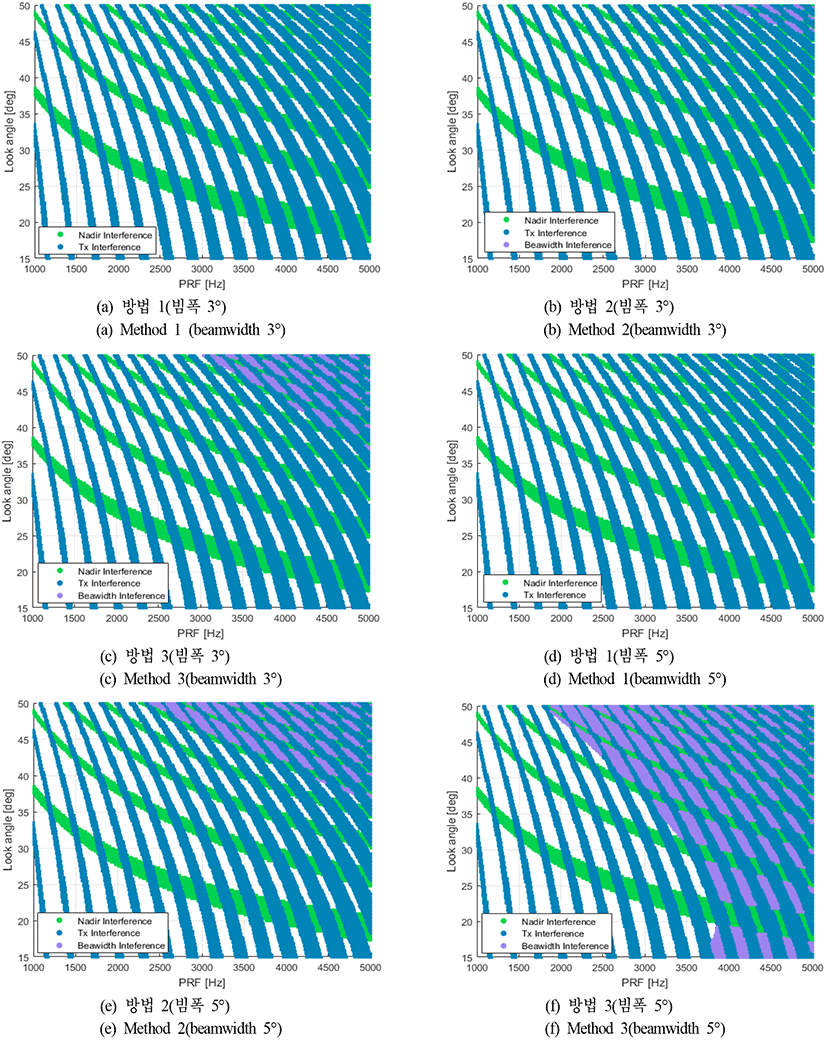
그림 5는 관측각 및 PRF의 변화에 따른 간섭의 영향을 나타낸다. 녹색, 파란색, 보라색은 각각 직하방 신호 및 송신 신호, 빔폭과의 간섭을 나타낸다. 특정 관측각에서의 흰색 바탕의 PRF 부분은 해당 PRF의 범위에서 파형을 설계하면 간섭이 발생하지 않음을 나타낸다.
먼저 각 방법 1, 2, 3 내에서 빔폭의 변화에 따른 간섭의 영향을 분석하면 아래와 같다. 방법 1을 이용한 그림 5(a) 및 그림 5(d)를 비교하면 빔폭이 3°에서 5°로 커져도 간섭의 영향은 변하지 않음을 알 수 있다. 이것은 방법 1에서 고려하고 있는 두 가지 간섭(직하방 신호 및 송신 신호의 간섭)에 영향을 미치는 요소인 관심 영역, 펄스폭, 고도 등이 빔폭의 변화와 무관하기 때문이다.
동일 조건에 대해 방법 2의 시뮬레이션 결과인 그림 5(b) 및 그림 5(e)를 비교하면 빔폭이 3°에서 5°로 증가함에 따라 보라색의 영역이 넓어졌다. 즉, 빔폭이 증가함에 따라 빔폭과의 간섭이 더 넓은 영역에서 발생했음을 알 수 있다. 동일 조건에 대해 방법 3의 시뮬레이션 결과인 그림 5(c) 및 그림 5(f)의 경우도 방법 2와 마찬가지로 빔폭이 증가함에 따라 빔폭과의 간섭이 더 넓게 발생했음을 알 수 있다.
다음으로 방법 1, 2, 3 상호 간의 빔폭에 변화에 따른 간섭의 영향을 분석하면 아래와 같다. 먼저 빔폭이 3°인 그림 5(a)~그림 5(c)의 경우를 비교하면 빔폭이 동일함에도 방법 3, 2, 1의 내림차순으로 빔폭과의 간섭이 많이 발생하였음을 알 수 있다. 빔폭이 5°인 그림 5(d)~그림 5(f)의 경우도 마찬가지이다.
그림 5의 결과를 종합하면 본 논문에서 제안하는 방법 3이 포함하는 빔폭과의 간섭은 빔폭이 커짐에 따라 간섭의 영향이 커지며, 특히 ESA를 사용하는 레이다의 경우 간섭의 영향이 더욱 커짐을 알 수 있다. 즉, 본 논문에서 제안하는 방법 3을 ESA 레이다에 이용하면 방법 1, 2에서 구분하지 못 하는 간섭을 식별하여 배제할 수 있음을 알 수 있다.
다음으로 간섭율 η를 이용하여 방법 1, 2, 3을 평가한 결과는 표 2와 같다.
| Case | Method | PRF (Hz) | Beamwidth (deg) | Look angle (deg) | η |
|---|---|---|---|---|---|
| 1 | 1 | 3,600 | 3 | 47 | 0 |
| 2 | 3,600 | 3 | 47 | 0 | |
| 3 | 3,600 | 3 | 47 | 12.37 | |
| 2 | 1 | 3,100 | 5 | 46 | 0 |
| 2 | 3,100 | 5 | 46 | 5.09 | |
| 3 | 3,100 | 5 | 46 | 100.00 |
표 2의 경우, 1, 2의 결과를 보면, 방법 1에서는 간섭율이 0으로 계산되는 조건에서도 방법 2와 3에서는 간섭을 식별할 수 있음을 알 수 있다. 특히 방법 3의 경우에서는 경우 1의 경우는 방법 2에서 식별하지 못한 간섭을 식별 하거나, 경우 2의 경우는 같은 조건에서 방법 3이 방법 2보다 간섭율이 더 크게 계산됨을 알 수 있으며, 관심 영역 전 구간에 대하여 간섭이 발생하였음을 알 수 있다. 이것은 방법 3이 방법 2와 비교하여 ESA의 빔폭의 퍼짐효과를 추가적으로 포함하고 있기 때문이다.
다음으로 신호 대 간섭비 Ψ를 이용하여 방법 1, 2, 3을 평가한 결과는 표 3과 같다. 이때, 계산의 단순화를 위하여 빔의 이득은 sinc 함수의 자승이라고 가정하였다.
경우 1의 결과를 보면 apparent range가 16.38 km일 때, 방법 1, 2에서는 간섭이 발생하지 않은 것으로 계산되나, 방법 3에서는 Ψ가 0.8 dB로서 간섭이 발생함을 알 수 있다. 경우 2, 3은 동일조건이나 apparent range만 다르게 설정하였다. 경우 2의 경우는 방법 1에서는 간섭이 발생하지 않으며, 방법 2, 3에서는 간섭이 발생하였음을 알 수 있다. 경우 3의 경우는 방법 1, 2의 경우에서는 간섭이 발생하지 않았으나, 방법 3에서는 Ψ가 2.34 dB로 간섭이 강하게 발생했음을 알 수 있다. 2.34 dB라는 수치는 신호 세기와 비슷한 세기의 간섭이 발생했음을 나타낸다.
시뮬레이션 결과를 정리하면, 같은 조건의 ESA 레이다에서 방법 1, 2를 사용했다면 식별하지 못하는 간섭들을 방법 3을 이용하면 식별할 수 있음을 알 수 있다. 즉, 방법 3을 이용했을 때, 더 많은 간섭을 식별할 수 있다는 것을 알 수 있다. 따라서 방법 3을 이용하면 간섭이 예상 되는 PRF의 범위를 효과적으로 제거하여 안정적인 PRF 설계가 가능함을 알 수 있다.
Ⅴ. 결 론
본 논문에서는 ESA 레이다의 성능 향상을 위하여 간섭을 회피하기 위한 개선된 PRF 설계 기법을 제시하였다. 또한 시뮬레이션 결과를 통해, 본 논문에서 제시하는 기법을 사용하면 기존의 방법이 배제하지 못하는 부적절한 PRF의 범위를 효과적으로 회피하여 PRF를 설계할 수 있음을 분석할 수 있었다. 추후 해당 설계 기법을 실제 개발에 활용하여, 예측한 만큼의 성능 개선이 이루어지는지 확인해 볼 필요가 있다.
본 논문의 기법은 ESA 레이다의 PRF 설계에 유용하게 쓰일 수 있으며, 그 중 특히 거리 영역에 대한 정보가 중요한 LPRF의 설계에 효과적으로 사용될 수 있을 것이다.