3개의 고 분해능 거리 프로파일을 이용한 유도탄의 위치 추정

Ⅰ. 서 론

국방 유도무기 개발 과정에서 유도탄의 정상비행 추적을 확인하고, 안전구역을 확보하기 위하여 계측 레이다가 사용된다. 계측 레이다는 실시간으로 유도탄의 시공간위치정보를 획득하고, 이를 중앙통제소에 전송하여 유도무기 체계의 성능을 평가한다.

일반적으로 추적 레이다는 모노펄스 레이다, 광대역 레이다, 도플러 레이다 등의 3가지로 분류된다^[1]～^[10]. 모노펄스 레이다는 짧은 시간 동안 펄스 형태의 신호를 발생시켜 좁은 빔폭 내에 들어오는 물체를 실시간으로 추적하는 장거리 유도무기 계측에 적합하다^[1]～^[3]. 하지만 낮은 거리 분해능과 방위각/고각에 대한 각도 오차로 유도탄의 위치 추정 오차가 크게 발생한다. 반면에 광대역 레이다는 선형주파수변조(linear frequency modulation: LFM) 방식을 사용하고, 주파수 대역폭에 따라 고 분해능 거리 프로파일 획득이 가능하다^[4]～^[6]. 하지만 방위각/고각 각도 빔폭이 모노펄스 계측레이다보다 넓기 때문에 1대의 광대역 레이다로는 유도탄의 정확한 위치 추정이 어렵다. 도플러 레이다는 다수의 배열 안테나를 사용하며, 표적에 반사되어 돌아오는 신호의 위상차를 이용하여 유도탄의 위치를 추정한다^[7]～^[10]. 유도탄의 거리 측정을 위하여 듀얼 오실레이터 모듈을 사용하고, 서로 다른 주파수를 이용하여 표적을 추적하는 MF(Multi-Frequency) 모드가 널리 알려져 있다.

다수의 레이다에서 얻어지는 거리 프로파일을 이용하여 표적의 위치를 추정하는 기법이 소개되었다^[11]～^[13]. 이 기법은 방위각과 고각 데이터를 사용하지 않기 때문에 각도 오차의 영향을 받지 않는다. 그리고 거리 분해능이 좋을수록 표적의 위치 추정 정확도가 높다. 하지만 표적의 비행자세에 따라 거리 측정 오차가 발생한다. 참고문헌 [11]에서는 거리 계측 오차에 의해 발생하는 3차원 위치 추정 오류를 줄이기 위하여 귀납 공식(recursion formula) 기법을 제시하였다. 참고문헌 [12]에서는 레이다에서 유도탄까지의 거리를 거리 계측 데이터와 거리 오차의 합으로 표시하였고, 거리에 따른 위치 추정 오차를 3차원 기하학 그래프로 분석하였다. 그리고 수평면 위치 추정 정확도는 무시할 수 있지만, 수직면 위치 추정 정확도는 거리 오차의 영향을 많이 받는다고 결론지었다. 참고무헌 [13]에서는 레이다에서 표적의 중심까지 거리를 알아내기 위하여 표적의 3차원 전자기 모델을 사용하였다. 고 분해능 레이다에서 계측된 거리 프로파일과 3차원 전자기 모델 시뮬레이션을 이용하여 계산된 거리 프로파일을 비교하여 표적 중심까지의 거리를 알아내었다. 하지만 이 방법은 표적의 자세와 위치 변화에 따른 모든 경우의 수에 대하여 전자기 수치해석 시뮬레이션 데이터를 획득해야 되는 단점이 있다. 따라서 본 논문에서는 유도탄의 비행자세에 따른 거리 보상을 통해 레이다에서 유도탄 원점까지의 거리를 알아내고 이를 이용하여 유도탄의 위치를 추정하는 방법을 제안한다. 그리고 전자기 수치해석 프로그램을 이용하여 거리 보상에 대한 시뮬레이션 검증을 수행하고, 고 분해능 레이다를 이용하여 위치추정 알고리즘을 검증한다.

Ⅱ. 거리 프로파일을 이용한 위치 추정

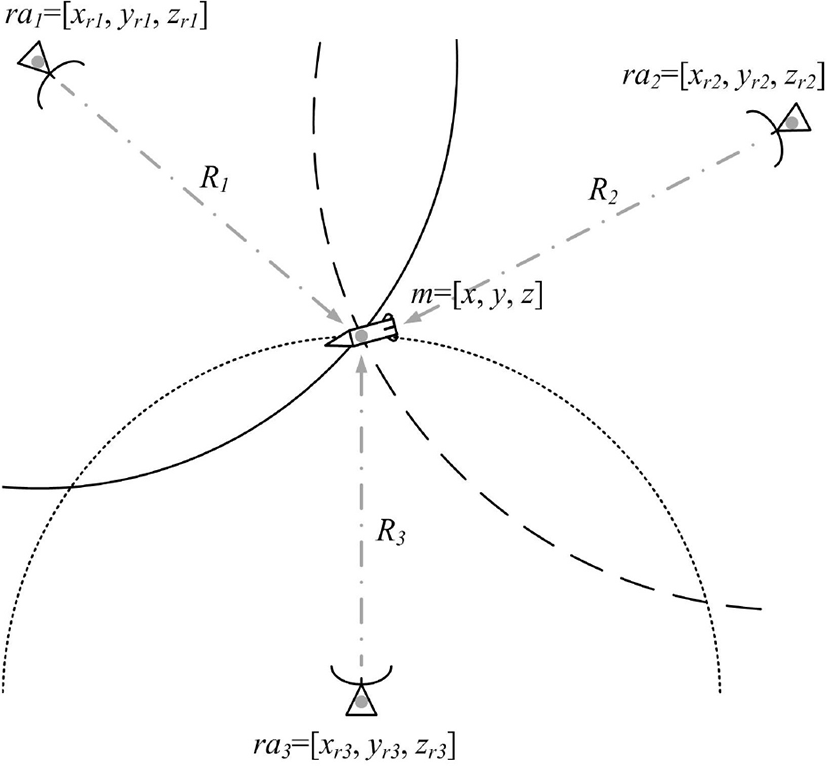
광대역 레이다 위치를 ra₁=[x_r1, y_r1, z_r1], ra₂=[x_r2, y_r2, z_r2], ra₃=[x_r3, y_r3, z_r3] 으로, 유도탄의 위치를 m=[x, y, z] 으로 나타낸다. 광대역 레이다에서 유도탄까지의 거리 R₁, R₂, R₃는 식 (1)～식 (3)으로 표현되며 이를 그림 1에 나타내었다.

그림 1. | Fig. 1. 광대역 레이다 3대의 유도탄 추적 | Missile tracking using 3 wide-band radars.

Download Original Figure

식 (1) 및 식 (2)으로부터 (R₁-R₂)와 (R₂-R₃)을 x에 대하여 풀이하면 각각 식 (4) 및 식 (5)를 얻을 수 있다.

이때 A, B, C는 수식 간략화를 위한 공통 변수이다.

식 (4)와 식 (5)의 x는 같기때문에 y에 대하여 재정리하면

이때 Y₁, Z₁은 수식 간략화를 위한 공통 변수이다.

광대역 레이다의 위치와 유도탄까지의 거리 R₁, R₂, R₃를 이미 알고 있기 때문에 A, B, C와 Y₁, Z₁은 상수로 표현된다. 따라서 식 (1)의 x에 식 (4)를 대입하고, y에 식 (9)를 대입하면 유도탄의 위치 z를 계산할 수 있다. 그리고 계산된 z를 식 (4)와 식 (9)에 대입하여 유도탄의 위치 [x, y, z]를 추정할 수 있다.

Ⅲ. 유도탄의 자세에 따른 거리 보상

3-1 유도탄 모델링

광대역 레이다에서 얻어지는 거리 프로파일에서는 유도탄의 원점이 아닌, 각도에 따른 유도탄의 표면까지의 거리(R_m)만 획득된다. 앞 장에서 기술한 거리프로파일을 이용한 위치 추정은 오차가 발생하므로, 상대적 위치를 고려한 거리 보상(R_c)이 요구된다. 이를 위하여 레이다 입사각에 따른 유도탄의 거리 보상에 대한 계산이 필요하다. 따라서 총 거리(R_total)는 식 (12)와 같이 측정 거리(R_m)와 거리 보상(R_c)의 합으로 표현된다.

$$R_{total}=R_m+R_c$$

(12)

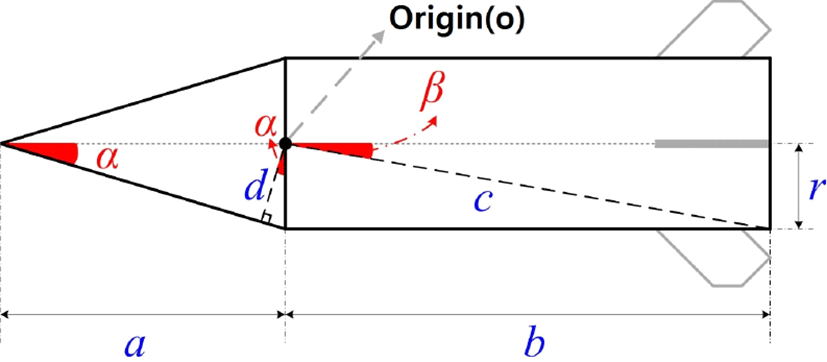
유도탄 모델링은 그림 2처럼 날개를 제외하면 원뿔과 원통으로 간략화 할 수 있다. 원뿔과 원통의 접합 중심을 원점(o)이라고 가정할 경우, 원뿔의 길이 a, 원뿔의 반지름 r, 원뿔 각도 $\alpha ={\tan }^{-1}\left(\frac{r}{a}\right)$, 원점에서 원뿔 표면까지의 직선거리 d=r×cos(α), 원통 길이 b, 원점에서 밑면 모서리까지의 대각선 길이 $c=\sqrt{b^2+r^2}$, 원점에서 밑면 모서리까지의 각도 $\beta ={\tan }^{-1}\left(\frac{r}{b}\right)$으로 나타낼 수 있다.

그림 2. | Fig. 2. 유도탄 모델링 | Missile modeling.

Download Original Figure

3-2 자세 변화에 따른 거리 보상 계산

유도탄 자세(Pitch, Yaw) 변화에 따른 거리 보상을 계산하기 위해서는 유도탄의 원점에서 레이다 방향으로 유도탄 표면까지의 직선거리 계산이 필요하다. 레이다 입사각 θ에 따른 거리 보상 R_c는 식 (13)～식 (16)으로 나타낼 수 있다. 그림 3은 유도탄 자세 변화에 따른 거리 보상을 그림으로 도시화하였다.

$$0\le \theta \le \beta ,R_c=\frac{b}{\cos \left(\theta \right)}$$

(13)

$$\beta \le \theta \le 90,R_c=c\times \cos \left(\theta -\beta \right)$$

(14)

$$90\le \theta \le \left(90+\alpha \right),R_c=r\times \cos \left(\theta -90\right)$$

(15)

$$\left(90+\alpha \right)\le \theta \le 180,R_c=a\times \sin \left(\theta -90\right)$$

(16)

그림 3. | Fig. 3. 자세 변화에 따른 거리 보상 | Compensated range according to missile position.

Download Original Figure

3-3 유도탄의 레이다 입사각 계산

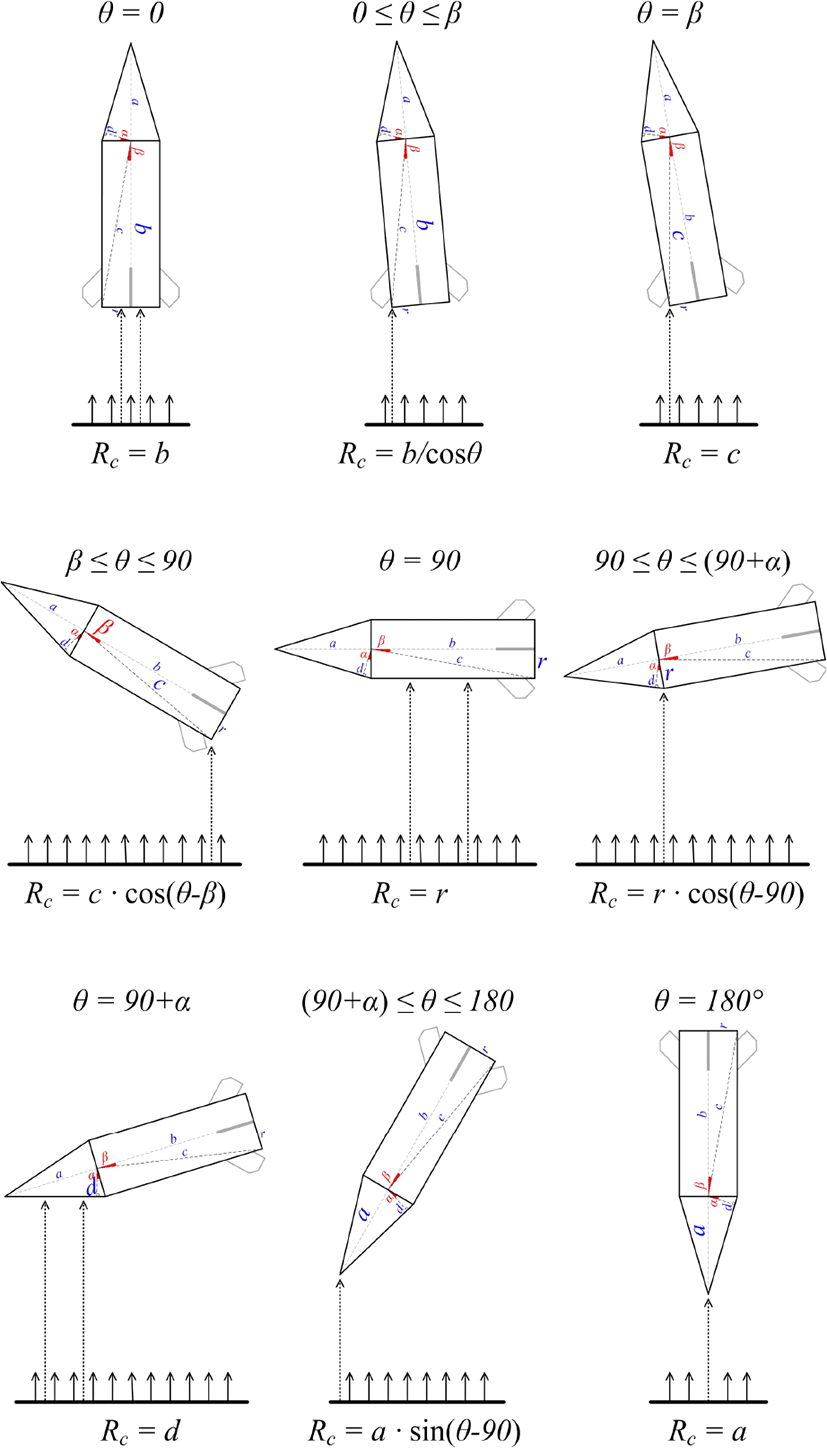
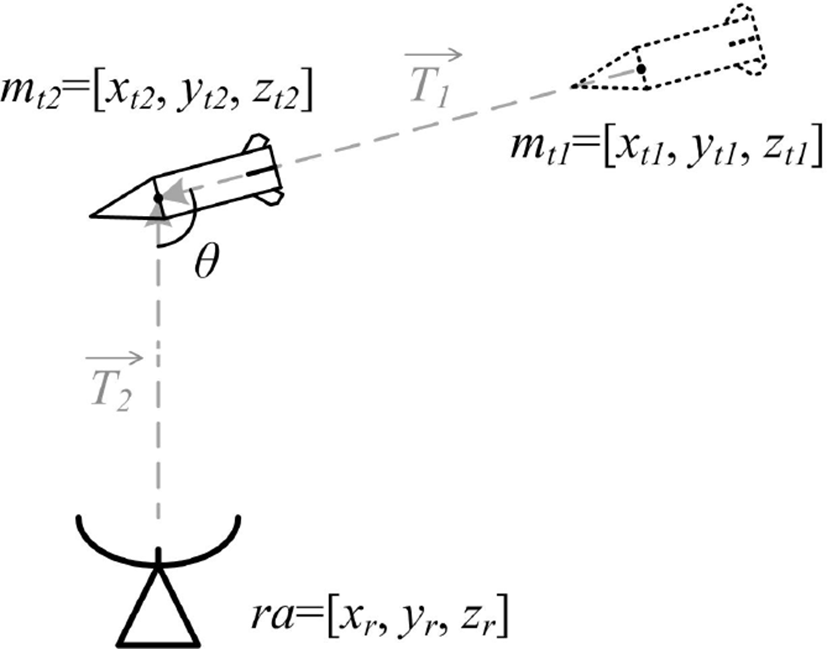
유도탄 자세 변화에 따른 거리 보상을 계산하기 위해서는 유도탄의 레이다 입사각 θ 계산이 필요하다. 이는 유도탄의 이동 궤적을 바탕으로 레이다와 유도탄 사이의 벡터 내적을 이용하여 계산이 가능하다. 그림 4는 유도탄 이동에 따른 레이다 입사각 계산 방법이다.

그림 4. | Fig. 4. 유도탄의 레이다 입사각 계산 | Aspect angle calculation of radar.

Download Original Figure

레이다 위치를 ra=[x_r, y_r, z_r], 유도탄이 m_t1=[x_t1, y_t1, z_t1]에서 m_t2=[x_t2, y_t2, z_t2]으로 이동한다고 가정할 경우, 유도탄 이동 벡터 $\overrightarrow{T_1}$를 식 (17)로, 레이다 추적 벡터 $\overrightarrow{T_2}$를 식 (18)로 나타낼 수 있다. 따라서 레이다 입사각 θ는 벡터 내적 공식에 의해 식 (19)로 계산될 수 있다.

$$\overrightarrow{T_1}=\left(\begin{array}{ccc}{x}_{t2}-x_{t1},& y_{t2}-y_{t1},& z_{t2}-z_{t1}\end{array}\right)$$

(17)

$$\overrightarrow{T_2}=\left(\begin{array}{ccc}{x}_{t2}-x_r,& y_{t2}-y_r,& z_{t2}-z_r\end{array}\right)$$

(18)

$$\theta ={\cos }^{-1}\left(\frac{\overrightarrow{T_1}\cdot \overrightarrow{T_2}}{\Vert \overrightarrow{T_1}\Vert \Vert \overrightarrow{T_2}\Vert }\right)$$

(19)

하지만 현재시간에서의 유도탄 위치를 미리 알 수 없기 때문에, 이전 시간에 대한 유도탄의 이동 벡터를 이용하여 레이다 입사각을 계산할 수 있다.

Ⅳ. 시뮬레이션

4-1 전자기 수치해석 모델링

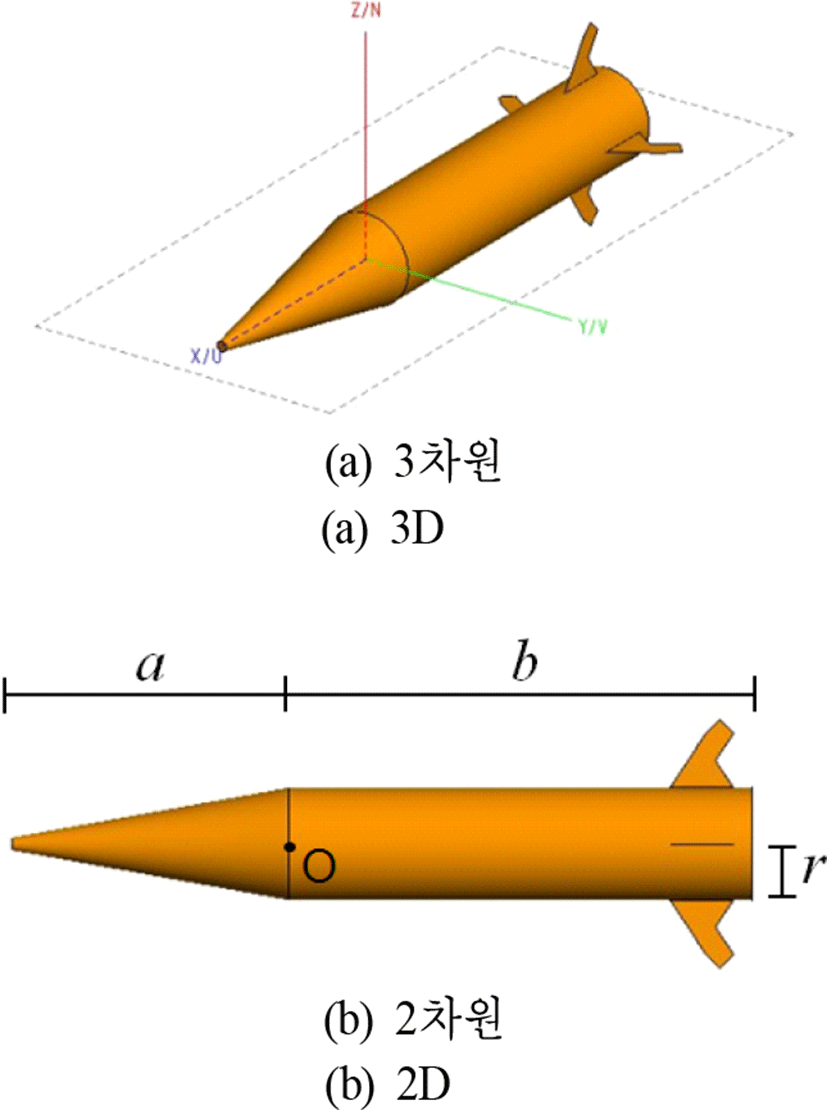
유도탄 전자기 분석을 통하여 입사각에 대한 반사 정도를 확인하고 시뮬레이션 검증을 수행하였다. 상용 도구인 FEKO를 사용하여 유도탄을 그림 5와 같이 모델링하였다. 표 1은 시뮬레이션에 사용된 유도탄 크기와 시뮬레이션 설정값이다.

그림 5. | Fig. 5. 유도탄의 모델링 | Missile modeling.

Download Original Figure

표 1. | Table 1. 설계 변수 및 시뮬레이션 설정 값 | Design variable and parameter.

Variable	Description	Value
a	Cone length	1.5 m
b	Cylinder length	2.5 m
r	Cylinder radius	0.3035 m
fc	Center frequency	10 GHz
BW	Bandwidth	1.5 GHz

Download Excel Table

전자기 수치해석 프로그램에서 선형간격 불연속점(linearly spaced discrete points) 기법을 적용하여 9.25 GHz에서 10.75 GHz까지 주파수를 사용하였다. 식 (20)은 거리 분해능 R_resolution을 계산하는 식이며, 주파수 대역폭 BW가 1.5 GHz이므로 거리 분해능은 0.1 m이다.

$$R_{resolution}=\frac{c}{2\cdot BW}$$

(20)

이때, c는 빛의 속도 3×10⁸ [m/s]이다.

4-2 거리프로파일 획득

전자기 수치해석 결과를 바탕으로 거리프로파일을 획득하기 위하여 유도탄의 레이다 입사각 θ를 0도에서 180도까지 10도 간격으로 변화시키며 전자기 수치해석을 진행하였다. 그림 6은 전자기 수치해석 결과로 얻어지는 *.ffe 파일이다. 설정한 주파수 대역폭 내에서 각 주파수에 해당하는 유도탄의 레이다유효반사면적(radar cross section: RCS) 값과 전기장(electric-field) 수치를 각각 실수 (real)와 허수(imaginary)로 얻을 수 있다. 이 중에서 phi와 theta로 저장된 전기장 수치를 실수와 허수끼리 더해준 뒤 이를 복소수 형태로 만들어 IFT(Inverse Fourier Transform)을 수행하면 3차원 유도탄 모델의 원점(o)을 기준으로 유도탄의 표면에 부딪혀 반사되는 신호의 거리 프로파일을 획득할 수 있다.

그림 6. | Fig. 6. 전자기 수치해석 결과 파일 (*.ffe) | Result file of electromagnetic numerical analysis.

Download Original Figure

그림 7(a)는 유도탄의 레이다 입사각이 0°일 때 유도탄의 거리프로파일을 그래프로 나타낸 것이며, 유도탄 모델의 원점(o)을 기준으로 −2.5 m에서 거리프로파일세기(range profile intensity: RPI)가 크게 획득되었다. 이는 레이다에서 송신된 신호가 유도탄의 뒷면을 맞고 반사된 것을 의미한다. 그림 7(b)는 유도탄의 레이다 입사각이 90°일 때의 결과이며, 레이다에서 송신된 신호가 유도탄의 측면에 부딪혀 반사된 신호가 −0.3 m에서 크게 획득되었다. 그리고 0 m에서도 거리프로파일세기가 크게 나타났는데, 이는 원점과 일직선에 위치한 꼬리 날개 측면에 반사되어 돌아오는 신호가 반영된 것이다.

그림 7. | Fig. 7. 레이다 입사각에 따른 거리프로파일세기 | Range profile intensity according to radar aspect angle.

Download Original Figure

4-3 레이다 입사각에 따른 거리 보상

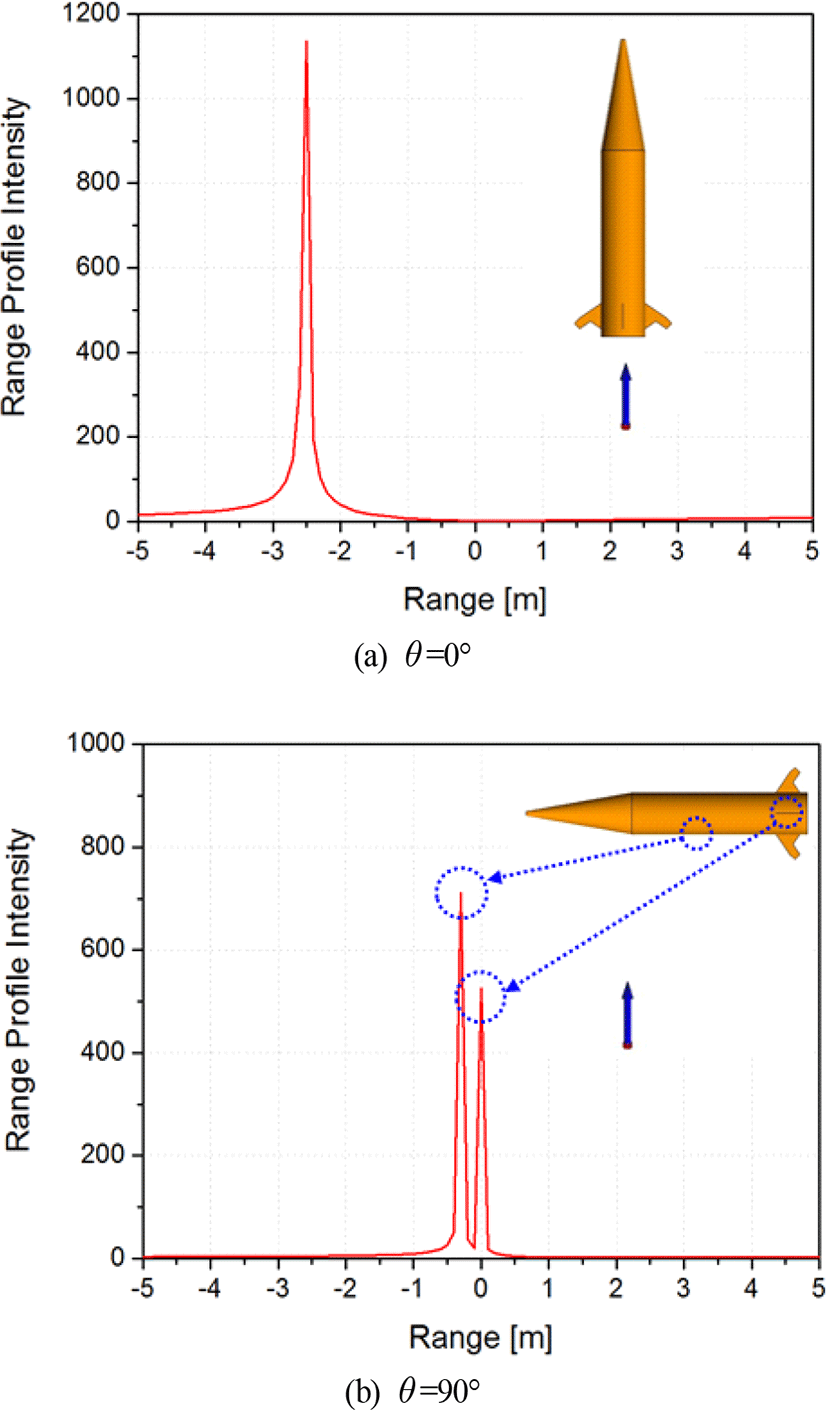
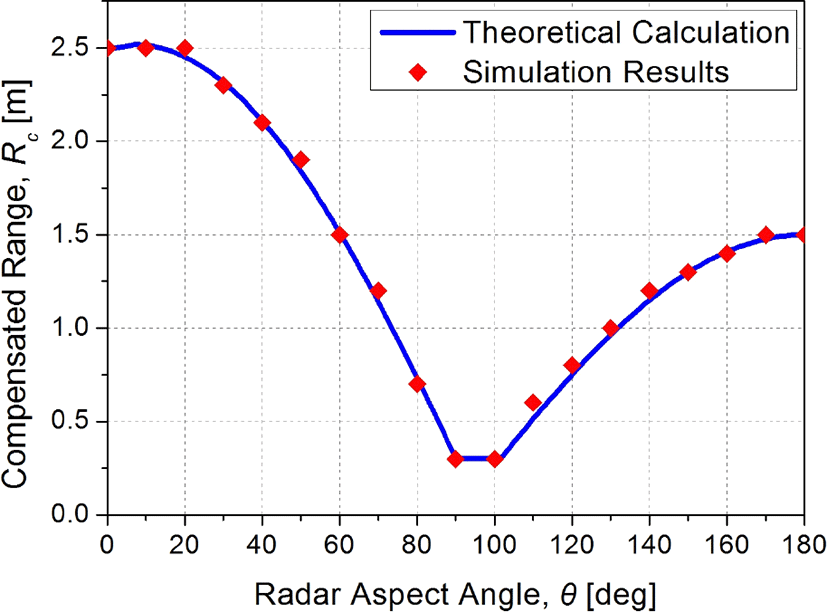
그림 8은 레이다 입사각에 따른 거리 보상 값을 비교한 것이다. 파란색 실선은 유도탄의 크기(a, b, r)를 식 (13)～식 (16)에 대입하여 거리 보상 값을 계산한 것이다. 빨간색 점은 전자기 수치해석 프로그램을 이용하여 레이다 입사각을 0°에서 180°까지 10° 단위로 변화하면서 획득한 거리 보상 값이다. 이론적으로는 레이다 입사각이 θ=β= 6.92°일 때, 최대 거리 보상 값이 2.518 m으로 계산되었다. 하지만 전자기 수치해석 결과에서는 거리 분해능이 0.1 m 이기 때문에 0°, 10°, 20°에서 동일하게 2.5 m로 획득되었다. 레이다 입사각이 90°일 때, 유도탄의 측면에 반사되어 돌아오는 신호의 세기가 크기 때문에 거리 보상 값이 0.3035 m로 동일하게 나타났다. 그 외에 발생하는 오차는 전자기 수치해석 프로그램의 주파수 대역폭 설정에 따른 거리 분해능 오차 ±0.05 m이므로, 주파수 대역폭을 크게 설정하면 오차를 최소화할 수 있다. 따라서 광대역 레이다에서 계측한 거리 R_m에 그림 8의 레이다 입사각 θ에 따른 거리 보상 R_c를 더하면 레이다에서 유도탄 원점까지의 총 거리 R_total을 알 수 있다.

그림 8. | Fig. 8. 레이다 입사각에 따른 거리 보상 값 비교 | Comparison of compensated range according to radar aspect angle.

Download Original Figure

Ⅴ. 검증 결과

그림 9(a)는 자료 검증에 사용된 고 분해능 레이다이다. 선형주파수변조(linear frequency modulation: LFM) 방식을 사용하고, 주파수 대역폭은 500 MHz, 거리 분해능은 0.33 m이다. 그림 9(b)는 유도탄 모의표적으로, ¼ 크기로 제작되었다. (a=0.375 m, b=0.625 m, r=0.075 m) 그림 9(c)는 측정에 사용된 레이다와 유도탄 위치를 지도에 나타낸 것이다. 이때 사용된 레이다와 유도탄의 xyz 좌표는 표 2와 같으며, 이를 식 (1)～식 (3)에 대입하여 레이다에서 유도탄까지의 이론적인 거리를 R₁=132.6268 m, R₂=118.8645 m, R₃=100.1135 m 으로 계산할 수 있다.

그림 9. | Fig. 9. 사진 (a) 레이다, (b) 모의표적, (c) 지도 | Picture (a) radar, (b) target, (c) field map.

Download Original Figure

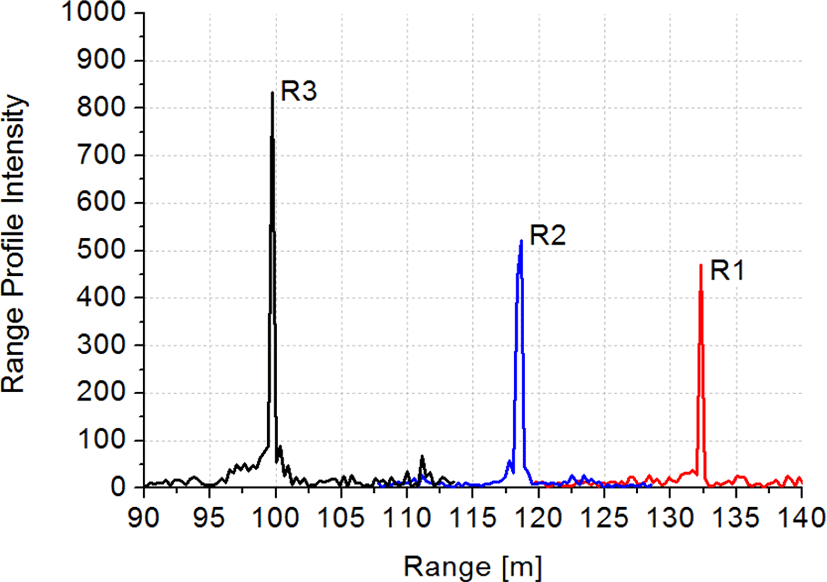
그림 10은 고 분해능 레이다로부터 획득한 거리프로파일이다. 표 3은 각 레이다가 유도탄을 측정한 거리 R_m, 유도탄의 레이다 입사각 θ, 거리 보상 R_c, 총 거리 R_total을 나타낸 것이다. 레이다 입사각 θ는 각각의 레이다에서 유도탄까지의 벡터와 유도탄의 이동 벡터를 식 (19)에 대입하여 계산하였다. 이 때 사용된 유도탄의 이동 벡터는 이전 시간에서의 유도탄 xyz 좌표 m_t1=121.1159, 37.9425, 12.6902와 표 2의 현재 유도탄 xyz 좌표 m_t2=123.8064, 47.5382, 1.4026으로 계산된다. 이를 식 (13)～식 (16)에 대입하면 거리 보상 값을 알 수 있고, 이로부터 총 거리를 계산할 수 있다. 따라서 레이다 계측 총 거리 R_total을 알 수 있기 때문에, 2장에서 소개한 식 (1)～식 (11)에 대입하여 유도 탄의 xyz 좌표를 m_estimation=123.8007, 47.5362, 1.5100으로 추정할 수 있다. 이는 표 2의 유도탄 xyz 좌표와 매우 유사한 결과이며, 최대 발생 오차는 0.1074 m이다.

그림 10. | Fig. 10. 고 분해능 레이다의 거리프로파일 | Range profile of high resolution radar.

Download Original Figure

Ⅵ. 결 론

본 논문에서는 3대의 광대역 레이다에서 유도탄을 측정한 거리를 이용하여 유도탄의 위치를 추정하는 방법에 대하여 소개하였다. 유도탄의 원점까지의 총 거리 계산을 위하여 레이다 입사각으로부터 거리 보상 값을 계산하였고, 이를 레이다 측정 거리에 더하여 레이다로부터 유도탄 원점까지의 총 거리를 알아내었다. 전자기 수치해석 프로그램을 이용하여 유도탄의 레이다 입사각에 따른 거리 보상 값을 시뮬레이션 검증하였고, 고 분해능 레이다를 이용하여 위치 추정 알고리즘을 검증하였다.