Ⅰ. 서 론
항공기 기반 SAR(Synthetic Aperture Radar) 영상복원을 위해서 시스템 특성에 적합한 다양한 영상복원 알고리즘과 신호처리 기법 등이 활발히 연구되고 있으며[1],[2], 이 중 back-projection 알고리즘은 항공기 요동보상에 대한 우수한 특성으로 다른 알고리즘 기반(예, range-Doppler, frequency scaling, range-migration 등) SAR 영상과의 비교연구를 위해서 활용될 수 있다[3]. 그러나 기존 back-projection 알고리즘은 우수한 요동보상의 장점이 있는 반면에, 긴 처리시간이 걸린다는 단점이 있다[4]~[6].
이와 같은 긴 영상처리시간 문제를 극복하기 위해서 고안된 고속 분할연산기법(fast factorized-BPA)[7],[8]은 처리속도 개선 측면에서 우수한 성능을 보이지만, 일반적으로 다층구조의 분할연산기법을 이용한 상대적으로 복잡도가 높은 알고리즘으로 사용자 측면의 활용도가 다소 제한적인 측면이 있다. 이를 보다 직관적이고 단순화된 단일구조의 분할연산기법으로 대체함으로써 SAR 영상복원의 처리속도와 사용자 편의성을 높이고자 하였다.
본 논문에서는 항공기 기반의 FMCW(Frequency Modulated Continuous Wave)-SAR 시스템의 레이다 영상복원을 위해 이용되는 back-projection 알고리즘에 간소화된 분할연산기법을 더한 수정된 back-projection 알고리즘을 제안한다. 단순화시킨 분할연산기법을 적용한 back-projection 알고리즘은 상대적으로 좁은 주사폭(swath width)과 긴 합성개구면(synthetic aperture)을 갖는 SAR 시스템의 영상복원에 적합하며, 획득된 신호영역과 복원영상 내 신호영역을 일정한 비율로 분할하여 각 영역 간 연산 중요도를 고려해 처리한다. 이때, 분할 영역 간의 영상처리 중 기여도가 낮은 영역 간의 계산과정을 생략함으로써 전체 연산시간을 단축시킬 수 있게 된다.
Back-projection 알고리즘의 기본 연산과정과 본 논문에서 제안된 간소화된 분할연산과정은 각각 2장과 3장에서 설명되며, 제안된 분할연산기법을 실제 항공기 기반 FMCW-SAR 원시자료에 적용하여 기존 알고리즘의 처리 결과와 그 특성을 4장에서 비교분석하였다.
Ⅱ. Back-Projection 알고리즘
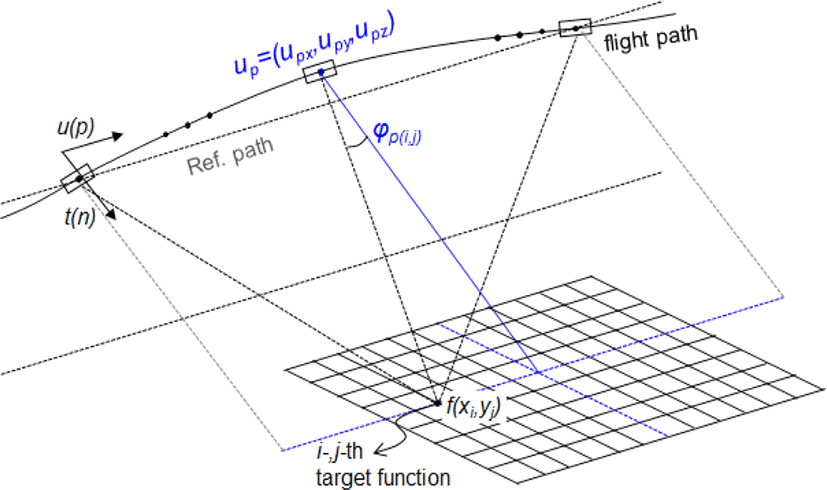
Back-projection 알고리즘은 항공기 요동보상기법과 SAR 신호처리 연구를 위한 기준영상과 비교자료 생성 등을 위해서 그 장점을 활용할 수 있으며, 항공기 기반 FMCW-SAR 시스템의 영상복원을 위해 적용된 신호모델과 back-projection 알고리즘의 기본 연산과정을 본 장에서 설명한다(그림 1 참조).
FMCW 신호기반의 레이다 시스템은 기준 송신 신호를 이용해 수신신호를 직접 주파수 하향변환(frequency down conversion)하여, 두 신호의 차에 해당하는 비트 주파수(beat frequency) 성분을 수신하고 샘플링하여 레이다 신호처리에 활용한다[1],[9]. 이와 같은 과정은 식 (1)~(4)로 정리될 수 있다. 식 (1)은 송신신호로 비트주파수 생성과 레이다 신호처리 과정 중 정합필터(matched filter)로 활용될 기준 신호가 되며, 식 (2)는 목표물 지연시간 τ을 적용한 수신신호가 된다. 식 (3)과 식 (4)는 송·수신신호를 주파수하향변환시켜 얻은 중간주파수(IF: Intermediate Frequency)의 수신신호와 복원영상 내 i-, j-번째 목표물의 지연시간 특성을 각각 나타낸다(여기서, t 샘플링 시간, u 안테나 위치, f0 중심주파수, Kr 변조율, c 광속을 각각 나타냄).
위 수식 식 (1)~(3)은 편의상 신호세기 성분이 생략되었으며, 안테나 빔패턴, 목표물 거리감쇄와 반사도 등이 고려되어야 한다[10],[11].
기존의 back-projection 알고리즘은 SAR 영상 내 i-, j-번째 픽셀의 목표물 복원을 위해서 아래 식 (5)~(7)과 같이 윈도우 함수(Wp)와 샘플링 시간(t)에 대한 푸리에 변환(Fourier transform)이 이루어진 수신신호(sIF,r(ω, up))를 적용한 정합필터과정을 거치게 되고, 이를 특정 레이다 송·수신 안테나 위치(up, p-번째 송신펄스 기준 안테나 위치)에 대해서 목표물(i-, j-번째 픽셀)과의 거리 및 지연시간(tdij)을 모든 안테나 위치에 대해 반복 계산하여 그 결과를 누적하는 과정을 수행한다.
위 과정에서 윈도우 함수는 거리(range) 방향과 방위(azimuth) 방향을 구분하여 적용할 수 있으며, 특히 방위 방향 위신호(aliasing 또는 azimuth ambiguity)를 낮추기 위한 목적으로 식 (8)과 같은 윈도우 함수를 안테나 위치(up)와 복원영상 내 i-, j-번째 픽셀 간의 편각(ϕp(ij)) 성분을 이용하여 식 (9)와 같이 정의할 수 있고, 이를 정합필터과정에 적용하였다(그림 1 참조). 또한, 최적화된 가중치 적용을 위해 가중치 계수(α)는 10~500 이내의 최적화된 값으로 설정할 수 있다.
그리고 기존 back-projection 알고리즘의 효율적 영상복원을 위해서 입력신호(sIF,r(ω, up))를 복원영상 내 목표물 지연 시간과 정합필터의 계산 결과가 최적화되도록 입력신호를 고해상 신호로 다시 샘플링(re-sampling)하는 과정을 포함하였다. 이때, 입력 신호는 내삽법(interpolation)을 이용하여 기존 신호 대비 10~100배의 고해상 신호로 변환하여 정합필터과정에 적용된다.
Ⅲ. 분할연산기법을 적용한 BPA
본 장에서는 효율적인 레이다 영상복원을 위해 기존 back-projection 알고리즘에 합성개구면을 기준으로 분할된 입력신호(레이다 수신신호, sIF,r(ω, u))와 출력 복원영상 영역 간의 연산을 기본으로 한 분할연산기법을 추가한 수정된 back-projection 알고리즘에 대해 설명하며, 모의실험을 통해 제안된 분할연산기법의 계산효율과 SAR 영상복원 특성을 검증한다.
Back-projection 알고리즘은 기본적으로 식 (7)에서와 같이 SAR 영상복원을 위해 설정된 각 픽셀과 안테나 간의 지연시간을 정합필터과정에 적용하여 각각의 계산결과를 해당 픽셀에 누적하는 연산과정을 반복적으로 수행하게 된다. 그러나 레이다 빔 중심에서 상대적으로 멀리 벗어난 픽셀의 경우, 그 계산결과가 복원영상에 미치는 영향은 적으나, 계산상의 중요도가 높은 연산과정과 비교해 동일한 계산시간을 소모하는 특성을 갖게 된다. 이와 더불어 고해상도의 영상복원을 위해 픽셀 수가 증가할수록 back-projection 알고리즘의 정합필터과정 식 (5)의 연산량이 그만큼 증가됨을 알 수 있다.
위 두 가지 관점의 문제점을 개선하기 위해서 간소화시킨 분할연산기법은 먼저 정합필터 연산과정의 계산효율이 최적화될 수 있도록 복원될 SAR 영상을 그림 2(a) 우측과 같이 특정 크기의 영상으로 분할하고, 이와 동일한 위치의 입력신호를 그림 2(a) 좌측과 같이 분할한다. 계산효율을 높이기 위해 소규모로 분할된 영역의 영상복원과정은 기존의 back-projection 알고리즘을 이용해 처리되며, 특정 분할영역의 SAR 영상 복원을 위해서 분할된 모든 입력 수신신호가 적용된다. 이때, SAR 영상 복원을 위해 분할된 영상과 상대적으로 먼 위치에 있어 계산결과에 영향을 덜 미치는 분할 입력신호를 연산과정에서 생략하여 계산시간을 더욱 단축시킬 수 있다.

예를 들어 그림 2(a)에서와 같이 두 번째 분할영상을 복원하기 위해 back-projection 알고리즘의 입력신호는 (1)~(M)-번째까지의 분할 입력신호가 적용될 수 있다. 이 중분할 입력신호와 분할 영상 (2)-(2)의 연산조합이 가장 높은 계산 중요도를 가지며, 상대적으로 가장 먼 거리의 (M)-(2)의 연산조합이 가장 낮은 계산 중요도를 갖게될 것이다. 이때, 각각의 연산조합이 가장 높은 중요도를 갖는 조합과 이루는 편각(예, ϕMc(2c)는 (M)-(2) 연산조합의 중심점 간 연장선과 (2)-(2) 연산조합 연장선이 이루는 각도)을 기준으로 계산 중요도를 결정할 수 있다.
각 분할 입력신호(1~M)와 분할 영상(1~N·n) 간의 연산조합과 그 계산 중요도는 그림 2(b)의 행렬 개념도로 도식화 할 수 있다. 그림 2(b)의 확장된 대각원소(점선 내 원소)들의 연산조합은 계산 중요도가 높아 SAR 영상복원 과정에 필수적이며, 상대적으로 먼 거리의 연산조합(점선 밖 원소)들은 계산과정에서 생략되어 계산시간 단축에 기여한다. 추가적으로 SAR 영상분할 시 거리방향 분할을 추가할 경우(n≥2), 그림 2(b)와 같이 동일한 분할 입력신호를 적용한 연산조합이 n만큼 반복된다.
상대적으로 좁은 빔폭과 긴 합성개구면을 갖는 항공기 기반 FMCW-SAR 시스템의 경우, 계산 중요도가 낮은 연산조합의 비율이 높아져 제안된 분할연산기법이 효과적으로 적용이 가능하며, 입력자료 분할과 분할연산기법의 적용은 정합필터과정의 연산량과 합성개구면 길이 등을 고려해 기존 back-projection 알고리즘에 쉽게 적용이 가능하다.
식 (10)과 식 (11)은 분할연산기법을 적용한 후, 계산 중요도의 임계치 적용 전·후를 비교한 것으로 전체 연산조합(M × N·n개)과 계산 중요도가 높은 연산조합(K≤M × N·n개)을 선택적으로 이용한 목표물 함수특성을 나타낸 것이다. 식(12)는 위의 조건별 목표물 함수의 복원특성을 정리한 것이다. 여기서, M번째 분할 입력신호의 p번째 송수신 안테나 위치는 uMp이며, N번째 분할 복원영상 영역 내 목표물과의 지연시간은 tdN(uMp)으로 표현된다.
다음으로 분할연산기법 적용을 위한 계산중요도 범위 설정 임계치는 송·수신 안테나의 반전력빔폭(ϕHPBW)을 기준으로 설정이 가능하며, 일반적으로 반전력빔폭 이상의 편각을 갖는 연산조합의 계산 중요도는 back-projection 알고리즘 특성상 그 중요도가 매우 낮아 연산과정에서 쉽게 생략될 수 있다. 반면에 반전력빔폭 이내의 편각을 임계치로 설정할 경우, SAR 영상복원 성능과 계산효율을 고려한 최적화된 임계치 설정이 필요하다.
분할연산기법을 적용한 back-projection 알고리즘의 성능분석을 위해 그림 3과 같은 모의실험을 수행하였다. 모의실험을 위한 설정 조건은 본 연구에 사용된 실제 항공기 기반 FMCW-SAR 시스템 설정값(표 1 참조)을 기준으로 하였으며, 목표물 거리 450 m, 주파폭 100 m 그리고 방위방향 거리 200 m의 SAR 원시신호(샘플개수 1,252×4,000 개)와 복원영상을 모의실험하였다. FMCW-SAR 시스템의 성능분석을 위해 분할연산기법 적용 전·후 특성과 계산중요도 범위설정을 위한 다양한 임계치(연산조합 간 편각 기준, ϕ=1°~6°) 적용 시 변화된 IRF(Impulse Response Function) 특성을 비교하였다. 점목표물의 특성 변화 분석은 분할연산기법 적용과 좁은 임계치 적용 시 그 특성변화가 민감할 것으로 예측되는 방위방향 양 끝단의 목표물 중 위쪽에 위치한 목표물을 기준으로 비교분석하였다.
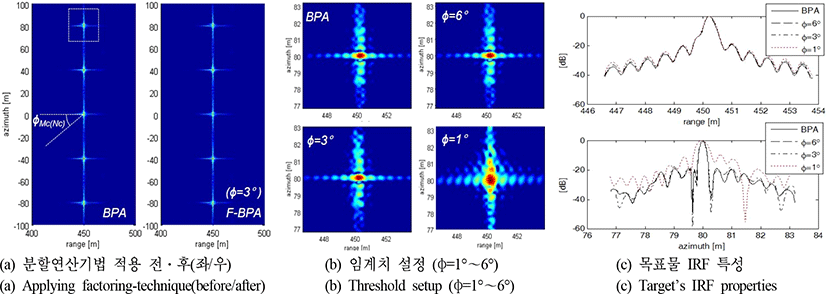
모의실험 결과, 분할연산기법의 설정 임계치 ϕ=1°인 경우, 거리/방위방향 해상도는 각각 0.29 m와 0.37 m로 설정 임계치 ϕ=3° 이상의 기준 해상도 0.29 m와 0.18 m보다 나빠지는 특성을 확인할 수 있다. 또한, 계산시간은 분할연산기법 적용 전 144.8초, 적용 후 임계치 ϕ=6°, 3°, 1°의 설정 조건에 따라 각각 30.2초, 21.26초, 7.1초로 감소하였으며, 모의실험 결과 분할연산기법의 계산 중요도 범위 설정을 위한 임계치는 FMCW-SAR 시스템의 송·수신 안테나의 반전력빔폭 기준 50 % 미만의 설정값(ϕ<3°)에서 복원영상의 급격한 왜곡을 확인 할 수 있었으며, 50 % 이상의 임계치 설정값(ϕ≥3°)을 권한다.
분할연산기법을 적용한 SAR 영상복원 및 신호처리 전 과정은 MATLAB 프로그래밍과 개인 연구용 PC(CPU i5 3.8 GHz, 메모리 16 GBytes)를 기반으로 수행되었다.
Ⅳ. 분할연산기법을 적용한 항공기 SAR 영상복원
간소화된 분할연산기법을 적용한 back-projrction 알고리즘 성능검증을 위해 실제 항공기 기반 FMCW-SAR 시스템으로부터 획득된 레이다 원시자료를 활용하였다. 사용된 항공기 기반 FMCW-SAR 시스템 제원은 표 1과 같으며, 이론적인 경사거리(slant-range) 해상도 30 cm의 성능을 갖는다.
분할연산기법을 적용한 SAR 영상복원 결과를 비교·검증하기 위해서 실제 항공기 기반 FMCW-SAR 시스템 으로부터 획득된 원시자료를 back-projection 알고리즘을 기반으로 SAR 영상을 복원하였다. 처리결과 비교분석을 위해서 2016년 1월 대부도 인근 지역에서 획득된 레이다 원시자료(합성개구면 길이 약 1.5 km, 주사폭 약 450 m, 샘플개수 1,024×28,000개, 용량 ~480 MBytes)를 이용하였다.
그림 4는 기존 back-projection 알고리즘과 간소화된 분할연산기법을 적용한 back-projection 알고리즘의 영상복원 결과를 각각 비교한 것으로, 그림 4(a)는 분할연산기법 적용 전의 기존 back-projection 알고리즘의 처리결과이고, 그림 4(b)와 그림 4(c)는 분할연산기법을 적용한 결과로 각각 모든 분할연산조합을 계산한 결과와 중요도가 높은 연산조합을 선택적으로 계산한 결과를 비교한 것이다. 다시 말해, 그림 4(b)의 반복연산횟수(K)는 분할연산조합의 전체 수(M×N·n)와 동일하며, 그림 4(c)는 계산중요도를 반영해 생략된 분할연산조합의 수만큼 줄어든 반복연산횟수(K<M×N·n, ϕ=5°)로 계산된 결과이다(식 (12) 참조).

그림 4의 각각의 처리결과는 기존 back-projection 알고리즘을 이용한 처리결과와 비교하여 간소화된 분할연산기법 적용과 계산중요도를 고려한 선택적 계산으로도 동급의 영상품질을 얻을 수 있음을 보여준다. 이때, 복원된 SAR 영상(픽셀 개수 1,534×4,756개) 내 픽셀크기는 거리/방위 방향 각각 30 cm로 계산되었다. 최적화된 영상복원을 위해 정합필터 과정의 입력신호는 20배 증가된 re-sampling 과정을 포함하였다.
그림 5는 동일한 합성개구면 길이(200 m)와 분할연산기법 적용을 위한 임계치 설정(ϕ=3°) 조건에서 복원영상의 해상도(영상 내 픽셀크기 1 m/0.5 m/0.3 m)를 변화시킨 것으로 동일한 관측 조건에서 획득된 자료에 대한 기존 back-projection 알고리즘과 분할연산기법을 적용한 영상복원 결과를 비교한 것이다. 이는 상대적으로 짧은 합성개구면을 이용한 관측 조건에서도 분할연산기법이 효율적으로 적용됨을 보이기 위한 것으로 그림 5의 (a), (c), (e)는 기존 back-projection 알고리즘을 이용해 복원한 영상이며, 그림 5의 (b), (d), (f)는 간소화된 분할연산기법을 적용한 결과이다.

분할연산기법을 적용해 복원된 SAR 영상의 비교분석을 위하여 앞선 그림 4의 예시에서 사용된 원시자료를 포함해 방위방향 샘플개수를 각 2,048/4,096/28,000개(합성개구면 길이 100/200/1,500 m)로 구분한 3종 9개의 원시자료 샘플을 이용해 각각의 처리속도를 비교분석하였다. 또한, 상대적으로 짧은 합성개구면 길이 200 m를 갖는 원시자료(샘플개수 1,024×4,096개)를 이용해 다양한 해상도(1 m/ 0.5 m/0.3 m)로 복원된 영상처리 결과를 비교분석하였다.
그림 6은 분할연산기법을 적용한 back-projection 알고리즘의 영상처리속도를 분석한 것으로 영상복원을 위한 분할연산기법의 계산효율을 두 가지 측면에서 비교한 것이다. 그림 6(a)는 복원영상의 동일한 해상도 조건을 기준으로 입력 원시자료의 합성개구면 길이와 자료용량 크기 변화를 비교한 것이며, 그림 6(b)는 상대적으로 짧은 합성개구면 조건에서 획득된 동일 자료의 SAR 영상복원을 위해 서로 다른 해상도를 적용시켜 픽셀 수 증가에 따른 연산량 변화를 분할연산기법의 처리속도 측면에서 비교/분석한 결과이다.
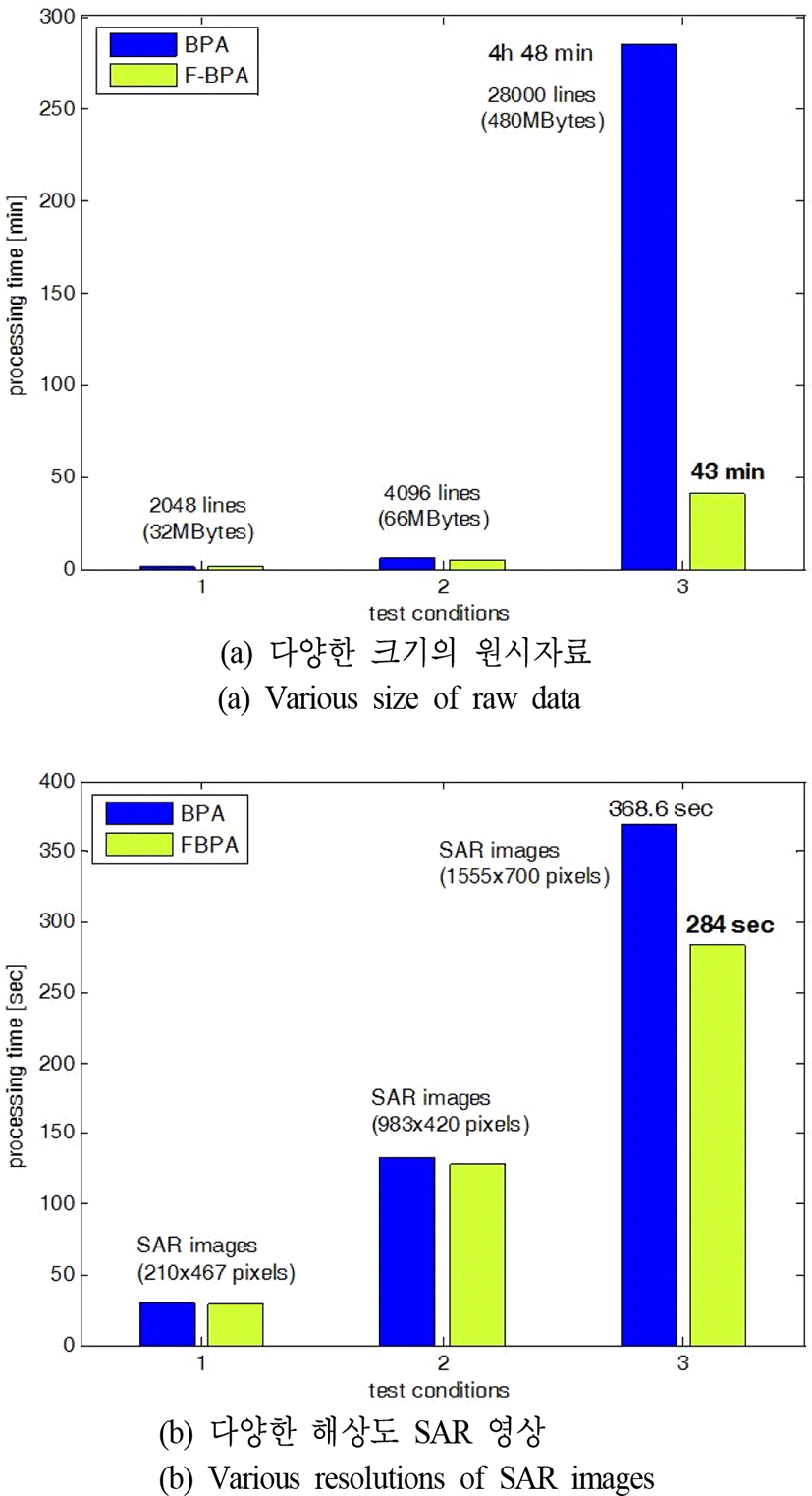
상대적으로 긴 합성개구면을 갖는 원시자료를 이용한 SAR 영상 복원 시 계산중요도를 고려한 분할연산기법의 임계치 설정과 그에 따른 연산량 감소는 처리속도 개선에 직접적인 영향을 미치며, 합성개구면이 길어질수록 다시 말해 입력 원시자료의 방위방향 자료길이가 커질수록 분할연산기법의 연산효율이 증가함을 알 수 있다. 이와 더불어 특정조건의 동일한 원시자료를 각기 다른 해상도를 갖도록 복원된 결과는 복원과정에서 픽셀 수가 증가하여 연산량이 증가될수록 분할연산기법의 효과가 두드러지게 된다. 그 이유는 최적의 연산효율을 위해 설정된 특정 픽셀 수를 기준으로 한 분할영역 크기 설정값이 상대적으로 많은 수의 픽셀로 구성된 영상복원과정에서 그 효과가 더욱 크게 나타나기 때문이다. 다시 말해, 상대적으로 적은 수의 픽셀로 구성된 SAR 영상의 경우 영상분할이 적게 이루어지고, 그만큼 분할연산기법의 기대효과가 점차 줄어들어 분할연산기법 적용 전 back-projection 알고리즘의 처리속도에 수렴되는 결과를 나타낸다.