Analysis of Radar Cross Section of the Integrated Mast Module for Battleship

Shin, Hokeun; Lee, Seokgon; Park, Dongmin; Shin, Jinwoo; Chung, Myungsoo; Park, Sanghyun; Park, Yong Bae

doi:10.5515/KJKIEES.2017.28.7.584

J. Korean Inst. Electromagn. Eng. Sci. 2017; 28(7):584-587

pISSN: 1226-3133, eISSN: 2288-226X

DOI: https://doi.org/10.5515/KJKIEES.2017.28.7.584

단편논문/SHORT PAPER

함정용 통합 마스트의 레이다 단면적 분석

신호근¹, 이석곤^*, 박동민^*, 신진우^**, 정명수^**, 박상현^**, 박용배¹^,^†

Analysis of Radar Cross Section of the Integrated Mast Module for Battleship

Hokeun Shin¹, Seokgon Lee^*, Dongmin Park^*, Jinwoo Shin^**, Myungsoo Chung^**, Sanghyun Park^**, Yong Bae Park¹^,^†

Author Information & Copyright ▼

¹아주대학교 전자공학과

^*한화시스템

^**국방과학연구소

¹Department of Electrical and Computer Engineering, Ajou University

^*Hanwha Systems

^**Agency for Defense Development

^†Corresponding Author: Yong Bae Park (e-mail: yong@ajou.ac.kr)

© Copyright 2019 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: May 30, 2017; Revised: Jul 10, 2017; Accepted: Jul 12, 2017

Published Online: Jul 31, 2017

요약

본 논문에서는 함정용 통합 마스트의 레이다 단면적을 분석한다. 레이다 단면적 분석을 위한 물리 광학법 및 물리 광학 회절이론 기반의 계산 프로그램을 개발하고, 상용 시뮬레이터와 비교를 통해 계산의 정확도를 확인한다. 함정용 마스트의 형상과 입사각, 편파에 따른 레이다 단면적 변화를 계산하고 분석한다. 마스트의 측면 기울기 변화 및 모따기가 있는 마스트 구조를 통해 레이다 단면적을 감소시킬 수 있고, 이것을 저 RCS 함정 마스트 개발에 활용할 수 있음을 확인한다.

Abstract

In this paper, the radar cross section of the integrated mast module for battleship is analyzed. The computation program based on physical optics and physical theory of diffraction is developed and the computed results are compared with those of commercial simulator to check the accuracy of computations. The radar cross section is calculated in terms of the mast shape, incident angle, and polarization. The radar cross section can be reduced through the change of the mast slope and the chamfered mast, which can be applied to a mast with a low radar cross section.

Keywords: Integrated Mast Module; Radar Cross Section; Physical Optics; Physical Theory of Diffraction

Ⅰ. 서 론

적의 레이다에 감지될 확률을 감소시키는 스텔스 기술은 함정의 생존성과 밀접한 관계가 있다. 2014년 4월 진수식을 가진 미국의 최첨단 스텔스 구축함 ‘줌왈트’호 역시 레이다에 소형 어선으로 표시될 정도로 스텔스 능력을 갖추고 있다. 이처럼 극단적인 스텔스 지향의 설계는 통합마스트(IMM: Integrated Mast Module) 기술 관련 시스템이 개발되어야 한다. 통합마스트란 기존의 레이다 등 선상에 노출된 정보 시스템이 레이다 단면적(RCS)을 높이기 때문에, 이 시스템들을 통합, 모듈화하여 RCS를 극단적으로 낮추는 기술이다. 통합마스트의 RCS 감소를 위한 가장 기본적이고 중요한 것이 마스트의 형상을 결정하는 것이다^[1],^[2]. 마스트 형상은 함정 설계의 초기단계에서 고려하기 때문에 미리 함정 마스트의 형상에 따른 RCS 특성을 알아야 한다.

본 논문에서는 함정용 레이다 체계 구조를 고려한 함정용 통합 마스트를 PEC로 가정하고, 마스트의 기하학적 형상 변화에 따른 모노스테틱 RCS를 S band에서 계산하고, 입사파의 입사각도와 편파에 따른 RCS 변화를 분석하였다.

Ⅱ. RCS 해석 방법

2-1 RCS 계산

고주파 영역에서 RCS를 계산하는 가장 대표적인 방법은 물리광학법이다. 물리 광학법은 식 (1)과 같이 산란체에 전자파가 직접 입사하는 경우에 대해서만 표면 등가 전류를 정의하고, 이로부터 산란파를 계산한다^[3].

J ¯ P O = {2 n^× H ¯ i illuminated region 0 shadow region

(1)

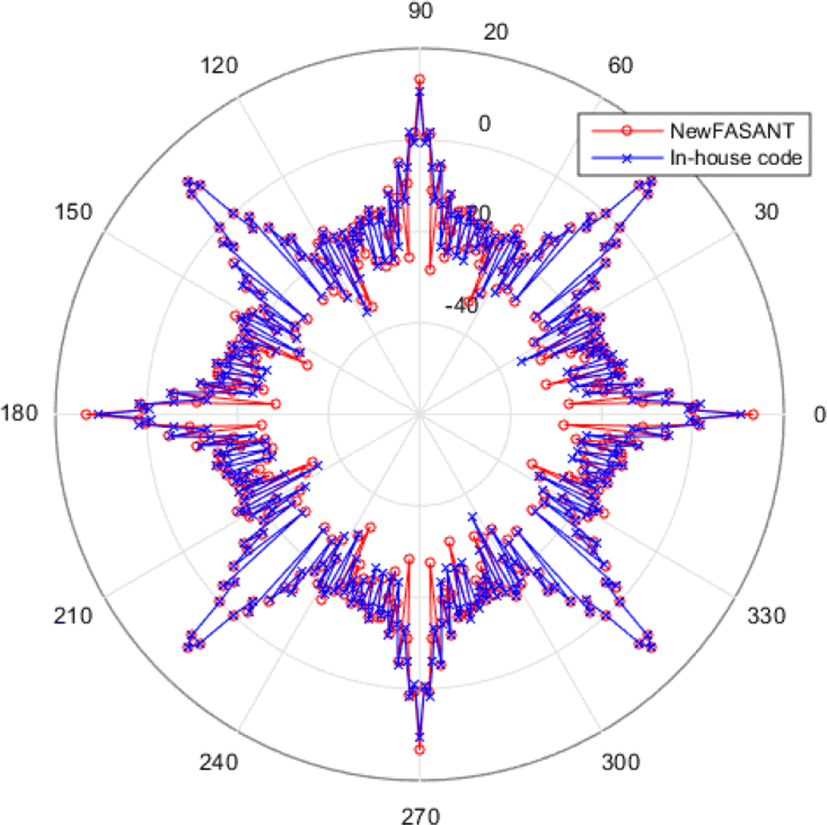
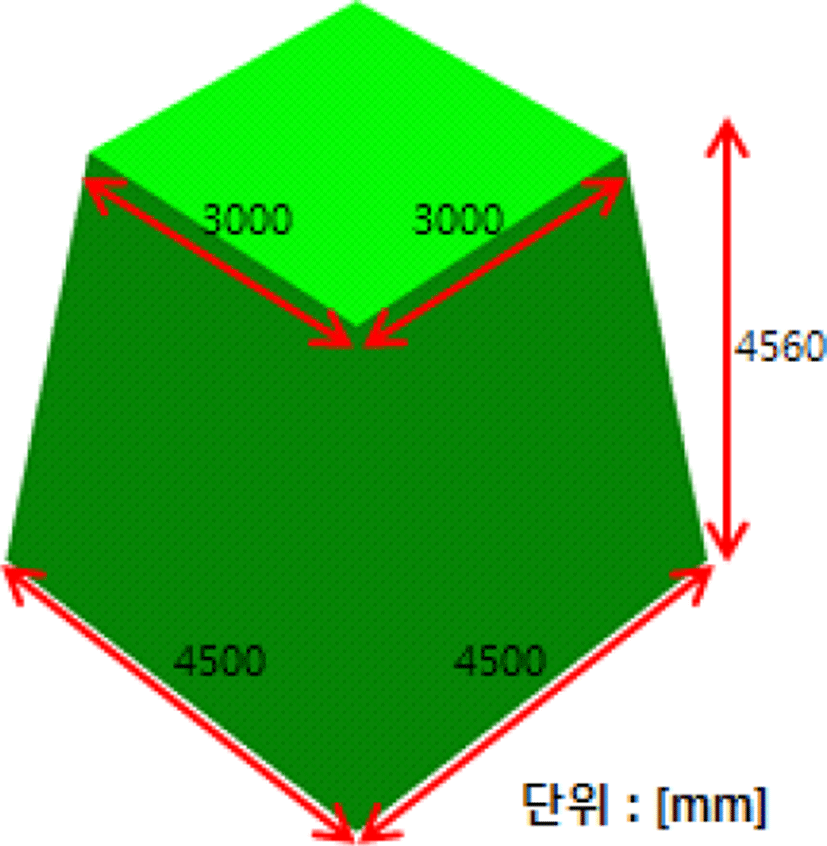
물리 광학법은 매우 정확한 산란파를 계산하지만, 산란체가 기하학적으로 불연속이 있을 때 오차를 발생시킨다. 이는 모서리에 의한 회절파의 영향으로, 이를 고려하는 물리 광학 회절이론을 함께 고려해 주어야 정확한 산란파를 계산할 수 있다^[4]. 그림 1과 같은 통합마스트 기본형상을 수평면에서 방위각이 0～360°로 변할 때, 자체적으로 개발한 프로그램으로 계산하여 EM 해석 시뮬레이터인 newFASANT^[5]의 시뮬레이션 결과와 함께 그림 2에 도시하였다. 본 구조에 대해서 개발한 프로그램의 계산 속도는 newFASANT보다 약 1.5배 빠르며, 두 결과가 잘 일치함을 확인할 수 있다. 논문의 RCS 계산은 자체적으로 개발한 프로그램을 이용하여 계산하였다.

그림 1. | Fig. 1. 통합마스트 기본 형상 | The basic shape of IMM.

Download Original Figure

그림 2. | Fig. 2. 통합마스트 기본 형상의 RCS 패턴(VV 편파) | RCS pattern on IMM basic shape(VV-pol).

Download Original Figure

2-2 RCS 대푯값

RCS 값은 전자파의 입사각도 및 편파특성에 따라 그 값이 변하기 때문에, RCS 성능의 기준치/목표치 달성을 위해 대푯값을 사용한다. 대푯값은 최대값, 최소값, 중간값, 평균값 등이 있다. 평균값은 산술평균과 기하평균을 사용하며 각각 식 (1) 및 식 (2)와 같다.

산술평균의 경우 큰 값의 RCS 성분이 더 가중되는 특 성이 있는 반면, 기하평균의 경우에는 작은 값의 RCS 성분이 가중되는 특성을 갖는다. 그러므로 산술평균과 기하평균이 큰 차이를 갖는다면, 특정구간에서 큰 RCS 값을 갖는 것을 알 수 있다^[6]. 이처럼 대푯값 선택에 따라 RCS 성능이 크게 바뀌기 때문에, 특정 대푯값을 선택하기 보다는 여러 가지 대푯값들을 비교 분석하여야 한다.

10 log 10 (1 N ∑ k = 1 N σ k) dBsm

(2)

1 N (10 log 10 σ 1 + 10 log 10 σ 2 + ... + 10 log 10 σ N) dBsm

(3)

Ⅲ. 시뮬레이션 결과 및 분석

3-1 통합마스트 측면 기울기 변화

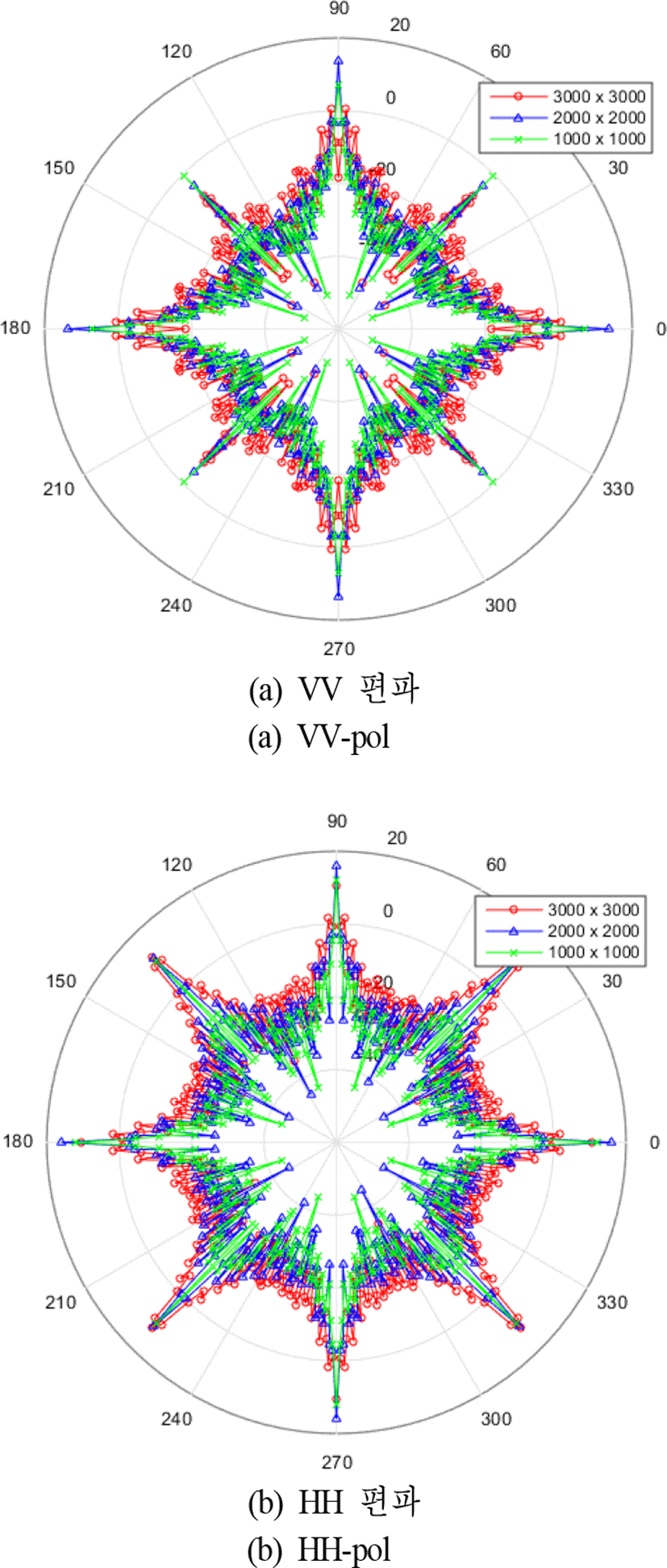
그림 1의 마스트 윗면을 각각 2,000×2,000, 1,000×1,000 mm로 변환하여 마스트 측면의 기울기 변화에 따른 RCS 패턴 변화를 그림 3에 도시하였다. 전체적인 RCS 패턴은 마스트 윗면의 크기가 감소하여 측면 기울기가 감소할수록 RCS 크기 역시 줄어드는 것을 볼 수 있다. 표 1을 살 펴보면 RCS 최대값과 산술평균은 증가 또는 감소하지만, 중간값 및 기하평균값은 윗면의 크기가 감소할수록 줄어드는 경향을 보였다. 산술평균은 큰 값에 더 가중치를 갖기 때문에 최대값의 증가로 산술평균이 증가한 것으로 보인다. 이는 RCS 패턴에서 확인할 수 있듯이, 특정각도에서 큰 RCS 값을 갖는 경우에 산술평균과 기하평균의 차가 크다는 관계도 확인할 수 있다. 결과적으로는 특정각도를 제외하면 마스트의 측면 기울기가 감소할수록 RCS 감소효과가 있음을 확인하였다.

그림 3. | Fig. 3. 통합마스트 측면 기울기 변화에 따른 RCS 패턴 | RCS pattern by IMM side slope change.

Download Original Figure

표 1. | Table 1. 마스트 측면 기울기 변화에 따른 RCS 대푯값 | RCS representative value by IMM side slope change.

Type	RCS(dBsm)
Size [mm]	3,000×3,000		2,000×2,000		1,000×1,000
Polarization	VV	HH	VV	HH	VV	HH
Maximum value	12	0.54	15.88	13.72	12.21	7.14
Median value	−16.48	−21.36	−21.76	−26.48	−24.08	−27.48
Geometric mean	−15.04	−21.69	−20.54	−24.49	−23.45	−26.39
Arithmetic mean	−1.81	−12.79	−1.29	−4.44	−4.34	−10.06

Download Excel Table

3-2 통합마스트 형상 변환

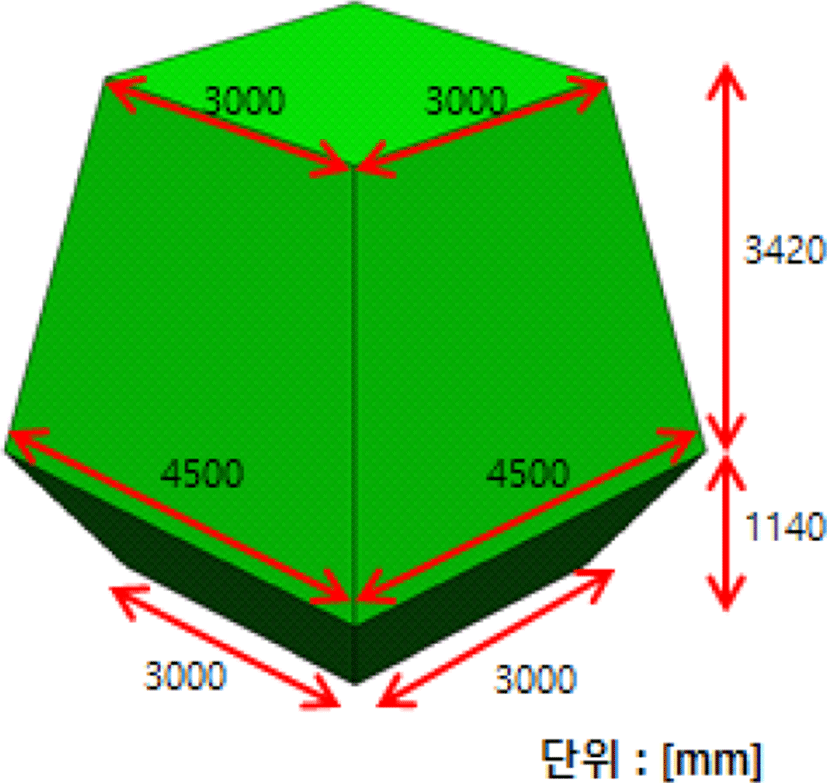
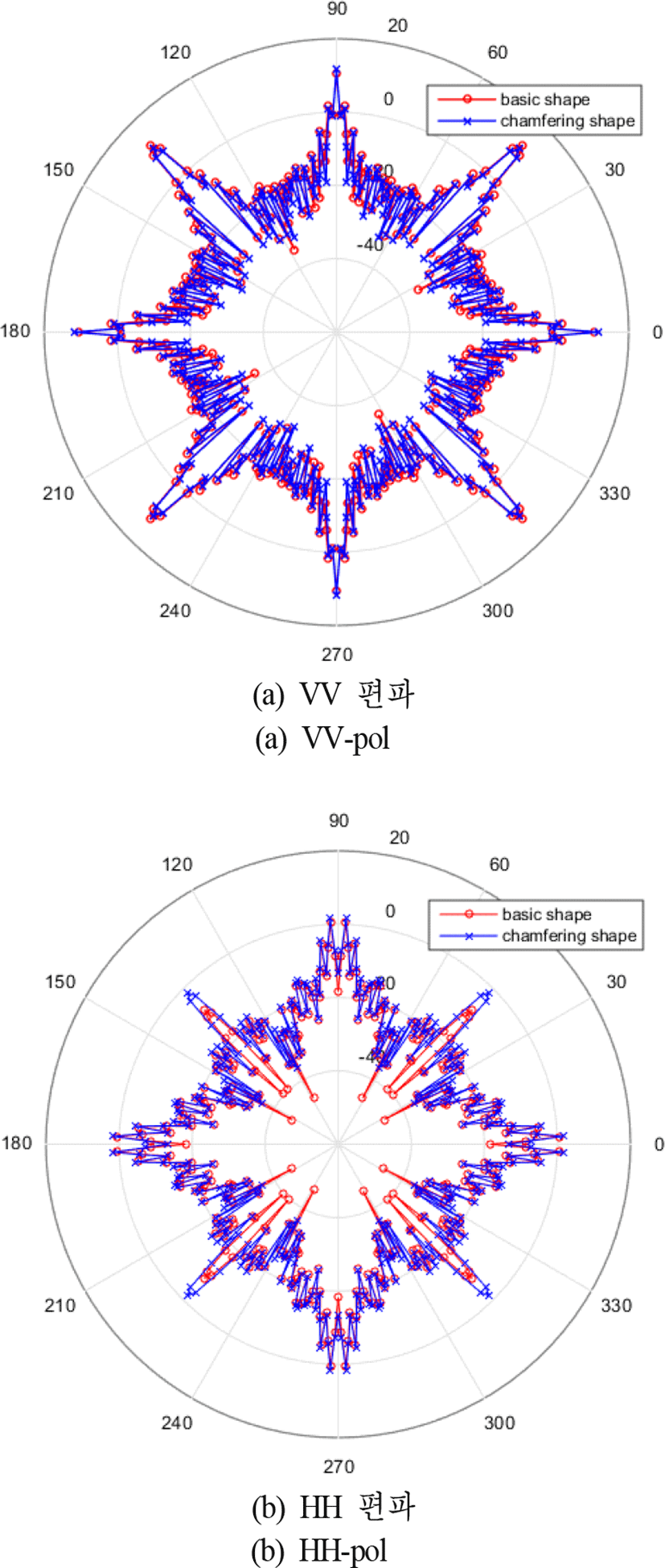
기본마스트 형상에서 그림 4와 같이 하단부에 모따기가 있는 형상으로 변환한 마스트의 RCS를 방위각 변화에 따라서 계산하였다. 계산 결과는 기본마스트 형상의 RCS 결과와 함께 각각 그림 5에 도시하였다. 전체적인 RCS 패턴을 살펴보면 VV 편파의 경우는 기존의 RCS 값보다 조금 감소한 반면에, HH 편파의 경우는 조금 증가함을 보였다. 표 2의 RCS 대푯값을 살펴보면 VV 편파는 기본마스트 형상보다 모든 대푯값 RCS가 감소함을 보인 반면에 HH 편파는 모든 대푯값 RCS가 증가함을 보였다.

그림 4. | Fig. 4. 모따기 형상의 통합마스트 | IMM of chamfering shape.

Download Original Figure

그림 5. | Fig. 5. 통합마스트 형상 변화에 따른 RCS 패턴 | RCS pattern by IMM shape change.

Download Original Figure

표 2. | Table 2. 통합마스트 형상 변화에 따른 RCS 대푯값 | RCS representative value by IMM shape change.

Type	RCS(dBsm)
Shape of IMM	Basic shape		Chamfering shape
Polarization	VV	HH	VV	HH
Maximum value	12	0.54	11.53	1.57
Median value	−16.48	−21.36	−17.62	−20.01
Geometric mean	−15.04	−21.69	−16.11	−19.66
Arithmetic mean	−1.81	−12.79	−2.38	−10.95

Download Excel Table

Ⅳ. 결 론

본 논문에서는 함정 마스트 형상 변화에 따른 모노스테틱 RCS를 분석하였다. RCS는 고주파 근사법인 물리광학법 및 물리 광학 회절이론을 이용하여 계산하였다. 마스트의 측면 기울기 변화로 RCS 감소 효과를 가져올 수 있음을 확인하였으며, 모따기가 있는 마스트 구조에서는 편파에 따라 RCS 값을 감소시킬 수 있음을 확인하였다. 이러한 결과를 토대로 측면 기울기 조정, 형상 변경 등을 통한 저 RCS 함정 마스트 개발에 활용될 수 있다.

Acknowledgements

이 연구는 한화시스템의 지원으로 연구되었음.

References

[1].

권현웅, 홍석윤, 이광국, 김종철, 나인찬, 송지훈, “첨단 함형의 레이다 반사면적 해석”, 해양환경안전학회지, 20(5), pp. 593-600, 2014년 10월.

[2].

안병준, 서상규, “함정 RCS 기준치 및 설계 목표치 설정을 위한 절차 연구”, 한국전자파학회논문지, 26(6), pp. 581-588, 2015년 6월.

[3].

C. A. Balanis, Advanced Engineering Electromagnetics, John Wiley & Sons., pp. 286-344, 2012.

[4].

E. F. Knott, T. Senior, “Equivalent currents for a ring discontinuity”, IEEE Trans. Antennas Propagation, vol. 21, no. 5, pp. 693-695, Sep. 1973.

[5].

newFASANT. [Online]. Available : www.fasant.com

[6].

안병준, “함정 RCS 저감 설계를 위한 최신 분석기법 연구”, 한국전자파학회논문지, 25(3), pp. 333-338, 2014년 3월.