SAR-GMTI에서 지상이동표적의 속도 추정 기법

Ⅰ. 서 론

현재 민수와 방위사업의 다양한 분야에서 지상이동표적을 관측하고자 하는 수요가 늘어나면서 SAR 시스템에 ground moving target indication (GMTI) 기능을 접목시킨 SAR-GMTI 시스템이 주목을 받고 있다^[1],^[2].

SAR-GMTI 시스템에서는 정지된 지형 이미징 외에 지상이동 표적의 속도로 인한 SAR 영상의 왜곡을 보상하기 위해 표적의 속도를 정확히 추정하는 것이 중요한 과제로 여겨지고 있다. 표적의 across-track 속도의 경우, 각 채널에 수신된 신호의 위상을 이용하는 along-track interferometry(ATI) 기법^[3]으로 간단히 추정이 가능하다.

Along-track 속도 추정은 linear frequency modulated (LFM) 형태의 azimuth 신호를 추정하는 과정과 동일하기 때문에 정합필터뱅크(matched filter bank), fractional Fourier transform(FrFT), 그리고 time frequency analysis와 같이 기존에 사용되는 LFM 신호 추정 기법들이 사용되고 있다. 대부분의 기법들은 높은 계산량과 구현상의 문제들로 실제 SAR-GMTI 시스템에 적용되기 힘든 점이 있다. 따라서 알고리즘을 개선시키거나 새로운 접근 방법을 통한 속도 추정 알고리즘 연구^[4]～^[9]가 최근에 많이 진행되고 있다.

계산량을 줄이기 위한 방법으로 실제 도로 환경에 대한 사전 지식(a priori knowledge)을 이용한 연구^[6]와 second order Wigner-Ville distributuion(WVD)을 통한 time-frequency analysis 기법^[7]을 이용한 연구 등이 진행되어왔다. 또한, multiple signal classification(MUSIC), Capon 기법을 이용하여 속도를 추정^[8]하거나 segmented keystone transform(SKT)과 Doppler Lv’s transform을 결합한 SKT-DLVT^[9]와 같은 새로운 방법에 대한 연구들도 계속해서 보고되고 있다.

본 논문에서는 합성 개구면(synthetic aperture)내의 subaperture 신호에 대한 푸리에 변환을 통해 공간 주파수 도메인에서 spectral center 위치 정보를 이용하여 표적의 along-track 속도를 추정하는 새로운 알고리즘을 제안한다. 이를 위해 2장에서는 SAR-GMTI 시스템 동작 개요를 설명하고, 3장에서는 표적의 속도 추정 알고리즘 및 이를 적용한 이동표적 SAR 이미징 방법을 제시하며, 4장에서는 시뮬레이션을 통해 제안한 알고리즘을 조사한다.

Ⅱ. 2채널 SAR-GMTI 시스템

지상이동표적에 대한 SAR 기하학적 구조는 그림 1과 같이 나타낼 수 있다. 그림 1에서 플랫폼은 y축 방향(azimuth)으로 v_p = (0, v_py)의 속도로 이동하고 있고, 표적은 v_t = (v_tx, v_ty)의 속도로 이동하고 있다. Azimuth 방향의 시간, 즉 slow-time t가 0일 때 플랫폼은 (0, 0)에 위치해 있고, 표적은 (r₀, 0)에 위치해 있다. 플랫폼이 이동하면서 표적으로부터 수신한 azimuth 신호의 위상 ϕ_a는 다음과 같이 표현할 수 있다.

그림 1. | Fig. 1. 지상이동표적에 대한 SAR 기하학적 구조 | SAR geometry for ground moving target.

Download Original Figure

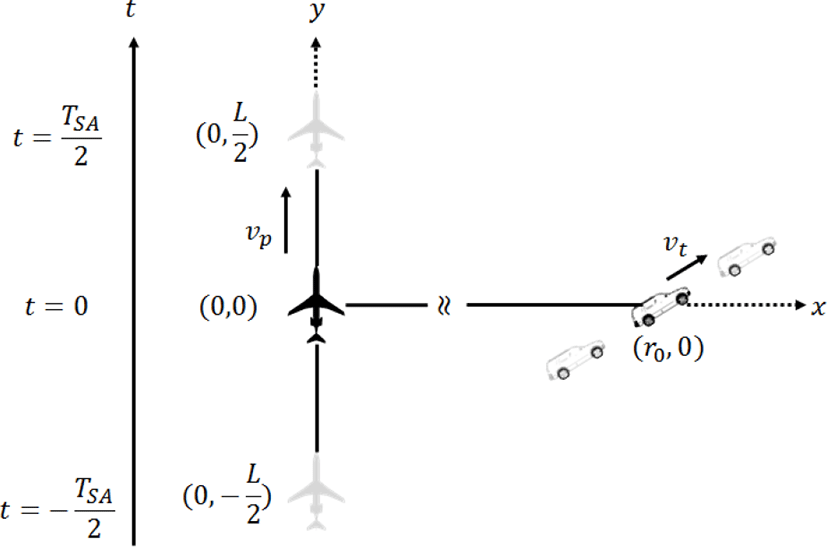
여기서 λ는 파장이다. 식 (1)을 시간에 대해 미분하면 도플러 주파수를 얻을 수 있으며, 이는 정지표적 신호의 것과 비교하여 DC 성분의 주파수가 존재하고, 변형된 기울기의 일차 주파수(linear frequency) 성분을 가짐을 확인할 수 있다. 이러한 성분들로 인하여 신호가 azimuth 방향의 정합필터를 통과함에 있어서 부정합(mismatch)이 발생하고, 그 결과 SAR 영상의 왜곡(퍼짐 및 이격)이 발생한다. 따라서 SAR 영상의 왜곡 현상을 보상하기 위한 표적의 속도 추정이 필요하다.

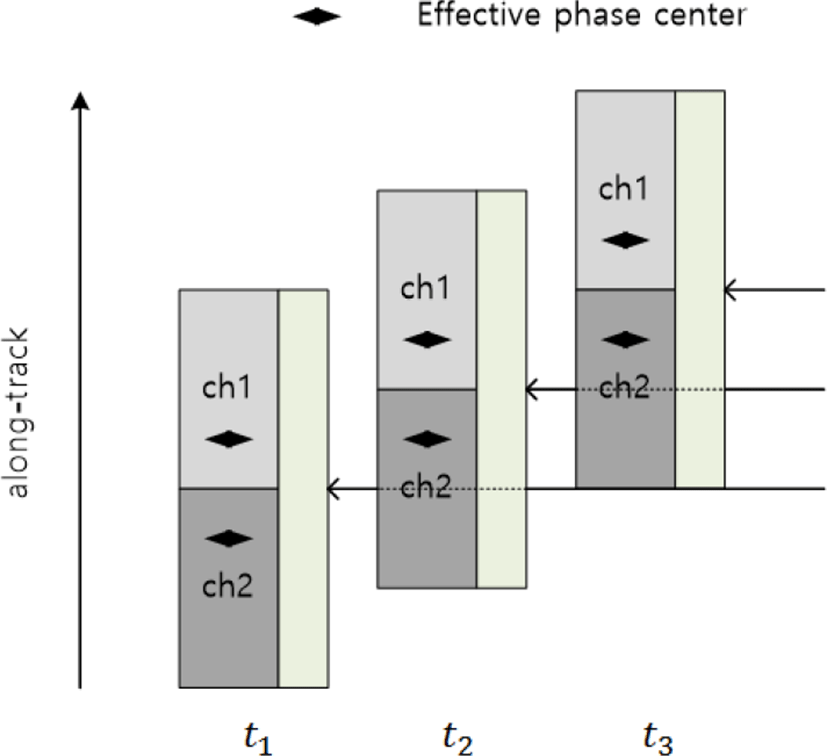
그림 2는 DPCA를 위한 2채널 SAR-GMTI 시스템 구조를 나타낸 것이다. DPCA는 이동표적의 속도를 추정하기 앞서 클러터 환경에서 이동표적을 탐지하기 위해 수행되며, DPCA 조건을 만족하기 위해 플랫폼은 t₁에서 채널 1의 effective phase center와 t₂에서 채널 2의 effective phase center가 일치하도록 이동한다. 이후 pulse repetition interval(PRI)이 Δt = t₂ − t₁이 되도록 설정하면 시스템은 DPCA 조건을 만족하게 된다.

그림 2. | Fig. 2. 2채널 SAR-GMTI 시스템 | 2-channel SAR-GMTI system.

Download Original Figure

Ⅲ. 표적 속도 추정

3-2 Along-Track 속도 추정

그림 3은 그림 1의 이동표적을 고정시킨 후 플랫폼의 상대적 움직임을 이용하여 기하학적 구조를 나타낸 것이다. 이때 레이다에 수신된 신호는 그림 1의 환경과 동일하다. 각각 v_t = (v_tx, v_ty), v_p = (0, v_py)의 속도로 이동하던 표적과 플랫폼은 새롭게 변형된 기하학적 구조(그림 3)에서 v′_t = (0, 0), v′_p = (v′_px, v′_py)의 새로운 상대속도로 이동하는 것으로 생각할 수 있다. 이때 v′_p은 이동표적의 속도와 플랫폼의 속도의 벡터적 합으로, 다음과 같이 표현할 수 있다.

$$v{‣}_p=\left(v{‣}_{px},v{‣}_{py}\right)=\left(-v_{tx},v_{py}-v_{ty}\right)$$

(3)

그림 3. | Fig. 3. 변형된 지상이동표적에 대한 SAR 기하학적 구조 | Transformed SAR geometry for ground moving target.

Download Original Figure

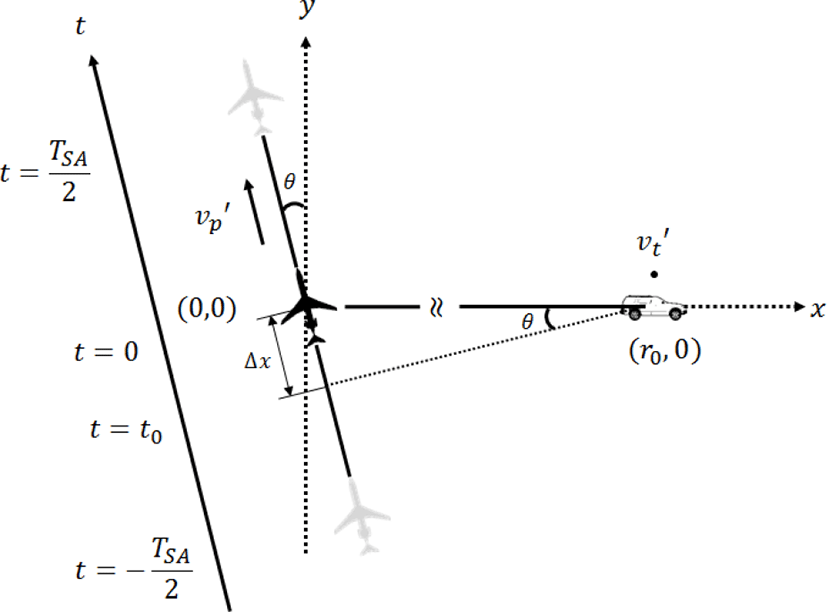
즉, 표적을 고정시킨 변형된 기하학적 구조는 플랫폼과 빔의 각도가 θ만큼 틀어지고(squinted), 플랫폼과 표적간의 가장 가까운 거리(표적의 위치에서 플랫폼의 이동궤적으로 내린 수선의 발)에 해당하는 지점이 Δx만큼 이격된 형태의 새로운 기하학적 구조를 가지는 것으로 생각할 수 있다. 이때 틀어진 각도 θ와 이격된 거리 Δx는 다음과 같이 구할 수 있다.

$$\begin{array}{l}\theta ={\tan }^{-1}\left(\frac{{x^{\prime }}_{px}}{{v^{\prime }}_{py}}\right)\hfill \\ \Delta x=r_0\sin \theta \hfill \end{array}$$

(4)

여기서 r₀는 t=0일 때의 플랫폼과 표적과의 거리이다. 플랫폼의 이동궤적의 중심으로부터 Δx만큼 이격된 지점은 표적과의 가장 가까운 거리임과 동시에 영 도플러(zero Doppler) 주파수를 갖는 지점이기도 하다. 따라서 Δx는 다음과 같은 관계식을 통해 나타낼 수 있다.

$$\Delta x={v^{\prime }}_{p}NT$$

(5)

여기서 N은 t = 0일 때 플랫폼과 표적에 의해 발생하는 도플러 주파수로부터 제로 도플러가 되는 지점인 t = t₀까지의 azimuth 샘플(sample) 개수로, 이는 다음(그림 4)과 같은 방법으로 구할 수 있다.

그림 4. | Fig. 4. Subaperture 푸리에 변환을 이용한 도플러 주파수 및 파라미터 N계산 과정 | Subaperture Fourier transform processing to acquire Doppler frequency and parameter N.

Download Original Figure

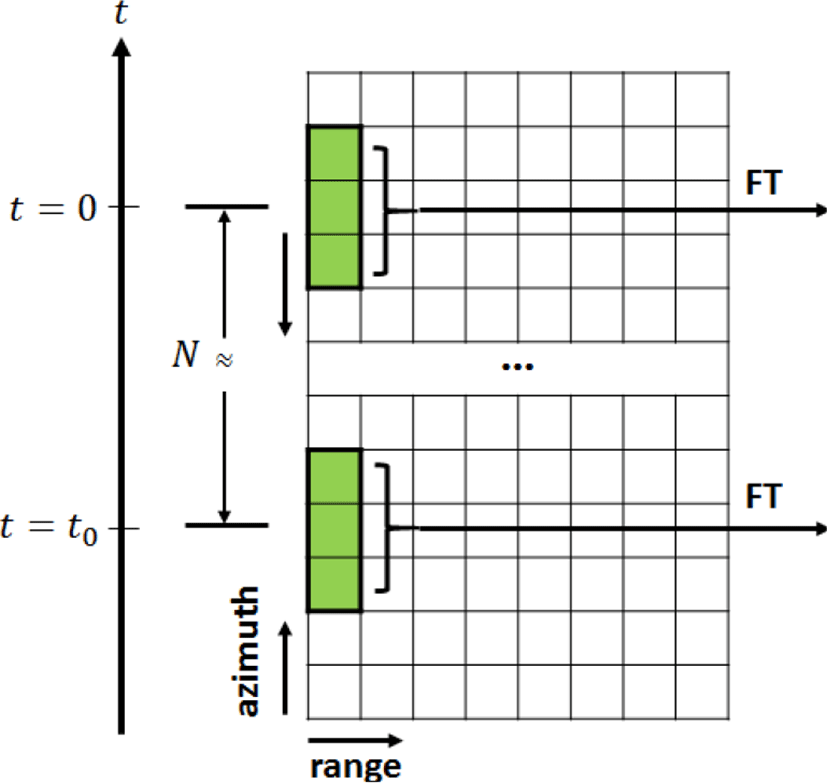
먼저 t = 0을 중심으로 유한한 크기의 subaperture 내의 azimuth 샘플에 대해 푸리에 변환(Fourier transform)을 수행하여 표적의 도플러 주파수, 즉 spectral center를 구한다. 이때 spectral center는 spectrum의 peak에 해당하고, 표적이 다수의 scatterer로 구성되는 환경에서는 peak 근처에서 1차 moment를 이용하여 구할 수 있다. 이후 subaperture의 중심점(t)을 이동해가며 각 subaperture의 spectral center를 조사하여 그 값이 영 도플러 주파수를 가질 때까지 이 과정을 반복하고, 이때의 중심점에 해당하는 인덱스와 최초 중심점 인덱스의 샘플 간격으로 N을 구한다. 각 샘플은 PRI 간격으로 샘플링이 되어 있으므로 NT는 플랫폼이 Δx만큼 이동하는데 걸린 시간 t₀가 된다. 지상의 고정 클러터 성분은 DPCA 과정으로 거의 제거가 가능하여 spectral center를 추정하는데 큰 어려움이 없지만 nonstationary 클러터가 존재하는 환경에서는 spectral center의 추정이 어려울 수 있다. 이 경우에는 subaperture의 크기를 줄임으로써 spectral center에 위치한 피크를 sharp하게 할 수 있으나, 이로 인해 공간 주파수의 해상도가 떨어지는 단점이 있다. 또한, subaperture의 크기는 푸리에 변환의 계산량과 직접적인 관계가 있으므로 알고리즘의 계산량은 subaperture의 크기에 따라 달라진다.

다음으로 식 (4)와 (5)를 v′_p에 대한 식으로 정리하면 다음과 같다.

$$\begin{array}{cc}{v^{\prime }}_p=\frac{r_0}{NT}\sin \theta & =\frac{r_0}{NT}\sin \left({\tan }^{-1}\left(\frac{\left|{v^{\prime }}_{px}\right|}{{v^{\prime }}_{py}}\right)\right)\\ & =\sqrt{{\left({v^{\prime }}_{px}\right)}^2+{\left({v^{\prime }}_{py}\right)}^2}\end{array}$$

(6)

여기서 |v′_px|은 Δx > 0인 조건을 만족하기 위해 사용된 것으로 v′_px의 값을 알고 있는 환경이므로 가능하다. a = |v′_px|, b = r₀/NT, x = v′_py로 치환하여 식을 정리하면 다음과 같은 x에 대한 4차 방정식을 얻을 수 있다.

$$x^4+2a^2{x}^2+\left(a^4-a^2{b}^2\right)=0$$

(7)

이때 식 (7)에 대한 해 x는 다음과 같다.

$$\begin{array}{c}{x}_{1,2}=\pm \sqrt{\frac{-2a^2+\sqrt{4a^4-4\left(a^4-a^2{b}^2\right)}}{2}}\\ x_{3,4}=\pm \sqrt{\frac{-2a^2-\sqrt{4a^4-4\left(a^4-a^2{b}^2\right)}}{2}}\end{array}$$

(8)

지상이동표적의 along-track 속도 v_ty가 v_py보다 작다고 가정한다면, 즉 v′_py = v_py-v_ty > 0이라면, 이때 x는 다음과 같은 단일 해를 가지게 된다.

$$x=\pm \sqrt{\frac{-2a^2+\sqrt{{\left(2a^2\right)}^2-4\left(a^4-a^2{b}^2\right)}}{2}}$$

(9)

최종적으로 식 (9)를 풀어쓰면 v′_py에 대한 식 (10)을 얻을 수 있다. 따라서 t = 0일 때의 플랫폼과 표적과의 거리 r₀, PRI T, 영 도플러까지의 인덱스 개수 N, 그리고 표적의 across-track 속도 v_tx(=−v′_px)를 이용하여 식 (10)을 계산하고, 이를 식 (3)에 대입하면 표적의 along-track 속도를 추정할 수 있게 된다.

$${v^{\prime }}_{py}=\frac{\sqrt{-2{\left|{v^{\prime }}_{px}\right|}^2+\sqrt{4{\left|{v^{\prime }}_{px}\right|}^4-4\left({\left|{v^{\prime }}_{px}\right|}^4-{\left|{v^{\prime }}_{px}\right|}^2{\left(\frac{r_0}{NT}\right)}^2\right)}}}{2}$$

(10)

Ⅳ. 시뮬레이션

본 절에서는 속도 보정이 이루어지지 않은 SAR-GMTI의 성능을 보이고, 이어서 표적 속도 추정 및 이에 따른 SAR-GMTI 성능을 비교하였다.

본 논문에서 표적의 속도 추정 시뮬레이션에서 사용한 파라미터는 표 1과 같다.

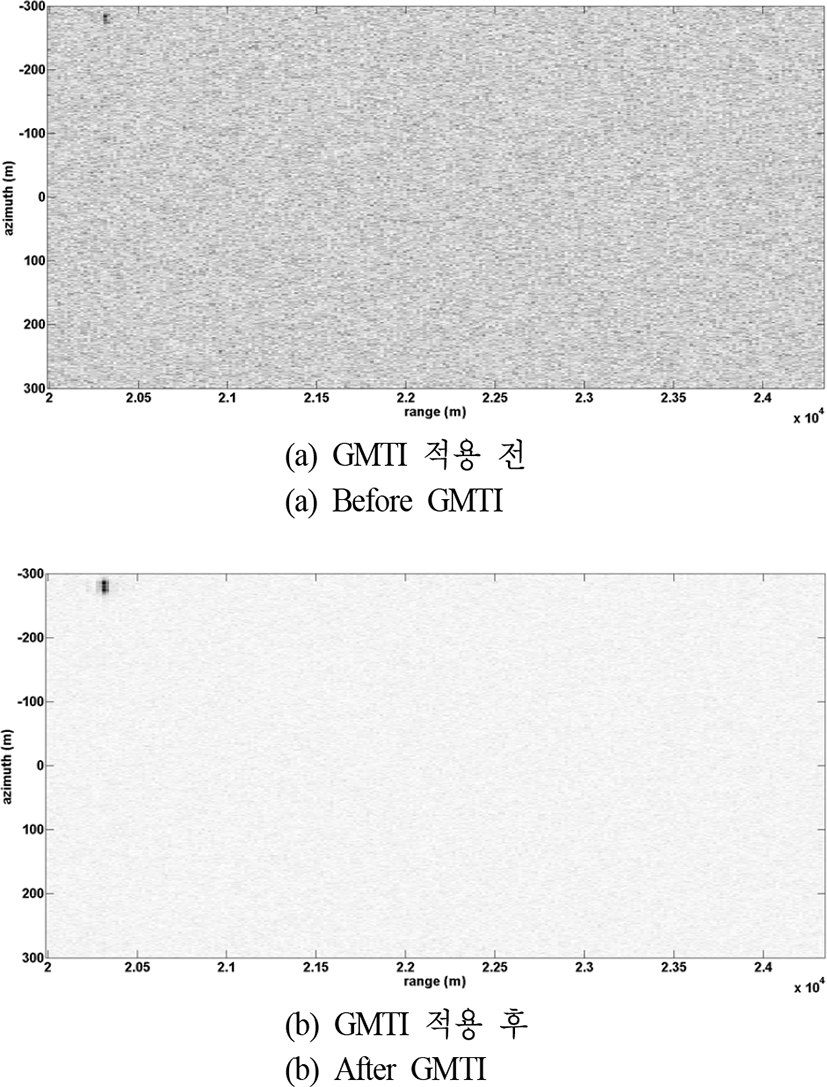
그림 5는 DPCA 방법의 GMTI를 통한 클러터 억제 및 이동표적의 탐지 성능 개선을 보인 것이다. 클러터의 경우, 지형 환경에 따라 다양한 분포로 모델링이 가능하므로 본 논문에서는 모든 셀에 걸쳐 가우시안 분포로 존재한다고 가정하였다. 또한, 시스템의 물리적 오차 및 바람과 같은 미세한 변화로 인한 동일한 장면간의 decorrelation을 나타내기 위해 1이 아닌 0.8의 상관인수(correlation factor)를 가지도록 생성하였다. 그림 5(a)는 GMTI를 수행하지 않은 이동표적에 대한 SAR 영상으로, 클러터로 인해 이동표적의 식별이 힘든 것을 확인할 수 있다. 그림 5(b)는 GMTI를 수행한 후의 결과로 클러터 레벨이 상당히 낮아지고, 그에 따라 이동표적이 뚜렷이 나타남을 확인할 수 있다. 하지만 그림 5(b)는 정지표적 파라미터를 이용하여 생성한 azimuth 정합필터를 통과한 결과로, 이동표적의 t = 0에서의 위치(20,300 m, 0)와 다른 곳에 이미지가 형성되었고, 또한 정합필터의 부정합으로 인하여 표적의 영상이 퍼지고, 최대 피크가 낮아짐을 확인할 수 있다.

그림 5. | Fig. 5. 지상이동표적 SAR 영상 | SAR image for ground moving target.

Download Original Figure

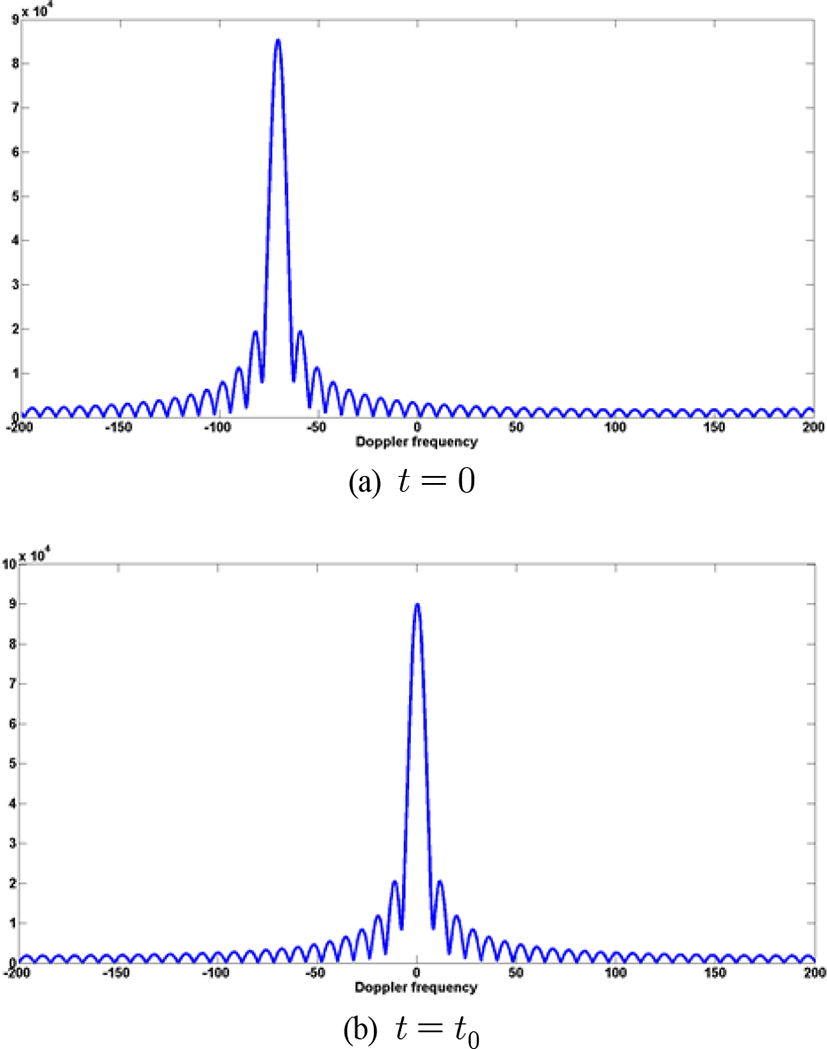
이동표적의 속도 추정을 위해서 50개의 azimuth 샘플을 갖는 subaperture를 이용하여 spectral center를 조사하였다. 그림 6(a)는 t = 0일 때 공간 주파수 축에서 표적 스펙트럼 분포를 나타내며, 그림 6(b)는 t = t₀에서의 표적 스펙트럼으로 영을 중심으로 위치해 있는 것을 확인할 수 있다. 이때 N은 772개로 이 N을 식 (10)에 대입시켜 변형된 기하학적 구조에서 플랫폼의 along-track 속도 $\widehat{v}{\prime }_{py}$를 구하였고, 이를 식 (3)에 대입하여 표적의 along-track 속도 $\widehat{v_{ty}}$를 구하여 표 3의 결과를 얻었다.

그림 6. | Fig. 6. 도플러 주파수 | Doppler frequency.

Download Original Figure

그림 7은 환경 변화에 따른 제안한 알고리즘의 추정성능을 확인하고자 상관인수를 바꾸어가며 평균 속도 추정 오차를 분석한 결과이다. 상관인수가 낮은 환경, 즉 두 장면간의 decorrelation이 강한 환경에서는 속도 추정 오차가 상당히 큰 것을 확인할 수 있다. 이는 상관인수가 낮을수록 DPCA를 통한 클러터 제거 성능열화가 발생하고, 이로 인해 표적의 spectral center를 정확히 추정할 수 없기 때문이다.

그림 7. | Fig. 7. 상관인수에 따른 속도 추정 오차 | Error of estimated velocity with respect to correlation factor.

Download Original Figure

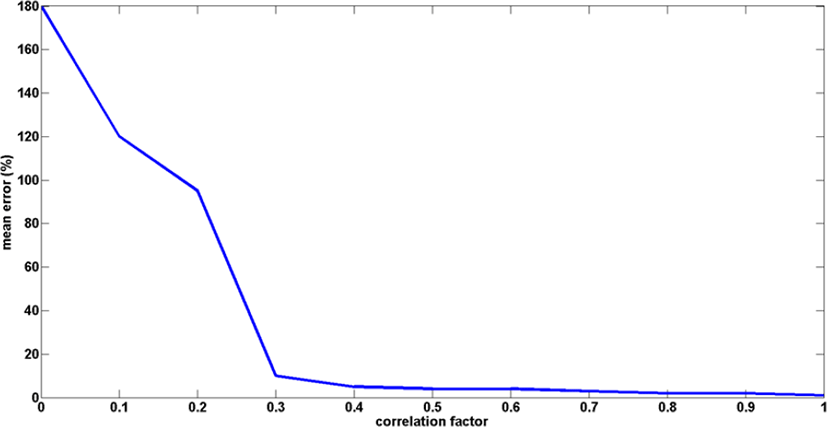
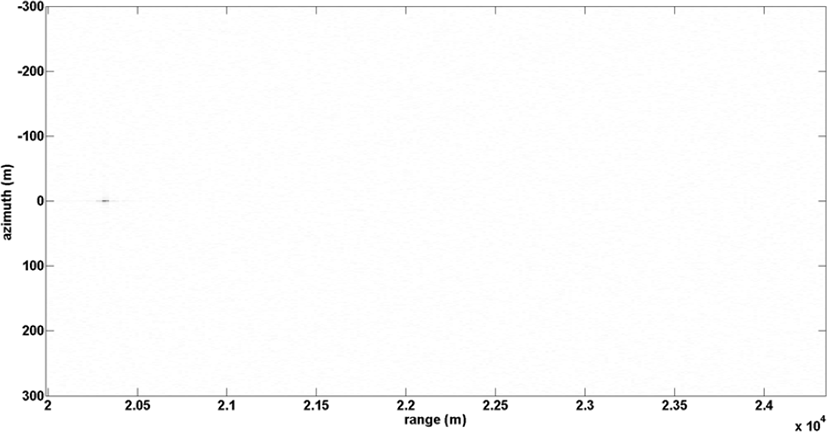
그림 8은 표 3의 추정된 속도를 바탕으로 생성한 azimuth 정합필터를 통과한 SAR 영상의 결과를 나타낸 것이다. 이격된 표적이 원하는 위치에 나타나는 것을 확인할 수 있고, 그림 5(b)와 비교하였을 때 표적의 해상도가 향상됨을 확인할 수 있다. 또한, 표적의 최대 피크가 증가함에 따라 셀의 SINR이 그림 5(b)의 27.1 dB에서 42.6 dB로 15.5 dB 증가함을 확인할 수 있다. 보상된 SAR 영상은 추후 이동표적의 식별 및 시각화를 위한 용도로 사용될 수 있다.

그림 8. | Fig. 8. 추정된 속도로 보상한 지상이동표적 SAR 영상 | Compensated SAR image for ground moving target using estimated velocities after GMTI.

Download Original Figure

Ⅴ. 결 론

본 논문에서는 2채널 SAR-GMTI 시스템에서 표적의 along-track 속도를 추정하는 알고리즘을 제안하였다. 이동하는 표적을 고정시킨 기하학적 구조에서 플랫폼의 움직임을 관측하고, 이로 인한 이동표적 SAR 영상의 왜곡 특성을 분석하였다. Azimuth 샘플들의 subaperture 푸리에 변환을 통하여 공간 주파수를 획득하고, 이와 관련된 파라미터들을 이용하여 이동표적의 along-track 속도를 구할 수 있는 관계식을 유도하였다. 추정된 속도(4.89 m/s)는 실제 속도(5 m/s)와 비교하여 약 2 %의 오차를 가지며 잘 추정된 것을 확인할 수 있다. 추정된 속도를 바탕으로 azimuth 정합필터를 설계하여 온전한 이동표적 SAR 영상을 복원한 결과 영상의 해상도가 향상되고 SINR이 증가함을 확인할 수 있었다.