Ⅰ. 서 론
밀리미터파 대역에서 송수신기에 대한 수요가 높아짐에 따라, 이 주파수 대역에서 회로 설계의 높은 신뢰도가 요구되고 있다. 설계된 회로의 신뢰도는 공정에서 제공하는 RF 소자 모델의 정확도에 의존하고, 이것은 소자의 측정값을 이용하기 때문에, 결과적으로 소자의 측정 정확도가 신뢰도에 영향을 미친다. 칩 상에서 RF 소자의 정확한 측정을 위한 여러가지 디임베딩 방식들이 소개되었고[1]~[3], multi-line THRU-REFLECT -LINE (mTRL) 교정도 그 중 하나이다[4]~[10].
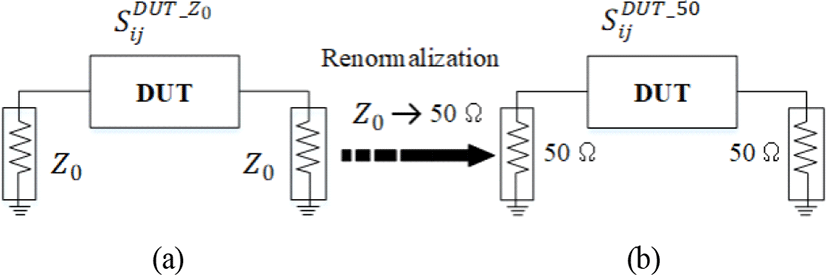
mTRL 교정을 이용하기 위해서는 LINE 표준기의 특성 임피던스를 평가하는 것이 중요하다. mTRL 교정으로 얻어지는 측정 시료(device under test: DUT)의 S-파라미터는 그림 1(a)와 같이 LINE 표준기의 특성 임피던스 Z0를 기준으로 얻어진다. 따라서 측정 시료 산란계수의 기준 임피던스를 그림 1(b)와 같이, Z0에서 50 Ω으로 재정규화(renormalization)해야 한다.
제작된 전송선로의 특성 임피던스를 결정하는 방법은 여러 가지가 있다. 가장 간단하게는 전자기 시뮬레이션과 식 (1)을 이용해서 임피던스를 구하는 방법이다[11].
위 식은 균일한 전송선로에 대하여 임피던스를 구할 때 적용할 수 있다. 여기서 Z0,S는 전자기시뮬레이션을 이용해 추출한 LINE의 특성 임피던스이고, ZSys는 그림 2(a)와 같이 전자기 시뮬레이션의 기준 임피던스로 보통 50 Ω이다. 이 방식은 선행 연구에서 밀리미터파 대역의 mTRL 교정에 이용되었다[11].
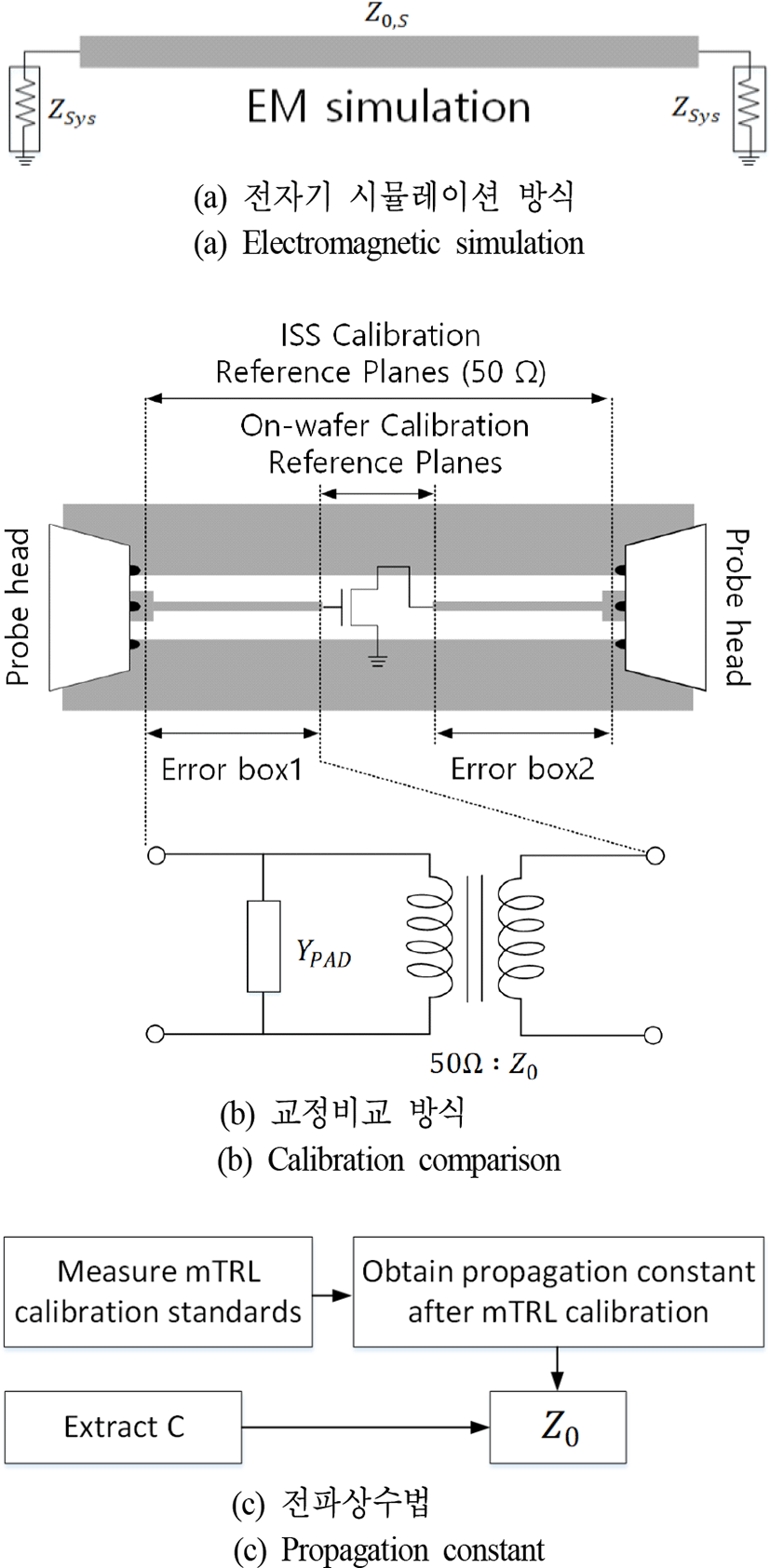
교정비교법[12],[13] 또한 임피던스 추출에 많이 이용되는 방식으로, 그림 2(b)와 같이 먼저 두 번의 교정을 통해서 패드부터 on-wafer 기준면까지의 Error box(디임배딩이 이루어지는 구간)의 산란계수를 결정한다. 이 산란계수의 T-매트릭스와 Error box를 패드 어드미턴스(YPAD)와 트렌스포머로 모델링을 해서 얻은 T-매트릭스를 비교하여 반사계수를 구하고, 최종적으로 전송선로의 임피던스를 추출하는 방식이다. 이 방식은 패드의 영향을 최소화하여 정확도를 높였으나, Error box에 해당하는 fixture에 via가 포함이 되거나, 패드 폭과 전송선로의 폭 차이가 클 경우 발생하는 인덕턴스의 영향에 의해 정확도가 떨어진다[11],[13]. 또한 첫 번 째 교정에서 정확히 얻은 임피던스가 정확히 50 옴이 아닐 경우, 이에 대한 오차가 특성 임피던스에 나타나 밀리미터파대역에서 낮은 정확도를 보인다[10].
마지막으로, 반도체 칩과 같이 기판의 손실이 적은 경우, 전파상수 γ와 단위 길이 당 캐패시턴스 C를 이용하여 식 (2)를 통해 임피던스를 구하는 방식(이하, 전파상수 법)이 있다[14].
여기서 기판 손실 G는 무시할 만큼 작다고 가정한다. 전파상수 γ는 mTRL 교정 과정에서 얻을 수 있는 값으로, 교정 표준기의 측정값을 이용하면 실제 전송선로의 전파상수 값을 얻을 수 있다. 즉, 실제 전송선로의 손실과 위상속도가 반영된 값이다. 전송선로의 C를 추출한 후, 식 (2)를 이용해서 특성임피던스 Z0를 얻는다. 이 과정을 그림 2(c)에 나타내었다.
C를 구하는 여러 가지 방식들도 이전 논문에 소개되었다[15]. 전송선로의 dc 저항을 측정하여 계산하는 방법, 전송 선로 끝단에 dc 저항을 위치시켜 반사계수를 이용하는 방법, 전송선로 치수를 이용해서 계산하는 방법 등이 제안되었다. 이 중, 칩 상에서 전파 상수법을 사용한 선행연구[6]에서는 전송 선로 끝단에 off-chip 저항을 위치시켜 dc 저항 값과 반사계수를 측정하여 C를 추출하였고, off-chip 저항으로 인해 큰 불확도를 야기하였다. 측정을 통해 C를 평가하는 방법은 Error box를 포함한 전송선로 상에 큰 반사를 야기할 수 있는 변화 구간이 포함될 경우, 오차를 야기할 수 있어 선로 설계 시 주의를 기울여야 한다. 전송선로의 치수를 이용해서 계산식을 이용하는 방법은 복잡한 다층 구조에 적합하지 않다.
본 논문에서는 칩 상의 트렌지스터를 평가하기 위해 mTRL 교정기를 CMOS 28 nm 공정을 이용하여 설계하였고, 전파상수법을 이용하여 LINE 표준기의 특성 임피던스를 구하였다. 이때, C 는 다층 기판의 임배디드 선로의 복잡한 구조를 계산하기위하여 전자기 시뮬레이션을 이용하였고, 정확도를 향상시키기 위하여 시뮬레이션에 이용한 기판의 유전 정보를 측정된 전파상수를 바탕으로 보정한 후 이용하였다. 또한, 보정된 기판의 전자기 시뮬레이션 결과에 식 (1)을 적용하여 구한 임피던스와 제안한 방식으로 구한 임피던스를 비교하여, 저주파수 대역에서 전파상수법이 칩 상의 전송선로 특성 임피던스를 평가하는데 적합함을 보였다. 최종적으로 동일한 칩 상에 제작한 트렌지스터의 고유 특성을 특성 임피던스에 따라 어떻게 변하는 지를 살펴보았다.
Ⅱ. mTRL 교정 표준기 설계
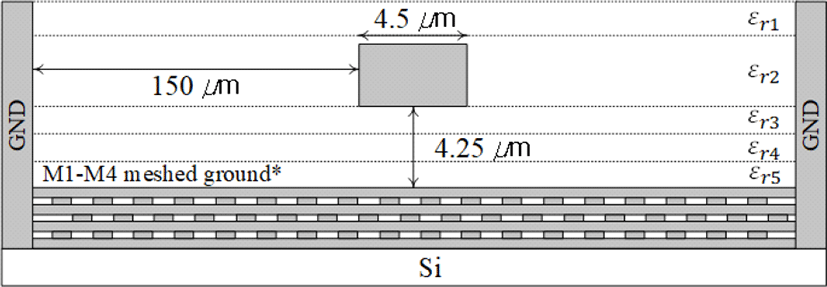
먼저, mTRL 교정에 이용할 50 Ω 전송선로를 설계하였다. 삼성 CMOS 28 nm 공정은 10개의 도체 층으로 구성되어 있고, 가장 두꺼운 최상위 도체판의 두께는 3.01 μm이다. 본 논문에서는 최상위 도체판을 이용하여 전송선로를 제작하였고, 맨 아래 4개층의 도체판을 이용하여 접지면을 구현하였다. 이 접지 도체판은 공정가이드에 따라 메시(mesh) 구조로 설계하여, 아래층 실리콘 기판의 영향을 최소화하도록 하였다. 접지 패드와 연결되는 접지 벽(wall)은 신호 선으로부터 150 μm의 거리로 충분히 넓은 공간에 배치하였다. 유전체의 비유전율은 3~4.5 사이의 값으로 층마다 다른 값을 가지며, Loss tangent는 0.002이다[16]. 높이와 각 층의 비유전율 값을 이용하여 유효 유전율 값을 얻었고, 마이크로스트립 선로 공식으로부터 선로의 폭을 결정하였다. 그림 3과 같은 기판 구조를 모두 반영한 전자기 시뮬레이션과 식 (1)을 통해 선로 폭을 조정하였고, 최종적으로 4.5 μm로 설계하였다. 본 논문에서 전자기 시뮬레이터로 Keysight Advanced Design System (ADS)의 Momentum을 이용하였다.
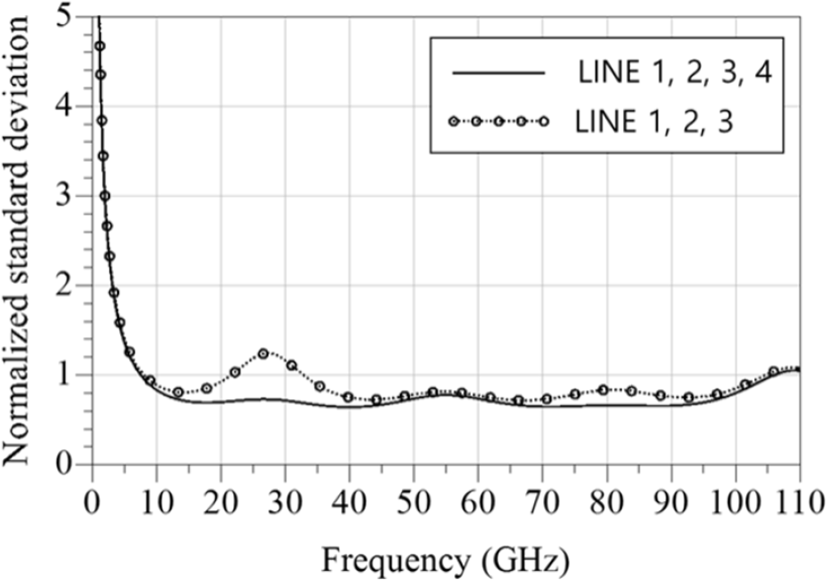
위 전송선로를 이용하여 mTRL 교정을 위한 THRU, REFLECT, LINE 표준기를 설계하였다. 110 GHz 대역까지 넓은 주파수 대역에서 mTRL 교정을 하기 위해서 여러 개의 LINE 표준기가 필요하다. 특정 주파수에서 가장 낮은 불확도를 얻기 위해서 90도의 선로 길이가 필요하다. 모든 주파수에서 90도 선로의 길이를 제작할 수 없기 때문에 통상 20도에서 160도 이내의 길이를 이용한다. LINE 표준기가 큰 면적을 차지하기 때문에, 적절한 길이의 선택으로 LINE 표준기 수를 제한할 필요가 있다. 본 논문에서는 위상 조건을 최대한 충족시키도록 150 μm (LINE 1), 650 μm (LINE 2), 2,800 μm (LINE 3) 세 가지 길이로 선택하였다. 설계된 LINE 표준기을 이용하여 mTRL 교정 시, 교정과정에서 산출되는 error term의 표준편차를 그림 4에 점선(원형)으로 나타내었다. 이는 mTRL의 정확도를 평가하기 위한 값이며, 작을수록 더욱 정확한 교정이 가능함을 나타낸다[17]. 그림 4의 28 GHz 대역에서 표준편차가 높게 나타나는 것은 LINE 2의 길이를 조절하여 낮출 수도 있지만, 본 논문에서는 1,400 μm(LINE 4) 하나 더 추가하여 그림 4의 실선과 같이 표준편차를 낮추었다. 한 칩에 그릴 수 있는 선로의 최대길이가 2,800 μm이기 때문에, 낮은 주파수에서는 표준편차가 증가한다. 이는 mTRL 교정이 저주파대역에서 불확도가 증가함을 의미한다.
THRU 표준기는 프루브팁 간의 커플링 효과를 줄이기 위하여, 측정 시료로부터 150 μm 만큼 거리를 두어 패드를 배치하였다[6]. REFLECT 표준기는 특정 값을 가질 필 요는 없으며, 큰 반사계수를 갖도록 OPEN이나 SHORT를 이용할 수 있다. 본 논문에서는 OPEN을 이용하였다.
그림 5는 삼성 CMOS 28 nm 공정으로 제작한 칩의 사진이다. 온-웨이퍼 교정법을 채택하여 mTRL 표준기와 측정시료가 동일한 반도체 칩 상에 제작하였다. 신호 패드의 사이즈는 32 μm×32 μm이며, 접지를 위한 패드는 75 μm부터 150 μm까지 간격을 갖는 GSG 프루브 측정이 가능하도록 설계 하였다.

Ⅲ. 특성 임피던스 결정
측정 시료 산란계수를 50 Ω 으로 재정규화하기 위해 전송선로의 특성 임피던스를 정확히 평가하는 것이 중요하다. 교정비교법의 경우, 첫번째 교정에서 50 Ω으로 정확히 교정이 되어야 하고, 패드와 전송선로 간의 인덕턴스가 무시할 만큼 작아야 하는 조건이 만족되어야 한다. 하지만, 첫번째 교정을 위해 잘 평가된 교정 표준기의 부재와 패드와 전송선로간의 via로 인한 인덕턴스를 높은 주파수대역에서 무시할 수 없어 교정비교법을 채택하지 않았다.
전자기 시뮬레이션과 식 (1)을 이용하여 특성 임피던스를 얻는 방법은 실제 제작 환경을 그대로 시뮬레이션에 반영하기 힘든 어려움이 있다. 계산량을 줄이기 위해 가정한 평평하고 무한한 접지면은 실제 메시 형태의 유한한 접지면이 줄 수 있는 유효 유전율과 실리콘 기판의 손실을 반영할 수 없다. 또한, 제작상의 공정오차도 알 수 없고, 다층으로 구성된 유전체의 비유전율 및 손실도 정확히 반영하기 어렵다. 특히, 파장이 길어 주변 환경의 영향을 많이 받는 낮은 주파수 대역일수록, 전자기 시뮬레이션으로 예측하기 어려워진다.
이것을 확인하기 위하여 전송선로 전파상수의 측정값과 시뮬레이션 값을 비교해 보았다. 먼저, 측정값은 제작한 표준기들을 측정한 후, mTRL 교정을 시행하는 과정에서 얻을 수 있다. 시뮬레이션값은 전송선로를 전자기 시뮬레이션을 통해 산란계수를 얻고, 식 (3)을 이용하여 전파상수를 얻을 수 있다.
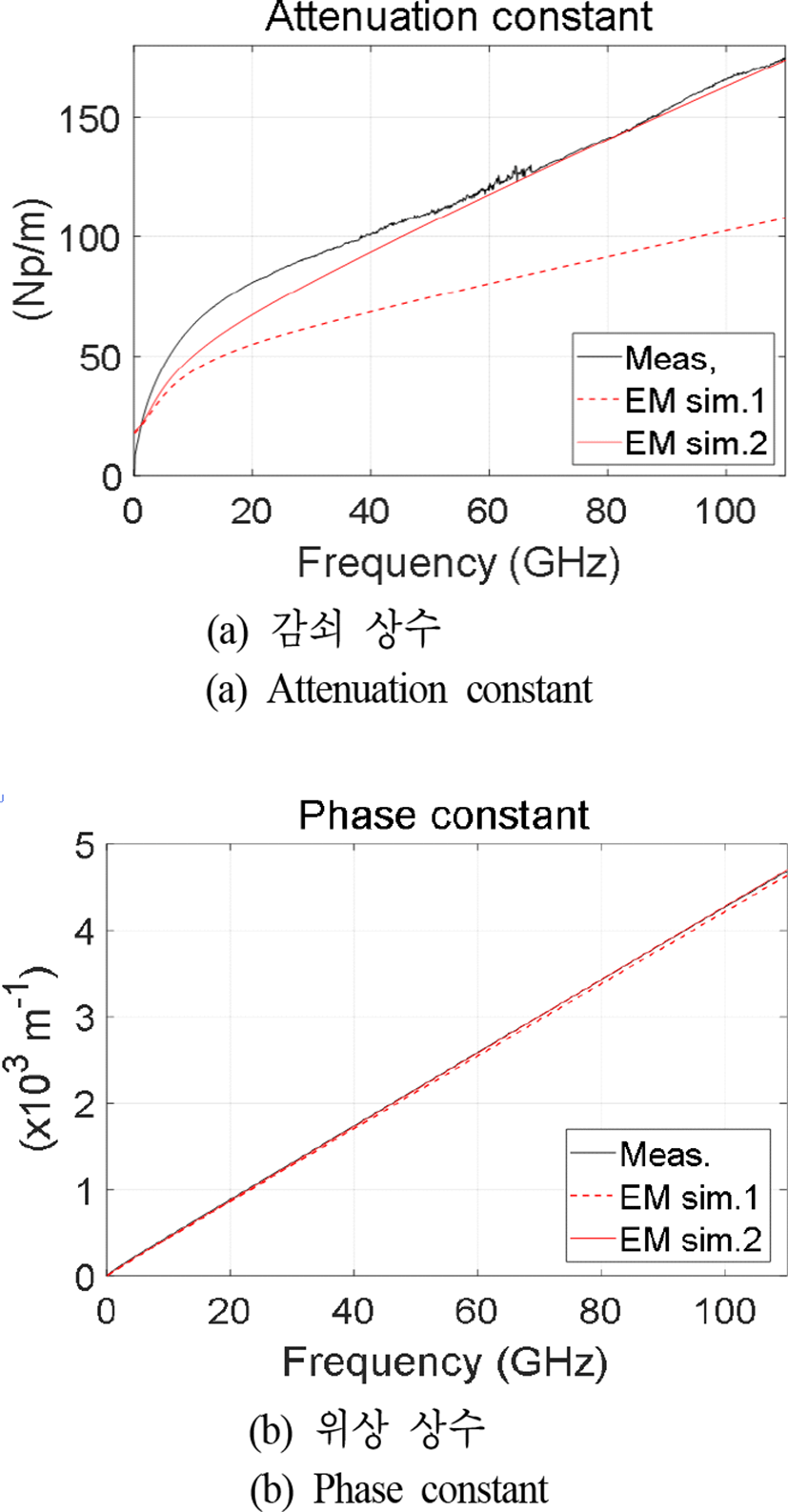
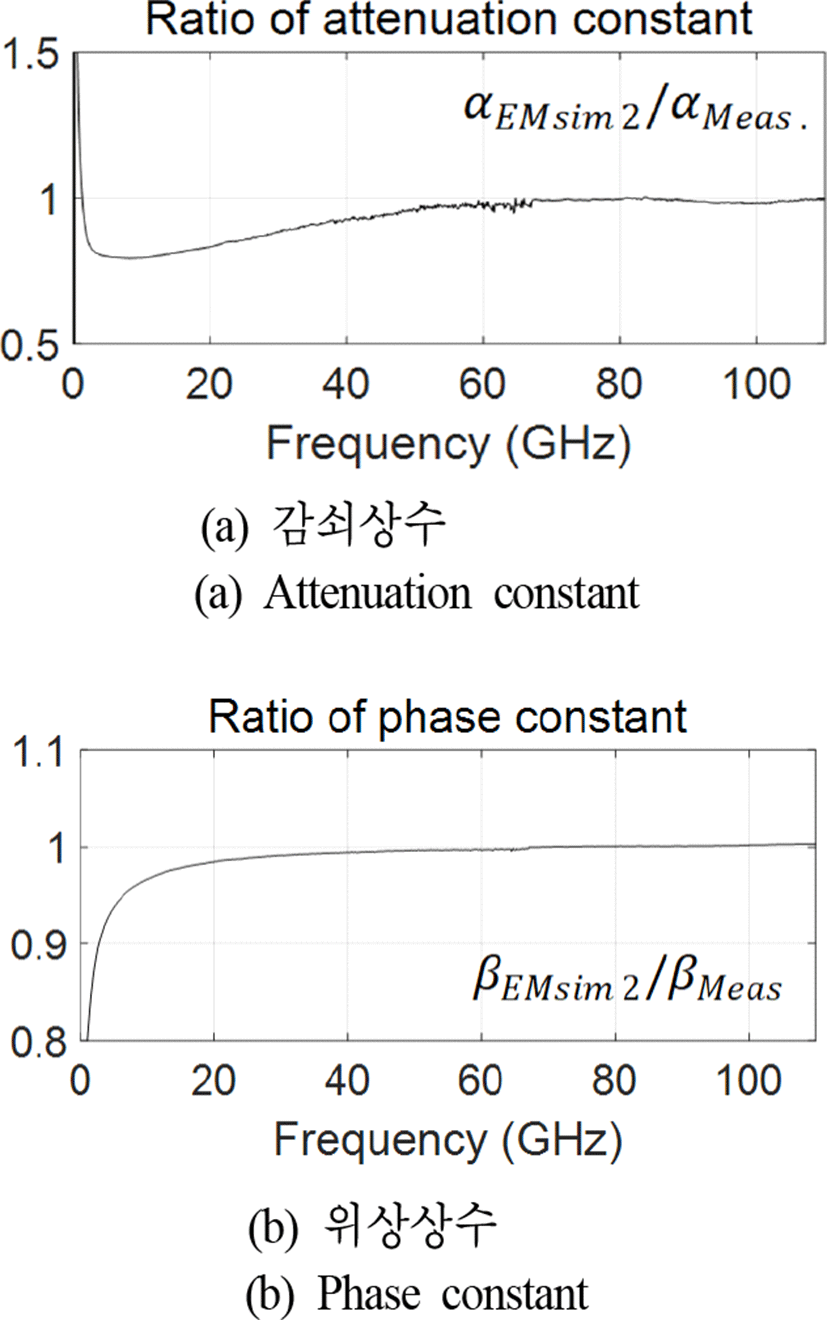
여기서 lTL은 전송선로의 길이이고, 아래첨자 S는 시뮬레이션을 나타낸다. 이렇게 얻은 측정한 값(검정)과 시뮬레이션 값(빨강)을, 실수부인 감쇠상수와 허수부인 위상상 수로 나누어, 그림 6에 나타내었다. EM sim.1은 파운더리 회사에서 제공한 비유전율과 이전 논문[16]을 참고한 loss tangent 값, 0.002를 이용한 결과이고, EM sim.2는 모든 유전층에 대하여 비유전율은 3 %, loss tangent는 15배를 증가시켜 측정으로 얻은 전파 상수와 매우 근접시킨 결과이다. 차이를 자세히 살펴보기 위하여, EM sim.2와 측정값의 비를 그림 7에 나타내었다. 감쇠상수는 50 GHz 이상에서 일치하였고, 저주파수로 갈수록 값의 차이가 커진다. 위상 상수의 경우도 밀리미터파 대역에서는 거의 일 치하는 결과를 보이지만, 저주파수로 갈수록 차이가 급격히 증가한다. 이렇듯, 저주파수 대역에서는 유전체 특성 조절만으로 예측하기 어려운 주변 환경의 영향이 있고, 주파수가 낮아질수록 그 영향은 더 커진다.
저주파수 대역에서 실제 칩 환경을 반영하여 임피던스를 추출하기 위해서는 전파상수의 측정값을 이용하는 전파상수법이 적합하다. 식 (2)를 실수부와 허수부로 나누어 나타내면, 식 (4)와 같이 나타낼 수 있다.
여기서 α는 전파상수의 실수부, 즉 감쇠상수이고, β는전파 상수의 허수부, 즉 위상상수이다. C는 단위 길이당 캐패시턴스로 본 논문에서는 전송선로의 전자기 시뮬레이션 산란계수와 식 (1), 식 (3), 식 (5)를 이용하여 도출하였다.
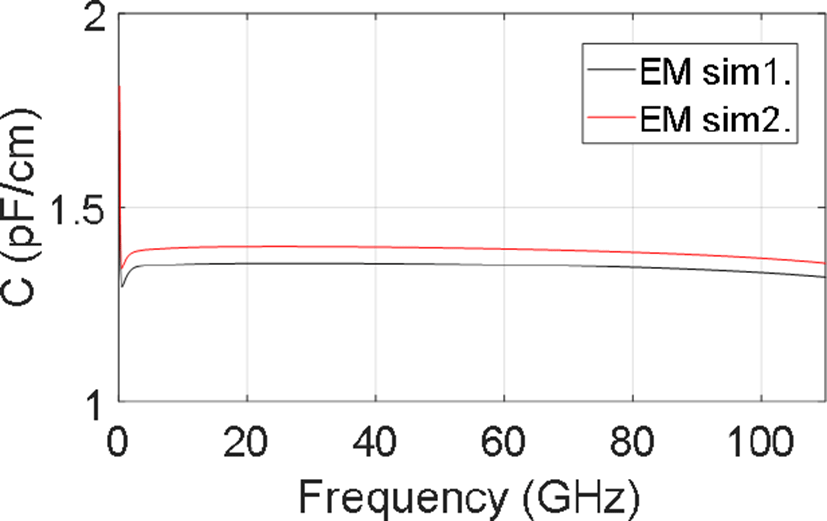
이전 논문[16]에서는 마이크로스트립라인 구조에 단층 구조로 전송선로의 치수를 이용하여 C의 간단한 수식적 계산이 가능했지만, 본 논문에서 다루는 칩 기판은 다층 구조이고, 임배디드 마이크로스트립 라인의 복잡한 기판 구조로 이루어져 있어 전자기 시뮬레이션을 활용했다. C를 구할 때, 식 (5)에서 의 허수부만 관여를 하고, Z0,S의 허수부는 작은 값을 갖기 때문에[11], γS 실수부인 감쇠 상수 αS 의 영향은 거의 나타나지 않는다. EM sim. 2의 결과에서 감쇠상수를 두 배 변화시켜도 C의 값은 0.1 %만 변함을 확인하였다. 전자기 시뮬레이션에서 나타나는 감쇠량의 측정값과의 차이는 무시할 수 있다. 위상 상수 βS는 값이 증가할 때 Z0,S 를 감소시켜 C에 더 큰 영향을 준다. EM sim.1과 EM sim. 2로 얻은 C 값을 그림 8에 나타내었다. 전 주파수 대역에서 대체적으로 평탄한 특성을 가지지만, 높은 주파수에서 감소하는 경향을 나타내는 것은 전송선로의 길이가 λ/2 정수배가 될 때마다 나타나는 공진현상이 원인으로, 그림 9(a)에 보여지 듯 Z0,S 실수부의 증가가 약하게 나타나기 때문이다. 이 영향을 최소화하기 위해 평탄한 특성을 가지는 50 GHz에서의 C 값을 이용하였다. EM sim. 2로 얻은 C값은 1.395 pF/cm로 EM sim.1의 결과인 1.355 pF/cm로 2.8 % 정도의 차이를 보인다.
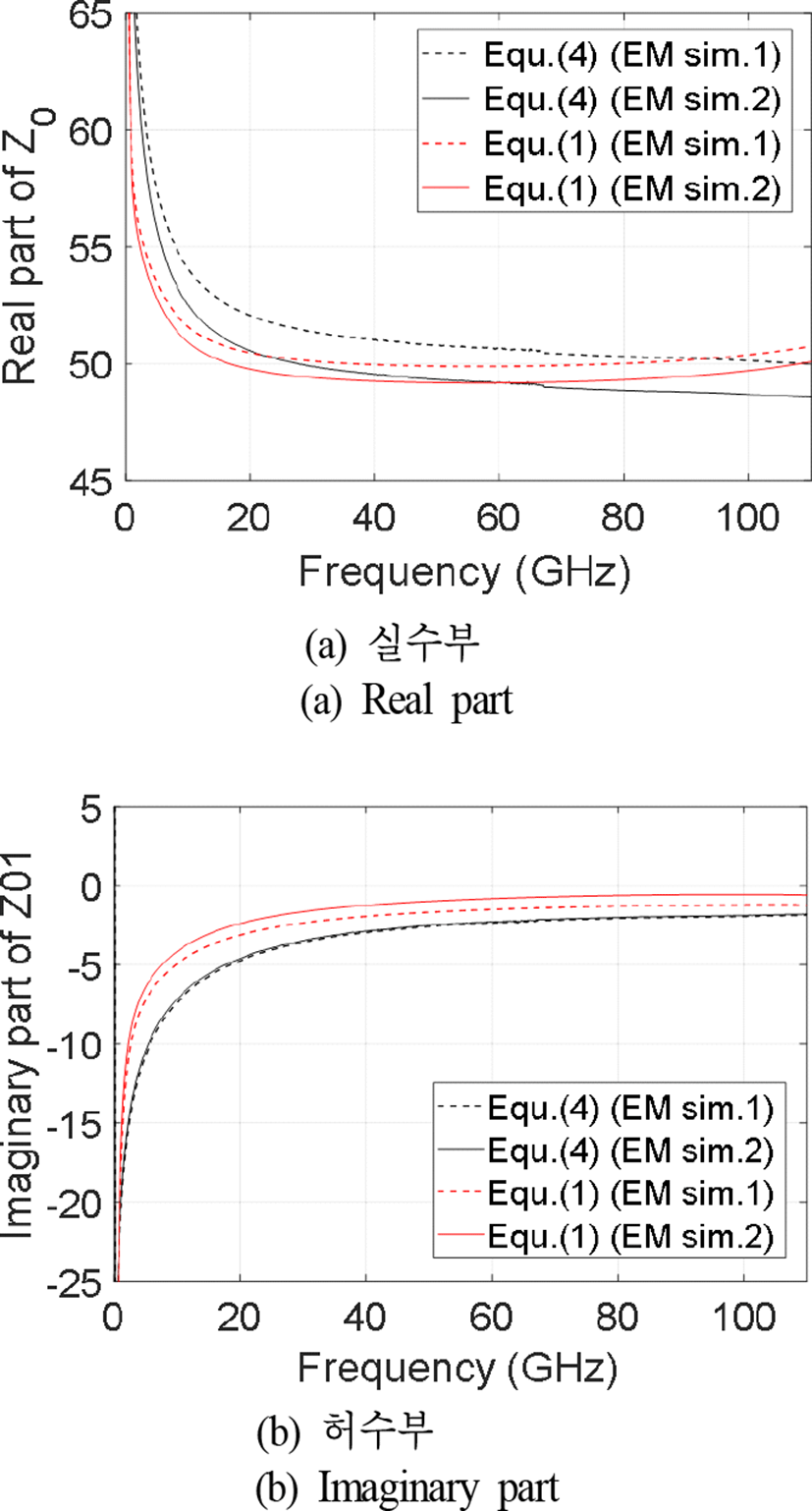
전자기 시뮬레이션으로 얻은 C와 식 (4)를 이용해서 계산한 특성 임피던스를 식 (1)을 이용해서 계산한 결과와 함께 그림 9에 도시했다. 비유전율을 조절하기 전 EM sim.1에 비해 EM sim.2의 결과는 실수부에서 0.7 Ω의 차이를 보인다. 빨간 선은 각각의 기판 정보를 이용해서 전자기 시뮬레이션을 통해 산란계수를 얻고, 식 (1)을 이용해서 얻은 특성 임피던스이다. 그림 9(a)에 나타나듯이, 식 (4)를 이용한 특성 임피던스 실수부는 식 (1)을 사용한 결과에 비해 저주파수 대역에서 변화가 완만하고, 고주파수 대역에서 평탄한 특성을 보인다. 그림 7 (b)에서 위상상수의 측정값이 저주파수 부근에서 나타났던 차이가 위상상수에 민감한 특성 임피던스 실수부를 계산할 때 반영되어 개선된 것으로 볼 수 있다. 식 (1)을 이용한 결과가 주파수가 올라가면서 증가하는 것은 앞서 C에서도 설 명한 바와 같이, 전송선로의 길이가 λ/2 정수배가 될 때마다 나타나는 공진현상이 원인으로 길이에 따라 조금씩 다른 결과를 보인다. 위상상수 측정값을 이용한 결과는 전송선로의 길이에 대한 영향 없이, 높은 주파수 대역에서 일정한 값을 나타낸다. 그림 9(b)는 특성 임피던스의 허수부로 식 (4)에서 확인할 수 있듯이 감쇠상수에 큰 영향을 받는다. 허수부도 측정값을 반영함으로써 저주파수로 갈수록 값의 차이가 크게 나타남을 확인할 수 있다. 이 차이로 개선된 결과는 다음 장의 재정규화된 산란계수를 살펴보면서 확인할 수 있다.
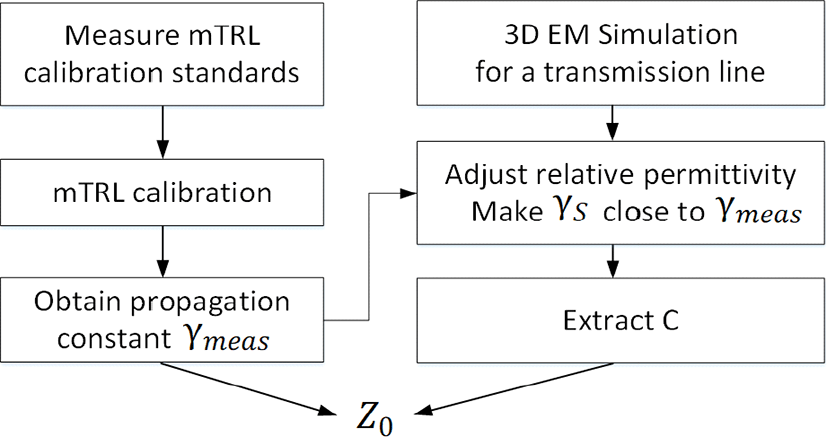
이 장에서는 전파상수의 측정값을 이용하고, 비유전율이 조절된 기판정보를 이용하여 전송선로의 단위길이 당 캐패시턴스를 사용해서 특성 임피던스를 계산하는 방식을 제안하였다. 이 방식의 순서도를 그림 10에 나타내었다.
Ⅳ. 산란계수의 임피던스 재정규화
앞 장에서 구한 특성 임피던스를 이용하여 측정 시료의 산란계수를 재정규화하였다. 측정 시료로 사용한 트랜지스터 게이트의 길이와 넓이는 각각 28 nm, 20 μm이고, 게이트 및 드레인 전압으로 모두 1 V를 인가해 주었다. 측정은 Keysight PNA N5247A를 이용하였고, mTRL 교정은 Wincal 소프트웨어를 이용하였다. 재정규화는 식 (5)를 이용하였다[18],[19].
S′ 는 50 Ω 기준 산란계수, S 는 LINE 표준기 임피던스 기준 산란계수, I는 단위행렬 (n 포트 일 경우, n×n)이다. G 는 식 (7)로 얻은 반사계수의 대각행렬로 식 (6)과 같이 나타낼 수 있으며, 포트 별로 다른 반사계수를 설정할 수 있다. 여기서는 동일하다고 가정하였다.
재정규화을 통해 얻은 게이트-드레인 종단에서 바라본 트렌지스터의 S11과 S21의 크기를 그림 11에 나타내었다. Off-chip 교정으로 이용하는 Impedance Standard Substrate (ISS)의 SHORT-OPEN-LOAD-THRU (SOLT) 교정을 이용해서 칩을 측정한 결과도 함께 도시하여 저주파 대역 결과의 기준으로 삼았다. 그림 11(a)의 S11의 크기는 크게 차이가 나타나지 않으나, 그림 11(b)의 S21 결과는 저주파 구간에서는 특성임피던스에 따라 차이가 크게 나타남을 보여준다. 특히, 식 (1)로부터 구한 특성 임피던스를 이용한 결과(보라)는 ISS SOLT 결과로부터 많이 벗어난다. 앞서 살펴본 바와 같이 간략화한 시뮬레이션 환경이 저주파수대역에서 전송선로의 특성을 정확히 예측하기 어려움을 보여준다. 이와 다르게 전파상수의 측정값과 식 (4)를 이용해서 구한 특성 임피던스를 이용한 결과(주황, 노랑)는 ISS SOLT 결과와 거의 일치하는 결과를 보여준다. 이것은 전파상수 실제 측정값이 반영되어, 저주파수 대역의 특성 임피던스가 바르게 얻어졌음을 보여준다.
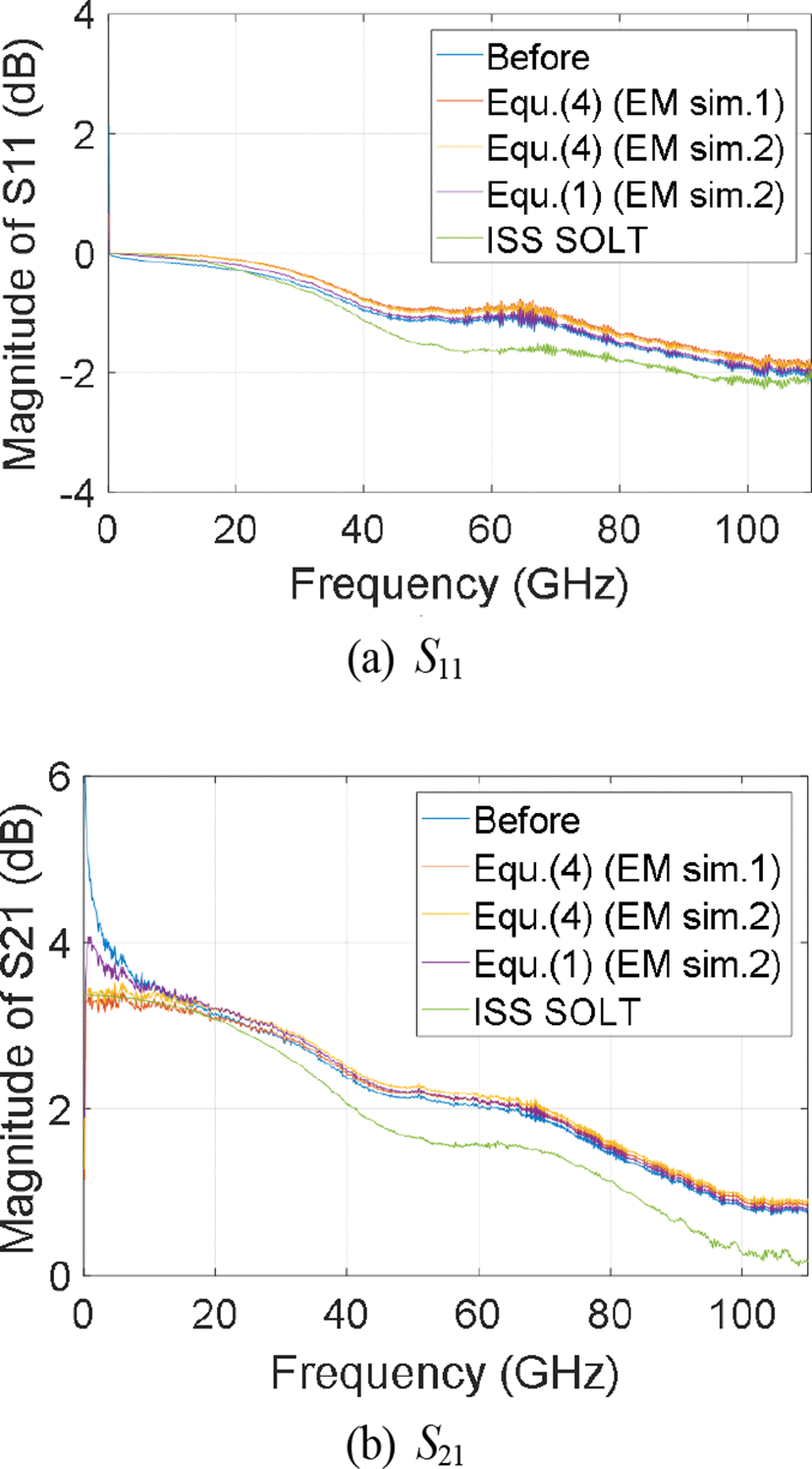
실제 전파 상수와 유사한 값을 얻기 위해 비유전율을 조절해서 얻은 EM sim.2의 결과는 ISS SOLT의 S21보다 조금 더 큰 값을 나타낸다. 이것은 칩 상의 패드로부터 게이트-드레인 종단까지 이르는 전송선로의 손실이 제거함으로써 얻을 수 있는 합당한 결과로 EM sim.1의 결과보다 개선된 결과임을 확인할 수 있다.
Ⅴ. 트랜지스터 고유 특성 추출
트랜지스터 고유 특성을 추출하기 위해서 한 가지 디임배딩 방식을 더 적용하였다. OPEN-SHORT 디임베딩 방식[1]으로 mTRL 교정 기준면으로부터 평가하고자 하는 트랜지스터의 도체판 층까지 이어진 access line에 대하여 추가 디임베딩을 수행함으로써, 주변 메탈을 제외한 트렌지스터 고유특성을 더욱 가깝게 얻을 수 있다[6]. 추가로 제작한 OPEN, SHORT 측정 시료에 대해서도 동일한 특성 임피던스를 이용하여 산란계수의 임피던스를 재정규화 하였다. 그리고 식 (8)을[1] 이용하여 추가 디임배딩한 어드미턴스 YOS를 얻었다.
여기서 YDUT,YOPEN,YSHORT는 각각 트렌지스터, OPEN, SHORT 측정 시료의 산란계수로부터 얻은 어드미턴스이다. 이후, 식 (9)를 이용하여 트랜지스터 등가 모델의 대표적인 파라미터들의 근사치를 계산하였다[20]~[22].
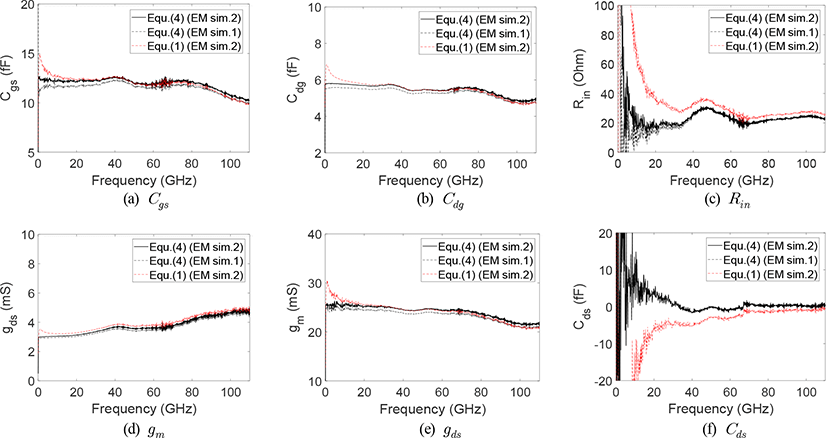
제안한 방식으로 얻은 임피던스를 이용한 결과를 그림 12에 검정 실선으로 나타내었다. 이 파라미터들은 트랜지스터의 고유특성으로 주파수의 의존도가 낮아, 주파수 전 영역에서 평탄한 특성을 갖는다. 본 논문에서는 트렌지스터 finger를 구성하는 메탈과 이를 합쳐서 게이트/드레인의 한 터미널로 연결하는 메탈층이 포함되었기 때문에, 평탄성이 깨어지는 구간이 있지만, 대체적으로 일정한 값을 나타낸다. 검정 점선은 기판의 유전정보를 보정하기 전의 값으로, 보정 후 Cgs와 Cdg에서 5 % 정도의 개선효과를 얻었다. 빨간 점선은 EM sim.1의 산란계수를 이용해 식 (1)로 구한 임피던스를 이용했을 때의 결과를 나타낸다. 기준 값에서 벗어났던 산란계수의 결과로부터 예측할 수 있듯이 밀리미터파 대역에서는 큰 차이가 나지 않지만, 저주파수 대역에서는 그 차이가 급격히 증가한다.
Ⅵ. 결 론
본 논문에서는 CMOS 28 nm 칩 상의 트렌지스터를 평가하기 위한 mTRL 교정을 위한 교정 표준기를 설계하였다. mTRL 교정으로 측정한 트렌지스터 산란계수를 LINE 표준기의 특성 임피던스에서 50 Ω으로 재정규화하기 위하여 LINE 표준기 특성 임피던스를 추출하였다. 기존의 전파상수 법을 이용하였고, 단위 길이 당 캐패시턴스를 전자기 시뮬레이션을 이용하여 계산하였다. 이 논문에서는 파운더리에서 제공받은 기판의 유전정보를 그대로 이용하지 않고, 측정값으로 얻은 전파상수에 맞춰 기판의 유전정보를 보정하였다. 수정된 기판을 이용하여 얻은 전자기 시뮬레이션 결과로부터 단위 길이 당 캐패시턴스를 얻었고, 이 값으로부터 얻은 특성 임피던스를 이용하여 재정규화된 산란계수의 결과에서 개선된 결과를 얻었다. 본 논문에서 이용한 CMOS 28 nm 공정은 비유전율 평가가 잘 되어 있어 큰 보정이 이뤄지지 않았지만, 공정에 따라 큰 개선도 가능할 것으로 예상된다.
또한, 전자기 시뮬레이션과 식 (1)로 부터 얻은 특성 임피던스를 이용한 결과와도 비교하였다. 간략화한 시뮬레이션 환경이 저주파수 대역에서 그 영향이 커져, 임피던스를 제대로 예측하지 못하였다. 이 방식은 이전 논문[11]에서 밀리미터파대역의 특성 임피던스 추출 방식으로 제안되었지만, 저주파수의 한계를 보여주지는 않았다. 본 논문에서는 그 한계를 산란계수뿐 아니라, 고유특성에서도 어떻게 나타나는지를 보여주었다.