The Journal of Korean Institute of Electromagnetic Engineering and Science

The Korean Institute of Electromagnetic Engineering and Science

J. Korean Inst. Electromagn. Eng. Sci. 2025; 36(8):766-778

pISSN: 1226-3133, eISSN: 2288-226X

DOI: https://doi.org/10.5515/KJKIEES.2025.36.8.766

논문/REGULAR PAPERS

사분면분할 수신 기반 이차원 위상비교 광대역 모노펄스 방향탐지에서 수신채널 오차에 의한 영향성 분석

이경민^†

, 안준일

, 유홍균

, 정운섭

, 김기백

Impact Analysis of Receiver Channel Errors in Quadrant Subapertures for Two-Dimensional Phase-Comparison Wideband Monopulse Direction Finding

Kyungmin Lee^†

, Junil Ahn

, Hongkyun Ryu

, Unseob Jeong

, Ghiback Kim

국방과학연구소

Agency for Defense Development

^†Corresponding Author: Kyungmin Lee (e-mail: kmlee55@add.re.kr)

© Copyright 2025 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Apr 01, 2025; Revised: Apr 28, 2025; Accepted: May 22, 2025

Published Online: Aug 31, 2025

요 약

서로 다른 위상중심을 가지는 안테나들로부터 수신된 다중 수신채널 환경은 수신된 신호 간의 조합으로 이차원 모노펄스 방향탐지 수행을 가능케 한다. 그중 배열안테나 내 사분면분할 수신구조를 활용한 개구면분할 모노펄스 방향탐지 기술은 분할개구면 조정을 통해 네 채널 이상 수신채널을 형성하여 광대역 주파수 신호에 대한 고각 및 방위각 방향탐지 임무 수행이 가능하다. 그러나, 사분면분할구조 내 부배열안테나 채널 간에 수신신호 세기 혹은 위상간 차이가 발생할 경우, 측정된 고각 및 방위각 정보가 오차가 많이 발생하게 되며, 특히 고각 방향탐지 결과가 수신신호의 방위각 성분에 영향을 받게 된다. 이에 본 논문은 사분면분할 배열안테나 구조에서 수신채널 별 신호간의 신호세기 및 위상오차 발생에 따른 모노펄스 방향탐지 영향을 시뮬레이션으로 분석하여 제시하였다.

Abstract

Two-dimensional direction finding can be conducted utilizing antennas segmented into quadrant subapertures, each with distinct phase centers. The azimuth and elevation angles of the received wideband signal were estimated via four receiver channels configured within the quadrant subaperture. However, the presence of amplitude or phase discrepancies, referred to as relative errors, between these channels results in increased errors in the estimated elevation and azimuth angles. Notably, the estimation of the azimuth angle is particularly sensitive to variations in the elevation angle. This study investigated the impact of relative errors, particularly amplitude and phase discrepancies, across the four receiver channels on the accuracy of monopulse direction finding within a quadrant subaperture array antenna.

Keywords: Electronic Warfare; Monopulse Direction Finding (DF); 2-D DF; Wideband Array Antenna

Ⅰ. 서 론

배열안테나 내 개구면 분할을 활용한 다중 수신빔 형성 및 이를 활용한 모노펄스 방향탐지(DF, direction fiding) 기술이 최근 다양한 연구분야에서 주목받고 있다^[1]~[4]. 배열안테나 내에 계획된 구조로 개구면을 분할하여 부배열 안테나들을 구성한 후 개별 개구면으로부터 수신빔패턴을 형성 및 도달 수신신호를 각 분할개구면 채널별로 수신한다. 각 수신채널은 분할된 개구면 별 안테나 위상중심 차이에 의한 서로 다른 위상 차이를 갖는 신호를 수신하게 되며, 해당 위상차를 활용하여 실시간 도래각(angle of arrival) 추정을 위한 모노펄스 방향탐지 기법을 수행할 수 있다^[5]. 또한 상기 방식의 개구면분할 배열안테나 구조는 수신빔 패턴의 빔폭 및 탐지각도 모호성 구간을 고려한 수신주파수에 따른 유동적인 개구면분할구조 변경 및 배열 이득 효과로 인한 높은 신호 대 잡음비(SNR, signal to noise ratio)의 수신신호 취득이 가능하기 때문에 광대역 주파수 신호 방향탐지에 유용하다^[5]~[7].

모노펄스 방향탐지 방식은 크게 진폭비교 방식과 위상비교 방식으로 구분될 수 있으며, 그 중 위상비교 방식은 수신신호가 각 부배열안테나 별 위상중심에 도달하는 시간 차이로 인해 발생하는 신호간 위상차를 활용한 방향탐지 방식이다^[5],[7],[8]. 위상차를 측정하는 방식으로는 두 수신신호간 위상차를 직접 측정하는 방법과 두 신호간 합, 차 패턴을 활용한 모노펄스 비 산출로 위상차를 측정하는 방법이 있으며, 본 논문에서는 합, 차 패턴을 활용한 모노펄스 비 산출 방법에 대해 기술한다^[8].

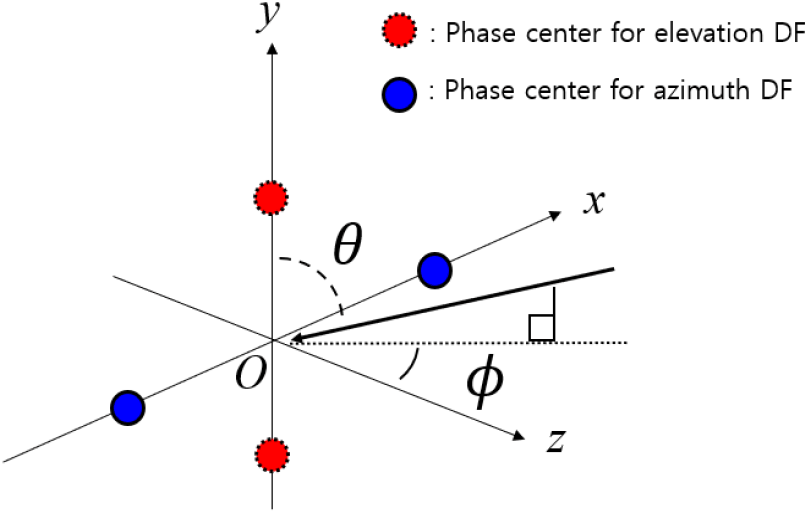
근래의 모노펄스 방향탐지 기술 연구는 단순 일차원의 방향탐지를 벗어나, 고각 및 방위각을 동시에 탐지하는 이차원 방향탐지 기술을 지향하고 있다^[1]~[5]. 그림 1과 같이, 배열안테나 중심으로부터 수신된 수신신호가 가지는 도래각은 고각과 방위각으로 나눌 수 있으며 이때 고각은 적색 원 위치에 해당하는 두 위상중심을 가지는 안테나로부터 수신된 신호간의 위상비교로, 방위각은 청색 원 위치에 수신되는 신호들로 모노펄스 방향탐지를 수행한다^[5],[8]. 상기 방법으로 고각 및 방위각을 추정하기 위해선, 최소 4개 이상의 수신채널이 필요하며, 이에 따라 이차원 모노펄스 방향탐지를 위한 분할개구면의 개수도 최소 4개 이상이 요구된다^[7].

그림 1. | Fig. 1. 이차원 모노펄스 방향탐지를 위한 안테나 위상중심 배치 | Antenna phase center configuration for two-dimensional monopulse DF.

Download Original Figure

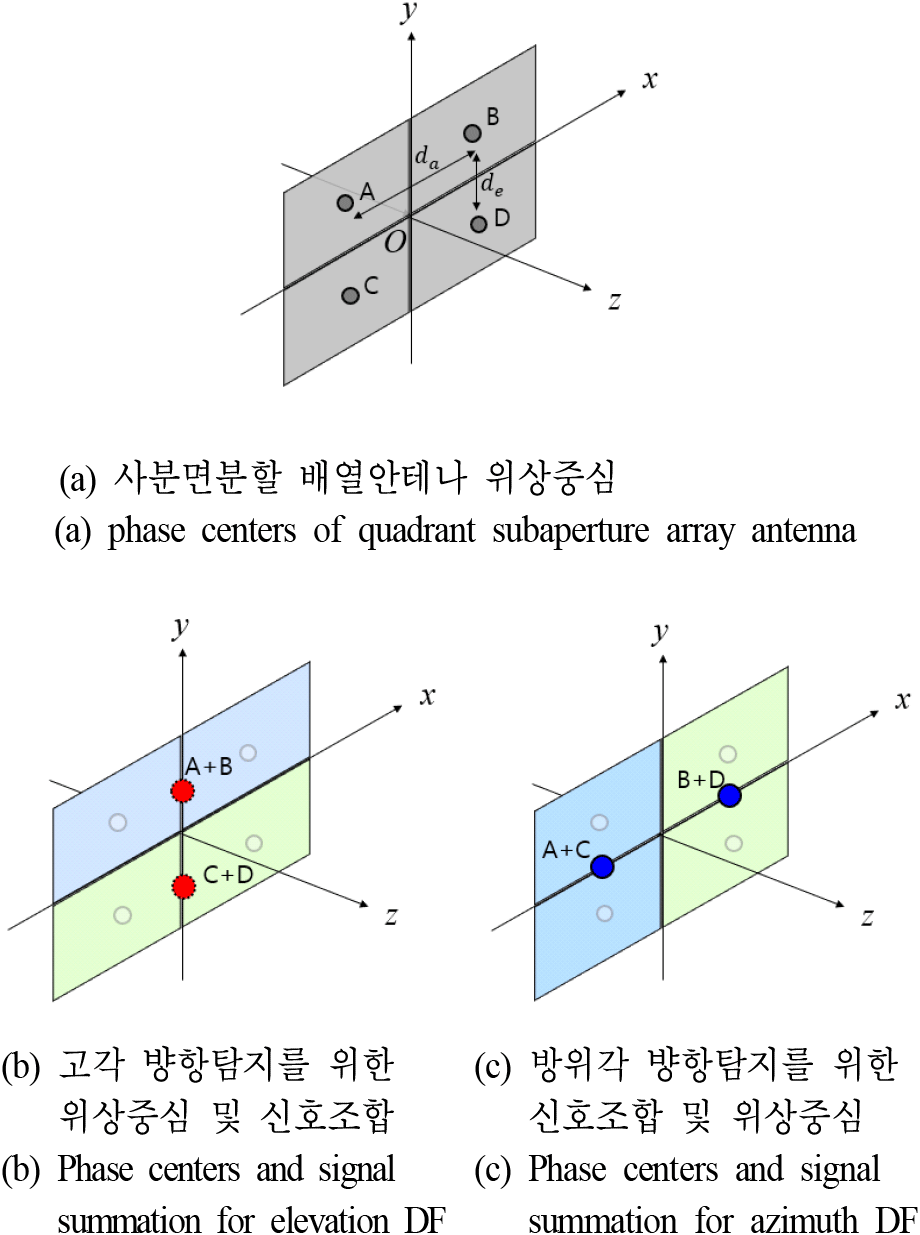
평면구조를 가지는 배열안테나에서의 개구면 분할 방식은 그림 2와 같이 부배열 안테나 간의 위상중심 배치가 상하, 좌우로 배치되는 십자 형태의 배치 방식과 사분면(quadrant) 구조로 부배열 안테나들의 위상 중심 배치 방식이 있다. 십자 형태의 분할 방식은 상하와 좌우의 안테나 중심을 활용하여 고각과 방위각을 바로 추정할 수 있으나, 사분면분할 방식은 그림 2 (b) 및 그림 2(c)와 같이 네 분할개구면간의 신호 조합으로 적색원과 청색원의 새로운 위상중심을 형성하여 고각 및 방위각을 추정한다^[6]. 채널간 신호세기 및 위상 오차가 없는 이상적인 환경에서는 고각 방향탐지 수행은 수신신호의 방위각 성분에 영향을 받지않는 독립적인 과정으로 도래각 추정이 가능하다^[9].

그림 2. | Fig. 2. 사분면분할 배열안테나 구조 | Array antenna structure of quadrant subaperture.

Download Original Figure

그러나 실제 방향탐지 장치에서는 초고주파 장비들의 장치 제작 오차들로 인하여 각 수신채널 간에 신호세기 및 위상 차이가 발생할 수 있으며, 수신채널간 신호 조합 과정에서 해당 상대오차(신호세기 및 위상 차) 성분들이 고각 및 방위각 모노펄스 방향탐지 결과에 악영향을 줄 수 있다. 특히, 수신채널간 상대오차가 발생한 환경에서 수신신호의 입사 방위각이 변화할 경우, 기존 이론적 수식과 달리 고각 모노펄스 방향탐지를 위한 합, 차 패턴 계산 과정에 영향을 주게 되어 방위각 변화에 따라 고각 모노펄스 방향탐지 결과가 변화하게 된다^{[4],[5],[10]~[12]}. 또한 광대역 주파수 수신신호를 취득하는 전자전 장비의 경우 협대역 주파수 신호를 사용하는 경우와 달리 탐지각도 모호성 구간이 주파수 별로 크게 변화하기 때문에 수신채널간 상대오차로 인한 전체 방향탐지 오차 영향이 상대적으로 더 크게 된다. 따라서 광대역 수신신호를 대상으로 하는 사분면분할 기반 위상비교 모노펄스 방향탐지에서는 수신채널 간 상대오차 영향을 고려한 성능분석이 필수적이다^[10]~[14].

본 논문은 사분면분할구조의 분할개구면 수신채널 간 상대오차를 고려한 이차원 모노펄스 방향탐지 성능 변화에 대한 분석의 필요성을 제안한다. 먼저 사분면분할개구면 구조의 이차원 모노펄스 방향탐지 과정에 대해 기술한 후, 각 수신채널간 상대오차가 방향탐지 결과에 미치는 영향을 수식 전개로 도출한다. 다음으로 이차원 모노펄스 방향탐지 시뮬레이션 환경을 구축하여 각 분할개구면 별 수신채널 간 신호세기 및 위상차 조합에 따른 이차원 모노펄스 방향탐지 오차 변화 경향을 확인하였으며, 상대오차 발생 환경에서 탐지각도 구간 내 방향탐지 오차의 정량적 변화를 확인하였다. 또한 수신채널간 상대오차가 발생한 환경에서 입사각의 고각 및 방위각 별 변화에 따른 상반된 각도의 방향탐지 결과에 가하는 오차의 영향을 확인하였다. 마지막으로 주파수 변화에 따른 광대역 수신신호의 방향탐지 오차 변화를 확인 및 분석하였다.

본 논문의 진행 순서는 다음과 같다. Ⅱ장에서는 수신채널간 오차가 없는 이상적인 환경에서의 사분면개구면분할 배열안테나의 모노펄스 방향탐지 수행과정에 대해 정리한다. Ⅲ장에서는 수신채널간 신호세기 및 위상 오차가 발생하는 환경에서 상대오차가 모노펄스 방향탐지 결과에 미치는 영향을 수식으로 도출한다. Ⅳ장에서는 수신채널간 상대오차가 반영된 시뮬레이션 환경에서의 이차원 모노펄스 방향탐지를 수행하여 방향탐지 결과 도출 및 분석을 다룬다. Ⅴ장에서는 결론 및 향후 연구 방향에 대해 기술한다.

Ⅱ. 사분면분할 배열안테나 2차원 모노펄스 방향탐지

사분면분할구조의 배열안테나는 그림 2(a)와 같이 4개의 부배열안테나로 개구면을 분할 후, 각 채널에서 신호를 수신한다. 각 채널을 그림 2(a)와 같이 좌상, 우상, 좌하, 우하 순서대로 A, B, C, D라 표기할 때, 동일한 세기의 수신신호를 각 채널에서 취득했다는 전제 하의 C 수신채널 기준 각 채널 별 상대 위상은 식 (1)과 같다^[5].

A = e j 2 π λ d e sin θ B = e j 2 π λ d a cos θ sin ϕ + d e sin θ C = 1 D = e j 2 π λ d a cos θ sin ϕ

(1)

여기서 d_a는 부배열안테나 위상중심 간 수평거리, d_e는 수직거리를, θ, ϕ는 수신신호의 배열안테나 중심(그림 2(a) O) 기준 입사 고각 및 방위각을, λ는 수신신호 파장을 의미한다. 수신된 네 채널의 신호들은 고각 및 방위각 추정을 위해 그림 2(b) 및 그림 2(c)와 같은 위상을 가지도록 조합되며 식 (2)와 같다.

U E L = A + B V E L = C + D L A Z = A + C R A Z = B + D Σ = A + B + C + D

(2)

여기서 아래첨자 EL과 AZ는 고각, 방위각 별 추정에 필요한 신호 조합을, Σ는 배열안테나 전 구간에 수신된 신호의 총합을 의미한다. 모노펄스 비 산출을 위한 고각 및 방위각 별 합차 비 계산은 식 (3)과 같다^[5],[6].

M E L = U E L − V E L / Σ = e j 2 π λ d e sin θ + e j 2 π λ d a cos θ sin ϕ + d e sin θ − 1 − e j 2 π λ d a cos θ sin ϕ e j 2 π λ d e sin θ + e j 2 π λ d a cos θ sin ϕ + d e sin θ + 1 + e j 2 π λ d a cos θ sin ϕ = e j 2 π λ d e sin θ − 1 e j 2 π λ d a cos θ sin ϕ + 1 e j 2 π λ d e sin θ + 1 e j 2 π λ d a cos θ sin ϕ + 1 = e j 2 π λ d e sin θ − 1 e j 2 π λ d e sin θ + 1 = tan π λ d e sin θ

(3)

M A Z = L A Z − R A Z / Σ = e j 2 π λ d a cos θ sin ϕ + d e sin θ + e j 2 π λ d a cos θ sin ϕ − 1 − e j 2 π λ d e sin θ e j 2 π λ d a cos θ sin ϕ + d e sin θ + e j 2 π λ d a cos θ sin ϕ + 1 + e j 2 π λ d e sin θ = e j 2 π λ d a cos θ sin ϕ − 1 e j 2 π λ d e sin θ + 1 e j 2 π λ d a cos θ sin ϕ + 1 e j 2 π λ d e sin θ + 1 = e j 2 π λ d a cos θ sin ϕ − 1 e j 2 π λ d a cos θ sin ϕ + 1 = tan π λ d a cos θ sin ϕ

(4)

고각 모노펄스 비에 방위각 성분은 분자, 분모에 공통인수로 남아 소거되며, 동일하게 방위각 모노펄스 비 과정에서도 고각 공통인수가 소거된다. 식 (4) 과정으로 계산된 고각 및 방위각 모노펄스 비(M_EL, M_AZ)를 활용한 각도 정보 추정은 다음 식 (5)와 같다.

θ = sin − 1 tan − 1 M E L ⋅ λ π d e ϕ = sin − 1 tan − 1 M A Z ⋅ λ π d a cos θ

(5)

상기 식 (1)~식 (5) 과정을 통해 방향탐지 장치는 고각 및 방위각의 모노펄스 비 값 M_EL, M_AZ을 계산 후 추정 각도 값인 $θ^, ϕ^$ 를 도출한다.

Ⅲ. 사분면분할구조 내 수신채널간 상대오차에 의한 모노펄스 방향탐지 성능 변화

Ⅱ장에서 다룬 사분면분할 배열안테나 구조 내 모노펄스 방향탐지 방법은 네 채널 수신신호 간 신호세기가 동일하다는 전제와 분할개구면 별 수신신호의 도달시간 차이에 의한 위상차 외 별도의 상대 위상오차가 없다는 전제가 가정된다. 그러나, 실제 장비의 동작 환경에서는 네 채널의 수신신호간 신호세기 및 위상차가 제작 오차 및 기타 요인으로 인해 발생할 수 있으며, 해당 상대오차는 사분면분할구조로 구성된 개구면분할 배열안테나에서 각각 방위각 및 고각 모노펄스 비 구성에 변화를 주어 이차원 방향탐지 성능에 악영향을 주게 된다. 본 장에서는 사분면분할 개구면구조 내 채널간 상대오차에 의한 고각 및 방위각 모노펄스 비 변화에 대해 기술한다.

3-1 상대오차가 반영된 모노펄스 비 수식

이전 장에서 다룬 모노펄스 비 산출 및 각도 추정 과정에 상대오차가 반영되었을 때의 수식 전개 과정의 변화에 대해 기술한다. 각 수신채널간 상대오차를 반영할 경우의 식 (1) 및 식 (2)의 변화는 식 (6)과 같다.

A e = K A e j 2 π λ d e sin θ B e = K B e j 2 π λ d a cos θ sin ϕ + d e sin θ C e = 1 D e = K D e j 2 π λ d a cos θ sin ϕ U E L, e = A e + B e V E L, e = C e + D e L A Z, e = A e + C e R A Z, e = B e + D e Σ e = A e + B e + C e + D e

(6)

여기서 K_A, K_B, K_D는 C 수신채널 기준 상대오차를 의미하며 식 (7)과 같다.

K A = ζ A e j ψ A K B = ζ B e j ψ B K D = ζ D e j ψ D

(7)

ζ_A, ζ_B, ζ_D는 C채널 대비 진폭 차이를, ψ_A, ψ_B, ψ_D는 위상차를 의미한다.

신호세기 및 위상오차가 포함된 환경에서의 모노펄스 비 산출 과정은 식 (8)과 같다.

M E L, e = U E L, e − V E L, e / Σ e = K A e j 2 π λ d e sin θ + K B e j 2 π λ d a cos θ sin ϕ + d e sin θ − 1 − K D e j 2 π λ d a cos θ sin ϕ K A e j 2 π λ d e sin θ + K B e j 2 π λ d a cos θ sin ϕ + d e sin θ + 1 + K D e j 2 π λ d a cos θ sin ϕ M A Z, e = U A Z, e − V A Z, e / Σ e = K B e j 2 π λ d a cos θ sin ϕ + d e sin θ + K D e j 2 π λ d a cos θ sin ϕ − K A e j 2 π λ d e sin θ − 1 K B e j 2 π λ d a cos θ sin ϕ + d e sin θ + K D e j 2 π λ d a cos θ sin ϕ + K A e j 2 π λ d e sin θ + 1

(8)

고각 θ의 경우, 개별 항에 sin(·), cos(·)삼각함수로 지수 항에 포함되기 때문에 명시적 수식 형태(explicit form)로 표현할 수 없다. 따라서 방위각 ϕ에 대해서만 수식을 다시 전개하면 식 (9)와 같다.

ϕ = sin − 1 λ 2 π d a cos θ arg M A Z, e K A e j 2 π λ d e sin θ + K A e j 2 π λ d e sin θ + M A Z, e + 1 K B e j 2 π λ d e sin θ + K D − M A Z, e K B e j 2 π λ d e sin θ − M A Z, e K D

(9)

여기서 arg(·)는 복소수의 편각을 의미한다.

기존의 고각 및 방위각 모노펄스 비는 분자, 분모에서 각각 방위각과 고각을 가진 공통인수가 소거됨에 따라 고각은 방위각 모노펄스 비에 cos(·) 성분으로만 영향을 주고, 방위각은 고각 모노펄스 비에 영향을 주지 않으나, 식 (8) 및 식 (9)와 같이 네 수신채널간 상대오차가 발생한 경우는 상반된 각도 정보가 소거되지 않으므로 측정 각도의 오차를 유발하는 요인으로 남게 된다. 특히, 수신신호의 입사 방위각에 의한 채널간 위상차가 고각 모노펄스 방향탐지 과정에서 상대오차로 인해 상쇄되지 못하고 잔여 성분으로 남아 고각 방향탐지 결과에 영향을 주게 된다. 따라서 수신채널간 상대오차가 발생할 경우, 수신신호의 고각과 방위각 성분은 서로 다른 각도의 모노펄스 방향탐지 결과에 영향을 주게 된다.

3-2 상대오차로 인한 고각 및 방위각 별 모노펄스 비 변화

본 장에서는 수신채널 별 상대오차로 인해 발생하는 고각 및 방위각 별 모노펄스 비 변화를 관측각도 구간 내 입사각 변화에 따른 이차원 모노펄스 비 곡면도로 확인하였다. 수신신호가 X-대역 내 RF 주파수를 가지고 고각과 방위각이 각각 ±15°인 관측구간에 신호가 입사할 때, 위상중심이 서로 대각에 있는 B, C 채널 간 신호세기 3 dB 혹은 위상차 45° 로 상대오차가 발생할 경우를 예시로 모노펄스 비를 산출하였으며 이는 그림 3과 같다.

그림 3. | Fig. 3. B-C 채널 간 상대오차 발생 시 모노펄스 비 변화 | Monopulse slope variation when the relative error between B and C occurs.

Download Original Figure

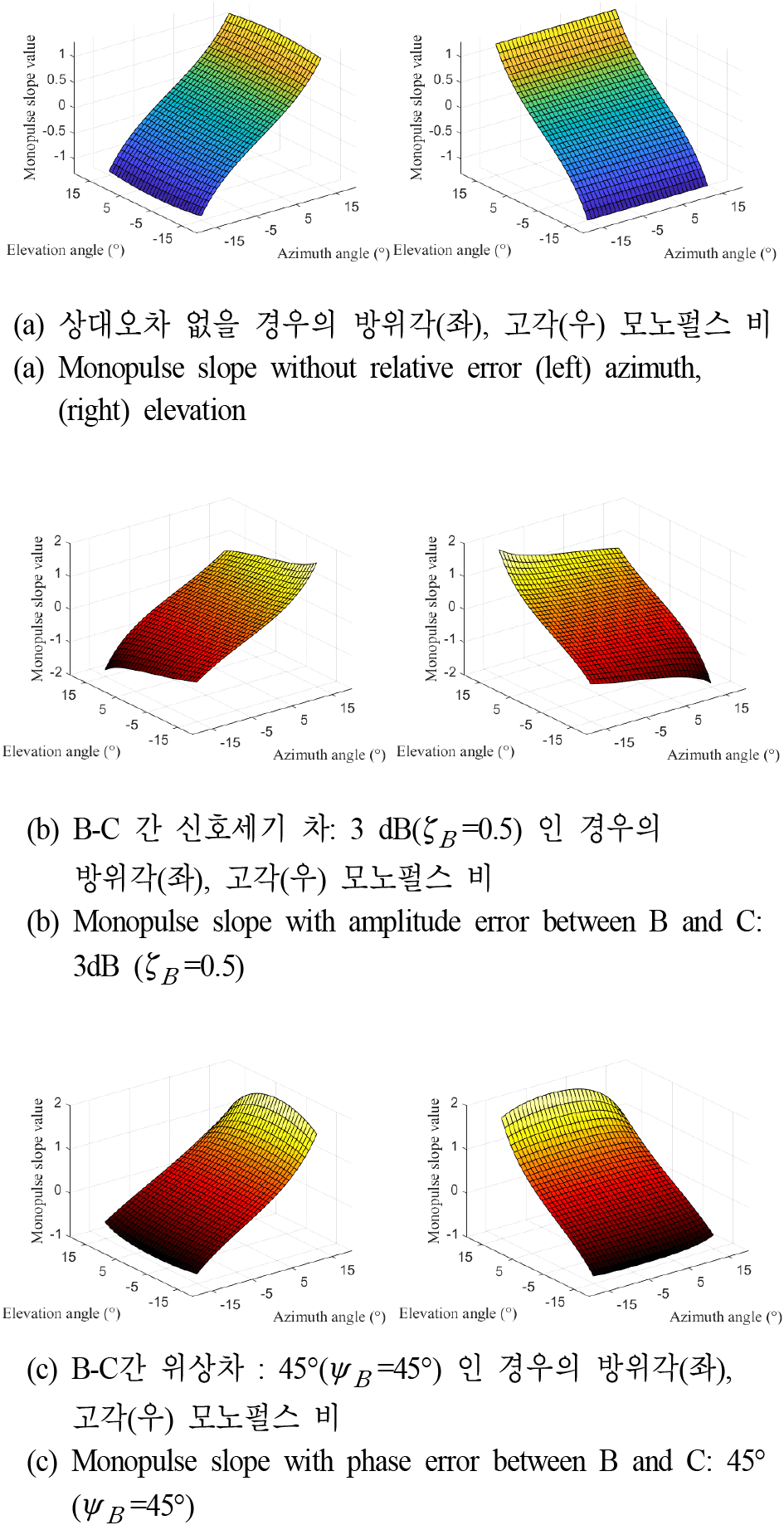
수신채널 별 상대오차가 없는 정상동작 시의 관측구간 내 고각-방위각 변화에 따른 이차원 모노펄스 비는 그림 3 (a)와 같으며, 상대오차가 없는 환경에서는 고각, 방위각 모노펄스 비는 다른 각도에 영향을 받지 않는 것을 볼 수 있다. 그러나 B-C 채널 간 신호세기 차이가 발생할 경우(그림 3(b)), 방위각 및 고각 모노펄스 비가 상반된 고각 및 방위각 변화에 영향을 받는 것을 볼 수 있으며, 특히 고각 모노펄스 비가 수신신호의 방위각 성분에 영향을 받게 되는 현상이 확인된다. 다음으로 수신채널 B-C 간의 상대 위상차가 45° 발생할 때의 고각-방위각 변화에 따른 이차원 모노펄스 비 변화를 확인하였으며(그림 3 (c)) B-C 신호간 위상차가 발생한 경우 또한 방위각 및 고각 변화에 따라 기존 정상 모노펄스 비 대비 상이한 고각 및 방위각 모노펄스 비를 가지는 것이 확인되었다. 따라서 각 수신채널 간에 상대오차가 발생할 시, 관측구간에 대한 모노펄스 비가 기존과 다른 형태로 변화하는 것을 볼 수 있다.

Ⅳ. 모노펄스 방향탐지 시뮬레이션 분석

본 장에서는 이전 장에서 다룬 사분면분할구조 내 수신채널간 상대오차로 인해 발생하는 이차원 모노펄스 비 변화가 방향탐지 결과에 미치는 영향을 확인한다. 이차원 방향탐지 영향을 분석하기 위한 전체 시뮬레이션 수행 과정은 그림 4와 같으며, 시뮬레이션에서 사용된 변수 정보는 표 1과 같다. 그림 2 (a)와 같이 좌상, 우상, 좌하, 우하 개구면 중심에 위상중심을 가지는 분할된 개구면에 좌표 중심 O 기준, 고각 및 방위각이 각각 ±15°인 관측구간 내 설정된 SNR의 신호세기를 가지는 입사신호를 A, B, C, D 네 분할개구면으로부터 얻는다. 이때 C채널 기준 각 A, B, D 수신채널에 신호세기는 −1 dB부터 −3 dB 까지, 위상은 15°, 30°, 45°로 상대오차 차이가 설정에 따라 발생한다. 상대오차가 포함된 네 채널의 수신신호는 식 (2) 및 식 (3)의 과정으로 합, 차 신호 조합 및 모노펄스 비 계산에 사용된다. 계산된 고각 및 방위각의 모노펄스 비는 식 (5)의 과정으로 고각 및 방위각 추정값 $θ^, ϕ^$ 을 도출하며 실제 입사 신호의 참값인 θ, ϕ와 비교하여 제곱평균제곱근(RMS, root mean square) 값을 계산한다. RMS 계산식은 식 (10)과 같이 정의한다.

그림 4. | Fig. 4. 사분면분할 배열안테나 구조 이차원 모노펄스 방향탐지 시뮬레이션 순서도 | Simulation flowchart for monopulse DF in quadrant subarray structure.

Download Original Figure

표 1. | Table 1. 시뮬레이션 변수 | Simulation parameters.

Parameter	Value
Frequency	C-, X-, Ku-Band
Elevation angle range	±15°
Azimuth angle range	±15°
Elevation angle step	1°
Azimuth angle step	1°
SNR	10 dB
Number of trial in each azimuth	100
Number of trial in each elevation	100
Number of trial for all azimuth (M)	3,100
Number of trial for all elevation (N)	3,100
Azimuth phase center interval (d_a)	0.03 m
Elevation phase center interval (d_e)	0.03 m

Download Excel Table

θ R M S = ∑ i = 1 N θ i − θ^i 2 N ϕ R M S = ∑ i = 1 M ϕ i − ϕ^i 2 M

(10)

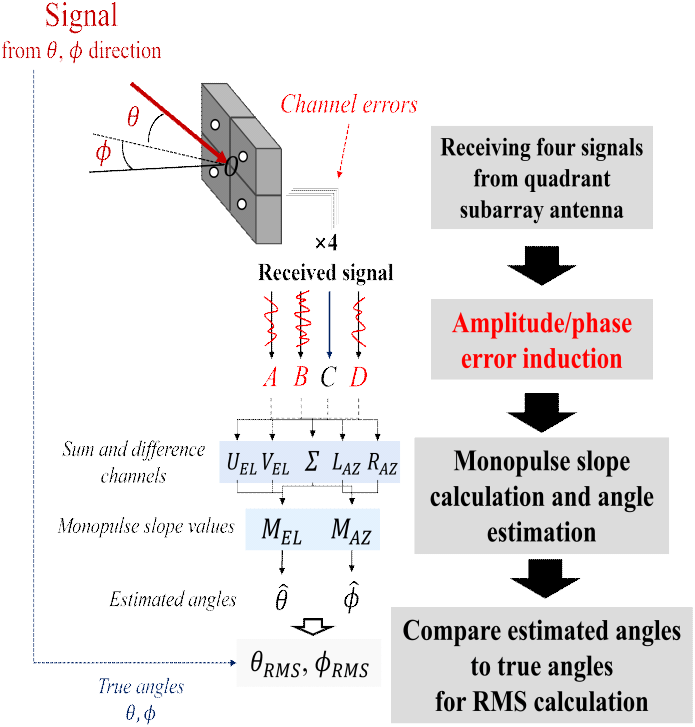
여기서 N, M은 각각 고각 및 방위각 별 관측각도 범위 내 방향탐지 총 수행 횟수이다.

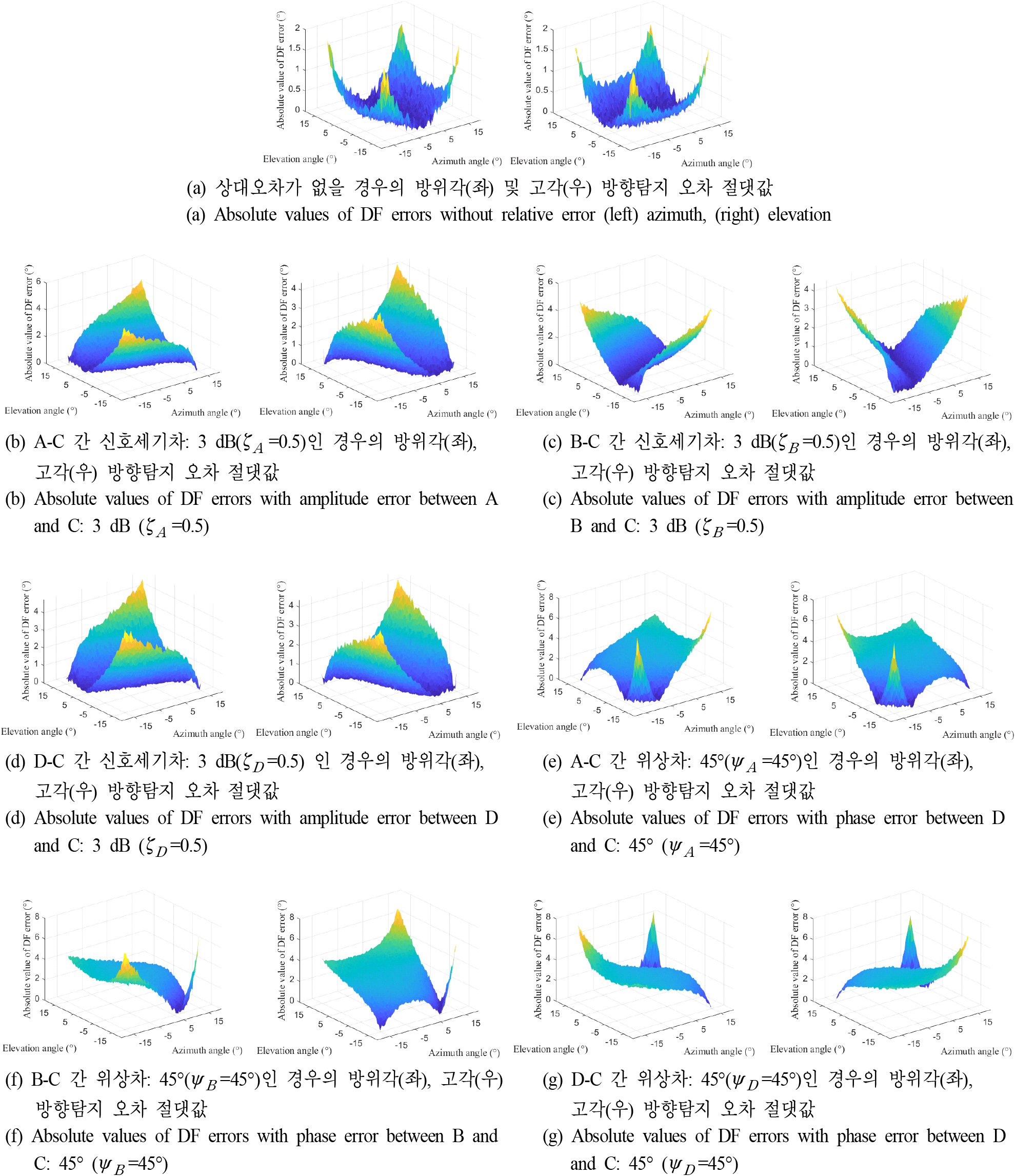
본 논문은 총 네가지 시뮬레이션 수행 결과에 대해 기술한다. 먼저, 상대오차가 발생한 시뮬레이션 환경 내 관측구간에서 입사각(고각, 방위각) 변화에 따른 방향탐지 오차의 변화 경향을 보여준다. 수신채널 C 기준 A, B, D 채널간 신호세기, 위상차가 3 dB, 45° 일 경우의 측정된 고각 및 방위각 각도와 실제 참값(ground-truth angle)간의 차이의 절댓값을 계산하여 관측구간 내 곡면도를 도시하였으며 이는 그림 5와 같다. 수신채널 간 상대오차가 발생하지 않는 경우(그림 5(a))에도 고각 및 방위각 변화에 따라 방향탐지 오차가 증가하는 것을 볼 수 있는데 이는 SNR이 10 dB 인 환경에서 잡음 신호가 방향탐지 결과에 영향을 주는 상황이며 기존 연구결과와 달리 고각 방향탐지 결과가 수신신호의 방위각 방향탐지 결과에 영향을 줄 수 있음이 상기 시뮬레이션 결과로 확인된다^[4]. 그림 5(b)부터 그림 5(d)는 각각 C 채널 기준 A, B, D 채널간 신호세기 차이가 3 dB 발생했을 때의 방향탐지 시뮬레이션 오차 결과이며 채널마다 서로 다른 방향탐지 오차 분포가 나타나며 고각 및 방위각 변화가 상반된 각도의 방향탐지 결과에 영향을 주고 있음이 확인된다. 그림 5(e)~그림 5(g)는 동일한 환경에서 채널간 위상차를 45° 줄 때의 방향탐지 오차 결과이며, 이 또한 각 채널마다 방향탐지 오차 분포가 상이하게 변화하며 고각 및 방위각 성분이 다른 각도의 방향탐지 결과에 영향을 줄 수 있음을 확인하였다.

그림 5. | Fig. 5. C채널 기준 채널간 상대오차 발생 시 고각(좌) 및 방위각(우)방향탐지 오차 변화 | DF error variation when the relative error occurs related with the C channel.

Download Original Figure

두번째로 C 채널 기준 각 A, B, D 채널 간의 신호세기차 혹은 위상차가 3 dB, 45° 발생했을 경우에 전체 관측구간(고각 ±15°, 방위각 ±15°)에서 수행된 방향탐지 결과의 RMS를 식 (10)에 따라 계산하였다. 각 채널간의 신호세기 및 위상차에 따른 RMS 계산결과는 표 2와 같다. C 채널 기준 각 채널간에 신호세기와 위상차가 증가할수록 전체 고각 및 방위각 방향탐지 오차의 RMS가 증가하는 것을 볼 수 있다. 따라서 각 수신채널간에 발생하는 상대오차가 전체 관측구간 내 이차원 방향탐지 성능에 악영향을 줄 수 있음을 보여준다.

표 2. | Table 2. C채널 기준 상대오차 변화에 따른 전 구간 방향탐지 오차 RMS 변화 | RMS variation when the relative error increases.
(uint: °)

Amplitude error (dB)	A		B		D
Amplitude error (dB)	Elevation	Azimuth	Elevation	Azimuth	Elevation	Azimuth
−1	0.76	0.79	0.73	0.77	0.76	0.79
−2	1.23	1.29	1.24	1.30	1.22	1.30
−3	1.71	1.80	1.71	1.80	1.71	1.81
Phase error	A		B		D
Phase error	Elevation	Azimuth	Elevation	Azimuth	Elevation	Azimuth
15	1.10	1.11	1.06	1.06	1.06	1.07
30	2.03	2.05	2.02	2.05	2.03	2.05
45	3.02	3.06	3.02	3.05	3.02	3.06

Download Excel Table

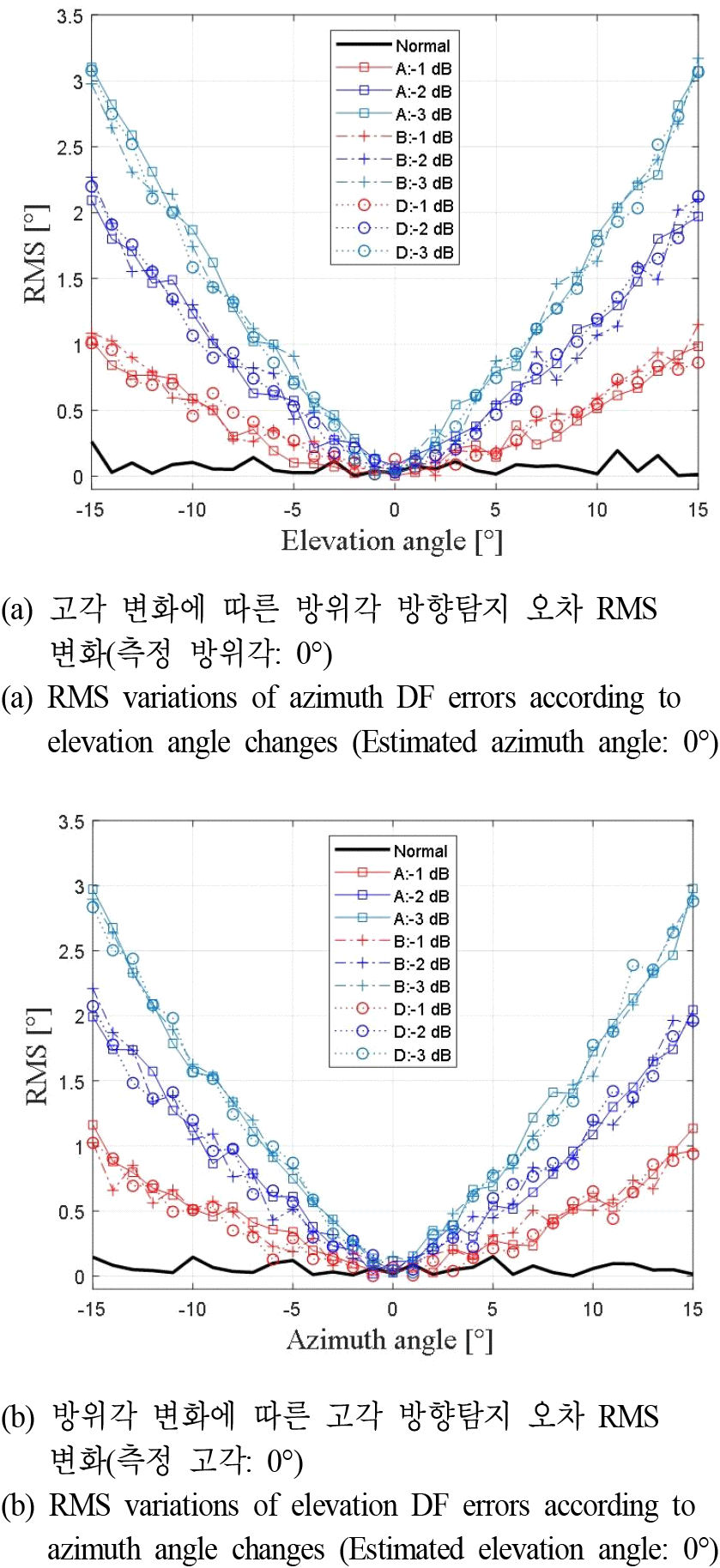
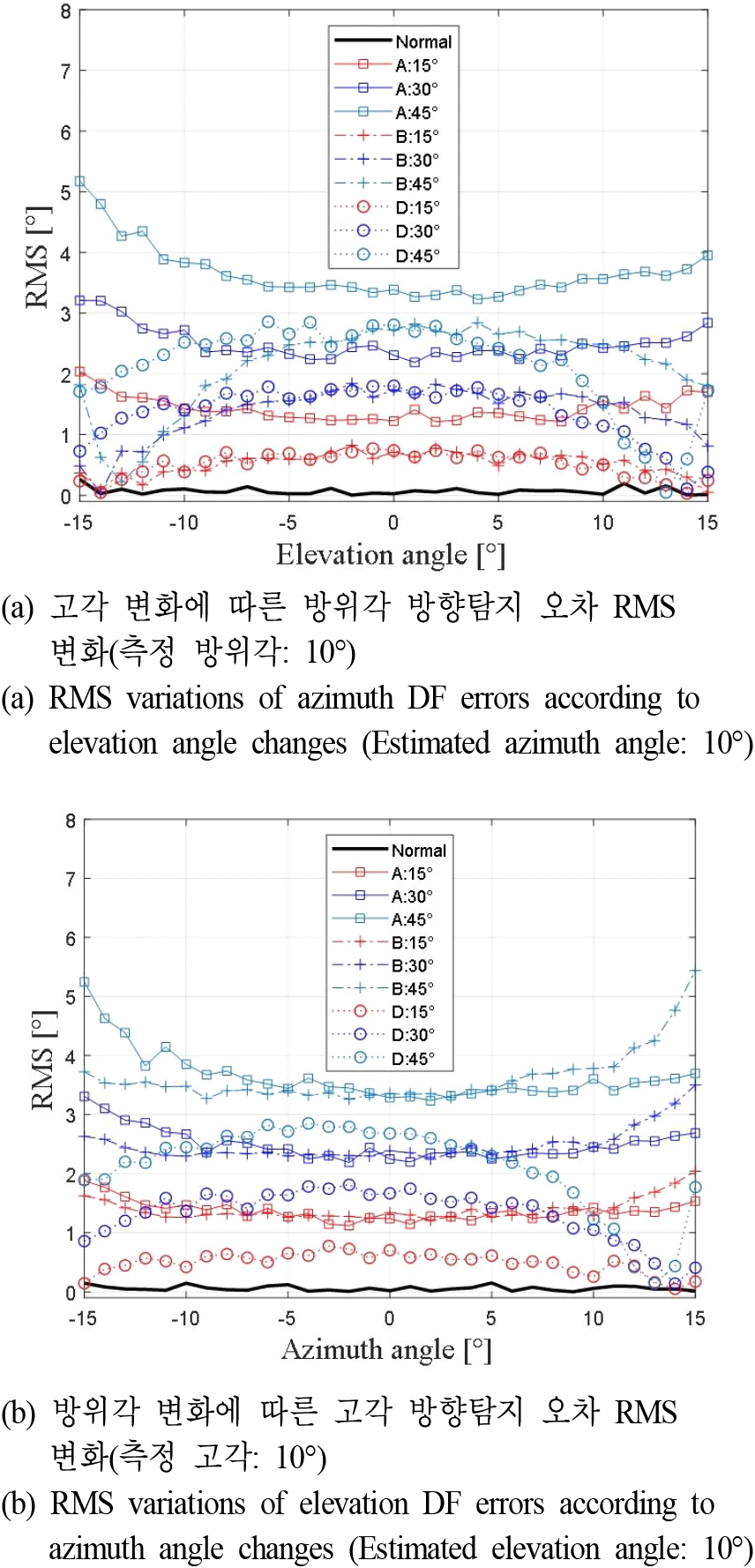
세번째로 수신신호 입사각의 고각 및 방위각 성분 변화가 다른 각도의 방향탐지에 미치는 영향을 분석하였다. C채널 기준 A, B, D 채널간 상대오차가 발생했을 때, 고각 변화에 따른 방위각 방향탐지 와 방위각 변화에 따른 고각 방향탐지 결과 오차를 RMS로 산출하였으며 그림 6 및 그림 7과 같다. 그림 6은 C채널 기준 각 채널간 신호세기 차이가 −1 dB, −2 dB, −3 dB 발생했을 때 각도 변화에 따른 방향탐지 결과를 도시한 것으로, 그림 6 (a)는 관측 방위각이 0°일 때 고각 변화에 따른 방향탐지 오차 RMS 변화를, (b)는 관측 고각이 0°일 때 방위각 변화에 따른 RMS 변화를 도시한다. 고각 및 방위각이 변화함에 따라 상반된 방위각 및 고각 방향탐지 오차 RMS가 증감하는 것을 볼 수 있으며 신호세기 차이에 따라 방향탐지 결과가 영향을 받는 것이 확인된다. 그림 7은 이전과 동일한 환경에서 C채널 기준 각 채널간 위상차가 15°, 30°, 45°일 경우에 각도변화에 따른 방향탐지 오차 RMS를 나타낸다. 채널간 위상차의 경우 신호세기와 달리 탐지 방위각 및 고각이 0°일 경우에 각도 변화에 따른 큰 변화가 나타나지 않기 때문에(그림3 및 그림 4) 관측 방위각이 10°, 고각이 10°인 경우의 RMS 변화를 확인하였다. 채널간 위상차가 발생하였을 때 각도 변화에 따른 방향탐지 RMS 변화는 기존 신호세기차 경우와 달리 채널간 조합에 따라 다양한 증감 형태를 보인다. 또한 채널간 위상차가 증가할수록 방향탐지 오차 RMS의 전반적 수치가 증가함을 볼 수 있다. 따라서 사분면분할개구면 구조의 배열안테나 환경에서 수신채널간 신호세기 및 위상차가 발생할 경우, 방위각 및 고각 방향탐지 결과는 서로다른 입사 각도 성분의 변화에 영향을 받을 수 있음이 확인되었다.

그림 6. | Fig. 6. C채널 기준 신호세기차 발생시, 입사각 변화에 따른 고각, 방위각 별 방향탐지 오차 RMS 변화 | RMS variation of DF error in elevation and azimuth according to incident angle changes when the amplitude errors occur between C-channel and others.

Download Original Figure

그림 7. | Fig. 7. C채널 기준 위상차 발생시, 입사각 변화에 따 른 고각, 방위각 별 방향탐지 오차 RMS 변화 | RMS variation of DF error in elevation and azimuth according to incident angle changes when the phase errors occur between C-channel and others.

Download Original Figure

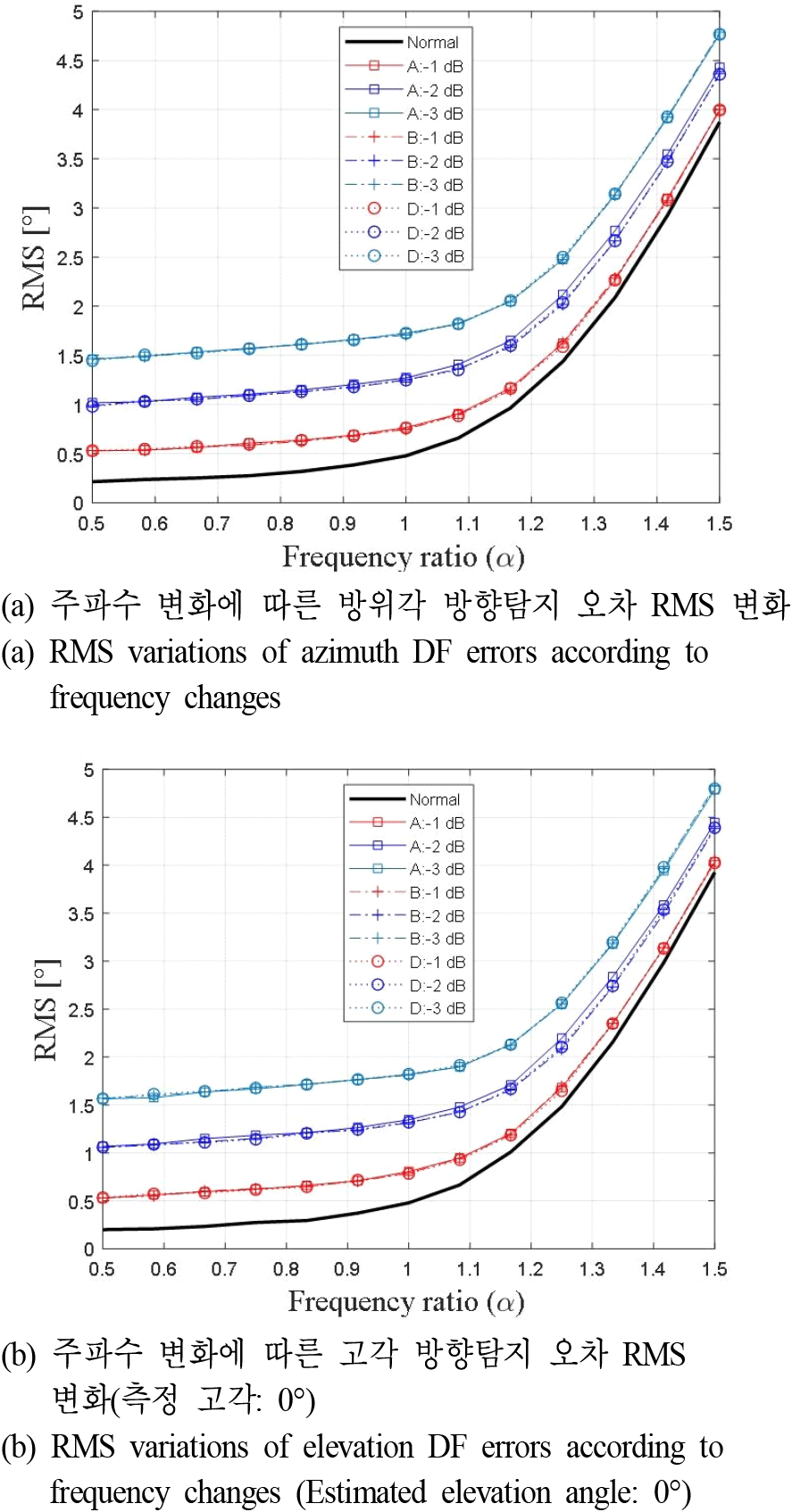
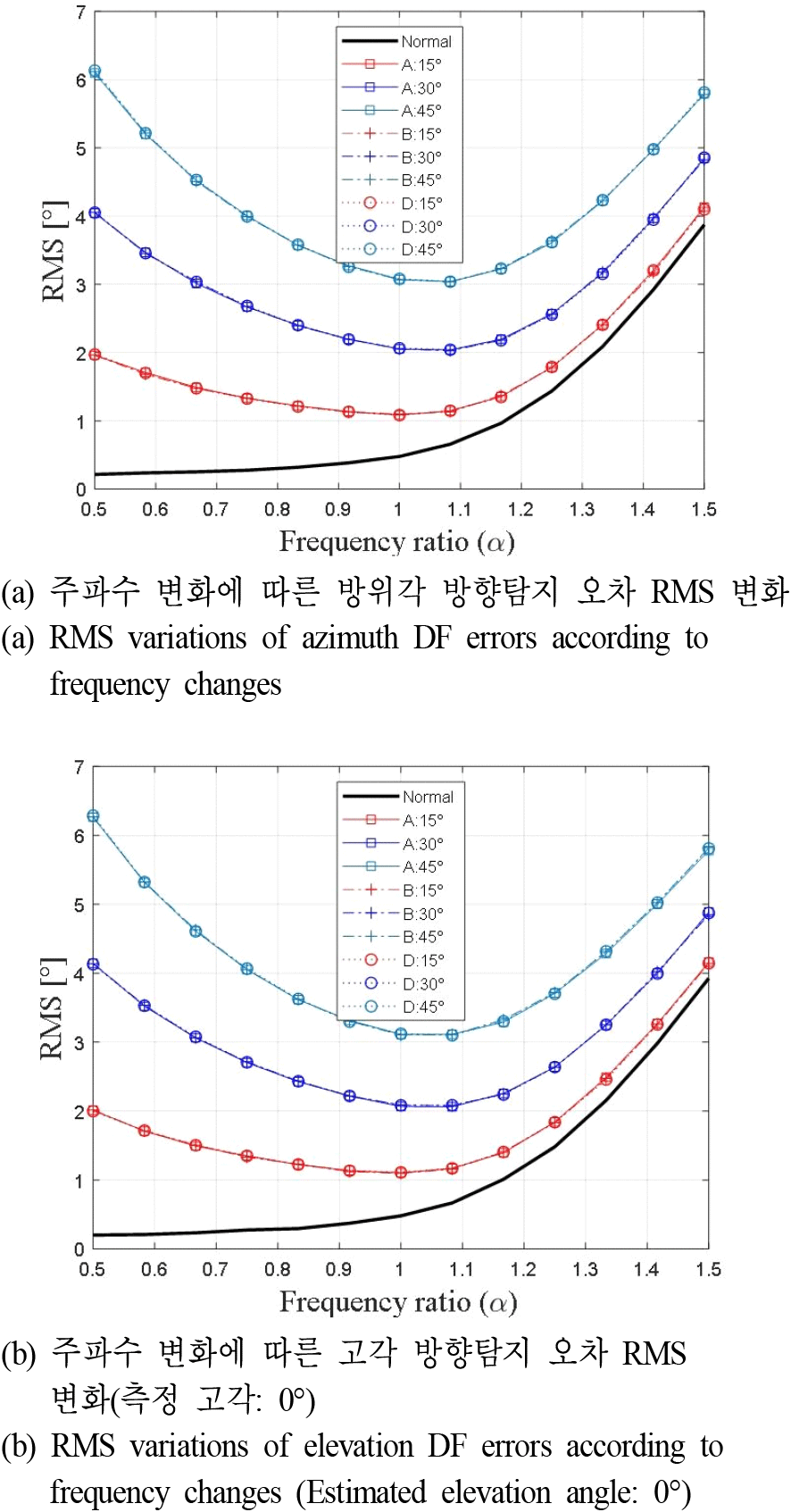
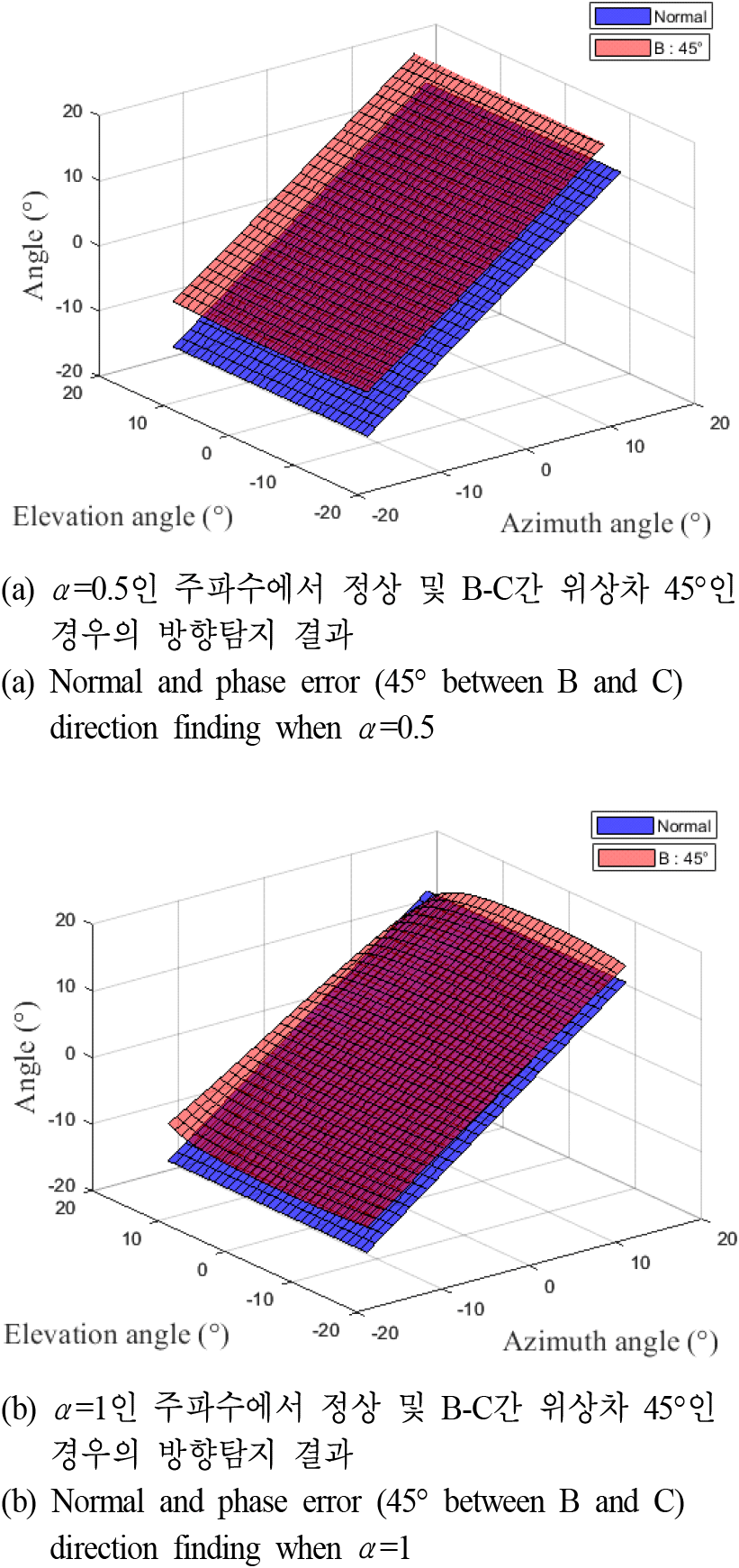
마지막으로 주파수 변화에 따른 이차원 모노펄스 방향탐지 결과의 RMS 변화를 확인하였다. 수신대상신호의 전체 주파수 스펙트럼의 중심주파수가 f_center로, α를 중심 주파수와의 비율이라 할 때, 0.5≤α≤1.5구간 내 주파수(αf_center) 대역폭 수신신호들의 관측구간 내 방향탐지 RMS 결과를 시뮬레이션으로 확인하였으며 이는 그림 8 및 그림 9와 같다. 그림 8은 신호세기 차가 발생할 때의 주파수 비율 α에 따른 방위각 및 고각 방향탐지 RMS 변화를 도시하고 있으며 주파수가 증가할수록, 또한 C채널과 A, B, D 수신채널의 신호세기 차가 증가할수록 방위각 및 고각 방향탐지 RMS 수치가 전체 주파수 대역에서 증가함을 보여준다. 그림 9는 위상차가 발생할 경우의 주파수에 따른 방향탐지 RMS 변화를 보여주며 전체 주파수에서 공통적으로 위상차 크기에 따라 RMS가 증가하는 것이 확인된다. 또한 낮은 주파수와 높은 주파수에서 상대적으로 높은 RMS 수치가 나타나는데 이는 위상차 발생에 따른 모노펄스 비 변화 및 방향탐지 결과 영향이 각 주파수 별로 상이하기 때문이다. 그림 10은 α=0.5 및 α=1일 경우의 정상 동작과 B-C간 위상차가 45°인 두가지 경우에 대해 관측 구간 전반에 고각 방향탐지 결과를 표현한 곡면도 예시이다. α=0.5에서의 방향탐지 결과가 상대적 고주파인 α=1보다 높은 편차를 가지는 것을 볼 수 있으며 평균 방향탐지 오차의 정량적 수치로는 α=0.5는 6.529°, α=1는 3.159° 이며 낮은 주파수에서 높은 RMS 오차를 가짐이 확인된다. 따라서 수신채널 간 상대오차가 있는 환경에서 광대역 주파수 신호 대상 방향탐지 결과가 주파수 변화에 영향을 받을 수 있음을 본 시뮬레이션 분석 결과로 확인하였다.

그림 8. | Fig. 8. C채널 기준 신호세기차 발생시, 주파수 변화에 따른 고각, 방위각 별 방향탐지 오차 RMS 변화 | RMS variation of DF error in elevation and azimuth according to frequency changes when the amplitude errors occur between C-channel and others.

Download Original Figure

그림 9. | Fig. 9. C채널 기준 위상차 발생시, 주파수 변화에 따른 고각, 방위각 별 방향탐지 오차 RMS 변화 | RMS variation of DF error in elevation and azimuth according to frequency changes when the phase errors occur between C-channel and others.

Download Original Figure

그림 10. | Fig. 10. B-C 간 위상차: 45°(ψ_B =45°)인 경우의 주파수 별 정상(청색) 및 위상차 발생(적색) 방향탐지 결 과 비교 | Comparison of direction finding results between normal and phase error between B and C: 45° (ψ_B =45°).

Download Original Figure

Ⅴ. 결 론

본 논문에서는 사분면분할구조 개구면분할 환경에서 수신채널간 상대오차가 발생할 경우 모노펄스 방향탐지 결과에 끼치게 되는 영향에 대해 분석하였다. 사분면분할구조의 분할개구면은 기존 십자 구조의 분할개구면과 다른 위상중심을 가지는 특성으로 인해 고각 및 방위각 별 모노펄스 방향탐지과정에 네 채널의 신호가 모두 사용되며, 실제 장비에서 발생하는 제작 오차로 인해 유발되는 각 채널 간 신호 세기 및 위상차가 방향탐지 결과에 영향을 줄 수 있음을 수식 전개 및 이차원 모노펄스 방향탐지 시뮬레이션 수행으로 확인하였다. 수행 결과, 사분면분할 수신채널 간 상대오차가 발생할 경우에 수신신호의 입사각의 변화에 따른 이차원 방향탐지 결과가 방위각, 고각별로 영향을 받으며, 각 수신채널별 상대오차 발생조합에 따라 이차원 방향탐지 오차 영향이 변화하였다. 또한, 각 채널 간 신호 세기 및 위상차가 증가할수록 방위각, 고각 ±15° 이내 관측구간 전체의 이차원 방향탐지 오차 RMS가 증가하였으며 수신신호의 방위각 및 고각 입사각 성분이 서로 다른 고각 및 방위각 방향탐지 결과에 영향을 줄 수 있음을 확인하였다. 마지막으로 주파수에 따른 상대오차 발생 환경에서의 방향탐지 RMS 변화를 확인하여 주파수에 따른 수신채널 간 상대오차 영향을 분석하였다.

본 논문은 사분면분할구조의 모노펄스 방향탐지 방식에서 수신채널 간 상대오차가 발생할 경우, 기존의 이론적 수식 결과와 다르게 되므로 사분면분할구조를 따르는 이차원 모노펄스 방향탐지 방법에 대한 새로운 접근 및 연구가 수행되어야 함을 제시하였다. 향후 연구로 각 채널 간 상대오차 발생 조합에 따라 관측구간 내 방향탐지 오차 변화가 달라짐에 따라, 각 분할개구면간의 위치와 방향탐지 오차와의 연관성에 대한 정밀한 분석이 요구된다. 또한 분할개구면 안테나에 추가적인 수신빔 조향 개념이 추가될 경우, 모노펄스 비 산출 식이 달라지므로, 수신빔 조향을 추가적으로 고려한 수신채널간 상대오차를 고려한 이차원 모노펄스 방향탐지 영향 분석이 필요할 것으로 예상된다.

Acknowledgements

본 연구는 2025년 정부의 재원으로 국방과학연구소의 지원을 받아 수행된 연구임(912971201).

References

[1].

B. J. Jang, “Direction finding technology: Tutorial, review, and research prospects,” The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 30, no. 8, pp. 607-617, Aug. 2019.

[2].

J. M. Yang, J. H. Choi, M. S. Kwon, T. W. Kim, I. T. Han, and J. H. Im, et al., “Study on a rRadar module for active phased array radars,” The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 35, no. 1, pp. 67-80, Jan. 2024.

[3].

K. K. Kim, S. M. Pyo, and J. W. Jung, “A study on phase weighting of reflectarray antenna system for dual-beamforming based on split beam,” The Journal of the Korea Institute of Electronic Communication Sciences, vol. 19, no. 5, pp. 799-808, Oct. 2024.

[4].

M. H. Chae, “Accuracy analysis of 2-D direction finding based on phase comparison,” The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 28, no. 8, pp. 653-660, Aug. 2017.

[5].

R. A. Dana, Monopulse Measurement with Active Electronically Scanned Arrays(AESAs), New York, NY, Springer, 2022.

[6].

B. R. Mahafza, Radar Systems Analysis and Design using MATLAB, New York, Chapman and Hall/CRC, 2005.

[7].

L. G. Bullock, G. R. Oeh, and J. J. Sparagna, “An analysis of wide-band microwave monopulse direction-finding techniques,” IEEE Transactions on Aerospace and Electronic Systems, vol. AES-7, no. 1, pp. 188-203, Jan. 1971.

[8].

S. M. Sherman, D. K. Barton. Monopulse Principles and Techniques, Norwood, MA, Artech House, 2011.

[9].

H. K. Sim, M. A. Jung, and S. C. Kim, “A performance analysis of phase comparison monopulse algorithm for antenna spacing and antenna array,” The Journal of Korean Institute of Communications and Information Sciences, vol. 40, no. 7, pp. 1413-1419, Jul. 2015.

[10].

A. D. Brown, Active Electronically Scanned Arrays: Fundamentals and Applications, Hoboken, NJ, John Wiley & Sons, 2021.

[11].

A. D. Brown, Electronically Scanned Arrays: MATLAB Modeling and Simulation, Oxfordshire, Taylor & Francis, 2012.

[12].

J. Jung, B. Satriyotomo, and S. Pyo, “A study of direction-of-arrival estimation with an improved monopulse ratio curve using beamforming for an active phased array antenna system,” Electronics, vol. 12, no. 24, p. 4906, Dec. 2023.

[13].

D. J. An, J. H. Lee, “Performance analysis of amplitude comparison monopulse direction-of-arrival estimation,” Applied Sciences, vol. 10, no. 4, p. 1246, Feb. 2020.

[14].

H. Rezaei, M. A. Sebt, N. Zarei, and G. S. Moghadam, “Unambiguous direction estimation and localization of two unresolved targets via monopulse radar,” Electronics, vol. 11, no. 22, p. 3780, Nov. 2022.