I. 서 론
현대 군사작전 환경에서는 로켓탄, 박격포와 같은 고속 탄체를 빠르게 탐지하고 식별하는 능력이 방어 체계의 대응 속도와 정밀도에 직접적인 영향을 미친다. 하지만 실전에서 운용되는 다양한 포탄에 대해 레이다 반사 신호를 실험적으로 확보하는 데에는 보안, 비용, 환경 통제 등 여러 제약이 따른다. 특히 적군이 사용하는 포탄의 세부 형상 정보는 대부분 기밀로 분류되어 있으며, 공개된 데이터 또한 제한적이지만, 효과적인 탐지 및 분류 알고리즘 개발을 위해 이에 대한 수치 해석 기반의 분석이 반드시 필요하다. 후방 산란(backscattering) 특성은 수치 해석 기반 분석 대상으로 레이다의 입사 방향과 관측 방향이 동일한 경우 발생하는 전자기 산란을 의미하며, 표적의 탐지, 식별, 궤적 추정 등에 있어 중요한 정보로 작용한다.
이러한 문제를 보완하기 위해, M&S(modeling and simulation) 기반의 전파 해석 기법이 활발히 활용되고 있다[1],[2]. 시뮬레이션 기반 해석은 고속성, 재현성, 변수 통제가 가능하다는 점에서 물리 실험의 한계를 보완하고, 해석 효율성과 정확도 향상을 동시에 추구할 수 있는 장점을 제공한다.
전자기 산란 해석에 사용되는 대표적인 수치 기법으로는 Full-wave simulation인 MoM(method of moments), MLFMM(multi-level fast multipole method)[3]와 고주파 근사 기반의 SBR(shooting and bouncing rays)[4] 및 IPO (iterative physical optics)[5] 등이 있다. MoM 정확도가 높지만 계산 자원 요구가 커 복잡한 형상이나 대형 표적 해석에는 실용적인 한계가 존재한다. 반면 SBR은 해석 속도가 빠르며, 형상이 단순하고 전기적으로 큰 물체의 해석에 적합하지만, 회절 등의 효과를 충분히 반영하지 못하는 한계가 있다. MoM과 SBR을 비교하여 기법별 정확도와 적용성을 분석한 연구가 진행되었다[6]. 해당 논문에서는 미사일 형상을 대상으로 bistatic 및 monostatic RCS를 비교하여, 고주파 근사 기법의 계산 효율성과 복잡 형상에서의 정확도 차이를 보고하였다.
본 연구에서는 122 mm 로켓 형상을 기준으로 탄체의 후방산란을 MoM과 SBR 방법으로 해석하고, 결과를 비교한다. 먼저 EFIE(electric field integral equation)와 가중치 0.2 및 0.8을 적용한 CFIE(combined field integral equation)를 포함한 총 3가지 MoM해석을 비교하여, 효율적이고 정확도가 보장되는 방법을 선택한다. 그 후 SBR 계산 시 날개 부분의 회절이 SBR 결과에 주는 영향을 분석한다.
II. MoM 및 SBR 비교
MoM 방법은 상업용 툴인 Feko의 EFIE 및 MFIE (magnetic field integral equation)을 조합한 CFIE 기반 MoM을 사용하였다. 비교를 위한 두 가중치(α)는 각각 0.2와 0.8을 사용하고, 이때 가중치가 작으면 EFIE의 영향이, 크면 MFIE의 영향이 커진다[3]. EFIE는 정밀한 해석이 가능하지만, 수렴속도가 느린 반면, MFIE는 수렴성이 양호하나 해석 정확도가 낮다. 이러한 단점을 보완한 CFIE는 가중치 0.2 수준에서 수렴성과 정확도 간 균형이 잘 맞는 것으로 보고되었다[7]. 역행렬 계산에 LU preconditioner를 이용하는 BicgStab 반복 기법이 사용되었다. 반복 횟수는 최대 500회로 제한되고, 수렴 기준의 잔차(residual error)는 3×10−3이다.
SBR방법의 후방산란을 계산하기 위해, Anycasting S/W인 Conerstone을 사용하였다. 광선 다발 (ray tube)의 수는 10, 반사회수 및 회절 각은 각각 5번 및 120도로 설정하였다. SBR방법은 최종 광선의 반사면에 PO(physical optics) 전류를 입혀, 산란을 계산한다[4].
해석 대상의 표면은 완전도체 (PEC, perfect electric conductor)이고, 주파수는 C-band 및 X-band를 고려하였다. 편파는 HH (horizontal to horizontal)로 설정한다. 관측 각도는 주어진 φ에 대해 θ를 0° 에서 180° 까지 1도 간격으로 변화한다. 그림 1은 해석 좌표를 보여준다.
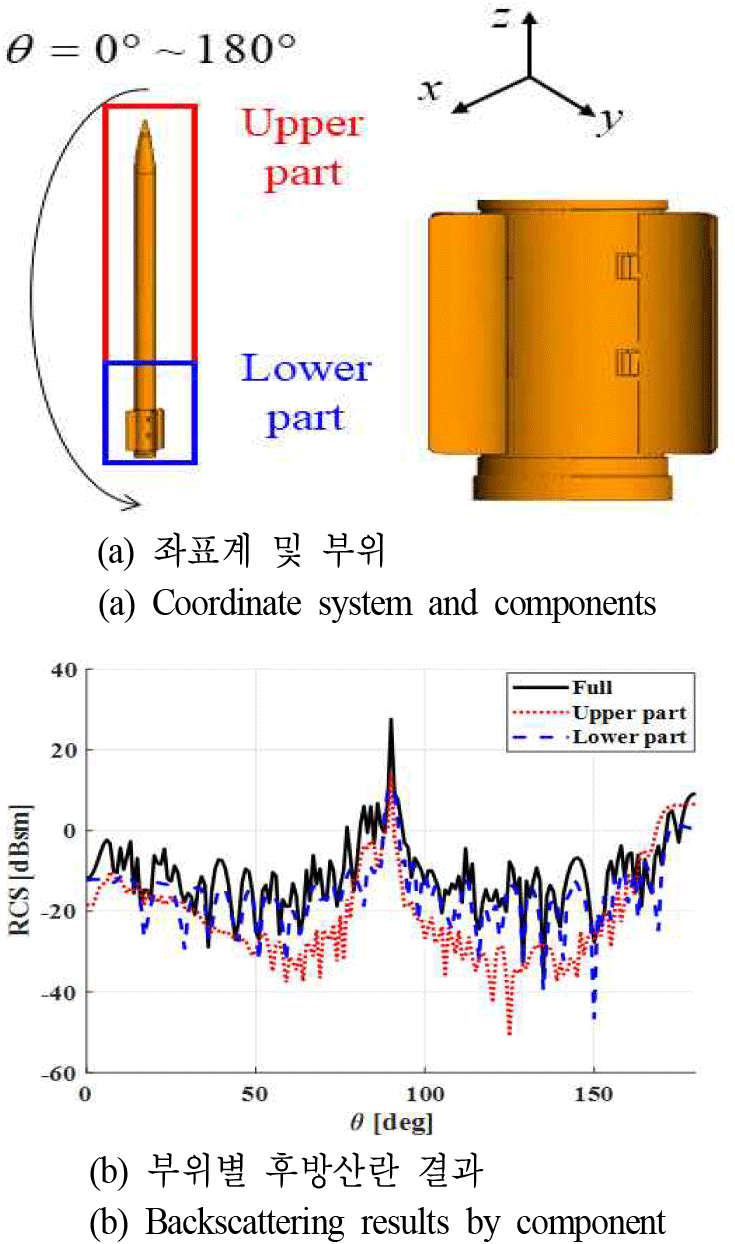
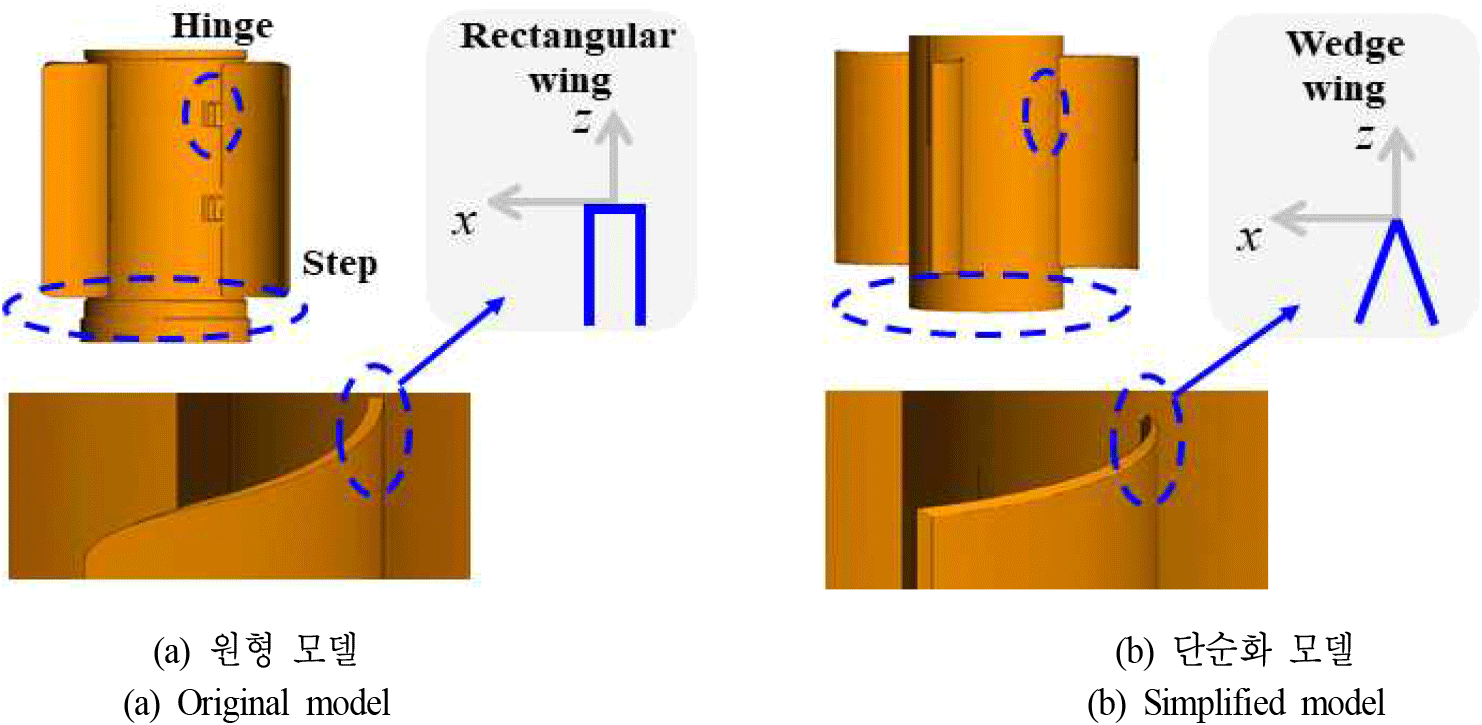
단순화 모델의 부위를 정하기 위해 먼저 그림 1(a)와 같이 두 분의 산란을 따로 계산한다. 해석 대상인 122 mm 로켓의 전체 길이는 2.875 m이고, 4개의 날개, 경첩 및 단차(step discontinuity)가 존재한다. 표적을 탄두부 (upper part)와 하부 구조 (lower part)를 분리하여 각각에 대한 가중치 0.2인 CFIE MoM 해석을 비교하였다. 그림 1(b)는 각 부위와 전체 형상에 φ0°에 대한 후방산란을 비교한 것으로, 대부분의 영역에서 하부 구조에 의한 산란이 주요함을 확인할 수 있다. 그러므로 하부 구조의 형상을 계산 효율성과 해석 정확도라는 두 가지 측면으로 비교하였다. 먼저 경첩과 같은 미소 형상은 전체 RCS에 미치는 영향이 미미한 반면, 세부 형상 표현을 위한 메쉬(mesh) 증가로 계산 시간을 증가시킨다. 반면 RCS 해석 정확도에 큰 영향을 미치는 날개는 기존 직각 형상에서 UTD(uniform theory of diffraction)이 유도된 쐐기 형상으로 바꾼다. 표 1은 원형(original) 형상과 단순화 형상의 비교이고 그림 2는 자세한 형상 차이를 보여준다.
| Original | Simplified | |
|---|---|---|
| Hinge | O | X |
| Step | O | X |
| Wing Shape | Rectangular | Wedge |
| # of Mesh | 160,038 | 147,966 |
| MoM time | 18 h | 5 h |
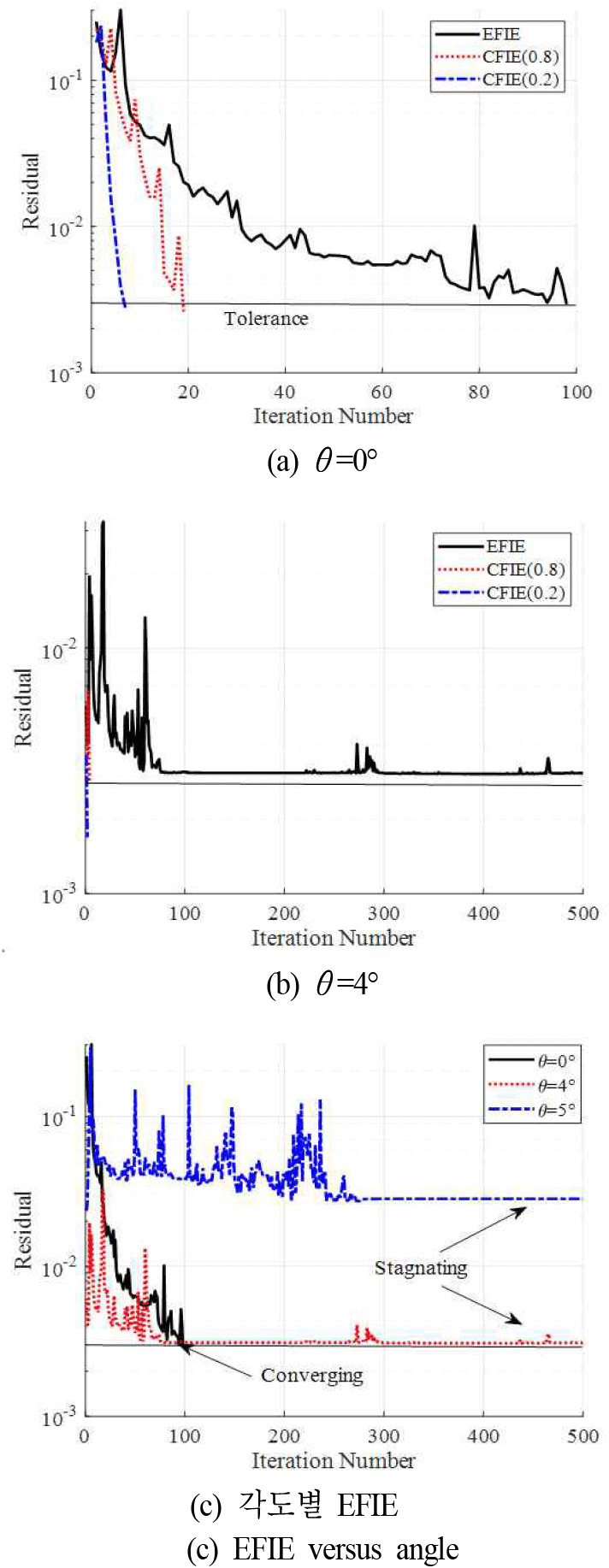
먼저 MoM 방법의 정확도를 비교한다. 즉, EFIE와 가중치 0.2 및 0.8을 사용하는 CFIE, 세 가지 방법의 결과를 비교하였다. 먼저 단순화하지 않은 원형 형상을 고려한다. 그림 3은 EFIE와 가중치 0.2 및 0.8로 설정된 CFIE의 수렴 특성을 보여준다. CFIE는 가중치에 상관없이 모든 각도에서 수렴하여 해석이 완료되었으나, EFIE는 θ=4°부터 수렴하지 않았다. 그림 3(a) 및 그림 3(b)는 φ=0°일 때, θ=0°와 4°의 MoM 해석의 잔차를 보여준다. θ=0°에서 EFIE는 수렴하는 데 반해 θ=4°에서는 잔차가 감소 후 일정 수준에서 정체되는 양상이 보인다. 그림 3(c)는 EFIE의 세 각도별 수렴 추이를 보여주며, 5°인 경우 상대적으로 높은 수준에서 잔차가 정체되었다. 또, 그림 3(a) 및 그림 3(b)에서 CFIE의 가중치 0.2가 0.8보다 빠르게 수렴하는 것을 확인할 수 있다.
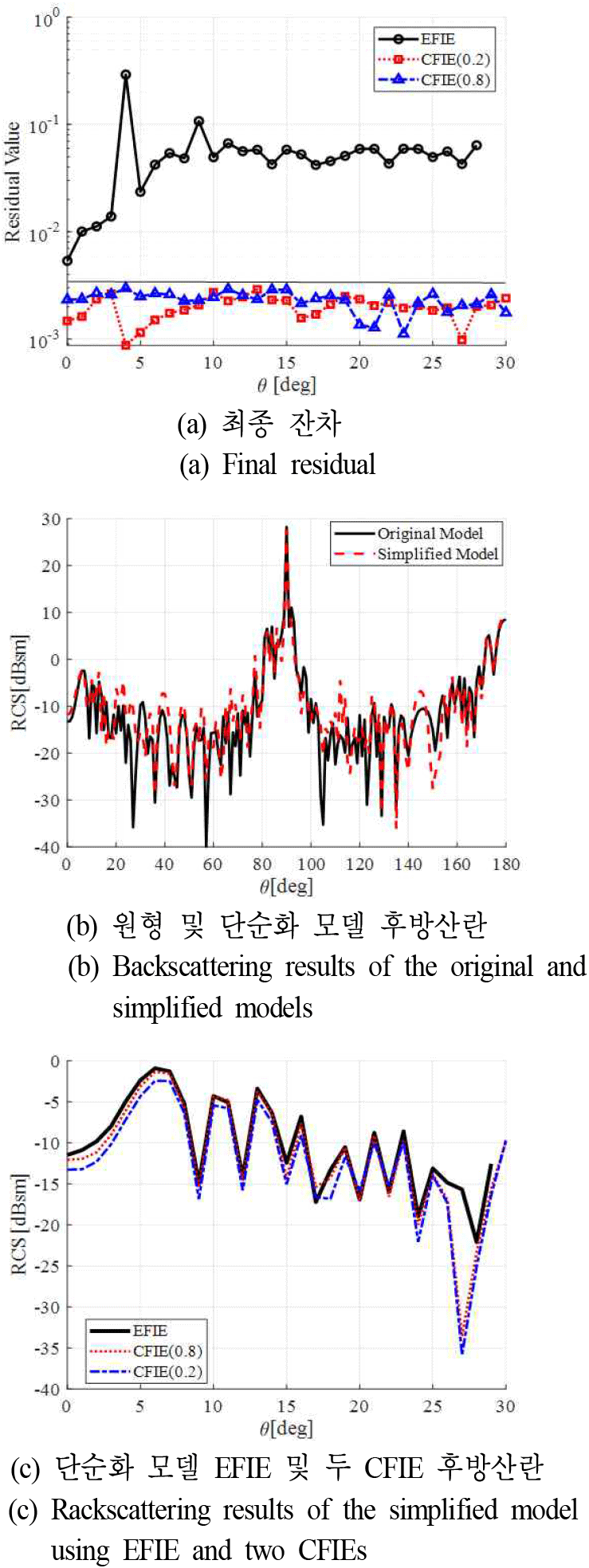
EFIE해석의 어려움이 원형 모델이 포함하고 있는 단차, 경첩 등 작은 구조에 의해 발생하는지를 확인하기 위해, 단순화를 진행한 모델의 해석 결과를 그림 4가 보인다. 먼저 해석이 끝난 후 최종 잔차의 값을 그림 4(a)가 보여준다. EFIE MoM의 잔차는 많이 줄어들었으나, 이 경우에도 수렴을 못 하였다. 그러므로. EFIE MoM은 두 CAD 모델에 사용할 수 없어, 본 연구에는 가중치 0.2 CFIE MoM을 사용한다. 원형 및 단순화 모델의 후방산란를 비교하기 위해 가중치 0.2 CFIE 결과를 그림 4(b)에 비교하였다. 전체적인 후방산란은 유사한 형태를 보이나, 단순화 형상에서는 일부 관측영역에서 후방산란 값이 감소하는 경향을 보인다. 이는 경첩이나 단차와 같은 작은 세부 구조가 제거되면서, 이의 효과가 줄어든 결과로 해석할 수 있다. 그림 4(c)는 EFIE 해석 결과를 얻은 각도 θ≤29°에서 세 방법의 결과 비교를 보여준다. EFIE MoM의 최종잔차가 크지 않아 전 범위에서 CFIE 결과와 비슷하나, θ=27° 근처에서는 후방산란이 매우 작아 적은 잔차에도 불구하고 EFIE MoM의 에러가 크다.
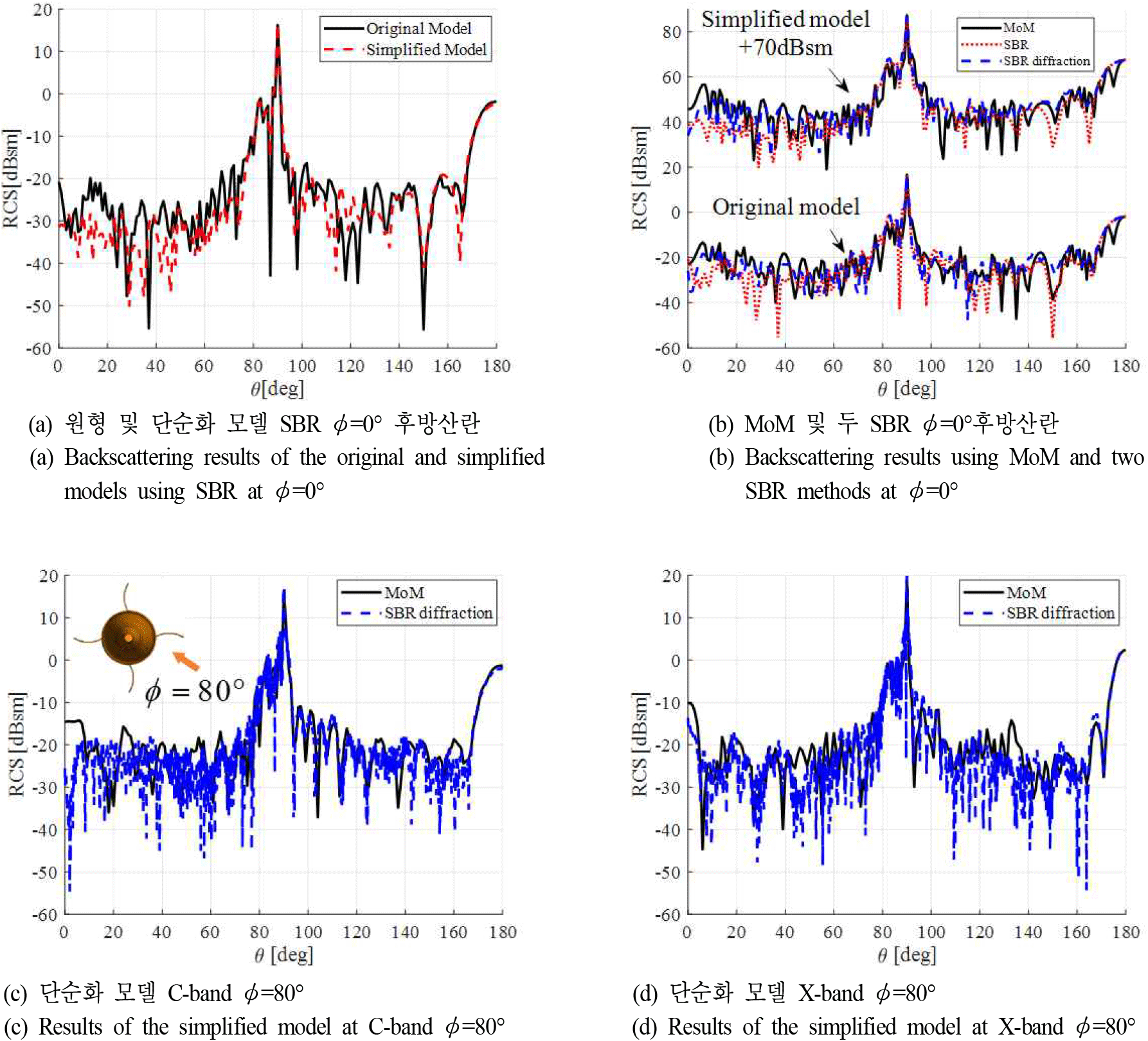
원형 모델과 단순화된 모델에 대해 가중치 0.2 CFIE MoM, SBR 및 회절 보정된 SBR을 사용한 후방산란 결과를 비교하였다. 그림 5는 두 모델에 대한 세 해석 방법의 C-band 및 X-band 후방산란 결과를 보여준다. 그림 5(a)는 원형 및 단순화 형상에 대한 SBR의 결과 비교이다. 탄두 쪽에서 입사하는 저각도 영역(θ=10°~25°)에서 약간의 차이가 존재하나 전체적인 후방산란 패턴은 MoM 해석 대비 크지 않은 것을 볼 수 있다. 그림 5(b)는 φ=0°일 때, 두 모델의 MoM, SBR 및 회절 효과가 적용된 SBR의 후방산란 해석 비교이다. 단순화 모델의 경우 70dBsm을 더하였다. 두 모델 모두 날개의 회절 효과가 SBR 결과에 정확히 반영되지 않아 오차가 존재하나, 날개 부분의 회절 성분을 추가한 SBR 결과는 MoM 결과와 차이를 크게 줄인다. 그림 1(b)에서 보듯이 θ=30°~80°영역에서는 이 회절 효과가 후방산란에 주된 영향이 된다. 마지막으로 그림 5(c) 및 그림 5(d)는 단순화 모델을 사용하여 φ=80°방향에서 C-band와 X-band에서 MoM과 회절을 고려한 SBR의 후방산란 결과이다. C-band에서는 SBR과 MoM 결과 간의 전체적인 패턴은 유사하게 유지되나, 저각도 영역에서 오차가 크게 발생한다. 그러나 X-band에서는 전기적 크기가 커짐에 따라 저각도 포함 전 영역에서 오차가 줄어든 것을 확인할 수 있다.
식 (1)로 정의된 NRMSE(normailized root mean square error)를 사용하여 에러의 수치 비교를 하였다.
식 (1)에서 σMoM,SBR는 각각 MoM과 SBR의 RCS 해석 결과이고, N은 관측점의 수이다. 각 해석 결과의 계산 시간 및 NRMSE는 표 2에 정리되어 있다.
‘SBR w/o D’과 ‘SBR w/ D’는 각각 회절을 고려하지 않은 그리고 고려한 SBR 결과이다.예측했던 데로 회절은 고려한 SBR의 속도는 느려지고, 정확도는 향상됨을 알 수 있다. 예측한 대로 단순화 모델인 경우 원형 모델보다 SBR의 정확도가 향상된다.
III. 결 론
본 연구에서는 로켓의 후방산란을 MoM 및 SBR을 이용해 계산하고 이의 결과를 비교하였다. 전반적인 후방산란에 큰 영향을 주지는 못하나, SBR 결과의 정확도에 영향이 미미한 모델의 작은 형상 예를 들면 경첩이나 단차 등을 제거하고, 또 날개의 형상을 UTD 해석에 맞는 쐐기 모양으로 변경한 단순화 모델과 원형 모델을 이용하여 비교를 수행했다. SBR은 원형 모델 결과보다 단순화 모델을 사용할 경우, 또 날개의 회절성분을 고려하는 경우 정확도가 높아진다. 또, 같은 모델에 대해 주파수가 높아지면 SBR의 정확도는 향상된다. 정확도의 한계에도, MoM에 비해 SBR의 매우 높은 수치 효율로 회절이 고려된 SBR은 큰 해석 대상의 후방산란 해석에 사용할 수 있고, 높은 정확도를 제공할 수 있다.




