Ⅰ. 서 론
최근 스마트 팩토리, 의료, 에너지 등 다양한 산업 분야에서 이음 5G(Private 5G)가 핵심 기술로 부상하고 있으며, 국내에서는 4.7 GHz 대역이 주요 주파수로 활용되고 있다. 이음 5G 네트워크의 안정적인 구축 및 운영을 위해서는 실제 환경에서의 정확한 전파 분석과 이를 시각화하는 전파맵 생성이 필수적이다. 그러나 4.7 GHz 대역에서 실측한 데이터의 특성으로 인해 이론적 모델이나 전통적인 공간 보간 기법인 크리깅(kriging)만으로는 실제 전파 환경을 정확히 반영하기에는 한계가 존재한다. 이러한 전파 환경 예측 정확도 향상을 위해 다양한 선행 연구들이 진행되어 왔다. 특히, 기존 크리깅 기법의 수동적인 베리오그램 파라미터 선택 문제를 개선하고자 SVM을 활용하여 베리오그램을 구현하는 연구는 예측 정확도 향상에 기여한 바 있다[1].
본 연구에서는 상기 명시한 한계를 극복하고 4.7 GHz 이음 5G 실측 데이터를 기반으로 보다 정확한 전파맵을 생성하기 위해 딥러닝과 잔차 크리깅(residual kriging)을 융합한 새로운 기법을 제안한다. 본 연구의 목표는 제안하는 딥러닝-잔차 크리깅 융합 기법의 전파맵 생성 성능을 평가하고, 기존 기법과의 비교를 통해 그 우수성을 입증하는 것이다. 이를 위한 본 논문의 구성은 다음과 같다. 제Ⅱ장에서 측정 환경 및 시스템을 설명하고, Ⅲ장에서 딥러닝-잔차 크리깅 융합 기법에 대하여 기술한다. Ⅳ장에서는 실측 데이터를 기반으로 한 전파맵 생성 결과 및 분석을 제시하며, 제Ⅴ장에서 결론을 내린다.
Ⅱ. 측정 환경 및 측정 시스템
4.7 GHz 이음 5G 대역의 실제 전파 특성을 파악하고자, 정부세종청사 인근 지역의 건물 밀집 환경에서 전파 데이터 측정을 하였다. 정부청사의 옥상 및 건물 내부에 위치한 기지국의 신호를 인근 도로에서 스펙트럼 분석기를 활용해 도보 및 차량으로 측정하였으며, 측정 지점들은 그림 1(a)에 나타내었다.
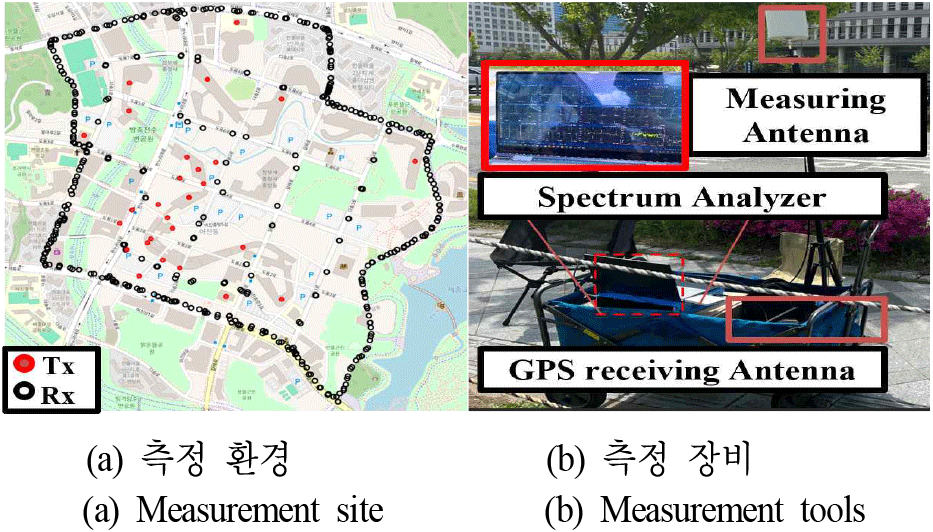
그림 1(b)는 전파 측정 시스템을 보여준다. 이 시스템의 수신부는 전파를 수신하는 측정 안테나, 측정 위치를 기록하는 GPS 수신 안테나, 그리고 수신된 전파를 분석하는 스펙트럼 분석기로 구성된다.
측정 안테나는 400 MHz~8 GHz까지의 주파수 대역에서 신호를 수신할 수 있으며, GPS 수신 안테나를 함께 사용해 각 측정 위치의 위도와 경도 데이터를 확보했다. 본 측정은 도보 및 차량 기반으로 측정하였으며, 총 407개의 지점에서 peak level을 측정하도록 설계하였다.
Ⅲ. 딥러닝-잔차 크리깅 융합 기법
베리오그램(variogram)은 공간 데이터의 공간적 자기상관성(spatial autocorrelation) 구조를 정량적으로 분석하는 핵심 도구이다. 이는 특정 거리에 위치한 두 지점에서의 자료 값 차이의 제곱에 대한 기댓값으로 정의되며, 거리가 증가함에 따라 공간적 비유사성 또는 변동성이 어떻게 변화하는지를 보여준다. 관측된 공간 데이터로부터 각 자료의 위치 정보를 활용하여 자료 값들 간의 거리에 따른 경험적 베리오그램(experimental variogram)이 식 (1)에 따라 계산된다.
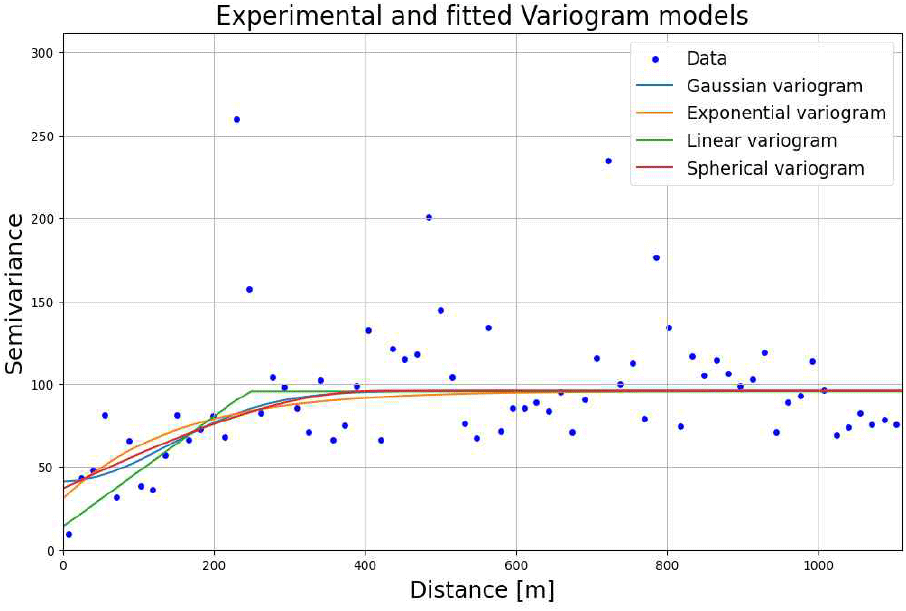
계산한 경험적 베리오그램을 기반으로 자료의 공간적 자기상관 구조를 이상적으로 표현하는 이론적 베리오그램(theoretical variogam) 모델을 적합(fitting)시킨다. 이론적 모델은 비교적 간단한 수식으로 표현되며, 경험적 베리오그램의 경향을 잘 반영하는 적절한 모델을 선택하는 것이 최종 크리깅 보간 결과의 정확도에 결정적인 영향을 미친다. 모델 적합 과정에서는 자료 값들 간의 거리와 베리오그램 값의 관계로부터 모델의 매개변수(nugget, sill, range)를 결정한다. Nugget은 거리가 0일 때의 베리오그램 값으로, 측정 오차나 관측 최소 거리보다 짧은 거리에서의 공간적 변동성을 나타낸다. Range는 베리오그램이 sill에 도달하는 거리로, 이 거리 이상에서는 공간적 자기 상관성이 거의 없다고 간주된다. Sill은 베리오그램 값이 더 이상 증가하지 않고 수평을 이루는 값으로, nugget과 partial sill(sill - nugget)의 합으로 표현되기도 한다. 그림 2는 계산된 경험적 베리오그램과 적합된 이론적 베리오그램 모델을 함께 제시하여, 자료의 공간적 구조 모델링 결과를 시각적으로 보여준다. 이론적 베리오그램의 수학적 수식은 식 (2)~식 (5)에 제시되어 있다. 각각 선형 모델, 구형 모델, 지수 모델, 가우시안 모델로 나타낸다.
크리깅은 공간적 분포된 데이터의 예측 및 보간을 위한 지구통계학적 기법이다. 이 방법은 앞서 설명한 정량적으로 모델링된 공간적 자기상관성 정보를 기반으로 관측되지 않은 지점에서의 값을 최적의 선형 비편향 예측(BLUP, best linear unbiased prediction) 방식으로 추정된다. 크리깅 예측 값 은 주변 관측 지점 xi에서의 자료 값 z(xi)들의 가중 선형 합으로 표현되며, 크리깅 예측 값의 일반적인 형태는 식 (6)과 같다.
크리깅은 경향성(trend) 추정 전제 조건과 가중치의 산출법에 따라 심플 크리깅(simple kriging), 정규 크리깅(ordinary kriging), 일반 크리깅(universal kriging)으로 구분된다. 이 중 정규 크리깅은 공간 데이터의 평균이 특정 지역 내에서는 상수로 유지된다는 가정을 기반으로 데이터를 보간한다. 그러나 전자파 측정과 같이 주변 환경(건물 밀집도, 장애물 등)에 따라 신호 감쇠와 같은 뚜렷한 전반적인 경향성이 존재하는 데이터의 경우, 이러한 경향성을 충분히 반영하지 못하여 예측 정확도가 떨어질 수 있다는 한계가 존재한다. 이러한 정규 크리깅의 한계를 효과적으로 보완하기 위해 본 연구에서는 딥러닝 기반 잔차 크리깅(deep learning-based residual kriging) 기법을 제안한다. 이 기법은 데이터에 내재된 비선형적이고 복잡한 전반적인 경향성을 딥러닝 모델이 먼저 학습하고 제거하여 잔차(residual)를 도출한 뒤, 이 잔차에 남아있는 공간적 자기상관성만을 정규 크리깅으로 보간하는 방식으로 동작한다. 딥러닝이 비선형적인 전반적인 경향성을 효과적으로 모델링하고 제거함으로써, 정규 크리깅이 가지는 평균 상수 가정의 제약을 완화하고, 이를 통해 측정 데이터의 특성을 더욱 정밀하게 반영하여 전파맵 생성의 예측 정확도를 크게 향상시킬 수 있다.
DNNRK(deep neural network residual kriging) 기법은 공간 데이터 Z(s)가 결정론적 추세 성분 m(s)과 확률론적 잔차 성분 ϵ(s)의 합으로 구성된다는 가정하에, 각 성분을 모델링하는 데 최적화된 기법을 적용하는 융합적인 접근 방식이다[2].
제안하는 딥러닝은 측정 지점의 경도와 위도를 입력값으로 사용하며, 다수의 은닉층(hidden layer)을 거친 후 단일 뉴런으로 구성된 출력층(output layer)에서 각 측정 지점에서의 peak level 추세 예측 값이 산출된다. 이 모델은 입력 데이터와 peak level 값 사이의 복잡한 비선형적인 상관관계(non-linear correlation)를 학습하여, 거리나 지형, 환경 요소 등 복잡한 전파 감쇠 요인을 효과적으로 반영한다[3].
신경망(neural network) 학습은 adam optimizer가 사용되었으며, 손실 함수(loss function)는 예측 값과 실제 peak level 값 간의 평균 제곱 오차(MSE, mean squared error)를 최소화하도록 설정되었다. 모델은 총 100 epoch 동안 학습이 진행되었으며, 배치 크기(batch size)는 32로 설정하여 효율적이고 안정적인 학습이 이루어지도록 하였다.
학습된 딥러닝 모델로 추세 성분을 예측한 후, 실제 관측된 peak level 값에서 예측된 추세 성분을 감하여 잔차를 계산하였다. 이 잔차는 딥러닝 모델이 포착하지 못한 국소적인 공간적 자기상관성을 포함하고 있다. 따라서 잔차 성분에 대해서는 정규 크리깅을 적용하여 공간 보간을 수행하였다.
크리깅 모델은 잔차 데이터의 공간적 보간성을 분석하고, 가우시안, 선형, 구형, 지수형 등과 같은 다양한 베리오그램 모델 중 최적의 형태를 선택하여 잔차의 분포를 추정한다. 이러한 과정은 딥러닝이 학습한 전역 추세와 크리깅이 보정한 지역적 변동(local correction)을 결합함으로써, 전체 영역에 대한 정밀한 전파 세기 예측이 가능하도록 한다.
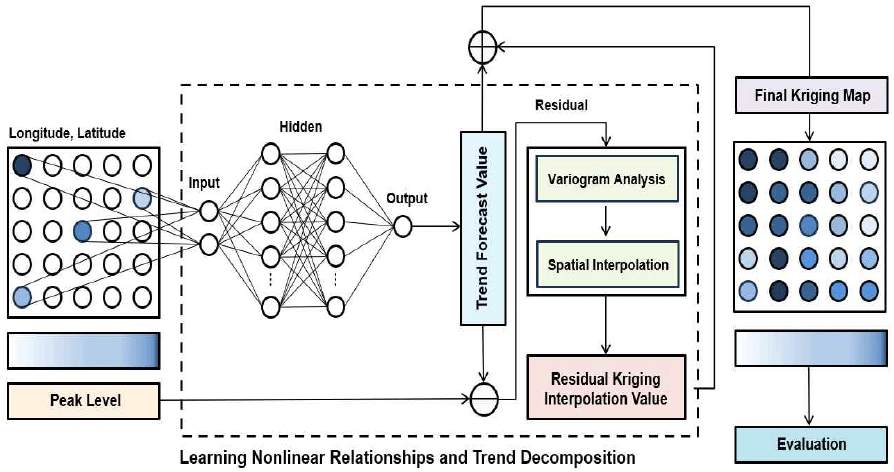
최종적으로 딥러닝 모델이 예측한 peak level 추세 값과 잔차 크리깅으로 보간된 잔차 값을 합산하여 연구 대상 지역의 최종 전파맵을 생성하였다. 그림 3은 제안하는 DNNRK 기반 전파맵 생성 개념도를 나타낸 것으로, 딥러닝 모델이 전역 패턴을 학습하고, 크리깅이 국소적 공간 특성을 보정함으로써 두 방법의 장점을 상호 보완적으로 결합한 구조임을 보여준다.
Ⅳ. 전파맵 생성 결과 및 분석
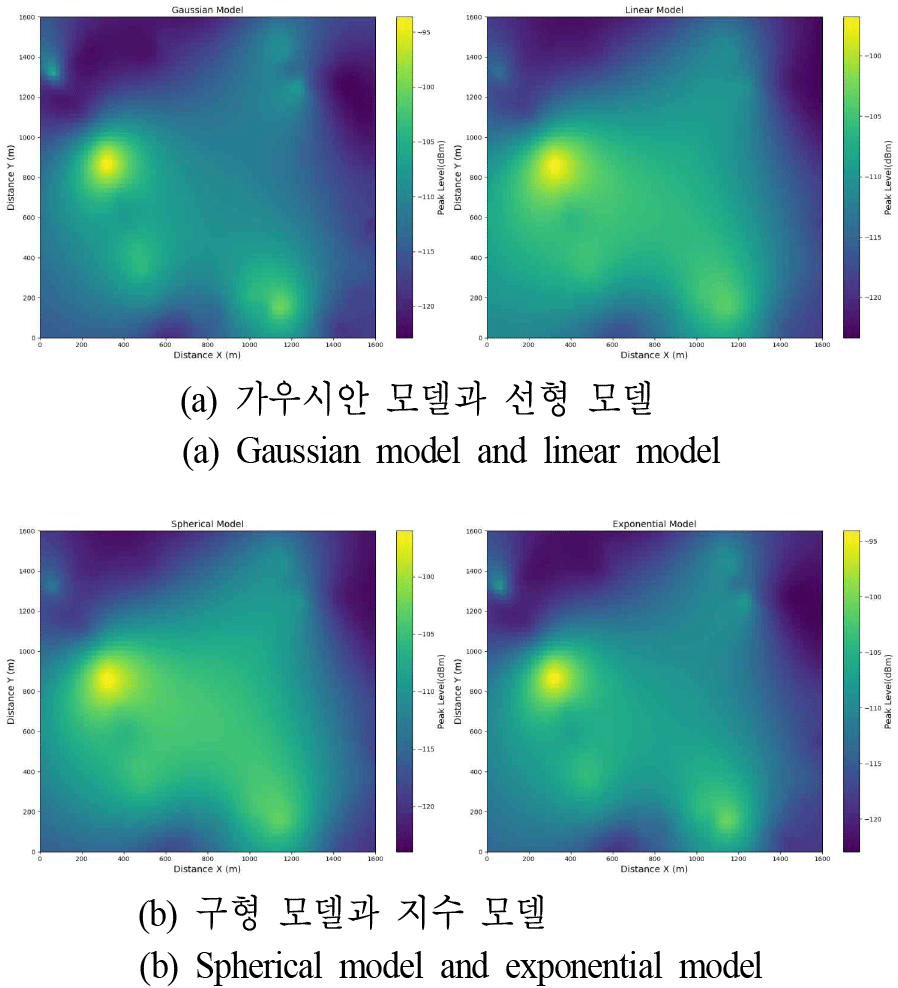
그림 4는 본 연구의 측정 장소에서 수집된 4.7 GHz 이음 5G 신호의 peak level 데이터 공간 분포를 나타내는 동시에 기존 보간 기법인 정규 크리깅을 적용하여 생성된 전파맵 결과를 함께 제시한다. 이는 이후 분석을 위한 기본 데이터셋으로 활용된다. 특히 데이터의 공간적 자기 상관성을 모델링하는 데 사용된 이론적 베리오그램 각각에 대해 생성된 전파맵을 비교 분석함으로써 정규 크리깅이 지니는 평균 정상성 가정의 제약이 복잡하고 비선형적인 공간 경향성을 효과적으로 모델링하기 어렵다는 기존 기법의 한계점, 그리고 모델 선택의 중요성을 시각적으로 보여준다.
생성된 전파맵을 보면, 구형 모델은 일정 거리 이상에서 급격히 평활화(smoothing)되어 전파 세기의 미세 변동이 완화되는 반면, 지수형 모델은 국소적 변화가 상대적으로 뚜렷하게 반영되는 경향을 보인다. 또한 선형 모델의 경우 거리 증가에 따른 감쇠가 단순 비례 관계로 표현되어 실제 관측된 비선형적 감쇠 특성을 충분히 반영하지 못하는 한계를 보여준다. 이러한 비교는 베리오그램 모델의 선택이 전파 세기 예측 결과의 세밀한 공간 패턴과 평활성에 직접적인 영향을 보임을 확인할 수 있다.
각 모델별 전파맵은 동일한 실측 데이터를 사용하였음에도 불구하고, 적용된 변이 함수 모델의 특성에 따라 예측된 peak level 값의 공간적 분포 및 평활성에서 차이를 보임을 확인할 수 있다. 이러한 차이는 정규 크리깅이 실제 환경의 다양한 전파 특성을 반영하는 데 한계가 있으며, 적용된 모델 유형에 따라 결과에 변화가 발생할 수 있음을 시사한다.
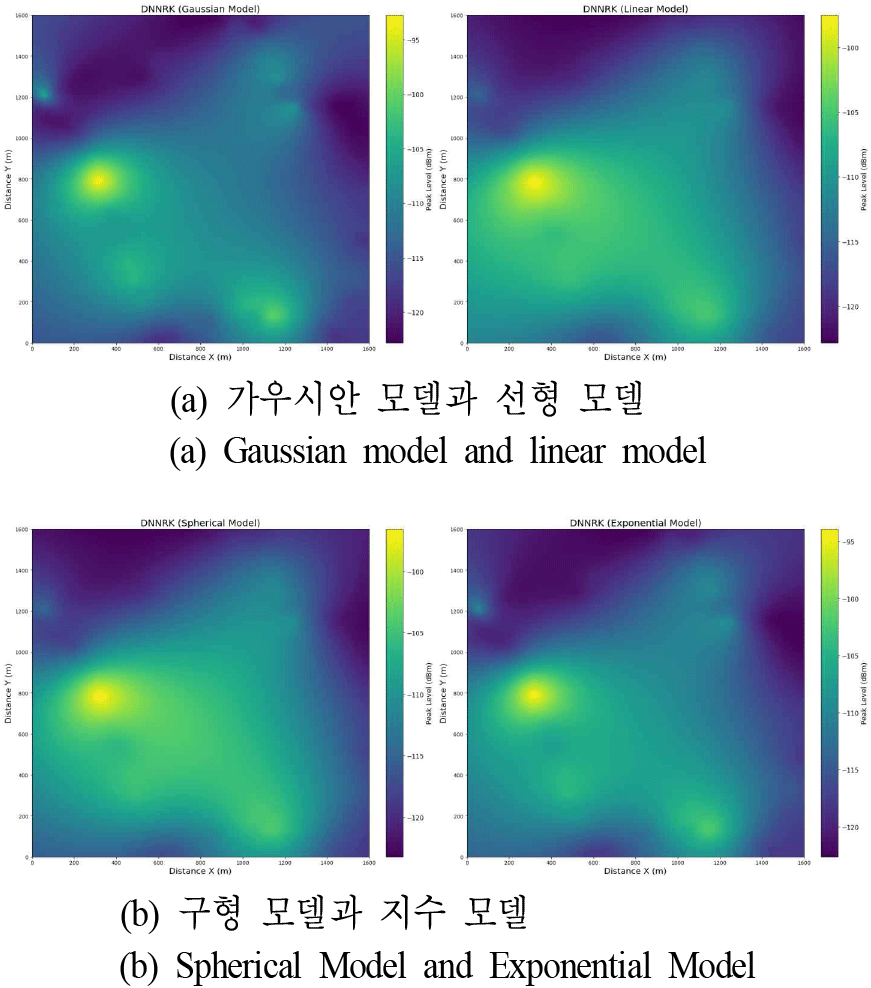
이러한 기존 기법의 한계를 극복하고자, 그림 5는 본 연구에서 제안하는 DNNRK 기법을 적용하여 생성된 전파맵 결과를 제시한다. 그림 4의 정규 크리깅 결과와 비교할 때, DNNRK는 높은 정밀도와 실제 전파 환경의 복잡한 패턴을 사실적으로 반영한 전파맵을 생성하였다. 이는 딥러닝 모델이 입력 변수들 간의 복잡한 비선형 관계를 학습하여 전역적 추세 성분을 효과적으로 예측하고, 잔차 크리깅이 딥러닝이 설명하지 못한 지역적 공간 변동을 보완함으로써, 두 접근법의 장접을 결함한 융함적 예측 모델의 결과이다.
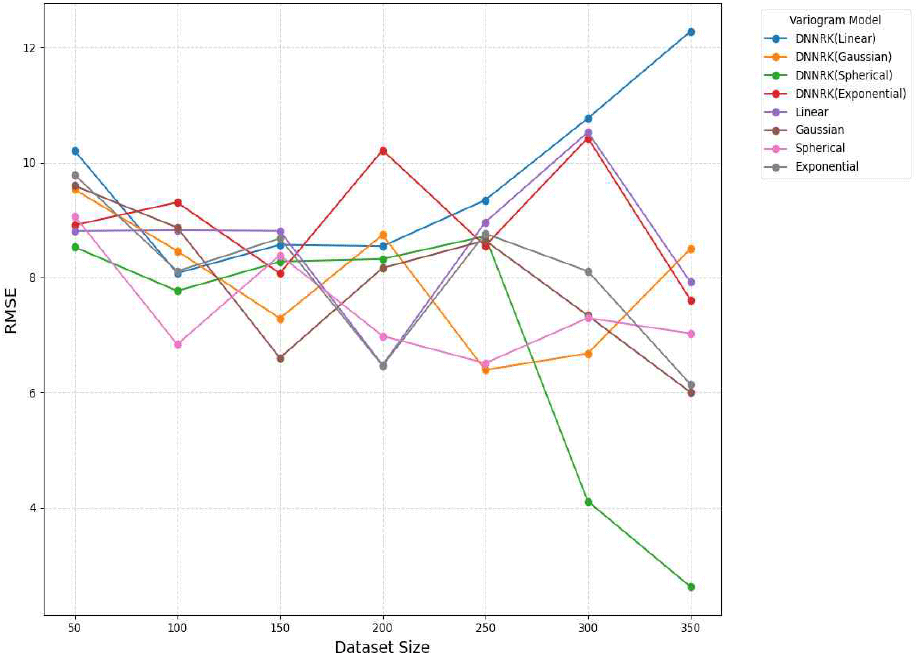
그림 6은 학습 데이터 개수 변화에 따른 기존 크리깅 기법과 제안하는 DNN 기반 잔차 크리깅 기법의 전파맵 예측 정확도(RMSE, root mean squared error) 변화를 비교한 결과이다. 본 연구에서는 모델의 예측 성능을 객관적으로 평가하기 위해 전체 데이터셋에서 다양한 개수의 샘플을 무작위로 추출하여 학습 데이터로 활용하고, 나머지 데이터를 검증 데이터로 사용하여 성능을 반복 측정하는 leave-in-leave-out 교차 검증(cross validation) 방식을 적용하였다.
특히, 학습 데이터 개수를 350개로 설정했을 때, 기존크리깅(구형 모델)의 RMSE는 약 7.0283이었으나, 제안하는 DNNRK(구형 모델)의 RMSE는 약 2.6243으로 낮은 오차를 보였다.
이는 제안하는 기법이 딥러닝의 비선형 추세 학습 능력과 잔차 크리깅의 공간 상관성 보완 능력을 결합한 하이브리드 접근법으로서 기존 기법 대비 우수한 예측 성능을 제공함을 시사한다. 더 나아가, 최근 주목받는 그래프 신경망(GNN, graph neural network) 구조를 도입하면 전파 수신 지점 간의 비정형 공간 관계를 모델링하여 복잡한 도심 환경에서도 보다 정교한 전파 예측이 가능할 것으로 기대된다.