Ⅰ. 서 론
항공기용 펄스 도플러 레이다를 항공기에 적재하고, 레이다 빔을 방사하여 비행시험을 하였다. 이런 비행시험을 통해 획득한 실제 항공기 항법 정보 및 레이다 운용/빔 조향 정보, 레이다 클러터 반사 신호 등의 데이터를 활용하여 지상/해상클러터 반사계수를 계산하는 방법과 항공기 레이다의 모의 지면클러터 신호 생성 모델을 개발하였다. 본 논문에서는 실측 데이터를 이용하여 지상/해상클러터 반사계수의 값을 계산하고, 그 계산 값을 기존 연구의 반사계수 값과 비교한다. 그리고 실측한 지상/해상클러터 신호 획득 결과와 제시한 방법으로 모의한 지상/해상클러터 신호 생성 결과를 비교하여 제시한다. 항공기 항법 및 빔 조향 정보 등을 이용하고, 실제 측정하여 획득한 지면과 안테나 빔 방사 지역의 지형 정보 등을 이용하여 지상과 해상의 클러터를 보다 세밀히 모사하는 모의 지상/해상클러터를 생성하여 보았다. 또한 실제 안테나 패턴 및 레이다 파라메타를 반영하여 제안한 신호 생성 모델이 실제 지면클러터를 잘 모의하도록 하였다. 실제 측정한 지면클러터와 모의 지면클러터와의 유사성 비교를 통해 지면클러터 신호 생성 모델 파라메타의 적절성 및 본 논문에서 제시한 지면클러터를 모사하는 지면클러터 신호 생성 모델의 유효성을 확인하였다.
Ⅱ. 지면클러터 분석/모의를 위한 비행시험 데이터
지상/해상클러터 획득을 위한 비행시험 환경은 펄스 도플러 레이다를 항공기에 설치하고, 안테나 송신 신호를 방사하여 지상/해상클러터 신호 및 항공기 항법 및 레이다 운용 정보를 획득하는 시험을 하였다. 실제 획득한 지면클러터의 반사계수 계산과 지면클러터 모의를 위해서는 항공기 및 레이다 측면에서 항공기 플랫폼의 NED (north, east, down) 속도, LLA(latitude, longitude, altitude) 위치, RPY(roll, pitch, yaw) 자세 등의 항공기 항법 정보와 항법장치대비 항공기 내에서 레이다가 설치된 위치 정보, 레이다 시스템 파라메타(전송주파수, 전송전력, 안테나 패턴 정보 등), 레이다 운용 PRI(pulse repetition interval)와 파형 정보, 레이다 안테나의 빔 조향 방향 정보 등이 필요하다. 이 외에 빔을 방사하고 비행한 지역의 지면 정보가 필요하다. 지상의 산악, 도로, 논 등의 지형 정보 및 지면 해발고도, 해상의 해상 상태 정보 등이다.
Ⅲ. 비행시험 데이터를 이용한 지면클러터 반사계수 계산 방법과 모의 지면클러터 신호 생성 모델 설계
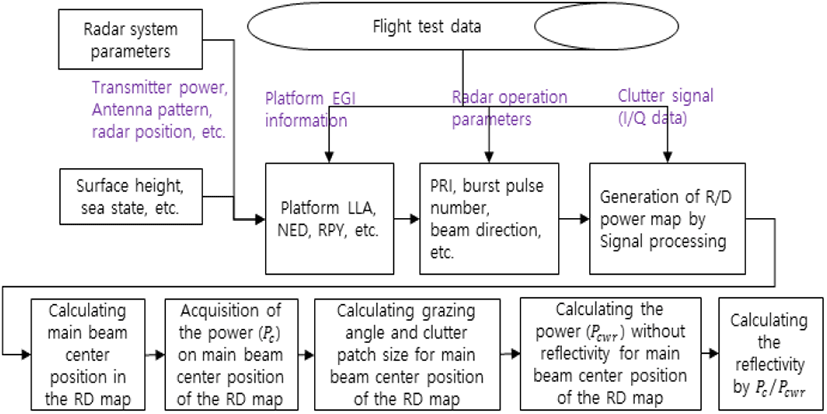
그림 1의 과정으로 비행시험에서 버스트(burst) 단위로 획득한 클러터 신호로부터 지면클러터 반사계수를 계산한다. 그림 1의 과정에서 볼 수 있듯이 비행시험 데이터에서 한 버스트의 RD(Range/Doppler) 맵[1,2]을 구하고(그림 1의 ‘generation of RD power map by signal processing’), 주엽클러터 중심에 해당하는 지점(그림 1의 ‘calculating main beam center position in the RD map’)의 클러터 전력(Pc)을 획득한다(그림 1의 ‘acquisition of the power Pc on main beam center position of the RD map’). 주엽클러터 중심의 클러터 전력 Pc는 식 (1)과 같다.
여기서 GT와 GR은 안테나 빔의 송신과 수신 이득을 나타내며, Rc는 주엽클러터 중심 지면과 안테나 사이의 거리, L은 전력 손실, λ는 전송파장, N는 한 버스트의 펄스수, WPCR는 펄스 압축비, ΔS는 해당 전력의 레이다 클러터 신호를 반사하는 클러터 패치(patch)의 넓이, σ0는 구하고자 하는 클러터 반사계수를 나타낸다. 그리고 CK는 이외에 레이다 신호전력을 결정하는 레이다 시스템의 파라메타 값들을 모두 포함하는 레이다 시스템 상수를 나타낸다. L은 거리 Rc에 해당하는 대기 손실과 신호처리 손실 및 빔 조향에 의한 이득 손실 등을 포함한다. 식 (1)에서 RD 맵의 주엽클러터 중심 지점에 해당하는 지면클러터 반사계수 σ0을 제외한 전력 값은 Pcwr를 나타낸다.
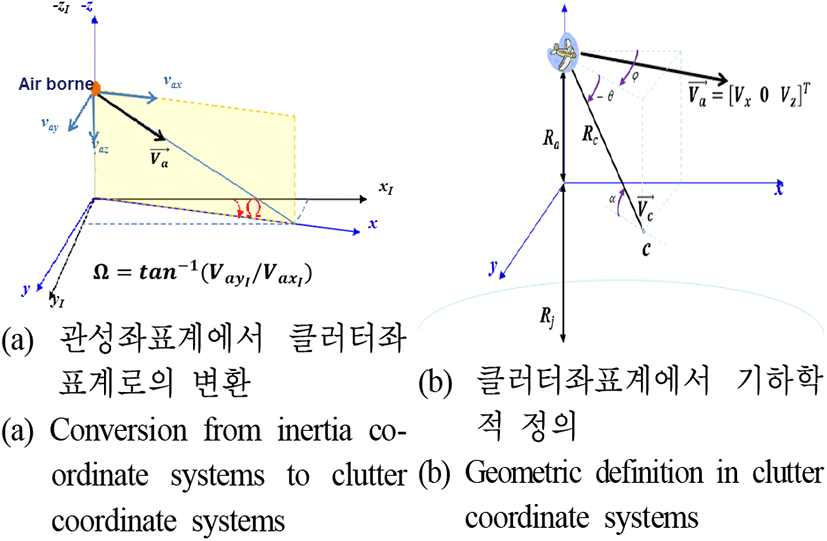
Pcwr의 값은 플랫폼 항법 정보와 빔 조향 방향 정보, 파형 운영 정보 등을 이용하여 계산할 수 있다. Pcwr을 계산한 후 식 (1)에서 σ0=Pc/Pcwr를 이용하여 지면클러터 반사계수 값을 계산한다. Pcwr의 계산을 위한 Rc와 RD 맵에서 주엽클러터 중심 위치 계산 및 주엽클러터 중심 위치에 해당하는 지면 패치의 면적 ΔS의 계산은 참고문헌 [3]을 참고하였다. ΔS 및 Rc 등의 계산의 편의성을 위해 안테나 빔 조향 방향 및 플랫폼의 항법 정보 등을 그림 2(a)와 같이 정의되는 클러터좌표계에서 그림 2(b)와 같이 표현한다[3]. 그림 2(b)에서 는 플랫폼 속도, Ra는 플랫폼 고도, Rj는 지구의 등가반경(effective radius), 지면지점 c는 안테나 주엽빔의 중심이 조향하는 지면지점, −θ는 안테나 빔 조향의 고각, ϕ는 안테나 빔 조향의 방위각, 는 빔 조향 중심 방향의 플랫폼 속도(주엽클러터 중심속도), 그리고 α는 빔 조향 방향(주엽클러터 중심)에 대한 지표각(grazing angle)을 나타낸다. 그림 2(b)와 같은 클러터좌표계에서의 안테나 빔 조향방향 표현(고각 θ, 방위각 ϕ)을 위해서는 안테나좌표계에서의 빔 조향 값을 플랫폼의 RPY 자세 정보를 반영하여 NED좌표계로의 값으로 변환하고, 다시 NED좌표계에서 클러터좌표계로의 값으로의 변환이 필요하다. 빔 조향 고각과 식 (2)로부터 지표각 α 및 거리 Rc를 구할 수 있다[3](그림 1의 ‘Calculating grazing angle and clutter patch size for main beam center position of the RD map’).
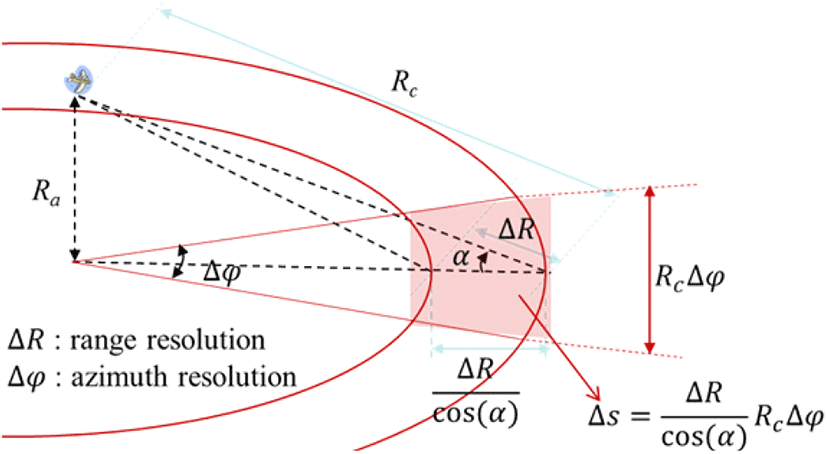
Pcwr의 계산에 필요한 지면 패치의 면적 ΔS의 계산은 한 RD 맵을 형성하는 한 버스트 파형의 거리 해상도와 방위 해상도(파형의 도플러 해상도에 의해 결정됨) 등을 이용하여 이루어진다. 그림 3은 ΔS를 나타낸다[3]. ΔS의 계산을 위한 Δϕ의 계산은 식 (3)으로 이루어진다[3](그림 1의 ‘Calculating grazing angle and clutter patch size for main beam center position of the RD map’).
여기서 Vc는 클러터 패치 방향의 플랫폼 속도 값을 나타내며, Vc=Vx cos(θ)cos(ϕ)-Vz sin(θ)로 구해진다(Vx와 Vz는 그림 2(b)에서 보듯이 플랫폼 속도 의 x축과 z축 성분임). cos(ϕ(Vc))는 앞의 Vc를 구하는 식에서 Vc 변수를 가정하여 cos(ϕ(Vc))=(Vc+Vz sin(θ))/Vx cos(θ) 로 다시 표현한 식이다. Δv는 파형의 속도 해상도를 나타내며, Δv=λΔf/2이다. Δf는 파형의 도플러 해상도를 나타내며, Δf=fPRF/N이다. fPRF는 파형의 PRF(pulse repetition frequency) 값을 나타낸다. 즉, 식 (3)은 RD 맵에서 도플러 쪽의 한 셀에 해당하는 방위 해상도를 파형의 속도 해상도를 이용한 ϕ(Vc-Δv/2)와 ϕ(Vc+Δv/2)와의 차이로 구한 것이다. 다시 말해서 식 (3)의 Δϕ(Vc)는 클러터 패치 방향의 플랫폼 속도가 Vc인 지점에 해당하는 RD 맵의 한 도플러 셀의 방위 해상도를 나타낸다(그림 1의 ‘Calculating the power Pcwr without reflectivity for main beam center position of the RD map’). 비행시험으로 획득한 클러터 신호에 의한 RD 맵과 식 (1), 식 (2), 식 (3), 그리고 Pc/Pcwr을 이용해서 주엽클러터 중심 영역에 해당하는 지면의 지표각 α에 해당하는 지면클러터 반사계수 σ0 (α)를 구할 수 있는 것이다(그림 1의 ‘Calculating the reflectivity by Pc/Pcwr’).
비행시험 데이터에서 확보한 버스트 단위의 항법 정보 및 레이다 운용 정보로 지면 클러터 신호를 모의한다면 앞에서 설명한 그림 2와 그림 3의 기하학적 정의와 식 (2) 및 식 (3)이 그대로 사용될 수 있다[3]. 클러터 신호 모의를 위해 먼저 클러터좌표계에서 관심거리 영역의 지면을 쪼개어 클러터 패치를 형성하고, 그 클러터 패치의 면적과 방향 (ϕ,θ) 및 LLA좌표 위치 값을 저장한다. 클러터 패치를 형성할 때는 거리 해상도와 파형의 도플러 해상도를 고려하여 그림 3과 식 (3) 등을 이용하여 관심거리 영역의 지면을 쪼개어 형성한다. 그리고 클러터 좌표계에서 생성한 클러터 패치의 위치 값은 플랫폼 자세 및 위치 정보를 이용하여 LLA좌표계의 값으로 변환한다. 이렇게 클러터 패치의 위치와 그 면적 정보가 형성되었으면 그 다음으로 플랫폼의 항법 정보와 레이다 운용 정보로 플랫폼 이동과 빔 조향을 모의하여 펄스 단위로 각 클러터 패치에서의 레이다 반사 신호 Cp(t)를 식 (4)와 같이 모의하고, 각 클러터 패치에 대한 모의 신호를 더하여 지면클러터 신호를 모의한다[1],[2].
여기서 는 안테나좌표계 기준 빔 조향 방향 (ϕa,θa)의 정규화된(normalized) 안테나 송신 패턴에서 클러터 패치 방향 (ϕc,θc)에 대한 이득이며, 는 빔 조향 방향 (ϕa,θa)의 정규화된 안테나 수신 패턴에서 클러터 패치 방향 (ϕc,θc)에 대한 이득 값이다. 안테나좌표계 기준 빔 조향 방향 (ϕa,θa)은 비행시험 데이터에서 얻을 수 있으며, 안테나좌표계 기준 클러터 패치의 방향 (ϕc,θc)은 클러터 패치를 형성할 때 저장해둔 클러터좌표계 기준 클러터 패치 방향 정보를 NED좌표계의 값으로 변환하고, 다시 플랫폼의 자세(RPY) 정보를 반영하여 안테나좌표계에서의 값으로 변환하여 구한다. f는 송신주파수, tc는 송신 신호가 안테나에서 출발하여 클러터 패치에서 반사되어 다시 수신되는 시간으로서 tc=2Rc/D이고, 여기의 Rc는 안테나와 클러터 패치사이의 거리로서 식 (2)와 클러터 패치 형성 때 저장해둔 클러터좌표계 기준 클러터 패치 고각 방향 정보를 사용하여 구할 수 있으며, D는 광속도이다. fd는 클러터 패치 방향의 도플러로서 fd=2vc/λ이며, 클러터 패치의 도플러 속도 vc는 다음 과정으로 구한다. 먼저 플랫폼의 ECEF(earth-centered, earth-fixed)좌표 값을 플랫폼 LLA좌표에서 획득하고, 클러터 패치의 LLA좌표 값을 ECEF좌표계 값으로 변환하여 ECEF좌표계에서 플랫폼 기준 클러터 패치 방향으로의 단위 벡터를 계산한다. 이 방향 단위 벡터를 NED좌표계 값으로 변환하고, 플랫폼 NED속도와의 내적을 계산하여 도플러 속력 vc를 구한다. 식 (4)의 Ac의 σ0는 지면클러터 반사계수 값이며, 참고문헌 [4], [5], [6] 및 [7]에서 기술되어 있는 지상과 해상의 여러 반사계수 모델들을 사용할 수 있다. 지면클러터 반사계수 모델 사용을 위해서는 해당 클러터 패치에 대한 지표각을 구해야 하며, 이는 식 (2)를 사용하여 구한다. 식 (4)의 Ac의 Δs는 해당 클러터 패치의 면적이며, Ernd (Δs)는 평균 Δs를 가지는 지수분포의 난수 값이다(exponential random number). 지수분포의 난수 값을 사용한 이유는 클러터신호 크기의 변칙적인 성질을 반영하기 위해서다. 식 (4)의 Ac의 Urnd는 0과 1 사이의 균일분포 난수 값이며(uniformly distributed random number), 를 사용한 이유는 클러터신호 위상의 변칙적인 성질을 반영하기 위해서다. ∏(t-tc)는 송신 펄스 파형의 포락선(envelope) ∏(t)의 tc 만큼의 시간지연을 나타낸다.
Ⅳ. 지면클러터 반사계수 계산 결과 및 모의 지면클러터 신호 생성 결과
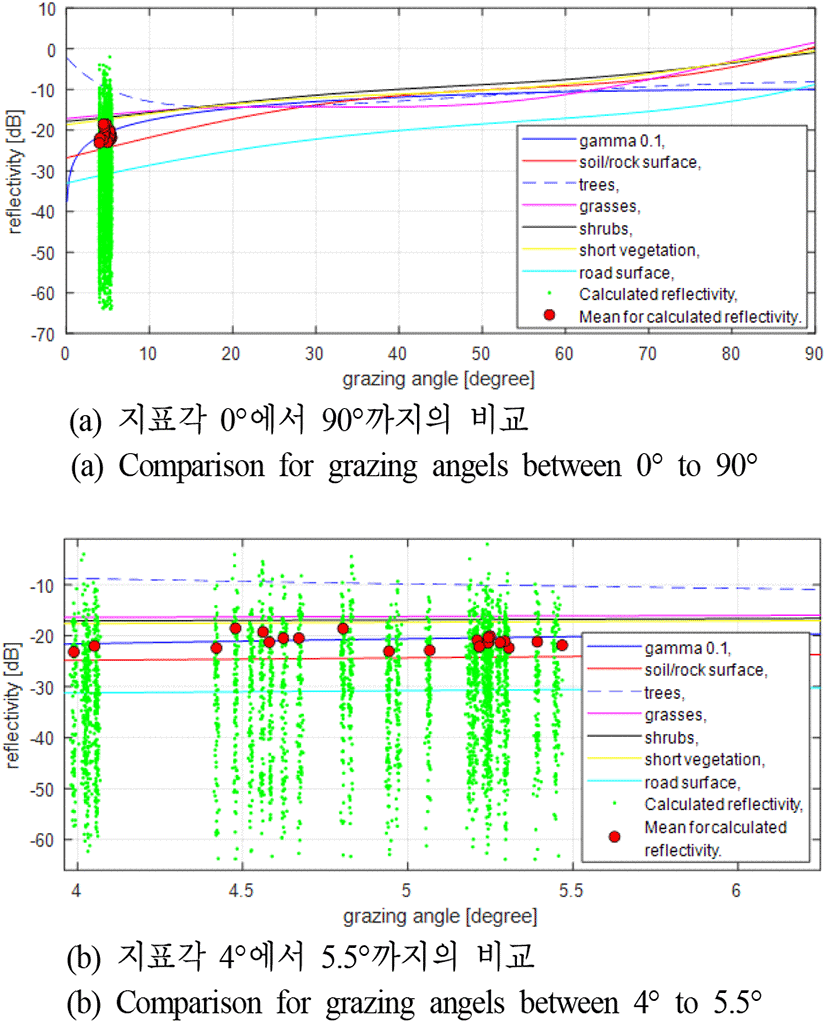
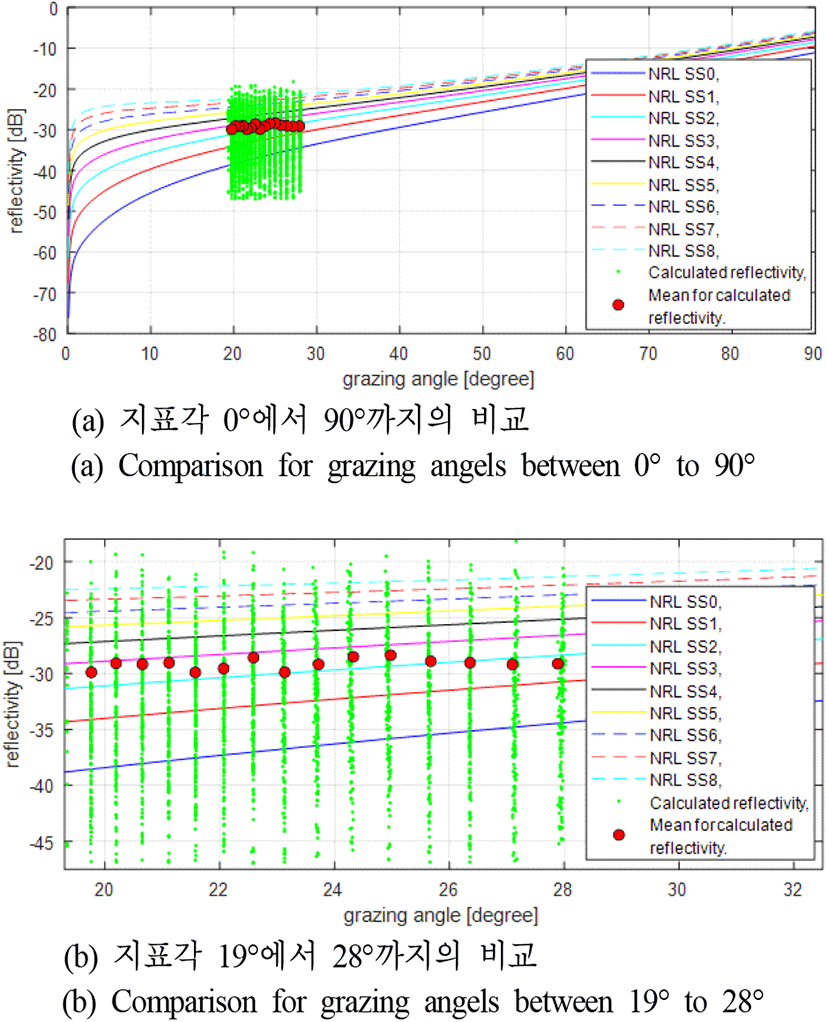
본 논문에서 기술한 방법으로 지면클러터 반사계수를 구해 보았다. 지상 지역의 비행 데이터와 클러터 신호를 수집하기 위하여 지상 지역을 비행하면서 빔을 평지의 흙 및 도로 등이 있는 영역에 조향하였다. 그림 4는 수집한 비행시험 데이터를 이용하여 계산한 지상클러터 반사계수 값을 나타낸다. 그림 4(a)의 그림은 지표각 0°에서 90°까지 여러 지상클러터 반사계수 모델[4],[5],[7]에서의 값과 계산한 지상클러터 값을 비교한 것이다(그림 4에서 gamma 0.1은 constant gamma 모델에서 gamma 값을 0.1로 사용한 모델이다). 그림 4(b)의 그림은 그림 4(a)에서 지표각 약 4°에서 5.5° 영역을 확대한 그림이다. 비록 제한된 비행시험 데이터와 지표각에서 계산한 값이지만 그림 4에서 보듯이 계산한 지상클러터 반사계수 값은 soil/rock surface 또는 constant gamma 0.1 모델과 유사하다. 빔 조향 방향이 평지의 흙 및 도로 등이 있는 영역인 것을 고려하면 유효한 결과를 얻은 것을 알 수 있다. 해상지역의 비행시험 데이터와 클러터 신호를 수집하기 위하여 해상지역을 비행하면서 빔을 해상영역에 조향하였다. 한국기상청 기상자료개방포털(https://data.kma.go.kr)에서 해상상태 정보를 수집하여 해상 비행시험 지역의 비행시험 때의 해상상태가 해상상태 2(sea state 2) 또는 3 정도임을 알 수 있었다[5]. 그림 5는 수집한 비행시험 데이터를 이용하여 계산한 해상클러터 반사계수 값을 나타낸다. 그림 5(a)의 그림은 지표각 0°에서 90°까지 해상에 관한 NRL(naval research lab.) 해상클러터 반사계수 모델[6]에서의 값과 계산한 해상클러터 값을 비교한 것이다(NRL SS0는 해상상태 0 모델, NRL SS1은 해상상태 1모델 등을 나타낸다). 그림 5(b)의 그림은 그림 5(a)에서 지표각 약 19°에서 28° 영역을 확대한 그림이다. 비록 제한된 비행시험 데이터와 지표각에서 계산한 값이지만 그림 5에서 보듯이 계산한 해상클러터 반사계수 값은 NRL SS2 또는 NRL SS3 모델과 유사하다. 해상 클러터 수집 당시의 해상상태 정보를 고려하면 유효한 결과를 얻은 것을 알 수 있다.
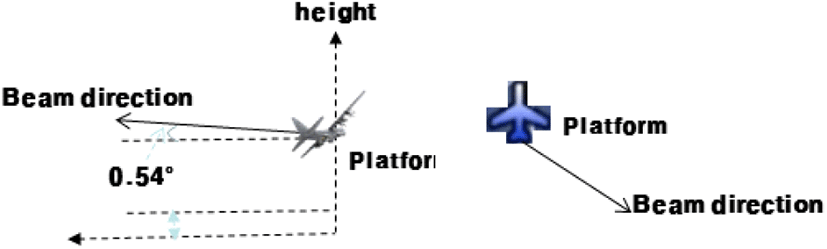
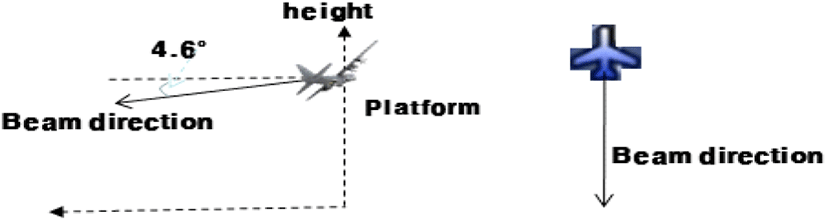
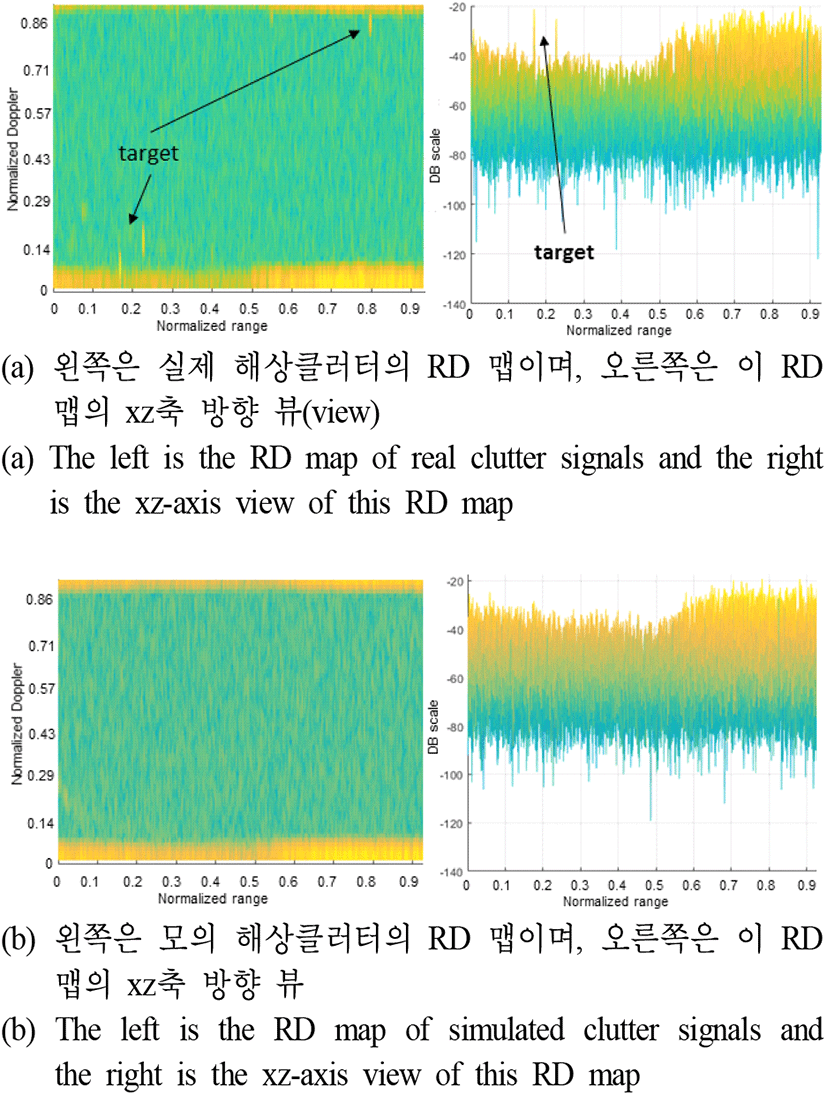
본 논문에서 기술한 방법으로 모의 지면클러터 신호를 생성해 보았다. 그림 6은 지상지역의 시험 데이터를 획득하기 위해 비행한 시나리오를 보인다. 지면클러터 신호 모의는 한 버스트 단위로 수행하였으며, 시나리오는 그림 6에서 보듯이 도로 및 논/밭이 있는 지역 위의 특정 해발고도에서 특정 비행 속도로 비행하면서 산악지역 쪽으로 안테나 빔을 고각 0.54°로 하여 조금 위의 방향으로 조향했다(안테나 빔 조향 방위각은 약 60°). 그리고 비행지역의 지상의 해발고도는 약 100 m 정도였다. 그림 7에서는 그림 6의 시험 데이터로 한 버스트의 지상클러터 신호를 모의하여(식 (4)로서 지상클러터 신호를 모의하고, 레이다 시스템 파라메타를 반영한 잡음 신호도 모의하여 합하였다.) RD 맵을 형성하고 해당 비행시험 데이터의 지상클러터 신호로 RD 맵을 형성한 것과 비교하였다. 그림 7(b)의 지상지역 지상클러터 모의에서 constant gamma 0.1의 반사계수 모델(그림 4 참고)을 사용하였다. 그림 7의 비교에서 보듯이 제안한 모의 지면클러터 신호 생성 모델의 유효성을 확인할 수 있다. 그림 8은 해상지역의 비행시험 데이터를 획득하기 위해 비행한 시나리오를 보인다. 한국기상청 기상자료개방포털에서 해상상태 정보를 수집하여 그림 8의 시험 지역의 시험 때의 해상상태가 해상상태 2 정도임을 알 수 있었다[5]. 해상클러터 신호 모의는 한 버스트 단위로 행하였으며, 시나리오는 그림 8에서 보듯이 해상 위의 특정고도에서 특정속도로 비행하면서 해상지역 쪽으로 안테나 빔을 고각 −4.6°로 하여 아래 방향으로 조향했다(안테나 빔 조향 방위각은 약 0°). 그림 9에서는 그림 8의 비행시험 데이터로 한 버스트의 해상클러터 신호를 모의하여(식 (4)로서 해상클러터 신호를 모의하고 레이다 시스템 파라메타를 반영한 잡음 신호도 모의하여 합하였다.) RD 맵을 형성하고 해당 비행시험 데이터의 해상클러터 신호로 RD 맵을 형성한 것과 비교하였다. 그림 9(b)의 해상지역 지면클러터 모의에서 NRL SS2의 반사계수 모델(그림 5 참고)을 사용하였다. 그림 9(a)의 RD 맵에는 기회표적이 보이고 있다.
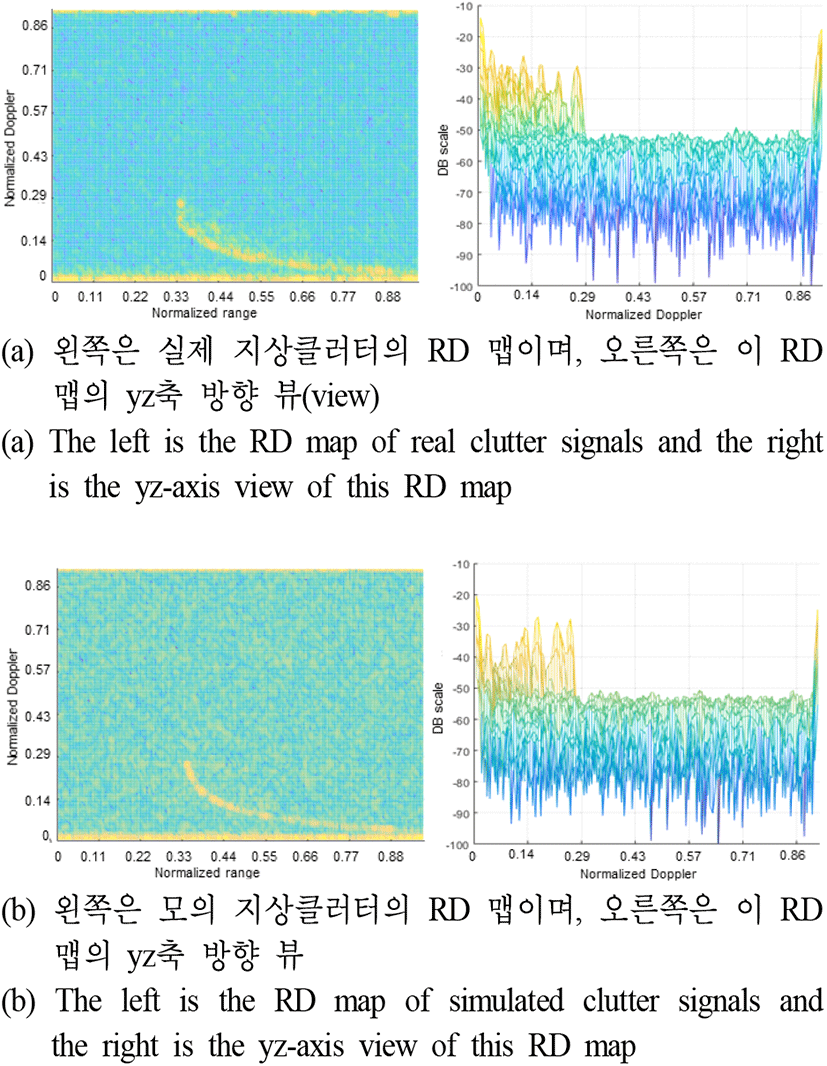
이것은 그림 8의 비행시험 때에 어선 등의 표적이 탐지된 것이며, 그림 8의 비행시험 데이터로 해상클러터 신호를 모의할 때 표적신호는 모의하지 않았다. 그림 9의 비교에서 보듯이 제안한 모의 지면클러터 신호 생성 모델의 유효성을 확인할 수 있다.
Ⅴ. 결 론
항공기 레이다를 이용한 지면클러터 반사계수를 계산하는 방법과 항공기 레이다의 모의 지면클러터 신호를 생성하는 모델을 제시하였다. 항공기 레이다를 항공기에 적재하고 빔을 방사한 비행시험을 통해 획득한 실제 항공기 항법 정보 및 레이다 빔 조향 정보, 지면클러터 신호 등을 이용하여 실제 지형의 지면클러터 반사계수를 구해보았다. 또한 지면클러터 신호를 모의해 보았다. 기존연구의 지면클러터 반사계수 모델과의 비교를 통해 제안한 지면클러터 반사계수 계산 방법의 유효성을 확인하였다. 또한 실제 지면클러터 신호에 대한 RD 맵과 모의 지면클러터 신호에 대한 RD 맵의 비교를 통해 제안한 항공기 레이다의 모의 지면클러터 신호 생성 모델의 유효성을 확인하였다.