해수면 같은 임피던스 평면 위의 다이아딕 그린함수에 관한 효율적 원거리 근사공식 선택 기준

Ⅰ. 서 론

지표면 위에 존재하는 산란체의 산란특성을 예측하기 위해서는 지표면의 효과는 매우 중요하다. 특히, 해수면과 같이 거친 지표면에 관하여 MoM(Method of Moment) 등의 수치해석 기법을 사용하여 산란 효과를 계산하는 경우, 거친 지표면을 모두 차분화해야 한다. 이 경우, 고려해야 하는 지표면의 크기가 매우 커 수치방법을 적용하기 어렵다. 거친 지표면을 고려하는 현실적인 방법은 거친 지표면을 매끈한 지표면으로 변환하여 매끈한 지표면의 다이아딕 그린함수(dyadic Green’s function)를 사용하여 MoM 방법의 복잡도를 낮추는 방법이다. 이 경우, 지표면 반사 특성만 고려할 수 있으나, 지표면 효과를 고려하는 four-ray 모델과 같은 경우도 반사특성만 고려하므로 정확도를 어느 정도 보장할 수 있다. 일반적으로 거친 지표면을 매끈한 지표면으로 변환하는 방법으로 임피던스 근사법을 많이 사용한다^[1].

임피던스 근사법을 사용할 경우, 다이아딕 그린함수의 효율적 계산 공식(exact image 공식)이 알려져 있어, MoM 행렬 계산을 높은 정확도로 계산할 수 있다^[2]. 일반적인 유전체 반 공간인 경우 필요적분 계산이 매우 복잡하다 ^[3]～^[5]. 그러나 exact image 공식도 적분이 포함되어 있어, MoM 행렬 계산 시 다중 적분 계산이 필요해 복잡도가 매우 높다. 이 적분의 효율적인 원거리 근사공식(far-filed approximation)은 두 특수 다항식, 르장드르(Legendre)와 라게르(Laguerre) 다항식을 이용하여 표현이 가능하다^[6],^[7]. 이 근사공식의 정확도는 가까운 거리에서도 매우 높다. 그러므로 MoM 행렬 계산에 이 두 다항식을 사용하면 계산량이 적은 MoM 행렬 공식을 얻을 수 있다. 그러나 두 다항식이 적용 가능한 조건이 명확하게 알려져 있지 않아, 본 논문에서는 관측점과 소스 사이의 상대적 위치, 표면 임피던스 등 중요 파라미터를 바탕으로 두 다항식의 적용 범위를 제안한다.

Ⅱ장에서는 좀머펠트 적분의 두 가지 원거리 근사공식을 서술하고, Ⅲ장에서는 그 정량적 경계조건을 유도한다. Ⅳ장에서는 좀머펠트 적분의 고차 편도함수의 간략화된 수식을 제안한다. 그리고 Ⅴ장에서는 시뮬레이션 결과를 바탕으로 제안된 기준/수식 등을 검증한다. e^−jwt를 가정한다.

Ⅱ. 두 가지 원거리 근사공식

그림 1과 같이, η = Z₁/Z₀의 정규화된 임피던스를 갖는 평면상에서 $\widehat{l}$방향으로 I가 흐르는 미소 다이폴 안테나에 의한 전계 $\overrightarrow{E^t}$는 다음과 같이 표현된다^[2],^[6],^[7].

그림 1. | Fig. 1. 임피던스 평면상의 소스와 관측점 | Source and observation over impedance plane.

Download Original Figure

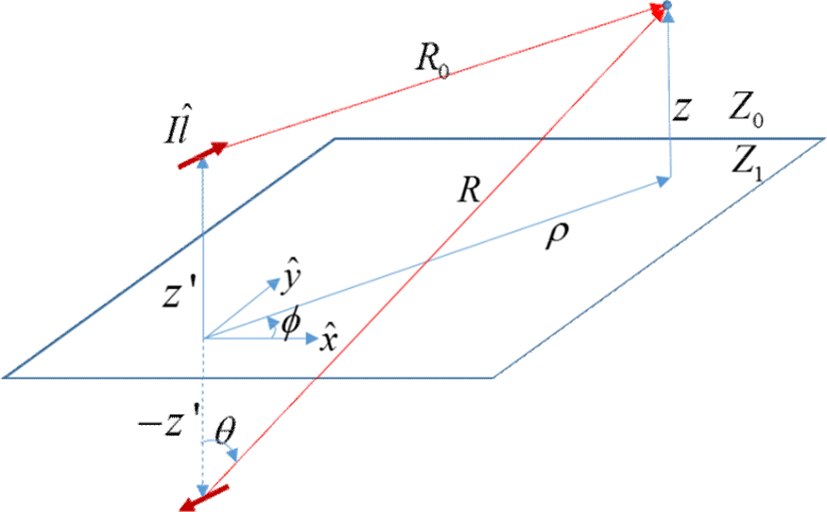
여기서 $\overrightarrow{E^i}$와 $\overrightarrow{E^{is}}$는 자유공간에서 각각 미소 다이폴과 그의 영상전하에 의한 전계이고, $\overleftrightarrow{G}$는 임피던스 평면에 의한 회절파를 나타내는 다이아딕 함수이다^[2]. $\overleftrightarrow{G}$는 좀머펠트 적분 f(q)에 관한 식으로 표현되며, f(q)는 다음과 같이 표현된다^[6].

여기서 $R\prime =\sqrt{{\left(x-x\prime \right)}^2+{\left(y-y\prime \right)}^2+{\left(z+z\prime +j\xi \right)}^2}$이고, R₀와 R은 각각 소스 또는 그의 영상전하와 관측점 사이의 거리를 나타낸다. J₀(·)은 0차 베셀함수이고, q는 k₀η 또는 k₀/η이다. 식 (2)의 마지막 적분 부분을 I(q)로 표현하면, 이의 점근급수(asymptotic series)는 다음과 같이 알려져 있다^[6],^[7].

여기서 P_m(·)과 L_m(·)은 m차 르장드르와 라게르 다항식을, α와 β는 각각 α = (j/2)(k₀-q)(R-z-z′), β =−(j/2)(k₀+q)(R+z+z′)이다. 위 두 수식은 거리가 멀수록(R ≫ 1) 결과의 정확도가 높아진다. 식 (3)은 분모의 |α+β| = |k₀(z+z′)+qR|이 매우 큰 경우에 정확하다. 그러므로 전자기파가 임피던스 평면 가까이 전파할 경우(z+z′ ≈ 0)에는 q가 매우 작으면 식 (3)은 부정확해진다. 반면에 식 (4)는 z+z′ ≈ 0일 때 분모가 |β| ~ |(1/2)(k₀+q)R|이므로 작은 q에도 사용될 수 있다. 그러므로 |α+β| ≥ |β|는 식 (3)과 (4)의 사용을 결정하는 기준이 될 수 있다.

Ⅲ. 원거리 근사공식의 선택 기준

앞서 언급한 바와 같이, |α+β| ≥ |β|인 경우에는 식 (3)을 선택하고, |α+β|<|β|인 경우에는 식 (4)를 선택하는 것이 일반적인 점근급수 선택방법이다. 부등식 |α+β| ≥ |β|를 q = k₀η 또는 q = k₀/η인 경우에 cosθ에 관한 식으로 나타내면 다음과 같다.

cosθ = (z+z′)/R이고, 사용된 계수들은 다음과 같다.

여기서 η = η_r+iη_i이다. 식 (5)와 (6)은 cosθ에 관한 포물선 식이므로, 부등식을 만족하는 영역은 최고차항 계수(A 또는 D)의 부호, 그리고 포물선과 cosθ축과의 교점에 따라 달라진다. 그 교점은 식 (5)의 경우에 (1,P)이고, 식 (6)의 경우에 (1,Q)이다. 즉, 하나의 교점은 1로 고정되고, 다른 하나의 교점(P 또는 Q)은 임피던스에 관한 함수이며, 다음과 같다.

부등식의 해 영역은 A(또는 D)와 P-1(또는 Q-1)의 부호 조합에 따라 다음과 같이 나누어진다.

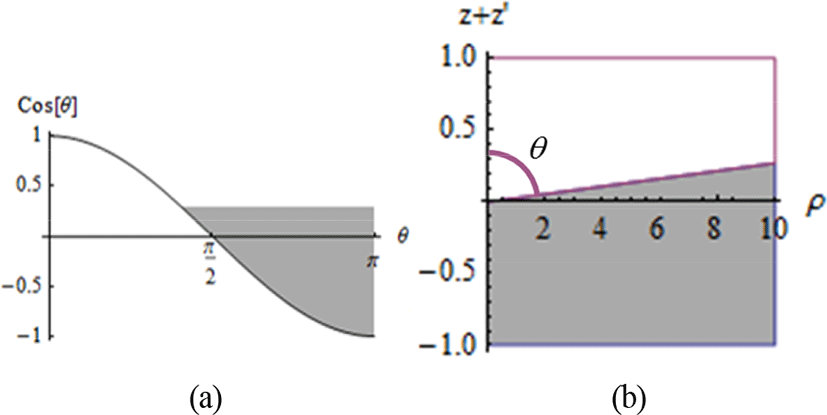
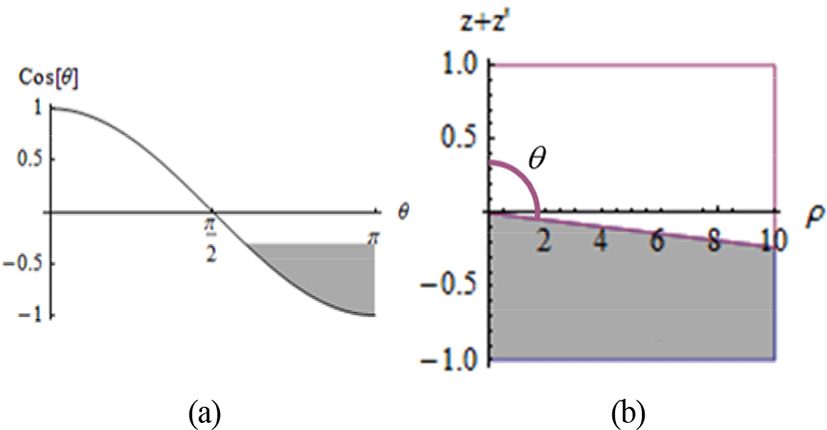
본 논문에서는 q = k₀η인 경우에 대해서만 서술하고, q = k₀/η인 경우에는 그 결과를 요약한다. CASE 1의 부등식이 나타내는 영역은 임피던스 복소수 평면 상에서 이고, 이 경우 식 (5)가 성립할 조건은 {cosθ < 1} ∪ {cosθ > P}이다. 즉, 평면의 임피던스 값이 에 해당될 경우 언제나 부등식 |α+β| ≥ |β|를 만족한다. CASE 4의 영역은 $\left\{{\left({\eta }_r+1\right)}^2+{\eta }_i^2>4\right\}$이고, 이 경우 식 (5)가 성립할 조건은 {cosθ > P} ∩ {cosθ < 1}이다. 이 때 P의 상계는 1이지만, 최소상 계는 −1보다 낮아진다: P > −1라고 가정하면 CASE 4의 전제는 $\left\{{\left({\eta }_r+1\right)}^2+{\eta }_i^2>4\right\}$인데, 부등식 P > −1의 영역은 이므로 모순이다. 따라서 P < −1이고, 식 (5)가 성립할 조건은 {cosθ > −1} ∩ {cosθ < 1}가 된다. 즉, 평면의 임피던스 값이 $\left\{{\left({\eta }_r+1\right)}^2+{\eta }_i^2>4\right\}$에 해당될 경우에 언제나 부등식 |α+β| ≥ |β|를 만족한다. CASE 3의 영역은 공집합이다. CASE 2의 영역은 0 < P < 1인 경우와 P < 0인 경우로 나누어 고려한다. {A > 0} ∩ {0 < P < 1}의 영역은 이고, 이 경우 식 (5)가 성립할 조건은 {cosθ < P} ∪ {cosθ > 1}이다. {A > 0} ∩ {P < 0}의 영역은 이고, 마찬가지로 식 (5)가 성립할 조건은 {cosθ < P} ∪ {cosθ > 1}이다. 두 경우, 식 (5)의 해 영역은 동일하나, 전자의 경우 {cosθ < P} ∩ {0 < P < 1}이므로 그림 2(a)의 음영 영역에서 |α+β| ≥ |β|를 만족한다. 이는 z+z′와 ρ의 좌표계에서 그림 2(b)의 음영 영역에 해당하며, 관측점이 멀어지면서 적합한 점근급수가 식 (4)에서 식 (3)으로 변함을 의미한다. 후자의 경우 {cosθ < P} ∩ {P < 0}이므로 그림 3(a)의 음영 영역에서 |α+β| ≥ |β|를 만족한다. 이는 그림 3(b)의 음영 영역에 해당하며, 소스와 관측점이 모두 임피던스 평면 위에 존재하기 때문에 z+z′ > 0인 영역에서 언제나 점근급수 식 (4)가 적합함을 의미한다.

그림 2. | Fig. 2. 부등식 {cosθ < P} ∩ {0 < P < 1}의 영역. | Solution region for {cosθ < P} ∩ {0 < P < 1}.

Download Original Figure

그림 3. | Fig. 3. 부등식 {cosθ < P} ∩ {P < 0}의 영역 | Solution region for{cosθ < P} ∩ {P<0}.

Download Original Figure

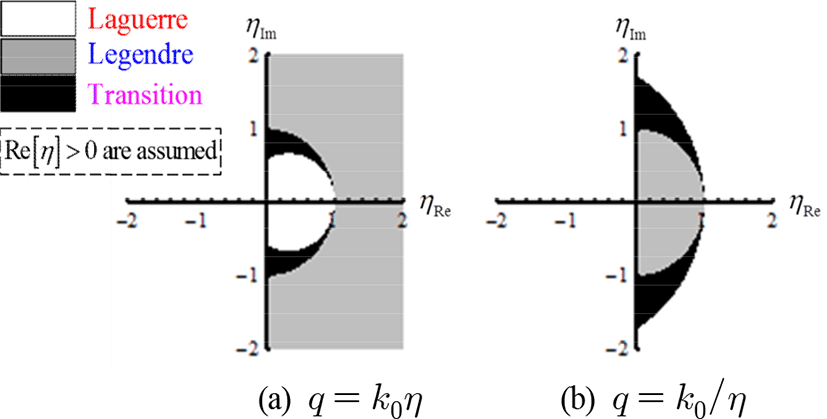
이런 범위를 정리하여 그림 4에 표시하였다. 그림 4(a)와 4(b)는 각각 q = k₀η와 q = k₀/η의 경우에 해당하며, 자연계에 존재하는 물질의 임피던스는 η_r > 0를 만족하므로 해당 영역만 나타내었다. 평면의 임피던스가 그림 4의 흰색 영역에 해당할 경우에는 라게르 급수를 사용한 식 (4)를, 회색 영역의 경우에는 르장드르 급수를 사용한 식 (3)을 각각 사용한다. 그리고 검정 영역에서 q = k₀η인 경우에는 관측점의 elevation angle이 θ = cos⁻¹(P)보다 클 때, 식 (4)를 작을 때 식 (3)을 각각 사용하고, q = k₀/η인 경우에는 관측점의 elevation angle이 θ = cos⁻¹(Q)보다 클 때, 식 (4)를 작을 때 식 (3)을 각각 사용한다. 검정 영역의 수식은 다음과 같다.

그림 4. | Fig. 4. 르장드르와 라게르 점근급수에 적합한 임피던스 영역의 분할 | Division of impedance space suitable for Legendre and Laguerre asymptotic series.

Download Original Figure

Ⅳ. 고차 편도함수의 간략화

임피던스 다이아딕 그린함수는 좀머펠트 적분 f(q)뿐만 아니라, 적분의 고차 편도함수들을 포함한다^[7]. 이를 정확하게 계산하는 것은 연산량 요구에 비해 정확도 항상은 미미하다. 원거리 영역에서는 R⁻ⁿ의 차수가 낮을수록 중요하다. 그러므로 f(q)의 고차 편도함수를 근사화 하기 위해 f(q)와 고차 편도함수의 비를 R⁻ⁿ에 관한 급수로 표현한다. 예를 들어 $\frac{\partial f(q)}{\partial x}/f(q)~{\displaystyle \sum }_{n=0}^N\frac{a_n}{R^n}$이면 $\frac{\partial f(q)}{\partial x}~f\left(q\right){\displaystyle \sum }_{n=0}^N\frac{a_n}{R^n}$로 근사화 할 수 있다. R⁻¹ 이상의 차수는 충분히 먼 거리에서 0으로 감소하기 때문에 상수항 a₀까지만 고려해도 충분하다. 르장드르 또는 라게르 다항식을 사용한 경우에 a₀를 구하면 다음과 같고, 이들은 파라미터 q(k₀η 또는 k₀/η)와 무관하게 동일한 값을 갖는다.

정리하면, 식 (1)에 사용되는 좀머펠드 적분식 (2)는 그림 4를 바탕으로 식 (3), (4) 몇 개의 항으로 계산될 수 있고, 좀머펠트 적분의 고차 편도함수는 계산된 값에 식 (17)～(21)의 상수항을 곱하여 간단히 얻을 수 있다.

Ⅴ. 시뮬레이션 검증

식 (1)을 서로 다른 방식으로 계산한 결과를 비교하였다. 아래의 모든 그림에서 Complete는 가우시안 구적법으로 정확하게 계산한 결과를 의미하고, Simple은 원거리 근사공식으로 계산한 결과를 의미한다. 이 때, 그림 4를 바탕으로 르장드르와 라게르 급수 중의 하나를 선택하였고, 고차 편도함수들은 식 (17)～(21)을 사용하였다. 주파수는 편의상 300 MHz를 가정하였다.

그림 5(a)는 임피던스가 η=1.3+1.1j인 평면 위의 z+z′=0.2인 위치에서 나선형 경로(spiral path) x = ϕ cos(ϕ), y = ϕ sin(ϕ)를 따라 식 (1)을 가우시안 구적법과 원거리 근사법으로 계산한 결과를 비교하여 나타내었고, 그림 5(b)는 수치적분 결과를 기준으로 계산한 원거리 근사법의 상대오차를 나타낸다. 미소 다이폴의 방향코사인은 $\widehat{l}=0.58\widehat{x}+0.58\widehat{y}+0.58\widehat{z}$를 가정하였다. 식 (1)에는 k₀η와 k₀/η에 관한 좀머펠트 적분이 모두 사용되며, 그림 4를 바탕으로 모든 경우 에 르장드르 급수가 사용되었다.

그림 5. | Fig. 5. z+z′=0.2, η=1.3+1.1j 임피던스 평면상에서 complete와 simple의 비교 | Comparison of the complete and simple methods over impedance plane of z+z′=0.2, η=1.3+1.1j.

Download Original Figure

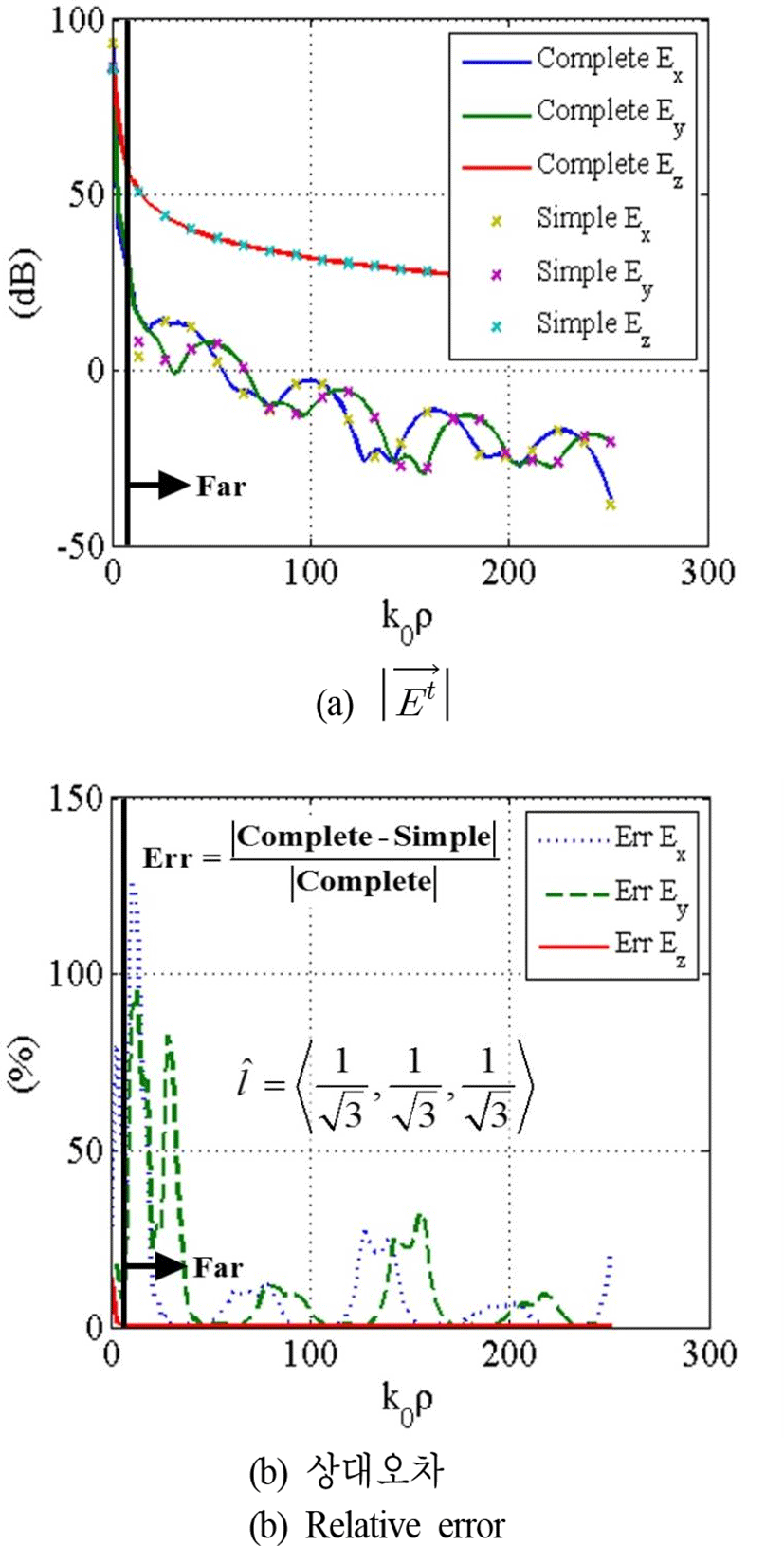
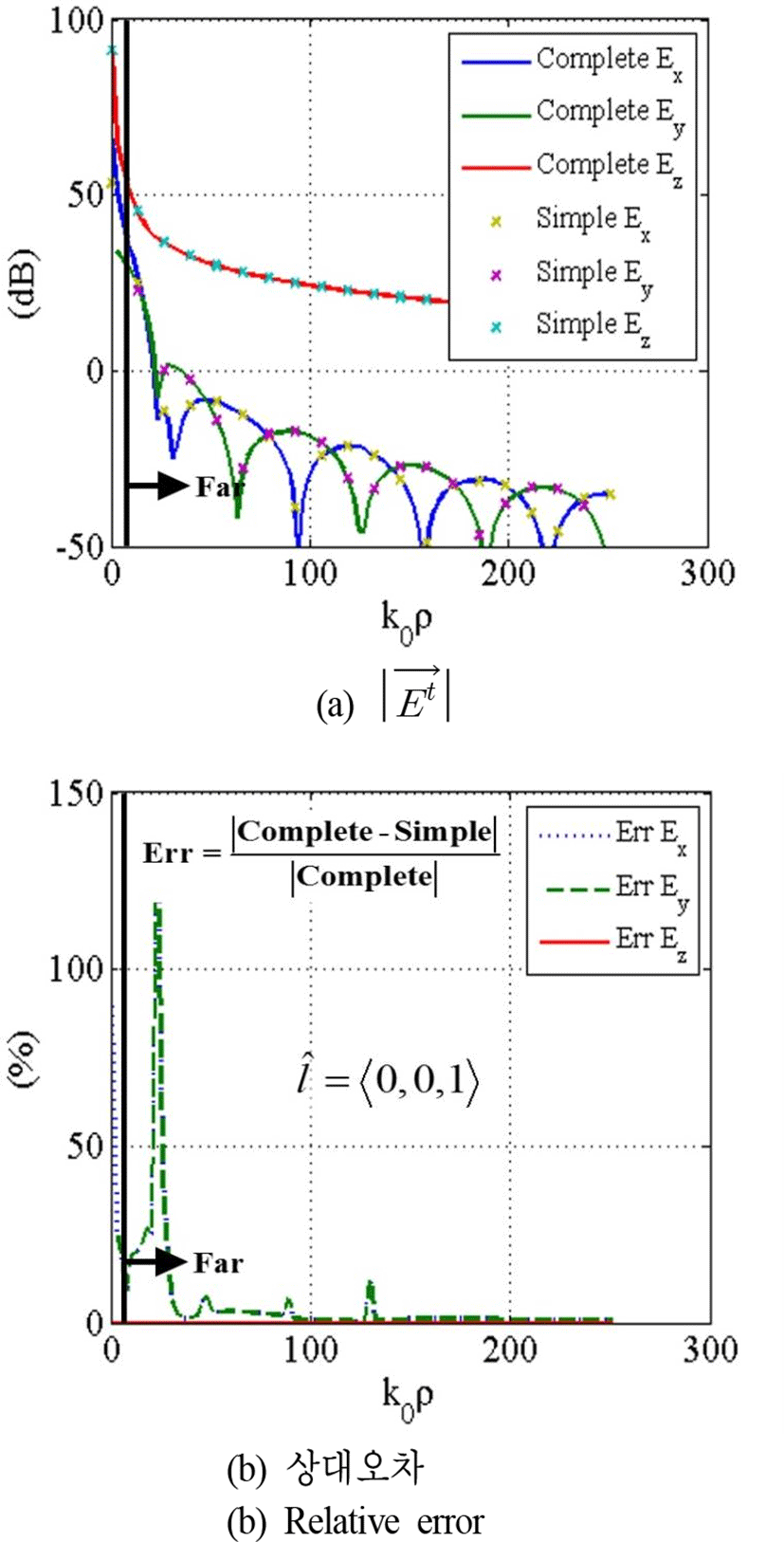
그림 6은 임피던스가 η=0.3+0.77j인 평면 위의 z+z′=0.3인 위치에서 동일한 경로를 따라 얻은 결과를 나타낸다. 수직 미소 다이폴 안테나를 가정하였다. 마찬가지로 그림 4를 기반으로, k₀η에 관한 적분은 르장드르와 라게르 급수를 모두 사용하였고, k₀/η에 관한 적분은 르장드르 급수를 사용하였다.

그림 6. | Fig. 6. z+z′=0.3, η=0.3+0.77j 임피던스 평면상에서 complete와 simple의 비교 | Comparison of complete and simple methods over impedance plane of z+z′=0.3, η=0.3+0.77j.

Download Original Figure

마지막으로, 그림 7은 주파수가 300 MHz일 때 실제 바닷물의 임피던스인 η=0.1129+0.0008j을 사용하였고^[8], 전자기파가 해수면에 매우 가까이 전파하는 상황(z+z′=0.1)을 가정하였다. 수직 미소 다이폴 안테나에 의한 전계를 동일한 경로에 대하여 계산하였고, k₀η에 관한 적분은 라게르 급수를, k₀/η에 관한 적분은 르장드르 급수를 각각 사용하였다.

그림 7. | Fig. 7. z+z′=0.1, η=0.1129+0.0008j 임피던스 평면에서 complete와 simple의 비교 | Comparison of the complete and simple methods over impedance plane of z+z′=0.1, η=0.1129+0.0008j.

Download Original Figure

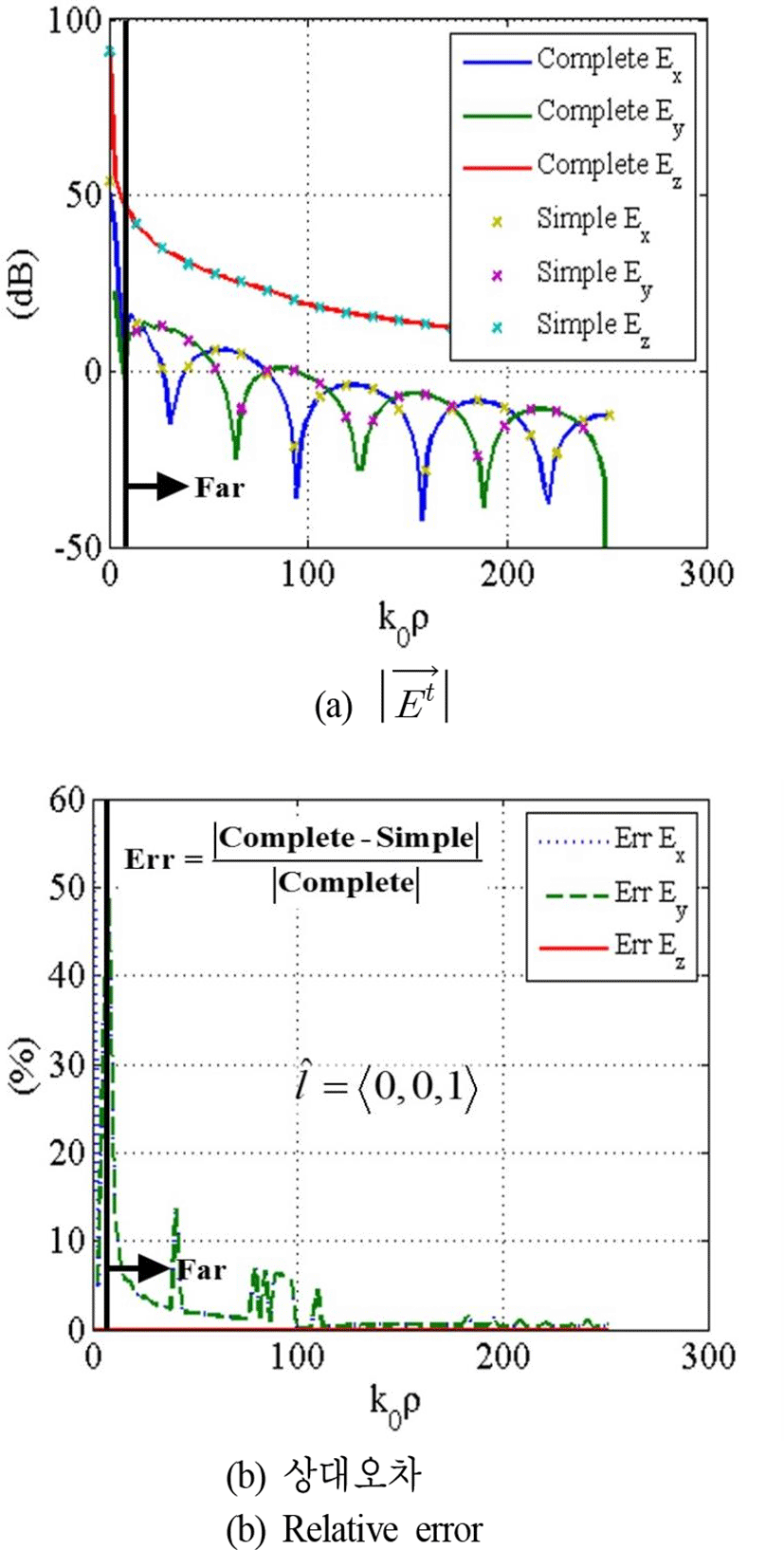
위 세 가지 경우의 시뮬레이션 결과에서 보듯이, 제안된 원거리 근사공식은 관측점의 거리가 멀어질수록 식 (1)의 정확한 수치적분의 결과와 매우 정확히 일치한다. 중간에 상대오차가 커지는 구간이 존재하지만, 이는 소스와 관측점의 거리가 가깝거나 또는 상대오차의 기준이 매우 작은 값을 갖기 때문이다. 가령 그림 5에서 보듯이, E_z는 전계의 주요 성분으로 상대오차가 거의 0이나, E_x와 E_y는 Complete와 Simple 모두 작은 값을 갖기 때문에 수치적으로 상대오차가 커질 수 있다.

Ⅵ. 결 론

임피던스 평면의 다이아딕 그린함수의 효율적인 계산을 위해, 두 개의 점근급수를 선택하는 기준을 제안하였다. 선택 기준은 관측점과 소스 사이의 상대적 위치 및 임피던스 값에 따라 결정이 된다. 다양한 경우에 제안된 선택 기준에 따라 임피던스 평면의 다이아딕 그린함수를 계산하고, 이를 정확한 수치계산과 비교하여 선택 기준의 정확도를 입증하였다. 또, 다이아딕 그린함수에 포함된 고차 편도함수의 간략한 공식 또한 제안하고, 수치적으로 검증하였다. 임피던스 근사법과 제안된 간략화된 원거리 공식을 사용하면 거친 표면 위 산란체의 산란 효과를 계산하는 수치 방법을 효율적으로 구현할 수 있다.