Ⅰ. 서 론
현대의 방공 및 미사일 방어 체계에서 조기경보 레이다와 다기능 레이다는 가장 핵심적인 감시 수단으로 자리 잡고 있다. 이러한 레이다는 고속으로 상승하는 탄도탄을 조기에 탐지하고 추적하여 교전 체계에 신뢰성 있는 표적 정보를 제공해야 한다. 특히 초기 상승 구간에서 레이다가 표적을 놓치지 않고 연속적으로 관측하기 위해서는 팬스 탐색(fence search) 운용이 요구된다. 팬스 탐색은 특정 고각 범위를 여러 층으로 나누고, 각 층에서 일정한 방위각 폭을 설정하여 탐색 빔을 분할 운용하는 방식으로 이루어진다. 이는 상승하는 표적이 필연적으로 일정 고각을 통과한다는 점을 활용한 방식으로, 조기경보 및 추적 인계 단계에서 중요한 역할을 한다[1],[2].
그러나 기존의 팬스 탐색 운용은 일반적으로 정해진 탐색 범위와 빔 성능에 의해 고정적인 운용을 수행한다. 이러한 접근은 구현이 단순하다는 장점이 있으나, 실제 상황에서 발생하는 불확실성을 반영하지 못한다는 근본적인 한계를 지닌다[3]~[5]. 발사 방향의 오차, 레이다 측정 잡음, 신호대잡음비(SNR, signal-to-noise ratio) 변화와 같은 요소가 존재하는 환경에서는 고정된 폭이나 펄스 수로는 탐지 신뢰도를 보장하기 어렵다. 결국 일부 층에서는 불필요하게 넓은 탐색 범위로 인해 시간 자원이 낭비되고, 다른 층에서는 펄스 수 부족으로 탐지 확률이 저하되는 문제가 발생한다.
이러한 한계를 극복하기 위해 최근 연구에서는 레이다 운용에서 확률적 기법과 최적화 기법을 도입하려는 시도가 나타나고 있다. 하지만 대부분은 표적 추적 필터 개선이나 자원관리 기법에 초점을 두고 있으며, 팬스 탐색 운용 자체를 확률적·수리적으로 재정립한 사례는 드물다. 따라서 팬스 탐색을 단순한 빔 분할 개념이 아니라, 확률적 제약 조건과 시간 자원 최적화를 동시에 고려하는 체계적 운용 문제로 바라보는 시각이 필요하다.
본 논문에서는 이러한 문제의식을 바탕으로, 칼만 필터(Kalman filter)를 활용하여 층별로 추정된 표적의 불확실도를 반영하고, 이를 통해 상층에서의 팬스 방위각 범위와 펄스 수를 자동으로 산출하는 새로운 운용 방법을 제안한다[6],[7]. 구체적으로, 1층에서 관측된 펄스 단위 데이터를 바탕으로 상태 추정을 수행하고, 이를 상층으로 예측하여 불확실도 분포를 도출한다. 이어서 확률 제약 기반의 수식을 통해 상층의 방위각 범위를 결정하고, 절약된 시간은 펄스 증액으로 환원하여 탐지 확률을 높이도록 설계하였다. 이러한 절차를 층별로 재귀적으로 반복함으로써, 기존 방식보다 더 높은 누적 탐지 확률을 확보할 수 있으며, 동시에 추적 인계 단계에서 더 정밀한 표적 정보를 제공할 수 있다.
본 논문의 의의는 기존의 단순한 팬스 운용을 벗어나, 확률적 제약 조건과 시간 자원 최적화를 결합한 새로운 방법론을 제시한다는 점에 있다. 이를 통해 탐지 신뢰성을 높임과 동시에 운용 효율을 개선할 수 있으며, 향후 실전 환경에 적용 가능한 참신한 운용 개념으로 발전할 수 있음을 시뮬레이션을 통해 보인다.
Ⅱ. 시스템 구성
팬스 탐색 운용을 단순한 빔 분할 규칙으로 정의하는 기존 접근은 실제 환경에서 발생하는 불확실성과 시간 자원 제약을 충분히 반영하지 못한다. 본 장에서는 제안된 방법을 수리적으로 정립하기 위하여 시스템 모델과 신호·잡음 특성을 기술하고, 이후 확률 제약 기반 섹터 폭 산출 및 펄스 최적 배분 절차를 단계적으로 제시한다. 특히 모든 과정은 층별로 재귀적으로 수행되며, 하위 층에서 추정된 결과가 상위 층의 팬스 운용을 직접적으로 규정하는 구조를 갖는다. 이를 통해 단일 층의 결과에 국한되지 않고, 전체 팬스 구조가 점진적으로 최적화되는 연속적 의사결정 과정을 구현할 수 있다.
상승 구간의 탄도 비행체는 포물선에 근사되는 궤적을 따라 이동하며, 레이다는 이를 거리, 방위각, 고각의 형태로 관측한다. 표적의 상태는 위치(m)와 속도(m/s)로 구성된 6차원 벡터로 식 (1)과 같이 표현할 수 있다.
이는 단순 중력장 내 운동방정식으로 기술되며, 외란 및 모델링 오차를 포함하기 위하여 상태 방정식은 식 (2)와 같이 표현된다.
여기서 f( · )는 비행체의 동역학을 나타내며, w(t)는 공분산 Q를 갖는 백색가우시안 잡음으로 불확실성을 반영한다.
레이다로부터의 측정은 표적의 상태를 거리, 방위각, 고각으로 변환한 형태로 식 (3)과 같이 주어지며, arg(x+jy)는 tan−1 (y/x)로 사분면을 고려하여 −π~+π 범위의 각도를 제공한다.
x,y,z: 표적의 위치(m)
xr,yr,zr: 레이다의 위치(m)
Re: 지구 반경(m)
νR,νθ,νϕ: 거리, 방위각, 고각 측정 잡음~Ν(0,σ2)
(gaussian measurement noise)
이와 같이 정의된 측정 모델은 단순한 기하학적 변환을 넘어, 곡률 효과를 명시적으로 포함하고 있어 수십 km 이상의 장거리 탐지에서도 정확도를 보장한다. 특히 방위각과 고각의 측정 분산은 레이다의 신호대잡음비(SNR)에 직접적으로 의존한다. 일반적으로 방위각 오차 분산은 식 (4)와 같이 근사할 수 있다.
여기서 βθ와 βϕ는 각각 방위각 및 고각 빔폭(rad), cθ와 cϕ는 실험적으로 결정되는 보정 상수(calibration constant)이다. 이는 곧, 표적의 SNR이 높을수록 각도 추정의 불확실도가 낮아짐을 의미한다. 이러한 관계식은 이후 확률 제약 기반 섹터 폭 계산에서 핵심적으로 활용된다. 앞서 정의한 상태-측정 모델은 칼만 필터(Kalman filter) 기반 추정을 가능하게 하고, 동시에 각도 추정 분산을 SNR에 연결함으로써 상위 층에서의 자동 팬스 폭 산출로 직결된다. 다시 말해, 시스템 모델 자체가 단순 궤적 예측을 넘어, 이후의 팬스 운용 최적화를 위한 기반 정보 구조를 제공하는 역할을 수행한다.
1층 팬스는 상층 계획의 기준을 형성한다. 목표는 1층 스윕 동안 펄스 단위로 표적을 관측하여 교차 시각 근방에서의 후단 추정치 와 공분산 을 얻는 것이다. 이 결과는 상층 중심 방위각 및 자원 분배 예측에 직접 적용되어, 확률 제약 기반 섹터 폭과 펄스 수가 자동으로 산출된다.
실제 운용에서는 1층 스윕을 중심으로 정렬해, 표적이 빔 중심을 통과할 때 빔 내(in-beam) 펄스 수가 최대가 되도록 시간을 배치한다. 빔 간격은 sθ=(1-ovθ)βθ이고, 1층 섹터 폭 Δθ1에서 빔 개수는 n1=⌈Δθ1/sθ⌉이다. 한 빔 체류 시간은 τdwell=Np,0/PRF로 두며, 스윕 전체 시간은 Tsweep=n1τdwell이다. 여기서 PRF(pulse repetition frequency)는 초당 송출되는 펄스 주기(Hz)를 의미한다.
1층에서의 상태 추정은 이산 시간 칼만 필터로 표현하며, 시간 갱신과 측정 갱신은 식 (5) 및 식 (6)과 같다[8],[9].
f( · ): 펄스 간 샘플링 시간에 대응하는 이산화 상태 천이
Fk−1=∂fd/∂X: 상태 천이 야코비안
Qk−1: 이산화된 공정 잡음 공분산 (모델 오차 포함)
h( · ): (R,θ,ϕ) 측정 비선형 변환
Hk=∂h/∂X: 측정 야코비안
Rk: 펄스 k에서의 측정 잡음 공분산 [R2,θ2,ϕ2]
Zk: 펄스 k의 측정 벡터 [R,θ,ϕ]⊤
여기서 1층 갱신의 중요 요소는 빔 내 펄스 선택과 SNR 의존 잡음 공분산이다. 실제로는 빔 중심과 빔 폭에 대해, 펄스가 빔 내에 있을 때만 갱신을 수행한다. 기하학적인 게이팅은 식 (7)과 같이 정의하며, 실제 갱신에 기여하는 유효 펄스 수 meff=∑gk 가 결정되면서 후단 공분산의 수렴 속도에 직접적인 영향을 준다.
θk,ϕk: 펄스 k에서의 방위각/고각(rad)
θb,ϕb: 현재 빔 중심 방위각/고각(rad)
βθ,βϕ: 3-dB 빔 폭(rad)
1( · ): 지시함수(참; 1, 거짓: 0)
측정 잡음 공분산은 펄스별 SNR에 따라 적응시킨다. SNR은 표준 단일 정방 산란체 가정하에 식 (8)과 같이 근사하며[10], 각도 분산은 CRLB(추정 가능한 오차 분산의 이론적 최솟값) 근사식을 사용하여 식 (4)를 통해 모델링하였다. 또한 거리 분산의 경우 시스템 사양에 따른 상수 로 두어 식 (9)와 같이 모델링하였으며, 이때 가 과도하게 작을 때의 수치 불안정성을 피하기 위해 는 적절한 상·하한으로 제한한다.
Pt: 송신전력(W), G: 안테나 이득(W/W)
λ: 파장(m), σrcs: 레이다 반사 단면적(m2)
Rk: 펄스 k에서의 슬랜트 거리(m)
κ: Boltzman’s constant [W/(Hz K)]
T0: 시스템 잡음 온도(K), B: 수신 대역폭(Hz)
Lsys: 시스템손실(W/W)
한 펄스 갱신의 정보 증분은 이며, 유효 펄스들이 누적되면 가 커지고 P=J−1이 감소한다. 여기서 ΔJk는 펄스 k의 피셔 정보 증분을 뜻한다. 결과적으로 근방에서 방위각의 주변 분산 가 충분히 축소되고, 이는 상층 확률 제약 섹터 폭의 초기 조건을 유리하게 만든다.
마지막으로 1층에서의 탐지 확률은 자원 계획의 보조 지표로 활용된다. 스윕 중 특정 빔에 대해 인-빔 펄스들의 선형 SNR 평균을 라 하면, Swerling case-1을 가정으로 비결합(noncoherent) 추적의 근사적 탐지 확률은 식 (10)과 같이 표현할 수 있다.
여기서 κ는 파형·탐지기 상수(waveform/detector- dependent constant)로 해당 식은 시간 예산 기반 펄스 배분에서 단조·포화 특성을 갖는 목적함수로 쓰이며, 1층에서 확보된 유효 펄스 수 meff와 SNR는 상층에서의 펄스 증액 필요성을 정량화하는 근거가 된다.
이와 같이 1층에서는 시간 정렬된 스윕과 빔 내 펄스 선별, SNR 기반 측정 잡음 공분산, 펄스 단위 칼만 갱신을 통해 와 를 얻는다. 이 결과는 상층 교차 시각으로의 예측을 통해 상층 방위각 평균과 불확실도로 변환되고, 확률 제약 섹터 폭 산출과 시간 예산 기반 펄스 배분으로 연결된다.
추가적으로, 만약 초기 층에서 탐지가 실패할 경우, 시스템은 동일 층을 한 차례 재탐색하도록 설정하여 상층 운용이 전적으로 무력화되는 상황을 방지하였다. 또한 확률 제약 조건에서 커버리지 하한(pcov, min)을 두어 초기 실패 시에도 상층 운용이 일정 수준 이상 보장되도록 설계하였다.
Ⅲ. 확률 제약 기반 팬스 운용 절차
본 운용 절차는 기본 방식의 고정 섹터 탐색을 기본으로 수행하며, 1층에서 탐지가 이루어질 경우에만 해당 정보를 이용하여 상층 섹터 폭을 줄이고 펄스를 최적화한다. 만약 1층에서 탐지가 이루어지지 않고 2층에서 최초 탐지가 발생하면, 2층이 새로운 기준 층으로 간주되어 이후 상층 운용이 적응형으로 전환된다. 이러한 구조는 초기 탐지 실패에 의한 운용 공백을 방지하면서, 탐지 성과가 발생하는 즉시 자원 효율을 극대화할 수 있도록 설계되었다.
1층에서 얻어진 추정치는 상층 팬스 운용의 기반이 된다. 특정 고각 αL에서의 표적 교차 시각 를 고려할 때, 1층 후단 상태 와 공분산 은 예측 연산을 통해 상층 시각으로 전달된다. 이를 통해 상층에서의 평균 방위각 μθ,L과 불확실도 σθ,L가 결정되며, 이후 확률 제약 기반 섹터 폭 산출의 직접적인 입력으로 사용된다. 예측 단계는 이산화된 전이 ϕ(Δt)를 이용하여 식 (11)과 같이 표현된다.
(discretized state transition matrix)
QΔ: 시간 Δt 동안 누적된 공정 잡음 공분산(state2)
이때 방위각은 예측된 위치 ()로부터 결정되며, 평균값은 식 (12)와 같이 정의된다.
불확실도는 선형 근사에 기반하여 예측 공분산으로부터 도출된다. 방위각의 1차 테일러 전개에서 야코비안 Jθ는 식 (13)과 같으며, 방위각 분산은 식 (14)와 같이 근사된다.
상층에서의 팬스 폭은 단순히 하층의 일정 수준을 줄이는 방식이 아니라, 예측된 불확실도를 직접 반영하여 확률적인 형태로 산출된다. 이를 통해 상층으로 갈수록 탐지 실패 위험을 일정 수준 이하로 제어하면서, 불필요한 시간 자원 낭비를 줄이는 효과를 얻는다.
방위각 예측치는 확률 분포 로 표현된다. 따라서 특정 확률 pcov 이상으로 표적을 포함하도록 섹터를 설계하기 위해서는 정규분포의 역누적분포함수(ICDF, inverse cumulative distribution function) 계수 zp=Φ−1(pcov)를 사용한다. 이때 반폭은 불확실도 항, 빔 반폭, 바이어스 보정 항을 합산하여 정의되며, 최종 섹터 폭은 식 (15)와 같이 주어진다.
zp: 커버리지 확률 pcov에 대응하는 정규분포 임계값
σθ,L: L층 예측 방위각 표준편차(rad)
βθ: 방위각 3-dB 빔 폭(rad)
δbias: 오차 보상을 위한 여유항(rad)
이 식을 통해 다음과 같은 사항을 알 수 있다. 첫째, 불확실도 항 zp σθ,L은 추정 공분산으로부터 직접 도출된 통계적 신뢰구간을 의미하며, 선택한 pcov 값에 따라 레이다 운용자가 원하는 신뢰 수준을 보장할 수 있다. 둘째, βθ/2 항은 빔 자체의 절반 폭을 포함하여, 이상적으로 표적이 빔 중심에 위치하지 않더라도 탐지 가능성을 유지한다. 셋째, δbias는 초기 큐의 편향이나 시스템 오차를 보정하는 추가 안전 여유를 제공한다. 결과적으로 불확실도와 레이다 물리 파라미터를 결합한 확률 제약 기반 자동 산출 결과가 된다.
계산된 섹터 폭을 기반으로 실제 운용에서 요구되는 빔 개수는 빔 간격을 고려하여 식 (16)을 통해 산출한다.
이와 같은 과정을 통해 각 층의 팬스는 표적을 일정 확률 이상으로 포함하도록 자동 설계된다. 특히, SNR이 충분히 크고 σθ,L가 작을 경우 ΔθL는 좁아지고, 반대로 불확실도가 크면 폭이 넓어지는 적응적 운용이 이루어진다. 이는 기존의 기계적 폭 축소 방식과 달리, 상황에 따라 최적화된 폭을 보장함으로써 시간 자원의 낭비를 최소화하는 동시에 탐지 신뢰도를 유지할 수 있는 장점을 제공한다.
확률 제약 기반으로 산출된 섹터 폭 ΔθL은 기존 베이스라인(예: 1층과 동일한 폭 유지) 대비 더 좁아진다. 이는 곧 스윕에 필요한 빔 개수와 전체 소요 시간의 감소를 의미하며, 절약된 시간을 상층의 펄스 증액에 활용할 수 있다. 시간 자원은 탐지 확률에 직접적으로 기여하므로, 이를 효율적으로 배분하는 것은 팬스 운용 최적화의 핵심 단계라 할 수 있다. 상층에서 절약된 총 시간(sec)은 식 (17)과 같이 정의된다.
N: 전체 팬스 층 수
NL: 제안 기법에서 산출된 L층 빔 개수
Np,0: 빔당 기본 펄스 수
이 시간을 상층에 배분할 때, 단순히 균등 분배하는 방식도 가능하지만 탐지 확률을 극대화하기 위해서는 각 빔의 SNR을 고려하는 것이 합리적이며, 앞서 식(10)과 같이 정의하였다. 해당 식은 펄스 수에 따라 단조 증가하지만 포화 특성을 가지므로, 한정된 시간 내에서 전체 탐지확률 Pd를 최대로 하기 위해서는 워터필링(water-filling) 형태의 최적화가 적합하다.
최적화 문제는 식 (18)과 같이 정의되며, 여기서 ΔTL은 팬스 L에 배정된 시간 예산이다.
Np,b: 빔 b에 할당된 펄스 수
이 최적화 문제는 2차 함수 형태를 가지므로, 전체 탐지확률을 최대로 하는 해는 유일하게 결정된다. 이를 제약식과 함께 풀면, 중심 빔에는 더 많은 펄스가, 주변 빔에는 최소 펄스만이 할당되는 가우시안 분배 형태의 결과가 얻어진다. 최종적으로 각 빔에 할당되는 펄스 수는 식 (19)와 같이 정의되며, 여기서 λ는 라그랑주 승수(Lagrange multiplier determined by total time constraint)로 시간 제약 조건으로 결정된다.
해당 방법은 높은 SNR을 가진 빔에 더 많은 펄스를 배분하고, 낮은 SNR 빔에는 최소 펄스만을 배정하여 전체 탐지 확률을 효율적으로 끌어올린다.
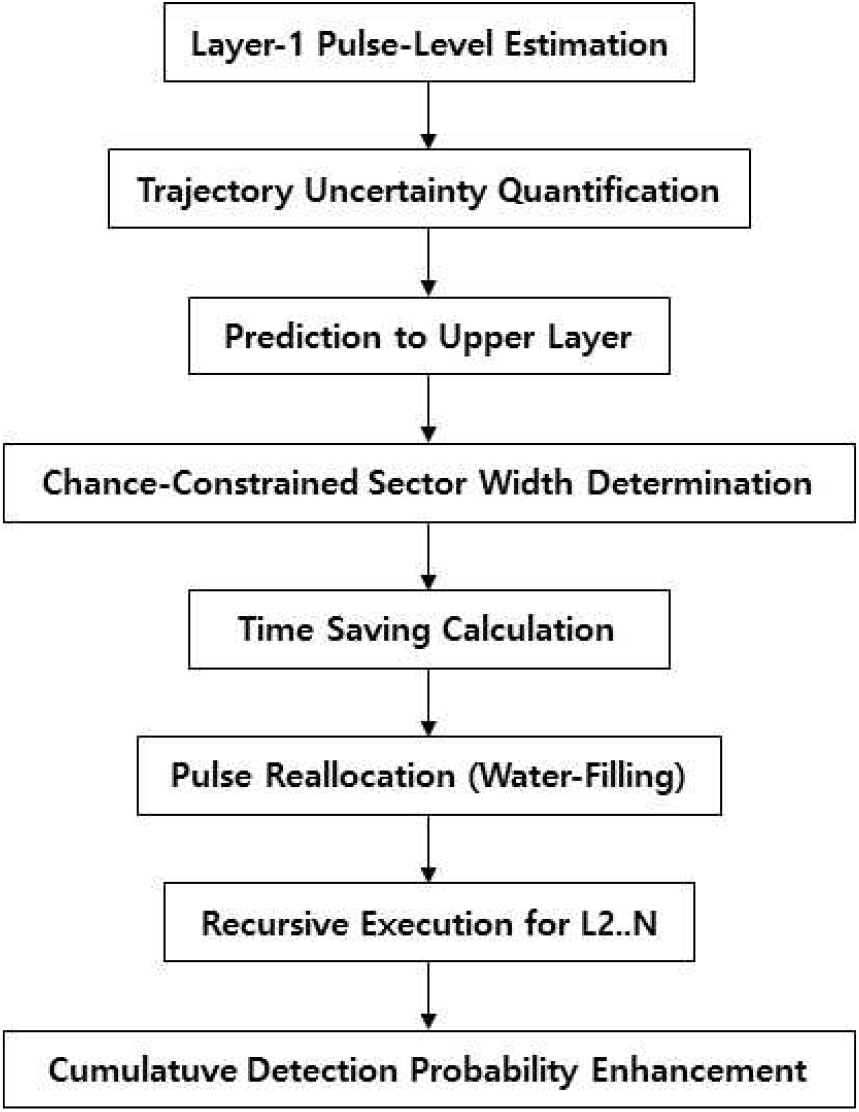
팬스 운용의 본질은 단일 층에서 끝나는 것이 아니라, 상승 궤적을 따라 연속적으로 형성되는 여러 층에서 반복적으로 수행된다는 점에 있다. 제안된 방법론에서는 1층에서의 추정 결과를 2층으로 예측하고, 2층에서 도출된 관측을 다시 적용하여 불확실도를 축소한 뒤, 동일 절차를 3층 이상으로 확장한다. 이와 같은 재귀 구조는 그림 1과 같이 각 층에서 얻어진 정보가 상층 운용의 입력으로 이어지는 순환적인 관계를 형성한다.
실제 다기능 레이다의 운용 환경 적용 가능성을 보면, 본 논문에서 사용된 EKF는 펄스 단위 샘플링 기반의 소규모 상태 갱신 구조로서, 복잡도가 O(n2)로 복잡도가 낮고, 계산이 빠르다. 또한 워터필링 기반 펄스 최적화는 2차 목적함수와 선형 제약조건으로 구성되어 유일한 해가 존재하여 실제 다기능 레이다 운용 환경에서도 실시간 처리에 충분히 적합하다.
Ⅳ. 시뮬레이션 및 분석
본 장에서는 제안된 적응형 팬스 운용 기법의 성능을 검증하기 위해 시뮬레이션을 수행하였다. 시뮬레이션은 실제 운용 환경을 반영할 수 있도록 레이다 위치, 표적 궤적, 빔 폭 및 중첩 비율, 파형 및 탐지기 파라미터 등을 입력으로 설정하였다. 전체 분석은 기존 방식(고정된 팬스 운용)과 제안 방식(적응형 운용)을 동일 조건에서 비교하는 형태로 진행되었다.
시뮬레이션에 적용된 입력 조건으로는 레이다 고도, 표적 초기 위치, 팬스 초기 설정 각도, 파형 특성 등이 있으며, 이에 대한 값은 표 1과 같다.
설정된 시나리오에 따라 기존 방식의 일반적인 팬스 그리드를 보면 그림 2와 같다[11]. 각 층은 동일한 방위각 폭을 가지며, 상층에서도 동일한 폭과 펄스 수가 유지된다. 이러한 방식은 구현이 단순하지만, 표적의 위치와 불확실도를 고려하지 않으므로 자원 효율성 측면에서 한계가 존재한다.
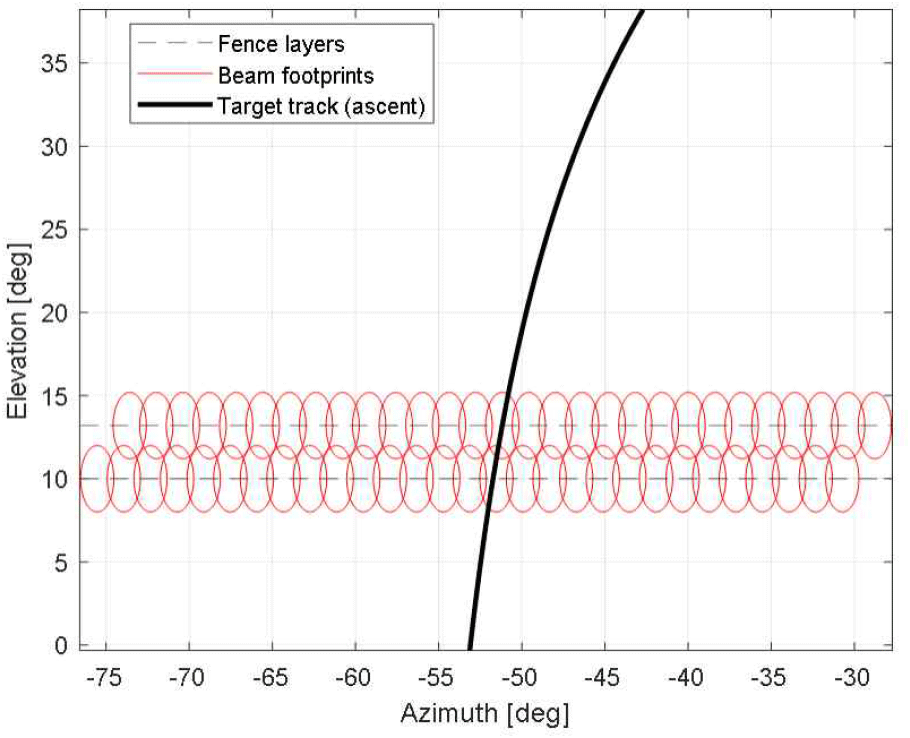
이에 비해 그림 3은 제안된 적응형 기법을 적용한 팬스 그리드이다. 1층에서의 추정을 바탕으로 상층의 불확실도가 줄어듦에 따라, 방위 범위가 점차 좁아지도록 설정된 것을 확인할 수 있다.
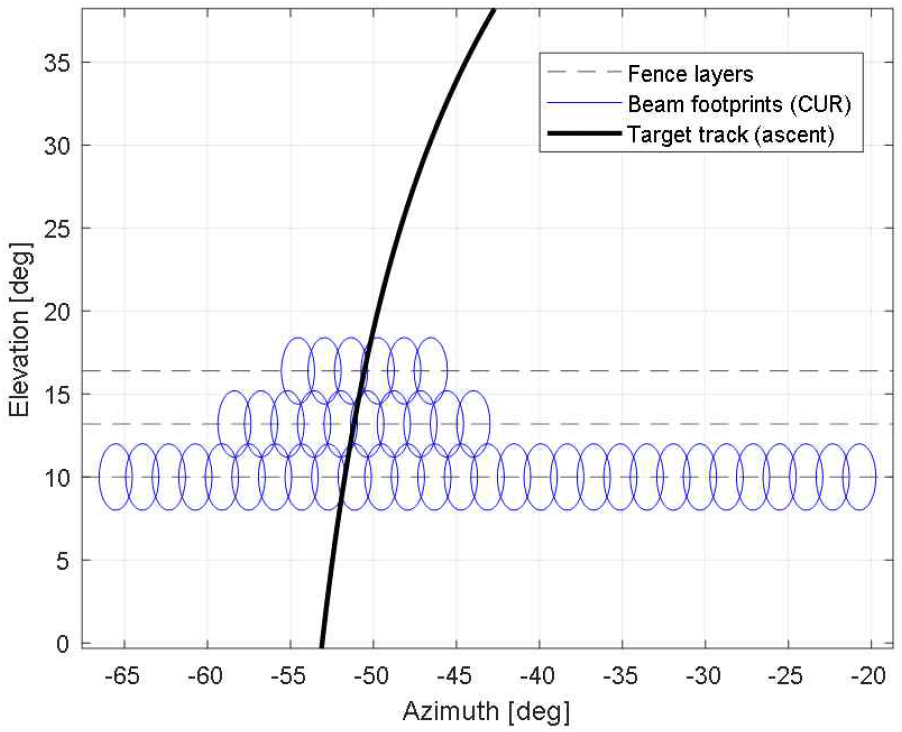
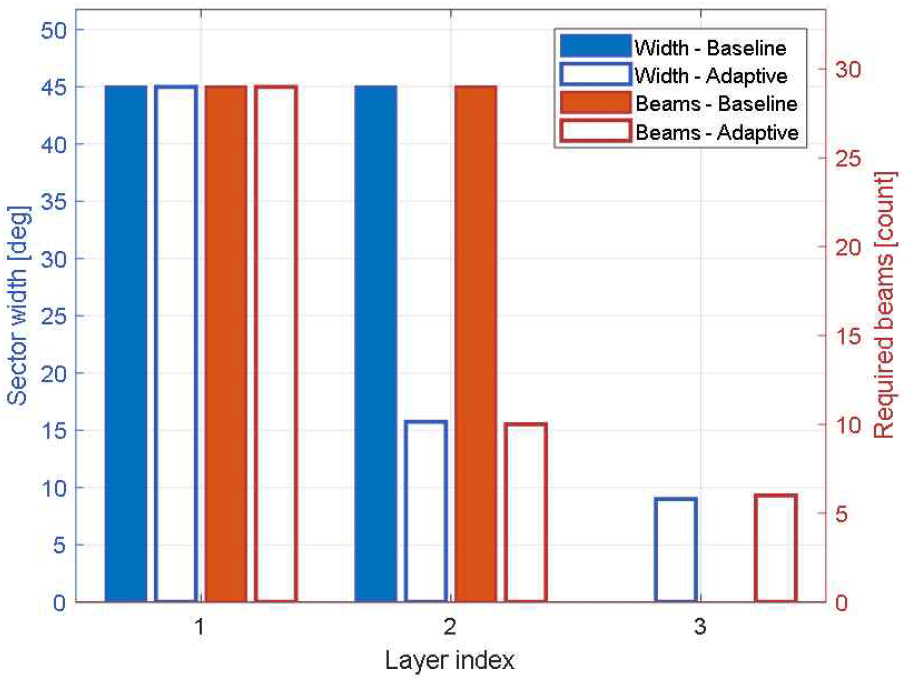
그림 4와 같이 기존 방식에서 2층의 방위 폭이 45도로 유지되었다면, 제안 방식에서는 2층은 약 15도, 3층은 약 3도로 축소되었다. 팬스 방위 범위가 줄어듦과 동시에 필요한, 사용된 빔의 수 또한 줄어든다. 기존 방식의 경우 총 29개의 빔이 사용됐지만 제안 방식의 경우 2층과 3층 각각 10개, 6개로 줄어든 것을 볼 수 있다. 이러한 차이는 불필요한 빔 운용을 줄이고, 절약된 시간을 펄스 증액에 활용할 수 있는 기반을 마련할 수 있다.
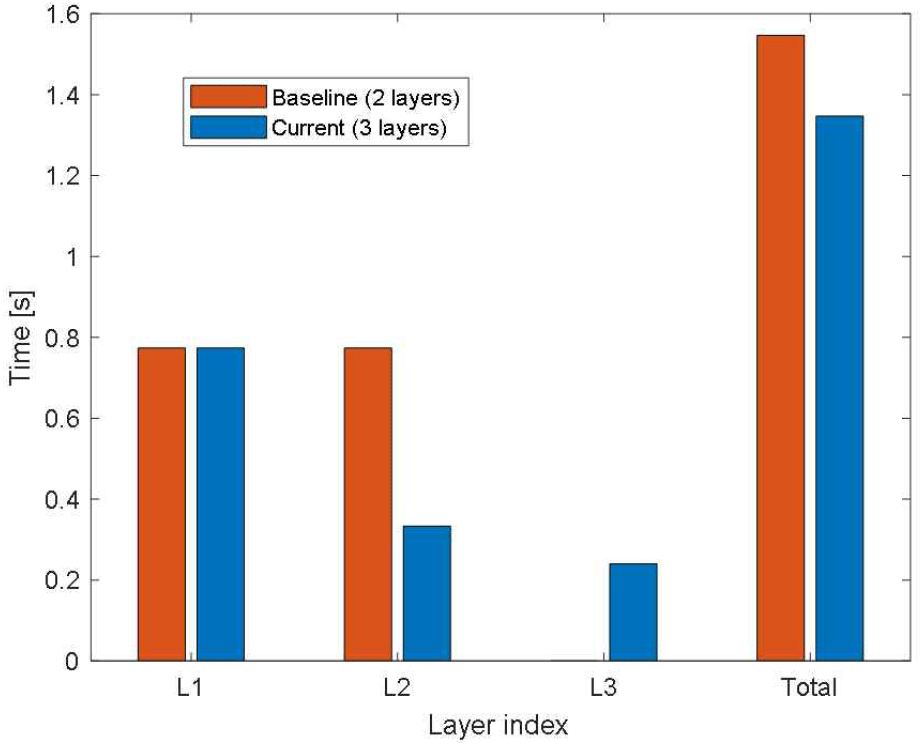
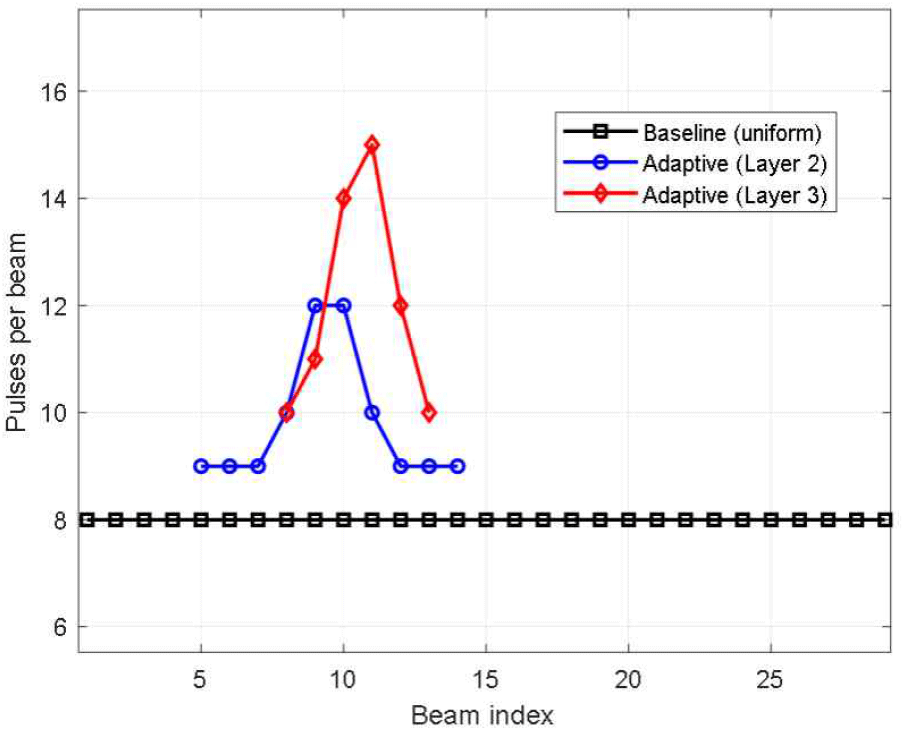
절약된 시간 자원에 대해 펄스 수를 증가한 결과 그림 5와 같이 기존 방식에서는 모든 층에서 동일한 펄스 수 8개가 유지되지만, 적응형 방식에서는 상층으로 갈수록 펄스 수가 2층과 3층 각각 빔당 약 평균 10과 12로 증가하는 것을 확인할 수 있었다. 특히 1층의 10번째 빔이 가장 큰 SNR을 가져 예측 궤적에 따라 2층의 9번 및 10번 빔에 동일한 펄스 수를 가지는 것을 보였다. 반면 3층의 경우 2층 빔들의 SNR 및 궤적 예측에 따라 11번째 빔의 펄스 수를 가장 크게 하여 SNR을 확보하는 것을 볼 수 있었다. 이는 좁아진 방위 범위 덕분에 절약된 시간을 상층에 집중 투입한 결과이며, 누적 탐지 확률 향상에 직접적으로 기여한다. 또한 비슷하게 층별 팬스를 탐색하는 데 걸리는 소요 시간을 비교하면 그림 6과 같다.
제안 방식은 하층에서는 기존 방식과 유사한 시간이 소요되지만, 상층에서는 폭 축소로 인해 탐색 시간이 줄어든다. 결과적으로 전체 소요 시간은 크게 증가하지 않으면서도, 상층에서 확보된 여유 시간으로 펄스를 증액하여 효율을 높였음을 알 수 있다.
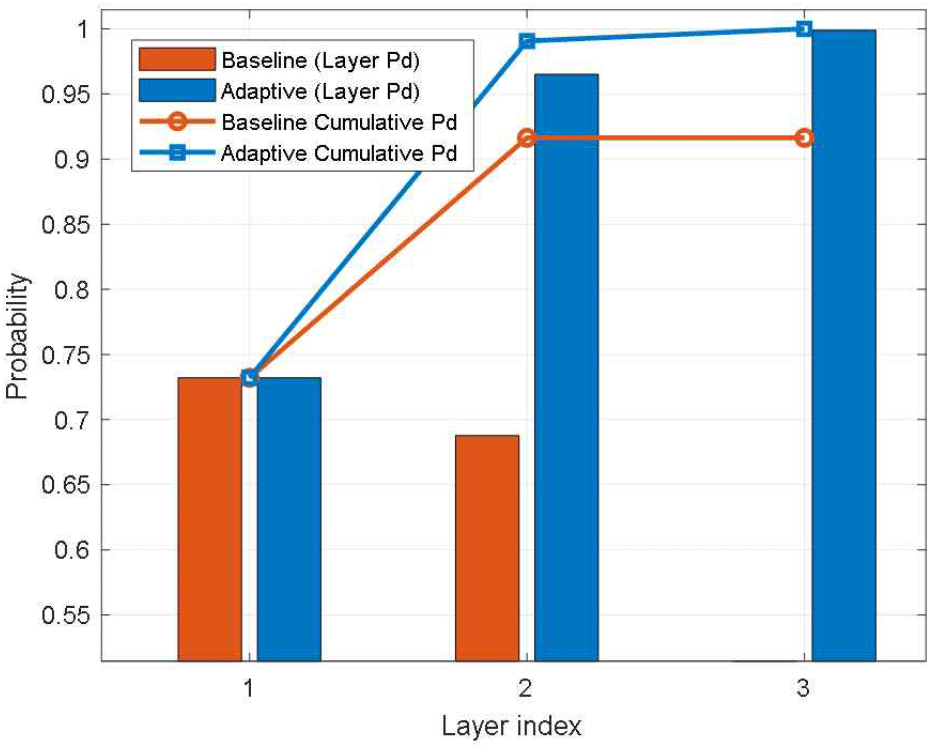
마지막으로 팬스에 걸린 탄도탄의 탐지 확률을 비교해보면 그림 7과 같다. 층별 탐지 확률은 표적 거리에 따라 일부 감소하는 구간이 존재할 수 있으나, 누적 탐지 확률은 적응형 방식이 기존 방식보다 일관되게 높은 값을 나타낸다. 이는 제안된 기법이 제한된 시간 자원 환경에서도 보다 안정적인 탐지를 보장함을 의미하며, 최종적으로 추적 인계의 신뢰성을 크게 향상시키는 결과로 이어진다.
그림 7에서 제시한 누적 탐지 확률 비교 결과를 포함하여, 다양한 운용 조건에서 분석된 성능 지표들을 종합하면 표 2와 같이 제안 기법이 시간 효율성과 탐지 신뢰도 향상 효과를 볼 수 있다.
추가 시뮬레이션으로 레이다 성능을 변화시켜 1층에서 상대적으로 높은 SNR이 확보되는 경우를 분석하였다. 이 경우 1층 추정치의 불확실도가 크게 줄어들어, 2층 팬스 섹터 폭은 그림 8과 같이 기존 대비(그림 3) 더 크게 축소되었다.
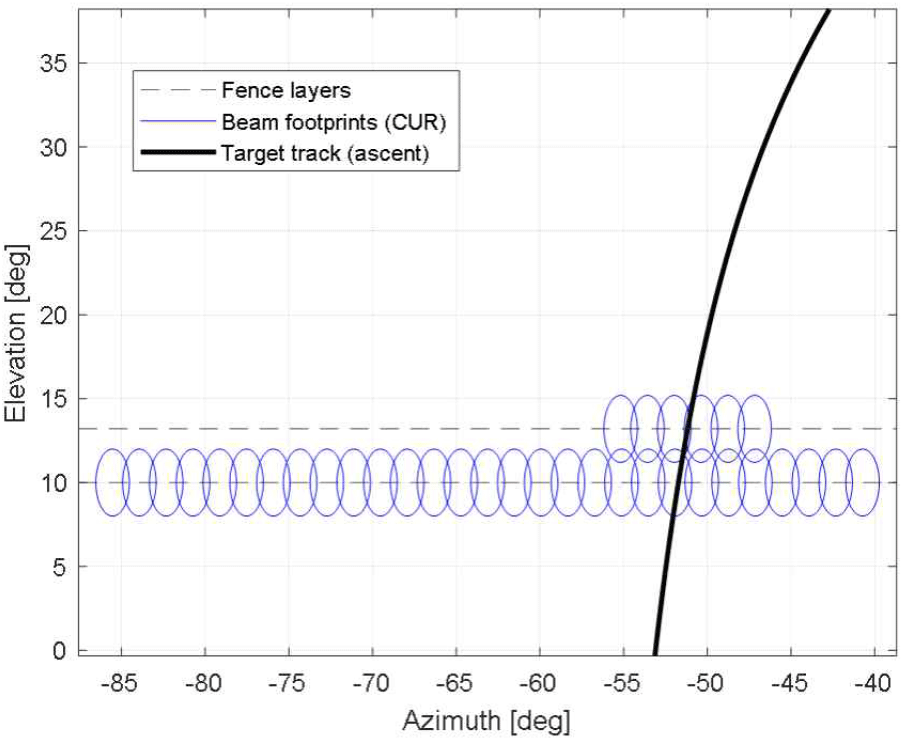
그에 따라 절약된 시간 자원은 2층 중심 빔에 집중적으로 재분배되어, 각 빔당 펄스 수가 평균 12펄스 수준으로 증가하였다. 이에 따라 2층에서의 누적 탐지 확률이 99.99 %로 상승하여, 이미 운용자가 설정한 기준 탐지 확률을 만족함을 보였다. 따라서 3층 운용은 추가 배정이 불필요하며, 이는 제안된 방식이 상황에 따라 상층 탐색을 생략하고 자원을 조기에 절약할 수 있음을 보여준다. 결과적으로 동일한 시간 제약 환경에서도 제안 기법은 자원 효율성과 탐지 신뢰성을 동시에 향상시킬 수 있음을 다시 한 번 확인하였다.
이러한 분석을 통해 제안된 확률 제약 기반 적응형 팬스 운용 기법이 기존의 단순 운용 방식 대비 시간 효율성과 탐지 신뢰도에서 뚜렷한 개선을 제공함을 확인할 수 있다.
Ⅴ. 결 론
본 논문에서는 기존의 기계적인 팬스 운용 방식과 달리, 확률 제약 기반의 적응형 팬스 운용 절차를 제안하였다. 제안된 방법은 1층에서의 펄스 단위 추정을 통해 표적 궤적의 불확실도를 정량화하고, 이를 상층 예측에 직접 반영함으로써 각 층의 중심 방위각 및 분산을 산출한다. 이어서 확률 제약식에 따라 섹터 폭을 자동으로 설정하고, 절약된 시간은 워터필링 기반의 최적화 해법을 통해 펄스로 재분배하였다. 이 절차는 층별로 재귀적으로 수행되며, 상층으로 진행될수록 탐지 신뢰도가 향상되는 구조를 갖는다.
분석 결과, 제안된 기법은 동일한 시간 자원 내에서 불필요한 빔 운용을 줄임으로써 효율성을 확보하는 동시에, 중심 빔에는 펄스를 집중 배분하여 탐지 확률을 높이는 효과를 제공한다. 특히 누적 탐지 확률 측면에서 기존의 절반 축소 기반 운용 방식보다 항상 우수한 성능을 보이며, 이는 추적 인계의 안정성을 크게 향상시키는 결과로 이어진다.
종합적으로, 제안된 적응형 팬스 운용 기법은 레이다 운용자가 제한된 시간과 자원 환경에서도 높은 탐지 신뢰도를 유지할 수 있는 실질적 방안을 제공한다. 이는 조기경보 레이다 운용뿐 아니라 다양한 다층 탐지 시나리오에서도 활용될 수 있는 확장성을 갖는다.