I. 서 론
다기능 레이다 MFR(multifunction radar)는 현대 전장 환경에서 다양한 기능을 통합적으로 수행할 수 있도록 설계된 핵심 센서 자산이다. 다기능 레이다는 단일 플랫폼에서 탐색, 추적, 식별, 무기 유도 및 탄도탄 대응 임무를 동시에 수행해야 하며, 이에 따라 제한된 시간·에너지 자원 내에서 다수의 기능이 상충 없이 병행되어야 한다[1],[2]. 특히 회전하지 않는 고정형 4면 구조의 다기능 레이다는 각 면(face)이 독립적인 구역을 담당하며, 면 단위 자원관리의 효율성은 전체 시스템의 성능 및 작전 수행 능력에 결정적인 영향을 미친다.
이러한 운용 환경에서는 자원의 효율적인 분배가 필수적이며, 특히 일반 운용 중 예기치 않게 고자원 소모 임무가 추가되는 상황은 매우 빈번히 발생한다. 하나의 예시로 일반 표적 탐색 및 추적 운용 중 탄도탄 위협이 발생하여 팬스(fence) 탐색 운용을 병행해야 하는 경우가 있다. 탄도탄을 탐색하기 위한 팬스 탐색은 긴 거리, 넓은 고각 범위, 짧은 반복 주기 등의 특성을 가진다. 이로 인해 해당 면의 총 자원 소모가 시스템이 허용하는 최대 자원 시간(탐색 갱신 시간)을 초과하는 상황이 빈번히 발생하며, 결과적으로 일부 구역의 탐색 거리 축소, 표적 추적 간격 증가, 혹은 특정 표적 추적 중단 등의 조치가 불가피하게 요구된다. 이러한 자원 충돌 상황은 다기능 레이다의 실시간 운용 성능과 전체 방공 체계의 신뢰도를 저하시킬 수 있기 때문에, 이를 체계적으로 분석하고 대응하는 방안이 필요하다.
기존의 레이다 자원관리 관련 연구들은 주로 탐색 및 추적 임무의 주기 조정 또는 타임슬롯 기반 스케줄링 기법에 집중되어 왔으며, 팬스 탐색과 같이 단시간에 높은 자원 사용을 요구하는 돌발 임무 발생 시의 자원 충돌 상황을 정량적으로 분석하고, 이를 실시간으로 해결하기 위한 최적화 관점의 접근은 상대적으로 부족하다[3]~[5]. 특히, 기존 연구들은 대부분 시간 기반(time-slot) 또는 우선순위 기반(priority-based) 자원관리 접근에 국한되어 있으며, 면 단위 운용 내에서 연속형(탐색 거리)과 이산형(추적 유지 여부) 변수를 동시에 고려한 섹터 기반 최적화(sectorbased optimization) 구조는 제시된 바 없다. 이러한 구조적 차이는 본 연구의 방법론이 단순한 스케줄링 개선이 아니라, 실제 다기능 레이다 면 운용을 반영한 상위 개념의 자원관리 프레임워크임을 의미한다. 따라서 기존 연구와의 수치적 비교는 모델 구조의 차이로 인해 직접적 의미가 제한적이며, 본 연구는 이러한 기존 접근법들을 특정 파라미터 조건하의 부분집합으로 포함할 수 있는 일반화된 모델로서 제안된다. 이에 본 논문에서는 다기능 레이다 운용 중 발생 가능한 자원 충돌 상황을 정량적으로 모델링하고, 섹터 기반 자원관리 구조를 바탕으로 팬스 운용과 일반 표적 운용 간의 자원 충돌을 해결하기 위한 최적화 기법을 제안한다.
제안된 모델은 섹터별 탐색 거리 조정, 표적 추적 해제 여부 등을 설계 변수로 정의하고, 전체 자원 초과 방지와 탐색 거리 손실 최소화를 복합적으로 고려하는 목적함수를 구성하여 자원 분배의 균형을 달성한다. 또한 본 논문은 유전자 알고리즘 GA(genetic algorithm), 입자 군집 최적화 PSO(particle swarm optimization)의 휴리스틱 최적화 기법을 적용하여 다양한 상황에 대한 시뮬레이션 분석을 수행하며, 각 기법의 수렴 특성과 자원 회복 성능을 비교 분석함으로써 실질적 운용 지침으로의 적용 가능성을 평가한다. 본 연구를 통해 단순한 자원 재분배를 넘어, 실전 운용 환경에서 발생 가능한 복합 임무 간 자원 충돌을 정량적·수학적으로 분석하고, 실시간 대응이 가능한 최적화 기반 자원관리 프레임워크를 제시함으로써, 다기능 레이다의 운용 효율성과 실시간 탄도탄 대응 능력 향상에 기여할 수 있는 기반을 마련하고자 한다.
II. 본 론
본 연구에서는 그림 1과 같이 각 면을 다시 4개의 방위각 섹터로 세분화하고, 이 섹터 단위로 자원을 관리하는 구조를 기반으로 최적화 문제를 정의한다.
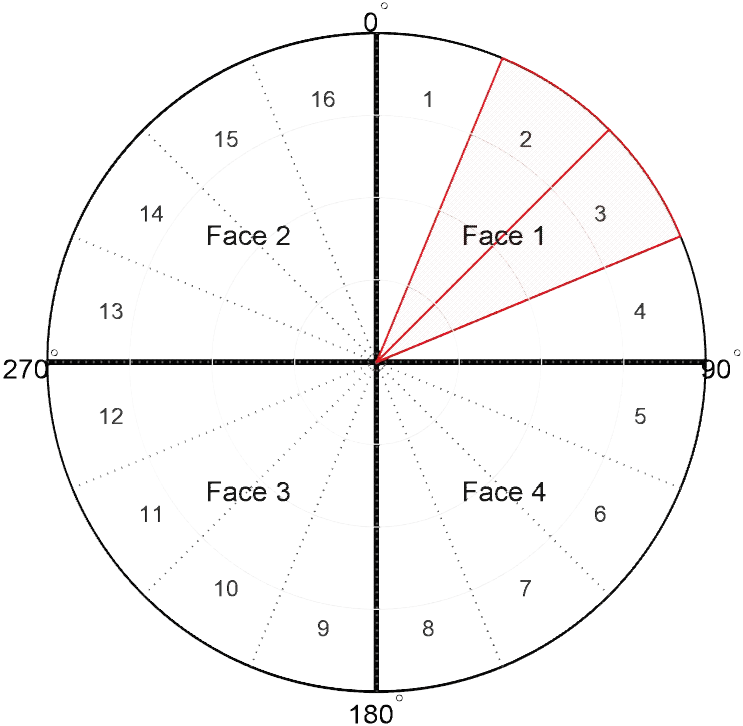
평시 운용에서는 섹터별 탐색 거리 및 표적 분포와 무관하게 탐색 자원과 추적 자원이 섹터별로 일정하게 분배되며, 자원 총합은 시스템이 정의한 면당 최대 자원 시간 이하로 제한된다. 그러나 특정 시점에 탄도탄 위협이 발생하면 팬스 운용이 추가되어야 하며, 이는 특정 섹터에 매우 높은 수준의 자원 요구를 야기하여 전체 자원을 초과하게 만든다. 이와 같은 자원 충돌 상황에서 탐색 거리 조정, 표적 추적 해제, 고각 범위 축소 등 다양한 자원 해소 전략을 종합적으로 적용할 수 있다[6]~[8].
우선, 하나의 섹터에 대한 탐색 자원 소모량은 다음과 같은 식 (1)로 정의된다. 소모(시간)되는 자원은 방위 및 고각 격자에 배치되는 빔 총수와 빔당 체류시간의 곱으로 정의할 수 있으며, 섹터에 소모되는 탐색 자원을 통해 한 면을 탐색하는 데 걸리는 시간을 계산할 수 있다. 여기서 Di는 섹터 i의 탐색 거리로 PRI=2Di/c의 관계를 가진다.
θi, φi: 섹터 방위각 및 고각 커버리지
θbw, φbw: 방위 및 고각 빔 폭(deg)
ρaz, ρel: 방위 및 고각 빔 겹침 정도
Np: 펄스 수, Nrev: 프레임 내 반복 횟수
τsw: 빔 전환 오버헤드 시간
이 모델은 공간 해상도와 탐색 커버리지를 기반으로 실제 레이다가 요구하는 총 탐색 시간을 정량화한다. 탐색 자원은 Di에 선형 비례하므로, 탐색 거리 축소는 자원 해소에 직접적인 영향을 미친다.
다음으로, 섹터 i에 존재하는 Ni개의 표적에 대한 추적 자원 소모는 식 (2)와 같이 모델링된다.
Nhit,j: 추적 빔당 펄스 수
PRItrack: 추적 빔 1회에 소모되는 시간
여기서 xi,j∈{0, 1}는 j번째 표적의 추적 유지 여부를 나타내는 이진 변수이다. 이 모델은 개별 표적의 갱신 주기와 레이다 리소스 요구량을 기반으로 추적 자원을 정량화하며, xi,j=0인 경우 해당 표적은 추적 대상에서 제외되어 자원이 절감된다[9]. 단, 모든 표적이 최적화 대상으로 고려되는 것은 아니며, 실전 운용에서는 교전 중 표적, 고속 접근체 등 반드시 추적을 유지해야 하는 대상이 존재한다. 본 연구에서는 각 표적에 대해 추적 우선순위를 정의하고, 일정 수준 이하의 우선순위를 가진 표적만을 추적 해제 가능 대상으로 설정하였다. 이에 따라 최적화 대상 이진 변수 xi,j는 제거 가능 표적에 대해서만 정의되며, 중요 표적에 대한 추적은 항상 유지된다.
마지막으로 탄도탄을 탐지하기 위한 팬스 탐색은 고정된 섹터 수와 팬스 층 수, 반복 주기에 기반한 자원 요구로 구성되며, 식 (3)과 같이 표현된다.
여기서 Rscan,i의 경우 식 (1)을 통해 탐색 자원 계산과 동일한 개념으로 팬스 범위와 팬스에 운용되는 빔 각도 등 팬스 운용 성능에 맞게 적용하여 계산할 수 있다. 이때 팬스 운용은 통상 큐(que) 신호 정보에 따라 일정 섹터에 대해 대상 목표 탐지 거리가 정해져 고정된 성능으로 수행되므로, 해당 자원 소모량은 일정하며 비가변 요소로 작용한다. 또한 한 면의 전체 탐색 프레임 시간이 길어질수록 추적 표적은 갱신 주기 안에 더 많은 자원을 요구하게 된다. 이러한 탐색-추적 간 상호의존성을 반영한 최종 소모되는 자원을 식 (4)를 통해 계산할 수 있으며, 자원 제약 조건은 식 (5)와 같다.
Tupd: 해당 표적의 추적 갱신 주기
그러나 팬스 운용 발생 시 기존 탐색 및 추적 자원을 유지한 채 Rfence가 추가되면, 대부분의 경우 최대 자원을 초과하는 상황이 발생하게 된다. 이에 따라, 일부 섹터의 탐색 거리 Di를 축소하거나, 표적 추적 변수 xi,j를 0으로 조정하는 방식으로 자원 초과량을 감소시켜야 한다. 이러한 조건하에서의 자원관리 문제는 식 (6)과 같은 목적함수를 최소화하는 최적화 문제로 정식화된다. 목적함수는 섹터별 탐색거리 축소에 따른 성능 손실, 면 단위 자원 초과 패널티, 추적 우선순위가 높은 표적을 해제할 때의 패털티를 함께 고려한다. 설계변수는 섹터별 탐색거리 D=[D1,…,DNs ector]와, 제거 가능 표적 집합 Κ에 한정한 이진 추적 유지 변수 X={xk∈(0, 1)∣k∈Κ}로 구성한다. 여기서 첫 번째 항은 탐색 성능 손실, 두 번째 항은 자원 초과 패널티, 세 번째 항은 우선순위 패널티를 의미한다.
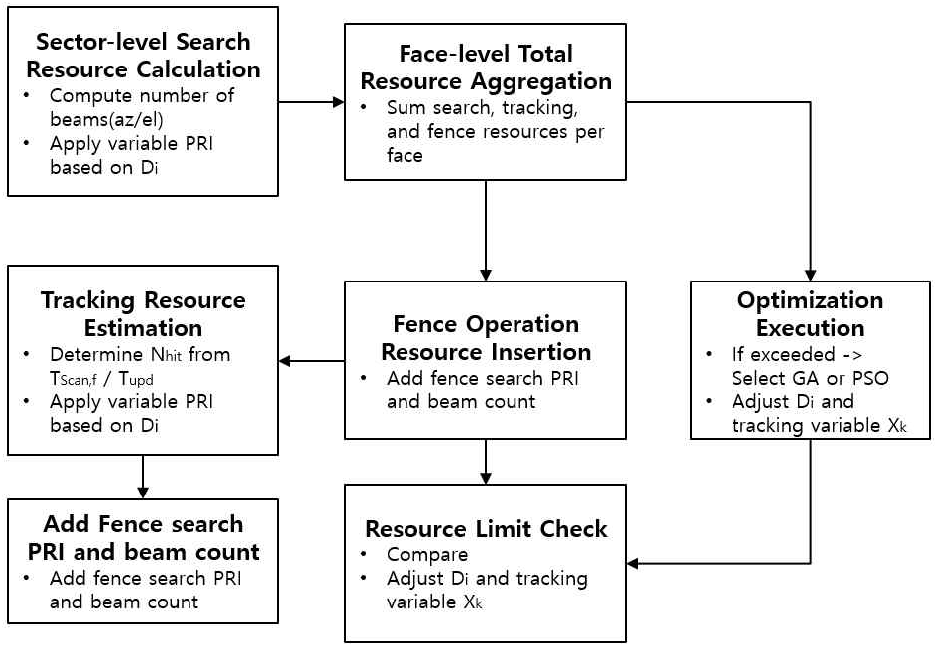
이 목적함수는 다목적 최적화 문제의 구조를 띠며, 각 항의 상대적 중요도에 따라 탐색 손실을 최소화하면서도 자원 제약을 만족하는 최적의 자원 재분배 조합을 탐색하게 되며, 그림 2와 같은 순서도를 가진다.
추후 적용될 최적화 기법은 이 설계 변수 공간을 탐색하여 자원 충돌 상황을 가장 효과적으로 해결할 수 있는 운용 해를 도출한다.
본 절에서는 앞서 정의한 자원 소모 모델을 기반으로, 실현 가능한 운용 파라미터 조합 중에서 가장 효율적인 해를 탐색하기 위한 최적화 기법을 수학적으로 정의하고, 알고리즘 적용 구조를 설계한다.
섹터 기반 자원관리 구조하에서 최적화의 설계 변수는 두 범주로 구분된다. 첫째는 탐색 거리 조정 변수이며, 이는 연속적 실수 공간에서 정의되는 변수 집합이다. 둘째는 추적 대상 선택 변수로, 이진 조합 공간에서 정의되는 이산 변수 집합이다. 두 설계변수의 경계 조건은 식 (7)과 같다.
탐색거리를 줄이면 해당 섹터의 탐색 펄스 반복 주기 PRI(pulse repetition interval)가 단축되고, 이는 곧 탐색자원 절감으로 이어진다. 본 모델은 이와 동시에 면 단위 탐색시간이 짧아지면 추적 갱신 횟수가 줄어들어 추적자원도 함께 절감되는 상호의존 구조를 가진다. 탐색 공간은 Ns ector개의 연속변수와 |Κ|개의 이진변수로 구성된 혼합정수 최적화 문제이며, 해 공간의 차원은 총 Ns ector+|Κ|이다.
본 연구에서는 대표적인 진화 기반 전역 최적화 알고리즘인 GA, PSO를 적용하였다. 이들 알고리즘은 각각 상이한 탐색 방식과 수렴 특성을 가지며, 조합형 설계 변수와 연속형 변수의 동시 최적화 문제에 적합하다.
GA는 각 해를 염색체(chromosome)로 인코딩하여 세대 단위로 진화를 수행하는 탐색 기법이다. 본 연구에서는 실수 기반 D와 이진 기반 X를 연결한 벡터를 단일 염색체로 구성한다.
선택(selection) 과정에서는 순위 기반으로 적합도에 비례하여 개체를 선택하였다. 교차 연산은 연속형 변수에는 모의 이진 교차(simulated binary crossover)를, 이진형 변수에는 균등 교차 방식을 적용하였다. 변이 연산의 경우, 탐색 거리를 조정하는 변수에는 가우시안 섭동 방식을, 추적 여부를 나타내는 변수에는 플립 변이를 적용하였다.
PSO는 각 해를 입자로 정의하고, 군집 내 정보 공유를 통해 위치를 갱신한다. 연속형 변수 D는 실수 공간에서 속도-위치 모델을 통해 갱신되며, 이진형 변수 X는 시그모이드(sigmoid) 함수 기반 확률 이진화(binary PSO) 기법을 통해 표현된다.
본 장에서 정의된 최적화 구조는 고정된 자원 제약조건 내에서 각 섹터의 운용 매개변수를 조정하여 팬스 운용을 성공적으로 삽입하고, 동시에 일반 탐색 및 추적 성능 손실을 최소화하는 최적 해를 탐색하는 것을 목표로 한다. 이후 장에서는 설정된 시나리오에 따라 각 최적화 기법의 성능을 비교하고, 자원 해소율, 탐색 거리 감소율, 계산 효율성 등의 지표를 기반으로 해석을 수행한다.
III. 시뮬레이션 및 결과 분석
시뮬레이션에서 사용된 주요 운용 조건은 다음과 같다. 총 4개의 면이 있으며, 각 면은 4개의 섹터로 구성되어 총 16개 섹터로 분할되어 있으며, 최대탐지거리는 300 km이며, 최적화 시 최소 30 km 이하로 감소하지 않게 설정하였다. 탄도탄용 팬스 탐색거리의 경우 일반 탐색거리보다 긴 450 km로 설정하였으며, 첫 번째 면의 2, 3번 섹터에 팬스를 운용하도록 하였다. 표적은 임의의 방위각과 거리로 분포하며, 총 50개의 표적이 최대탐지 내에 존재한다. 각 표적에는 1~3의 추적 우선순위(priority)가 부여되며, 1은 반드시 추적이 유지되어야 하는 고위험 표적을 의미하고, 2와 3은 추적 해제가 가능한 중/저위험 표적으로 간주된다. 레이다 제원 및 빔 운용에 대한 보다 상세한 분석 시나리오 설정은 표 1과 같다.
또한 본 연구에서 적용된 최적화 알고리즘의 하이퍼파라미터 구성은 표 2와 같다. 목적함수의 가중치 파라미터 α, β, γ는 각각 탐색 성능 손실, 자원 제약 위반, 추적 손실 패널티의 상대적 중요도를 나타내며, 전체 목적함수의 균형적 수렴을 위해 0.5:0.3:0.2의 비율로 설정하였다.
GA와 PSO의 파라미터는 수렴 안정성과 계산 효율성 간의 균형을 고려하여 사전 민감도 분석을 통해 결정하였다. GA의 경우 탐색 다양성 확보와 연산 시간의 균형을 위해 개체 수(population)를 50, 세대 수(generation)를 100으로 설정하였으며, 교차 확률 0.8과 변이 확률 0.1은 전역 탐색 능력과 지역 수렴 속도를 동시에 확보할 수 있는 조합으로 확인되었다. PSO의 경우 관성 계수(inertia weight) w=0.7과 인지·사회적 계수(c1, c2)=1.5를 적용하였으며, 이는 0.4<w<0.9의 안정 영역 내에서 군집 수렴 특성을 유지하면서도 계산 시간이 짧은 구간으로 판단되었다.
각 파라미터는 사전 실험을 통해 목적함수의 수렴률, 제약 위반 정도, 탐색·추적 손실의 민감도를 비교하여 최종 선정하였다. 이러한 설정은 동일 조건에서의 재현 가능성을 보장하며, 알고리즘 성능 비교 시 변수 간 영향이 최소화되도록 통제된 조건으로 기능한다.
본 연구에서는 다기능 레이다 자원관리 최적화에서 GA와 PSO의 성능을 정량적으로 비교하기 위해 다섯 가지 핵심 지표를 설정하였다. 첫 번째 지표인 목적함수값 OFV(objective function value)는 제약 위반 패널티, 탐지 성능, 추적 성능을 종합하여 계산한 단일 수치로, 값이 작을수록 자원 제약을 준수하면서도 운용 성능이 우수한 해를 의미한다. 두 번째 지표인 제약 만족도 CS(constraint satisfaction)는 면별 소요 자원이 최대 허용값을 초과한 정도를 나타내며, 0 이하일 경우 모든 면에서 시간 제약을 만족하는 운용안을 의미한다. 세 번째 지표인 탐색 커버리지 SCR(search coverage ratio)은 각 섹터의 탐지거리를 최대 탐지거리로 정규화하여 평균한 값으로, 값이 클수록 탐색 영역이 넓어 운용 상황인식 능력이 높다. 네 번째 지표인 추적 유지율 TRR(tracking retention ratio)은 전체 표적 중 유지되는 표적의 비율을 나타내며, 높은 값은 자원 제약 속에서도 고·중위험 표적을 효과적으로 유지하고 있음을 보여준다. 다섯 번째 지표인 계산 시간 CT(computation time)는 알고리즘 실행에 소요된 총 시간으로, 짧을수록 실시간 운용 환경에서 적용 가능성이 높다. 마지막으로 평가 횟수는 최적화 과정에서 목적함수가 호출된 총 횟수를 의미하며, 적을수록 동일한 성능을 더 적은 연산으로 달성했음을 나타낸다. 이와 같은 지표를 통해 두 알고리즘의 해의 품질, 제약 조건 만족 여부, 운용 성능, 계산 효율성을 종합적으로 평가할 수 있다.
다기능 레이다의 자원관리 최적화 성능을 분석하기 위해 세 가지 단계로 시뮬레이션을 수행하였다.
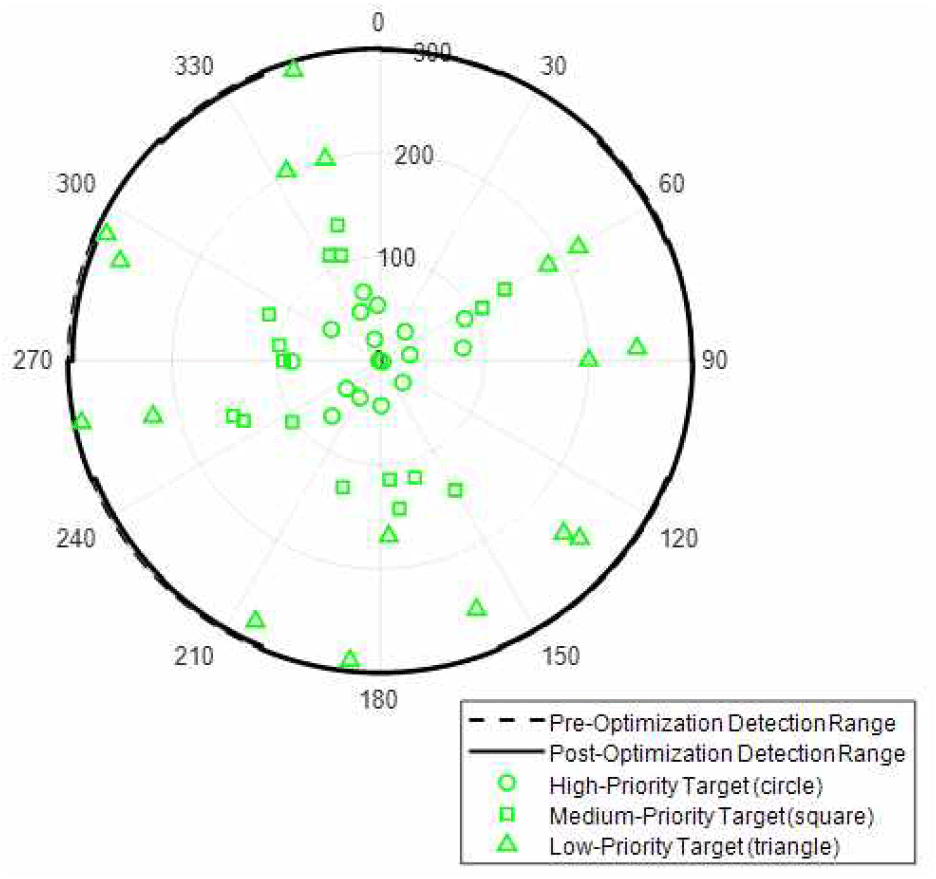
첫째, 자원이 충분한 상황에서의 다기능 레이다 운용 결과를 보면 그림 3과 같다. 이 경우 탄도탄 팬스 운용이 없으며, 모든 섹터가 최대 탐지 거리로 설정되고 표적 추적의 탈락이 발생하지 않는다. 탐색 커버리지와 추적 유지율 모두 1이며, 제약 만족도는 음수 값을 유지하여 자원 초과가 발생하지 않는다. 이는 정상 운용 환경에서 레이다가 안정적으로 전 영역을 탐지 및 추적할 수 있음을 의미한다.
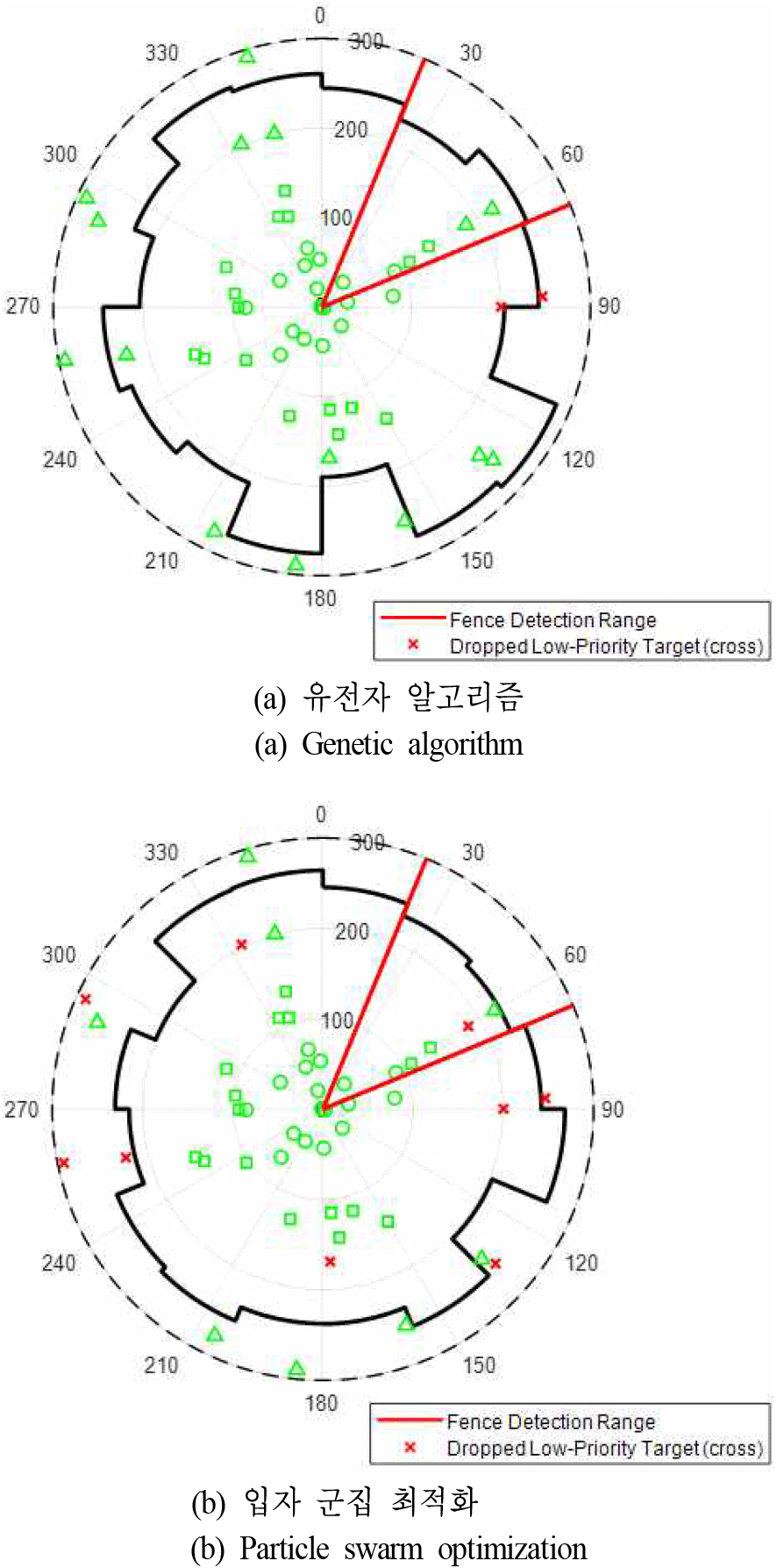
둘째, 탄도탄 팬스 운용에 따른 자원 제약 상황에서 GA와 PSO 기반 최적화를 각각 적용한 결과 그림 4와 같다. 두 알고리즘 모두 팬스 운용으로 증가한 탐색 부하를 보상하기 위해 일부 섹터에서 탐지거리를 축소하거나, 저위험 표적 위주로 추적을 중단하는 전략을 사용하였다. 두 알고리즘 모두 섹터별 최적화 후 탐색 커버리지가 줄어들었으며, 위험도에 따라 표적별 추적 유지 및 탈락된 것을 볼 수 있다. 특히, PSO의 경우 상대적으로 저위험 표적에 대한 추적 탈락 수가 더 많아지는 경향이 관찰되었으며, 이는 동일한 탐색 커버리지 수준을 유지하는 대신, 추적 측면에서 더 많은 조정을 통해 자원 여유를 확보하는 특성으로 해석된다.
셋째, 동일 조건에서 다양한 시나리오에 따라 최적화 알고리즘 결과를 비교하기 위해 1,000회 몬테카를로 시뮬레이션을 수행하였고, 그 결과는 표 3과 같다.
| Metric | GA | PSO |
|---|---|---|
| Objective function value | 82160.614 | 70349.053 |
| Constraint satisfaction | −2.591 | −4.906 |
| Search coverage ratio | 0.803 | 0.803 |
| Tracking retention ratio | 0.945 | 0.844 |
| Computation time | 1.202 | 0.466 |
목적함수값은 GA 82,160.614, PSO 70,349.053으로 PSO가 소폭 낮아(더 우수) 자원 초과 억제와 탐지·추적 균형의 측면에서 더 유리한 해를 도출하였다. 제약 만족도는 GA −2.591 ms, PSO −4.906 ms로 두 방법 모두 제약을 만족했으며, PSO가 더 큰 음수(절대값 기준)로 자원 여유가 더 큼을 보여준다. 탐색 커버리지는 양측 모두 0.803로 동일하여, 탐지거리 축소의 비율이 평균적으로 동일함을 보였다. 반면 추적 유지율은 GA 0.945, PSO 0.844로 차이가 나타났는데, 이는 PSO가 탐지 성능과 제약 준수를 우선시하는 과정에서 상대적으로 더 많은 표적을 추적에서 제외했기 때문으로 해석된다. 나아가 탐색 커버리지 및 추적 유지율의 경우 레이다에서 중요한 성능 지표로 GA와 PSO의 탐색 커버리지 및 추적 유지율의 변동성을 비교하였으며, 그 결과는 그림 5와 같다. 탐색 커버리지의 표준편차는 GA가 0.0065, PSO가 0.0035로 나타나 두 알고리즘 모두 매우 낮은 변동성을 보였다. 특히 PSO는 GA 대비 약 46 % 낮은 표준편차를 기록하여, 다양한 시나리오에서도 탐지 성능이 일정하게 유지되는 안정성이 더 높은 것으로 확인되었다. 반면, 추적 유지율의 표준편차는 GA가 0.0381, PSO가 0.0420으로, 탐색 커버리지보다 변동 폭이 크게 나타났다. 이는 추적 유지율이 시나리오별 자원 분배 결과에 더 민감하게 반응함을 의미한다. 또한 PSO의 표준편차가 GA보다 다소 큰 것은 PSO가 일부 시나리오에서 추적 대상을 더 과감하게 축소하여 자원을 확보하는 경향을 반영한다. 종합적으로, 탐색 안정성 측면에서는 PSO가, 추적 안정성 측면에서는 GA가 상대적으로 우수하다는 점을 확인할 수 있다.
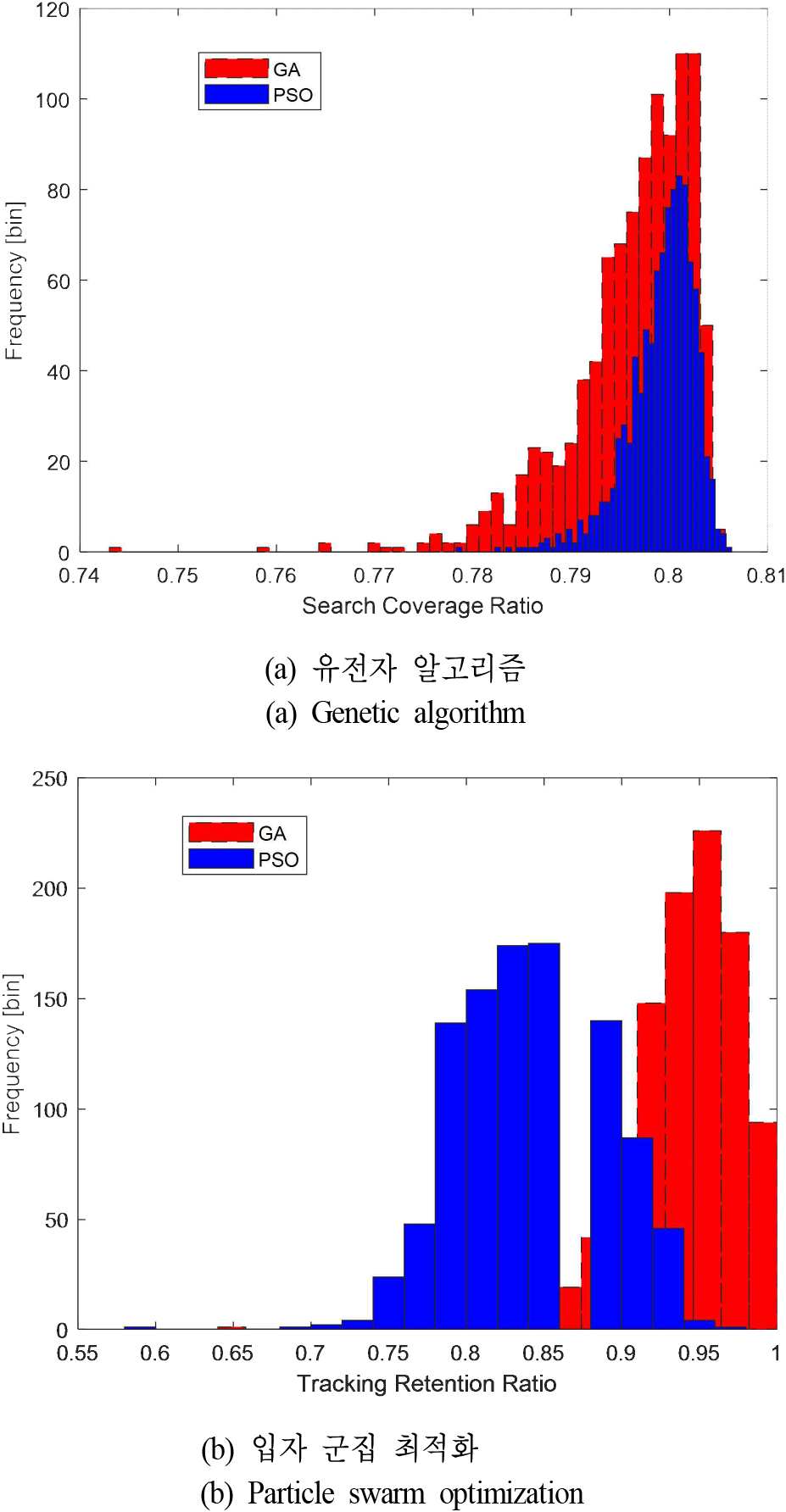
마지막 성능 지표인 계산 시간은 PSO 0.466 s, GA 1.020 s로 PSO가 약 2.19배 빠른 처리 속도를 보였으며, 이는 실시간 또는 준실시간 운용 환경에서 유리하게 작용할 수 있다. 종합하면, PSO는 낮은 OFV와 더 큰 자원 여유, 짧은 계산 시간을 확보하는 대신, TRR을 희생하는 경향이 있으며, GA는 상대적으로 추적 유지성을 높게 유지하는 성향을 보인다.
이러한 결과는 동일한 운용 조건에서 PSO가 GA 대비 전반적으로 높은 성능과 빠른 계산 속도를 제공함을 보여주며, 특히 탐색 커버리지 및 자원 효율성 측면에서 우수함을 확인할 수 있다.
IV. 결 론
본 논문에서는 다기능 레이다 운용 환경에서 발생할 수 있는 자원 충돌 문제를 해결하기 위해, 섹터 기반 자원관리 구조를 바탕으로 최적화 알고리즘을 활용하여 탐색 거리 조정 및 표적 추적 해제를 통한 자원관리 방안을 제안하였다. 특히, 탄도탄 위협 상황에서 추가적으로 수행되는 팬스 탐색 운용이 기존 자원 운용 계획을 초과하는 경우, 각 섹터의 탐색 거리 및 저우선순위 표적의 추적 여부를 조정함으로써 자원 제약을 만족시키는 실시간 운용 방안을 수립하는 데 중점을 두었다.
이를 위해 본 연구에서는 탐색 거리, 추적 대상, 팬스 운용 등 다차원 요소를 수식화한 자원 소모 모델을 구성하였으며, 면 단위 자원 제한 조건을 기반으로 한 목적함수를 정의하였다. 탐색 성능 손실, 자원 초과 페널티, 중요 표적 해제 패널티 등을 종합적으로 고려한 목적함수를 기반으로, GA와 PSO를 각각 적용하여 최적의 자원 분배 전략을 도출하였다. 또한 각 표적에 추적 우선순위를 부여하고, 제거 가능 표적에 한하여 최적화 변수로 정의함으로써 실제 운용 가능성을 고려한 모델링 구조를 제시하였다.
시뮬레이션 결과, PSO는 GA 대비 더 낮은 목적함수값 과 더 큰 자원 여유, 더 짧은 계산 시간을 달성하였다. 반면 추적 유지율은 GA가 유의하게 높아, 임무가 추적 유지성에 더 민감한 경우에는 GA가 선호될 수 있다. 즉, PSO는 탐지/제약 준수/계산 효율을, GA는 추적 유지성을 상대적으로 강조하는 해를 산출하는 것으로 판단된다. 이러한 결과는 탐색 커버리지 유지와 실시간성이 최우선이면 PSO, 고·중위험 표적의 추적 지속이 최우선이면 GA가 유리한 것과 같이 미션 요구도에 따른 알고리즘 선택 기준을 제시할 수 있다.
이렇듯 본 연구는 팬스 운용이라는 실전 운용 상황을 정량화하여 수식화하고, 이를 기반으로 실제 운용 가능한 자원관리 최적화 전략을 제시하였다는 점에서 이론적 기여와 실용적 적용 가능성을 동시에 가진다. 제안된 모델은 향후 다기능 레이다의 운용 알고리즘 설계, 전술 기반 자원 스케줄링, 실시간 운용 의사결정 지원체계 등에 활용될 수 있을 것으로 기대된다.
아울러, 본 연구의 결과는 국내 다기능 레이다 개발 및 방공체계 운용 환경에도 직접적으로 기여할 수 있다. 팬스 탐색과 같은 고자원 임무가 빈번히 발생하는 실제 운용 환경에서는, 본 연구에서 제시한 최적화 기반 자원관리 기법을 실시간 운용소프트웨어에 내장함으로써 시스템 효율성을 높일 수 있다. 또한 GA와 PSO는 각각 추적 안정성과 실시간성을 강조하는 특성을 가지므로, 임무 단계별 운용정책 수립(예: 초기 대응 시 PSO, 안정 추적 단계에서 GA) 에 유용한 설계 기준을 제공한다. 따라서 본 논문은 국내 방공체계의 자율운용 및 통합자원관리 체계 설계에 있어 참고 가능한 기술적 기반을 마련하였다는 점에서 학술적·실무적 의의를 갖는다.