The Journal of Korean Institute of Electromagnetic Engineering and Science

The Korean Institute of Electromagnetic Engineering and Science

J. Korean Inst. Electromagn. Eng. Sci. 2026; 37(1):33-42

pISSN: 1226-3133, eISSN: 2288-226X

DOI: https://doi.org/10.5515/KJKIEES.2026.37.1.33

논문/REGULAR PAPERS

소스 및 부하 임피던스를 고려한 3상 EMI 필터의 상전압 전달 특성 분석

한병진

, 권태욱

, 최경륜

, 나완수^†

Analysis of Phase Voltage Transfer Characteristics of a Three-Phase EMI Filter Considering Source and Load Impedances

Byeongjin Han

, Taewook Kwon

, GyeongRyun Choi

, Wansoo Nah^†

성균관대학교 전자전기컴퓨터공학과

Department of Electrical and Computer Engineering, Sungkyunkwan University

^†Corresponding Author: Wansoo Nah (e-mail: wsnah@skku.edu)

© Copyright 2026 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Sep 19, 2025; Revised: Oct 02, 2025; Accepted: Oct 13, 2025

Published Online: Jan 31, 2026

요 약

본 논문은 150 kHz~30 MHz의 대역폭을 갖는 3상 EMI 필터의 임피던스 및 주파수 의존적인 상전압 전달 특성을 분석하기 위한 모델링 기법을 제안하였다. 임의의 주파수 성분을 갖는 펄스가 1차측에 인가될 때, 2차측의 출력 전압 및 전류 응답과 이득을 예측하는 것을 목표로 하였으며, 소스, 필터, 부하를 각각 나타내는 세 개의 ABCD 파라미터 네트워크를 연쇄 결합(cascading)함으로써 시스템 수준의 전달 모델을 구성하였다. 제안 모델은 소스 및 부하 임피던스의 변화를 반영한 조건에서 필터 전달 특성을 해석할 수 있고, 실제 회로 환경에서 EMI 필터 성능 평가를 위한 신뢰성 있는 해석 기반을 제공한다.

Abstract

This paper presents a modeling approach for analyzing the impedance- and frequency-dependent phase voltage transfer characteristics of a three-phase EMI filter with a bandwidth of 150 kHz to 30 MHz. The analysis focuses on predicting the output voltage and current responses, as well as the output side voltage gain of the filter, when arbitrary frequency pulses are applied to the input side. A system-level model is constructed using three cascaded ABCD-parameter networks representing the source, EMI filter, and load. This study analyzed the EMI filter transfer characteristics under operating conditions, which demonstrate changes in the source and load impedance, and provides a reliable analytical framework for evaluating the performance of EMI filters in actual circuit environments.

Keywords: Voltage Transfer Characteristic; S-Parameters; ABCD Parameters; Three-Phase EMI Filter; Multiport Network Analysis

Ⅰ. 서 론

최근 산업용 시스템에서 사용되는 150 kHz~30 MHz 대역의 3상 EMI(전자파 간섭) 필터에서 출력 상전압 단자와 섀시 접지 사이에 그림 1과 같이 아킹(arcing) 흔적이 관찰되었다. 반면 입력 단자는 정상이었다. 이는 출력 단자에서 발생한 예기치 않은 고전압에 따른 절연 파괴로 추정되며, 고전압은 임의의 펄스 입력에 의해 유도된 것으로 판단된다. 이러한 이상 전압의 원인 규명을 위해 3상 EMI 필터의 전압 전달 특성 분석이 요구된다.

그림 1. | Fig. 1. 3상 EMI 필터의 출력단 상전압 단자와 섀시 접지 간 아킹 흔적 | Arcing trace between the output phase terminal and chassis ground in a three-phase EMI filter.

Download Original Figure

일반적으로 EMI 필터의 전달 특성은 소스 및 부하 임피던스가 각각 50 Ω일 때의 삽입 손실(insertion loss)로 특정된다^[1]. 앞선 EMI 필터의 고장 분석 사례에서도 입출력 단 임피던스를 50 Ω으로 정합하여 성능을 측정하였다^[2]. 그러나 실제 환경에서는 소스 및 부하 임피던스가 이상적이지 않으며, 이는 필터의 전달 특성에 영향을 미칠 수 있다^[3],[4]. 아울러 최근 연구에서는 IEC와 같은 표준에서 요구하는 150 kHz 이상에서의 EMI 특성이 아닌 150 kHz 미만 대역의 전도성 교란과 왜곡의 중요성을 지적한다^[5]. 이에 따라 EMI 필터 성능이 보장되지 않는 1 kHz부터 규격 경계부인 200 kHz까지를 관심 주파수로 설정한다.

본 연구는 소신호(small-signal) S-파라미터에 기초한 6×6 ABCD 파라미터 모델을 이용하여, 3상 EMI 필터의 1차측에서 2차측으로의 임피던스 및 주파수에 따른 상전압 전달 특성을 수식적으로 분석하기 위한 기법을 제안하였다. 소스, 필터, 부하를 각각 ABCD 파라미터로 표현하고, 이를 연쇄 결합(cascading)하여 전체 시스템 전달 특성을 해석하였다. 소스 및 부하 임피던스는 일반적인 산업 조건을 고려하여 설정하였으며, 제안 모델이 다양한 임피던스 및 주파수 조건에서 3상 EMI 필터의 상전압 및 전류 전달 특성을 예측할 수 있음을 보였다.

본 논문의 구성은 다음과 같다. Ⅱ장에서는 6포트 EMI 필터의 S-파라미터를 측정하고, 이를 기반으로 6×6 ABCD 파라미터 변환 방법을 설명한다. Ⅲ장에서는 소스, 필터, 부하의 ABCD 파라미터를 연쇄 결합한 전압 전달 이론을 제시한다. Ⅳ장에서는 다양한 소스 및 부하 임피던스 조건에서의 시뮬레이션으로 고전압 발생 조건을 예측한다.

Ⅱ. 3상 EMI 필터의 ABCD 파라미터

그림 2의 3상 EMI 필터는 정격 500 V_AC, 250 A이며, 150 kHz~30 MHz 범위에서 전도성 노이즈 감쇠 성능을 가지며 50/60 Hz의 전원 주파수에서 동작한다. 입력 단자는 R, S, T상이며 대응되는 출력 단자는 U, V, W상으로 구성된다. 따라서 3상 EMI 필터는 3 포트 입력과 3 포트 출력을 가지는 6 포트 네트워크로 정의되며 포트 1, 2, 3은 입력(R, S, T)에, 포트 4, 5, 6은 출력(U, V, W)에 각각 대응된다.

그림 2. | Fig. 2. 3상 EMI 필터 | Three-phase EMI filter.

Download Original Figure

S-파라미터 측정을 위해 각 포트에 SMA 커넥터를 장착하였고, 2포트 VNA인 Agilent사의 E5061B ENA series network analyzer를 이용하여 1~200 kHz까지 총 1,601개 포인트의 주파수 영역 측정을 수행하였다. 측정 시 사용하지 않는 포트는 모두 50 Ω으로 종단하여 임피던스 매칭을 유지하고 반사를 최소화하였다. 그림 3(a)와 같이 2포트 VNA를 사용하여 전체 6×6 S-파라미터 행렬을 구성하기 위해서는 포트 쌍의 모든 조합에 대해 측정이 필요하다. 이때 필요한 측정 조합 수는 15개 조합(6C2=15)이다^[6]. 그림 3(b)와 같이 2포트 측정의 반사 및 전달 특성을 통합하여 6×6 S-파라미터 행렬을 구성할 수 있다.

그림 3. | Fig. 3. 6×6 S-파라미터 측정 조합 및 결과 | Measurement combinations and results for 6×6 S-parameter matrix.

Download Original Figure

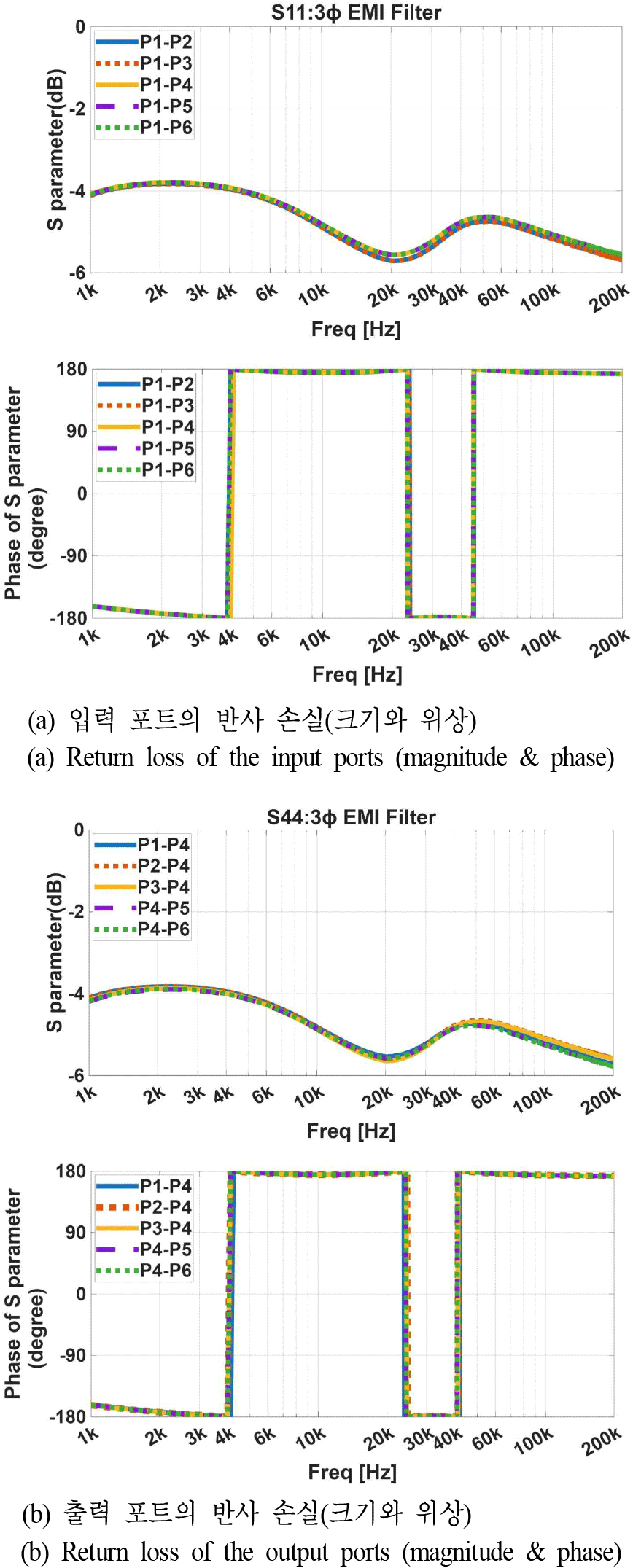
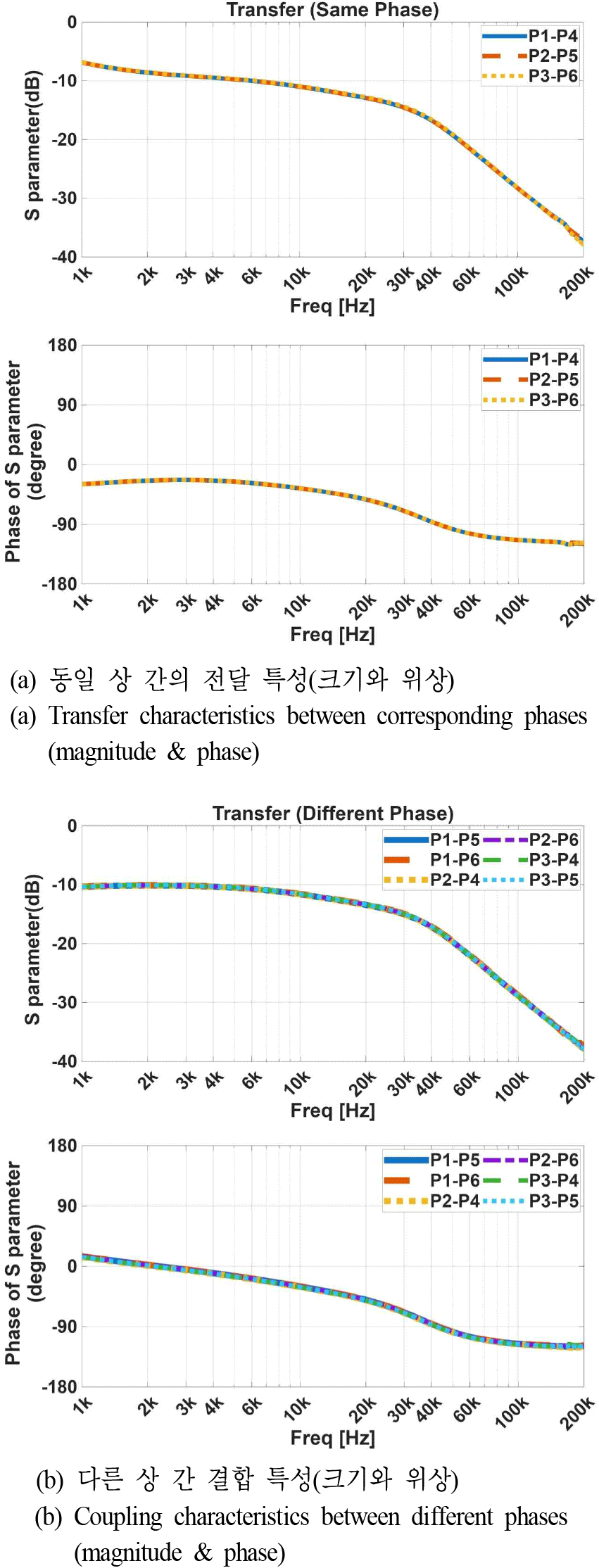
그림 3(a)의 측정 조합에 따라 반사 손실(return loss)은 포트별로 5회 반복 측정된다. 그림 4의 포트의 반사 손실 |S₁₁|과 |S₄₄|는 5회 측정 결과 높은 일치도를 보였고, 나머지 포트들도 동일한 경향을 확인하였다. 그림 5(a)는 동일 상 간 전달 특성(S₁₄, S₂₅, S₃₆), 그림 5(b)는 상 간 결합 특성(S₁₅, S₁₆, S₂₄, S₂₆, S₃₄, S₃₅)을 보여준다. 동일하게 각 전달 특성이 일관되게 나타나 측정된 S-파라미터의 신뢰성을 뒷받침한다. 또한 150 kHz 이상 대역에서는 삽입 손실이 −30 dB 이하로 EMI 필터 감쇠 성능을 나타낸다.

그림 4. | Fig. 4. 3상 EMI 필터 각 포트 반사 손실 | Return loss at each port of a three-phase EMI filter.

Download Original Figure

그림 5. | Fig. 5. 3상 EMI 필터 전달 및 결합 특성 | Transfer and coupling characteristics of the threephase EMI filter.

Download Original Figure

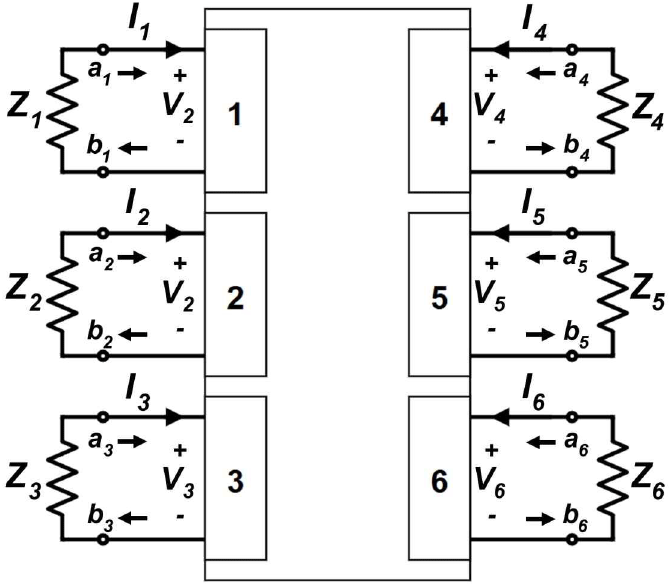
측정된 반사 및 전달 특성을 통합하여 6×6 S-파라미터 행렬을 구성하였고, 이를 ABCD 파라미터로 변환하였다^[7]. 입력 포트 3개와 출력 포트 3개를 가지는 6 포트 S-파라미터는 포트 n의 입사파 a_n과 반사파 b_n의 식 (1)로 정의된다. a_n과 b_n은 식 (2) 및 식 (3)과 같이 해당 포트의 전압 V_n 및 전류 I_n의 관계로 표현할 수 있다. Z_n는 포트 n의 종단 임피던스이며 gn는 식 (4)로 정의된다^[8]. 그림 6은 6 포트 네트워크의 a_n, b_n, V_n, I_n, Z_n을 나타낸다.

그림 6. | Fig. 6. 6 포트 네트워크 | 6-ports network.

Download Original Figure

식 (2) 및 식 (3)을 식 (1)에 대입하면 입력 포트 전압, 전류와 출력 포트 전압, 전류의 식 (5)가 유도된다. 행렬 P와 Q는 식 (6) 및 식 (7)과 같다. I는 단위행렬이다.

b 1 b 2 b 3 b 4 b 5 b 6 = S 11 S 12 S 13 S 14 S 16 S 16 S 21 S 22 S 23 S 24 S 25 S 26 S 31 S 32 S 33 S 34 S 35 S 36 S 41 S 42 S 43 S 44 S 46 S 46 S 51 S 52 S 63 S 54 S 5 S 56 S 61 S 62 S 63 S 64 S 65 S 66 a 1 a 2 a 3 a 4 a 5 a 6

(1)

a n = g n 2 V n + Z n I n

(2)

b n = g n 2 V n − Z n * I n

(3)

g n = 1 Re Z n

(4)

P V 1 V 2 V 3 I 1 I 2 I 3 = Q V 4 V 5 V 6 I 4 I 5 I 6

(5)

P = I − S p p g p − Z p * + S p p Z p g p − S q p g p − S q p g p Z p p = 1, 2, 3, q = 4, 5, 6 = 1 − S 11 g 1 − S 12 g 2 − S 13 g 3 − 1 + S 11 Z 1 g 1 − 1 + S 12 Z 2 g 2 − 1 + S 13 Z 3 g 3 − S 21 g 1 1 − S 22 g 2 − S 23 g 3 − 1 + S 21 Z 1 g 1 − 1 + S 22 Z 2 g 2 − 1 + S 23 Z 3 g 3 − S 31 g 1 − S 32 g 2 1 − S 33 g 3 − 1 + S 31 Z 1 g 1 − 1 + S 32 Z 2 g 2 − 1 + S 33 Z 3 g 3 − S 41 g 1 − S 42 g 2 − S 43 g 3 − S 41 g 1 Z 1 − S 42 g 2 Z 2 − S 43 g 3 Z 3 − S 61 g 1 − S 62 g 2 − S 63 g 3 − S 61 g 1 Z 1 − S 62 g 2 Z 2 − S 63 g 3 Z 3 − S 61 g 1 − S 62 g 2 − S 63 g 3 − S 61 g 1 Z 1 − S 62 g 2 Z 2 − S 63 g 3 Z 3

(6)

Q = S p q g q S p q g q Z q S q q − I g q S q q g q Z q + g q Z q * p = 1, 2, 3, q = 4, 5, 6 = S 14 g 4 S 15 g 5 S 16 g 6 S 14 g 4 Z 4 S 15 g 5 Z 5 S 16 g 6 Z 6 S 24 g 4 S 25 g 5 S 26 g 6 S 24 g 4 Z 4 S 25 g 5 Z 5 S 26 g 6 Z 6 S 34 g 4 S 35 g 5 S 36 g 6 S 34 g 4 Z 4 S 35 g 5 Z 5 S 36 g 6 Z 6 S 44 − 1 g 4 S 45 g 5 S 46 g 6 S 44 + 1 g 4 Z 4 S 45 + 1 g 5 Z 5 S 46 + 1 g 6 Z 6 S 54 g 4 S 55 − 1 g 5 S 56 g 6 S 54 + 1 g 4 Z 4 S 55 + 1 g 5 Z 5 S 56 + 1 g 6 Z 6 S 64 g 4 S 65 g 5 S 66 − 1 g 6 S 64 + 1 g 4 Z 4 S 65 + 1 g 5 Z 5 S 66 + 1 g 6 Z 6

(7)

식 (5)의 행렬 P를 이항하여 식 (8)로 나타내면 ABCD 파라미터의 전압, 전류 관계와 동일함을 알 수 있다. 결과적으로 행렬 P와 Q로 ABCD 파라미터가 유도된다. 위첨자 H는 에르미트(Hermitian) 전치를 의미한다.

V 1 V 2 V 3 I 1 I 2 I 3 = P H P − 1 P H Q V 4 V 5 V 6 I 4 I 5 I 6 = A 11 A 12 A 13 B 11 B 12 B 13 A 21 A 22 A 23 B 21 B 22 B 23 A 31 A 32 A 33 B 31 B 32 B 33 C 11 C 12 C 13 D 11 D 12 D 13 C 21 C 22 C 23 D 21 D 22 D 23 C 31 C 32 C 33 D 31 D 32 D 33 V 4 V 5 V 6 I 4 I 5 I 6

(8)

Ⅲ. ABCD 파라미터 연쇄 결합 전압 전달 모델

선행 연구에서는 단상 시스템에 대해 소스-시스템-부하 모델을 이용한 전압 전달 특성이 제시된 바 있다^[9]. 그러나 본 연구의 3상 EMI 필터는 그림 7(a)와 같이 상 간 부하(Z_UV, Z_VW, Z_UW)가 연결되는 Δ(delta) 결선 구조를 사용하므로, 단상 모델을 직접 적용하기 어렵다. 그림 7(b)는 제안하는 3상 소스-필터-부하 모델이다. 식 (9)의 Δ-Y 변환을 이용해 부하를 Y 결선으로 등가화하여, 상간 전압 대신 중성선 전압으로 시스템 출력을 단순화하였다^[10]. 해당 모델의 각 요소는 소스 전압(V_R, V_S, V_T), 전류(I_R, I_S, I_T), 임피던스(Z_R, Z_S, Z_T), EMI 필터 입력 전압(V₁, V₂, V₃), 전류(I₁, I₂, I₃), EMI 필터 출력 전압(V₄, V₅, V₆), 전류(I₄, I₅, I₆), 부하 임피던스(Z_U, Z_V, Z_W), 전류(I_U, I_V, I_W), 중성점 전압(V_N)으로 정의된다.

Z U = Z U V Z U W Z U V + Z V W + Z U W Z V = Z U V Z V W Z U V + Z V W + Z U W Z W = Z V W Z U W Z U V + Z V W + Z U W

(9)

그림 7. | Fig. 7. 3상 시스템의 소스-필터-부하 모델 | Block diagram of three-phase source-filter-load model.

Download Original Figure

3-1 소스 및 부하 임피던스의 ABCD 파라미터 표현

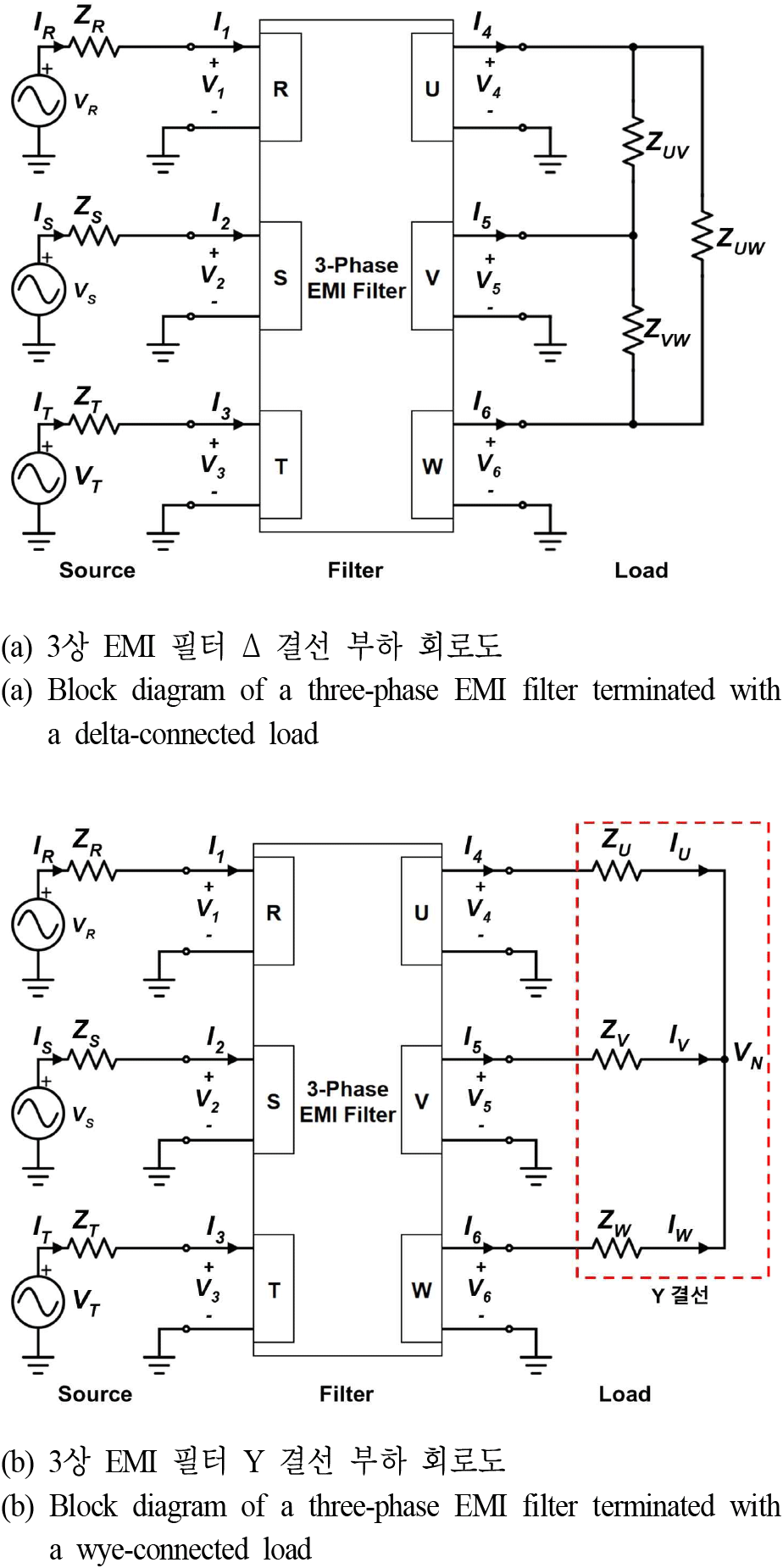
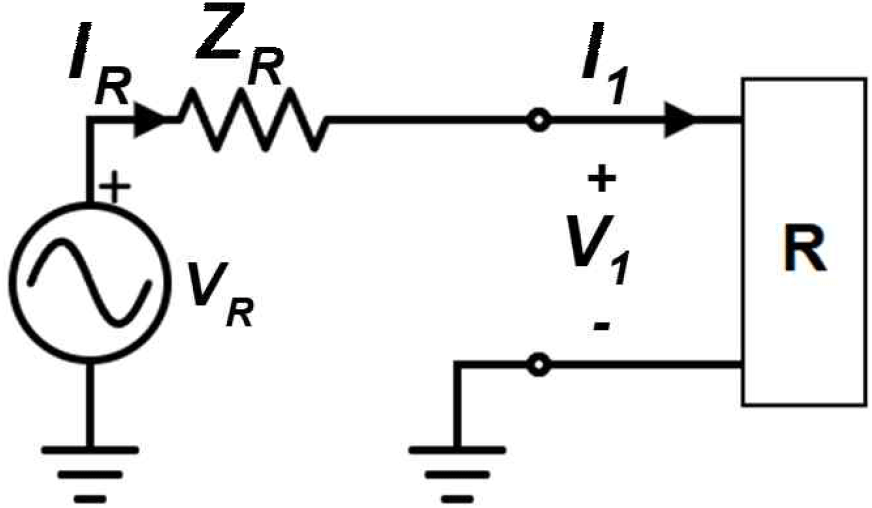
그림 8은 포트 1의 소스와 필터 입력단 회로이다. 소스 전압과 전류(V_R, I_R) 그리고 입력단 전압과 전류(V₁, I₁)의 관계를 소스 임피던스 Z_R이 포함된 ABCD 파라미터로 식 (10)과 같이 표현하였다. 이를 3상으로 확장하여 소스 임피던스 Z_R, Z_S, Z_T를 포함하는 6×6 ABCD 파라미터 식 (11)로 정리하였다.

V R I R = 1 Z R 01 V 1 I 1 V R = V 1 + I 1 Z R I R = I 1

(10)

V R V S V T I R I S I T = 100 Z R 00 0100 Z S 0 00100 Z T 000100000010000001 V 1 V 2 V 3 I 1 I 2 I 3

(11)

그림 8. | Fig. 8. 포트 1 소스-필터 입력 회로 | Source-filter input circuit at port 1.

Download Original Figure

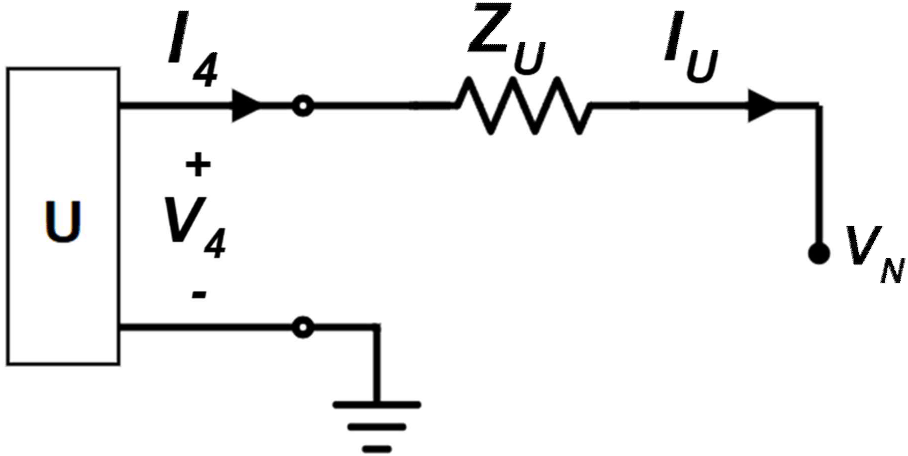
그림 9는 포트 4의 필터 출력단과 부하 회로이다. 필터 출력단 전압과 전류(V₄, I₄) 그리고 부하의 Y결선 중성점의 전압과 전류(V_N, I_U) 관계를 부하 임피던스 Z_U를 포함하는 ABCD 파라미터로 식 (12)에 정의하였고, 동일하게 이를 3상으로 확장하여 부하 임피던스 Z_U, Z_V, Z_W를 포함하는 6×6 ABCD 파라미터 식 (13)을 도출하였다.

V 4 I 4 = 1 Z U 01 V N I U V 4 = I U Z U + V N I 4 = I U

(12)

V 4 V 5 V 6 I 4 I 5 I 6 = 100 Z U 00 0100 Z V 0 00100 Z W 000100000010000001 V N V N V N I U I V I W

(13)

그림 9. | Fig. 9. 포트 4 필터 출력-부하 회로 | Filter output-load circuit at port 4.

Download Original Figure

3-2 ABCD 파라미터 연쇄 결합 모델

소스, EMI 필터, 부하의 6×6 ABCD 파라미터를 연쇄 결합하면 식 (14)와 같이 시스템 전압 및 전류 관계가 성립하며, 식 (15)는 중성점 전류의 합이 0임을 나타낸다. 식 (14) 및 식 (15)를 이용하면 임의의 소스 V_R, V_S, V_T에 따른 중성점 전압(V_N), 소스 전류(I_R, I_S, I_T), 부하 전류(I_U, I_V, I_W)를 소스 및 부하 임피던스와 EMI 필터의 ABCD 파라미터의 관계로 정의할 수 있다. 정의된 전압, 전류를 식 (11) 및 식 (13)에 적용하면 EMI 필터 입력 전압(V₁, V₂, V₃), 전류(I₁, I₂, I₃), EMI 필터 출력 전압(V₄, V₅, V₆), 전류(I₄, I₅, I₆)를 유도할 수 있다. 따라서 3상 소스-필터-부하 모델의 전압, 전류를 임피던스와 ABCD 파라미터를 이용한 수식으로 모두 도출하였다.

V R V S V T I R I S I T = 100 Z R 00 0100 Z S 0 00100 Z T 000100000010000001 S o u r c e × A 11 A 12 A 13 B 11 B 12 B 13 A 21 A 22 A 23 B 21 B 22 B 23 A 31 A 32 A 33 B 31 B 32 B 33 C 11 C 12 C 13 D 11 D 12 D 13 C 21 C 22 C 23 D 21 D 22 D 23 C 31 C 32 C 33 D 31 D 32 D 33 F i l t e r × 100 Z U 00 0100 Z V 0 00100 Z W 000100000010000001 L o a d × V N V N V N I U I V I W

(14)

I U + I V + I W = 0

(15)

3-3 제안 모델의 수식 검증

전압 전달 특성은 전압 이득(voltage gain)으로 나타내며, 식 (16)과 같이 G_V로 정의하였다. 전압 이득을 앞서 유도한 수식을 이용한 계산값과 실제 측정값을 비교하여 모델을 검증하였다.

G V = V O u t V I n

(16)

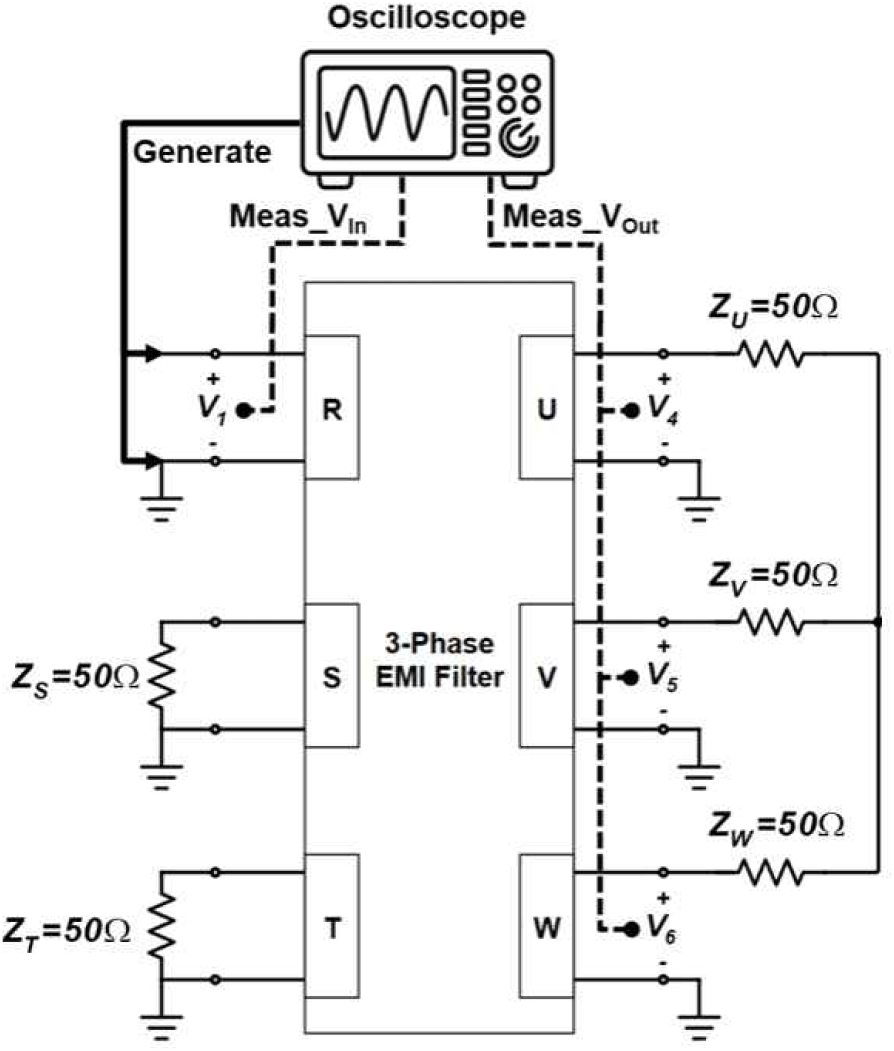
그림 10과 같이 Keysight사의 DSOX1102G 오실로스코프를 사용하였다. 내장된 함수 발생기(function generator) 에서 1~200 kHz 주파수 범위에서 로그 스케일로 20개 포인트(1~9 k[1 k 간격], 10~90 k[10 k 간격], 100 k, 200 k)를 선정하여 R상에 단일 주파수 사인파를 인가하였고, R, U, V, W 각 상의 전압을 측정하였다. 즉, 소스 전압 V만 인가되는 조건(V_S=V_T=0V)에서 포트 1 입력 전압(V₁)과 포트 4, 5, 6의 출력 전압(V₄, V₅, V₆)을 측정하였다. 소스 임피던스 Z_S, Z_T와 부하 임피던스 Z_U, Z_V, Z_W는 모두 50 Ω으로 설정하였다.

그림 10. | Fig. 10. 전압 이득 측정 셋업 | Voltage gain measurement setup.

Download Original Figure

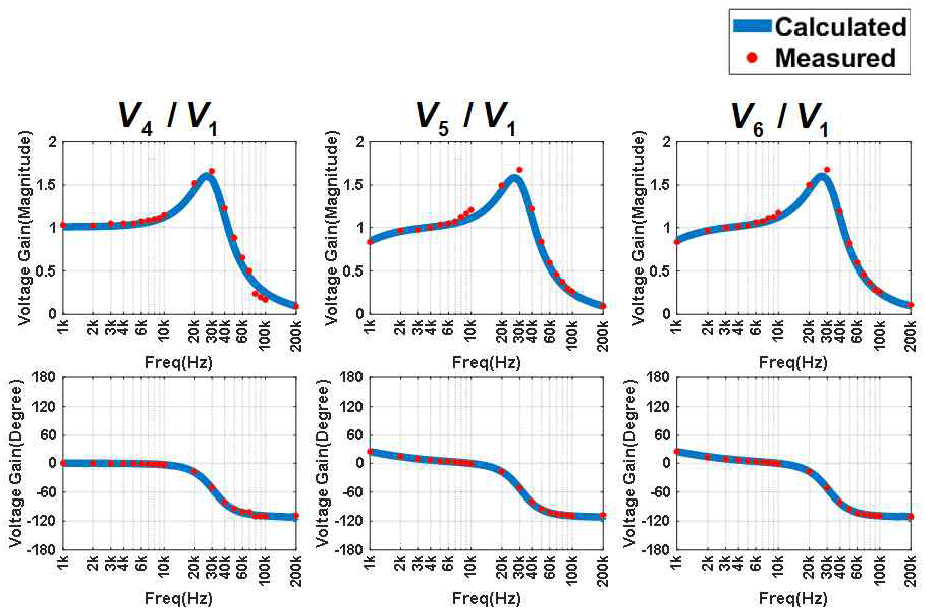
전압 이득 V₄/V₁, V₅/V₁, V₆/V₁의 계산값과 측정값은 그림 11과 같다. 실선으로 표기된 계산값과 20개 주파수 측정값이 전반적으로 잘 일치하였다. 이를 통해 도출한 수식의 타당성과 모델의 신뢰성을 검증하였다.

그림 11. | Fig. 11. 단일 소스에 대한 전압 이득 계산 및 측정 결과 (크기와 위상) | Calculated and measured voltage gain for a singlephase excitation (magnitude & phase).

Download Original Figure

Ⅳ. 소스 및 부하 임피던스에 따른 전압 전달 특성

Ⅲ장에서 검증한 수식을 이용하여 3상 EMI 필터 시스템의 전압 전달 특성을 분석하였다. 3상 소스의 주파수와 위상차 그리고 소스 및 부하 임피던스 조합에 따라 최대 전압 이득이 나타나는 조건이 고전압 발생 조건이 된다. 분석에 사용한 조건은 표 1과 같다. 주파수 범위는 1~200 kHz이며, 임의의 주파수 입력인 3상 소스의 크기는 각각 1 V이다. V_R의 위상은 0°, V_S와 V_T는 −180°~180° 범위를 10° 간격으로 정의하여 다양한 입력 조건을 정의하였다. 소스 임피던스(Z_R, Z_S, Z_T)는 이상적인 0 Ω 또는 50 Ω으로 설정하였다. 부하는 실제 시스템을 모사하는 Δ 결선 상 간 임피던스(Z_UV, Z_VW, Z_UW)를 50 Ω 또는 부하의 개방(open) 상태를 의미하는 1 MΩ으로 설정하고, 계산 과정에서 식 (9)를 사용하여 Y 결선 임피던스(Z_U, Z_V, Z_W)로 변환하였다. 이에 따라 총 82,944개 조합에 대한 전압 이득을 Matlab으로 시뮬레이션하였다.

표 1. | Table 1. 3상 소스 전원 및 임피던스 조건 | Condition of 3-phase source voltages and impedance.

Condition		Number of cases
Frequency	1～200 kHz	-
Magnitude of V_R, V_S, V_T	1 V	-
Phase of V_R	0°	-
Phase of V_S	−180°～180° (10° interval)	36
Phase of V_T	−180°～180° (10° interval)	36
Source impedance (Z_R, Z_S, Z_T)	0 Ω, 50 Ω	2×2×2=8
Load impedance (Z_UV, Z_VW, Z_UW)	50 Ω, 1 MΩ(open)	2×2×2=8
Total		82,944

Download Excel Table

각 출력 전압(V₄, V₅, V₆)에 대한 최대 전압 이득 시뮬레이션 결과는 그림 12이다. 그림 12(a) V₄ 기준 소스 주파수 41 kHz, 위상차 V_S=180°, V_T=110°, 소스 임피던스 Z_R, Z_S, Z_T=0 Ω, 부하 임피던스 Z_UV, Z_VW, Z_UW는 모두 개방(1 MΩ)인 조건에서 최대 이득 2.66배를 보였다.

그림 12. | Fig. 12. 입력 전압에 대한 출력 전압 비(크기와 위상) | Voltage gain relative to source volatage (magnitude & phase).

Download Original Figure

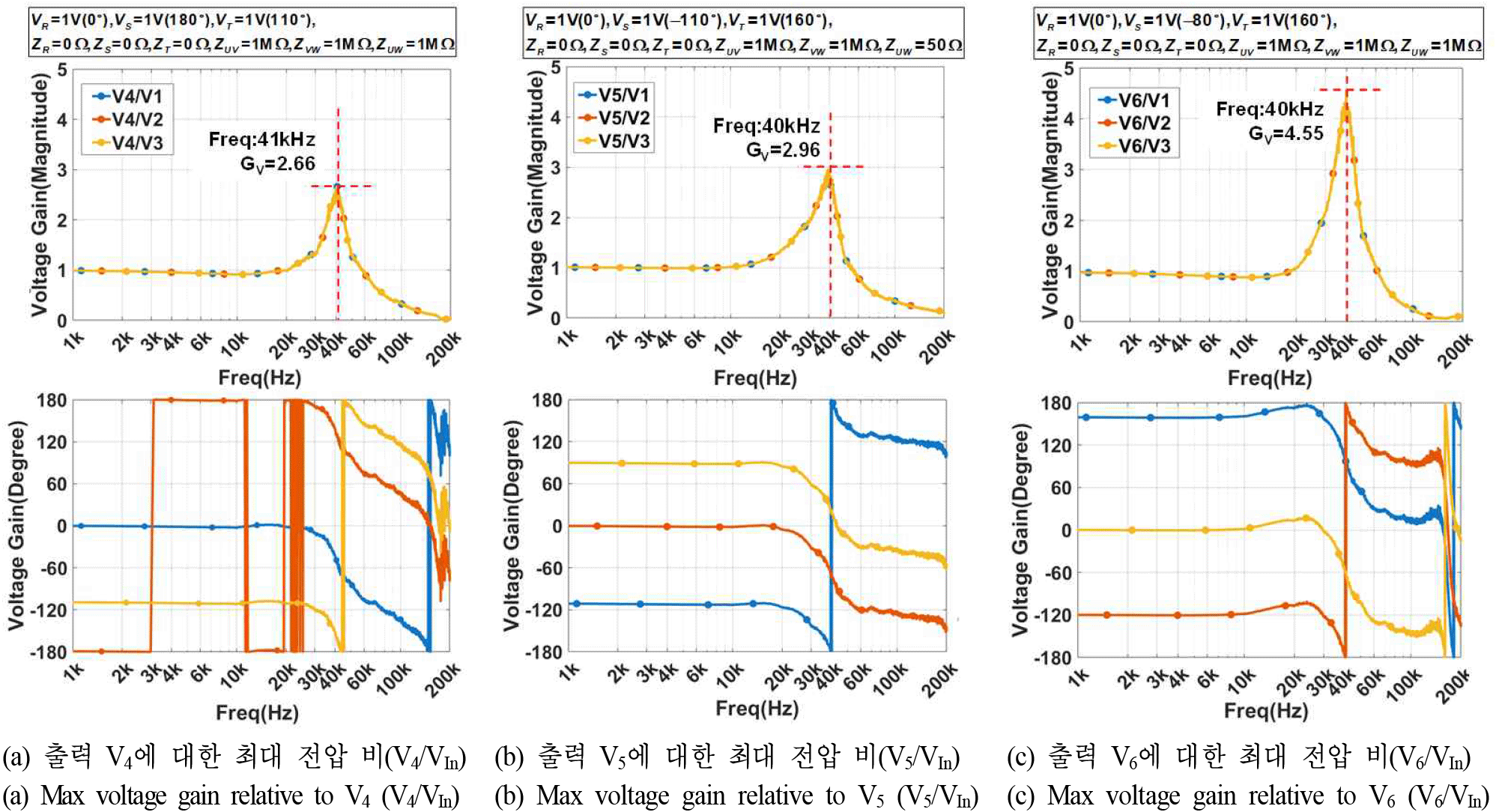
그림 12(b) V₅에 대해서는 소스 주파수 40 kHz, 위상차 V_S=−110°, V_T=160°, 소스 임피던스 Z_R, Z_S, Z_T=0 Ω, 부하 임피던스 Z_UV, Z_VW=1 MΩ, Z_UW=50 Ω일 때 최대 이득 2.96배가 확인되었다. 마지막으로 그림 12(c) V₆에서 모든 출력 중 가장 높은 전압 이득 4.55배가 관찰되었다. 조건은 소스 주파수 40 kHz, 위상차 V_S=−80°, V_T=160°, 소스 임피던스 Z_R, Z_S, Z_T=0 Ω, 부하 임피던스 Z_UV, Z_VW, Z_UW=1 MΩ이다.

Ⅴ. 결 론

본 논문은 150 kHz~30 MHz 대역의 3상 EMI 필터를 대상으로, 소스, 필터, 부하를 6×6 ABCD 파라미터로 모델링하고 이를 연쇄 결합하여 시스템 수준의 상전압 전달 특성을 해석하는 방법을 제안하였다. 제안 모델은 임의의 소스 전압과 소스 및 부하 임피던스 변화가 전압 이득에 미치는 영향을 정량적으로 평가할 수 있게 하였다.

모델의 타당성은 1~200 kHz 구간에서 계산값과 오실로스코프 측정값의 전반적인 일치로 검증되었다. 또한 총 82,944개 조합을 비교하여 소스 주파수 40 kHz, 위상차 V_S=−80°, V_T=160°, 소스 임피던스 0 Ω, 부하 임피던스 부하 개방(1 MΩ) 조건에서 최대 전압 이득(최대 4.55배)이 발생함을 확인하였다. 이는 실제 운영 조건에서의 임피던스 변화를 반영하여 고전압 발생 위험을 사전에 식별할 수 있음을 보여준다.

제안 모델은 (i) S-파라미터 기반의 측정 가능 파라미터로 구성되어 재현성이 높고, (ii) 임피던스 불일치 및 운전 조건 변동을 모델 수준에서 직접 반영할 수 있으며, (iii) 주파수, 위상, 임피던스 조합에 대한 의존성 분석에 바로 적용 가능하다는 점에서 실무적 효용이 크다. 향후 유사 전력전자 시스템 해석에 폭넓게 활용될 것으로 기대된다.

Acknowledgements

이 연구는 2023학년도 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. 2023R1A2C2008116).

References

[1].

S. Wang, F. C. Lee, and W. G. Odendaal, “Characterization and parasitic extraction of EMI filters using scattering parameters,” IEEE Transactions on Power Electronics, vol. 20, no. 2, pp. 502-510, Mar. 2005.

[2].

S. B, Jung, J. B. Yoon, “A study on failure analysis and improvement for the input EMI filter of power converter unit,” Journal of the Korean Society of Mechanical Technology, vol. 25, no. 3, pp. 410-416, Jun. 2023.

[3].

S. J. Briggs, D. J. Savignon, P. T. Krein, and M. S. Kim, “The effects of nonlinear loads on EMI/RFI filters,” IEEE Transactions on Industry Applications, vol. 31, no. 1, pp. 184-189, Jan.-Feb. 1995.

[4].

S. Jiang, Y. Liu, H. Wang, G. Wang, J. Yan, and J. Peng, “Effective EMI filter design method of single-phase inverter based on noise source impedance,” in 2018 IEEE International Power Electronics and Application Conference and Exposition(PEAC), Shenzhen, Nov. 2018.

[5].

Z. Tang, F. Johansen, and P. Davari, “Closed-loop impedance modeling and analysis of three-phase active rectifier below 150 kHz frequency range,” in 2023 25th European Conference on Power Electronics and Applications (EPE'23 ECCE Europe), Aalborg, Sep. 2023.

[6].

K. Kim, W. Nah, “High frequency transfer characterization of a three phase transformer using two-port vector network analyzer,” in 13th International Conference on Development in Power System Protection 2016(DPSP), Edinburgh, Mar. 2016.

[7].

M. Ma, F. You, M. Wei, T. Qian, Y. Chen, and M. Pan, et al., “A generalized multiport conversion between S parameter and ABCD parameter,” in 2022 International Conference on Microwave and Millimeter Wave Technology (ICMMT), Harbin, Aug. 2022.

[8].

D. M. Pozar, Microwave Engineering, Hoboken, NJ, John Wiley & Sons, 2009.

[9].

K. Kim, S. Kim, and W. Nah, “Voltage transfer characteristics of an insulation transformer up to 1 MHz,” IEEE Transactions on Electromagnetic Compatibility, vol. 58, no. 4, pp. 1207-1216, Aug. 2016.

[10].

J. D. Irwin, R. M. Nelms, Basic Engineering Circuit Analysis, Hoboken, NJ, John Wiley & Sons, 2015.