Ⅰ. 서 론
최근 재사용 로켓 기술과 소형 위성 제작 기술의 발전으로 로켓 발사 및 위성 제작 비용이 크게 절감됨에 따라, 전 세계적으로 위성 발사, 우주 탐사, 저궤도 통신 네트워크 구축 등 우주활동이 가속화되고 있다[1],[2]. 이로 인해 인공위성이나 우주 쓰레기(debris)와 같은 인공우주물체의 수가 매년 급증함에 따라, 우주물체 간 충돌이나 지상 추락 위험이 크게 높아지고 있다[3]. 이러한 문제를 사전에 식별하고 효과적으로 대응하기 위해, 저궤도 위성과 우주물체의 위치를 정확하게 파악하고 효율적으로 감시·관리하는 기술이 필수적으로 요구된다. 이러한 배경에서 우주감시레이다(space surveillance radar)는 지구 저궤도에 위치한 표적을 탐지하고, 위치를 추정하는 핵심 감시 수단으로 활용되고 있다.
우주감시레이다는 지상에서 우주를 향해 고출력 전파를 송신하고, 표적에서 반사되어 돌아온 신호를 다수의 수신 소자를 통해 포착한 뒤, 신호 처리를 통해 표적의 거리와 방향을 추정하여 3차원 위치를 계산한다[4]. 일반적으로 우주감시레이다 시스템에서는 전파가 자유공간(free space)을 진행한다고 가정하고 표적의 위치를 추정한다.
하지만 레이다와 표적 사이를 오가며 지구 대기권을 통과하는 전파는 대기의 영향을 받아 특성이 변화한다. 따라서 자유공간을 가정하는 경우, 표적의 위치 추정에 대기에 의한 굴절이나 시간 지연과 같은 전파 특성의 변화가 반영되지 않아, 오차가 발생할 수 있다[5],[6]. 일반적으로 대기에 의한 영향은 전파가 대기권을 통과하는 경로 길이에 비례하여 증가한다. 특히 우주감시레이다 시스템에서 탐지·추적하고자 하는 우주 물체는 130~2,000 km 고도에 위치하고 거리(range)가 수천 km에 이르는 초장거리 표적이므로, 일반적인 지상 기반 장거리 레이다 시스템에서 중단거리 표적을 탐지하는 경우와 비교하여, 전파가 대기의 영향을 더 크게 받게 된다. 이로 인해 우주 물체의 위치에는 최대 수 km 수준의 위치 오차가 발생할 수 있다[7]. 따라서 우주물체의 위치를 정확히 계산하기 위해서는 굴절률과 전리층의 전자 밀도 등 대기권의 매질 특성을 종합적으로 고려해야 한다.
기존에는 국내 기상관측소의 고층 기상 관측 데이터를 기반으로 지역 및 계절별 굴절률 프로파일을 모델링하고, 광선추적법(ray tracing)을 적용하여 주파수별 전파의 시간 지연 및 표적의 고도별 굴절 오차 등을 정량적으로 분석한 연구가 수행되었다[8]. 또한, 3차원 비균질 전자 밀도 데이터를 활용해 전리층을 통과하는 전자파의 전파 경로를 모의하고, 고도각·주파수·태양활동 등 다양한 변수에 따라 전리층에 의한 표적의 굴절 오차를 정밀하게 계산한 연구도 수행되었다[9]. 하지만 이러한 방법론을 우주감시레이다 시스템에 적용하여 모의된 우주 환경에서 다수 표적에 대한 오차 보정 연산을 GPU(graphic processing unit)를 활용하여 가속화한 연구는 수행되지 않았다. 실제 운용 환경에서는 표적 획득 당시의 대류권 및 전리층 데이터를 적용하여 능동형 위상배열 안테나가 수신한 수천에서 수만 개에 이르는 표적 정보를 짧은 시간 안에 처리해 보정된 위치로 변환해야 하므로, 이를 가능하게 하는 GPU 기반 병렬처리 알고리즘에 대한 연구가 요구된다.
본 논문에서는 고층 기상 관측 데이터 및 전리층 전자 밀도 데이터를 바탕으로 모의된 우주 환경에서, 광선추적법을 활용하여 다수의 표적에 대한 우주 환경 오차 보정을 가속화하는 GPU 기반 병렬처리 알고리즘을 제안한다. 제안된 알고리즘은 엔비디아(NVIDIA)에서 개발한 GPGPU (general-purpose computing on graphics processing units) 아키텍처인 CUDA(compute unified device architecture)를 기반으로 구현되었으며, 각 표적에 대한 연산을 GPU의 개별 코어에 병렬 분산하여 수행함으로써 전체 연산 시간을 효과적으로 단축할 수 있도록 설계되었다.
본 논문은 다음과 같이 구성된다. Ⅱ장에서는 우주 전파 환경을 모델링하는 방법에 대해 설명하였다. Ⅲ장에서는 모델링 결과를 바탕으로, 대류권과 전리층을 통과하는 전자파의 전파 경로 및 시간 지연 특성을 모델링하는 방법과 우주 환경에서의 전파 특성 분석 결과를 제시하였다. Ⅳ장에서는 대기에 의해 발생하는 레이다 오차 특성을 계산하는 알고리즘을 제안하고, 오차 특성을 분석하였다. Ⅴ장에서는 GPU를 활용하여 다수의 표적에 대한 오차 보정 알고리즘을 구현하고, 기존 CPU 기반 연산 방법과의 연산 시간을 비교하였다. 마지막으로 Ⅵ장에서 본 논문의 결론을 기술하였다.
Ⅱ. 우주 전파 환경 모델링
전자파는 서로 다른 굴절률을 갖는 두 매질의 경계면에서 굴절 및 반사하는 특성을 갖는다[10]. 그리고 대기권은 고도에 따라 서로 다른 굴절률을 갖는 다수의 매질로 구성되어 있다. 따라서 대기권 각 층의 굴절률을 알면, 대기권을 통과하는 전자파의 전파 특성을 예측할 수 있다. 대기권은 전자파와의 상호작용 특성에 따라 대류권(troposphere)과 전리층(ionosphere)으로 구분된다. 대류권은 고도 0~30 km에 이르는 영역으로, 대류권을 통과하는 전자파의 전파 특성은 대기 굴절률에 의해 결정되며 다음과 같은 식에 의해 계산된다[11].
식 (1)~식 (2)에서 n은 굴절률, N은 굴절 계수(N-units), T는 절대 온도(K), P는 기압(hPa), e는 수증기압 (hPa)을 나타낸다[12]. 대기 굴절률의 예측에 필요한 기온·기압·상대습도 데이터는 라디오존데(radiosonde)를 이용해 획득할 수 있다. 라디오존데는 온도·압력·습도 센서를 탑재한 무선 송신 장치와 이것이 부착된 헬륨 또는 수소를 채운 기구로 구성되며, 최대 30 km 고도까지 상승하면서 다양한 기상 정보를 실시간으로 수집한다[13]. 본 논문에서는 전파가 한반도 상공의 대기를 통과하는 시나리오를 가정하고, 대기에 의한 전파 특성 변화를 예측하기 위해 한반도 상공의 대기 굴절률을 활용하였다. 대기 굴절률은 대한민국 및 주변국 9개 기상관측소(백령도, 포항, 창원, 흑산도, 제주도 등)에서 제공하는 라디오존데 관측 데이터를 활용하여 예측할 수 있지만[14], 관측 데이터는 기상 관측소가 위치한 일부 지점에서만 제공되기 때문에, 본 논문에서는 일부 관측 데이터와 공간보간법을 활용하여 미관측 지점의 대기 굴절률을 예측하였다[15]. 그림 1은 관측 데이터와 공간보간법을 활용하여 예측된 2025년 4월 10일 00:00:00 UTC 기준 한반도 상공의 대기 굴절률을 시각화한 것이다. 해당 시각, 예측에 활용된 관측소의 대기 굴절률 기울기는 표준 대기 상태에서의 기울기(약 −40 N-units/km)에 가까웠기에, 이를 통해 예측된 전체 영역의 대기 상태 또한 표준 대기와 유사한 특성을 보였다. 이러한 과정으로 예측된 대기 굴절률의 3차원 분포는 고도 범위 0~30 km의 대류권을 통과하는 전자파의 전파 특성 예측에 활용된다.
전리층은 고도 90~1,000 km에 이르는 영역으로, 이곳의 대기 구성 입자들은 태양의 극자외선 및 X선에 의해 전자와 양이온으로 분리되어 플라즈마 상태로 존재한다[16]. 이러한 플라즈마는 전파가 전리층을 통과할 때 전파 경로, 속도, 위상 등에 영향을 미친다. 이와 같은 영향은 전리층의 굴절률을 통해 정량적으로 계산할 수 있으며, 전리층의 굴절률은 주파수, 전자 밀도, 지구 자기장, 전자 충돌 주파수 등을 입력 변수로 하는 Appleton-Hartree 방정식으로 계산된다. 우주 감시 레이다 시스템에서 주로 사용되는 수 GHz 이상의 주파수 대역에서는 전자의 충돌 및 지구 자기장이 전파 특성에 미치는 영향이 무시할 수 있을 정도로 작아지므로, 전리층에서의 굴절률은 식 (3)과 같이 근사하여 나타낼 수 있다[17],[18].
식 (3)에서 N은 전리층 전자 밀도(electron/m3), e는 전자의 전하량(C), ω0는 각 주파수(rad/s), ε0는 자유공간 유전율(F/m), m은 전자의 질량(kg)을 나타낸다. 전리층의 굴절률은 대기 굴절률과 달리 1보다 작은 값을 갖는데, 이는 대기의 중성 분자와 달리, 전리층의 자유전자는 전파와 상호작용하며 위상이 앞선 파동을 재방출해, 전체 파동의 위상 속도를 빛의 속도보다 빠르게 만들기 때문이다[19]. 이로 인해, 전리층은 주파수에 따라 굴절률이 급격히 변하는 분산(dispersion) 매질의 특성을 나타낸다.
전리층 굴절률을 결정하는 핵심 변수인 전리층 전자 밀도 데이터를 획득하기 위해 고려할 수 있는 대표적인 모델로는 NeQuick과 IRI(international reference ionosphere)가 있다. NeQuick은 두 지점의 위치, 시간, 태양활동 지수 등을 입력으로 받아 두 지점 간의 총 전자 함유량(TEC, total electron content)을 빠르게 제공하는 장점이 있다[20]. 그러나 특정 좌표와 좌표 사이의 TEC를 제공할 뿐, 전파 경로를 예측하기 위한 위도·경도·고도 기반의 3차원 전자 밀도 프로파일을 제공하지 않는다. 반면, IRI 모델은 다양한 위성 및 지상 기반 관측 자료를 바탕으로 구축되어 시공간적으로 변화하는 실제 전리층의 비균질성을 잘 반영할 뿐만 아니라, 전파 경로의 세밀한 모델링을 위해 필수적으로 요구되는 위도·경도·고도 기반의 3차원 전자 밀도 프로파일을 제공한다[21].
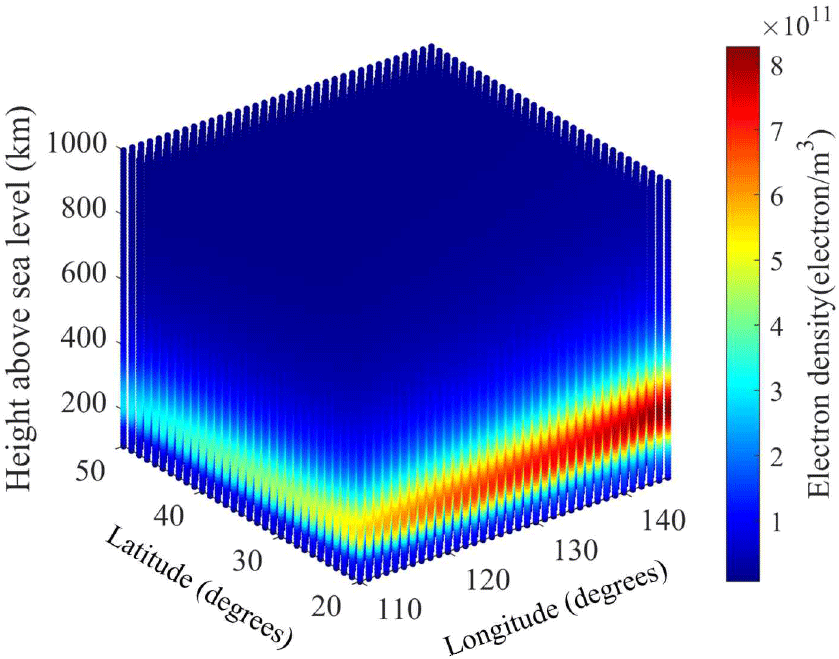
따라서 본 논문에서는 NASA에서 제공하는 IRI 2016을 활용하여 한반도 상공의 전리층 전자 밀도 데이터를 확보하였다[22]. 그림 2는 IRI 2016으로부터 획득한 2025년 4월 10일 00:00:00 UTC 기준 한반도 상공의 전리층 전자 밀도 분포를 시각화한 것이다. 이렇게 획득한 전리층 전자 밀도의 3차원 분포는 고도 범위 90~1,000 km의 전리층을 통과하는 전자파의 전파 특성 예측에 활용된다.
이처럼 0~30 km, 90~1,000 km 고도에서는 각각 고층 기상 관측 데이터와 전자 밀도 모델을 이용하여 굴절률을 추정할 수 있다. 그러나 30~90 km 또는 1,000 km 이상의 고도에서는 굴절률을 추정할 수 있는 관측 기반 데이터가 부족하므로, 본 논문에서는 대류권과 전리층의 고도별 밀도 특성과 이온화 경향을 바탕으로 해당 고도에서의 굴절률을 추정하였다.
그림 3(a)는 2025년 4월 10일 00:00:00 UTC에 특정 레이다 사이트(36.0°N, 128.0°E)에서 대기 굴절률의 고도별 프로파일을 나타낸 것이다. 일반적으로 대류권에서는 고도가 높아질수록 대기의 밀도가 감소하며, 이에 따라 대기 굴절률도 감소한다. 특히 대류권 상층부에서는 고도가 높아질수록 대기의 밀도가 더욱 희박해져, 매질은 자유공간(n=1)과 유사한 상태가 된다. 그림 3(b)는 전리층 굴절률의 고도별 프로파일을 나타낸다. 전리층 하층부에서는 고도가 낮아질수록 굴절률이 감소하여 점차 1로 수렴하는데, 이는 태양 복사에 의한 대기 분자의 이온화가 줄어들면서 전자 밀도가 감소하기 때문이다. 이러한 대류권 상층부와 전리층 하층부에서 나타나는 굴절률의 수렴 특성을 고려할 때, 고도 30~90 km 구간에서는 매질을 자유공간(n=1)으로 근사할 수 있다.
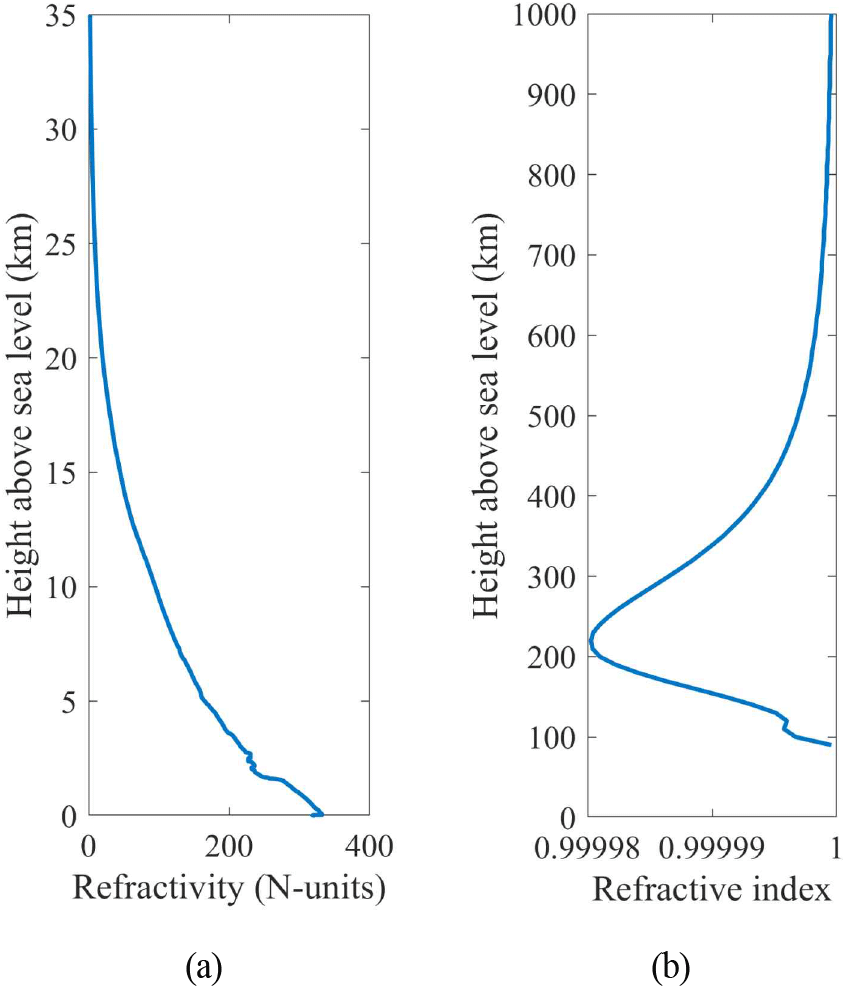
전리층에서는 고도가 증가함에 따라 태양 복사에 의한 이온화가 활발해져 전자 밀도가 증가한다. 그러나 일정 고도 이상에서는 대기 밀도의 급격한 감소로 인해 이온화된 대기 분자의 수가 줄어들기 시작하며, 대기 분자가 희박한 전리층 상층부에서는 고도가 높아질수록 굴절률이 점차 1로 수렴한다. 이러한 전리층 상층부에서의 수렴 특성을 고려했을 때, 1,000 km 이상의 고도에서는 매질을 자유공간(n=1)으로 근사할 수 있다[23].
Ⅲ. 우주 전파 환경에서의 전파 특성
대기에 의한 표적의 위치 오차를 보상하기 위해서는 대기를 통과하는 전자파의 전파 경로 및 전파 시간을 정밀하게 계산해야 한다. 이를 위한 대표적인 방법 중 하나인 포물형 방정식(PE, parabolic equation)은 스플릿-스텝 푸리에 변환(SSFT, split-step Fourier transform)과 같은 수치 기법을 활용하여 거리 및 고도에 따라 굴절률이 연속적으로 변화하는 비균질 대기 내에서의 전파 특성을 효과적으로 계산할 수 있다. 하지만 본 기법은 해면 또는 대류권 내에서의 전파 해석에 적합하나, 전리층과 같은 고고도 환경에서는 적용이 제한되는 한계가 있다 [24]. 또한 대기권과 같이 굴절률이 연속적으로 변화하는 불균일 매질(inhomogeneous medium)에서는 맥스웰 방정식을 직접 적용하기 어렵기에, 파동을 광선(ray)으로 근사하는 고주파 근사(high-frequency approximation) 기반의 수치해석 기법인 광선추적법이 활용된다. 광선추적법에서 대기권은 굴절률이 서로 다른 다수의 층으로 분할되고, 분할된 각 층의 경계면에서 광선의 진행 경로는 스넬의 법칙(Snell’s law)에 의해 계산된다. 서로 다른 굴절률(n1, n2)을 갖는 두 매질의 입사각과 굴절각 사이의 관계를 정의하는 이 법칙은 식 (4)와 같이 나타낼 수 있다.
θ1은 매질 1에서 매질 2로 전파가 입사할 때의 입사각이며, θ2는 매질 2에서의 투과각을 나타낸다. 이처럼 스넬의 법칙을 이용한 경로 계산을 전파가 통과하는 모든 경계면에 대해 목표 고도까지 연쇄적으로 반복하면, 최종적으로 대기 굴절률과 전리층 전자 밀도 같은 복잡한 대기 효과가 정밀하게 반영된 전파 경로를 얻을 수 있다.
대류권을 통과하는 전자파의 전파 시간은 매질의 굴절률에 의해 결정된다. 대류권을 고도에 따라 변화하는 굴절률에 따라 N개의 층으로 분할했을 때, i번째 층(i=1, 2, ··· ,N)에서의 전파 속도 vi는 식 (5)와 같이 계산되고, 대류권을 통과하는 데 걸리는 총 시간은 식 (6)과 같이 각 층을 통과하는데 걸리는 시간의 합으로 계산된다. 식 (6)에서 Ri, ni는 각각 분할된 i번째 층에서의 경로 길이와 대기 굴절률을 나타낸다.
전리층을 통과하는 전자파의 전파 시간은 주파수와 전리층의 총 전자수(TEC, total electron content)에 결정된다[25]. 이론적으로 TEC는 전파 경로를 따라 전자 밀도를 선적분하여 계산되지만, 실제 전자 밀도 데이터는 해석적인(analytic) 함수로 주어지지 않는 경우가 일반적이다. 따라서 본 논문에서는 전파 경로에 따라 변화하는 전자 밀도 분포를 고려하여, 전리층을 M개의 균일한 전자 밀도를 가진 층으로 분할하여 모델링하였다. j번째 층의 TEC는 해당 층 내 전자 밀도(Nej)와 해당 층을 통과하는 전파의 경로길이(Rj)의 곱으로 계산되며, 전체 경로에 대한 TEC는 식 (7)과 같이 각 층의 TEC를 합하여 수치적으로 계산된다. 전리층을 통과하는 동안 발생하는 전파의 시간 지연 Δtiono은 전체 전파 경로의 총 전자수를 이용하여, 식 (8)과 같이 계산된다. e는 전자의 전하량, ε0는 자유공간 유전율, me는 전자의 질량, f는 주파수를 나타낸다. 따라서 전리층을 통과하는 전자파의 총 전파 시간은 전리층으로 인해 발생하는 추가적인 시간 지연과 전파가 총 경로 길이를 자유 공간에서 통과하는 데 소요되는 시간을 합하여 식 (9)와 같이 계산할 수 있다.
그림 4는 2025년 4월 10일 00:00:00 UTC에 특정 레이다 사이트(36.0°N, 128.0°E, 고도 250 m)에서 1 GHz 주파수로 방사된 전파가 자유공간과 대기 환경(대류권 및 전리층 고려)을 통과할 때 나타나는 전파 특성의 변화를 고각에 따라 나타낸 것이다. 실제 대기 환경을 고려한 전파 경로 및 시간 계산을 위해서, 대기 굴절률은 해당 날짜 및 좌표에서의 고도별 굴절률 프로파일을 사용하였으며, 전리층 전자 밀도 분포는 IRI 2016 모델에서 제공하는 동일 시점의 특정 지리적 범위에 대한 3차원 데이터를 활용하였다. 그림 4(a)는 전파가 특정 지상 거리(ground range)에 도달했을 때, 자유공간을 통과한 전파의 최종 도달 지점과 대기 환경을 통과한 전파의 최종 도달 지점의 고도 차이를 나타내며, 그림 4(b)는 전파가 특정 고도(altitude)에 도달했을 때, 자유공간을 통과한 경우 소요된 시간과 실제 대기 환경을 통과하며 소요된 시간 간의 차이를 나타낸다.
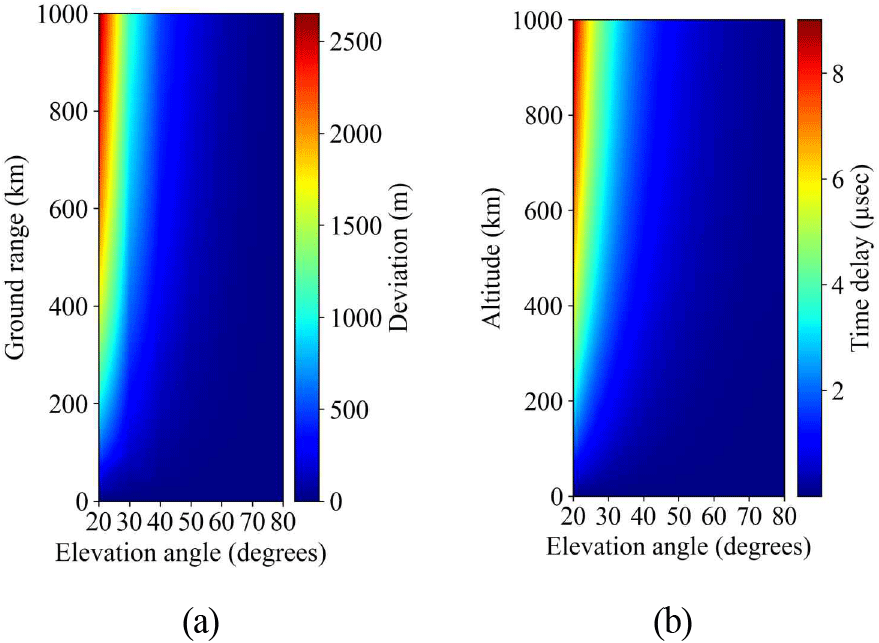
그림 4(a)에서 모든 고각 범위에서 고도 차이는 항상 양의 값을 갖는 것을 확인할 수 있다. 이는 전파의 출발 고각에 상관없이 자유공간을 가정했을 때의 전파 도달 고도가 실제 대기 환경을 고려했을 때의 전파 도달 고도보다 항상 높다는 것을 의미한다. 이러한 현상은 고도가 낮아질수록 대기 밀도가 증가하여 굴절률이 커지는 일반적인 대류권의 특성과 전리층 내 전자 밀도 분포에 따른 굴절 효과가 복합적으로 작용한 결과로 해석된다.
그림 4(b)는 모든 고각 범위에서 전파가 특정 목표 고도에 도달하기까지 소요된 시간이 자유공간과 비교하여 실제 대기 환경을 통과할 때 항상 더 길게 나타남을 보여준다. 이는 전파가 대기를 진행할 때, 대기 굴절률 및 전리층의 전자 밀도로 인해 전파 속도가 감소하기 때문이다. 또한, 그림 4(a)의 고도 차이와 그림 4(b)의 시간 지연 모두 고각이 낮아짐에 따라 그 차이가 비선형적으로 증가하는 경향이 관찰된다. 이는 고각이 낮을수록 전파가 대기층을 통과하는 경로의 길이가 증가하게 되고, 이로 인해 대기 및 전리층 매질과의 상호작용이 누적되어 굴절 및 지연 효과가 더욱 커지기 때문으로 분석된다.
그림 4의 시뮬레이션 결과는 대기를 통과하는 전파가 지표면을 향해 굴절하고, 전파 속도가 감소하여 시간 지연이 발생함을 보여준다. 이러한 경로 왜곡과 시간 지연의 정도는 전파의 초기 출발 각도가 낮을수록 비선형적으로 증가한다. 이러한 특성은 표적의 위치 추정에 대기환경으로 인한 오차가 발생할 수 있는 주요 원인이 된다.
Ⅳ. 우주 환경 오차 추정 및 보상
레이다 시스템은 전파를 표적에 방사하고, 표적으로부터 반사되어 수신되는 반향 신호를 이용하여 표적의 위치를 계산한다. 자유공간을 가정했을 때, 전파는 광속으로 직진하므로, 표적까지의 거리는 레이다와 표적 간 왕복 전파 시간의 절반에 해당하는 단방향 전파 시간에 광속을 곱하여 계산할 수 있다. 표적의 방위각과 고각은 반향 신호가 최대 강도로 수신되거나 최초로 탐지되는 순간의 안테나의 주 빔(main lobe) 중심축이 지향하고 있는 기계적 또는 전자적인 각도 값으로 결정된다.
그러나 실제 레이다 운용 환경에서는 지구 대기의 영향으로 인해 전파가 굴절되고, 추가적인 전파 지연이 발생한다. 따라서 안테나 주 빔이 특정 방위각과 고각으로 지향(steered)된 상태에서 총 왕복 전파 시간 τ가 측정되었을 때, 대기의 영향을 고려하여 보정된 표적의 위치는 해당 방위각 및 고각으로 방사된 전자기파가 실제 대기 매질 내에서 단방향 전파 시간인 τ/2 시간 동안 진행하여 도달한 공간상의 지점으로 정의된다.
그림 5는 레이다에서 고각 θ, 방위각 ϕ로 방사된 전파가 모델링된 대기 환경 내에서 τradar 시간 동안 진행하였을 때 도달한 위치를 계산하는 과정을 나타낸 것이다. 대기권 내의 전파 특성을 고려하기 위해서, 레이다 반향 신호 수신 시점의 대기 굴절률 n과 전리층의 전자 밀도 Ne가 입력파라미터로 설정된다. 전파 경로를 모델링하기 위해, 대기권은 굴절률, 전자 밀도의 변화에 따라 다수의 층으로 분할된다. 레이다의 위치에서 초기 고각 θ0, 방위각 ϕ0으로 전파가 송신되면, 다음 층 경계면에 도달 지점이 결정되고, 해당 지점에서 다음 층으로 진행하는 전파의 방향(고각 및 방위각)은 스넬의 법칙에 의해 계산된다. 이 때, 전파가 레이다 사이트부터 분할된 대기의 n번째 층의 경계면에 도달하는 데 소요된 총 시간을 τn으로 정의한다. 그리고 각 단계에서 n을 1씩 증가시켜가며, |τn-τradar |<ε이 될 때까지 전파 경로를 계속해서 추적한다. 이때, ε은 분할된 층의 높이를 기준으로 결정된다. 만약 ε이 분할된 층의 두께에 비해 상대적으로 큰 값으로 설정되면, |τn-τradar |이 증가하여 이 차이에 비례하는 오차가 발생한다. 반대로, 작은 값으로 설정되면, |τn-τradar |<ε를 만족하는 n을 얻을 수 없다. 본 논문에서는 이를 고려하여, 최적의 ε를 설정하였다. 특정 n에서 |τn-τradar |〈ε 조건이 만족되면, 광선 추적을 종료하고 광선의 도달 위치를 출력한다. 이때의 위치가 대기에 의한 굴절, 시간 지연 효과가 보정된 표적의 위치가 된다.
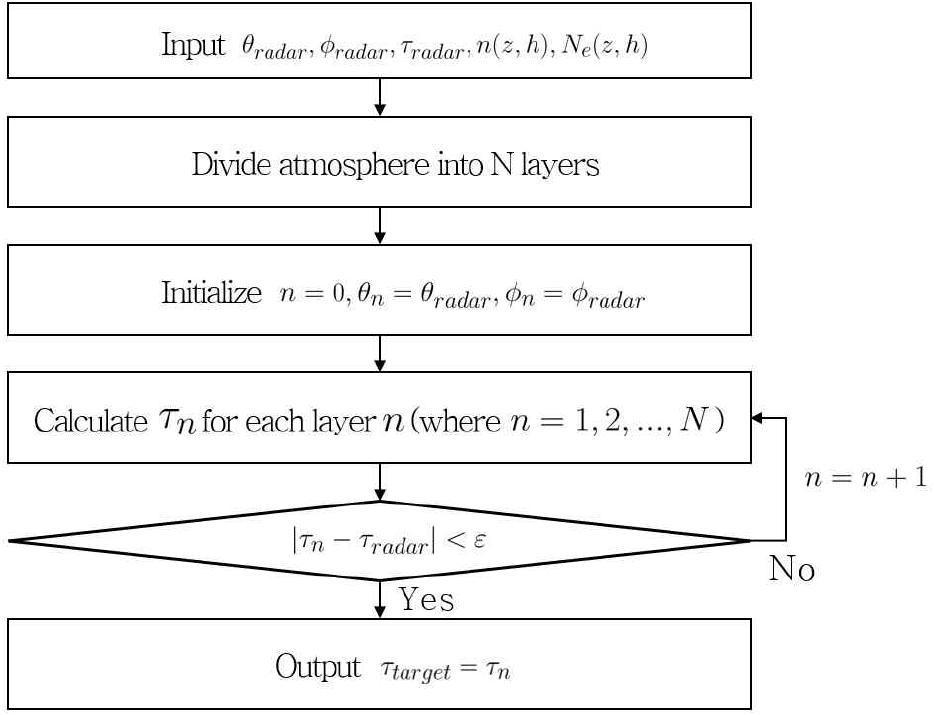
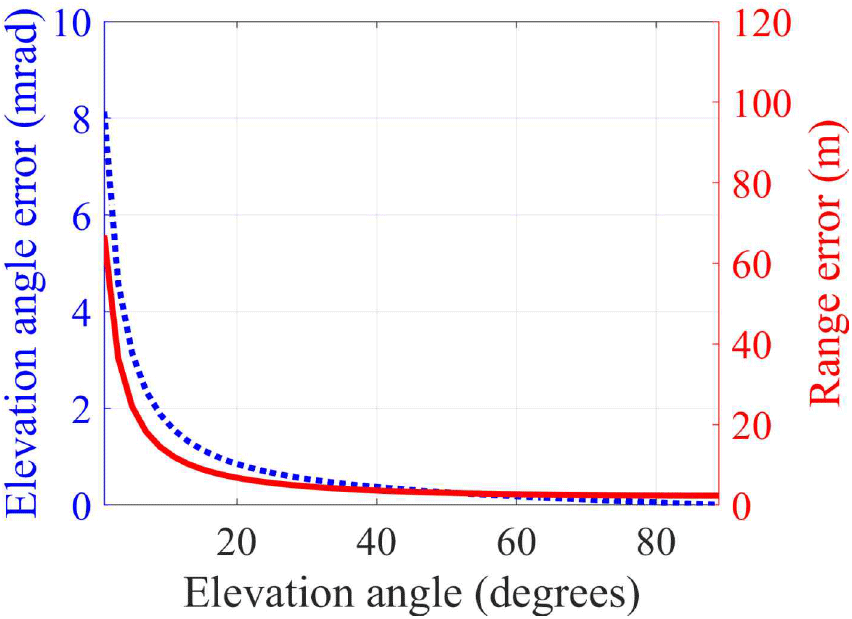
그림 6은 2025년 4월 10일 00:00:00 UTC에 특정 레이다 사이트(36.0°N, 128.0°E, 고도 250 m)에서 수신된 신호를 이용하여 표적의 위치를 추정하였을 때, 신호 획득 시점의 대기 굴절률, 전리층 전자 밀도를 활용하여 계산된 표적의 고각 오차와 거리 오차를 표적의 고각에 따라 나타낸 것이다. 예를 들어 레이다 수신 신호로 추정된 표적의 고각이 20°인 경우, 고각 오차는 0.8514 mrad, 거리 오차는 6.7714 m로 계산된다. 이는 대기의 영향을 보정했을 때, 보정된 표적이 레이다가 관측한 표적에 비해 약 0.0488°(0.8514 mrad) 아래에 위치하며, 6.7714 m 더 가까운 거리에 존재함을 의미한다. 그림 6에서 표적의 고각이 낮을수록 두 오차가 모두 증가하는 경향이 나타난다. 이러한 특성은 낮은 고각의 표적을 관측할 때, 전파가 대기를 통과하는 경로 길이가 길어져 전파 경로의 변화가 누적되고, 시간 지연 효과가 증가하기 때문이다. 고각이 90°에 가까운 표적의 경우에는 고각 오차에 비해 거리 오차가 두드러지는데, 이는 고각이 증가할수록 굴절률 변화에 의한 전파 경로의 변화보다는, 대기 굴절률과 전리층 전자 밀도에 의한 시간 지연 효과가 더 크게 작용하기 때문이다.
Ⅴ. GPU 기반의 오차 보정 가속화
실제 우주감시레이다 운용 환경에서는 한정된 탐색 프레임 시간 내에 다수 표적의 오차를 보정해야 한다[26]. 그러나 다수의 표적에 대한 오차 보정을 순차적으로 수행할 경우, 연산 시간은 표적의 수에 비례하여 선형적으로 증가하므로, 전체 연산 시간이 급격히 늘어나는 문제가 발생한다. 이러한 한계를 극복하기 위한 효과적인 접근법은 병렬 처리이며, 표적별 광선 추적 연산은 상호 독립적으로 수행되므로 병렬화에 최적화된 구조를 이룬다. 이러한 연산 특성은 GPU의 SIMT(single instruction, multiple thread) 아키텍처에 이상적으로 부합하기에, 본 논문에서는 NVIDIA의 병렬 프로그래밍 플랫폼인 CUDA를 활용하여 다수 표적에 대한 오차 보정을 병렬적으로 수행하였다.
그림 7은 다수의 표적에 대한 우주 환경 오차 추정 및 보상 알고리즘의 전체적인 실행 과정을 나타낸다. 알고리즘은 크게 메모리 할당, 데이터 전송, 병렬 처리, 결과 회수의 4단계로 구성된다. 첫 번째 단계에서는 프로그램이 CUDA malloc 함수를 호출하여 GPU 메모리 공간을 할당한다. 이때 할당되는 메모리는 입력 데이터를 위한 공간과 결과를 저장할 공간으로 구분된다. 두 번째 단계에서는 cudaMemcpy 함수를 사용하여 호스트 메모리에 준비된 대기 굴절률(n(z,h)) 및 전자 밀도(Ne (z,h))를 디바이스 메모리(device memory)로 복사한다. 이와 같은 환경 파라미터는 시간에 따라 변하지 않는 정적 데이터이므로, 프로그램 초기화 시 한 번만 전송하여 모든 탐색 프레임 타임에서 반복적으로 활용된다. 세 번째 단계에서, 각 표적(Target 1, 2, ···, k)은 독립적인 CUDA 스레드에 할당되어 병렬적으로 처리된다. 각 스레드는 글로벌 메모리에서 해당 표적의 정보를 읽어오고, 동일한 ray tracing 커널을 실행하여 연산을 수행한다. 이때, 모든 스레드가 동일한 명령어를 실행하지만, 서로 다른 데이터에 대해 작업하는 SIMT 방식으로 동작한다. 최종적으로, 모든 CUDA 스레드의 연산이 끝난 뒤, 결과 데이터는 cudaMemcpy를 통해 GPU에서 CPU로 복사된다.
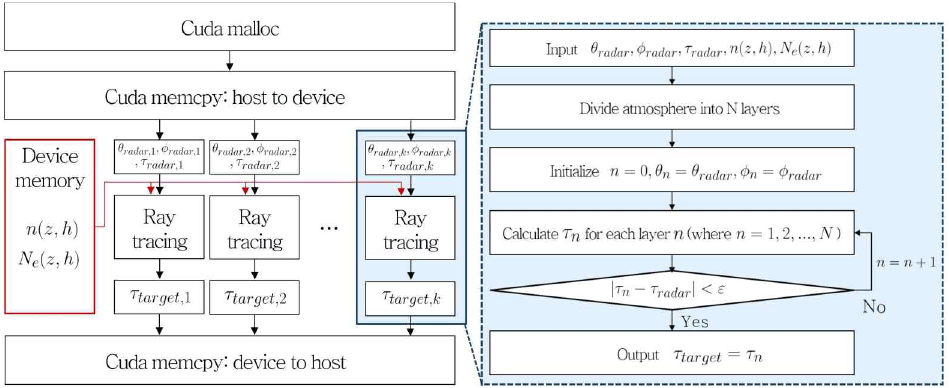
단순한 표적별 스레드 할당만으로는 GPU의 연산 자원을 충분히 활용하기 어렵기 때문에, 본 논문에서는 GPU 하드웨어의 메모리 계층 구조와 연산 최적화 특성을 고려한 다양한 기법을 적용하였다. 먼저, 광선 경로를 따라 참조되는 대기 굴절률 및 전리층 전자 밀도 데이터는 3차원 텍스처 메모리(texture memory)에 바인딩함으로써, 공간적으로 국소화된 접근 패턴에 최적화된 캐시 활용이 가능하도록 하였다. 이러한 접근 방식은 글로벌 메모리 접근을 줄이고, 데이터 로딩 지연을 약 20% 감소시키는 효과를 보였다. 또한 연산 효율을 극대화하기 위해 혼합 정밀도(mixed-precision) 연산을 도입하였으며, 반복 연산이 집중되는 루프 내 계산은 FP16으로 수행하고, 정밀도가 요구되는 결과값에 대해서만 FP32 연산을 적용하였다. 이를 통해 연산 속도와 메모리 효율을 모두 확보하면서도 결과의 정확성을 유지할 수 있었다[27].
본 논문에서는 CPU를 이용한 순차 처리 방식과 GPU를 활용한 병렬 처리 방식의 연산 시간을 비교하기 위해, 그림 8과 같이 우주 물체가 150~2,000 km 고도에 존재한다고 가정하고, 36.0°N, 128.0°E, 고도 250 m에 위치한 레이다가 고각 10°에서 90°사이 그리고 거리 150~2,000 km 이내로 정의되는 영역을 탐색하여, 레이다 반향 신호를 획득하는 구체적인 시나리오를 가정하였다. 그림 8에서 apparent target은 레이다 반향 신호를 통해 자유 공간을 가정하는 기존 방식에 따라 예측된 표적의 위치를 나타내고, true target은 대기에 의한 영향이 보정된 표적의 위치를 나타낸다.
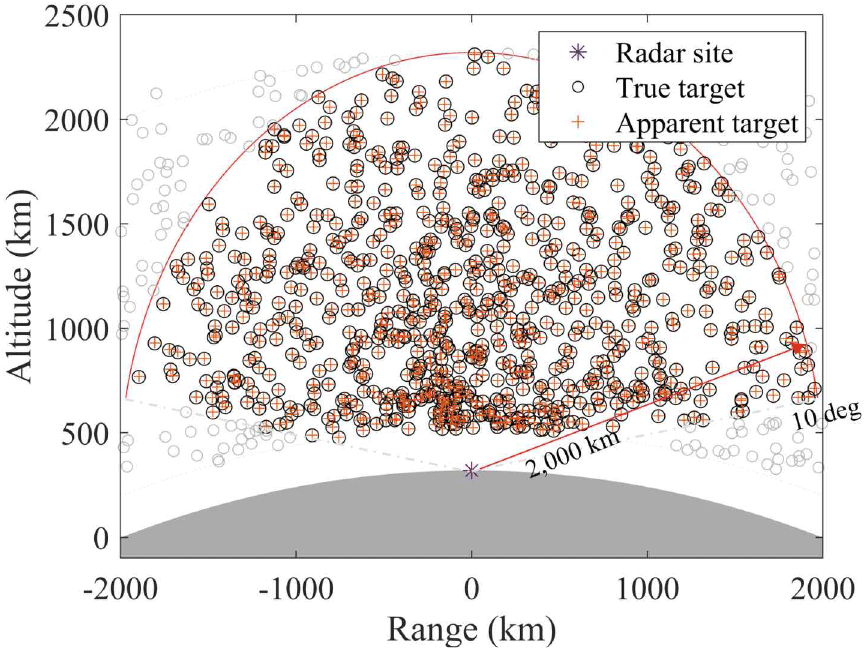
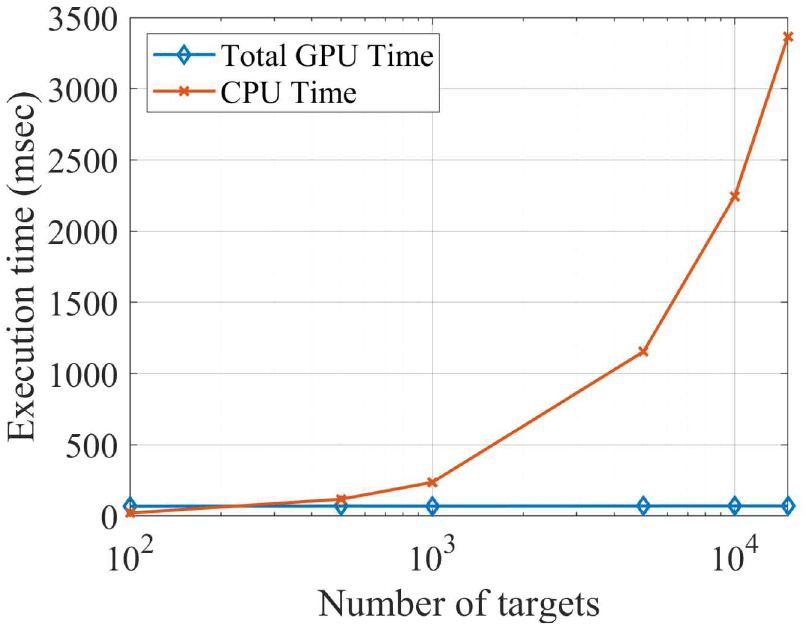
그림 9는 앞서 제시한 레이다의 우주 물체 탐지 시나리오에서, 레이다가 획득한 표적 신호의 개수에 따라 CPU 기반 순차 처리 방식과 GPU 기반 병렬 처리 방식의 연산 시간을 시뮬레이션한 결과를 나타낸 것이다. 시뮬레이션에 사용된 하드웨어 제원은 표 1과 같다. 병렬 처리 알고리즘을 이용하여 모든 표적의 오차를 보정하는 데 소요되는 전체 시간은 호스트 메모리에서 디바이스 메모리(device memory)로의 데이터 전송 시간, 커널 실행 시간, 그리고 결과를 디바이스 메모리에서 호스트 메모리로 전송하는 시간의 합으로 정의된다. 시뮬레이션 결과, CPU를 이용한 순차 처리 방식을 이용한 연산 시간은 표적의 개수가 증가할수록 연산 시간이 21 ms에서 2,244 ms까지 크게 증가하였다. 반면, GPU를 활용한 병렬 처리 방식의 경우에는 표적의 개수와 관계없이 총 연산 시간이 약 69~70 ms 범위로 일정하게 유지되었다. 일반적으로 CPU의 단일 코어 연산 속도는 GPU의 개별 코어보다 빠르기 때문에, 표적의 개수가 적을 때는 순차 처리가 오히려 효율적일 수 있다. 그러나 표적 수가 일정 수준을 초과하면, GPU의 병렬 처리 능력으로 인해 전체 연산 시간이 급격히 단축되는 이점이 나타난다. 이러한 결과는 GPU 기반 병렬 처리 기법이 한정된 프레임 타임 내에 수천에서 수만 개에 이르는 다수의 표적에 대한 오차 보정을 효과적으로 수행하는 데 매우 적합한 방법임을 보여준다.
| CPU | GPU | |
|---|---|---|
| Model | AMD Ryzen 7 5800X 8-Core processor | NVIDIA GeForce RTX 3070 |
| Core | 8 core | 5,888 CUDA core |
| Memory | 128 GB DDR4 | 8 GB GDDR6 |
| Clock | 3.80 GHz | 1.50 GHz |
제안된 보정 알고리즘은 총 M개의 표적에 대해 각각 N개의 광선을 추적하는 구조로 구성되며, CPU 기반의 순차 처리 방식에서는 전체 연산량이 O(M×N)의 시간 복잡도를 갖는다. 반면, GPU 기반 병렬 처리 방식에서는 각 표적과 광선 단위의 연산을 동시에 병렬로 수행할 수 있으므로, 이론적으로 전체 연산 복잡도를 O(N) 수준으로 줄일 수 있다.
Ⅵ. 결 론
본 논문에서는 NVIDIA의 병렬 프로그래밍 플랫폼인 CUDA를 활용하여 다수의 표적에 대해 우주 환경으로 인한 위치 오차를 정밀하게 보정하는 알고리즘을 제안하였다. 이를 위해, 라디오존데 관측 자료를 기반으로 대기 굴절률을 추정하고, IRI 모델을 이용하여 전리층 전자 밀도 데이터를 획득함으로써, 대류권 및 전리층 환경을 정밀하게 모델링하였다. 이후, 해당 환경 정보를 입력으로 하여 광선추적법을 적용함으로써, 전파가 지구 대기권을 통과할 때 발생하는 굴절 및 시간 지연 특성을 정량적으로 분석하였다. 분석 결과, 레이다에서 방사된 전파는 우주를 향해 진행할 때 지면 방향으로 굴절하며, 이 과정에서 대기 및 전리층 특성에 의해 시간 지연이 발생하는 것으로 나타났다. 특히 이러한 영향은 전파의 출발 고각이 낮을수록 더욱 크게 나타났다. 이러한 분석을 바탕으로, 레이다 반향 신호와 환경 데이터를 입력으로 받아 우주 환경 오차를 보정하는 알고리즘을 설계하였으며, 이를 CUDA 커널로 구현하여 GPU 기반의 병렬 처리가 가능하도록 구성하였다. 시뮬레이션 결과, 제안한 알고리즘은 기존의 CPU 기반 순차 처리 방식에 비해 연산 시간을 최대 30배까지 단축하였으며, 이를 통해 제한된 탐색 프레임 시간 내에도 다중 표적에 대한 실시간 보정이 가능함을 확인하였다.
본 논문에서 제안한 GPU 병렬처리 기반 오차 보정 기법은 대규모 우주 물체 감시가 요구되는 우주 감시 레이다 시스템 뿐만 아니라, 다중 표적을 동시에 추적해야 하는 다양한 레이다 시스템에도 적용 가능하다. 예를 들어, 공중조기경보통제기(airborne early warning and control)나 해상에서 운용되는 다기능 위상배열 레이다(multi-function radar)와 같이, 빠르게 변화하는 전파 환경 속에서 수십 개 이상의 항공기나 미사일을 실시간으로 탐지·추적해야 하는 시스템에서는 각 표적에 위치 오차 보정을 병렬로 수행하는 것이 필수적이다. 특히, 고속 기동 표적의 위치 오차가 수 미터 단위 정밀도로 요구되는 작전 환경에서는, 본 연구에서 제안한 GPU 병렬 보정 기법이 제한된 탐지 시간 내에 고정밀 궤도 추정과 오차 보정을 동시에 수행할 수 있는 핵심 기술로 작용할 수 있다.




