The Journal of Korean Institute of Electromagnetic Engineering and Science

The Korean Institutes of Electromagnetic Engineering and Science

J. Korean Inst. Electromagn. Eng. Sci. 2025; 36(9):897-910

pISSN: 1226-3133, eISSN: 2288-226X

DOI: https://doi.org/10.5515/KJKIEES.2025.36.9.897

논문/REGULAR PAPERS

인공지능 기반의 한반도 특화 전리층 전자밀도 모델을 이용한 패러데이 회전 분석

이도현^*

, 양준모^*

, 문효상^**

, 정재훈^**

, 이명식^**

, 박용배^*^,^***^,^†

Faraday Rotation Analysis Using an Artificial Intelligence-Based Ionospheric Electron Density Model Specialized for the Korean Peninsula

Do Hyeon Lee^*

, Junmo Yang^*

, Hyosang Moon^**

, Jaehoon Jung^**

, Myungsik Lee^**

, Yong Bae Park^*^,^***^,^†

^*아주대학교 AI 융합네트워크학과

^**LIG 넥스원

^***아주대학교 전자공학과

^*Department of AI Convergence Network, Ajou University

^**LIG Nex1 Co., Ltd.

^***Department of Electrical and Computer Engineering, Ajou University

^†Corresponding Author: Yong Bae Park (e-mail: yong@ajou.ac.kr)

© Copyright 2025 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Jul 28, 2025; Revised: Aug 05, 2025; Accepted: Aug 11, 2025

Published Online: Sep 30, 2025

요 약

본 논문은 인공지능 기반의 한반도 지역에 특화된 전리층 전자밀도 모델을 설계하고, 이를 이용하여 전리층을 통과하는 전자파의 전파 특성 중 하나인 패러데이 회전을 분석한다. 설계한 인공지능 모델, 이오노존데 관측 자료, 그리고 전 지구적 경험 모델인 IRI-2016의 전자밀도를 이용하여 계산한 패러데이 회전값을 비교하여 전자밀도 모델 간 차이를 분석하였다. 또한 기존의 단순화된 패러데이 회전 계산 방법과 광선추적법 및 Appleton-Hartree 방정식에 기반한 정확한 계산법 간의 오차를 평가하였다. 본 연구 결과는 한반도 지역에서 전리층을 통과하는 전자파의 전파 특성 예측의 정확도를 향상시키는 데 기여할 수 있다.

Abstract

In this study, an artificial intelligence (AI)-based ionospheric electron density model specialized for the Korean Peninsula was developed and used to analyze the Faraday rotation, a propagation characteristic of radio waves passing through the ionosphere. The Faraday rotation values calculated using the developed AI model, ionosonde observation data, and global empirical model IRI-2016 data were compared to analyze the differences among the electron density models. In addition, the errors between the simplified Faraday rotation calculation method and a more accurate approach based on ray tracing and the Appleton-Hartree equation were evaluated. The results of this study can contribute to improving the accuracy of predicting radio wave propagation characteristics in the ionosphere over the Korean Peninsula.

Keywords: Ionosphere; Electron Density; Faraday Rotation; Artificial Intelligence; Electromagnetic Wave Propagation

Ⅰ. 서 론

위성 통신(satellite communication), 우주 감시 레이다 (space surveillance radar), 위성 항법 시스템(GNSS, global navigation satellite system)과 같이 전자파가 대기권을 통과하는 상황에서 전자파는 대기권 고도 약 90~1,000 km에 해당하는 전리층(ionosphere)의 영향을 받게 된다. 전리층은 대기권 내의 원자 또는 분자가 태양의 X선 및 극자외선에 의해 이온화되어 양이온과 전자로 분리된 플라즈마 상태의 영역이다. 전자파가 이러한 전리층 영역을 통과하는 경우 굴절, 감쇠, 시간 지연, 편파 회전 등의 영향을 받게 된다^[1]. 이 중 전자파가 전리층을 통과할 때, 자유 전자와 지구 자기장의 상호작용으로 발생하는 패러데이 회전(Faraday rotation)은 전자파의 편파면을 회전시켜 송수신 안테나 간의 편파 불일치(polarization mismatch)를 유발하여 편파 손실을 증가시키고, 이는 통신 및 레이다 시스템의 성능 저하를 초래하는 주요 원인이다^[2]. 따라서 패러데이 회전각(FRA, Faraday rotation angle)의 정확한 예측은 신호 손실을 최소화하고 수신 신호 세기를 예측하기 위한 필수 조건이다.

기존의 FRA 계산 방법은 평균 지자기값을 사용하거나 준-종단(QL, quasi-longitudinal) 전파 가정을 기반으로 수행된다^[3][4]. 그러나 실제 전파 시나리오에서는 전리층을 통과하며 전파가 굴절됨에 따라 파동 벡터(wave vector)와 지자기장이 수직인 준-횡단(QT, quasi-transverse) 조건이 발생할 수 있다. 이로 인해 기존의 계산 방법은 전리층의 3차원적인 비균질성과 지자기장의 공간적 변화를 반영하지 못해 특정 전파 조건에서 큰 오차가 발생한다. 따라서 본 연구에서는 광선 추적법(ray tracing)을 이용하여 전리층을 통과하는 전자파의 전파 경로를 계산하고 AppletonHartree 방정식을 기반으로 3차원 전자밀도 및 지자기장 분포를 고려하여 패러데이 회전각을 정확하게 계산하는 방법을 제안한다.

한편, 위 계산의 정확도를 확보하기 위해서는 패러데이 회전에 직접적인 영향을 주는 전자밀도의 3차원 분포를 실제에 가깝게 모델링하는 것이 중요하다. 특히 위도·경도·고도에 따른 공간적 변화를 고려한 전자밀도 분포는 전리층을 통과하는 전자파의 전파 특성을 예측하는 데 필수적이다. 그러나 기존의 국제적으로 널리 사용되는 전리층 전자밀도 모델인 IRI(international reference ionosphere)2016 모델은 전지구적 통계에 기반한 경험적 모델로서, 평균적인 전자밀도 경향을 추정하는데는 유용하지만, 국지적이며 단기적인 전리층 변화와 특성을 충분히 반영하지 못하는 한계를 가진다^[5],[6]. 이러한 한계를 극복하기 위해서는 해석 대상 영역의 전리층 관측 자료를 기반으로, 국지적 특성을 반영한 예측 모델의 개발이 필수적이다.

이에 본 연구에서는 인공지능(AI) 기반의 한반도 지역에 특화된 전리층 전자밀도 모델을 설계하였다. 제안된 인공지능 기반 전자밀도 모델은 기존의 경험적 모델에 비해 실제 관측값에 더 근접한 전자밀도 분포를 추론하였으며, 이를 통해 실제 전파 환경이 고려된 패러데이 회전각 분석을 진행하였다.

본 논문의 구성은 다음과 같다. Ⅱ장에서는 인공지능 기반의 한반도 특화 전리층 모델 설계 과정을 다루며, Ⅲ장에서는 광선 추적법 및 Appleton-Hartree 방정식 기반의 FRA 계산 방법을 서술한다. Ⅳ장에서는 기존의 전리층 모델과 인공지능 모델을 활용하여 산출된 FRA 결과를 비교 분석하고, Ⅴ장에서 결론을 제시한다.

Ⅱ. 인공지능 기반의 한반도 특화 전리층 모델 설계

2-1 전리층 모델 예측값과 실측값 간 오차 분석

전리층을 통과하는 전자파의 전파 특성은 전리층의 굴절률(n)에 의해 결정되며, 이는 Appleton-Hartree 방정식에 지구 자기장(B), 전자 충돌 주파수(v), 전리층 전자밀도(N_e), 주파수(f)를 입력으로 하여 계산할 수 있다^[1]. 이때 300 MHz 이상의 주파수에서는 지구 자기장 및 전자 충돌의 영향을 무시할 수 있으므로, simplified AppletonHartree 방정식이 적용된다^[7]. 이에 따라 전리층 굴절률(n)은 전자밀도(N_e)와 주파수(f)의 함수로 식(1)과 같이 표현되며, 전리층의 전자밀도는 전리층을 통과하는 전자파의 전파 특성을 결정짓는 핵심 변수이다.

n 2 = 1 − X = 1 − N e e 2 ϵ 0 m e ω 2 = 1 − 80.64 N e f 2

(1)

일반적으로 전리층의 전자밀도는 IRI-2016 모델과 NeQuick와 같은 경험적 모델을 통해 산출된다. 그러나 이러한 전 지구적 통계 모델 혹은 물리 기반 모델은 지자기 폭풍(geomagnetic storm)이나 국지적 이상 현상(local anomaly) 등 전리층의 동적인 변화로 인한 일시적·지역적 특성을 정밀하게 반영하지 못하는 한계가 있다^[8].

그림 1은 태양 중간기 시점(2022년)의 이천 지역에서의 전리층 수직 전자밀도 분포의 모델 예측값과 실제 측정값을 비교한 결과이다. 모델의 예측값은 국제 참조 전리층 모델인 IRI-2016 모델과 NeQuick2 모델로부터 산출하였으며, 관측값은 이오노존데(ionosonde)를 통해 측정되었다^[9]. IRI-2016 모델은 전리층 분야의 공식 ISO 표준으로 전 지구 월평균 전자밀도 분포를 제공하며, NeQuick2 모델은 ITU-R 권고에 따라 GNSS 전리층 지연 예측용으로 채택된 모델로서 두 모델은 전 세계적으로 가장 보편적으로 사용되는 전리층 모델이다^[10].

그림 1. | Fig. 1. 전자밀도 모델 예측값과 이오노존데 측정값 비교 | Comparison between predicted electron density model values and ionosonde measurements.

Download Original Figure

전리층 전자밀도 모델 예측값과 실제 측정값 간에 오차가 존재하는 것을 확인할 수 있으며, 이러한 결과는 기존의 전 지구적 전리층 모델이 한반도와 같은 특정 지역의 국지적 단기적 전리층 특성을 정밀하게 반영하지 못한다는 한계를 나타낸다. 전리층 모델이 실제 상태를 정확히 반영하지 못하는 경우 전리층의 전파 특성인 굴절, 감쇠, 시간 지연, 편파 회전 등에 대한 정확한 계산이 제한된다. 이로 인해 GNSS 정밀 측위, 위성통신, 우주 감시 레이다 등 고정밀 시스템의 성능에 유의미한 수준의 오차가 발생할 수 있다.

2-2 인공지능 모델 아키텍처

본 연구에서는 IRI-2016 모델의 전자밀도 자료를 인공지능 모델의 학습 데이터로 활용하였다. 또한, 국내 이천 및 제주 지역의 이오노존데 관측을 통해 얻은 고도별 전자밀도 프로파일을 추론 단계의 입력값으로 사용하였다. 이를 바탕으로 한반도 지역에 특화된 3차원 전리층 전자밀도 분포를 추론하는 인공지능 모델을 제안한다.

제안한 인공지능 모델은 소수 지점의 전자밀도 관측만으로 전체 분포를 복원할 수 있도록 설계되었으며, 이를 위해 초해상도 합성곱 신경망(SR-CNN, super-resolution convolutional neural network)의 고해상도 생성 능력과 U-Net의 스킵 연결 구조를 결합하여 공간 정보 보존과 학습 안정성을 동시에 확보하였다.

그림 2는 제안한 U-Net 기반 SR-CNN 모델의 전체 흐름을 나타낸 것이다. 본 모델은 이천과 제주 두 지역의 전자밀도 데이터를 입력으로 사용하며, 각 지점의 위도, 경도, 전자밀도 값으로 구성된 (2, 3) 배열이 입력층에 주어진다. 이를 바탕으로 32×36 공간 해상도를 갖는 2차원 전자밀도 마스크가 생성되며, 각 지점의 위치에는 정규화된 전자밀도 값이 삽입되고 나머지 영역은 0으로 채워진다. 이 희소한 형태의 마스크는 전체 전자밀도 분포를 복원하기 위한 모델의 입력으로 사용된다.

그림 2. | Fig. 2. 인공지능 전리층 복원 모델 아키텍처 | Architecture of the AI-based ionospheric reconstruction model.

Download Original Figure

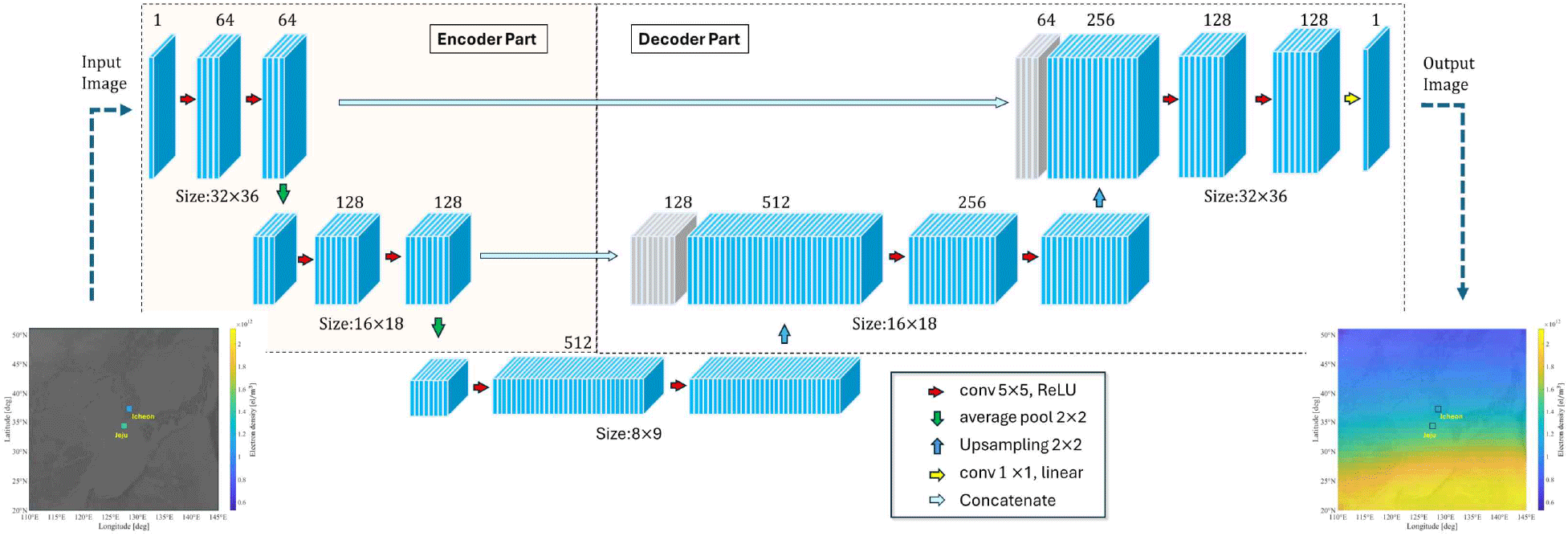
인코더는 3단계로 구성되며, 각 단계는 두 개의 5×5 합성곱 계층(convolutional layer)과 하나의 평균 풀링 계층(average pooling layer)으로 이루어진다. 합성곱 계층에는 ReLU 활성화 함수가 적용되며, 단계가 진행될수록 해상도는 절반으로 축소되지만, 추출되는 특징은 점차 더 복잡하고 추상적인 형태로 발전한다. 초기 단계에서는 국소 전자밀도 분포를, 이후 단계에서는 전역적인 공간 패턴을 학습하도록 설계되었다.

디코더는 인코더의 출력 특징을 고해상도로 복원하는 역할을 하며, 각 단계는 업샘플링 계층과 합성곱 계층으로 구성된다. 인코더의 출력은 skip connection을 통해 대응되는 디코더 단계에 전달되어 국소 정보를 효과적으로 보존한다. 출력층은 1×1 커널의 합성곱 계층과 선형 활성화 함수로 구성되며, 결과는 입력 마스크와 동일한 32×36 크기의 전자밀도 분포 맵이다. 모델은 희소한 입력만으로 전체 전자밀도 지도를 예측하는 방식으로 학습되며, 실측값이 부족한 실제 환경에서의 활용을 고려해 설계되었다.

이와 같이 본 모델은 SR-CNN의 고해상도 생성 능력과 U-Net의 국소 정보 보존 구조를 결합하여, 제한된 입력으로도 정밀한 전자밀도 분포 복원이 가능하도록 최적화되었다. 전통적인 보간 기법인 크리깅(kriging)이나 IDW (inverse distance weighting)는 관측 지점 간 거리를 기반으로 수학적으로 값을 추정한다. 이러한 방법은 계산이 빠르고 구현이 간단하다는 장점이 있지만, 전리층의 복잡하고 비선형적인 물리 특성 및 공간 패턴을 학습하지는 못한다. 반면 본 모델은 대규모 데이터 학습을 통해 물리적으로 타당한 분포를 생성하며, U-Net의 스킵 연결(skip connection)을 활용해 공간 정보 손실을 최소화함으로써 정교한 복원이 가능하다. 한편, GAN(generative adversarial network) 기반 모델은 학습 불안정성과 실제와 다른 허상(artifact) 생성의 위험이 있어, 안정적인 복원 성능이 중요한 본 연구에는 U-Net 기반의 SR-CNN 모델 구조를 적용하였다.

2-3 인공지능 모델 학습 데이터 구성 및 학습 절차

본 연구에서 제안한 모델은 제한된 지역의 관측 자료만을 활용하여 전체 영역의 전자밀도 분포를 복원하는 문제를 해결하기 위해, 희소 관측 기반의 지도 학습(supervised learning) 구조를 채택하였다. 입력 데이터와 타겟 데이터는 모두 IRI-2016 모델의 시뮬레이션 결과를 기반으로 생성되었으며, 관측값이 아닌 모델 출력값을 정답으로 사용하는 준참값(surrogate truth) 접근을 적용하였다. 이러한 방식은 관측 자료가 부족한 환경에서 대규모 학습 데이터를 확보하기 위한 일반적이고 효과적인 방법으로 활용되고 있다.

이와 같이 시뮬레이션 결과를 학습 데이터로 구성하는 방식은 실제 전리층의 3차원 전자밀도 분포를 전 영역에 걸쳐 측정한 ‘정답’ 데이터의 현실적인 부재로 인해 발생한다. 실측 데이터가 부족한 환경에서 대규모 학습데이터를 확보하기 위해, 국제적으로 널리 활용되는 IRI-2016 모델의 출력값을 준참값으로 활용함으로써 인공지능 모델은 IRI-2016의 물리적 공간 상관관계를 학습하여, 추론 과정에서 제한된 실제 측정값만으로 전체 분포를 복원한다.

학습 과정의 입력은 IRI-2016으로부터 특정 고도에서 추출된 2차원 전자밀도 맵을 기반으로, 이천과 제주 위치의 값만 남기고 나머지 영역은 0으로 초기화하여 32×36 해상도의 희소 마스크로 구성된다. 모든 값은 전역 최대값을 기준으로 정규화된다. 타겟은 동일한 공간 범위의 정답 전자밀도 맵으로, 같은 방식으로 정규화되며, 해상도 불일치 보정을 위해 하단에 패딩을 추가하여 (32×36×1) 형태로 고정된다.

이러한 구성은 실제 관측이 제한된 상황을 모사하며, 모델이 제한된 정보만으로도 전체 전자밀도 분포를 효과적으로 복원할 수 있도록 설계되었다. 학습 과정 전반에서 이오노존데 실측 데이터는 사용되지 않으며, 입력과 타겟 모두 IRI-2016 모델의 출력으로부터 구성된다. 모델은 U-Net 기반 SR-CNN 구조를 사용하여, 입력된 희소 마스크를 인코더-디코더 경로를 통해 다운샘플링 및 업샘플링하면서 복원한다. Skip connection을 통해 공간 정보를 보존하며, 최종적으로 고해상도 전자밀도 맵을 생성한다. 최적화는 adam 옵티마이저를 통해 이루어지며, 손실 함수로는 weighted_masked_mse를 사용한다. 이 손실 함수는 관측값이 존재하는 지점에 높은 가중치를 부여하고, 나머지 영역은 손실 계산에서 거의 영향을 미치지 않도록 설계되어, 모델이 유효한 입력 중심으로 학습되도록 유도한다. 학습은 오차 역전파(backpropagation) 방식으로 수행되며, 출력과 타겟 간 손실을 기준으로 각 계층의 파라미터가 반복적으로 갱신된다. 이 과정을 통해 모델은 점진적으로 예측 정확도를 향상시킨다.

2-4 모델 추론 및 데이터 복원

본 연구에서 학습된 인공지능 모델은 극히 제한된 관측값만을 입력으로 받아, 전 지구 전리층의 전자밀도 분포를 복원하도록 설계되었다. 추론 시에는 90 km부터 1,000 km까지의 고도 범위에 대해, 각 고도에서의 2차원 전자밀도 맵을 순차적으로 예측하고 이를 누적함으로써 최종적으로 3차원 전자밀도 구조를 재구성한다. 추론 과정의 입력은 이오노존데 장비를 통해 수집된 이천과 제주 지역의 전자밀도 값이며, 실제 운용 환경을 반영하기 위해 이 두 지점의 데이터만을 사용한다. 해당 값은 학습 시 사용된 전역 최대값을 기준으로 정규화되며, 위도 및 경도 좌표와 함께 배열 형태로 모델에 입력된다. 이후 나머지 위치는 0으로 채워져 희소 형태의 입력 마스크가 생성된다. 모델은 이 희소 입력을 바탕으로 전체 영역의 전자밀도 분포를 정규화된 상태로 출력한다. 따라서 물리적 단위로의 변환을 위해 다음과 같은 후처리 과정을 거친다. (1) 입력 관측값과 학습 기준값을 비교하여 상대적 스케일 계수를 계산하고, (2) 해당 계수를 이용해 출력 결과를 조정한 뒤 전역 최대값을 곱하여 el/m³ 단위로 복원한다. 제안된 접근법은 제한된 관측값을 기반으로 전리층의 3차원 전자밀도 분포를 효과적으로 복원할 수 있도록 설계되었다.

그림 3은 제안한 인공지능 모델을 통해 복원된 전자밀도 분포 결과를 시각화한 것으로, 모델의 공간적 복원 성능과 전리층 구조 재현 능력을 종합적으로 평가하기 위해 구성되었다. 그림 3(a)는 고도 90 km부터 1,000 km까지의 전자밀도 분포를 3차원으로 시각화한 결과로, 색상은 상대적 전자밀도 크기를 나타낸다. 수직 방향(F1, F2층 등)뿐만 아니라 수평 방향(위도-경도)에서도 구조적 연속성이 뚜렷하게 표현되어, 모델이 전리층의 공간 패턴을 효과적으로 학습했음을 시사한다. 그림 3(b)는 고도 440 km에서의 수평 전자밀도 분포를 위도-경도 평면에 나타낸 것으로, 제한된 입력만으로도 광역적인 연속성과 물리적 타당성을 갖춘 분포가 복원됨을 보여준다. 그림 3(c)는 이천 지역에서의 수직 전자밀도 프로파일로, F2층의 최대 전자밀도(NmF2)와 그에 대응하는 고도(hmF2)가 뚜렷하게 나타나 있어, 모델이 고도별 구조적 특성 또한 정확히 재현했음을 확인할 수 있다.

그림 3. | Fig. 3. 제안된 인공지능 모델을 이용하여 추론된 전자밀도 분포 | AI-inferred electron density.

Download Original Figure

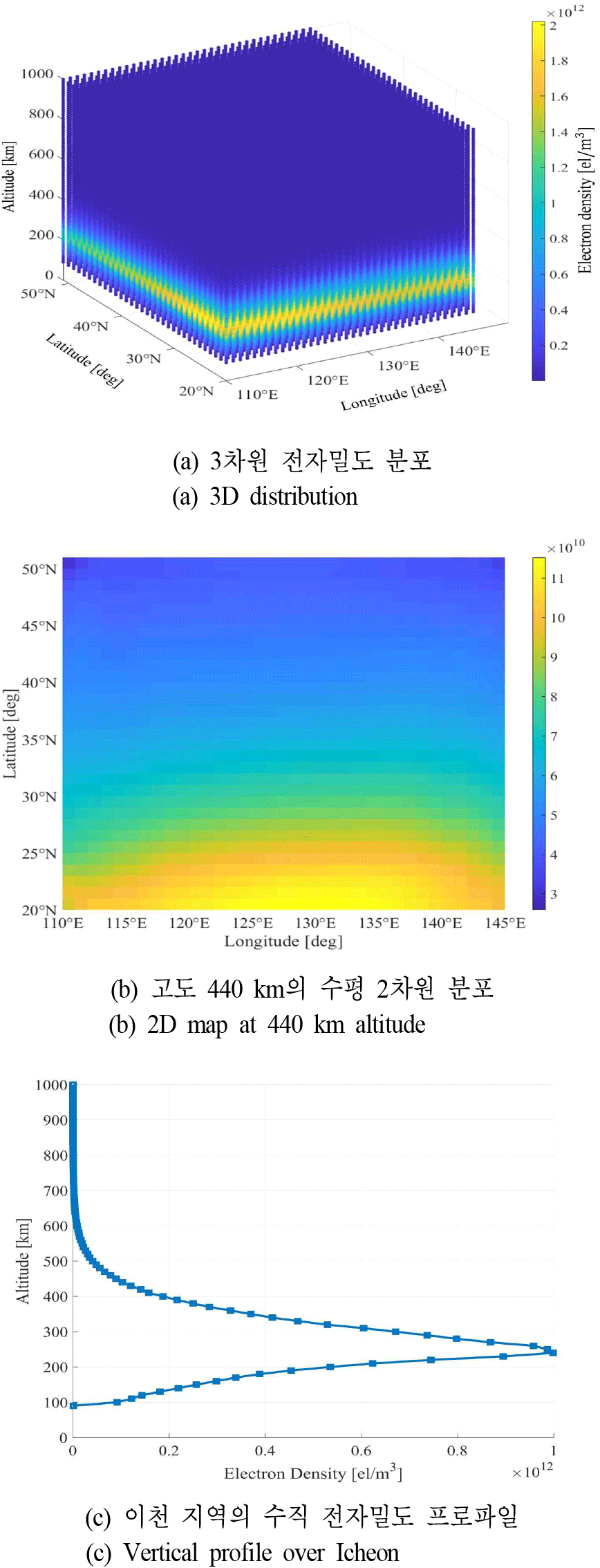
이러한 결과는 극히 제한된 관측값만으로도 전자밀도 분포를 고해상도로 예측할 수 있는 모델의 성능을 입증한다. 특히, 복원된 분포는 고도에 따른 변화 양상과 F2층의 물리적 특성을 잘 반영하고 있어, 모델이 전리층의 물리적 일관성을 유지하며 신뢰성 있는 결과를 생성함을 보여준다. 따라서 본 모델은 실측 자료 확보가 어려운 지역에서도 전자밀도 추정을 위한 유용한 도구로 활용될 수 있다.

제안된 인공지능 모델의 복원 성능을 검증하기 위해, 태양활동 중간기(2022년)인 4월 15일을 기준으로 제주(위도 33.5°N, 경도 126.5°E)와 이천(위도 37.3°N, 경도 128.9°E) 관측소에서의 수직 전자밀도 프로파일(EDP)을 비교 분석하였다. 분석에는 IRI-2016 모델 예측값, 이오노존데 실측값, 그리고 SR-CNN 기반 모델의 복원 결과에서 추출한 EDP가 사용되었다. 전자밀도 프로파일은 고도 90 km부터 1,000 km까지 10 km 간격으로 샘플링하여 구성되었으며, 실측값을 기준으로 각 모델의 예측 정확도를 정량적으로 평가하였다. 모델 성능 평가는 이오노존데 자료를 기준으로 하여, IRI-2016과 제안 모델의 예측값과의 차이를 정규화 평균 제곱근 오차(NRMSE)로 계산하였다.

N R M S E = 1 n ∑ i = 1 n y i − y i^2 y ¯ × 100 (%)

(2)

식 (2)에서 y_i는 i번째 고도에서의 관측 전자밀도, $y i^$ 는 해당 고도에서의 모델 예측값, $y ¯$ 는 관측값의 평균값이며, n은 전체 고도 지점의 수를 의미한다. 이를 통해 각 모델이 실제 전리층 특성을 얼마나 정확히 반영하는지를 평가하였다.

표 1에 따르면, IRI-2016 모델의 NRMSE는 이천과 제주에서 각각 144.4 %, 142.9 %의 현저한 오차를 기록하였는데, 이는 해당 모델이 중간기 전리층의 시공간적 변동성과 비선형적 특성을 효과적으로 반영하지 못함을 의미한다. 반면, SR-CNN 모델은 동일 조건에서 이천 7.8 %, 제주 28.3 %의 낮은 NRMSE를 나타내어, 각각 136.6 %, 114.6 %의 오차 감소를 달성하였다. 특히 이천 지역에서의 NRMSE가 10 % 미만으로 유지된 점은 제안한 인공지능 모델이 경험 기반 모델보다 정밀하게 전리층 전자밀도 분포를 복원할 수 있음을 의미한다. 이처럼 SR-CNN 모델은 두 지역 모두에서 일관되게 낮은 NRMSE 값을 기록하였다. 이는 본 모델이 전리층의 고도별 비선형성 및 지역적 특성을 효과적으로 학습함으로써, 복잡한 전자밀도 변동성을 정밀하게 반영할 수 있음을 나타낸다.

표 1. | Table 1. 모델 예측값과 이오노존데 관측값 간 NRMSE(%) | NRMSE (%) between model predictions and ionosonde observations.

		Electron density model
		IRI-2016	SR-CNN
Location	Icheon	144.4 %	7.8 %
Location	Jeju	142.9 %	28.3 %

Download Excel Table

그림 4는 태양활동 중간기(2022년) 조건에서 이천 관측소의 수직 전자밀도 프로파일(EDP)을 비교한 결과를 나타낸다. 각 그래프에는 IRI-2016 모델의 예측값, 이오노존데 실측값, 그리고 제안된 SR-CNN 모델의 복원 결과가 함께 도시되어 있다.

그림 4. | Fig. 4. 전자밀도 모델의 예측값과 실제 이오노존데 측정값의 비교 | Comparison between predicted electron density from the model and actual ionosonde measurements.

Download Original Figure

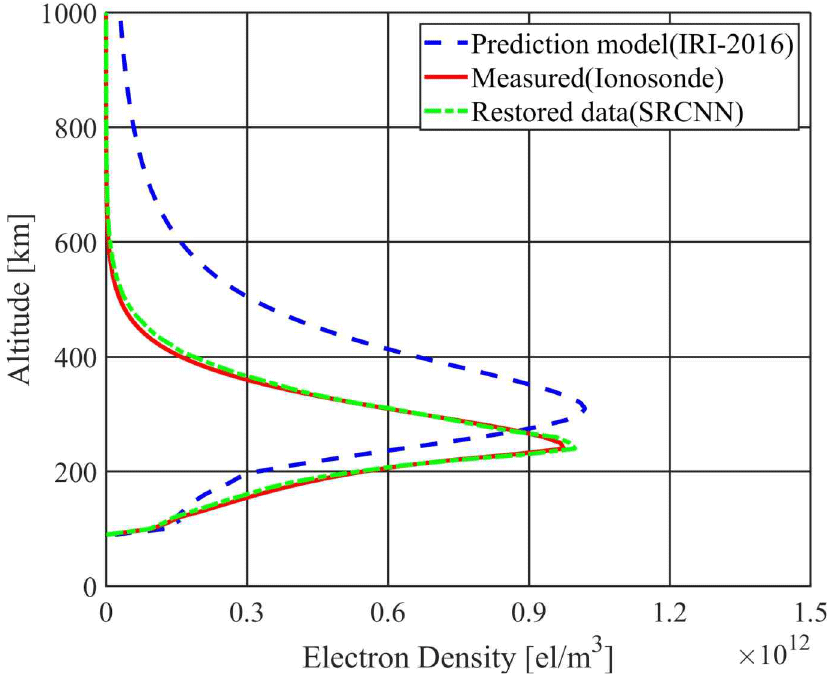
IRI-2016 모델은 전반적으로 관측값에 비해 전자밀도를 과대 예측하는 경향을 보이며, 이러한 편차는 특히 F2층의 최대 전자밀도가 위치한 고도(약 220~320 km)에서 두드러지게 나타난다. 반면, 제안된 SR-CNN 모델은 관측값과 유사한 전자밀도 분포를 재현하며, 고도 전 구간에서 실측값에 근접하는 양상을 보인다. 특히 F2층 고도에서도 전자밀도 수준과 분포 형태를 안정적으로 복원함으로써, 기존 경험적 모델에 비해 높은 예측 정밀도를 입증하였다.

이러한 결과는 제안된 인공지능 모델이 전리층의 수직 구조와 전자밀도 분포의 공간적 특성을 효과적으로 학습하고, 이를 기반으로 물리적으로 타당한 복원 결과를 생성할 수 있음을 보여준다. 제안된 모델의 복원 성능을 가장 정확히 검증하기 위해서는, 이천과 제주 외 제3의 독립된 관측 지점에서의 예측값과 실측값을 비교하는 것이 이상적이다. 그러나 현재 대한민국에서 운용 중인 이오노존데는 이 두 곳으로 한정되며, 인접 국가의 데이터 또한 접근성 문제로 활용이 불가능하여 해당 방식의 검증은 현실적인 한계가 있다.

따라서 본 연구에서는 다음과 같은 2단계 검증을 통해 모델의 신뢰성을 확보하였다. 첫째, 입력 데이터로 사용된 이천, 제주 지점에서 모델의 복원 결과가 실제 측정값과 매우 낮은 오차로 일치하는지를 확인하여 ‘정량적 정확성’을 검증하였다. 둘째, 복원된 3차원 전자밀도 분포가 물리적으로 타당하며 공간적으로 연속적인 패턴을 보이는지를 평가하여 모델이 국소적인 값에만 과적합되지 않고 일반화된 공간 복원 능력을 갖추었음을 확인하였다.

Ⅲ. 광선 추적법 및 Appleton-Hartree 기반 FRA 계산 방법

플라즈마 상태의 전리층은 지구 자기장의 영향을 받아 비등방성(anisotropic) 특성을 갖는다. 이에 따라 선형 편파(linearly polarized wave)를 갖는 전자파가 전리층을 통과할 때, 전자파는 서로 반대 방향으로 회전하는 두 개의 타원 편파(elliptically polarized wave)로 분리된다. 특히 30 MHz 이상의 고주파수 영역에서는 이 두 타원 편파를 원형 편파(circularly polarized wave)로 근사할 수 있으며, 각각 정상파(ordinary wave, O-wave)와 비정상파(extraordinary wave, X-wave)로 구분된다. 정상파와 비정상파는 전리층 내에서 서로 다른 굴절률(refractive index)을 가지므로 각기 다른 위상 속도를 갖게 된다. 따라서 전리층을 통과하는 동안 두 파 사이에는 위상 차가 누적되며, 전파가 전리층을 빠져나올 때 이 두 파가 다시 결합하여 하나의 선형 편파 전자파를 형성하게 된다. 이때 최종적으로 형성된 편파면은 초기 입사파의 편파면에 비해 회전된 상태로 나타나는데, 이를 패러데이 회전(Faraday rotation)이라고 한다^[11].

본 연구에서의 패러데이 회전 계산 절차는 다음과 같다.

첫째, 전리층의 전자밀도 분포(electron density profile)를 산출하기 위해 국제 기준 전리층 모델인 IRI-2016, 제안된 인공지능 기반 모델, 그리고 국내 이오노존데 관측자료의 세 가지 데이터를 활용하였다.

둘째, 얻어진 전자밀도 데이터를 기반으로 Simplified Appleton-Hartree 방정식 (1)을 적용하여 각 고도에서의 굴절률을 계산하였다.

셋째, 계산된 굴절률을 이용하여 전리층을 통과하는 전자파의 실제 전파 경로를 광선 추적법을 통해 모델링하였다. 이 과정에서는 안테나의 초기 위치(위도, 경도, 고도), 지향 방향(방위각, 고도각), 그리고 운용 주파수가 고려되었다. 전리층의 굴절률이 고도에 따라 연속적으로 변화하므로, 전파 경로는 직선이 아닌 곡선 형태로 나타난다. 이러한 전파 경로는 전리층을 여러 개의 층으로 나누어 각 층마다 스넬의 법칙(Snell’s law)을 적용하여 계산하였다^[12].

넷째, 광선 추적법을 통해 얻어진 전파 경로를 기반으로 국제 지자기 기준장 모델(IGRF-13)을 이용하여 경로상의 각 지점에서의 지자기 벡터를 획득하였다.

마지막으로, 전자 충돌이 무시될 수 있는 1 MHz 이상의 주파수 영역을 가정하고, 전자 충돌을 무시한 AppletonHartree 방정식 (3)을 이용하여 정상파와 비정상파의 굴절률을 계산한다.

n o, e 2 = 1 − X 1 − Y 2 (sin θ) 2 2 (1 − X) ± Y 4 (sin θ) 4 4 (1 − X) 2 + Y 2 (cos θ) 2 1 / 2

(3)

X는 정규화된 플라즈마 주파수이며, 식 (4)와 같이 정의된다.

X = f p 2 f 2 = 80.62 N e f 2

(4)

Y는 정규화된 전자 자이로 주파수의 절댓값이며 식 (5)와 같다.

Y = | Y | = 2.80 × 1010 | B | f

(5)

θ는 파동 벡터(wave vector)와 지자기 벡터 사이의 각도이며, + 부호는 정상파, −부호는 비정상파의 굴절률이다.

이렇게 계산된 두 전자파의 굴절률 차이를 이용하여, 전파 경로를 따라 적분함으로써 최종 패러데이 회전각(Ω)을 식 (6)을 이용하여 계산할 수 있다.

Ω = ω c ∫ S i S f n o − n e 2 d s

(6)

ω는 전자파의 각주파수, c는 진공에서의 빛의 속도, n₀와 N_e는 각각 정상파와 이상파의 굴절률이며, S_i와 S_f는 전파 경로상의 시점과 종점을 나타낸다.

그림 5는 전리층을 통과하는 전자파의 패러데이 회전 각 계산을 위한 과정을 정리한 프로세스 흐름도이다. 위 과정을 통해 전리층을 통과하는 전자파의 패러데이 회전을 모델링하고 분석한다.

그림 5. | Fig. 5. 전리층을 통과하는 전자파의 패러데이 회전 계산을 위한 프로세스 흐름도 | Process flowchart for calculating Faraday rotation of electromagnetic waves passing through the ionosphere.

Download Original Figure

기존의 패러데이 회전각 계산은 준-종단(QL, quasilongitudinal) 근사식을 기반으로 계산된다. 이 근사식은 전파의 진행 방향이 지구 자기장 벡터와 거의 평행한 경우, 즉 전파 경로를 따라 지자기장의 종방향 성분이 지배적인 경우 유효하며, ITU-R 권고안에 따른 계산식은 다음과 같이 단순화된 식 (7)을 통해 패러데이 회전각(Ω, [radian])을 산출할 수 있다^[4].

Ω = 2.36 × 10 − 14 B a v N T f 2

(7)

이때, B_av는 전파 경로 상 평균 지자기 세기[Wb × m⁻² or T], N_T는 총 전자함유량(TEC, total electron content)[el × m⁻²], f는 운용 주파수이다.

더욱 정확한 패러데이 회전 계산을 위해, QL 근사 조건 하에서 패러데이 회전 각은 식 (8)을 이용하여 계산할 수 있다^[13],[14].

Ω = e 3 8 π 2 ϵ 0 c m e 2 f 2 ∫ 0 h s N e B 0 → × k → d s = 2.3646 × 104 f 2 ∫ 0 h s N e B 0 → × k → d s

(8)

$k →$ 는 파동 벡터, $B 0 →$ 는 지자기 벡터이며 이 두 벡터의 내적을 통해 ITU-R에 제시된 근사식보다 더욱 정확한 QL 조건하에서의 FRA를 계산할 수 있다.

하지만 실제 전리층을 통과하는 전자파의 경우 고도에 따라서 변화하는 굴절률에 의해 전파가 굴절되고, 그에 따라 $k →$ 와 $B 0 →$ 사이의 각도는 연속적으로 변화한다. 특히 특정 고도각 및 방위각 조건에서는 $k →$ 와 $B 0 →$ 가 서로 수직에 가까워지는 준-횡단(QT, quasi-transverse) 전파 조건이 나타날 수 있다. 이 경우 QL 근사법을 그대로 적용할 경우 상당한 오차가 발생할 수 있다.

따라서 이러한 오차를 최소화하기 위해, QL 근사식의 적용 조건식 (9) 및 QT 근사식의 적용 조건식 (10)은 다음과 같이 정의된다.

Y T 4 ≪ 4 (1 − X) 2 Y L 2

(9)

Y T 4 ≫ 4 (1 − X) 2 Y L 2

(10)

이때, $Y = ω B ω = B 0 | e | m ω$ , Y_T=Ysinθ, Y_L=Ycosθ, θ는 파동 벡터와 지자기 벡터 사이의 각도이다.

이 중 QT 조건(10)이 만족될 경우에는, QT 근사 조건 하에서의 FRA를 아래 식 (11)과 같이 계산할 수 있다^[1].

Ω = e 4 32 π 3 ϵ 0 c m e 3 f 3 ∫ 0 h s N e B 02 sin 2 θ d s = 3.3098 × 1014 f 3 ∫ 0 h s N c B 02 sin 2 θ d s

(11)

이때 QL 조건하의 FRA 계산식 (8)과 QT 조건하의 식 (11)을 비교해 보면, QL 근사는 주파수의 제곱에 반비례하고, QT 근사는 주파수의 세제곱에 반비례함을 알 수 있다.

이는 동일한 전파 환경 및 전파 경로 조건에서도 사용되는 근사식에 따라 FRA 계산 결과가 달라질 수 있음을 의미한다. 실제로 QL 및 QT 근사는 유효한 추정값을 제공하지만, 적용 조건이 충족되지 않을 경우 정확도는 급격히 저하된다. 이에 본 논문에서는 전파의 굴절 경로와 지자기 성분 간의 정확한 각도 관계를 반영하기 위해 Appleton-Hartree 방정식을 이용하여 정상파 및 비정상파의 굴절률을 계산하고, 이를 기반으로 앞서 제시한 식 (6)을 통해 FRA를 도출한다.

특히, 패러데이 회전각 계산에 기존의 QL 근사식를 적용할 경우, 전파가 QT 조건에서 이루어질 때 상당한 오차가 발생할 수 있다. 이에 따라 본 연구에서는 기존 근사법들과 본 논문에서 제안한 정확한 계산 방법 간의 패러데이 회전각 계산 정확도를 비교 분석한다.

Ⅳ. FRA 계산 결과 비교·분석

전리층 시작 지점인 90 km에서 송신된 전파가 전리층을 통과하는 동안 발생하는 굴절 현상과 지구 자기장 분포를 그림 6에 도시하였다. 전파가 전리층을 통과하면서 굴절될 때, 지구 자기장 $B 0 →$ 의 방향도 고도에 따라 함께 변화하게 되며, 이로 인해 파동 벡터 $(k →)$ 와 지구 자기장 $B 0 →$ 사이의 각도도 지속적으로 달라진다.

그림 6. | Fig. 6. 전리층을 통과하는 전자파의 전파 경로 및 지구 자기장 분포 | Propagation path of an electromagnetic wave through the ionosphere and the distribution of the geomagnetic field.

Download Original Figure

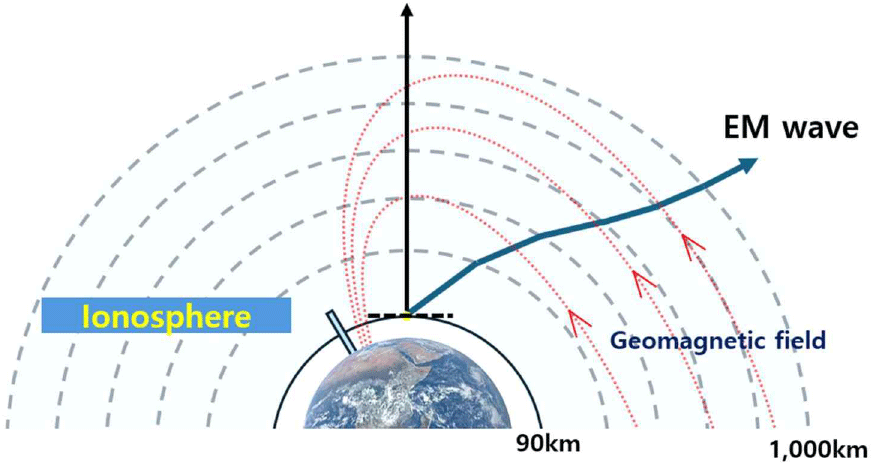
전자 밀도 및 지구 자기장의 3차원 공간 분포를 정밀하게 반영함으로써, 제안된 방법은 전리층을 통과하는 전자파의 FRA를 정확하게 계산할 수 있다.

그림 7은 전체 전리층 영역(90~1,000 km)에서 주파수에 따른 FRA을 분석한 결과를 나타낸다. 본 분석은 인공지능 기반 전자밀도 모델을 통해 추정된 전자밀도 분포를 바탕으로, 제안된 FRA 계산 방법을 적용하여 도출되었다. 시뮬레이션 조건은 2022년 4월 15일 04:00 UTC 기준이며, 사용된 주파수는 1, 2, 4, 8 GHz이다. 안테나의 지향 방향은 방위각 0도, 고도각 30도로 설정하였고, 전파 송신 지점은 북위 36도, 동경 128도, 고도 90 km에 위치하는 것으로 가정하였다.

그림 7. | Fig. 7. 전체 전리층 영역에서 주파수에 따른 FRA 비교 | Comparison of FRA as a function of frequency over the entire ionospheric region.

Download Original Figure

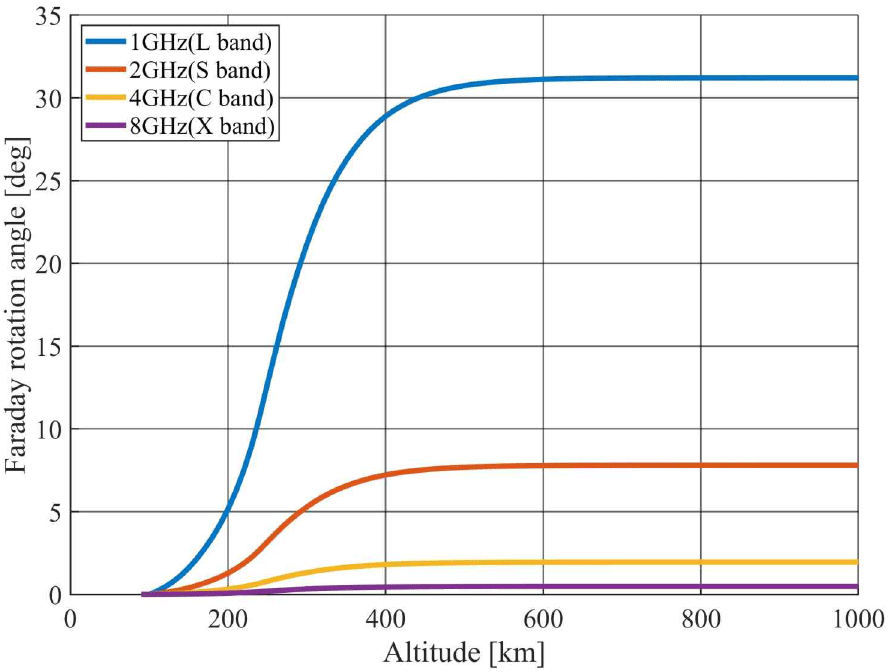
다양한 주파수에 대해 수행한 분석 결과, 주파수가 증가할수록 FRA은 감소하는 일관된 경향을 나타낸다. 본 결과는 제안된 계산 방법을 통해 도출된 것으로, FRA가 주파수에 따라 역비례함을 설명하는 기존 이론과 일치한다.

일반적으로, 전파 경로에 대해 지자기장의 종방향 성분이 지배적인 경우(QL 조건)에는 식 (7) 및 식 (8)과 같이 FRA가 주파수의 제곱에 반비례(∝1/f²)하며, 반대로 횡방향 성분이 주를 이루는 경우(QT 조건)에는 식 (11)과 같이 세제곱에 반비례(∝1/f³)하는 경향을 보인다. 제안한 방법으로 계산된 결과 또한 이러한 주파수 의존성을 반영하고 있으며, 특히 고주파 대역에서 FRA의 감소가 더욱 뚜렷하게 나타난다.

그림 8은 IRI-2016 모델, 제안한 인공지능 기반 모델, 그리고 이오노존데 관측을 통해 획득한 전자밀도 데이터를 이용하여 계산한 FRA을 비교한 결과를 나타낸다. 시뮬레이션에 사용된 주파수는 1 GHz이며, 나머지 조건은 그림 7과 동일하다. 제안한 인공지능 기반 전자밀도 모델을 이용하여 계산한 FRA은 30.70°로 나타났으며, 이오노존데 측정을 통해 획득된 전자밀도 데이터를 기반으로 계산한 FRA는 31.21°이다. 두 결과 간의 차이는 0.51°로, 1° 이하의 매우 작은 편차를 보였다. 반면, IRI-2016 모델을 이용하여 계산된 FRA는 50.61°로, 관측값과 비교하여 과대 추정하였음을 확인할 수 있다.

그림 8. | Fig. 8. 전자밀도 모델 및 측정치에 따른 FRA 비교 | Comparison of FRA based on electron density models and measurements.

Download Original Figure

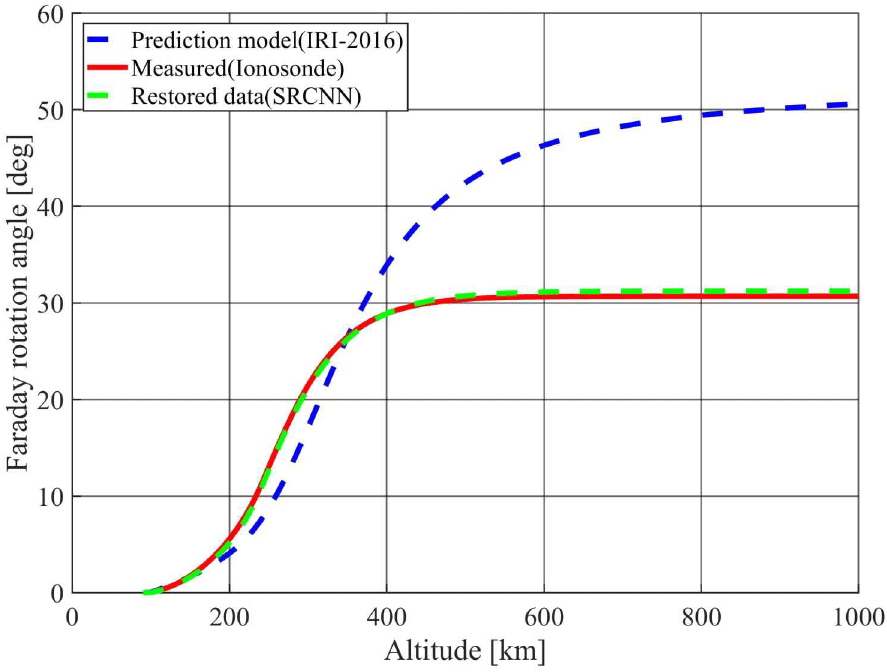
이오노존데는 전리층의 전자밀도 분포를 시간 및 고도에 따라 직접 측정할 수 있는 신뢰도 높은 관측 장비이며, 이를 기반으로 계산된 FRA은 실제 전리층 상태를 반영한 참값으로 간주할 수 있다. 제안한 인공지능 기반 모델로부터 추정된 전자밀도를 이용해 계산한 FRA가 이오노존데 관측 전자밀도를 기반으로 계산한 FRA와 수치적으로 근접한 결과를 보였다는 점은, 본 모델이 기존의 전지구적 경험적 모델보다 실제 전리층의 특성을 보다 정밀하게 재현할 수 있음을 나타낸다.

그림 9는 이오노존데를 통해 측정된 전자밀도 데이터를 이용하여 제안하는 방법에 따른 FRA와 QL 근사식 및ITU-R 권고에 따른 근사식으로 계산된 FRA 비교한 결과를 나타낸다. 제안한 방법에 따른 FRA는 30.70°로 계산되었으며, QL 근사식에 따른 FRA는 34.23°, ITU-R 권고에 따른 근사식으로 계산한 FRA는 16.20°로 계산되었다.

그림 9. | Fig. 9. 계산 방법에 따른 FRA 비교 | Comparison of FRA according to calculation methods.

Download Original Figure

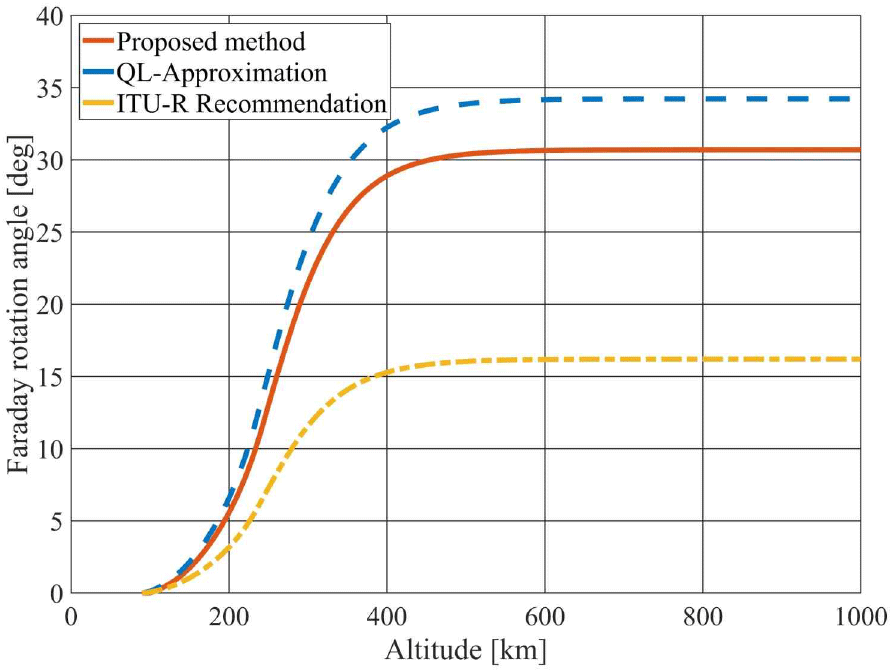
QL 근사식은 전파 경로상에서 파동 벡터 $(k →)$ 와 지구 자기장 벡터 $B 0 →$ 가 서로 평행하다고 가정하고 FRA를 계산하는 방식이다. 그러나 실제 전파 환경에서는 전리층의 굴절 현상과 지자기장의 공간적 변화로 인해 $k →$ 와 $B 0 →$ 사이의 각도가 전파 경로를 따라 지속적으로 변화하게 되며, 이로 인해 QL 근사 조건(식 (9))이 만족되지 않는 구간이 발생한다. QL 근사식는 이러한 단순화된 조건하에서 FRA가 주파수의 제곱에 반비례(∝1/f²)한다고 근사하고, QT근사는 주파수의 세제곱에 반비례(∝1/f³)한다고 근사한다. 하지만 실제로 전파는 전리층을 통과하면서 굴절되고 $k →$ 와 $B 0 →$ 간의 각도는 연속적으로 변하므로, 단일한 QL 또는 QT 근사 조건이 전 경로에 대해서 일관되게 유지되지 않는다.

이에 반해, 본 논문에서 제안하는 Appleton-Hartree 방정식 기반의 계산 방법은 전파 경로상에서 발생하는 파동 벡터와 지자기장 벡터 간의 각도 변화를 연속적으로 고려할 수 있으며, QL 및 QT 근사식이 각각 적용 가능한 극한 상황 사이의 실제 주파수 의존성을 정밀하게 반영한다. 이러한 방식은 단순 근사식이 가지는 이상화된 가정의 한계를 극복하며, 정확한 FRA 산출이 가능하다.

특히 QL 근사식을 전파 경로의 실제 기하학적 조건이나 지자기장의 구조를 고려하지 않고 적용할 경우, 실제보다 FRA를 과대 추정하는 경향이 나타난다. 이는 전파의 진행 방향이 지자기장과 수직에 가까운 QT 조건에 근접할수록 더욱 두드러지며, 해당 조건에서는 QL 근사의 적용이 타당하지 않기 때문이다.

한편, ITU-R 문서에 제시된 FRA 근사 계산식 역시 전파의 진행 방향과 지자기장 벡터가 평행한 경우에만 유효하며, 총 전자 함유량(TEC)과 평균 지자기장 세기 (B_av)값을 이용해 FRA를 계산한다.

그러나 이 방법은 고도에 따른 전자밀도 및 자기장 세기의 공간적 분포, 그리고 전파 경로의 굴절을 반영하지 않기 때문에, 전리층의 불균일성이 크거나 전파 경로가 길고 복잡한 경우에는 지속적으로 FRA를 과소 추정하는 경향을 보인다. 특히 고각이 낮아져 전파 경로가 길어지는 경우, 누적되는 패러데이 회전량을 정밀하게 산출하지 못하므로 수신 지점에서의 FRA가 실제보다 낮게 계산된다. 이와 같이 평균값 기반의 ITU-R 근사식은 계산 속도 측면에서는 효율적일 수 있으나, 위성 통신이나 우주 감시 시스템 등 정밀한 편파 보정이 요구되는 응용 분야에서는 적용에 명확한 한계가 존재한다.

본 연구에서는 이오노존데 관측치와 제안한 AppletonHartree 방정식 기반 계산법을 통해 도출된 FRA 값인 30.70°를 기준 참값으로 설정하고, 이를 바탕으로 IRI-2016, 제안 AI 모델, 이오노존데 관측치로 구성된 세 가지 전자밀도 모델과 ITU-R 권고식, QL-근사식, 제안 방법의 조합에 의해 산출된 FRA 값들의 상대오차를 다음과 같이 분석하였다. 표 2에는 세 가지 전자밀도 모델과 세 가지 계산 기법 조합별로 산출된 FRA 값과 그에 대한 참값 대비 상대오차(%)를 괄호 안에 함께 제시하였다.

표 2. | Table 2. 전리층 전자밀도 모델 및 계산 기법에 따른 패러데이 회전각 계산 결과 | Faraday rotation angle and relative error according to ionospheric electron density models and calculation methods.

Calculation method	Electron density model
Calculation method	IRI-2016 model	Proposed AI model	Ionosonde measurement
ITU-R recommendation	27.38° (10.81 %)	16.49° (46.29 %)	16.20° (47.23 %)
QL-approximation	58.65° (91.04 %)	34.87° (13.58 %)	34.23° (11.49 %)
Proposed method	50.61° (64.85 %)	31.21° (1.66 %)	30.70° (True value)

Download Excel Table

ITU-R 권고에 따른 근사식은 TEC와 평균 자기장 세기를 이용해 FRA를 계산하기 때문에, 모든 전자밀도 모델에서 FRA를 과소 추정하였다. 구체적으로 IRI-2016 모델에서는 27.38°로 오차가 10.8%에 불과했으나, 제안된 AI 모델은 16.49°, 이오노존데 관측치는 16.20°로 45 % 이상의 큰 오차를 보였다.

또한, QL-근사식은 전파 파동 벡터와 지자기장이 평행하다고 가정하여 FRA를 과대 추정한다. 이 근사식을 적용한 결과, IRI-2016 모델에서는 58.65°로 실제값의 거의 두 배에 이르는 과대 추정을 보였으며, 제안 AI 모델은 34.87°, 이오노존데 관측치는 34.23°로 각각 약 11~14 % 수준의 과대 추정이 확인되었다.

반면, 제안된 appleton-hartree 방정식 기반 방법은 전파 경로 상에서 파동 벡터와 지자기장 벡터 간의 각도 변화를 연속적으로 반영한다. 이 방법을 IRI-2016 모델에 적용한 결과 IRI 모델 자체의 전자밀도 분포의 과대 추정으로 50.61°로 계산되었으나, 제안된 인공지능 전자밀도 모델의 분포를 사용했을 때는 31.21°로 1.66 %의 오차를 보이며 참값에 가장 근접하는 성능을 보였다.

이러한 결과는 ITU-R 근사식과 QL 근사식이 전리층의 공간적 불균일성과 전파 굴절 효과를 충분히 반영하지 못해 상당한 오차를 초래하는 반면, 제안된 AppletonHartree 방정식 기반 방법은 전파 경로상에서 파동 벡터와 지자기장 벡터 간 각도 변화를 연속적으로 고려함으로써 예측 정밀도를 향상시킴을 보여준다. 특히, 제안된 AI 기반 전자밀도 모델은 실제 이오노존데 관측치에 근접한 전자밀도 분포를 제공하여 전리층 전파 특성 계산의 정확도를 크게 향상시킨다.

Ⅴ. 결 론

본 연구에서는 한반도 지역에 특화된 인공지능 기반 전리층 전자밀도 모델을 개발하고 이를 활용하여 전리층을 통과하는 전자파의 패러데이 회전 특성을 정확하게 계산하는 방법을 제안한다.

제안된 전자밀도 모델은 초해상도 SR-CNN과 U-Net 구조를 결합하여, 제한된 지점(이천, 제주)의 이오노존데 관측값만으로 전체 전리층 전자밀도 분포를 효과적으로 복원한다. 분석 결과, 개발된 인공지능 모델은 기존의 국제참조 전리층 모델(IRI-2016)에 비해 실제 이오노존데 관측 데이터와 높은 일치도를 보였으며, 특히 전리층의 비선형성과 지역적 특성을 더욱 정확하게 반영하였다.

또한, 전리층을 통과하는 전자파의 주요 전파 특성인 패러데이 회전각을 정확히 계산하기 위해 광선추적법과 Appleton-Hartree 방정식을 결합한 새로운 계산 기법을 제안하였다. 이 기법은 전파 경로상의 굴절 효과와 파동 벡터 및 지구 자기장 벡터 간의 각도 변화를 연속적으로 고려하여, 기존의 준종방향(QL) 근사법 및 국제전기통신연합(ITU-R) 권고안에 따른 근사식 대비 높은 정확도를 달성하였다.

제안된 인공지능 기반 전자밀도 모델과 정밀 FRA 계산법은 위성통신, GNSS 정밀측위, 우주 감시 레이다 등 전자파가 대기권을 통과하는 상황에서 전리층이 미치는 영향을 정확히 예측하고, 편파 손실을 최소화하는 데 기여할 것으로 기대된다.

Acknowledgements

본 논문은 정부(방위사업청)의 재원으로 국방기술진흥연구소의 지원을 받아 수행된 연구임(KRIT-CT-23-052).

References

[1].

K. G. Budden, Radio Waves in the Ionosphere, Cambridge, Cambridge University Press, 1961.

[2].

R. D. Hunsucker, J. K. Hargreaves, The High-Latitude Ionosphere and its Effects on Radio Propagation. Cambridge, Cambridge University Press, 2007.

[3].

J. E. Allnutt, Satellite-to-Ground Radiowave Propagation, 2nd ed. Stevenage, Institution of Engineering and Technology(IET), 2011.

[4].

P. Series, Ionospheric propagation data and prediction methods required for the design of satellite services and systems, Recommendation ITU-R, pp. 531-513, 2016.

[5].

Community Coordinated Modeling Center, 2024. Available: https://ccmc.gsfc.nasa.gov

[6].

D. Bilitza, “Iri the international standard for the ionosphere,” Advances in Radio Science, vol. 16, pp. 1-11, Sep. 2018.

[7].

S. H. Bickel, R. H. T. Bates, “Effects of magneto-ionic propagation on the polarization scattering matrix,” Proceedings of the IEEE, vol. 53, no. 8, pp. 1089-1091, Aug. 1965.

[8].

D. Bilitza, D. Altadill, V. Truhlik, V. Shubin, I. Galkin, and B. Reinisch, et al., “International reference ionosphere 2016: From ionospheric climate to real-time weather predictions,” Space Weather, vol. 15, no. 2, pp. 418-429, Feb. 2017.

[9].

Korea Space Weather Center Korea AeroSpace Administration, “Ionosonde plasma frequency measurements at Icheon and Jeju,” 2025. Available: https://spaceweather.kasa.go.kr/main.do

[10].

P. Coïsson, S. M. Radicella, and B. Nava, “Comparisons of experimental topside electron concentration profiles with iri and nequick models,” Annals of Geophysics, vol. 45, no. 1, pp. 111-116, Feb. 2002.

[11].

G. H. Millman, “Ionospheric electron content effects on Earth-space radio propagation: A review,” in Scientific and Engineering Uses of Satellite Radio Beacons, Warsaw, Mar. 1981, pp. 323-343.

[12].

D. H. Lee, J. Yang, S. Lim, I. H. Choi, and Y. B. Park, “Analysis of ionospheric radio-wave propagation paths over the Korean Peninsula based on three-dimensional electron density data,” Journal of Korean Institute of Electromagnetic Engineering & Science, vol. 35, no. 11, pp. 920-928, Nov. 2024.

[13].

A. C. Cushley, K. Kabin, and J. M. Noel, “Faraday rotation of automatic dependent surveillancebroadcast (ads-b) signals as a method of ionospheric characterization,” Radio Science, vol. 52, no. 10, pp. 1293-1300, Oct. 2017.

[14].

M. Singh, M. H. Bettenhausen, “An accurate and efficient algorithm for faraday rotation corrections for spaceborne microwave radiometers,” Radio Science, vol. 46, no. 4, pp. 1-16, Aug. 2011.