저피탐 레이다를 위한 펄스 압축 최적화 연구

Ⅰ. 서 론

레이다(Radar)는 안테나에서 전파를 방사한 뒤, 물체에 맞고 돌아오는 전파의 수신 시간을 측정하여 물체와의 거리를 계산하는 시스템이다. 레이다는 그 시스템 특성상 표적을 향해 전파를 보내게 되고, 피탐 대상에 전파가 도달하게 된다. 이 과정에서 피탐 대상에 설치된 전자전 장비(electronic warfare support)는 아군 레이다가 보낸 신호를 수신하게 되고, 피탐 대상은 어디선가 자신을 탐지하려고 시도하고 있음을 알게 된다^[1]. 상대방의 전자전 장비는 아군 레이다가 보낸 신호의 대역폭을 알 수 없으므로 넓은 주파수 범위를 탐색해야 하며, 크기, 전력 등의 이유로 안테나 성능 또한 제한되기에 아군 레이다에 비하면 처리 이득이 낮지만, 신호를 일방적으로 수신하기 때문에 낮은 처리 이득을 보완할 만큼 거리에서 이점을 얻는다^[2].

이와 같은 레이다의 특징으로 인해 LPI 기능을 가지는 레이다는 상대방에게 탐지되지 않기 위해 송신 신호의 파형을 첨두 전력은 낮추고, 신호의 길이는 늘이는 방식으로 변조하여 송신하게 된다. 이때, 신호의 변조 방식으로는 PSK (phase shift keying) 및 FSK(frequency shift keying) 등이 있으며, 특히 FRANK 코드와 COSTAS 코드 기반의 변조 기법이 널리 사용된다. 이러한 송신 기법들은 전자전 장비가 잡음 속에서 신호를 탐지하기 어렵게 만든다는 장점이 있지만, 같은 이유로 아군 레이다에서도 수신 감도가 저하된다는 단점 또한 존재한다. 하지만 아군 레이다는 송신 신호를 알고 있으므로 이를 기반으로 정합 필터를 만들 수 있고, 필터링을 통해 잡음 속에 묻혀있는 신호를 탐지할 수 있다.

정합 필터를 통과한 수신 신호의 출력은 모호 함수(AF, ambiguity function)와 같은 형태를 가지며, 해당 출력에서 메인 로브(main lobe)와 사이드 로브(side lobe)의 비율로 정의되는 PSLR(peak to sidelobe ratio)값은 수신기의 탐지 성능을 나타내는 핵심 지표가 된다. PSLR 값은 송신 신호 변조 시 사용한 코드 길이에 따라 달라지며, 일반적으로는 코드의 길이가 길수록 필터를 거친 뒤 사이드 로브가 억제되기 때문에 PSLR 값이 커진다^[3]. 이를 바탕으로 하면 어떤 환경에서든 길이가 긴 코드를 사용하는 것이 수신 신호 검출에 유리하다고 생각할 수 있지만, 실제로는 수신 신호의 샘플 수 및 잡음이 수신기 성능에 영향을 주게 되고, 이로 인해 코드 길이와 수신기 출력이 비례하지 않게 된다.

이에 본 논문에서는 수신기 성능의 최적화를 위해 총 샘플 수, 코드 길이, 잡음 전력, 그리고 PSLR 값 사이의 상호 관계를 이론적으로 분석하고 관계식을 유도하였으며, 이를 시뮬레이션을 통해 검증함으로써 실제 레이다 운용환경에서의 설계 지침을 제시하고자 한다.

Ⅱ. PSLR 식 유도

수신 신호를 r(t), 정합 필터를 h(t)라 하면 필터 출력은 y(t)=r(t)*h(t)가 되며, 신호와 필터 간의 시간 지연 및 도플러 편이 정도에 따라 메인 로브 혹은 사이드 로브가 발생한다. 이때, 잡음은 없고 샘플 수가 무수히 많은 이상적인 환경에서 측정한 메인 로브의 크기(magnitude)를 같은 환경에서의 사이드 로브의 크기로 나누어 PSLR 값을 구하면 COSTAS 코드를 쓴 FSK의 경우에는 COSTAS 코드 길이인 p와 같으며, FRANK 코드를 쓴 PSK의 경우에는 식 (1)과 같다^[4],[5].

여기서 N_c는 FRANK 코드 길이를 의미한다. 식 (1)은 샘플 수 및 잡음을 고려하지 않은 값으로, 샘플 수가 유한하고, 잡음이 존재하는 실제 레이다 운용환경에는 적용할 수 없다. 따라서 본 논문 Ⅱ장에서는 샘플 수와 잡음을 고려하여 메인 로브와 사이드 로브의 평균 전력을 각각 유도한 후, 이를 바탕으로 현실적인 PSLR 값을 새롭게 도출하였다. 식을 단순화하기 위해 수신 신호가 지연되지 않았다고 가정하였고, 이에 따라 송신 신호를 s(t), 신호 수신 시 발생한 잡음을 n(t)라고 정의하면 수신 신호는 시간 구간 [0,T]에서는 $r(t)=s(t)e^{j2\pi f_{d}t}+n(t)$이며, t>T 에서는 잡음으로만 구성된다. 여기서 f_d는 도플러 주파수, T는 펄스 폭의 길이이다. 또한, n(t)는 평균이 0, 분산(=잡음 전력)이 σ²인 WSS(wide sense stationary) 랜덤 프로세스로 가정하였으며, 서로 다른 시간에서의 잡음 값들은 uncorrelated 한다고 간주한다.

2-2 사이드 로브의 평균 전력

메인 로브와 달리, 수신 신호가 AF 상에서 사이드 로브를 형성하기 위해서는 신호와 필터 간에 정합이 이루어지지 않아야 하며, 이는 신호와 필터 사이에 시간 지연이 존재하거나, 수신 신호에 도플러 편이가 발생하거나, 혹은 이 두 상황이 동시에 발생하면 나타난다. 신호와 필터 사이의 시간 지연을 T_c로 정의하게 되면 앞서 설정한 수신 신호를 기준으로 사이드 로브는t=T±T_c에서 발생할 수 있는데, 수신 신호는 지연되지 않았다고 가정하였으므로 t=T+T_c에서의 사이드 로브 크기를 PSLR 식 유도에 사용하기로 한다. 이후, 사이드 로브의 크기를 구하기 위해 y(t)=r(t)*h(t)를 전개한 뒤, t=T+T_c를 대입하면 식 (8)과 같다.

$$\begin{array}{l}y\left(T+T_c\right)={\displaystyle {\int }_{T_c}^{T+T_c}\left(s(\tau )e^{j2\pi f_d\tau }\right)}{s}^{*}\left(\tau -T_c\right)d\tau \hfill \\ +{\displaystyle {\int }_{T_c}^{T+T_c}n}(\tau )s^{*}\left(\tau -T_c\right)d\tau \hfill \end{array}$$

(8)

식 (8)에서 사이드 로브가 발생하기 위한 구체적인 조건은 송신 신호의 변조 방법이 짝수 코드 길이의 FRANK 코드일 때는 $T_c=\frac{\sqrt{N_c}}{2}\times \frac{T}{N_c}$, f_d=0이며, 홀수 코드 길이의 FRANK 코드일 때는 $T_c=\frac{\sqrt{N_c}-1}{2}\times \frac{T}{N_c}$, f_d=0 이다. COSTAS 코드라면 $T_c=\frac{T}{p}$, f_d=RΔf이어야 하며, 여기서 R은 COSTAS 배열에서 선택된 어떤 두 주파수 간의 인덱스 차이를 나타내는 정수이고, 1~(p−1) 사이의 값을 가진다. Δf는 FSK 변조 신호의 최소 주파수이며, $\Delta f=\frac{p}{T}$를 만족해야 한다^[6].

식 (8)에서 잡음 성분이 사이드 로브 출력에 미치는 영향을 알아보기 위해 잡음이 포함된 항에 τ−T_c=τ’을 적용하고, 해당 항을 전개하면 식 (9)와 같다.

$${\displaystyle {\int }_0^{T}n}\left({\tau }^{\prime }+T_c\right)s^{*}\left({\tau }^{\prime }\right)d{\tau }^{\prime }$$

(9)

식 (9)는 식 (2)의 잡음 항과 비교했을 때, 잡음을 시간 축에서 T_c만큼 이동시킨 후 적분한 형태이다. 이때, 필터 구간 안에 포함되는 잡음의 양은 식 (2)와 같고, 앞서 가정한 잡음의 특성상 시간 이동은 잡음의 평균, 분산과 같은 통계적 특성에 영향을 주지 않기 때문에 잡음 항을 $\frac{1}{Fs}{S}^{H}N$로 근사하여도 사이드 로브의 평균 전력에는 유의미한 차이를 주지 않는다. 본 논문에서는 필터 출력의 통계적 특성을 살펴보기 위해 메인 로브 및 사이드 로브의 평균 전력을 기준으로 PSLR 값을 유도하므로 식 (9)와 같은 잡음 항은 $\frac{1}{Fs}{S}^{H}N$으로 근사하여 사용한다. 다음으로, 사이드 로브의 크기를 식 (4)와 유사한 형태로 표현하기 위해 식 (8)에서 신호와 필터의 곱에 해당하는 항을 펄스 폭 T와 어떤 상수 K의 비로 나타내게 되면 사이드 로브의 크기는 $\frac{T}{K}+\frac{1}{Fs}{S}^{H}N$가 된다. 이때, 잡음이 없다고 가정하면 $\frac{1}{Fs}{S}^{H}N=0$이 되어 식 (4)에서 메인 로브의 크기는 T가 되고, 사이드 로브의 크기는 $\frac{T}{K}$가 된다. 이후, 메인 로브의 크기를 사이드 로브의 크기로 나누면 K가 되며, 이는 이상적인 환경에서의 PSLR 값과 같아진다. 한편, 잡음이 존재하는 환경에서의 사이드 로브의 크기를 $\frac{T}{K}+\frac{1}{Fs}{S}^{H}N$으로 정의하였는데, 이는 식 (4)에서 T만 $\frac{T}{K}$로 바뀐 것이므로 사이드 로브의 평균 전력은 메인 로브의 평균 전력을 유도할 때와 같은 방식으로 구할 수 있고, 그 결과는 식 (10)과 같다.

$$E\left[y\left(T+T_c\right)y{\left(T+T_c\right)}^{*}\right]={\left(\frac{T}{K}\right)}^2+\frac{T}{Fs}{\sigma }^2$$

(10)

마지막으로, 식 (7)을 식 (10)으로 나누면 평균 전력 기반의 PSLR 값을 식 (11)과 같이 유도할 수 있다.

$$PSL{R}_{real}=\frac{1+\frac{{\sigma }^2}{M}}{\frac{1}{K^2}+\frac{{\sigma }^2}{M}}$$

(11)

여기서 K는 송신 신호 변조 시 사용한 코드가 짝수 FRANK 코드면 $N_c\sin \left(\frac{\pi }{\sqrt{N_c}}\right)$, 홀수 FRANK 코드면 $2N_c\sin \left(\frac{\pi }{2\sqrt{N_c}}\right)$, COSTAS 코드면 p 이다.

식 (11)을 보면 $\frac{{\sigma }^2}{M}$항을 통해 총 샘플 수 M이 증가할수록 잡음의 영향을 줄일 수 있음을 알 수 있으며, 이는 반대로 잡음이 적은 환경에서는 총 샘플 수가 PSLR 값에 미치는 영향이 미미함을 의미한다. 또한, 해당 항이 커질수록 K의 변화가 PSLR 값에 미치는 영향이 감소함을 알 수 있고, 이는 잡음이 심하거나 샘플 수가 적다면 코드 길이는 PSLR 값의 변화에 크게 작용하지 않는다는 것을 의미한다. 한편, FRANK 코드와 COSTAS 코드는 같은 코드 길이를 사용하더라도 K값에 있어 차이가 있는 것을 볼 수 있는데, 무잡음 환경이라 가정하고 N_c와 p를 1부터 100까지 사용하여 K²을 나타내면 그림 1과 같다.

그림 1. | Fig. 1. FRANK와 COSTAS의 K² 값 비교 | Comparison of K² values between FRANK and COSTAS codes.

Download Original Figure

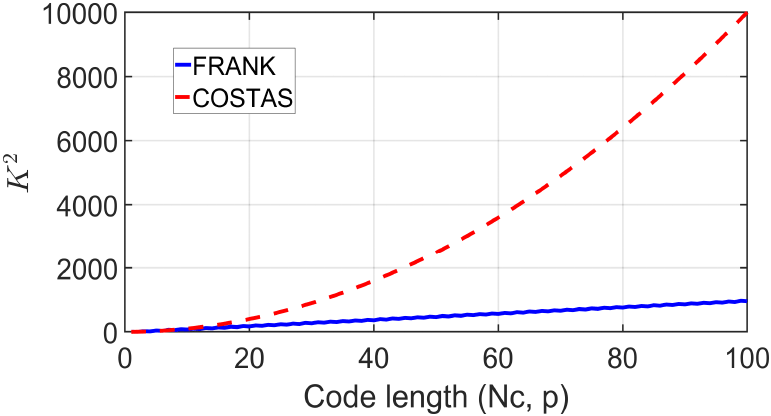
그림 1을 보면 FRANK 코드 방식은 COSTAS 코드 방식보다 코드 길이에 따른 PSLR 값의 변화가 상대적으로 작은 것을 알 수 있다.

Ⅲ. PSLR 식 검증 및 시뮬레이션 분석

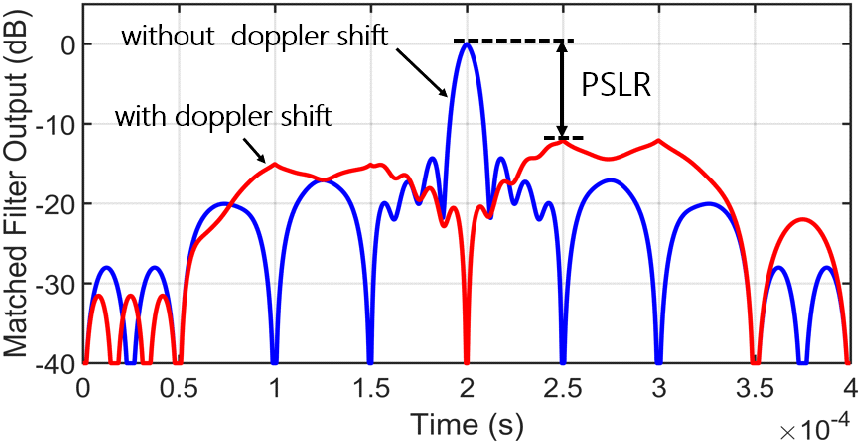
유도한 PSLR 식을 검증하기 위해 수신 신호가 정합 필터를 통과한 후 메인 로브 및 사이드 로브가 발생하는 환경을 설정하여 PSLR 값을 측정하였다. 그림 2는 잡음이 없는 환경에서= T=200 μs, p=4, T_c=50 μs를 적용하여 COSTAS 코드로 변조된 신호의 PSLR을 예시로 나타낸 것인데, 도플러 편이가 없는 경우에는 t=T 에서 peak가 발생하고, 도플러 편이가 있는 경우에는 t=T+T_c 에서 peak가 발생하는 것을 볼 수 있다. 이러한 peak 값들을 각각 수신 신호의 AF 상에서 메인 로브 및 사이드 로브로 정의되며, PSLR 값 계산을 위해 사용된다.

그림 2. | Fig. 2. COSTAS 코드로 변조된 신호의 PSLR | PSLR of a Costas-coded signal.

Download Original Figure

식 (11)에 따르면 실제 레이다 운용환경에서의 이론적인 PSLR 값은 코드 길이, 총 샘플 수, 그리고 잡음 전력에 의해 결정된다. 본 논문에서는 코드 길이를 조절하여 수신기 성능을 최적화하고자 하며, 샘플 수가 잡음 전력에 끼치는 영향을 분석하기 위해 다양한 잡음 환경과 총 샘플 수 파라미터를 조합하여 시뮬레이션을 진행하였다. 잡음 환경을 고려하여 각 파라미터 조합에 대해 총 1,000회의 반복 시뮬레이션을 수행하였고, 각 조합에 대한 평균값을 시뮬레이션 결과로 채택하였다. 이론적인 PSLR 값과 시뮬레이션 결과는 그림 3 및 그림 4에 나타내었으며, 시뮬레이션에 사용된 주요 파라미터는 표 1과 같다.

그림 3. | Fig. 3. FRANK(PSK) 코드 길이에 따른 PSLR 값 | PSLR values according to the length of the FRANK (PSK) code.

Download Original Figure

그림 4. | Fig. 4. COSTAS(FSK) 코드 길이에 따른 PSLR 값 | PSLR values according to the length of the COSTAS (FSK) code.

Download Original Figure

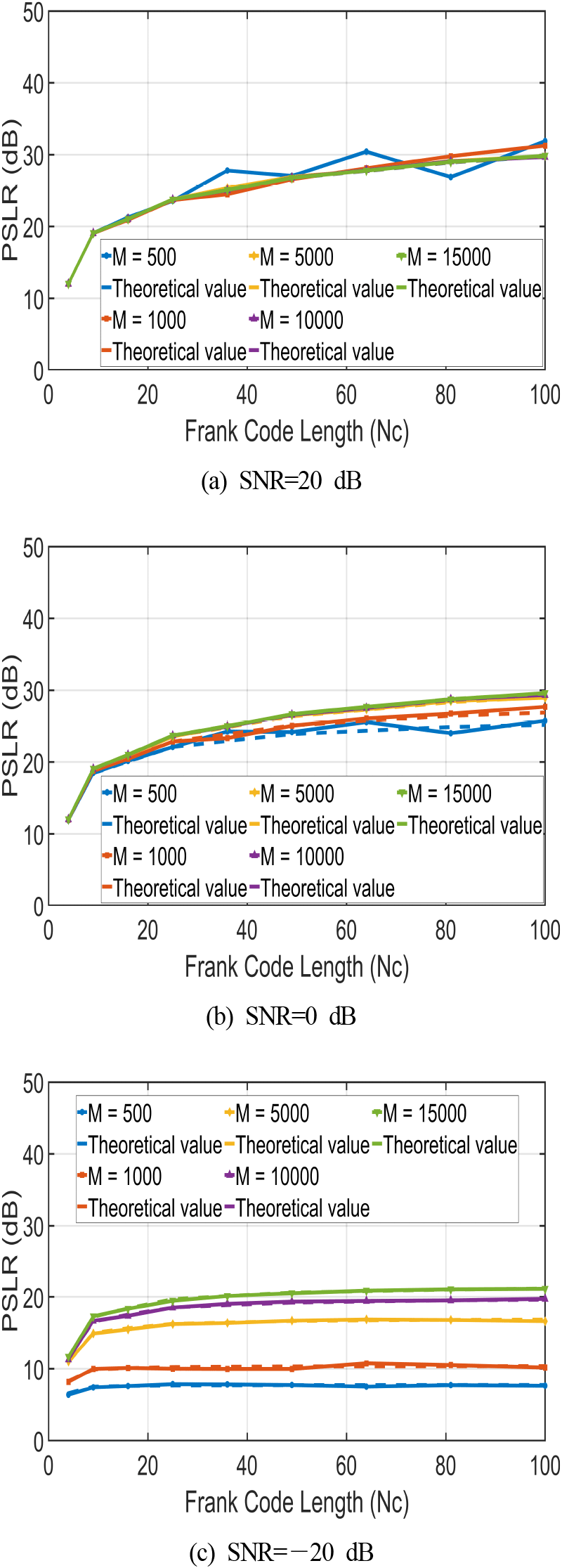
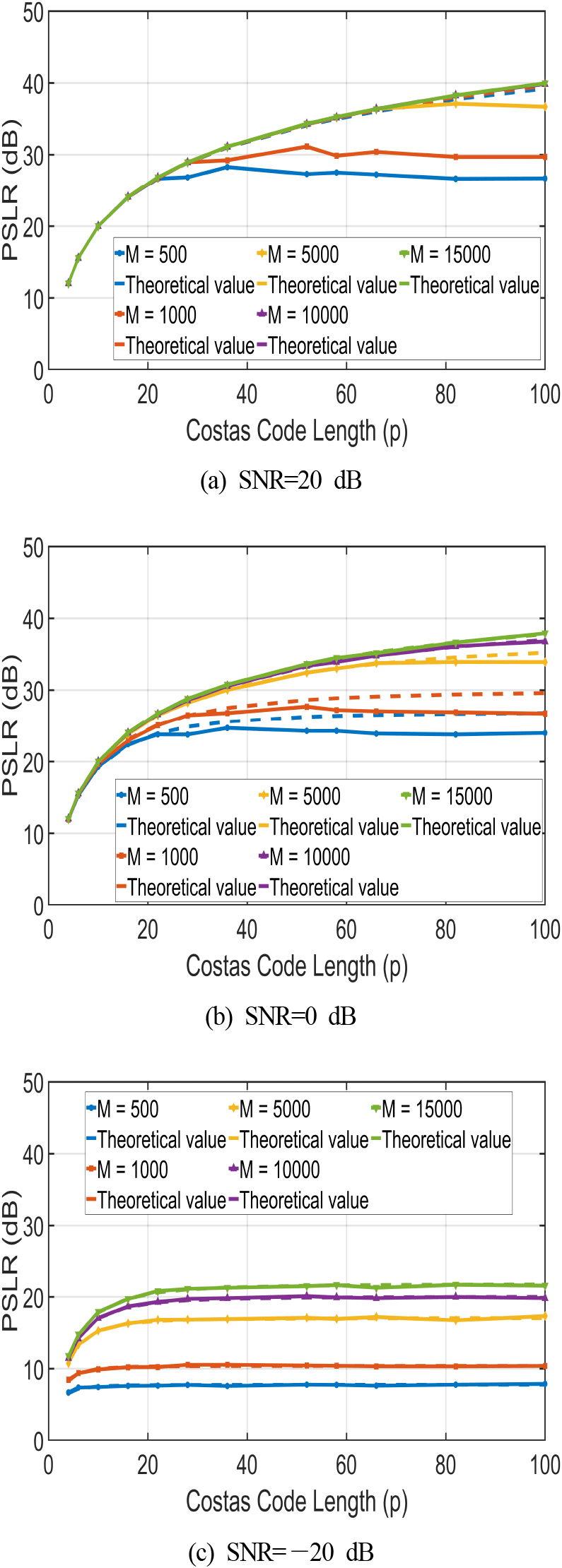
그림 3 및 그림 4에서 점선은 식 (11)에 의해 계산된 이론적 PSLR 값을, 실선은 시뮬레이션 결과를 나타낸다. 그림 4(a) 및 그림 4(b)를 제외하면 샘플 수에 따라서 약간의 차이가 있긴 하나, 전반적으로 점선과 실선이 일치하며, 이를 통해 유도한 PSLR 식이 유효함을 알 수 있다.

그림 3은 식 (11)에서 보인 바와 같이 SNR이 높을 때는 샘플 수에 상관없이 PSLR 값이 비슷하며, SNR이 낮아질수록 총 샘플 수가 많은 시뮬레이션의 PSLR 값이 큰 것을 볼 수 있다. 이와 달리, 그림 4는 그림 3과는 다른 경향을 보이는데, 그림 4(a)를 보면 총 샘플 수가 10,000개, 15,000개인 경우에는 샘플 수에 따른 PSLR 값의 차이가 거의 나타나지 않지만, 그 이외의 경우에는 샘플 수가 적을수록 이론값에 도달하지 못하고 조기에 포화하는 경향을 보인다. 그림 4(b)는 잡음의 영향으로 샘플 수에 따라 이론값 자체가 변하는데, 적은 샘플 수로 인해 PSLR 값이 조기에 포화하는 경향은 동일하게 관찰된다. 이러한 현상은 COSTAS 코드로 변조된 신호의 주파수 특성과 관련이 있다. 신호가 가지는 최대 주파수 f_max는 아래와 같이 정의되는데, 이는 샘플링 주파수 선정의 기준이 된다.

아날로그 신호를 샘플링하기 위해서는 나이퀴스트(Nyquist) 이론을 만족해야 하며, 본 시뮬레이션에서는 신호를 만들 때 복소 신호를 이용했기 때문에 샘플링 주파수는 신호의 최대 주파수 이상이기만 하면 된다^[7]. 정리하면 식 (13)과 같다.

따라서, 수신기가 받은 신호를 왜곡 없이 샘플링 하기 위해서는 식 (13)을 만족하는 충분한 총 샘플 수가 확보되어야 한다. 그림 4를 예시로 살펴보면 총 샘플 수가 500인 경우에는 코드 길이 28부터 식 (13)을 만족하지 못하며, 총 샘플 수가 1,000개인 경우에는 코드 길이 36부터 식 (13)을 만족하지 못하고, 총 샘플 수가 5,000개인 경우에는 코드 길이 82부터 식 (13)을 만족하지 못한다. 오직 총 샘플 수가 10,000개 이상인 경우에만 모든 코드 길이에 대해 식 (13)을 만족할 수 있어 샘플 수 부족으로 인한 성능 저하가 발생하지 않고, 이론값과 시뮬레이션 값이 일치하게 된다. 한편, 그림 4(c)에서는 총 샘플 수와 상관없이 이론값과 시뮬레이션 값이 전반적으로 일치하는데, 코드 길이가 p=28이 되기 전부터 PSLR 값이 포화하는 것으로 보아 총 샘플 수로 인한 제약보다 잡음이 수신기 성능에 더 큰 영향을 끼친 것을 알 수 있다.

이론적으로, 총 샘플 수를 무한히 늘릴 수 있다면 식 (11)의 $\frac{{\sigma }^2}{M}$항은 0으로 수렴할 것이다. 그러나, 이는 현실적으로 불가능하므로 잡음 억제에는 한계가 존재한다. 결과적으로, 코드의 길이를 증가시켜도 그림 3(c) 및 그림 4 (c)처럼 잡음의 영향으로 인해 어느 순간 PSLR 값이 일정 수준 이상으로 향상되지 않고 포화하는 모습을 볼 수 있고, 이런 상황에서 코드 길이를 늘이는 것은 신호의 대역폭만 증가시키는 결과를 초래하므로 성능 대비 효율 측면에서 바람직하지 않다. 신호가 차지하는 대역폭은 FRANK 코드의 경우 $BW=\frac{N_c}{T}$이므로 코드 길이에 선형적으로 비례하여 증가하며^[2], COSTAS 코드의 경우는 식 (12)에 의해 $BW=\frac{p^2}{T}$의 관계식을 가지므로 코드 길이의 제곱이 비례하여 증가하게 된다. 넓은 대역폭의 사용은 신호 간 간섭을 일으킬 수 있으며, 하드웨어에 부담을 주기 때문에 비슷한 성능을 낼 수 있다면 코드 길이가 짧은 것을 사용하는 것이 좋다.

Ⅳ. 결 론

본 논문은 저피탐 레이다 운용에 필수적인 펄스 압축 기법의 최적화를 다루었다. 실제 레이다 운용환경에서는 확보할 수 있는 샘플 수가 제한적이며, 잡음 또한 존재하므로 코드 길이와 수신기 성능이 비례하지 않게 된다.

이에 본 논문에서는 실제 레이다 운용환경에 적용 가능한 총 샘플 수, 잡음 전력, 코드 길이로 이루어진 PSLR 식을 유도하였으며, 시뮬레이션을 통해 제안 식의 유효성을 검증하였다.

시뮬레이션 결과, 잡음 환경에서 PSK 및 FSK 변조 방식 모두 샘플 수를 가능한 한 많이 확보하는 것이 잡음 억제 측면에서 효과적임을 확인하였으며, 특히 FSK 변조 방식의 경우, 수신 신호의 왜곡을 방지하기 위해서는 일정 수준 이상의 샘플 수를 확보해야 한다는 점도 확인하였다. 그러나, 확보할 수 있는 샘플 수에는 한계가 있어 잡음을 완전히 억제하지는 못하며, 잡음이 없더라도 부족한 샘플 수로 인해 샘플링 과정에서 왜곡이 발생하기도 하므로 코드 길이와 PSLR 값이 비례하지 않을 수 있게 된다. 따라서, 펄스 압축 최적화를 위해서는 본 논문에서 제안한 PSLR 공식을 활용하여 PSLR 값이 더는 향상되지 않는 한계 코드 길이를 산출한 뒤, 해당 코드 길이까지만 변조에 적용하는 것이 대역폭 효율성 및 하드웨어 복잡성 측면에서 바람직하다.