단일 채널을 활용한 1 cm 이하의 고정밀 UWB 구현 및 응용

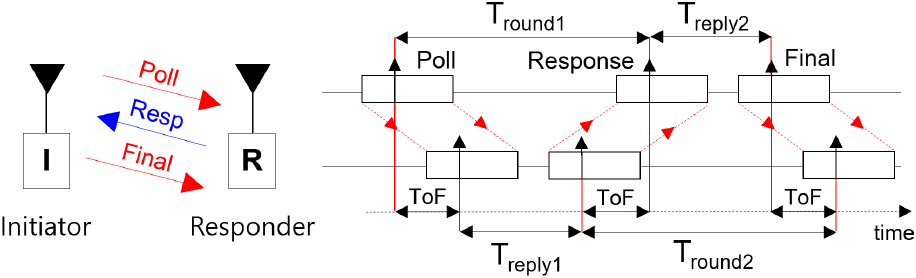
UWB에서 거리를 측정하는 원리로는 DS-TWR(double-sided two-way ranging) 방식이 주로 사용된다. DS-TWR은 2개의 UWB 기기(initiator와 responder라 각각 명함) 사이에 3번의 패킷 교환을 통해 UWB 기기 간의 전파도달 시간인 ToF(time of flight)를 계산한다. 특히, DS-TWR 방식은 3개의 패킷 교환으로 클럭 오프셋(clock offset)을 보정할 수 있어, 2개의 패킷을 교환하는 SS-TWR 방식보다 거리 측정 정밀도가 높은 장점이 있다. 그림 1은 DS-TWR 방식의 원리를 보여주며, 식 (1)을 통해 전파 도달 시간을 계산할 수 있다^[8],[9].

DS-TWR 방식에서 사용되는 패킷에서 국부발진기의 위상특성은 다음과 같이 기저대역 신호에 영향을 준다. 먼저 Initiator를 구성하는 DW3000 UWB IC에서는 기저대역에서 생성된 펄스 신호에 IC 내부의 국부발진기에서 발생한 UWB 채널 9 주파수인 7.9872 GHz의 반송파 주파수를 곱하여 실수 송신신호를 생성하게 된다. 이 신호가 Responder에 의해 주파수는 같지만 위상오차가 있는 7.9872 GHz 주파수와 곱해져 송신기와 수신기의 국부발진기의 위상 특성이 기저대역으로 변환된다. DW3000 UWB IC 내부의 수신기는 직교복조기 구조를 가지므로 I(inphase) 신호와 Q(qudrature) 신호의 복소수 형태로 출력된다. 이때 송신 후 다시 수신하기까지, 또는 수신 후 송신하기까지의 과정에서 지연시간이 필연적으로 발생한다. 이로 인해, 시간에 따른 위상의 변화가 발생되는데 이러한 위상 변화에는 국부발진기의 주파수 오프셋(frequency offset)과 초기 위상 오프셋(initial phase offset)이 포함된다.

이제 DW3000 UWB IC에서 DS-TWR 거리측정과 함께 제공하는 두 UWB 기기 사이의 무선채널의 특성을 알려주는 CIR(channel impulse response) 데이터를 이용하면 가시선(line-of-sight) 환경에서 수신된 패킷의 첫 번째 도착한 전파의 순시 위상을 식 (2)와 같이 계산할 수 있다.

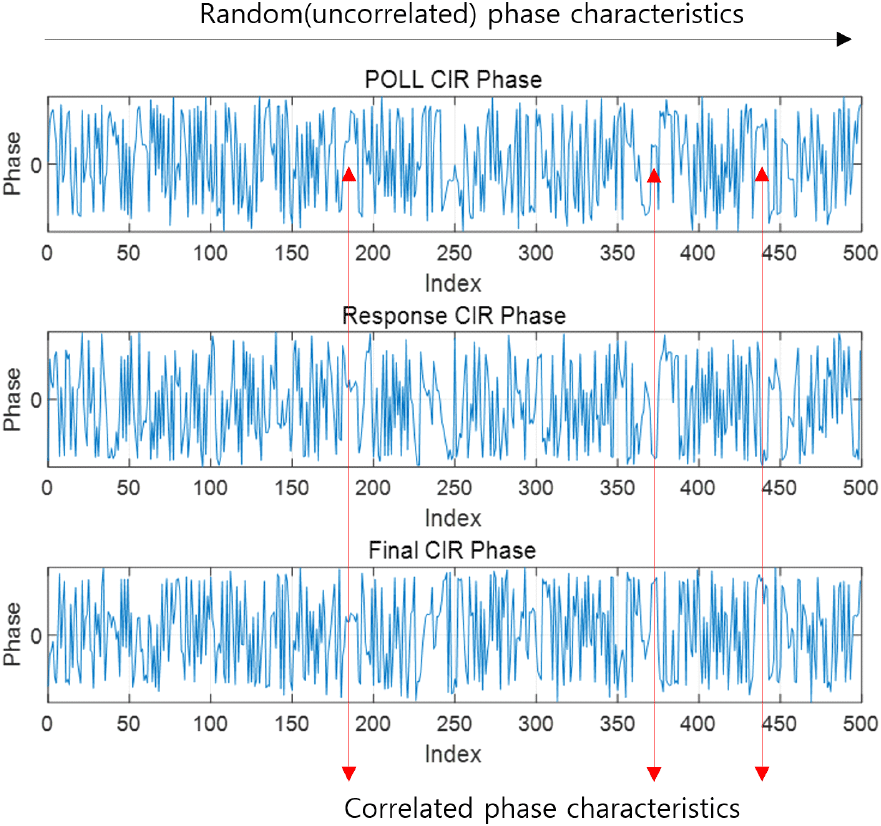
이제 UWB DS-TWR 방식에서 거리 측정을 수행하고 이때 사용되는 3개의 패킷 사이의 위상 특성을 살펴보았다. 먼저, DW3000 UWB IC를 임베디드 프로그래밍하여 DS-TWR 방식을 구현하고 이때 CIR 데이터로부터 첫 번째 도착한 전파의 순시 위상을 계산하였다^[10]~[14]. 그림 2는 고정된 거리에서 DS-TWR 방식으로 거리를 500회 측정하기 위해 Poll, Response, Final 패킷을 교환하고 이때 함께 측정되는 CIR을 저장한 후 식 (2)를 통해 계산된 각각의 패킷의 첫 번째 도착한 펄스의 위상값의 측정 결과를 보여준다. 그림에서 알 수 있듯이 위상의 시간적인 변화(가로축)는 패킷이 발생 시점이 랜덤하게 변화되므로 랜덤하게 변화되지만 거리측정에 사용된 3개의 패킷은 정해진 시간에 교환되므로 패킷의 위상 특성에는 유사성이 있음을 알 수 있다. 또한, poll과 final 패킷의 위상 특성과 response 패킷의 위상 특성을 비교하면 전파의 전달 방향에 따라 180°의 위상차가 발생함을 확인할 수 있었다. 이는 참고문헌 [7]에서 제시된 결과와 일치하며 이를 통해 DW3000 IC에서도 패킷 간의 순시 공통 위상 오차를 제거할 수 있는 가능성을 확인할 수 있었다.

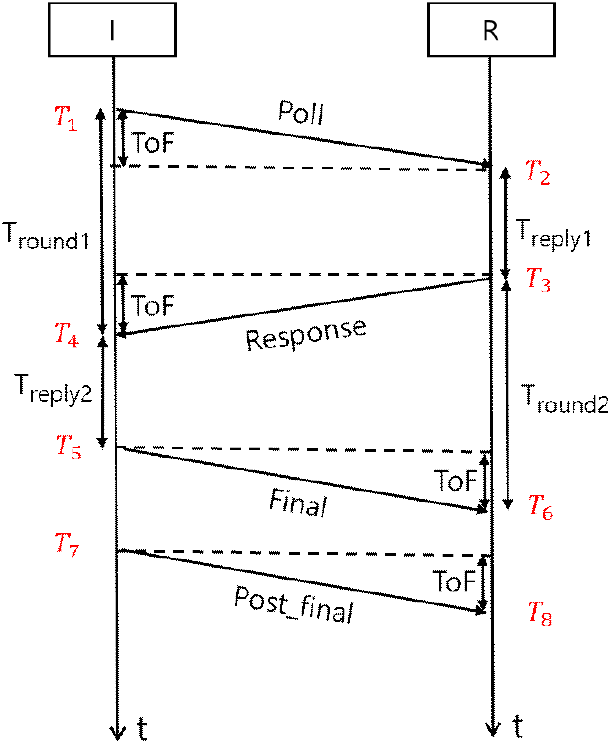
DS-TWR 방식에서 initiator와 responder는 그림 3과 같이 동일한 전파 경로를 갖지만, 패킷의 전송 방향이 서로 반대이다. 따라서, initiator와 responder 각각의 기기에서 발생하는 시간에 따른 위상의 변화량은 서로 부호가 반대인 형태로 표현될 수 있다. 이는 그림 3과 같다. 먼저 initiator에서 responder 방향의 패킷의 위상은 그림 3(a)와 같이 표현할 수 있고, 그 반대 방향은 그림 3(b)와 같이 표현 된다. initiator와 responder 사이 LOS 환경에서 그림 3의 표현은 CIR에 대한 식 (3)으로 정리된다.

여기서 2πf_cτ는 경로시간 τ에 의해 발생하는 실제 위상(actual phase), 2πΔf_c는 CFO(carrier frequency offset), ${\varphi }_i^{tx}$와 ${\varphi }_i^{rx}$는 각각 송신기와 수신기 국부발진기의 초기위상을 의미한다. 이때 Δf_c는 송신기와 수신기 간의 PLL (phase locked loop)의 미세한 주파수 차이에 의해 발생한다. Initiator에서 responder 방향으로 향하는 poll 패킷의 CIR에 의한 위상은 식 (4)와 같이 주어진다.

다음으로 responder에서 initiator 방향으로 향하는 Response 패킷의 위상은 식 (5)와 같이 주어진다.

식 (4) 및 식 (5)를 비교하면 송신기와 수신기의 CFO와 초기위상의 부호가 반대이므로 이를 더하게 되면 CFO와 초기위상을 제거할 수 있음을 알 수 있다.

이제 기존의 DS-TWR 방식에서 responder가 final 패킷을 수신 후 식 (1)로 거리 계산을 마치고, 시간에 따른 위상 변화량을 없애기 위해 post final 패킷을 하나 더 주고받는다. post final 패킷은 다른 패킷과 다르게 payload 부분에 ToF 정보가 존재하지 않는다. post final 패킷으로 정보를 주고 받는 것이 아닌 UWB IC의 위상오차를 제거하기 위해 기존의 DS-TWR 방식의 마지막에 추가되는 것이다^[7]. 이러한 과정은 그림 4와 같고 이를 고정밀 DS-TWR 방식이라 부르도록 한다. 단, post_final 패킷을 추가한 고정밀 DS-TWR 방식에서 각 기기의 송신 후 수신까지의 지연시간, 수신 후 송신까지의 지연시간을 동일하게 설정해야 한다. 이러한 방식으로 패킷의 전송방향을 고려하여 poll 패킷과 response 패킷의 위상정보를 더하면 식 (6)이 되고, final 패킷과 post final 패킷을 빼면 식 (7)이 된다.

이제 식 (6)에서 식 (7)을 빼면 식 (8)과 같이 CFO가 제거된 최종 위상을 구할 수 있다.

식 (8)의 최종 위상 계산식은 반송파 주파수의 2배인 주파수와 Initiator와 Responder가 떨어진 거리에 비례하여 2 π 주기로 반복되는 위상값을 얻을 수 있다. 이제 DS-TWR 방식으로 구한 거리 측정값을 사용하여 식 (8)을 보정하게 된다. 식 (10)의 정수값 N은 측정된 거리인 D_measured와 식 (9)와 같이 반송파 주파수의 2배인 주파수의 파장으로 나누어 구할 수 있다. 이제 식 (8) 및 식 (10)을 이용하여 보정된 거리값 D_adj을 식 (11)과 같이 구할 수 있다.

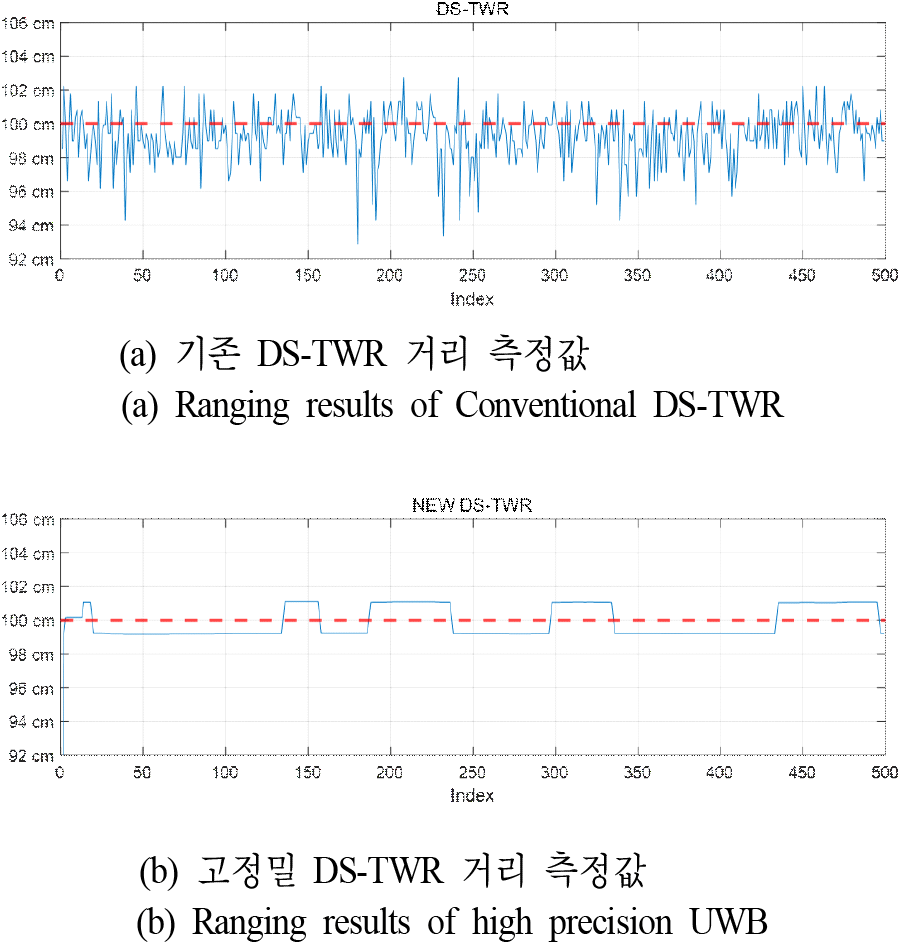
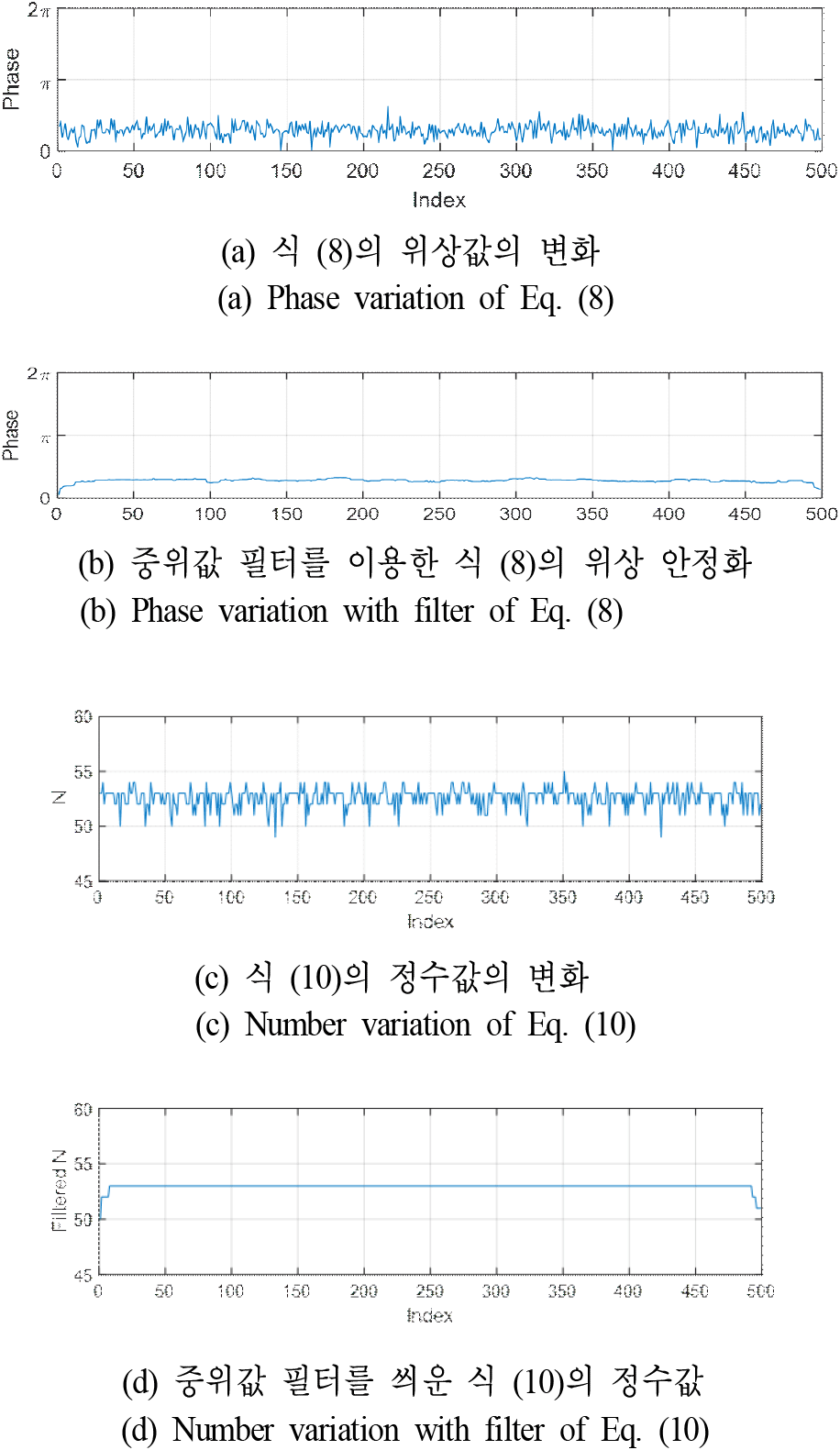
이상의 방식을 통해 구현된 고정밀 UWB의 정밀도를 확인하기 위하여 기존의 DS-TWR 방식의 결과와 비교한 결과가 그림 5에 보여진다. 이를 위하여 initiator와 responder를 바닥에서 1 m 높이의 삼각대로 고정하고 두 기기 사이 간격을 1 m로 고정하여 설치하였고, 서로 마주보는 LOS 환경에서 거리 측정을 500회 실시하였다. 그림 5(a)는 기존의 DS-TWR 거리 측정 정확도를 보여주며 그림 5(b)는 고정밀 DS-TWR 거리 측정 정확도를 나타낸다. 그림 5(a)에서 볼 수 있듯이 기존의 DS-TWR 방식은 실제 거리값 1 m를 중심에 두고 거리 측정 500회 동안 최대는 약 103 cm까지, 최소는 94 cm로 최대 10 cm의 오차범위를 갖는 것을 확인할 수 있었다. 반면, 그림 6(b)와 같이 고정밀 UWB 방법으로 위상오차를 제거하면 오차 범위가 1 cm 이내로 개선되었음을 확인할 수 있다. 하지만 위상모호성에 의해 실제 측정 시 거리값 D_measured에도 파장의 2배 만큼씩 거리 오차가 가끔 발생하게 된다. 참고문헌 [7]에서는 이를 2개의 주파수를 고정밀 TWR을 수행하고 이 둘의 차이를 이용하여 보상하는 방식으로 해결하였으나 국내 기술기준에서는 적용이 불가능한 방식이다. 따라서 본 연구에서는 움직임이 상대적으로 적어 거리 측정을 여러 번 할 수 있다면 간단한 중위값(median) 필터를 사용하는 방식을 사용하는 방식을 제안하였다. 즉, DS-TWR 방식에서 측정된 거리의 변화가 없다면 움직임이 없다고 보고 여러번 측정하여 위상모호성에 의해 거리 측정값이 튀는 값을 필터링하는 방법을 사용하는 것이다. 중위값 필터가 적용되는 부분은 식 (8)의 위상값과 식 (10)의 N값에 해당한다. 제안한 방법의 타당성을 보기 위하여 500번 측정한 결과에서 중위값 필터를 적용해 보았다. 그림 6은 그 결과를 보여준다. 먼저 그림 6(a)와 그림 6(c)는 고정밀 DS-TWR 방식으로 500번 거리 측정한 후 식 (8)로 구한 위상 정보의 변화와 식 (10)에서 구한 N값의 변화를 보여준다. 거리가 고정되어 있음에도 불구하고 위상과 정수 N값이 위 아래로 흔들림을 알 수 있다. 이제 크기가 25인 중위값 필터를 적용한 결과는 그림 6(b)및 그림 6(d)와 같다. 이 결과를 통해 식 (8) 및 식 (10)에서 발생하는 오차를 최소화하여 정밀한 거리측정이 가능함을 확인할 수 있었다. 단, 빠른 움직임이 있어 같은 거리에도 여러번 측정이 어려운 경우에는 불가능한 방식이라는 단점은 존재한다. 하지만 거리측정이 1 msec 이내에 이루어지므로 속도가 적은 손의 움직임 등을 추적할 때는 적용이 가능할 것으로 판단된다.

2-2절에서 국내 기술기준을 만족하는 고정밀 DS-TWR 방식을 제안하였다. 본 절에서는 제안한 방식을 이용하여 구현한 고정밀 DS-TWR 방식과 기존 DS-TWR 방식의 성능 분석 결과를 제시한다. 특히, 위상 기반 거리 측정의 특성상, 장거리로 갈수록 위상 정보의 변동성이 커지고 위상 래핑(phase wrapping) 현상이 반복적으로 발생하므로 실험에서는 10 m 거리 환경에서 수행하여, 제안된 고정밀 거리 측정 보정 기법의 유효성을 검증하였다.

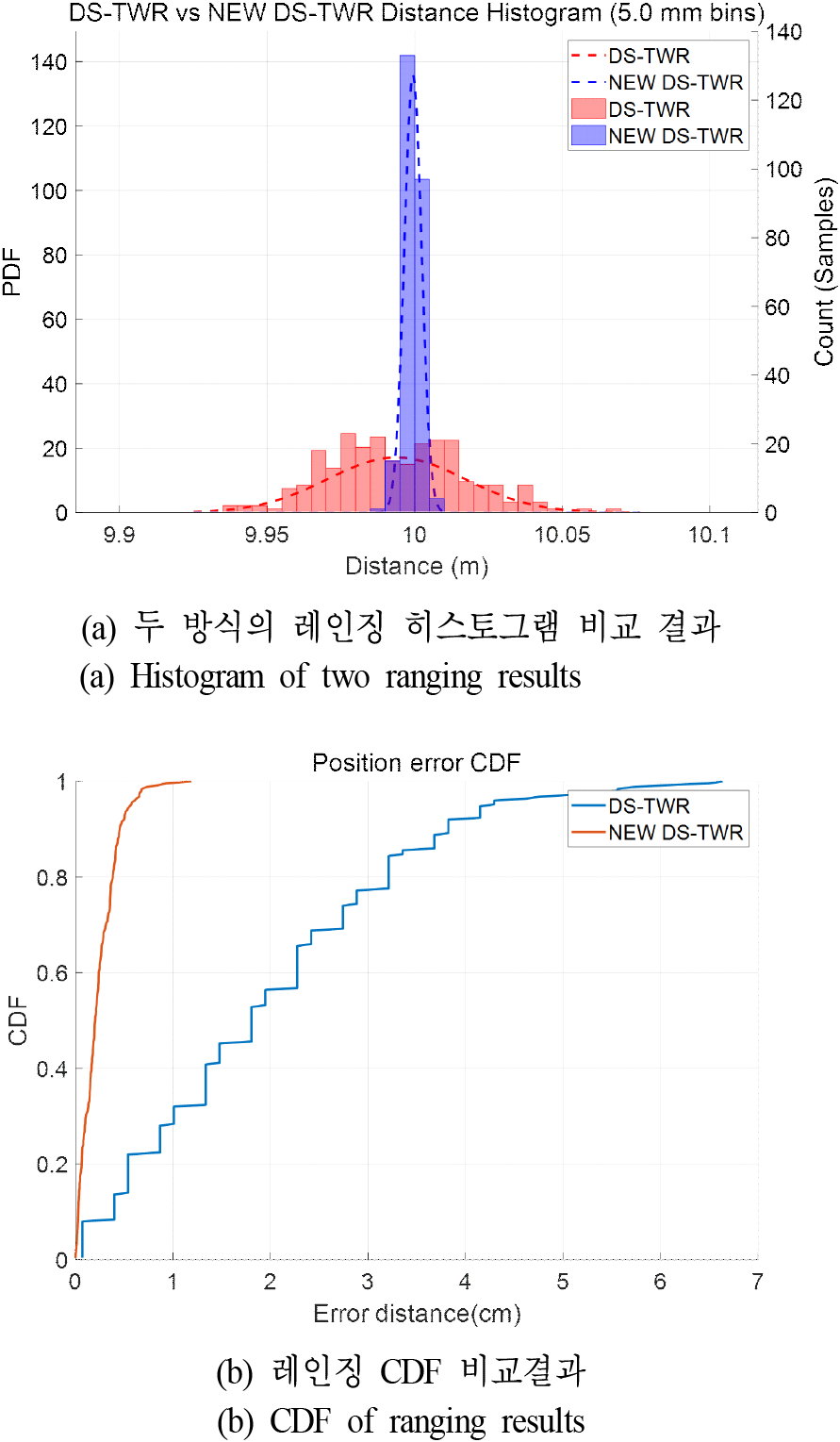
그림 7(a)는 기존 DS-TWR 거리 측정값과 고정밀 DS-TWR 레인징 방법의 히스트로그램을 비교한 결과를 보여준다. 고정밀 가능성을 확인하기 위하여 initiator와 responder 사이 간격을 10 m로 고정하여 설치하였고, 서로 마주보는 LOS 환경에서 거리 측정을 500회 실시하였다. 그림 7(a)에서 볼 수 있듯이 기존의 DS-TWR 방식은 실제 거리값 10 m를 중심에 두고 거리 측정 500회 동안 최대는 약 10.04 m까지, 최소는 9.94 m로 최대 10 cm의 오차범위를 갖는 것을 확인할 수 있었다. 반면, 본 연구에서 구현한 고정밀 UWB 방법으로 위상오차를 제거하면 오차 범위가 1 cm 내외로 개선되었음을 확인할 수 있다. 이를 확률분포로 표현하면 그림 7(b)와 같다. 기존 DS-TWR 방식과 제안된 고정밀 DS-TWR 방식을 비교한 결과, 그림 7(a)에서 제안 기법은 오차 분포가 매우 좁은 구간에 집중되어 기존 방식 대비 정밀도가 현저히 향상된 것을 확인할 수 있었다. 또한, 그림 7(b)의 CDF 분석에서는 1 cm 이하의 오차 구간에서 누적 확률이 급격히 증가하며, 전체 샘플의 90 % 이상이 1 cm 이내의 오차 범위에 포함되는 것으로 나타났다. 기존 TWR 방식은 누적 확률 10 % 기준 오차가 3.82 cm였던 반면, 제안된 방식은 동일 기준에서 0.45 cm로 나타나, 오차의 분산이 효과적으로 개선되었음을 입증하였다. 이는 제안한 보정 기법이 위상 오차와 정수값 N의 보정 및 중위값 필터링을 통해 거리 정확도가 향상됨을 확인할 수 있었다.