The Journal of Korean Institute of Electromagnetic Engineering and Science

The Korean Institute of Electromagnetic Engineering and Science

J. Korean Inst. Electromagn. Eng. Sci. 2025; 36(7):696-707

pISSN: 1226-3133, eISSN: 2288-226X

DOI: https://doi.org/10.5515/KJKIEES.2025.36.7.696

논문/REGULAR PAPER

바이스태틱 FMCW SAR 거리 해상도 향상에 관한 연구

김현동^†

, 이인혁

, 조민곤

, 신희섭^*

, 옥재우^*

, 백민영^*

, 유응노^*

, 김경태

Study on Range Resolution Improvement for Bistatic FMCW SAR

Hyun-Dong Kim^†

, In-Hyeok Lee

, Min-Gon Cho

, Hee-Sub Shin^*

, Jae-Woo Ok^*

, Min-Young Back^*

, Eung-Noh You^*

, Kyung-Tae Kim

포항공과대학교 전자전기공학과

^*LIG넥스원(주)

Department of Electrical Engineering, Pohang University of Science and Technology

^*LIG Nex1 Co. Ltd

^†Corresponding Author: Hyun-Dong Kim (e-mail: hdkim927@postech.ac.kr)

© Copyright 2025 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Apr 14, 2025; Revised: May 12, 2025; Accepted: May 29, 2025

Published Online: Jul 31, 2025

요 약

합성 개구 레이다는 전천후 고해상도 영상 획득이 가능해 다양한 분야에 활용되며, 최근에는 경량·저전력 구조의 FMCW SAR가 드론 등 소형 플랫폼에 적합한 기술로 주목받고 있다. 하지만 이러한 경량 플랫폼 기반의 FMCW SAR는 하드웨어 제약으로 인해 거리 해상도가 저하되는 한계가 존재한다. 이를 극복하기 위한 해상도 향상 기법들이 제안되어 왔으며, 그 중 하나로 바이스태틱 구조를 활용한 거리 해상도 향상 방식이 있다. 하지만, 실제 드론 운영 시 필요한 안전거리 확보로 인해 레이다 간 간격이 커지면 스펙트럼 사이에 공백이 생기고, 이로 인해 신호 합성이 어려워지는 문제가 발생한다. 이에 본 연구에서는 레이다 간 간격 증가로 인한 스펙트럼 공백 구간을 보완하고, 이를 통해 더 넓은 유효 대역폭을 갖는 연속 신호를 합성하여 향상된 거리 해상도를 달성하는 기법을 제안한다. 이를 위해 mutual coherent processing 기반 접근법을 적용하며, 각 대역 신호에 대해 모델 차수를 결정하고 ESPRIT 알고리즘을 통해 초기 pole을 추정한다. 이후 두 신호의 상호 관계를 바탕으로 위상 정렬 및 보상을 수행하고, 전체 대역에 대한 all-pole 모델을 정밀 추정하여 공백 구간을 채운다. 시뮬레이션 결과, 스펙트럼 성공적으로 추정하여 거리 프로파일을 제대로 형성하였으며, 늘어난 대역폭을 통해 향상된 해상도를 확인할 수 있었다.

Abstract

Synthetic aperture radar (SAR) enables high-resolution imaging, regardless of weather or lighting conditions. Frequency-modulated continuous wave (FMCW) SAR has emerged as a promising solution for use with lightweight, low-power platforms, such as drones. However, FMCW SAR systems suffer from limited range resolution, owing to hardware constraints. Bistatic configurations have been proposed to overcome this problem, but maintaining safe distances between platforms introduces spectrum gaps that hinder signal synthesis.

This study proposes a range-resolution improvement method that compensates for the spectrum gaps caused by increased bistatic separation. Using a mutually coherent processing-based approach, we estimated the initial poles by employing the ESPRIT algorithm and performed phase alignment between the signals. The all-pole model was then refined to fill these gaps. Simulation results demonstrated successful spectrum estimation and proper range profile formation, thus confirming improved resolution owing to the expanded bandwidth.

Keywords: Synthetic Aperture Radar; Bistatic Radar; Frequency Modulated Continuous Wave; Range Resolution Improvement

Ⅰ. 서 론

합성 개구 레이다(SAR, synthetic aperture radar)는 고해상도의 지상 영상을 획득할 수 있는 능력으로 인해 정찰, 감시, 환경 모니터링, 재난 대응 등 다양한 분야에서 활발히 활용되고 있는 이미징 기술이다^[1]. SAR는 플랫폼의 움직임을 활용해 가상의 대형 안테나(합성 개구)를 형성함으로써, 비교적 작은 안테나 크기로도 높은 해상도의 이미지를 생성할 수 있다. 최근에는 압축 센싱(compressive sensing), 자동 초점 기법(autofocus), 지능형 안테나 설계 등과 결합한 고성능 SAR 영상화 기법들이 활발히 연구되고 있으며, 영상 품질 향상과 연산 효율 개선을 동시에 달성하기 위한 다양한 접근법이 제안되고 있다^[2]~[7].

주파수 변조 연속파(FMCW, frequency-modulated continuous wave)를 사용하는 FMCW SAR는 기존의 펄스 기반 SAR에 비해 하드웨어 구성이 간단하고^[8], 경량화 및 저전력 구현이 가능하다는 장점이 있어 드론이나 무인항공기와 같은 소형 이동체에 탑재하기에 적합하다^[9]. 이러한 특성은 FMCW SAR을 활용한 다중기(multistatic) 또는 군집형 드론 기반 SAR 구성의 실현 가능성을 높이고 있으며^[10], 저비용 고유연성 시스템에 대한 수요를 충족시키고 있다.

그러나 경량 플랫폼에 탑재되는 FMCW SAR은 필연적으로 하드웨어 성능의 한계를 가지며, 이로 인해 영상의 해상도가 저하되는 문제가 있다. 아날로그-디지털 변환기의 샘플링 속도, 사용 가능한 주파수 대역폭, 그리고 안테나 빔폭 등의 제약이 해상도 저하의 주요 원인으로 작용한다. 이러한 제약을 극복하기 위해 다양한 거리 해상도 향상(RRI, range resolution improvement) 기법이 제안되어왔다.

단일 FMCW 레이다를 이용한 거리 해상도 향상 기법이 제안된 바 있으나, 이는 모노스태틱 구성에 국한되며, 다양한 톱니파형 FMCW 신호를 활용함에 따라 하드웨어 복잡도가 증가하는 단점이 존재한다^[11]. 이러한 한계를 극복하기 위해, CTI(cross-track interferometry) 구성을 활용하여 바이스태틱 레이다 구조에서 거리 해상도를 향상시키는 기법이 제안되었다^[12],[13]. 해당 기법은 두 레이다에서 수신한 신호 간 위상 차이를 보상한 후, 시간 영역에서 신호를 처리하여 더 넓은 대역폭을 갖는 하나의 신호로 합성함으로써 향상된 해상도를 확보한다. 그러나 이 방법은 드론 위치의 자유도를 보장하지 못해 실제 환경에서 적용하기 어렵다. 최근에는 바이스태틱 레이다 환경에서의 왜곡 보정, 압축 센싱 기반 영상화 등 다양한 기법이 제안되었으며^[14]~[17], 본 연구에서는 그 중 거리 해상도 향상 기법의 일반화에 집중하였다.

드론 기반 SAR 시스템에서는 두 레이다 플랫폼 간의 최소 안전거리를 확보해야 한다. 이는 실제 드론 운용 시 충돌을 방지하기 위한 필수 조건으로, 일정 수준 이상의 간격 유지를 요구한다. 그러나 레이다 플랫폼 간의 거리가 멀어질수록 수신 신호의 스펙트럼 간 간격 또한 증가하게 되며, 이로 인해 앞서 언급한 참고문헌 [12] 및 참고문헌 [13] 기법을 이용한 신호 합성이 어려워지는 한계가 있다. 이에 본 연구에서는 두 레이다 간 간격 증가로 인해 수신 신호 간 스펙트럼에 공백이 발생하는 조건을 분석하고, 스펙트럼 사이를 채워 넣음으로써 더 넓은 유효 대역폭을 갖는 하나의 연속된 신호로 합성하고, 이를 통해 더욱 향상된 거리 해상도를 확보하는 방법을 제안한다.

공백이 발생한 스펙트럼 구간을 보완하기 위해, 본 연구에서는 상호 위상 정합 처리(mutual coherent processing) 기법을 활용한다^[18]. 제안된 드론 SAR 시스템은 비행 중 SAR 데이터를 수집한 후, 지상에서 고정밀 후처리를 수행하는 방식으로 설계되었다. 1) 수신된 신호에 all-pole 모델을 적용하면, 신호는 복소 지수 함수들의 중첩 형태로 모델링될 수 있다. 2) 각 대역에 대해 MDL(minimum description length)^[19],[20]을 이용하여 유효한 신호원의 수를 추정한 뒤, 이를 바탕으로 ESPRIT(Estimation of Signal Parameters via Rotational Invariance Techniques) 알고리즘을 적용하여 초기 극값을 결정한다^[21]. 3) 이후, 두 대역 간의 상호 위상 정합 관계를 기반으로 신호 간 오차를 보상하고, 4) 마지막으로 공백 구간을 포함한 전체 대역에 대한 global all-pole 모델을 Levenberg-Marquardt 알고리즘을 통해 추정한다^[22].

제Ⅱ장에서는 바이스태틱 구조에서 기하구조를 활용한 RRI기법에 대해 기술하고, 스펙트럼 공백이 발생하는 제약 조건을 분석한 후 간단한 시뮬레이션을 통해 이를 검증한다. 제Ⅲ장에서는 제안된 기법의 이론적 배경과 처리 과정을 상세히 서술한다. 제Ⅳ장에서는 MATLAB 기반의 시뮬레이션을 통해, 제안된 기법이 제약 조건 하에서도 RRI를 효과적으로 수행하며 향상된 거리 해상도를 달성함을 확인한다.

Ⅱ. CTI를 활용한 바이스태틱 FMCW 레이다 RRI 기법과 제약조건 분석

2-1 바이스태틱 FMCW 레이다 RRI 기법

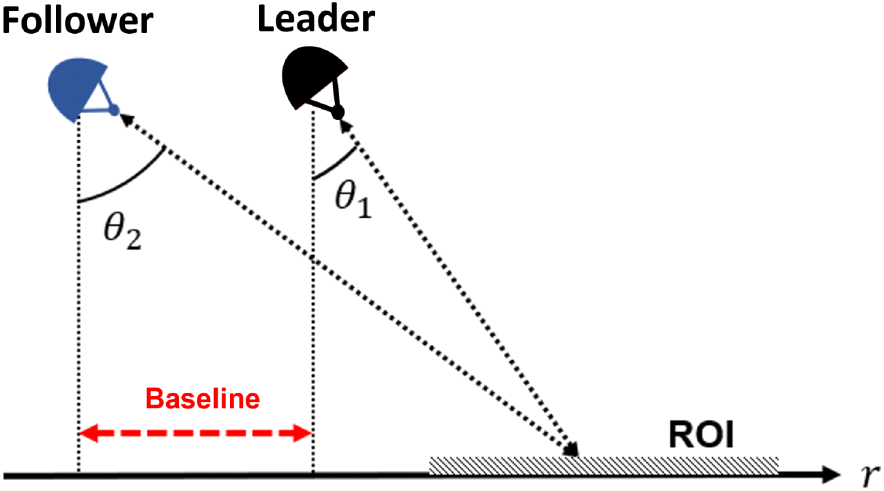
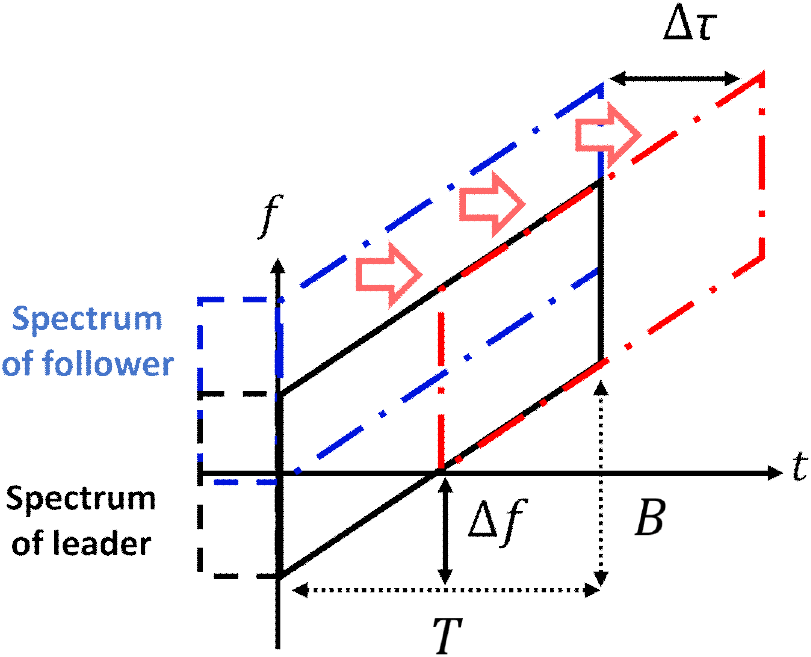
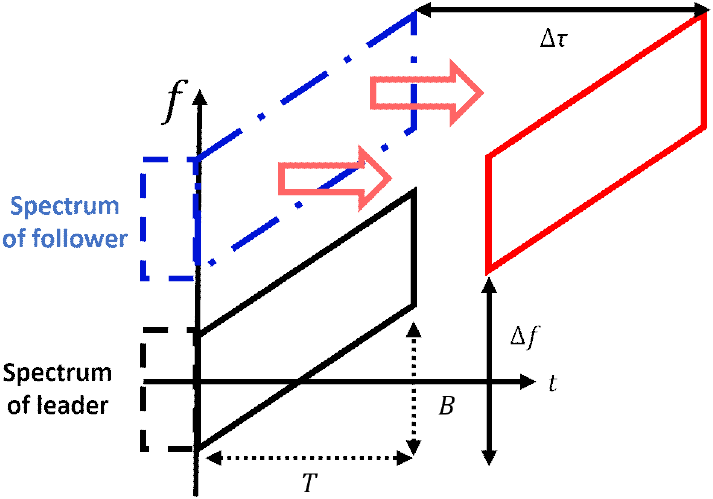
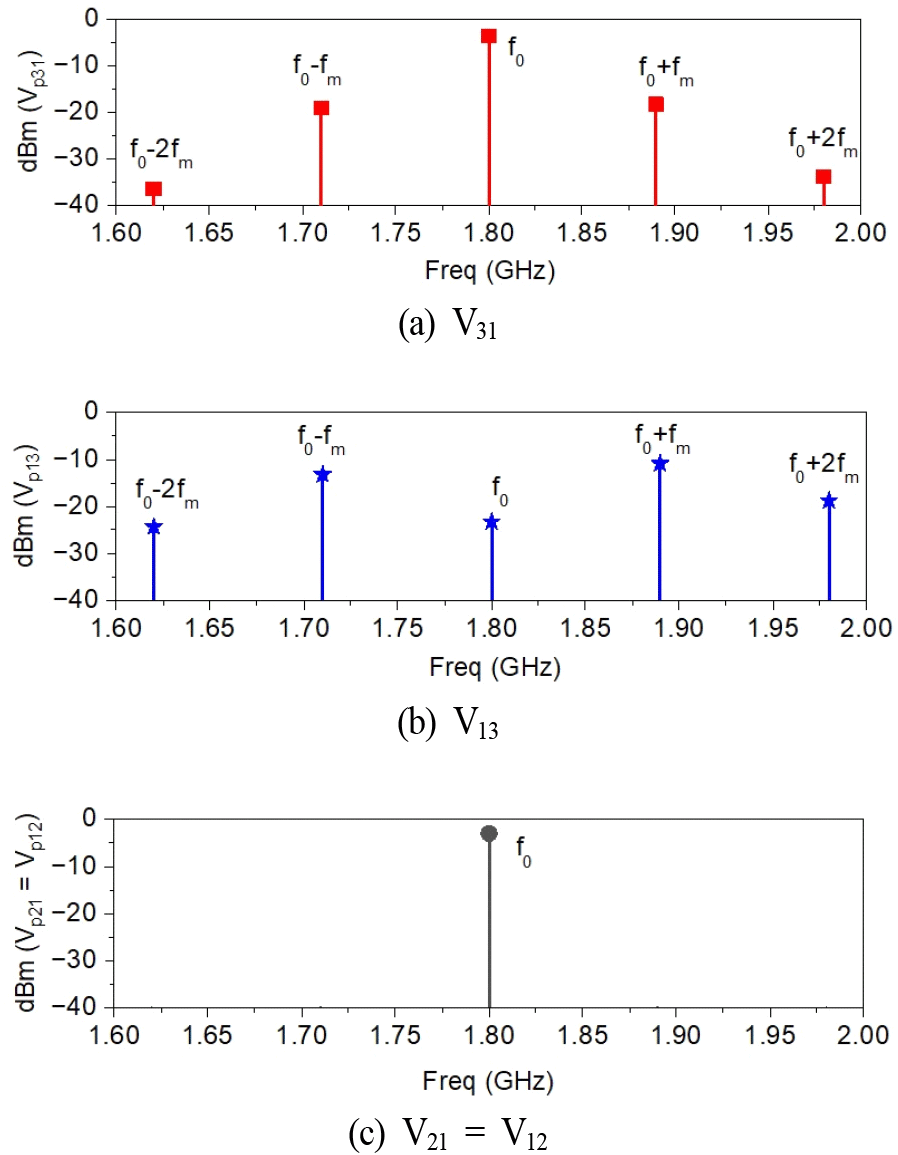
바이스태틱 FMCW 레이다의 수신 신호 스펙트럼 정보를 분석하기 위한 기하구조는 다음 그림 1과 같다. 이때, 관심영역(ROI, region of interest)와 가까운 드론을 선행 개체(leader), 먼 드론을 후행 개체(follower)로 지정하면 leader와 ROI 사이의 관측 각도는 θ₁, follower와 ROI 사이의 관측 각도는 θ₂이다. 두 드론에서 수신한 레이다 신호의 스펙트럼은 다음 그림 2와 같이 구해지며, T는 시간 지연, B는 신호의 대역폭을 나타낸다. 검은색 실선으로 표시한 부분은 leader가 수신한 신호의 스펙트럼이며, 파란색 파선으로 표시한 부분은 follower가 수신한 스펙트럼이다. 두 스펙트럼 사이의 주파수 변이 Δf는 식 (1)과 같이 정리된다.

Δ f = c Δ θ λ tan θ m

(1)

그림 1. | Fig. 1. 바이스태틱 FMCW 레이다 구조 | Bistatic FMCW radar configuration.

Download Original Figure

그림 2. | Fig. 2. 기존 RRI 기법 개념 | Concept of conventional RRI method.

Download Original Figure

여기서 c는 빛의 속력, λ는 레이다 신호의 파장을 의미하며, 두 수신기가 동일한 선형 주파수 변조(LFM, linear frequency modulated) 파형을 사용한다고 가정한다. θ_m은 (θ₁+θ₂)/2으로 두 각도의 평균값, Δθ는 (θ₂−θ₁)으로 두 각도의 차이를 표현한다. RRI를 수행하기 위하여 기존 RRI 기법에서는 FMCW 특성을 활용해 스펙트럼을 이동시켜준다. 식 (1)을 통해 얻은 Δf과 LFM 신호의 처프 기울기 K_r사이의 관계를 통해 시간 축에서의 지연 Δτ 를 계산하면, 식 (2)와 같이 표현된다.

Δ τ = Δ f K r

(2)

Δτ를 이용해 시간축에서 파란색 스펙트럼을 빨간색 스펙트럼으로 이동시켜주면 더 넓은 주파수 스펙트럼을 획득할 수 있다. 이는 곧, 향상된 해상도를 지닌 고해상도 거리 프로파일 (HRRP, high resolution range profile)을 얻는 것을 가능하게 해준다(거리 해상도 $Δ r = c 2 B$ ).

2-2 바이스태틱 FMCW 레이다 RRI 기법 제약조건 분석

앞서 언급한 기존 기법을 활용하여 RRI를 수행하기 위해서는 두 스펙트럼 간에 일정 부분 겹침이 존재해야 한다. 그러나 드론에 FMCW 레이다를 탑재하여 SAR 영상을 획득하는 경우, 운용상 드론 간의 안전거리를 확보해야 하며, 이에 따라 두 드론간 거리(baseline)는 필연적으로 증가하게 된다. Baseline이 증가하면 Δθ가 증가하게 되지만 θ_m역시 증가하게 되므로 Δf의 크기 변화를 확인하기 위해서는 정량적 분석이 필요하다.

이를 위해, 식 (1)의 분모 tanθ_m에 대하여 테일러 급수 전개를 적용하면, (θ₁+θ₂)/2로 근사할 수 있으며, baseline에 따른 각도 변화 역시 θ₂=θ₁+ϵ로 표현이 가능하다. 이때, 식 (1)은 식 (3)과 같이 근사할 수 있다.

Δ f ≈ c θ 2 − θ 1 λ θ 1 + θ 2 / 2 = 2 c ⋅ 2 ϵ λ 2 θ 1 + ϵ

(3)

식 (3)을 ϵ에 대해 미분하면 양의 값을 가지므로, ϵ가 증가함에 따라 전체 Δf 값도 증가하게 된다. 즉, baseline이 증가할수록 두 스펙트럼 간의 간격 또한 커지며, 기존 기법으로는 RRI 수행이 제한된다.

두 FMCW 신호를 RRI 기법을 통해 결합하기 위해서 시간 축에서 신호 결합을 수행한다. leader와 follower에서 수신한 신호는 식 (4) 및 식 (5)와 같이 표현된다.

s r, 1 (t) = e j 2 π f c τ d, 1 ⋅ e j 2 π K τ d, 1 2 ⋅ e j 2 π K τ d, 1 t

(4)

s r, 2 (t) = e j 2 π f c τ d, 2 ⋅ e j 2 π K τ d, 2 2 ⋅ e j 2 π K τ d, 2 t

(5)

여기서, τ_d,1과 τ_d,2는 레이다와 ROI 사이의 왕복 시간이다. 식 (2)를 통해 늘어난 Δτ만큼 s_r,2 (t)를 이동시켜주면 식 (6)과 같이 구성된다.

s R R I (t) = s r, 1 (t) + s r, 2 (t − Δ τ)

(6)

최종적으로, RRI를 통해 획득한 HRRP, I(f)는 식 (7)과 같이 구해진다.

I (f) = ∫ − ∞ ∞ s R R I (t) e − 2 π f t d t

(7)

RRI를 수행한 후 그림 3과 같이 시간-주파수 도메인 상에서 시각화하면 스펙트럼 간 간극(spectrum gap)이 발생한다. 해당 현상은 Δf 가 증가하여 Δf>B 일 때 발생하며, 이를 θ₁과 θ₂로 정리한 식은 식 (8)과 같다. 여기서, f_c는 레이다의 중심 주파수 이다.

θ 2 > 1 + B / f c 1 − B / f c θ 1

(8)

그림 3. | Fig. 3. Baseline의 증가로 인한 RRI 제약 조건 상황 | RRI constraint condition with increasing baseline.

Download Original Figure

2-3 바이스태틱 FMCW 레이다 RRI 기법 제약조건 시뮬레이션

식 (8)의 조건이 만족되는 경우, 스펙트럼 간 간극이 발생하게 되며, 이 상태에서 기존 RRI 방식으로 신호 처리를 수행할 경우, HRRP 상에서 정확한 PSF(point spread function)을 얻기 어렵다. 이 현상을 간단한 시뮬레이션으로 검증해 보았다. 본 시뮬레이션은 f_c는 77 GHz, B는 410 MHz, θ₁은 60°, θ₂는 61.88 °로 설정하여 식 (8)의 제약 조건에 해당하는 상황을 구성하였다. 해당 조건하에서 3개의 표적에 대해 기존 RRI 기법을 적용하여 HRRP를 획득한 결과는 그림 4에서 나타난다.

그림 4. | Fig. 4. 제약 조건에서의 모노스태틱 레이다와 기존 기법을 통해 획득한 HRRP | HRRPs obtained by monostatic radar and conventional RRI method under constraint condition.

Download Original Figure

그림에서 붉은 점선은 leader 레이다의 스펙트럼, 파란 파선은 follower 레이다의 스펙트럼을 나타내며, 기존 RRI 기법을 적용한 결과는 검은 실선으로, 실제 표적의 위치는 ‘o’로 표시하였다. 모노스태틱 레이다(leader 또는 follower 단독)의 경우 PSF는 정상적으로 형성되었으나, 해상도가 낮아 약 8 m 지점에 위치한 두 표적을 분리하지 못하는 한계를 보인다. 반면, 바이스태틱 레이다 구성에서 기존 RRI 기법을 적용한 경우에는 PSF 자체가 왜곡되어 정확한 거리 정보를 획득하지 못하는 문제가 발생한다.

이에 본 연구는 바이스태틱 레이다 구조에서, baseline 증가로 인해 발생하는 스펙트럼 공백을 보완하고, 이를 통해 고해상도 SAR 영상 복원이 가능한 신호 처리 기법을 제안한다.

Ⅲ. 제안된 기법

본 절에서는 baseline이 증가함에 따라 leader와 follower 간의 주파수 대역이 분리되며 발생하는 스펙트럼 상의 공백 영역, 즉 스펙트럼 간 간극을 효과적으로 복원하여, 결과적으로 하나의 연속적이고 넓은 대역폭을 갖는 신호를 구성하는 방법을 제안한다.

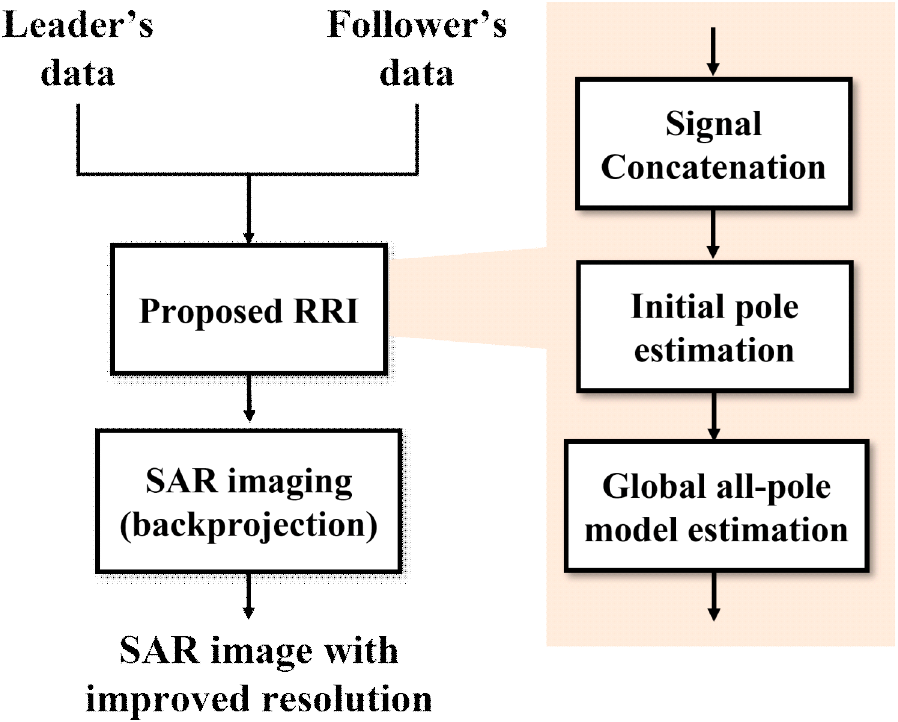
제안하는 기법은 다음의 세 단계로 구성된다. 첫째, 시간 도메인에서의 신호 합성 단계로, 이는 식 (6)에서 제시된 절차에 따라 수행되며, 본 장에서는 중복 설명을 생략한다. 둘째, 개별 스펙트럼 구간에 대해 all-pole 모델 기반의 스펙트럼 해석을 수행하고, 해당 모델의 극점(pole)에 대한 초기 추정을 수행한다. 이는 스펙트럼 간 간극을 보완하기 위한 구조적 기반을 마련하는 단계이다. 셋째, 추정된 극점 정보를 바탕으로 전체 스펙트럼을 대표하는 글로벌 all-pole 모델을 구축하고, 이를 통해 스펙트럼의 공백 구간을 복원하여 연속적인 넓은 대역의 스펙트럼을 생성한다.

3-1 All-Pole 모델 기반 초기 극점 추정

RRI를 수행하기 위해서는 두 개의 독립된 플랫폼이 필요하며, 각기 다른 플랫폼에서 신호를 수집하는 경우, 수신된 신호 간에 상호 위상 정합이 보장되지 않을 수 있다. 이에 따라, 본 연구에서는 각 수신기에서 수신한 신호의 위상 및 시간 정렬을 맞추기 위해 상호 위상 정합 처리(mutual coherent processing) 기법을 적용한다.

Mutual coherent processing을 하기 위해, 각 스펙트럼의 신호는 all-pole 모델을 기반으로 표현한다. 해당 모델은 복소 지수 함수들의 선형 조합으로 구성되며, FMCW 신호의 특성상 시간 축과 주파수 축이 일대일로 대응되기에 시간 도메인에서 표현하면 식 (9)와 같다.

M t n = ∑ k = 1 P a k p k n

(9)

여기서, a_k는 각각의 산란체에 대응하는 진폭이고, p_k는 산란체의 거리 및 감쇠 특성을 반영하는 극점이다. 각각의 데이터에 대하여, 전방 예측 행렬(forward prediction matrix)을 설정해주면 다음 식 (10) 및 식 (11)로 표현된다.

H r, 1 = s 0 s 1 ⋯ s L − 1 s 1 s 2 ⋯ s L ⋮ ⋮ ⋱ ⋮ s N r, 1 − L s N r, 1 − L + 1 ⋯ s N r, 1 − 1

(10)

H r, 2 = s N − N r, 2 s N − N r, 2 + 1 ⋯ s N − N r, 2 + L r, 2 − 1 s N − N r, 2 + 1 s N − N r, 2 + 2 ⋯ s N − N r, 2 + L r, 2 ⋮ ⋮ ⋱ ⋮ s N r, 2 − L r, 2 s N r, 1 − L r, 2 + 1 ⋯ s N − 1

(11)

N_r,1은 0 − T초에 해당하는 leader의 스펙트럼의 샘플 수, N_r,2는 이후 시점 Δτ − T+Δτ에 해당하는 이동된 follower 스펙트럼의 샘플 수, 그리고 N은 0 − T+Δτ에 해당하는 총 샘플 수를 의미한다. 그러므로 leader의 스펙트럼에서의 index인 n = 0,···,N_r,1, follower의 스펙트럼에서의 n = N − N_r,2,···,N-1까지 나타낸다. 여기서 전방 예측 행렬은 Hankel 행렬 H_r,1과 H_r,2로 표현하였으며^[23], 이는 all-pole 모델에서 형성된 지수함수의 선형 구조를 부각하기 위해서이다. 이때, L은 상관 윈도우 길이(correlation window length)로 일반적으로 각 데이터의 1/3로 설정한다.

얻어진 H_r,1과 H_r,2에 대하여 특잇값 분해(SVD, singular value decomposition)를 각각 수행해 주면, H_r,1 = U_r,1S_r,1V_r,1와 H_r,2 = U_r,2S_r,2V_r,2 형태로 구해진다. 여기서, S는 각 데이터에 대한 특잇값을 포함한 대각 행렬로서, 이를 나타내면 식 (12)와 같다.

S r, 1 = σ 0 ⋯ 0 ⋮ ⋱ ⋮ 0 ⋯ σ N r, 1 − 1

(12)

S r, 2 = σ N r, 2 ⋯ 0 ⋮ ⋱ ⋮ 0 ⋯ σ N − 1

(13)

획득한 S_r,1과 S_r,2에서의 신호 성분 개수를 추정하기 위해, 본 연구에서는 MDL 기법을 활용한다. MDL은 정보 이론에 기반한 모델 차수 추정 방법으로, AIC(Akaike information criterion)와 비교했을 때 과도한 모델 차수 선택을 억제하는 경향이 강하다^[19],[20]. 이에 따라 불필요하게 많은 신호원을 추정하는 것을 효과적으로 방지할 수 있다. MDL을 이용한 신호원 수 추정은 다음 식 (14)와 같이 수행되며 차수에 대하여 각각 MDL 값을 구한 다음, 그 값이 가장 작은 차수를 최종 추정치로 선택한다. 여기서, $L (θ^(k))$ 는 추정된 로그 우도(loglikelihood)값이다.

M D L (k) = − 2 ln L (θ^(k)) + 2 [k (2 p − k) + 1] ln N

(14)

이후, MDL 기법을 통하여 각 스펙트럼에서의 모델 차수를 바탕으로 ESPRIT 기법을 적용하여 초기 극값을 추정한다^[21]. 1) V_r,1과 V_r,2에 대하여 신호 부공간을 앞서 구한 모델 차수를 통하여 $V r, 1 s, V r, 2 s$ 로 분리해준다. 2) Shift invariance 구조를 활용하기 위해 선택 행렬 J_r,1=[I_r,1 0]과 J_r,2=[I_r,2 0] 를 구성해준 후, shift 신호 부공간 행렬 $R r, 1 = J r, 1 V r, 1 s, R r, 2 = J r, 2 V r, 2 s$ 를 구성한다. 3) 이들 간의 관계 R_r,2≈R_r,1Φ에 대하여 LS(least squares)를 통해 추정하여 회전 연산자 $Φ = R r, 1 H R r, 1 − 1 R r, 1 H R r, 2$ 를 구해준다. 4) Φ의 고윳값을 구하여 초기 극값 $z k ≈ λ k = e j θ^k$ 를 구한다. 이는 기존의 참고문헌 [18]에서 제안한 root-MUSIC(multiple signal classification) 알고리즘 기반 극값 추정 방식과 비교했을 때, 수치적 해를 직접적으로 제공함으로써 더 높은 정확도를 보장한다.

3-2 Global all-pole 모델 추정

ESPRIT을 통해 얻은 초기 극값을 바탕으로, 보다 정확한 모델 기반 파라미터 추정을 위해 후처리 절차를 수행한다. 두 수신기에서 얻은 모델 간의 위상 불일치를 보정하기 위한 상호 위상 보상(mutual coherent compensation) 단계가 수행된다. 이때 식 (15)의 목적함수를 최소화하여 위상 보정 파라미터 Δθ와 크기 보정 파라미터 A를 추정한다.

argmin A, Δ θ ∑ n = 0 N − 1 A M r, 1 t n e j Δ θ n − M r, 2 t n 2

(15)

여기서, M_r,1(t_n)와 M_r,2(t_n)은 각 데이터에서의 추정된 초기 all-pole 모델이다. 추정된 파라미터들을 통해 수신된 신호들을 식 (16)과 같이 보정한다.

s ¯ = s ⋅ e j Δ θ + arg A ∗

(16)

한편, 전체 데이터를 설명하는 global all-pole 모델을 구성하면, 식 (17)과 같이 표현된다.

M t n; p k, a k = ∑ k = 1 P a k p k n

(17)

이때, P는 전체 모델 차수로 추정된 두 모델 차수 중 큰 값으로 선택한다. 이때, 주어진 신호와 모델간의 오차를 최소화 하는 비선형 최소 자승 문제는 식 (18)과 같이 설정된다.

min p k, a k ∑ n ∈ Ω r, 1 s ˜ n − M t n 2 + ∑ n ∈ Ω r, 2 s ˜ n − M t n 2

(18)

본 연구에서 해당 최적화 문제를 잔차와 Jacobian을 이용해 파라미터를 반복적으로 갱신하는 방식인 LM(Levenberg–Marquardt) 방법을 이용하여 해결한다^[22]. 최적화된 global all-pole 모델은 스펙트럼 간극이 복원된 형태로, 식 (19)와 같이 정리된다.

s R R I t n = ∑ k = 1 P a^k p^k n

(19)

이후, 역투영(backprojection) 알고리즘을 활용하여 최종 SAR 영상을 획득한다. 전체 처리 과정을 정리한 제안 기법의 순서도는 그림 5에 제시되어 있다.

그림 5. | Fig. 5. 제안된 기법의 순서도 | Flowchart of the proposed method.

Download Original Figure

Ⅳ. 시뮬레이션 결과 및 분석

본 절에서는 제안한 알고리즘의 성능을 검증하기 위하여 두 가지 시뮬레이션을 수행해 보았다.

4-1 FMCW 바이스태틱 레이다 시뮬레이션

첫 번째 시뮬레이션에서는 리더와 팔로워 레이다는 동일한 높이인 4 m로 설정되었으며, 횡방향으로 분리되었다(그림 6). 각 레이다는 동일한 FMCW 레이다 시스템을 사용하였으며, 시스템의 주요 사양은 표 1에 요약되어 있다.

그림 6. | Fig. 6. 바이스태틱 FMCW 레이다 시스템 기하구조 | Geometry of bistatic FMCW radar systems.

Download Original Figure

표 1. | Table 1. 시뮬레이션 1 변수들 | Simulation 1 parameters.

Parameters	Values
Carrier frequency	77 GHz
Frequency bandwidth	410 MHz
Chirp rate	8.014 MHz/μs
Time duration	51.2 μs
Look angle (Leader)	60°
Look angle (Follower 1,2)	60.48°, 61.88°
Height	4 m
Baseline length (Follower 1,2)	0.14 m, 0.56 m

Download Excel Table

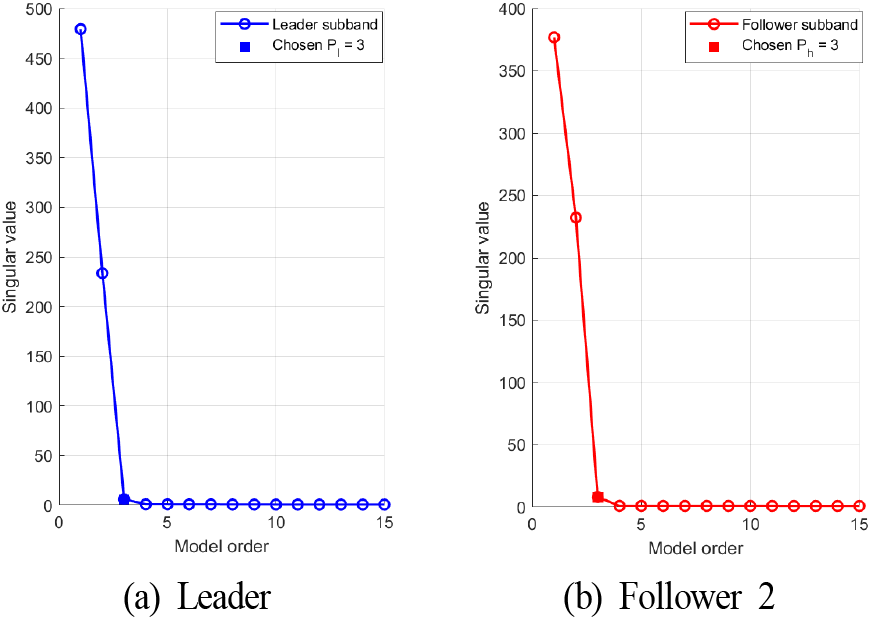
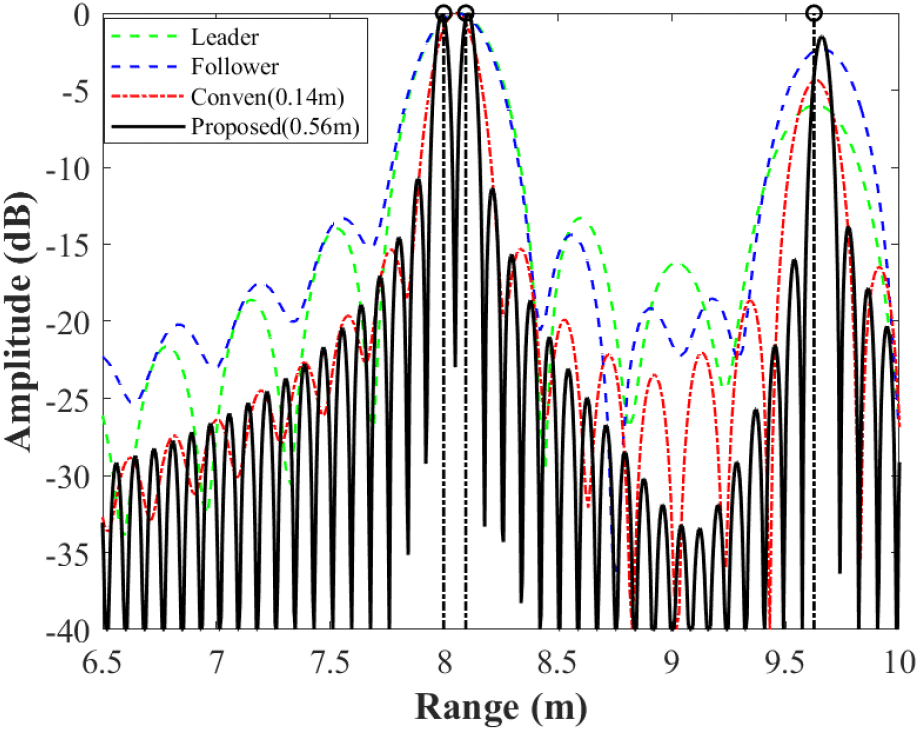
Follower는 총 2개를 설정했으며, follower 1은 제약조건을 벗어나지 않는 관측각으로 설정하여 참고문헌 [12]에서 제안한 기존 RRI 기법을 적용했으며, 이때의 baseline은 0.14 m이다. 반면, follower 2의 경우에는 spectrum gap이 발생하는 관측각으로 설정하여 제안된 RRI 기법을 적용했으며, 이때 baseline은 0.56 m이다. leader와 follower 2에서 수신한 신호에 대하여 신호 합성을 수행한 후, 각 스펙트럼에 대하여 SVD를 수행하여 특잇값을 추출한 결과는 다음 그림 7과 같다.

그림 7. | Fig. 7. MDL 수행 결과 | MDL results.

Download Original Figure

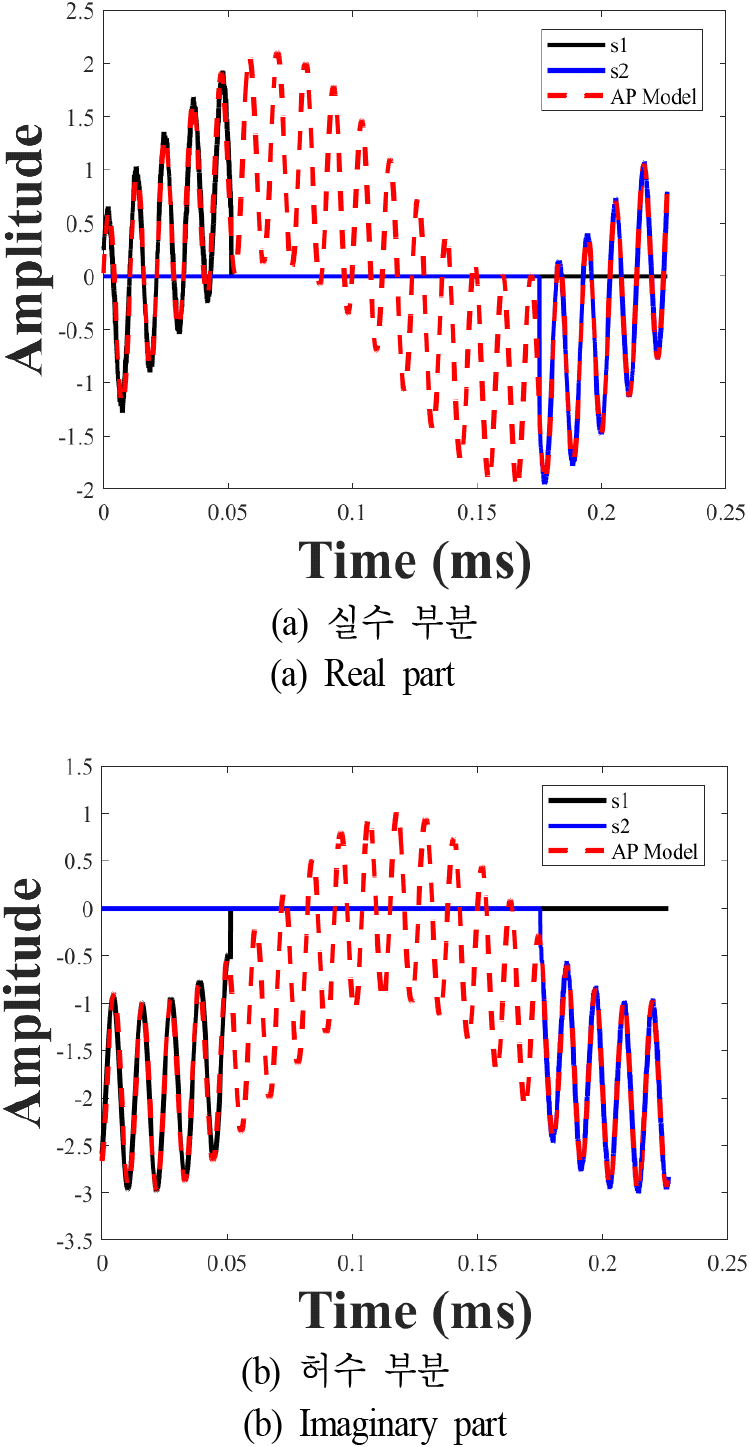
MDL 결과, (a)와 (b) 모두에서 신호원의 개수가 3으로 추정되었으며, 이는 실제 표적 수와 일치한다. 추정한 신호원의 개수를 바탕으로 제안된 기법을 적용하여 global all-pole 모델을 구성한 결과는 그림 8과 같다. 여기서, 검은 실선은 leader, 파란 실선은 follower 2 신호이며, 빨간 점선은 추정한 global all-pole 모델이다. 실수 부분과 허수 부분 모두 실제 신호와 유사하게 추정한 것을 확인할 수 있었으며, global all-pole 모델에 대하여 획득한 HRRP는 그림 9에서 나타난다.

그림 8. | Fig. 8. 추정한 global all-pole 모델 결과 | Results of the estimated global all-pole model.

Download Original Figure

그림 9. | Fig. 9. 시뮬레이션 1에서 획득한 HRRP | HRRP obtained from simulation 1.

Download Original Figure

이때, 녹색과 파란색 점선은 모노스태틱 레이다에서(leader와 follower) 각각 HRRP를 구한 결과이며, 빨간 파선은 leader와 follower 1을 사용해 기존 RRI 기법을 적용하여 HRRP를 획득한 결과이며, 검정 실선은 leader와 follower 2을 사용해 제안한 RRI 기법을 적용하여 HRRP를 획득한 결과이다.

모노스태틱 레이다에서의 이론적 해상도는 c/2B로 약 0.37 m이다. 한편, 바이스태틱 레이다에서의 이론적 해상도는 c/2(B+Δf)로 주어지며, 이때 Δf는 식 (1)을 통해 계산된다. 이를 바탕으로 계산한 leader와 follower 1간의 이론적 해상도는 0.19 m이며, follower 2간의 이론적 해상도는 0.08 m이다. 한편, 8 m 부근에는 해상도 향상을 확인하기 위해 0.11 m 간격으로 두 표적을 두었다.

그림 9에서 확인할 수 있듯이, 모노스태틱 레이다(leader 와 follower 단독 운용)의 경우 낮은 해상도로 인해 8 m 부근에 위치한 두 표적을 분리할 수 없다. 기존 RRI 기법을 적용한 경우에는 해상도가 일부 향상되었으나, 여전히 표적 간 거리(0.11 m)보다 해상도가 낮아 두 표적을 구분하지 못한다. 반면, 제안된 기법을 적용한 결과 충분한 해상도를 확보하여, 8 m 부근의 두 표적을 명확하게 분리할 수 있음을 확인하였다.

획득한 HRRP를 바탕으로 거리 해상도를 구해본 결과, 모노스태틱 레이다에서는 0.37 m, 기존 기법은 0.2 m, 제안된 기법은 0.10 m로 제안된 기법에서 가장 향상된 해상도를 획득할 수 있었다. 단일 점 표적을 기준으로 ISLR (integrated sidelobe ratio)과 PSLR(peak to sidelobe ratio)을 계산한 결과, 각각 −9.7008 dB, −9.7011 dB, −9.6983 dB 및 −13.2613 dB, −13.2609 dB, −13.2634 dB로 나타났다. 이를 통해 제안한 기법은 해상도를 향상시키는 동시에, 이상적인 PSF에 가깝게 성능을 유지하여 전체적인 영상 품질을 효과적으로 개선할 수 있음을 확인하였다.

한편, 제안한 기법은 스펙트럼 간극이 존재하는 환경에서도 신호 간 위상 정합성을 기반으로 거리 해상도 향상을 실현할 수 있도록 설계되었으나, 추가 시뮬레이션 결과 baseline이 증가함에 따라 두 대역 간 위상 정합성이 점차 약화되고, 이로 인해 모델 기반 복원의 수렴 안정성과 연산 효율이 저하되는 양상이 확인되었다. 따라서 제안한 기법을 효과적으로 활용하기 위해서는 거리 해상도 향상과 알고리즘의 수렴 특성 간의 균형을 고려하여 플랫폼 간 간격을 적절히 설정하는 것이 중요하다.

4-2 바이스태틱 FMCW SAR 시뮬레이션

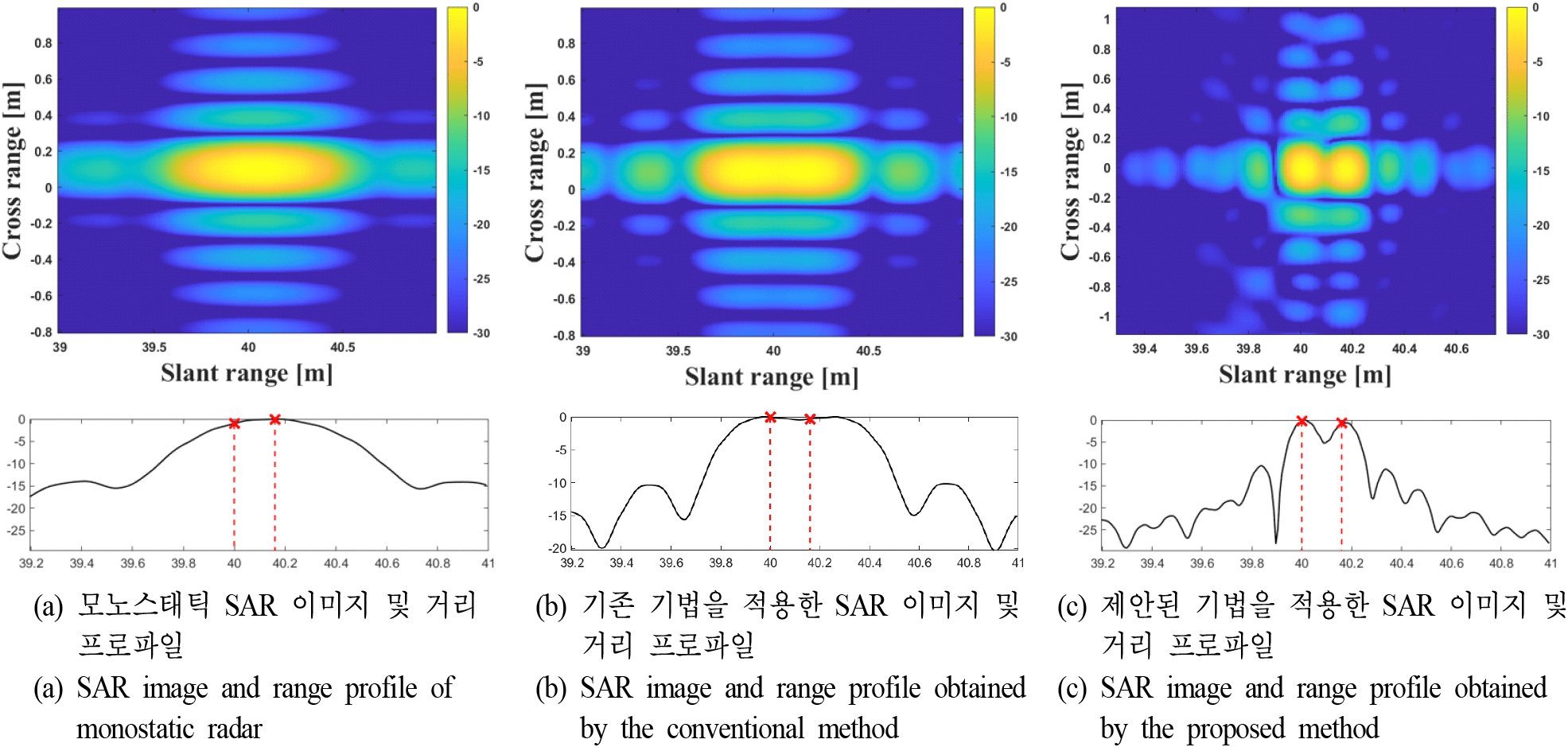
두 번째 시뮬레이션에서는 참고문헌 [13]의 SAR 시나리오로 설정했으며 레이다와 표적 사이의 기하구조는 그림 10을 통해 나타난다. 주요 변수들은 표 2와 같으며, 레이다 변수들은 시뮬레이션 1과 동일하다.

그림 10. | Fig. 10. 바이스태틱 FMCW SAR 시스템 기하구조 | Geometry of bistatic FMCW SAR system.

Download Original Figure

표 2. | Table 2. 시뮬레이션 2 변수들 | Simulation 2 parameters.

Parameters	Values
h₁, h₂, h₃	40 m, 41.42 m, 41.42 m
b₁₂, b₁₃	1.7 m, 3 m
v₁, v₂, v₃	1 m/s
x_c	40 m
Look angle (Leader)	45°
Look angle (Follower 1,2)	45.19°, 46.07°
Coherent processing interval	0.5 s
Pulse repetition frequency	1 kHz

Download Excel Table

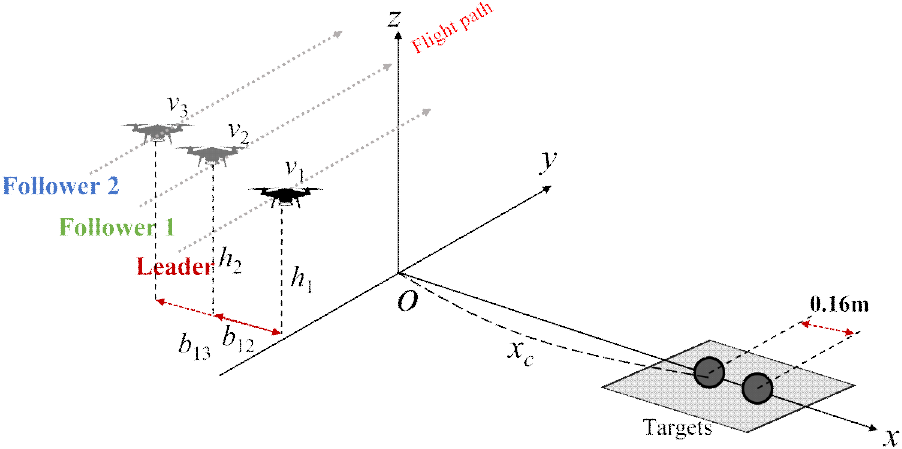
표 2에서 제시한 각 드론들의 관측각을 바탕으로 계산한 모노스태틱 레이다에서의 이론적 해상도는 약 0.37 m, 바이스태틱 레이다에서의 leader와 follower 1간의 이론적 해상도는 0.23 m, follower 2간의 이론적 해상도는 0.08 m이다. 표적 2개를 0.16 m 간격을 두고 SAR 이미지를 획득한 결과 다음 그림 11와 같이 나타난다. 이때, 표적들의 실제 위치는 빨간 'x' 마크로 표시한다. 그림 11(a)는 모노스태틱 레이다 기반 SAR 영상 결과로, 두 표적이 분리되지 않은 모습을 확인할 수 있다. HRRP에서도 마찬가지로 두 표적이 하나의 신호로 합쳐져 나타나 분리가 불가능함을 보여준다.

그림 11. | Fig. 11. 시나리오 2 시뮬레이션 결과 | Simulation results of the scenario 2.

Download Original Figure

참고문헌 [12]의 기존 RRI 기법을 적용한 그림 11(b)에서는 모노스태틱 대비 다소 향상된 해상도를 보이지만, 여전히 0.16 m 간격의 두 표적을 구분하기에는 해상도가 부족하다. 반면, 제안된 기법을 적용한 그림 11(c)에서는 SAR 영상 상에서 두 표적이 명확히 분리되어 나타나며, HRRP에서도 각각의 표적이 실제 위치에서 뚜렷한 피크로 검출되는 것을 확인할 수 있다.

Ⅴ. 결 론

본 연구에서는 드론 기반 FMCW SAR 시스템에서 발생하는 스펙트럼 공백 문제를 해결하여 거리 해상도를 향상시키기 위한 새로운 RRI 기법을 제안하였다. 제안된 기법은 바이스태틱 SAR 구성에서 수신된 신호 간의 상호 일관성을 기반으로 스펙트럼 공백을 보완하고, 이를 통해 연속된 넓은 대역의 신호를 구성함으로써 해상도를 개선한다. 시뮬레이션 결과, 제안된 방법은 플랫폼 간 간격 증가로 인한 제약 조건 하에서도 효과적인 거리 해상도 향상을 달성하였으며, 드론 기반 SAR 시스템의 실용성과 성능 향상 측면에서 유의미한 가능성을 확인하였다.

Acknowledgements

이 연구는 LIG NEX1 산학협력과제 지원으로 연구되었음.

References

[1].

I. G. Cumming, F. H. Wong, Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation, Boston, MA, Artech House, 2005.

[2].

M. S. Kang, J. M. Baek, “Compressive sensing-based Omega-K algorithm for SAR focusing,” IEEE Geoscience and Remote Sensing Letters, vol. 22, p. 4003405, Jan. 2025.

[3].

M. S. Kang, J. M. Baek, “SAR image reconstruction via incremental imaging with compressive sensing,” IEEE Transactions on Aerospace and Electronic Systems, vol. 59, no. 4, pp. 4450-4463, Aug. 2023.

[4].

M. S. Kang, J. M. Baek, “Efficient SAR imaging integrated with autofocus via compressive sensing,” IEEE Geoscience and Remote Sensing Letters, vol. 19, p. 4514905, Oct. 2022.

[5].

M. S. Kang, K. T. Kim, “Automatic SAR image registration via Tsallis entropy and iterative search process,” IEEE Sensors Journal, vol. 20, no. 14, pp. 7711-7720, Jul. 2020.

[6].

M. S. Kang, K. T. Kim, “Compressive sensing based SAR imaging and autofocus using improved Tikhonov regularization,” IEEE Sensors Journal, vol. 19, no. 14, pp. 5529-5540, July 2019.

[7].

M. S. Kang, Y. J. Won, B. G. Lim, and K. T. Kim, “Efficient synthesis of antenna pattern using improved PSO for spaceborne SAR performance and imaging in presence of element failure,” IEEE Sensors Journal, vol. 18, no. 16, pp. 6576-6587, Aug. 2018.

[8].

A. Meta, P. Hoogeboom, and L. P. Ligthart, “Signal processing for fmcw sar,” IEEE Transactions on Geoscience and Remote Sensing, vol. 45, no. 11, pp. 3519-3532, Nov. 2007.

[9].

A. Bekar, M. Antoniou, and C. J. Baker, “Low-cost, high-resolution, drone-borne sar imaging,” IEEE Transactions on Geoscience and Remote Sensing, vol. 60, p. 5208811, Jun. 2021.

[10].

Y. Liu, Y. K. Deng, R. Wang, and O. Loffeld, “Bistatic FMCW SAR signal model and imaging approach,” IEEE Transactions on Aerospace and Electronic Systems, vol. 49, no. 3, pp. 2017-2028, Jul. 2013.

[11].

S. Neemat, F. Uysal, O. Krasnov, and A. Yarovoy, “Reconfigurable range-Doppler processing and range resolution improvement for FMCW radar,” IEEE Sensors Journal, vol. 19, no. 20, pp. 9294-9303, Oct. 2019.

[12].

K. M. Lee, I. H. Lee, M. G. Cho, and K. T. Kim, “Range resolution improvement using cross-track interferometry for fmcw radar,” IEEE Geoscience and Remote Sensing Letters, vol. 20, p. 3506405, Jul. 2023.

[13].

K. M. Lee, I. H. Lee, M. G. Cho, and K. T. Kim, “Two dimensional resolution improvement for FMCW synthetic aperture radar using multistatic configuration,” in IEEE International Radar Conference, Sydney, Nov. 2023.

[14].

M. S. Kang, S. H. Lee, K. T. Kim, and J. H Bae, “Bistatic ISAR imaging and scaling of highly maneuvering target with complex motion via compressive sensing,” IEEE Transactions on Aerospace and Electronic Systems, vol. 54, no. 6, pp. 2809-2826, Dec. 2018.

[15].

M. S. Kang, B. S. Kang, S. H. Lee, and K. T. Kim, “Bistatic-ISAR distortion correction and range and crossrange scaling,” IEEE Sensors Journal, vol. 17, no. 16, pp. 5068-5078, Aug. 2017.

[16].

M. S. Kang, K. T. Kim, “Ground moving target imaging based on compressive sensing framework with singlechannel SAR,” IEEE Sensors Journal, vol. 20, no. 3, pp. 1238-1250, Feb. 2020.

[17].

B. S. Kang, J. H. Bae, M. S. Kang, E. Yang, and K. T. Kim, “Bistatic-ISAR cross range scaling,” IEEE Transactions on Aerospace and Electronic Systems, vol. 53, no. 4, pp. 1962-1973, Aug. 2017.

[18].

K. M. Cuomo, J. E. Pion, and J. T. Mayhan, “Ultrawide-band coherent processing,” IEEE Transactions on Antennas and Propagation, vol. 47, no. 6, pp. 1094-1107, Jun. 1999.

[19].

M. Wax, I. Ziskind, “Detection of the number of coherent signals by the MDL principle,” IEEE Transactions on Acoustics, Speech, and Signal Processing, vol. 37, no. 8, pp. 1190-1196, Aug. 1989.

[20].

M. Wax, T. Kailath, “Detection of signals by information theoretic criteria,” IEEE Transactions on Acoustics, Speech, and Signal Processing, vol. 33, no. 2, pp. 387-392, Apr. 1985.

[21].

R. Roy, T. Kailath, “Esprit-estimation of signal parameters via rotational invariance techniques,” IEEE Transactions on Acoustics, Speech, and Signal Processing, vol. 37, no. 7, pp. 984-995, Jul. 1989.

[22].

A. Ranganathan, “The levenberg-marquardt algorithm,” Tutoral on LM algorithm, vol. 11, no. 1, pp. 101-110, Jun. 2004.

[23].

S. Y. Kung, K. S. Arun, and D. V. Bhaskar Rao, “State-space and singular-value decomposition-based approximation methods for the Harmonic retrieval problem,” Journal of the Optical Society of America, vol. 73, no. 12, pp. 1799-1811, Dec. 1983.