Ⅰ. 서 론
IR-UWB(impulse radio - ultra wide band) 레이다는 넓은 주파수 대역의 짧은 펄스를 전송하여 물체의 위치, 움직임, 심박 및 호흡과 같은 생체 신호를 정밀하게 측정할 수 있는 기술로 주목받고 있다[1]. IR-UWB 레이다는 높은 공간 및 시간 해상도를 제공하며, 저전력 소비 및 비접촉 센싱이 가능하다는 점에서 다양한 응용 분야에서 활용되고 있다. 특히, IR-UWB 레이다는 높은 투과력을 갖추고 있어, 기존 레이다 기술과 달리 짧은 펄스를 활용하여 벽이나 장애물을 투과할 수 있다. 또한, 비접촉 방식의 센싱이 가능하므로 보안 감시, 생체 신호 측정 및 실내 위치 추정 등의 분야에서 폭넓게 활용되고 있다[2]~[5].
최근 IR-UWB 레이다와 머신러닝 및 딥러닝 기술을 융합한 연구가 활발히 진행되고 있다. 머신러닝 및 딥러닝 모델을 활용하면 IR-UWB 레이다에서 수집된 신호를 더욱 정밀하게 분석할 수 있으며, 이를 통해 보다 향상된 신호처리 및 패턴 인식이 가능하다. 예를 들어, 딥러닝 기반 신호 분석을 활용한 인원 수 추정[6], 모션 인식[7] 및 자세 분석[8]과 같은 응용 분야에서 높은 성능을 보이는 연구 결과가 수행되고 있다. 하지만, 머신러닝과 딥러닝 모델을 학습하기 위해서는 대규모 측정 데이터를 직접 수집해야 하는데, 이 과정에서 데이터 확보가 쉽지 않다는 문제점이 있다. 머신러닝 및 딥러닝 알고리즘에서는 충분한 양과 높은 품질의 데이터 확보가 필수적이지만, 인원 수 추정, 모션 인식 및 자세 분석과 같은 분야에 필요한 측정 데이터를 수집하려면 막대한 시간과 노력이 요구된다.
이에 따라, 측정 데이터를 효과적으로 확보하기 위한 방안으로 생성적 적대 신경망(GAN, generative adversarial network)을 활용한 데이터 증강 기법이 주목받고 있으며 연구되고 있다[9], [10]. GAN은 소량의 측정 데이터를 기반으로 새로운 데이터를 생성하여 데이터의 양을 확장하는 데 활용될 수 있으며, 이미지 데이터, 비디오 데이터, 자연어 처리 데이터, 음성 데이터, 그리고 시계열 데이터와 같은 다양한 형태의 데이터를 증강하는 기법으로 사용되고 있다. 이러한 방법을 IR-UWB 레이다 수신 데이터에도 적용하면, 적은 양의 측정 데이터를 기반으로 신뢰성 높은 학습 데이터를 생성할 수 있으며, 이를 통해 보다 정확한 신호 분석 및 패턴 인식이 가능하다. 하지만, GAN을 학습시키기 위해서도 최소한의 데이터가 확보되어야 한다. 부족한 데이터로 GAN이 학습된다면, 특정 패턴의 데이터만 생성하고 다양성을 잃는 모드 붕괴(mode collapse) 현상과, 데이터의 분포를 일반화하지 못하고 주어진 샘플과 거의 동일한 데이터를 생성하는 과적합(overfitting) 현상, 및 훈련 불안정성과 같은 문제가 발생한다. 이러한 문제를 해결하기 위한 방안으로, WGAN-GP(Wasserstein GAN with gradient penalty) 모델이 널리 활용되고 있다[11], [12]. WGAN-GP는 Wasserstein distance(지구 거리)를 이용하여 학습 안정성을 향상시키고, gradient penalty 기법을 적용하여 훈련이 불안정해지는 문제를 완화한다. 이를 통해 모드 붕괴를 방지하고, 데이터의 다양성을 증가시키며, 과적합을 완화하여 보다 일반화된 데이터 생성을 가능하게 한다.
따라서, 본 논문에서는 소량의 측정 데이터로도 높은 머신러닝 분류 정확도를 확보하기 위해 WGAN-GP 딥러닝 모델을 적용한 데이터 증강 방법을 제안한다. 레이다 수신 데이터에서 PCA(principal component analysis) 기법[13]을 통해 추출한 특징들을 WGAN-GP로 학습하여 실제 측정 데이터와 유사한 특징 데이터를 생성한다. 이후, 데이터 증강 전후의 머신러닝 분류 성능을 비교 분석하여 제안한 데이터 증강 방법의 타당성을 검증한다.
Ⅱ. 데이터 측정 및 수집
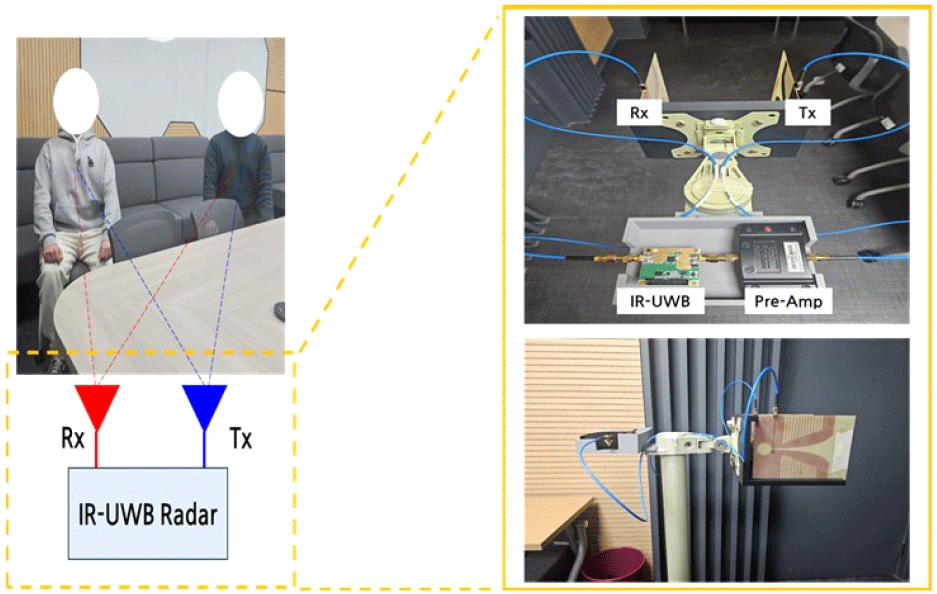
데이터를 측정하기 위해 사용되는 IR-UWB 레이다 칩NVA6100(Novelda 社)은 1~9 GHz의 1차 가우시안 미분 형태의 광대역 임펄스 신호를 사용하며, 순시 출력 진폭은 450 mV/s을 갖는다. 임펄스 신호를 주고 받는 송, 수신 안테나로는 1~9 GHz의 대역폭을 갖는 광대역 비발디 안테나(자체 제작)를 사용하였고[14], 송신 단에는 1~9 GHz 대역에서 25~35 dB 이득을 갖는 UBBV2 (AARONIA 社) Pre-Amplifier를 사용하였다. 그림 1은 측정 환경을 단순하게 나타낸 모식도이다. 실제 IR-UWB 레이다 운용 환경을 고려하여 책상과 의자와 같은 정적 클러터가 존재하는 방 안을 측정 장소로 선정했으며, 측정 인원 수는 0~3명으로 설정하였다. IR-UWB 레이다의 수신 데이터는 인체 신호, 클러터, 잡음이 포함된 행렬 형태로 구성되며, 측정 환경에 따라 1,000×512(0명, 1명 측정한 경우) 또는 1,000×1,024(2명, 3명 측정한 경우) 크기의 데이터 행렬이 생성된다. 이러한 데이터는 고해상도의 2D 이미지로 해석될 수 있으며, 그대로 학습 데이터로 사용할 경우 높은 계산 복잡도를 초래할 수 있다. 따라서, 본 논문에서는 수집된 데이터에서 특정 패턴을 추출하여 학습하는 방식을 적용하고자 한다.
Ⅲ. 주성분 분석을 활용한 특징 추
클러터와 잡음을 제거하고 인체 신호만의 특징을 추출하기 위해서 주성분 분석(PCA) 기법을 레이다 수신 데이터에 적용한다. PCA는 데이터의 공분산 행렬의 고유값 분해로, 고차원 데이터의 차원을 축소하면서 주요 정보를 유지하는 대표적인 기법이다. PCA는 분산(variance)를 최대화하는 방향으로 새로운 직교 좌표계를 구성하여, 데이터의 가장 중요한 특징을 보존하면서 불필요한 차원을 제거한다. 이를 통해 데이터의 노이즈를 줄이고, 계산 효율성을 높일 수 있다[13]. 측정된 레이다 수신 데이터에 PCA를 적용하여 얻어낸 주성분들이 레이다 수신 데이터에서 어떤 물리적 의미를 갖는지 분석하였다. 각 주성들분이 레이다 수신 데이터에서 어떤 물리적 의미를 갖는지를 수식적으로 명확히 해석하는 데에는 한계가 있다. 이에 본 논문에서는 주성분을 하나씩 제거하는 방법을 통해, 각 주성분이 레이다 수신 데이터에서 어떤 의미를 갖는지를 실험적으로 분석하였다. 그림 2는 첫 번째 주성분의 의미를 확인하기 위해, 가장 큰 고유값을 의미하는 첫 번째 주성분을 제거하기 전후의 range Doppler map의 예시이다. 그림 2(a)는 첫 번째 주성분을 제거하기 전의 range Doppler map으로 넓은 대역에 노이즈가 존재하고, zero Doppler 영역에서는 세기가 5×104 이상의 성분을 갖는다. zero Doppler 성분은 측정 환경에서의 책상, 의자, 벽 등과 같은 정적 클러터를 의미한다. 그림 2(b)는 첫 번째 주성분을 제거한 후의 range Doppler map으로, 넓은 대역이 존재하는 노이즈가 대부분 제거되었고, zero Doppler 영역에서는 세기가 0에 가까운 성분을 갖는다. 따라서, 첫 번째 주성분은 레이다 수신 데이터에서 정적 클러터와 노이즈를 의미한다는 것을 알 수 있다. 그림 3은 인체 신호를 의미하는 주성분들을 찾아내기 위해, 정적 클러터와 노이즈를 의미하는 첫 번째 주성분을 제외한 가장 큰 상위 20개(2~21번째)의 고유값을 의미하는 주성분을 제거하기 전후의 range Doppler map의 예시이다. 그림 3(a)는 상위 20개의 주성분을 제거하기 전의 range Doppler map으로 명확하게 측정된 인체 신호가 나타난다. 그림 3(b)는 상위 20개의 주성분을 제거한 후의 range Doppler map으로 인체 신호가 사라진 모습이다. 따라서, 상위 20개의 주성분은 레이다 수신 데이터에서 인체 신호의 세기를 의미한다는 것을 알 수 있다. 따라서, PCA 기법을 통해 얻어낸 주성분들 중 인체 신호를 찾아내는 과정을 거치면, 1,000×512 또는 1,000×1,024 크기의 레이다 수신 데이터 행렬을 상위 20개의 고유값을 나열한 하나의 행 또는 열 형태의 벡터로 나타낼 수 있다.
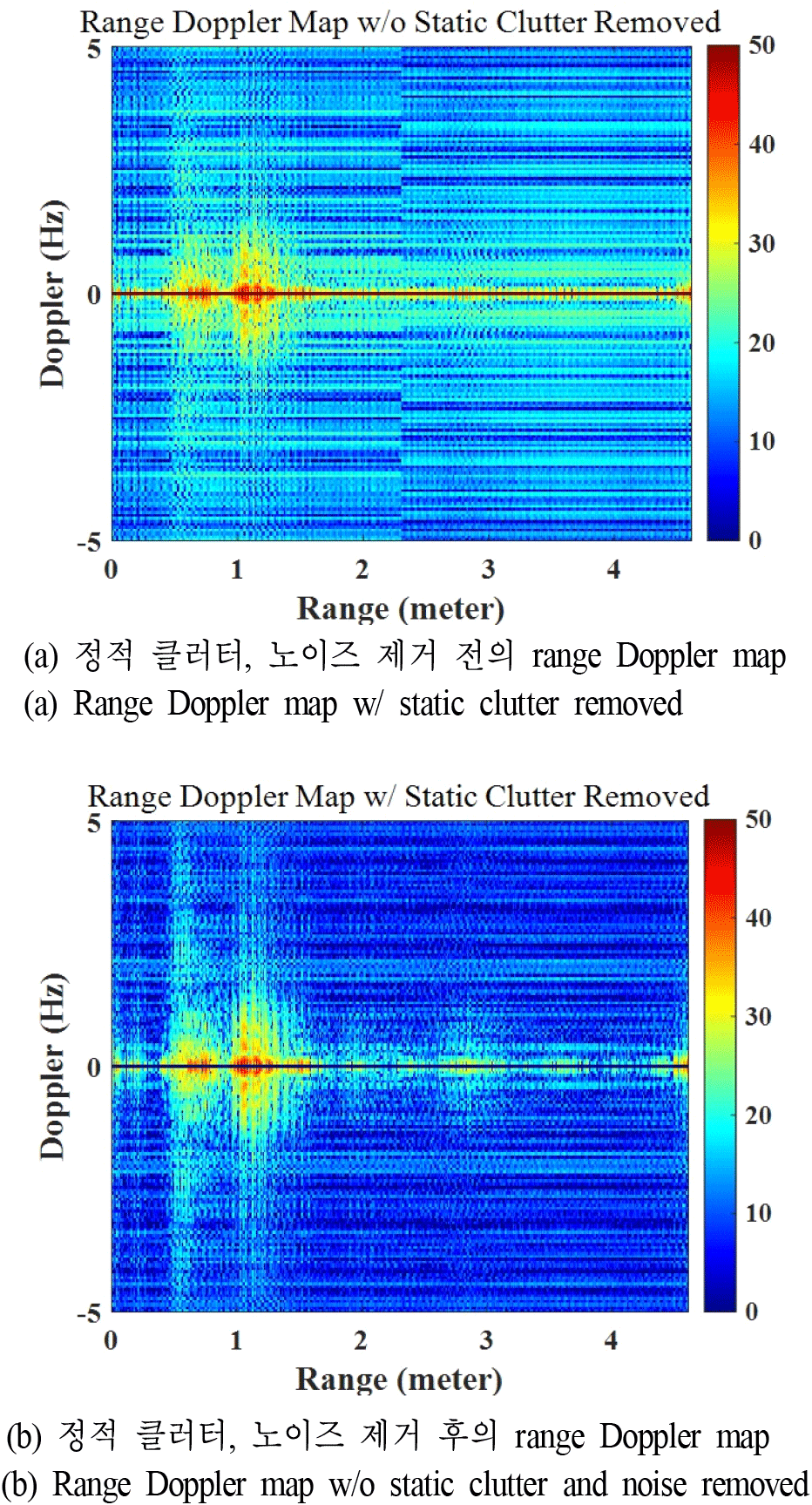
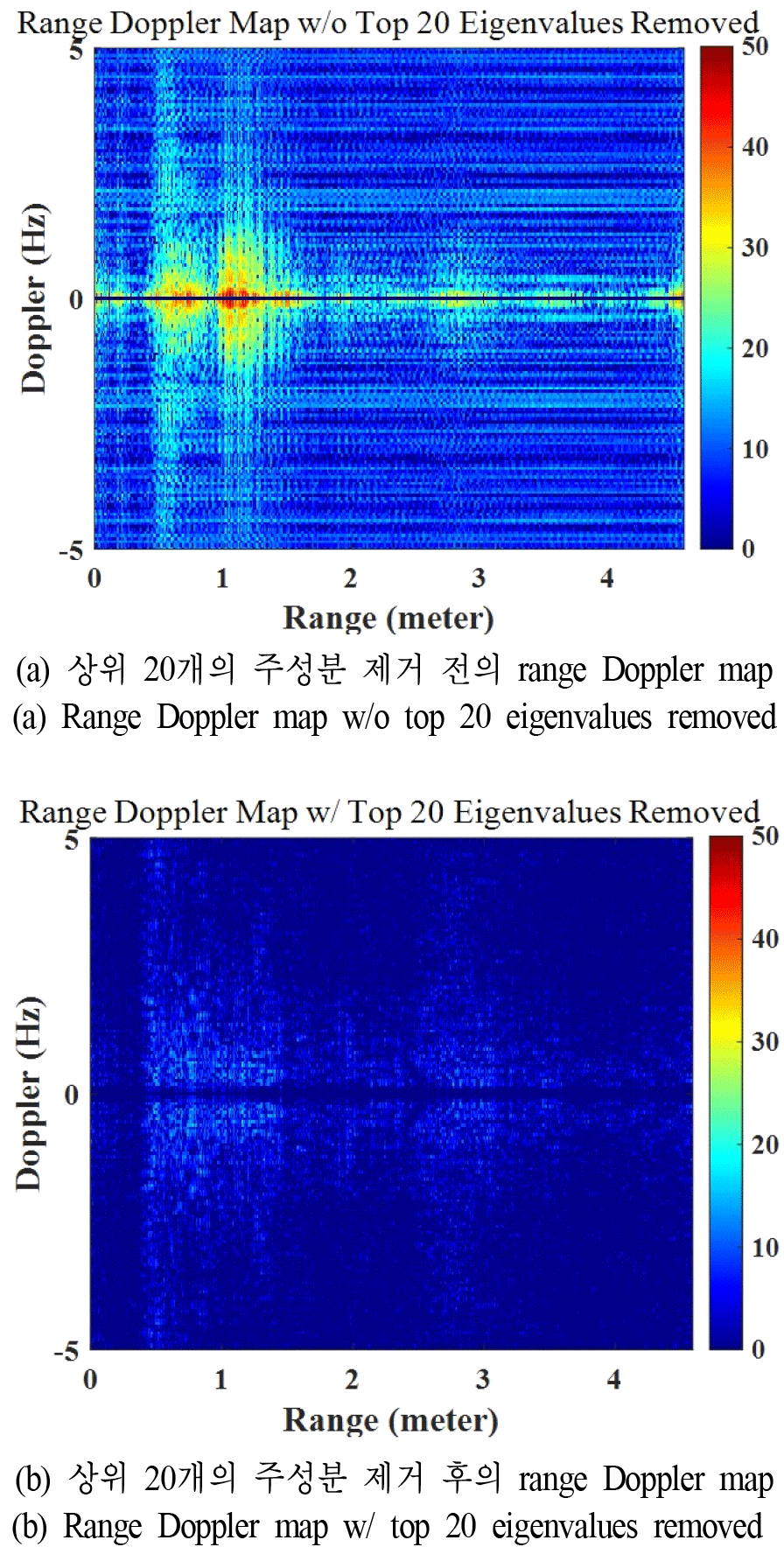
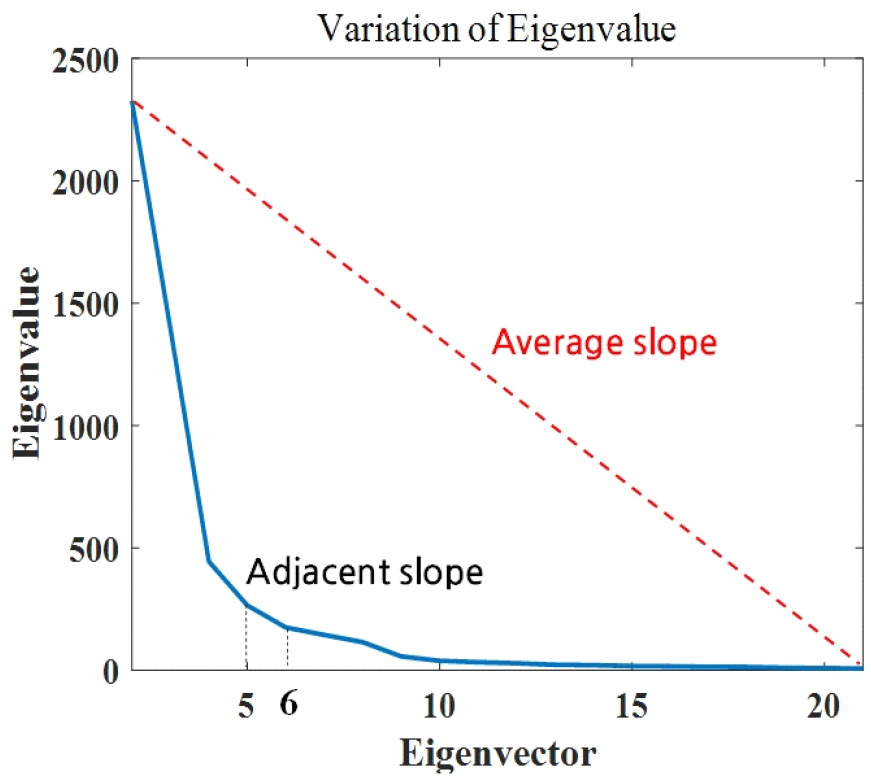
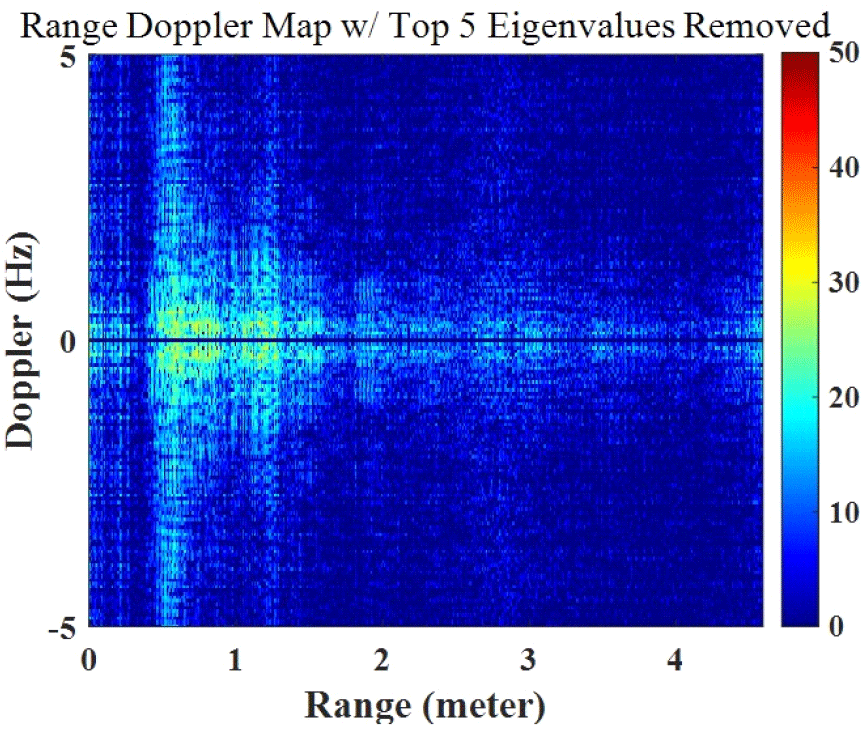
그림 4는 상위 20개의 고유값들을 시각화한 그래프이다. 상위 20개의 고유값들 중 인체 신호를 나타내는 데에 주요한 역할을 하는 고유값들만을 선별하여 사용할 수 있다면, 계산 효율성을 더욱 증대할 수 있다. 본 논문에서는 고유값들간의 기울기 차이를 기반으로 주요한 신호 성분의 수를 추정하는 EGM(eigenvalue gradient method)을 적용하였다[15]. EGM은 고유값들의 인접 기울기를 계산하고 전체 고유값들의 평균 기울기와 비교하여 신호 성분과 잡음 성분을 구분한다. 전체 고유값들의 평균 기울기보다 작은 기울기를 갖는 구간을 찾아, 해당 구간의 시작 인덱스를 기준으로 주요한 신호 성분의 수를 추정한다. 이를 통해, 데이터 내에 존재하는 의미 있는 인체 신호의 수를 정량적으로 분석할 수 있다. 상위 20개의 고유값들에 대한 평균 기울기와 각각의 인접 기울기를 비교한 후, 인접 기울기가 평균 기울기보다 작아지는 상위 5개의 고유값을 학습시킬 최종 데이터로 선정하였다. 따라서, 학습시킬 최종 데이터는 상위 5개의 고유값을 성분으로 갖는 벡터 형태로 구성된다. 그림 5는 상위 5개(2~6번째)의 고유값을 의미하는 주성분만을 남기고 나머지를 제거한 후의 range Doppler map의 예시이다. 원래의 range Doppler map인 그림 2(a)와 비교하면 1 Hz 미만의 저주파 신호들이 사라진 모습을 확인할 수 있다. 이는 인체의 호흡 및 심박 주파수가 일반적으로 약 1 Hz 내외인 점을 고려할 때, 상위 5개의 고유값을 의미하는 주성분은 인체 신호 중 호흡 및 심박 신호의 세기라는 것을 알 수 있다. 측정 환경(0명, 1명 측정한 경우와 2명, 3명 측정한 경우)에 따라 데이터 행렬의 크기는 달라졌지만, 최종적으로는 데이터 행렬에서 호흡 및 심박 신호의 세기만 추출하여 사용하였기 때문에, 원본 데이터의 크기 차이는 학습 및 인원 수 추정 과정에 직접적인 영향을 미치지 않는다.
Ⅳ. WGAN-GP 기반 데이터 증강
본 논문에서는 WGAN-GP(Wasserstein GAN with gradient penalty)를 학습 모델로 사용한다. WGAN-GP는 Wasserstein distance 기반의 GAN에 gradient penalty 기법을 적용하여 기존 GAN의 불안정성과 모드 붕괴 문제를 해결한 모델이다[11]. 기존 GAN은 JSD(Jensen-Shannon Divergence)를 사용하여 두 분포를 비교하는 방식을 채택하지만, 이는 학습이 불안정해지는 원인이 될 수 있다. 반면, WGAN은 Wasserstein distance를 활용하여 두 분포 간 차이를 보다 부드럽게 측정함으로써 학습 안정성을 향상시킨다. 또한, WGAN-GP에서 gradient penalty는 Lipschitz 조건(함수의 기울기가 일정 범위를 넘지 않도록 제한하는 조건)을 만족시키기 위한 규제 항(regularization term)으로 추가된다. 이는 일반적인 WGAN에서 사용되는 weight clipping 기법을 대체하며, critic의 그래디언트 크기를 1에 가깝게 유지하도록 유도하여 모델의 학습 안정성을 더욱 향상시킨다. 따라서, 데이터가 부족한 상황에서도 안정적인 학습이 가능하여 본 연구의 목적에 가장 적합한 모델로 선정되었다. 그림 6은 WGAN-GP의 학습 구조를 나타낸다. WGAN-GP의 학습 과정에서 생성자(generator)는 랜덤 노이즈를 입력으로 받아 가짜 데이터를 생성하고, 비판자(critic)는 진짜 데이터와 가짜 데이터의 분포 차이를 기반으로 학습한다. 비판자의 출력을 활용하여 생성자를 업데이트함으로써 점점 더 현실적인 데이터를 생성하도록 유도한다. 기존 GAN과 달리 WGAN-GP는 판별자(discriminator) 대신 비판자(critic)를 사용하며, Wasserstein distance(지구 거리)를 활용하여 진짜 데이터와 생성된 데이터 간의 차이를 평가한다. 또한, 비판자의 학습 과정에서 gradient penalty를 적용하여 Lipschitz 조건을 유지하고 학습의 안정성을 보장한다. 이를 통해 WGAN-GP는 기존 GAN보다 안정적이며, 더욱 실제와 유사한 데이터를 생성할 수 있다.
생성자는 20 차원의 랜덤 노이즈를 입력으로 받아, 64개의 채널을 갖는 은닉층 1(hidden layer 1)과 128개의 채널을 갖는 은닉층 2(hidden layer 2)를 거쳐 학습된다. 최종적으로 출력층(output layer)에서 실제 학습 데이터와 유사한 5개의 성분을 갖는 벡터를 생성한다. 생성자의 은닉층은 점진적으로 차원을 확장하며 복잡한 패턴을 학습하도록 설계되었다. 은닉층의 수가 증가함에 따라 출력 차원이 단계적으로 확장되는 구조는 고해상도의 복잡한 데이터를 생성하는 데 적합한 특징을 가지며, 생성자가 보다 정교한 패턴을 학습할 수 있도록 돕는다. 일반적으로 GAN 계열 모델에서 2~4단의 은닉층 구조는 간단한 데이터 생성 작업에서 널리 사용되는 기본 구성 중 하나이다. 본 논문에서 생성 대상이 되는 데이터는 5차원 고유값 벡터로 비교적 저차원 특성을 갖기 때문에, 복잡한 네트워크 구조를 사용할 필요 없이 2단 은닉층만으로도 충분한 학습 성능을 확보할 수 있다.
비판자는 실제 데이터 또는 생성자가 생성한 데이터를 입력으로 받아 128개의 채널을 갖는 은닉층 1(hidden layer 1)과 64개의 채널을 갖는 은닉층 2(hidden layer 2)를 거쳐 학습된다. 최종적으로 출력층(output layer)에서 입력된 데이터에 비판자가 부여한 점수를 출력한다. 비판자의 은닉층은 점진적으로 차원을 축소하며 데이터를 특징 공간에서 압축하여 진짜 데이터인지 가짜 데이터인지 판별하도록 설계되었다. 비판자의 출력은 생성된 데이터에 부여된 점수를 기반으로 계산되는 생성자 손실(generator loss)과 실제 데이터와 생성된 데이터 간의 점수 차이를 기반으로 결정되는 비판자 손실(critic loss)의 계산에 활용된다. 각각의 손실 함수는 다음 식 (1) 및 식 (2)와 같이 정의된다.
x는 실제 데이터, 는 생성된 데이터, f(x)는 비판자가 입력 x에 대해 산출하는 점수 값, 는 비판자가 입력 에 대해 산출하는 점수 값, Pr는 실제 데이터 분포, Pg는 생성된 데이터 분포, λ는 gradient penalty의 중요도를 조절하는 하이퍼파라미터, GP는 gradient penalty 항이다. 식 (1)에서 생성자는 비판자가 생성 데이터 에 대해 높은 점수를 주도록 학습된다. 이는 비판자가 실제 데이터와 생성 데이터를 구분하지 못하게 만들기 위함으로, 생성자는 비판자를 속이는 방향으로 점점 더 실제와 유사한 데이터를 생성하도록 유도된다. 식 (2)에서 비판자는 실제 데이터 x에는 높은 점수를, 생성된 데이터 에는 낮은 점수를 부여하도록 학습된다. 이를 통해 두 데이터 분포 간의 Wasserstein distance를 최대화하게 되며, 이는 WGAN에서 실제와 생성 데이터 분포 간 차이를 측정하는 핵심 지표로 작용한다. 학습이 원활하게 진행된다면, 생성자는 비판자를 효과적으로 속이며 실제와 유사한 데이터를 생성하게 되고, 비판자는 진짜 데이터와 생성된 데이터에 유사한 점수를 부여하게 된다. 이로 인해, generator loss는 적절한 음수 값에 수렴하며, critic loss는 0에 수렴하게 된다. 또한, gradient penalty와 관련된 항들은 상대적으로 작은 값이므로 critic loss 값에 미치는 영향은 제한적이다.
WGAN-GP을 안정적으로 학습시키기 위해서는 최소한의 데이터 양이 확보되어야 한다. 인체가 0명 또는 1명인 경우에는 데이터 측정 및 수집이 비교적 용이했지만, 2명과 3명인 경우에는 데이터 확보에 큰 어려움이 있었다. 이를 그대로 WGAN-GP 학습 데이터로 사용한다면, 모드 붕괴, 과적합, 학습 불안정성 문제가 발생할 수 있다. 이에 따라, 2명과 3명의 경우에는 레이다 수신 데이터를 크게 왜곡하지 않도록, 데이터의 표준 편차의 10 %에 해당하는 가우시안 랜덤 노이즈를 추가하여 원본 데이터의 2배인 64개씩 생성하여 데이터 증강을 수행하였다. 표 1은 1차 데이터 증강을 하기 전후의 데이터 양을 나타낸다. 인체가 2명과 3명인 경우에는 32개에서 96개로, 1차 데이터 증강이 이루어졌음을 확인할 수 있다. 1차 증강된 데이터를 최종 WGAN-GP 학습 데이터로 선정하여 학습을 진행하였다. 학습에 사용되는 하드웨어의 리소스를 고려하여 배치 사이즈는 16, 에포크는 1,000으로 설정하였다.일반적으로 WGAN-GP의 비판자의 개수는 5개, Gradient Penalty의 가중치 λ를 10으로 설정한다[11], [12]. 학습 과정에서 생성자 손실과 비판자 손실을 지속적으로 모니터링한 결과, gradient penalty의 가중치를 유지한 상태에서 비판자 개수를 20으로 늘렸을 때 가장 안정적인 학습 성능을 보였다. 생성자와 비판자의 학습률은 0.00003~0.00005 범위 내에서 조정되었으며, 이 설정이 손실 수렴과 생성 데이터 품질의 균형 측면에서 가장 효과적이었다. 인체가 0~3명인 4가지 경우 모두에서 비판자 손실이 0에 잘 수렴하였으며, 생성자 손실이 적절한 음수 값을 갖거나 수렴하였다. 이에 따라, 4가지 경우 모두에서 적절하게 학습이 진행되었다고 판단하였으며, 각각 200개의 데이터를 추가적으로 생성하였다. 표 2는 WGAN-GP을 통해 2차 데이터 증강을 하기 전후의 데이터 양을 나타낸다. 인체가 0명인 경우에는 360개, 인체가 1명인 경우에는 311개, 인체가 2명인 경우에는 296개, 인체가 3명인 경우에는 296개로, 2차 데이터 증강이 이루어졌음을 확인할 수 있다.
| Case | Number of data | |
|---|---|---|
| Before | After | |
| 0 Humans | 160 | 160 |
| 1 Humans | 111 | 111 |
| 2 Humans | 32 | 96 |
| 3 Humans | 32 | 96 |
| Case | Number of data | |
|---|---|---|
| Before | After | |
| 0 Humans | 160 | 360 |
| 1 Human | 111 | 311 |
| 2 Humans | 96 | 296 |
| 3 Humans | 96 | 296 |
Ⅴ. 머신러닝을 활용한 분류 및 성능 평가
데이터 증강의 효과를 확인하기 위해서 고전적인 머신러닝 분류 모델들을 이용하여 데이터 증강 전과 데이터 증강 후의 분류 결과를 비교하였다. 증강된 데이터(인체가 0명인 경우에는 360개, 인체가 1명인 경우에는 311개, 인체가 2명인 경우에는 296개, 인체가 3명인 경우에는 296개)를 학습 데이터로 사용하였고, 새로 측정된 데이터(인체가 0명인경우에는 15개, 인체가 1명인 경우에는 15개, 인체가 2명인 경우에는 15개, 인체가 3명인 경우에는 15개)를 검증 데이터로 사용하였다. 일반적으로 머신러닝 분류에서는 학습 데이터의 일부를 검증 데이터로 활용하여 모델의 정확도를 평가한다. 그러나 본 논문에서는 학습 데이터의 대부분을 딥러닝을 통해 생성한 데이터로 구성하였기 때문에, 기존 방식과 달리 학습 데이터의 일부를 검증 데이터로 사용하지 않고, 대신 새롭게 측정된 실제 데이터를 검증 데이터로 활용하여 제안된 방법의 타당성을 검증하였다. 이때, 로지스틱 회귀(logistic regression), 서포트 벡터 머신(SVM, suppor vector machine), K-최근접 이웃(KNN, K-Nearest neighbors), 랜덤 포레스트(random forest), XG부스트(XGBoost, eXtreme gradient boost) 모델을 사용하여 성능을 평가하였다.
그림 7은 데이터 증강 전의 머신러닝 분류 정확도를 나타낸 막대 그래프이다. 정확도는 다음 식 (3)과 같이 정의된다.
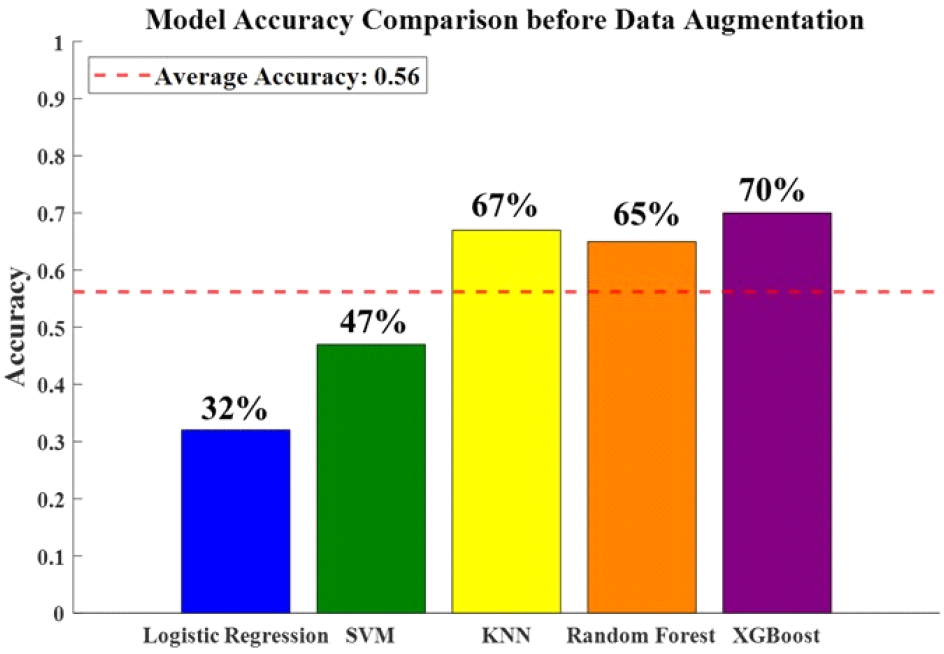
5가지 모델의 평균 정확도는 56 %이며, 가장 높은 정확도를 기록한 모델은 XGBoost로 70 %의 정확도를 보인다. 그림 8은 가장 높은 정확도를 나타내는 모델인 XGBoost의 데이터 증강 전 분류 결과를 나타낸 혼동 행렬(confusion matrix)이다. 혼동 행렬은 가로 축은 모델이 예측한 라벨을 의미하며, 세로 축은 실제 라벨을 의미한다. 대각 성분에 해당하는 값이 높을수록 모델이 정확하게 분류한 샘플이 많다는 것을 의미하며, 대각 성분이 아닌 값들은 분류 오류를 나타낸다. 인체가 1명인 경우와 2명인 경우를 제대로 분류하지 못한다는 사실을 확인할 수 있다. 그림 9는 데이터 증강 후의 머신러닝 분류 정확도를 나타낸 막대 그래프이다. 5가지 모델의 평균 정확도는 70 %로 데이터 증강 전에 비해 14 % 향상되었다. 가장 높은 정확도를 기록 한 모델은 XGBoost로 85 %의 정확도를 보이며, 데이터 증강 전에 비해 15 % 향상되었다. 그림 10은 가장 높은 정확도를 나타내는 모델인 XGBoost의 데이터 증강 후 분류 결과를 나타낸 혼동 행렬이다. 혼동 행렬의 대각 성분 값이 데이터 증강 전과 비교하여 증가한 것을 확인할 수 있으며, 이는 모델의 분류 성능이 향상되었음을 의미한다.
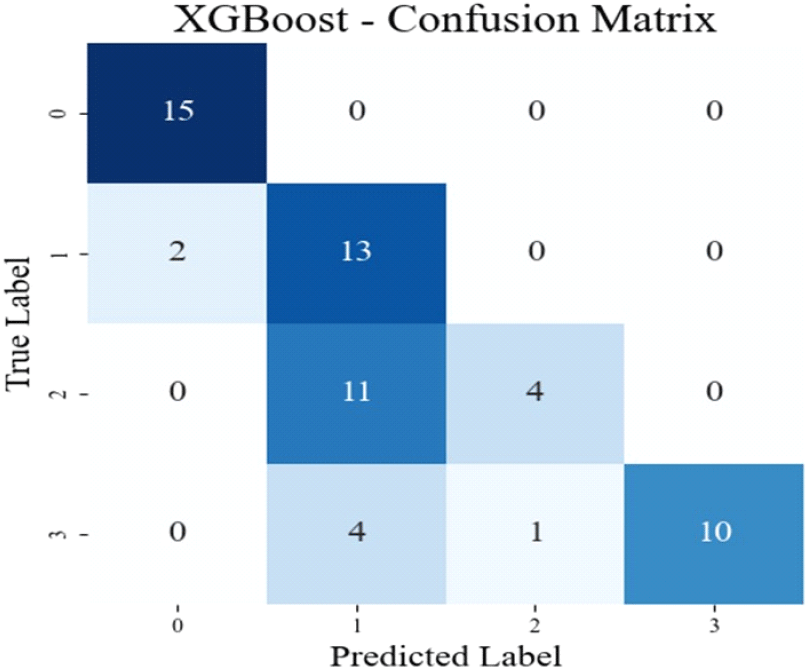
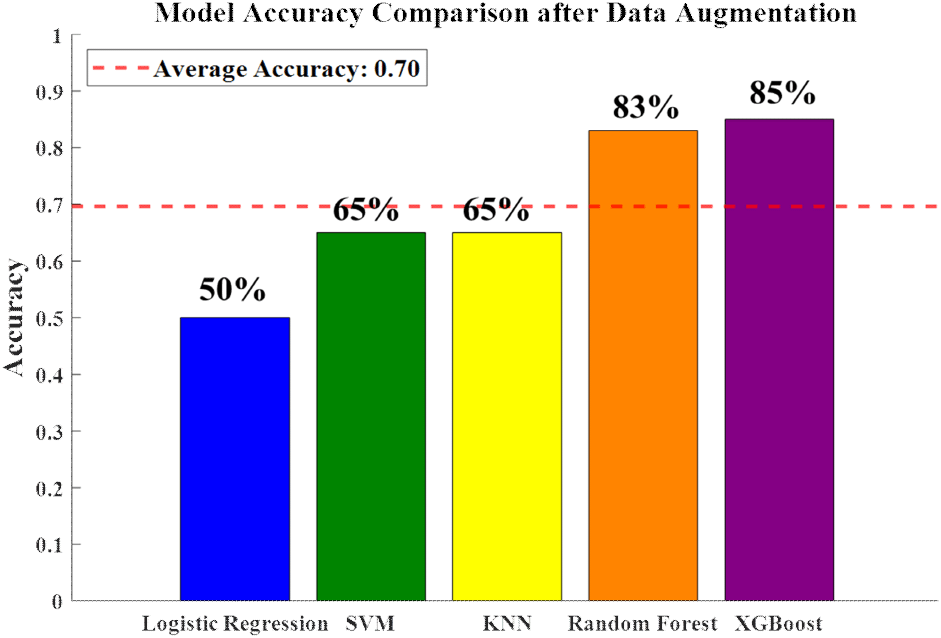
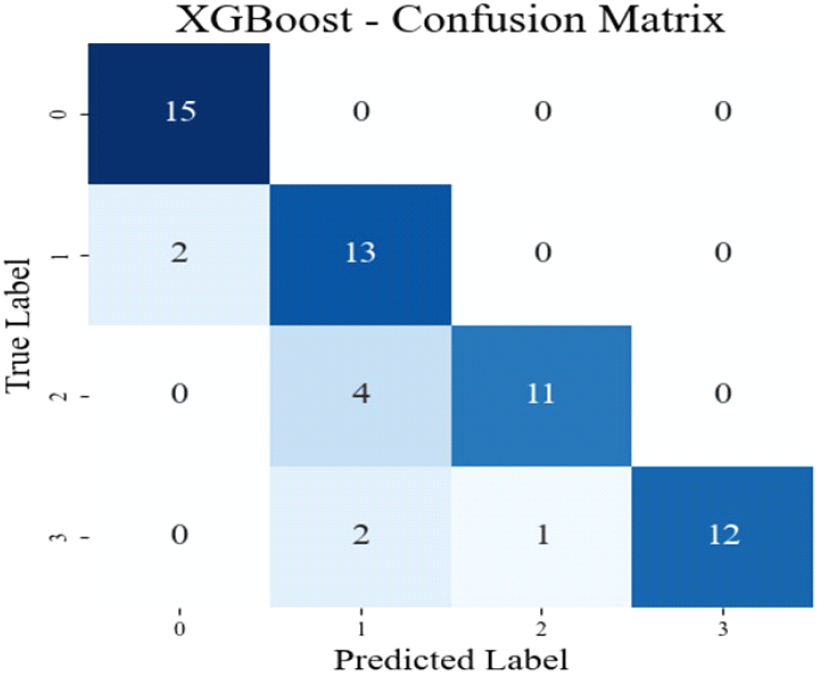
표 3은 사용한 모든 모델에 대해서 증강 전과 증강 후의 정확도(Acc.)를 비교한 결과를 나타낸다. KNN을 제외한 모든 모델들의 분류 정확도가 크게 향상되었다. 특히, SVM과 random forest의 분류 정확도가 18 %로 가장 크게 향상되었다. 이는 본 논문에서 제안하는 데이터 증강 방법이 모델의 분류 성능을 높이는데 중요한 역할을 한다는 점을 보여준다. 반면, KNN은 데이터들 간의 거리 기반 분류 방식이므로, 생성된 데이터가 기존 데이터 분포를 유지하는 특성 때문이라고 해석할 수 있다.
| Model | LogR | SVM | KNN | RF | XGB | |
|---|---|---|---|---|---|---|
| Before | Acc. | 32 | 47 | 67 | 65 | 70 |
| After | Acc. | 50 | 65 | 65 | 83 | 85 |
Ⅵ. 결 론
본 논문에서는 IR-UWB 레이다를 활용한 인원 수 추정 정확도를 향상시키기 위해 WGAN-GP 기반 데이터 증강 방법을 제안하였다. 제안된 기법을 통해 소량의 측정 데이터에서 추가적인 학습 데이터를 생성하고, 생성된 데이터가 기존 데이터의 특징을 유지하면서도 모델 학습에 효과적으로 기여하는지 검증하였다. 데이터 증강의 효과를 평가하기 위해 다양한 머신러닝 모델을 활용하여 데이터 증강 전후의 분류 성능을 비교 분석하였으며, 그 결과 데이터 증강을 적용한 경우 머신러닝 모델들의 평균 정확도가 약 14 % 향상되었고, XGBoost의 경우 15 %의 성능 향상이 이루어졌다. 본 연구에서 제안한 데이터 증강 방법은 데이터가 부족한 환경에서도 효과적으로 분류 성능을 개선할 수 있으며, 적절한 머신러닝 모델을 함께 활용할 경우 더욱 높은 정확도를 달성할 수 있음을 확인하였다. 따라서, 제안된 방법은 IR-UWB 레이다 기반의 인원 수 추정뿐만 아니라, 다양한 데이터 부족 문제를 해결하는 데 적용 가능성이 높다. 이를 통해, 향후 보안 및 감시 시스템, 재난 구조 활동 지원 등의 다양한 분야에 적용될 수 있을 것으로 기대된다.