Ⅰ. 서 론
레이다 단면적(RCS, radar cross section) 측정은 스텔스 플랫폼의 설계 및 대책 수립과 같은 군사 분야뿐 아니라, 무선 주파수 식별(RFID, radio frequency identification) 및 자율 주행 성능 평가와 같은 다양한 민간 분야에서도 필수적으로 활용되고 있다[1]~[4]. RCS 측정 시에는 평면파의 입사 및 반사를 전제로 하는 원전계 조건을 만족해야 하며, 이를 위해서는 전용 평가 시설의 구축이 요구된다. 그러나 이러한 시설은 흡수체, 정밀한 안테나 배치, 충분한 거리 확보 등으로 인해 막대한 경제적, 공간적 비용이 수반된다.
이에 따라 실내에서 흡수체를 활용한 무반향 챔버 기반의 RCS 측정 방식이 널리 연구되고 있으나, 챔버 구축 자체에 필요한 자원 역시 적지 않다[5]. 특히 빠른 설계 피드백이 요구되는 초기 개발 단계에서는 이러한 점이 병목 요소로 작용할 수 있다. 이를 해결하기 위한 대안으로, 흡수체를 제한적으로 사용하거나 흡수체 없이 일반 실내 환경에서 측정한 후, 신호 대 잡음비(SNR, signal-to-noise ratio)를 향상시키고 클러터를 저감하기 위한 후처리 기법을 적용하는 방식이 활발히 연구되고 있다[6]~[8].
일반적으로 이러한 후처리에는 세 가지 기법이 순차적으로 활용된다. 첫째, 랜덤 잡음을 줄이기 위한 코히어런트 적분(CI, coherent integration), 둘째, 시험 대상체(TUT, target under test)를 제외한 환경 산란을 제거하는 배경 차감(BS, background subtraction), 셋째, TUT로부터의 반사 신호 외의 잔류 신호를 제거하기 위한 시간 영역 게이팅(TG, time-domain gating)이다.
최근에는 이러한 방식으로 얻어진 비 무반향 챔버 환경의 RCS 측정 데이터를 실제 분석에 활용하는 사례가 증가하고 있으며, 원전계 조건 만족 여부에 따른 TUT의 RCS 비교 연구도 진행된 바 있다[9]. 그러나 참고문헌 [9]에서 제시된 잡음 등가 RCS(NERCS, noise equivalent RCS) 평가만으로 RCS 측정 시스템의 정확도를 평가하는 것은 평가 지표가 부족할 수 있으며, 특히 RCS 측정 재현성에 대한 체계적인 검토는 아직 부족하다. 따라서 본 논문에서는 비 무반향 챔버 환경에서의 RCS 측정 정확도를 두 가지의 오차 지표를 활용하여 심층적으로 분석하고, 반복 측정을 통한 재현성 역시 분석한다. 더불어 증폭기 사용 여부에 따른 측정 정확도의 변화를 비교 및 평가한다.
Ⅱ. RCS 측정 방법 및 시나리오
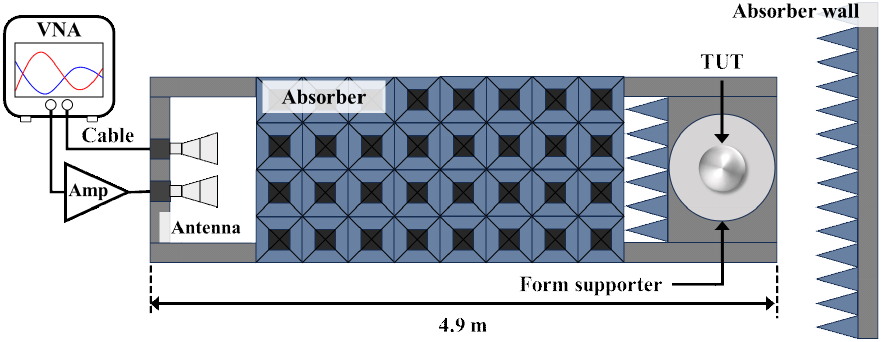
그림 1은 본 연구에서 활용된 비 무반향 챔버 환경을 나타낸다. 측정은 준-모노스태틱 방식으로 수행되었으며, 2개의 DRH-002G-018G 안테나와 Anritsu의 MS46122B 벡터 네트워크 분석기(VNA, vector network analyzer)가 활용되었다. 모든 측정은 2~18 GHz 대역에서 수행되었으며 CI 적용을 위해 2회 반복 측정되었다. 또한, VNA의 중간 주파수 대역폭(IFBW, intermediate frequency bandwidth)는 200 Hz로 설정되었다. 안테나와 TUT 사이 거리는 약 4.3 m이다. TUT 서포터는 유전율이 공기와 유사한(ϵr≈1.03) 스티로폼으로 제작되었다.

해당 환경에서 후처리 과정을 포함한 RCS 측정은 다음과 같다[9].
-
벡터 네트워크 분석기(VNA, vector network analyzer)의 케이블 보정을 수행한다.
-
TUT 및 배경의 S-파라미터 측정을 수행한다.
-
보정 대상 및 배경의 S-파라미터 측정을 수행한다.
-
단계 2)와 3)에서 모두 CI 적용을 위한 반복 측정을 수행한다. CI는 측정시 필연적으로 발생하는 열잡음을 포함한 랜덤잡음을 효과적으로 줄일 수 있는 방법으로 식 (1)과 같이 수행된다.
여기서 M은 총 반복 측정 회수이며, Re{·}|m과 Im{·}|m은 각각 m-th 측정값의 실수부와 허수부를 의미한다.
-
TUT 및 보정 대상 측정값과 각각의 배경 측정값을 이용한 BS를 수행한다. BS는 식 (2)과 같이 수행된다.
-
TUT 및 보정 대상에 역 퓨리에 변환(IFT, inverse Fourier transform) 혹은 역 Chirp-Z변환(ICZT, inverse Chirp-Z transform)을 적용하여 거리 프로파일을 획득한다.
-
TUT 및 보정 대상의 거리 프로파일에서 Hamming 윈도우를 활용한 TG를 수행한다.
-
TUT 및 보정 대상에 퓨리에 변환 혹은 Chirp-Z 변환을 통해 다시 주파수 영역 데이터 획득한다.
-
RCS 보정을 수행한다.
그림 2(a)는 12×12 cm 금속판의 S-파라미터 측정 결과 예시로, 원시 데이터, BS 적용 결과, 그리고 TG까지 적용된 결과를 비교한 것이다. 두 개의 안테나를 사용하는 준-모노스태틱 환경에서는 송신기와 수신기(TX-RX, transmitter-receiver) 간의 간섭이 발생하며, 특히 저주파 영역에서 회절에 의해 간섭이 더 크게 나타나는 것을 확인할 수 있다. 또한, 비 무반향 챔버 환경이므로, 다양한 환경 반사에 의한 복잡한 신호가 존재함을 알 수 있다. BS를 적용하면 TX-RX 간섭이 상당히 줄어들며, 환경적 요인에 의한 불필요한 신호들도 효과적으로 제거된다.
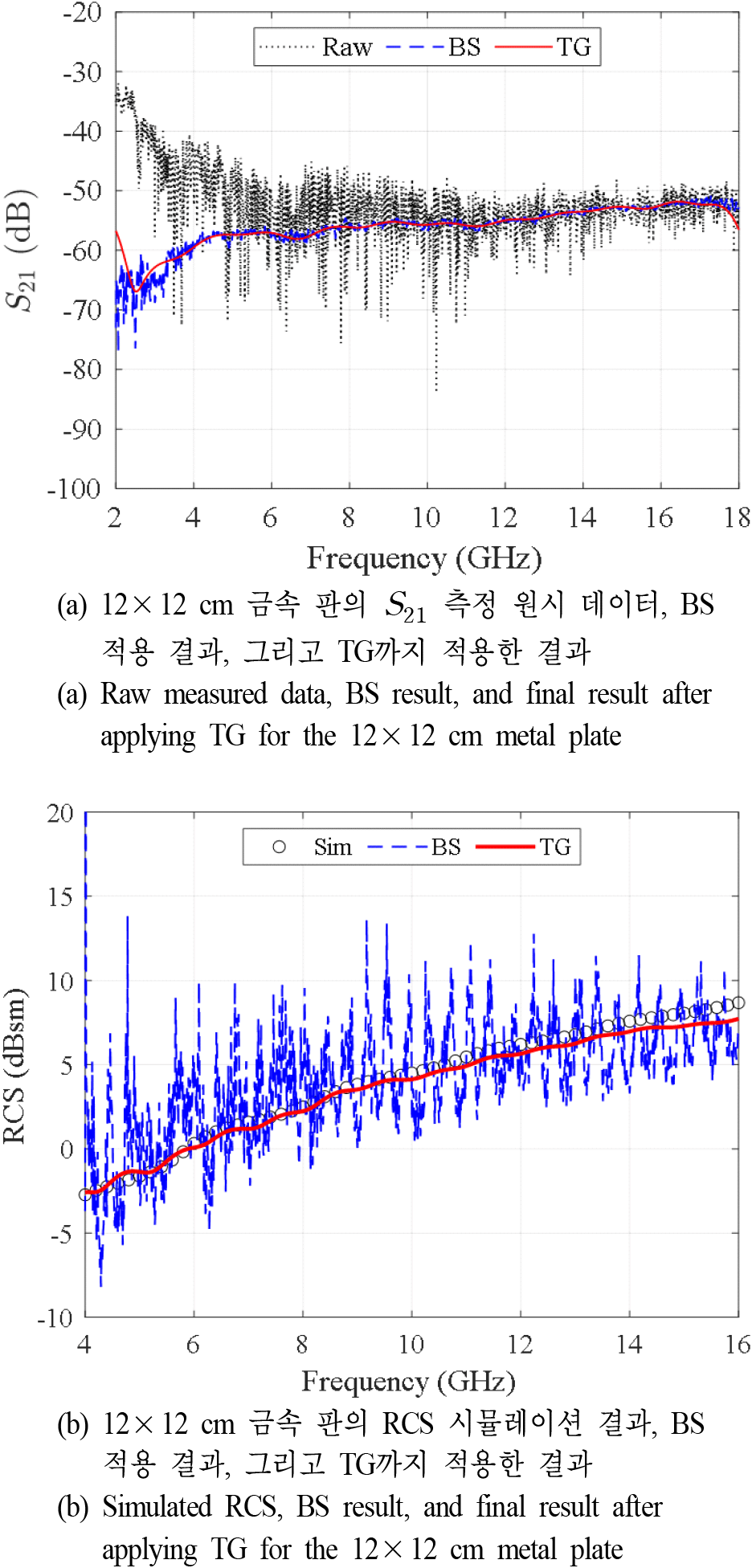
최종적으로 TG를 적용함으로써 가장 부드러운 형태의 결과를 얻을 수 있으나, 윈도우 함수의 영향으로 인해 측정 대역 양 끝에서 가파른 왜곡이 발생하는 것을 확인할 수 있다[10],[11]. 이러한 왜곡은 윈도우 함수의 너비가 데이터를 전부 포함하고 있지 않기 때문에 발생하며[12], TUT뿐 아니라 보정 대상에도 동일하게 발생한다. 이에 따라 본 연구에서는 4~16 GHz 대역을 기준으로 측정 정확도를 평가하였다.
그림 2(b)는 12×12 cm 금속판의 RCS 시뮬레이션 결과와 측정 결과를 비교한다. 그림 2(a)의 결과와 마찬가지로 BS만 적용된 경우 측정값에서 매우 큰 폭의 변동이 발생하며, TG 까지 적용된 경우 시뮬레이션 결과와 가장 가까우며 매끄러운 결과를 얻을 수 있다.
비 무반향 환경에서 RCS 측정 정확도 및 재현성을 확인하기 위해, 그림 1에 제시된 환경에서 표 1에 제시된 원전계 조건을 만족하는 금속 구의 RCS를 5회 반복 측정하였다. 원전계 조건 rFF는 식 (3)과 같다.
여기서 D는 측정 대상의 최대 선형 크기이며, λ는 측정 주파수의 파장이다. 1회 측정은 모든 금속 구에 대한 측정을 한 사이클로 간주한다. 한 사이클이 완료된 후, VNA 설정은 초기화되며 2-1에 제시된 1)단계부터 다시 반복 측정이 수행된다. 측정은 증폭기가 사용된 경우와 사용되지 않은 경우에 대해, VV-편파(VV-pol, VV-polarization)와 HH-편파(HH-pol, HH-polarization)에 대해 각각 수행된다. 금속 구의 monostatic RCS는 VV-pol과 HH-pol에서 같은 값을 갖지만, 비챔버 실내 환경의 경우 환경적 요인에 의해 두 값이 달라질 수 있기 때문에 두 편파에 대해 검증해야 한다. 증폭기는 그림 3에 제시된 구성도와 같이 TX 앞 단에 적용된다.
Ⅲ. RCS 측정 결과 및 분석
거리 프로파일은 주파수 영역에서 얻어진 측정 데이터를 거리 영역으로 변환하여 얻는 결과로, TUT에서 반사되는 신호와 주변 환경에서 반사되는 신호를 직관적으로 확인할 수 있다. TUT가 존재하는 위치에서는 높은 신호 수준을 보이고, 존재하지 않는 영역에서 낮은 잡음 및 클러터 수준을 보이는 것이 바람직하다. 그림 4는 VV-pol 측정에서 얻어진 반지름 60 mm 금속 구의 거리 프로파일을 나타낸다. 5회 측정된 값의 평균을 나타내며, 그림 4(a)및 그림 4(b)는 각각 BS를 적용하기 전과 후이다. 그림 4(a)에서 0 m 부분의 신호는 케이블과 안테나 간의 부정합에 의해 발생하며 약 1 m 부분의 신호는 TX-RX 간섭을 나타낸다. BS 적용을 통해 부정합과 TX-RX 간섭에 의한 신호가 효과적으로 제거되는 것을 확인할 수 있으며, 비챔버 실내 환경 특성상 발생하는 높은 잡음 수준 역시 상당히 저감되는 것을 알 수 있다. 또한, 증폭기를 사용한 경우 잡음과 TUT에서의 반사 신호 모두가 증폭되는 것을 확인할 수 있다.
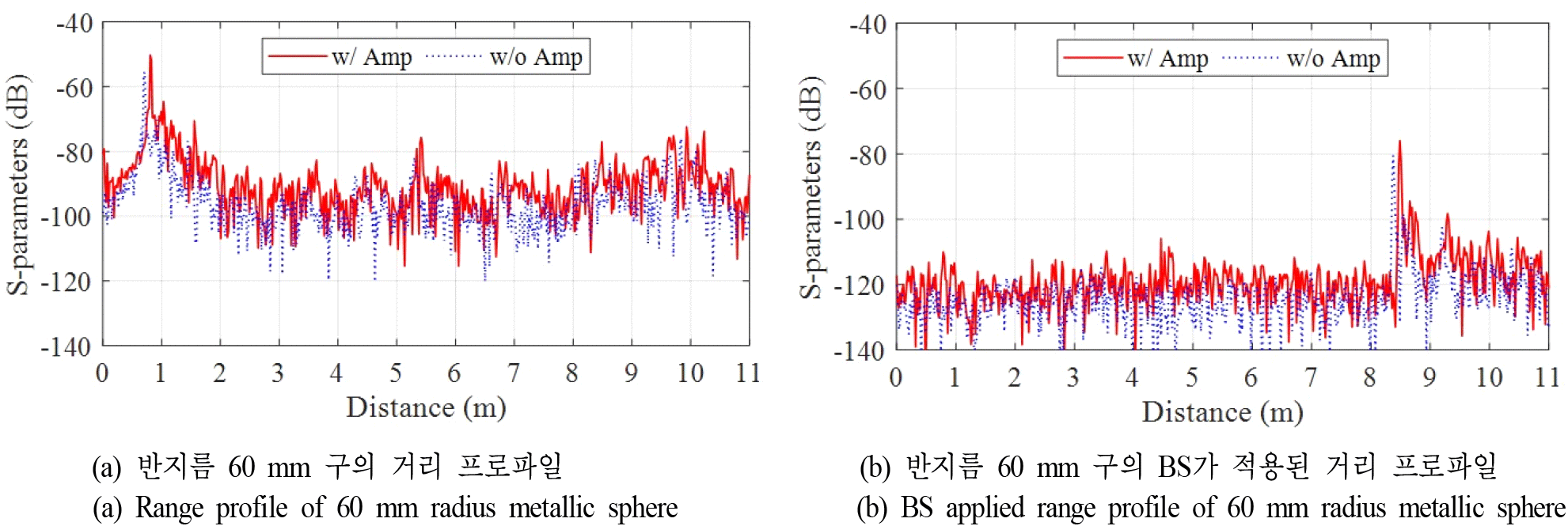
그림 5는 측정된 금속 구에 대해 VV-pol에서 증폭기 및 BS 적용 여부에 따른 잡음 바닥 수준을 나타낸다. 잡음 바닥은 TUT가 존재하지 않는 0~8 m 구간에서 측정된 S-파라미터의 평균값이다. 또한 5회 측정된 값의 평균을 나타낸다. 그림 4의 결과와 마찬가지로, BS를 적용하면 잡음 바닥 수준이 저감되며, 증폭기를 사용한 경우에는 잡음 바닥이 상승하는 것을 알 수 있다. HH-pol 역시 유사한 경향의 데이터를 얻을 수 있다.
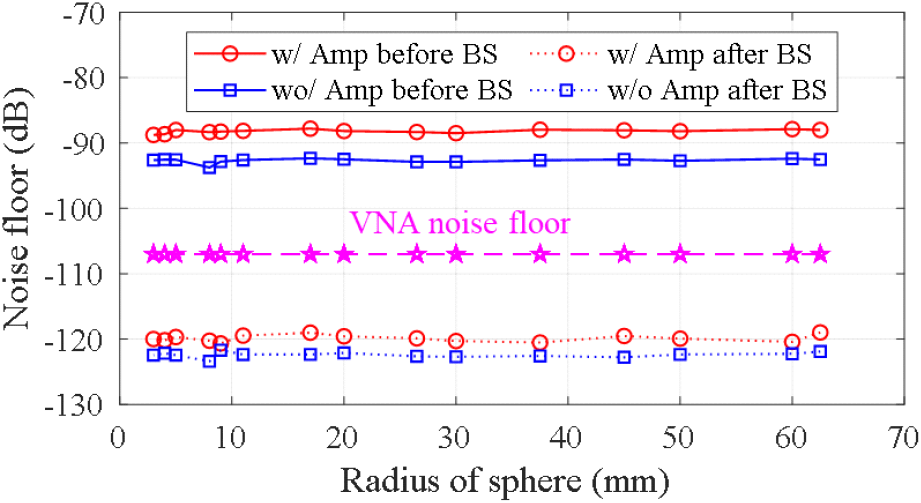
그림 6은 측정된 금속 구에 대한 VV-pol에서 증폭기 사용 여부에 따른 거리 프로파일 피크값을 나타내며, 5회 반복 측정된 결과의 평균이다. 피크값은 TUT가 존재하는 8~9 m 구간에서 측정된 S-파라미터의 최댓값으로 정의된다. BS를 적용하지 않은 경우 금속 구의 반지름에 따른 피크값의 차이가 유의미하게 나타나지 않으므로, BS를 적용한 후의 최댓값을 분석 대상으로 사용한다. 금속 구의 반지름이 작아짐에 따라 거리 프로파일의 피크값이 작아지는 경향을 보이며, 증폭기를 사용한 경우가 사용하지 않은 경우보다 더 큰 값을 나타낸다. HH-pol에서도 유사한 경향의 결과를 얻을 수 있다.
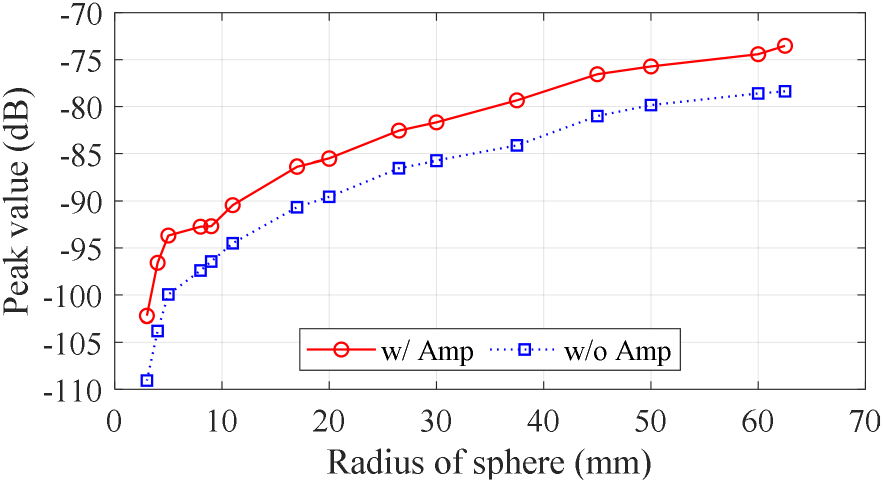
그림 7은 측정된 모든 금속 구에 대해 VV-pol에서 증폭기 사용 여부에 따른 피크값 대 잡음 바닥 비(PNR, peak value-to-noise floor ratio)를 나타내며, PNR은 식 (4)와 같이 정의된다.
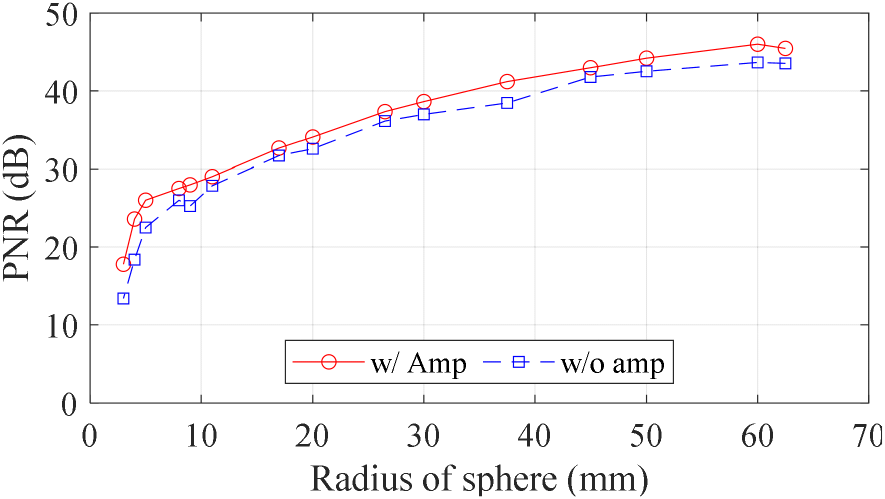
여기서 peak valuedB는 BS 적용 후 검출된 range profile의 피크값이며 noise floordB는 BS 적용후 산출된 거리 프로파일의 noise floor이다. 증폭기를 사용한 경우가 사용하지 않은 경우보다 더 높은 PNR을 나타내며, HH-pol에서도 유사한 경향의 결과를 얻을 수 있다. 추가적으로 적용되는 TG는 피크값과 거리가 먼 잡음을 더욱 효과적으로 제거하기 때문에, 잡음의 평균값으로 정의된 잡음 바닥을 이용한 PNR이 RCS 정확도를 완전히 결정하지는 않지만, 일반적으로 PNR이 높을수록 더 정확한 측정 결과를 얻을 수 있다.
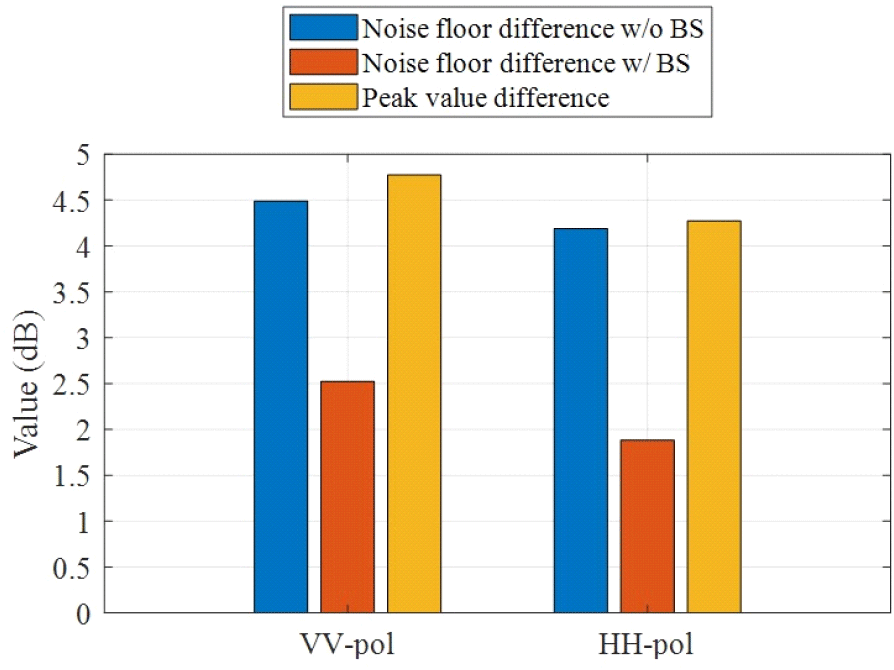
그림 8은 증폭기 사용 여부에 따라 BS 적용 전후의 잡음 수준 차이와 거리 프로파일의 피크값의 차이를 나타낸다. 증폭기 사용으로 인해 잡음과 피크값이 모두 증가하지만, BS를 적용함으로써 증폭기로 인해 추가되는 잡음 수준은 저감될 수 있다. 따라서 증폭기 사용을 통한 피크값 증가는 잡음 수준 증가보다 더 유효하게 크기 때문에, 결과적으로 더 높은 PNR을 확보할 수 있다.
최종적으로 얻어진 반지름 60, 26.5, 9, 4, 3 mm 금속 구의 RCS가 그림 9에 제시되어 있으며, 해석해와 비교된다. 제시된 결과는 5회 측정값의 평균이다. 증폭기를 사용한 경우, VV- 및 HH-pol 모두에서 반지름 3 mm 금속 구까지 높은 정확도의 RCS 측정 결과를 얻을 수 있다. 반면, 증폭기를 사용하지 않은 경우, 반지름 3 mm 금속 구의 측정 결과는 해석해와 비교했을 때 상당한 오차를 나타낸다.
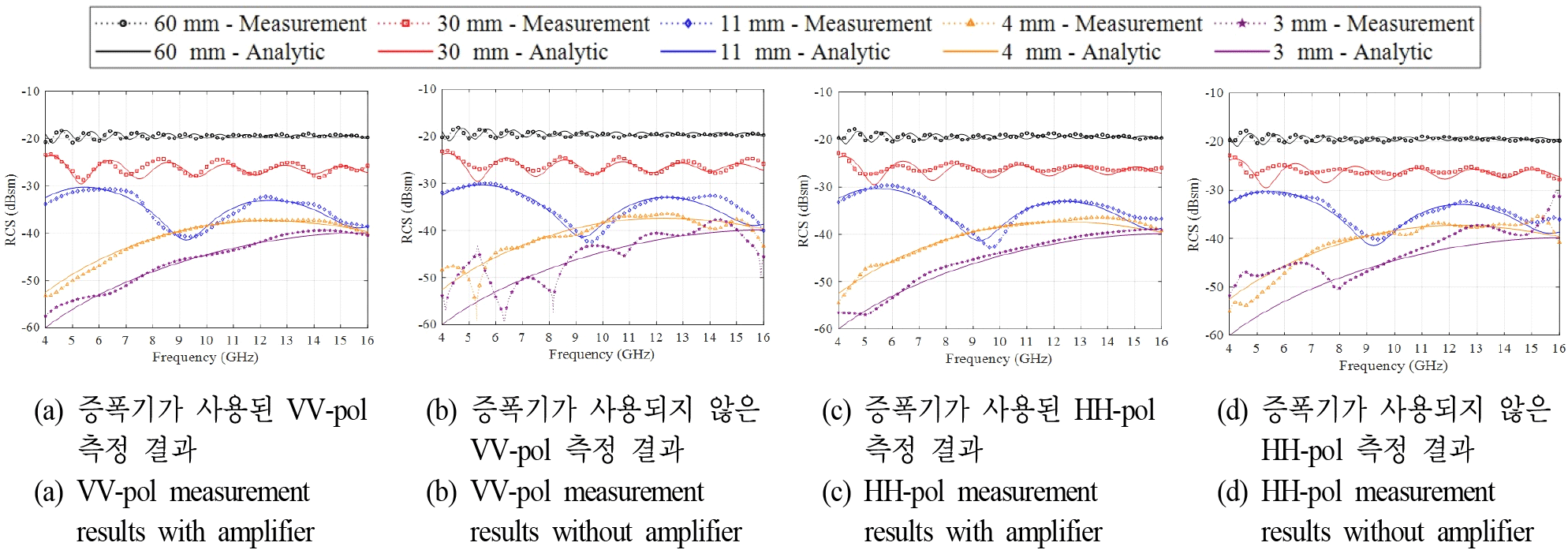
그림 10은 VV- 및 HH-pol에서 증폭기 사용 여부에 따른 평균 RCS를 해석해의 평균 RCS와 비교한 것이다. 마커는 5회 측정값의 평균을 나타내며, 범위는 측정값의 최대-최소 범위를 의미한다. 평균 RCS σmean은 식 (5)와 같이 정의된다.
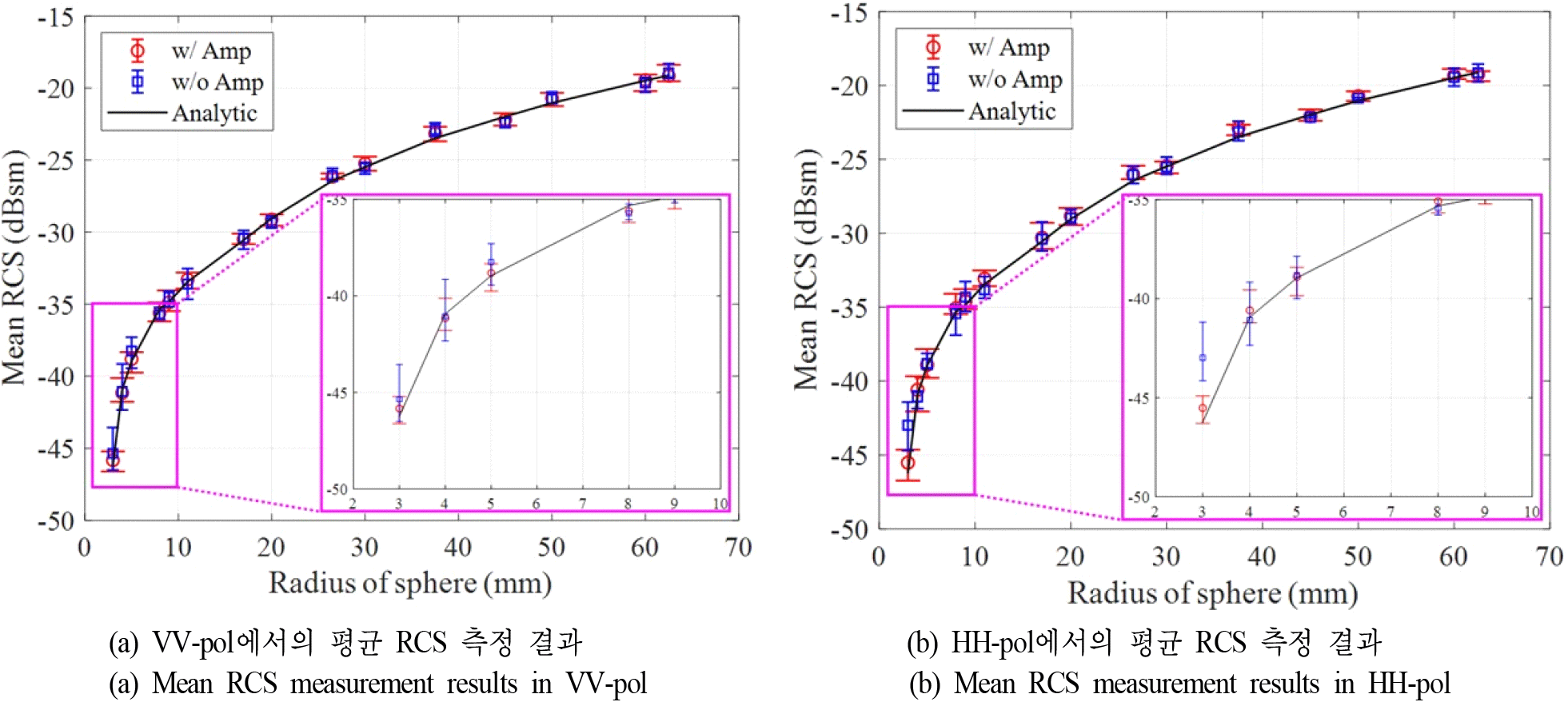
여기서 N은 측정된 모든 주파수 샘플 수이며 σdB [n]은 n번째 주파수 샘플에서의 RCS이다.
그림 11은 VV= 및 HH-pol에서의 평균 RCS 오차를 나타낸다. 평균 RCS 오차는 전반적인 RCS 수준의 측정 지표로 활용될 수 있으며, 해석해의 평균 RCS와 측정값의 평균 RCS 간 차이의 절댓값으로 정의된다. 마커는 5회 측정값의 평균을 나타내며, 범위는 측정값의 최대-최소 범위를 의미한다. 그림 9에서 제시된 결과와 마찬가지로, 증폭기를 사용한 경우 반지름 3 mm 금속 구의 평균 RCS 오차는 허용 가능한 수준으로 나타난다. 반면, 증폭기를 사용하지 않은 경우에는 오차가 급격히 증가하는 것을 확인할 수 있다.
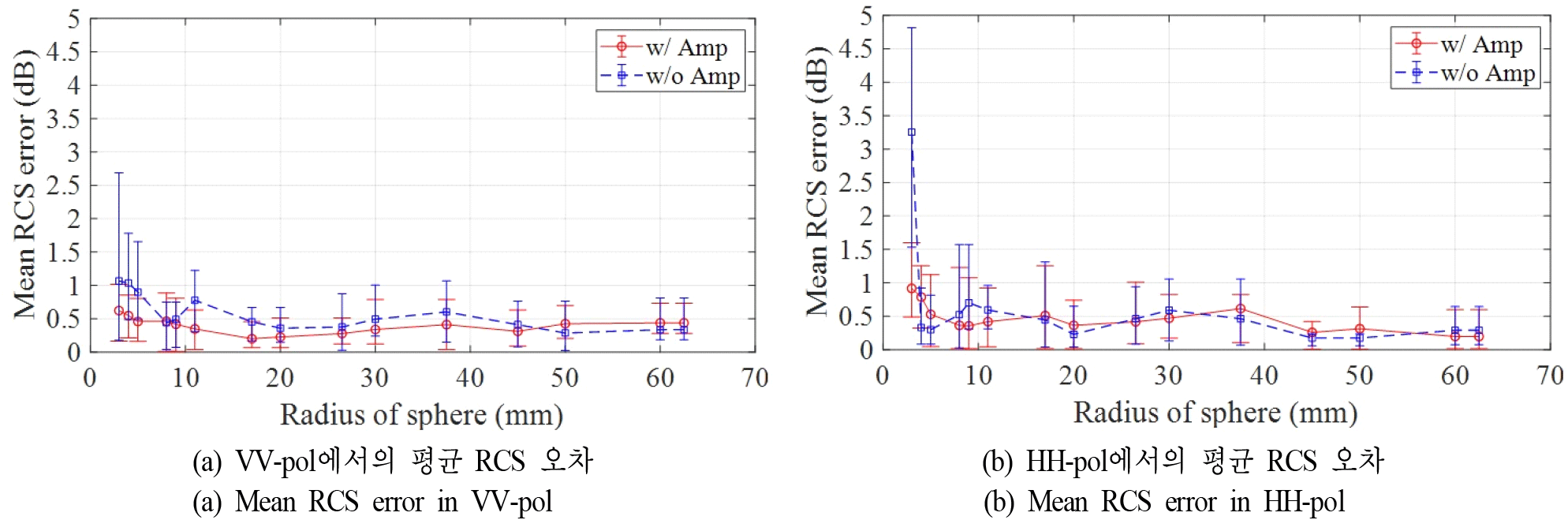
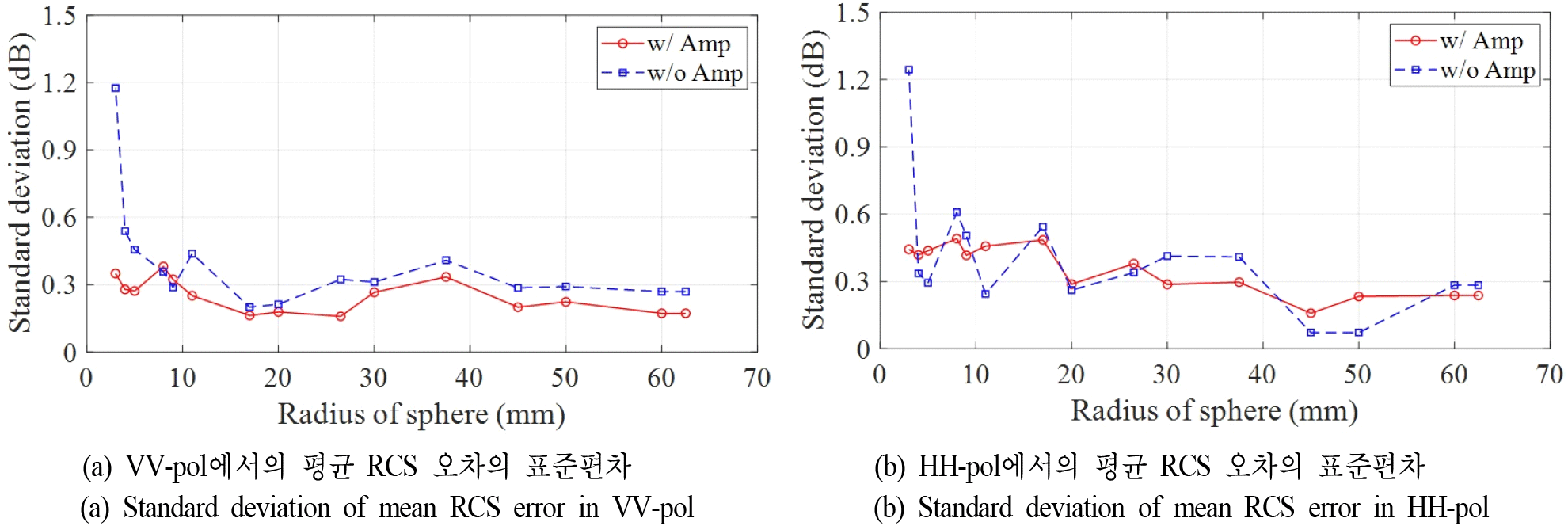
그림 12는 그림 11에 제시된 평균 RCS 오차의 표준편차를 나타낸다. 오차의 표준편차는 측정 결과의 신뢰성과 재현성을 판단하는 지표로 활용될 수 있다. VV= 및 HH-pol에서 증폭기 사용 여부와 관계없이, 반지름 4 mm 금속 구까지는 낮은 표준편차를 나타내지만, 반면 반지름 3 mm 금속 구의 경우 증폭기를 사용하지 않으면 매우 큰 표준편차를 보이는 것을 확인할 수 있다.
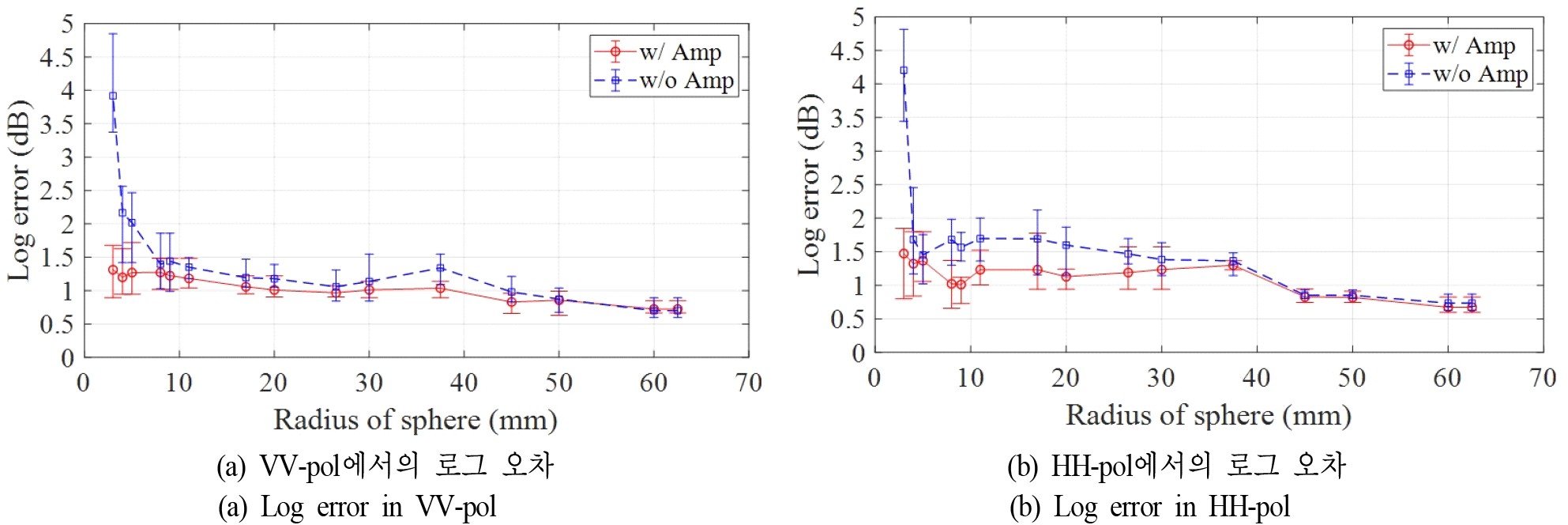
측정된 전반적인 RCS 수준뿐만 아니라, 비단조 및 진동 특성을 갖는 금속 구의 RCS 측정 정확도를 판단하기 위해서는, 모든 주파수에서 전반적인 RCS 수준을 평가하는 평균 RCS 오차만으로는 충분하지 않을 수 있다. 따라서 식 (6)과 같이 정의된 로그 오차 를 확인함으로써, 주파수에 따른 측정 경향성의 일치도를 평가한다.
여기서 은 n번째 주파수 샘플에서의 해석해이다. 그림 13은 VV- 및 HH-pol에서의 로그 오차를 나타낸다. 평균 RCS 오차와 유사하게, 증폭기를 사용한 경우에는 반지름 3 mm 금속 구까지 비교적 높은 정확도의 측정이 가능하다. 반면, 증폭기를 사용하지 않은 경우에는 반지름 3 mm 금속 구에서 로그 오차가 급격히 증가하는 것을 확인할 수 있다.
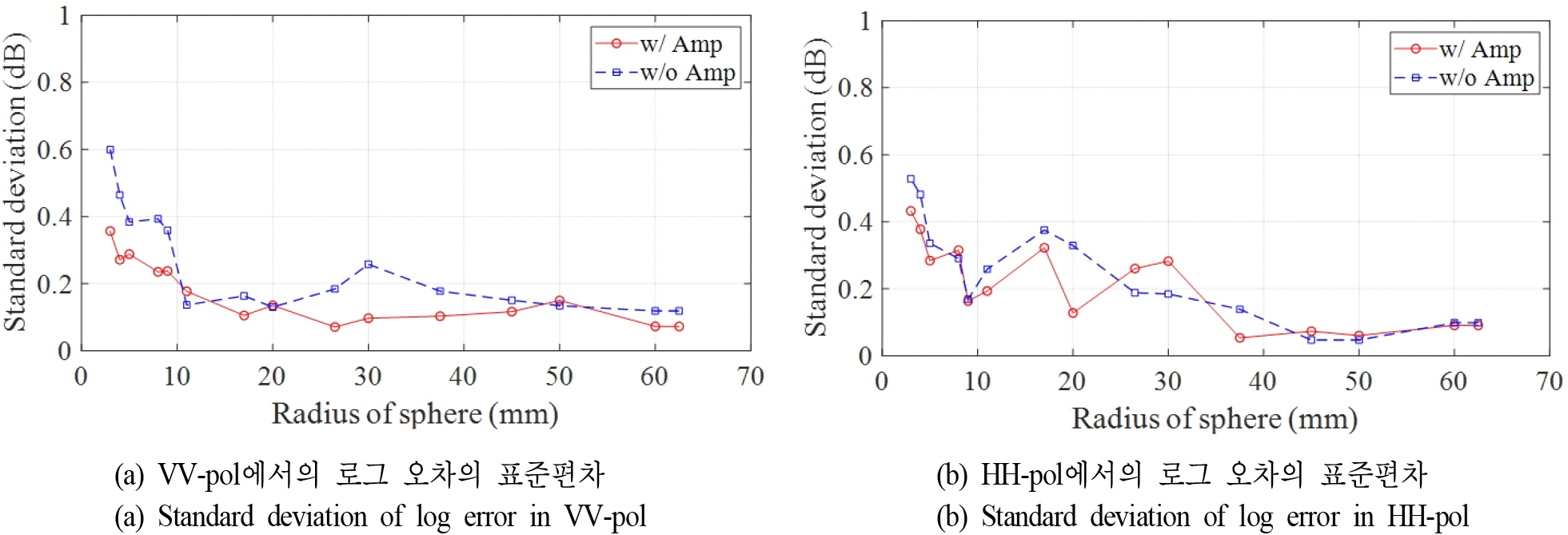
평균 RCS 오차와 마찬가지로, 재현성 분석을 위해 로그 오차의 표준편차가 그림 14에 제시되어 있다. 평균 RCS 오차의 표준편차와 달리, 증폭기를 사용하지 않은 경우에서도 로그 오차의 표준편차는 반지름 3 mm 금속 구에서 급격히 증가하지는 않는 것으로 나타난다. 하지만 그림 13에 제시된 결과를 고려하면, 이미 로그 오차가 큰 상태에서의 표준편차이므로 이를 긍정적인 결과로 판단하기는 어렵다.
제시된 평균 RCS 오차, 평균 RCS 오차의 표준편차, 로그 오차, 그리고 로그 오차의 표준편차를 통해, 비 무반향 챔버 환경에서의 RCS 측정 시스템의 NERCS를 확인할 수 있다. 측정 가능한 범위에서는 정확성과 재현성이 모두 달성되어야 하므로, 네 가지 지표 중 하나라도 급격히 증가하는 지점을 참고문헌 [9]에서 언급한 NERCS로 판단할 수 있다. 표 2는 최근 RCS 측정 문헌들과 제시된 연구 결과의 간략한 비교이다. 대부분의 연구들에서 측정 환경 및 시스템의 최소 측정 범위를 제시하지 않으며, 제시한 경우 하나의 지표만 근거로 삼는다. 본 연구에서는 비챔버 실내 환경에서 NERCS를 두 가지 오차와 각 오차들의 표준편차를 지표로 측정하고 측정법을 제시한다.
| Study | Minimum TUT linear size*[λ] | Measurement environment | NERCS evaluating metric |
|---|---|---|---|
| [2] | 9.12 | Anechoic chamber | - |
| [5] | 4.8 | Anechoic chamber | - |
| [7] | 8 | Non-anechoic chamber | - |
| [8] | 8 | Anechoic chamber | - |
| [9] | 0.32 | Anechoic chamber | Mean RCS error |
| This work | 0.32 | Anechoic chamber | Mean RCS error, log error, standard deviation of each errors |
본 연구에서 제시된 환경에서, 증폭기를 사용하지 않은 경우 반지름 3 mm 금속 구에서 로그 오차의 표준편차를 제외한 모든 지표가 급격히 증가하였다. 따라서 NERCS는 반지름 3 mm 구의 측정된 평균 RCS인 −43 dBsm으로 판단할 수 있다. 증폭기를 사용한 경우, 반지름 3 mm 금속 구까지 합리적인 측정 결과를 얻을 수 있었기 때문에 NERCS를 직접적으로 확인할 수 없다. 하지만 그림 7에 제시된 PNR 경향을 고려할 때, 반지름 2 mm 금속 구의 측정은 불가능할 것으로 예측된다. 따라서 증폭기를 사용한 경우, NERCS는 반지름 3 mm 구와 2 mm 구의 평균 RCS 중간값인 −51 dBsm으로 간접적으로 확인할 수 있다.
Ⅳ. 결 론
본 논문에서는 빠른 설계 피드백이 요구되는 경우 병목 요소로 작용할 수 있는 RCS 측정 시설의 경제적, 공간적 부담을 크게 완화한 비 무반향 챔버 환경에서의 RCS 측정 정확도를 분석하였다. 또한 기존 연구에서 제시되지 않았던 재현성 측면을 조사하기 위해 5회의 반복 측정을 수행하였다. 평균 RCS 오차, 평균 RCS 오차의 표준편차, 로그 오차, 로그 오차의 표준편차의 총 네 가지 지표가 제시되었다. 분석에는 반지름 62.5 mm부터 3 mm까지의 금속 구가 활용되었으며, 증폭기 사용 여부에 따른 결과가 비교 분석되었다.
결과적으로, 본 연구에서 사용된 측정 환경에서 증폭기를 사용하지 않은 경우 NERCS는 −43 dBsm으로 직접 확인되었으며, 증폭기를 사용한 경우에는 −51 dBsm으로 간접적으로 확인되었다.
본 연구에서 제시된 모든 방법은 다양한 환경에서도 일반적으로 활용될 수 있으므로, 향후 무반향 챔버를 보유하지 않은 소규모 연구소에서도 간이 측정 시설을 구축하고, 그 측정 정확도를 판단하는 지표로 활용될 수 있을 것으로 예상된다. 또한, 다양한 지표를 통해 NERCS를 정확히 확보함으로써, NERCS 이상의 RCS가 예상되는 대상에 대해 초기 설계를 위한 빠른 피드백을 제공할 수 있다. 결과적으로, 스텔스 플랫폼 설계의 가속화에 기여할 수 있을 것으로 기대되다.
추가적으로, 제시된 바와 같은 간이 RCS 측정 시설이 보다 유용하게 활용되기 위하여 근거리 측정을 보완하기 위한 근전계-원전계 변환 기법과, 식 (3)에 제시된 거리 근처에서의 측정시 발생하는 거리에 따른 RCS 값의 변화를 보정 할 수 있는 기법들이 연구되어야 한다.




