I. 서 론
최근 센서 기술의 고도화와 더불어, 다양한 환경에서 객체의 위치 및 운동 정보를 정확하게 인식하고 추적하는 기술에 대한 수요가 지속적으로 증가하고 있다. 이를 위해 고해상도 영상 기반의 비전 센서와 속도 측정에 특화된 레이다 센서는 각각 꾸준히 발전해왔으며, 다양한 응용 분야에서 독립적으로 활용되어왔다.
하지만 이러한 센서들은 각기 다른 물리적 특성과 측정 원리로 인해 고유의 한계를 지닌다. 예를 들어, 레이다 센서는 환경 변화에 강인하고 거리 및 속도 추정이 가능하나, 횡방향으로 이동하는 객체에 대해서는 정확한 탐지가 제한되는 반면, RGB-D (depth) 센서는 객체의 시각적 특성과 깊이 정보를 기반으로 다양한 방향의 운동을 추정할 수 있으나, 깊이 센서의 탐지 거리 제약 및 레이다 대비 상대적으로 낮은 깊이 정보 정밀도에 의해 실내 또는 근거리 환경에 주로 제한된다.
이러한 센서들의 단점을 보완하기 위해 상호보완적인 특성을 지닌 센서 퓨전(sensor fusion) 기술이 활발히 연구되고 있다[1],[2]. 특히 최근에는 딥러닝 기반의 센서 융합 기법이 주목받고 있으며[3],[4], 이는 복잡한 비선형 관계를 자동으로 학습할 수 있다는 장점을 가진다. 그러나 실제 환경에서는 대규모 학습 데이터 확보의 어려움, 비전과 레이다 데이터 정보량 차이에 따른 정보 손실[5],[6], 연산 자원의 부담 등으로 인한 한계가 존재한다.
딥러닝 기반 센서 퓨전의 한계점을 보완하기 위해, 명확한 수학적 모델에 기반한 해석 가능한 알고리즘 연구가 제안되었다 [7],[8]. 칼만 필터(Kalman filter) 및 그 확장 기법들은 센서로부터 얻은 위치 및 속도 정보를 통합하여, 단일 센서 대비 객체의 상태 (state)의 정확도를 성공적으로 향상하였다. 하지만, Zewge 등[7]의 연구는 수학적 모델링 기반의 시뮬레이션을 통해 정량적인 정확도 향상을 확인하였으나, 다양한 실제 측정 환경에서의 객체 상태(ground truth)와의 비교를 통한 정량적 검증이 미흡하다는 한계가 존재한다. Huang 등[8] 연구는 실제 환경에서 위치에 대한 정확도 향상을 보여주나, 속도에 대한 정확도 향상을 보여주지는 않는다.
따라서, 본 연구에서는 딥러닝 기반이 아닌, 해석 가능한 센서 융합 알고리즘을 제안하고 다양한 실제 조도 환경에서의 객체의 위치, 속도에 대한 정확도 향상을 살펴본다. MIMO(multi-input multi-output) 레이다의 3차원 위치 정보와 RGB-D 센서의 ROI(region of interest) 기반 추적 정보를 기반으로, 객체의 위치 및 속도를 전방위적으로 추정할 수 있는 칼만 필터 기반 융합 알고리즘을 설계하였다.
mmWave 레이다 센서는 종방향 운동에 대한 객체 추적을 정밀하게 측정할 수 있지만, 횡방향 운동은 안테나 개수와 빔 폭에 따른 한계가 존재하며, 클러터(clutter) 제거를 필요로 한다. 반면, RGB-D 센서는 객체 외형 기반의 ROI 추출과 깊이 정보를 활용하여 모든 방향의 속도 추정이 가능하며, IR(infrared) 센서를 포함하여 낮은 조도 환경에서도 일정 수준 이상의 탐지가 가능하다.
본 논문의 구성은 다음과 같다. 제 Ⅱ장에서는 제안된 센서 퓨전 알고리즘 적용을 위한 센서 구성 및 객체 이동 플랫폼을 설명하고, 제 Ⅲ장에서는 칼만 필터 기반의 센서 퓨전 알고리즘 및 각 센서의 처리 과정을 상세히 기술한다. 이어서 제 Ⅳ장에서는 실제 환경에서의 실험을 통해 측정된 결과를 바탕으로 성능을 정량적으로 분석하고, 연구의 결론과 향후 연구 방향에 대해 논의한다.
Ⅱ. 측정 시스템 구성
본 장에서는 제안된 센서 퓨전 알고리즘의 적용을 위한 측정 시스템의 구성, 취득 데이터와 객체 이동 플랫폼에 대하여 설명한다. 측정 시스템은 레이다와 비전 센서로 구성되어 있으며, 사용된 mmWave 레이다 센서는 그림 1과 같이 Texas Instrum사의 IWR1443 비전 센서는 Intel사의 RealSense Depth Camera D455 이다. 레이다 센서의 경우 3D-point cloud 기반의 위치 데이터를 취득할 수 있으며, 거리 해상도는 약 4 cm이다. 비전 센서의 경우 640×480 크기의 RGB, Depth 그리고 IR 데이터를 수집한다. 비전 센서의 프레임 속도는 30 fps이고, 레이다의 프레임 속도는 10 fps 로 동일한 프레임 속도를 구성하기 위하여 비전 센서의 프레임 속도를 10 fps로 고정하였으며, 동일한 FoV (field of view)를 가지도록 설정하였다. 또한, 단일 Python 스크립트에서 데이터 취득 명령을 순차 실행하는 방식으로 소프트웨어 수준의 시간 동기화를 수행하였으나, ms 수준의 미세한 시간 오차가 발생할 수 있다. 하지만 본 연구에서 사용된 표적의 속도는 0.1 m/s 수준으로 10 ms 의 시간 동기화 오차로 인해 발생하는 표적의 위치 오차는 최대 0.001 m가 발생할 수 있다.
객체 이동 플랫폼의 경우 정확한 속도로 움직일 수 있는 레일 기반의 스텝모터를 활용하였으며, 레일의 유효 길이는 약 0.85 m이다. 알고리즘 성능 검증을 위해 객체는 레이다 반사경(corner reflector)으로 선정하였다.
Ⅲ. 제안된 센서 퓨전 알고리즘
그림 2는 제안된 센서 퓨전의 과정을 명시한다. 각 센서에서는 우선적인 객체 상태 추정을 수행하며, 이를 위해 전처리 과정이 포함된다. 센서별 전처리 과정을 설명한 이후 퓨전 과정을 설명한다.
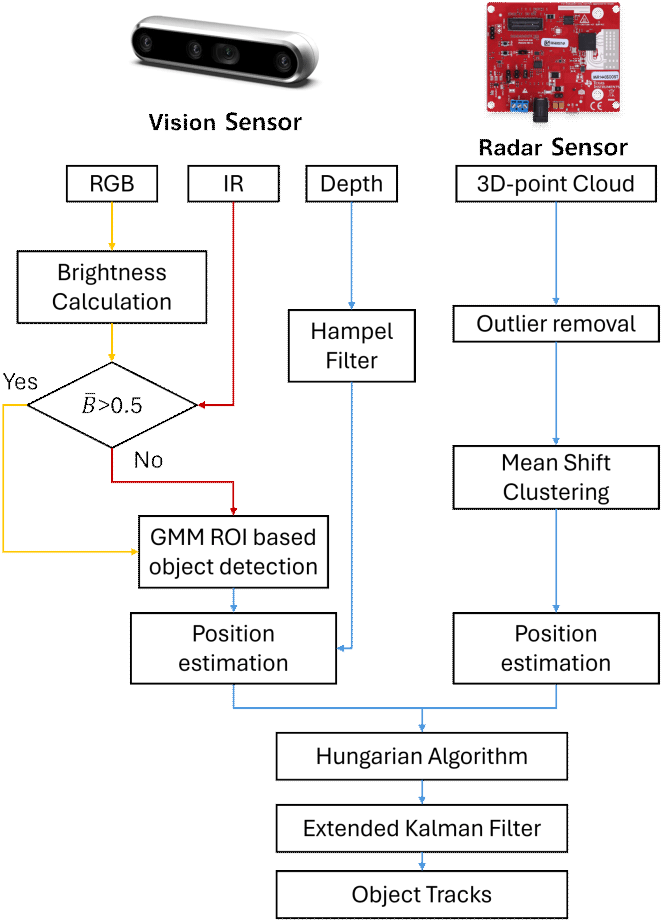
조도 환경에서 강인한 처리를 위해서는 RGB 영상의 주관적 특성을 배제하고, 객관적이고 정량적인 밝기 추정 기준이 요구된다. 본 연구에서는 이러한 기준으로 Bezryadin 등이 제안한 BCH(brightness-chroma-hue) 모델을 채택하여, 전체 영상에 대한 인지 기반 평균 밝기를 계산하였다[9].
입력된 sRGB 영상은 먼저 감마 디코딩을 수행하여 선형 RGB로 변환되며, 이어서 CIE 1931 XYZ 색공간으로 투영된다, 이후, XYZ 성분은 Cohen 등[10]의 실험 기반 가중치 행렬(MBCH)을 적용하여 인지 좌표계(D,E,F)로 사상된다. 해당 가중치 행렬은 다음과 같다.
각 픽셀의 인지적 밝기 Bi는 식 (1)과 같이 정의된다.
여기서 i는 픽셀의 인덱스를 의미하며, 전체 영상의 평균 인지적 밝기 는 식 (2)와 같이 정의된다.
여기서 N은 영상내의 총 픽셀 개수를 나타낸다. 수식 (2)를 통해 계산된 가 임계값 이상인 경우에는 RGB 데이터를 활용하며, 반대로 저조도 환경일 때는 IR 데이터를 활용하도록 한다.
이후 GMM(gaussian mixture model) 기반으로 운동 객체와 배경을 분리하고, bbox(bounding box)를 생성한다[11]. GMM은 정적인 배경과 동적인 객체의 ‘움직임’ 차이를 기반으로 대상을 구분하므로, 본 연구의 제어된 환경뿐만 아니라 복잡한 배경에서도 특정 패턴에 국한되지 않는 탐지 강인성을 확보할 수 있다. 생성된 bbox 내부의 depth 영상 데이터에 대해서는, Hampel 필터를 적용하여 측정 오차로 인한 이상치를 제거한 후 센서의 내부 파라미터를 반영하여 최종적인 객체 위치를 계산한다[12].
레이다 센서로부터 획득한 원시 데이터는 3D point cloud 형태로 수신되나, 낮은 elevation 해상도로 인해 x(횡방향), y(종방향) 의 2D 데이터만을 활용한다. point cloud 데이터는 복잡한 반사 환경 및 주변 물체로부터의 잡음으로 인해 노이즈와 클러터(clutter)가 포함되어 있으며, 이는 객체 추적 정확도를 저해하는 주요 원인 중 하나이다. 따라서 본 연구에서는 신뢰성 있는 객체 추적을 위해 전처리 과정을 선행적으로 수행하였다.
먼저, 레이다 점군 데이터에 대해 이상치 제거(outlier removal)를 수행하여, 반사율이 비정상적으로 낮거나 주변 간섭에 의해 FoV 외부에 생성된 비정상 점들을 제거하였다. 이를 통해 클러터에 의한 오류 가능성을 최소화하였다. 이후, 단일 객체에 대응하는 다수의 점들을 통합하여 대표 위치를 산출하기 위해 Mean shift 클러스터링 알고리즘을 적용하였다. Mean shift는 비모수 밀도 추정 방식을 기반으로, 각 점의 국소 밀도를 고려하여 클러스터 중심을 탐색하여, 객체의 중심 위치를 명확히 추출하는 데 효과적이다.
센서 퓨전 단계에서는, 각기 다른 로컬 좌표계(local coordinate system)를 기준으로 측정된 비전 센서와 레이다의 위치 정보를 단일 공통 좌표계로 변환하는 과정을 수행한다. 이를 위해, 레이다의 모든 측정 좌표에 사전에 측정한 두 센서 중심 간의 물리적인 거리 차이를 보정하여 카메라 좌표계 기준으로 통일하였다. 이어서, 동일한 물리 객체에 대응하는 센서 정보를 정합(match)한 후 퓨전을 수행한다. 이는 특정 센서에서 발생하는 클러터를 제거하고 안정적인 객체 추적을 제공한다. 이를 위하여 헝가리안 알고리즘(Hungarian algorithm)을 적용하여 센서 간 객체 간의 최적 정합을 수행한다. 헝가리안 알고리즘은 비용 행렬을 바탕으로 이분 매칭에서 모든 일대일 할당의 총 비용을 최소로 하는 최적의 해를 효율적으로 찾아주는 알고리즘이며, 본 연구에서는 각 센서에서 탐지된 객체를 정합시키는데 활용되었다. 식 (3)은 헝가리안 알고리즘을 위한 비용 행렬 (cost matrix)이다.
여기서 는 비전 센서에서 추정된 i번째 객체의 위치, 레이다 센서에서 추정된 j번째 객체, || · ||2는 유클리드 길이를 의미한다. 비용 행렬에서 사전에 정의된 임계값(Dmax)을 초과하는 경우 해당 쌍은 예외 처리가 된다. 이후 비전 센서에서 추정된 Nc개의 객체와 레이다 센서에서 추정된 Nr개의 객체 사이의 매칭을 식 (4)를 기반으로 수행한다.
여기서 SN은 N개의 객체에 대해 가능한 모든 순열(permutations)의 집합, σ(i)는 비전 객체 i번째에 매칭되는 레이다 객체 j를 의미한다.
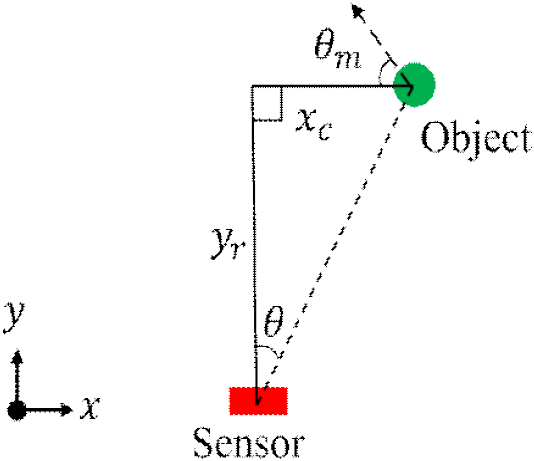
센서 정합 결과를 기반으로 그림 3과 같이 레이다 데이터의 종단 거리(yr), 비전 데이터의 횡단 거리(xc)를 활용하여 객체의 거리 및 각도(θ=arctan(xc/yr))를 계산하며, θm은 객체의 운동 각도를 의미한다.
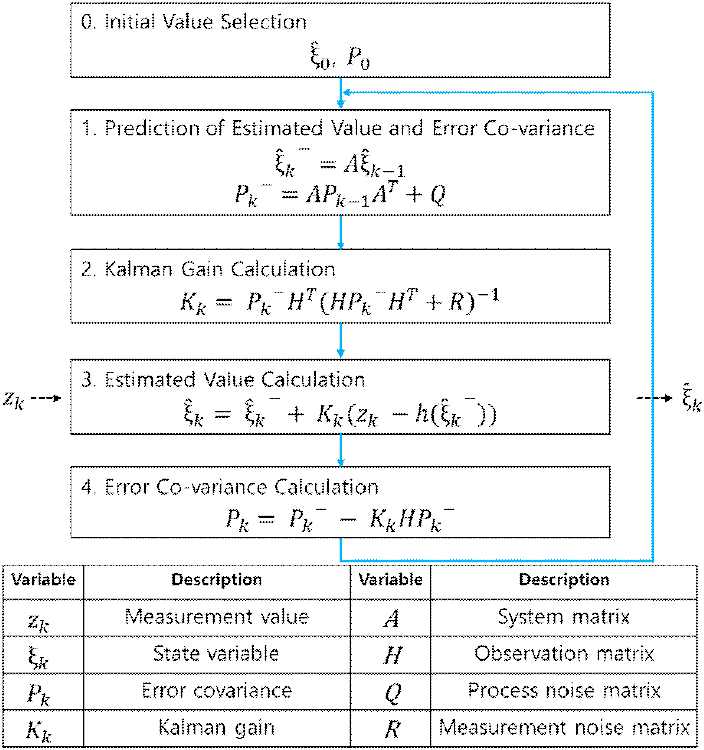
이를 기반으로 본 연구에서는 확장 칼만 필터(EKF, extended kalman filter)를 활용하여 시간에 따른 객체의 상태를 실시간으로 추정하였다. 확장 칼만 필터는 비선형 시스템을 매 단계 자코비안으로 선형 근사하여 시스템의 오차값 보정 및 상태를 추정하는 알고리즘이다[13]. 본 연구에서는 측정된 객체 위치를 바탕으로 객체의 보정된 위치 및 속도를 계산하는데 활용되었으며 상태 벡터는 다음과 같이 정의된다.
여기서 xk,yk는 센서 기준 객체의 위치, 는 벡터에 따른 속도 성분을 의미한다. 센서 측정 벡터는 레이다 센서 기반 종단 거리(y)와 센서와 객체 사이의 각도(θ)로 구성되며, 다음과 같이 표현된다:
이 측정값은 다음의 비선형 모델을 통해 상태와 연계된다.
이때, 비선형 모델을 EKF에 적용하기 위한 자코비안 (Jacobian) 행렬 Hk는 다음과 같이 유도된다:
이러한 측정 모델과 선형화 기반의 EKF 알고리즘을 그림 4에 나타내었으며, 해당 구조를 적용하여 객체 상태 추정 수행하였다.
Ⅳ. 객체 상태 추정 결과
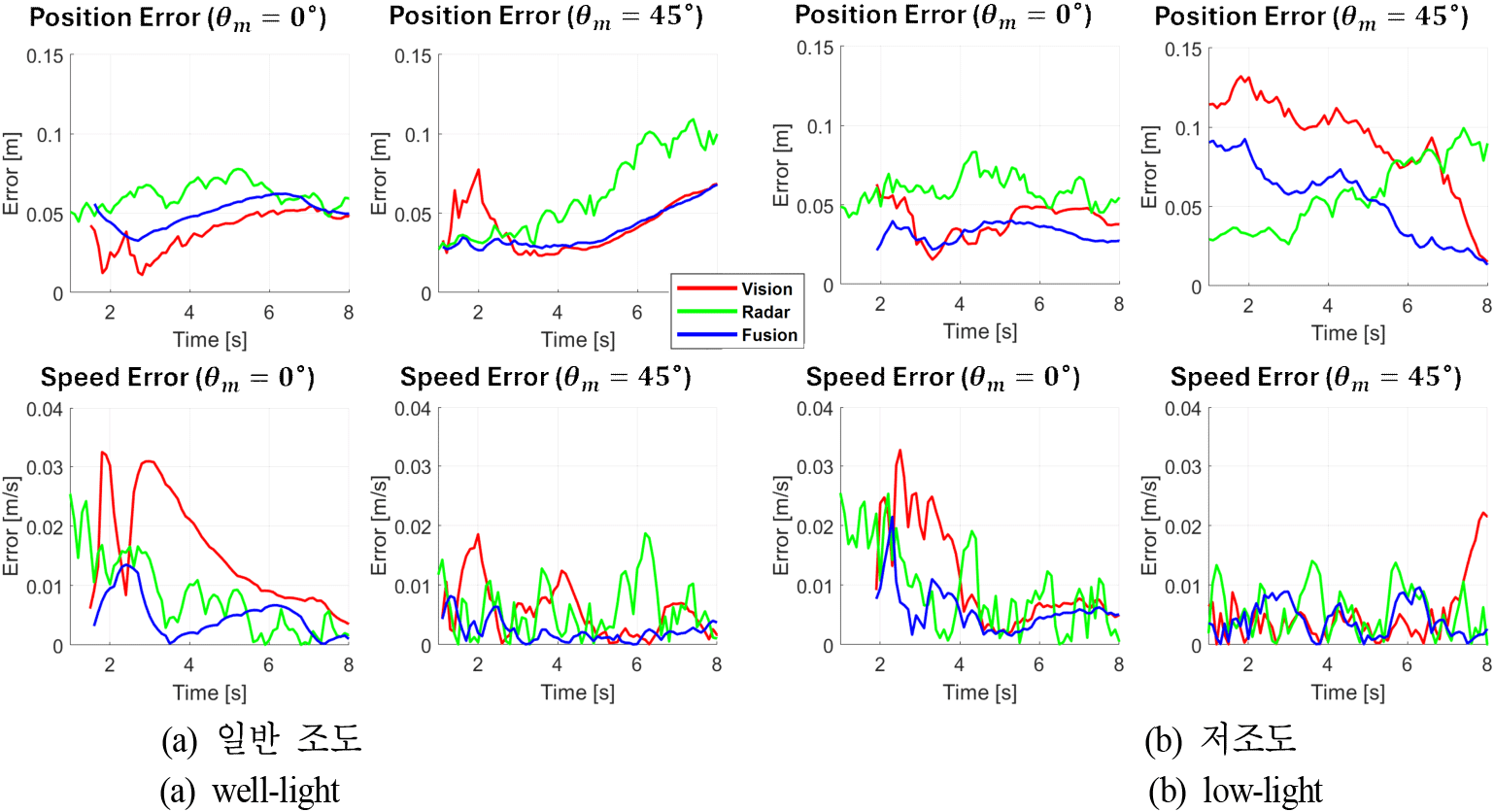
제안된 센서 퓨전 알고리즘의 성능을 정량적으로 검증하기 위해, 앞선 제 Ⅱ장에서 설명한 측정 시스템과 이동 플랫폼을 활용하여 실내 환경에서 실험을 수행하였다. 실험은 다양한 조도 조건과 레이다 탐지 특성에 영향을 미치는 객체의 운동 각도 조건을 설정하여 진행되었다. 구체적으로, 그림 5에 도시된 바와 같이 일반 조도 및 저조도 환경 각각에 대해 객체 운동 각도 (θm)을 0°와 45°로 설정하여 총 네 가지 조건을 구성하였다.
θm=0°에서는 횡방향 운동만 존재하는 상황을 의도적으로 유도하였으며, θm=45°은 횡방향 및 종방향 운동이 동시에 존재하는 경우를 모사하였다. 또한 조도 변화에 따른 비전 센서의 민감도를 실험적으로 분석하고자, 동일 조건에서 실내 조명을 변화시켜 비교 분석을 가능하게 하였다. 각 조건에서 객체는 일정한 속도 0.1 m/s 로 이동하며 반복 측정을 수행하였다. 그림 6은 실험 결과를 보여주며, θm=0°에서는 비전 센서의 추정이 x축 위치에 대해 높은 정확도를 나타낸 반면, y축 위치는 레이다 거리 정보에 기반한 추정이 더 안정적인 성능을 보였다. 이는 RGB-D 센서의 깊이 추정에서 종방향 (y축) 오차가 상대적으로 크기 때문으로 분석된다. 한편, 그림에서 레이다 탐지 결과가 비전 및 퓨전 결과보다 먼저 시작되는 것은, 비전 탐지에 사용된 GMM 알고리즘이 안정적인 배경 모델 구축을 위해 초기 학습 시간을 필요로 하기 때문이다.
θm=45°에서도 비전 센서가 제공하는 x축 위치 정보와 레이다 기반 y축 위치 정보 간의 상호 보완적인 구조가 유지되었으며, 이를 기반으로 한 EKF 기반 상태 추정 결과는 각 축의 속도 성분까지 안정적으로 도출되었다. 조도 변화 실험에서는 저조도 환경에서 IR 데이터를 통한 보완이 효과적으로 작동하여 센서 퓨전 기반 추정이 성공적으로 진행되었다.
해당 결과의 정량적 분석을 위해, 프레임 단위 객체 상태 추정 결과에 대해 오차는 식 (9) 및 식 (10)와 같이 계산하였다.
여기서 xgt,ygt,는 이동 플랫폼에 의해 운동 객체의 벡터별 위치와 속도, xest,yest,는 센서 또는 퓨전을 통해 추정된 객체의 벡터별 위치와 속도, n은 프레임 인덱스를 의미한다. 그림 7은 식 (9) 및 식 (10)에 대한 결과를 보여주며, 제안된 센서 퓨전 알고리즘은 단일 센서 기반 추정 방식에 비해 위치 및 속도 추정의 정확도 측면에서 유의미한 향상을 나타냈다.
구체적으로, 위치 추정(표 1)에 대한 RMSE(root mean square error)는 센서 간 정합 및 융합 처리를 통해 단일 센서 최소 오차 대비 평균 17.8 % 감소하였다. 이는 센서간 시간 동기화 오차를 감안하여도 다중 센서가 제공하는 상호보완적인 정보가 객체 위치 추정의 정확도를 향상시키는 데 기여했음을 의미한다. 또한 속력 추정 오차(표 2)에 있어서도, 융합 전 대비 평균 29.2 % 이상의 오차 감소가 확인되어 제안된 알고리즘의 오차 감소 성능을 검증하였다.
| Sensor | Vision | Radar | Fusion | |
|---|---|---|---|---|
| θm | ||||
| 0° | well-light | 0.0396 | 0.0595 | 0.0499 |
| low-light | 0.0400 | 0.0587 | 0.0311 | |
| 45° | well-light | 0.0446 | 0.0609 | 0.0413 |
| low-light | 0.0854 | 0.0575 | 0.0500 | |
| Sensor | Vision | Radar | Fusion | |
|---|---|---|---|---|
| θm | ||||
| 0° | well-light | 0.0139 | 0.0118 | 0.0079 |
| low-light | 0.0104 | 0.0138 | 0.0088 | |
| 45° | well-light | 0.0054 | 0.0064 | 0.0043 |
| low-light | 0.0059 | 0.0059 | 0.0042 | |
이와 같이, 제안된 알고리즘은 복잡한 환경 변화 속에서도 센서 개별 성능의 한계를 극복하고, 객체 상태 추정에서 뛰어난 정량적 성능을 보이는 것으로 확인되었다.
Ⅴ. 결 론
본 논문에서는 조도 변화에 강인한 레이다-비전 기반 센서 퓨전 알고리즘을 제안하였다. RGB-D 센서와 밀리미터파 레이다의 위치 정보를 정합하고, 확장 칼만 필터를 통해 객체의 위치 및 속도를 프레임 단위로 추정하였다. 실험은 객체 운동 각도 0°/45° 및 일반/저조도 환경의 총 4가지 조건에서 수행되었으며, 제안된 알고리즘은 단일 센서 대비 뛰어난 정밀도와 추적 안정성을 보였다. 특히 위치 오차는 평균 17.8 %, 속도 오차는 평균 29.2 %의 정확도 향상을 확인하였다. 이를 통해 제안된 알고리즘이 센서 간 상호보완적 정보를 효과적으로 융합함으로써 다양한 환경에서도 높은 신뢰성을 확보할 수 있음을 보였다. 향후에는 레이다의 도플러 속도 정보를 통합하여 다중 객체 및 복잡한 동작 환경에서도 확장 가능한 구조로 발전시킬 예정이다. 또한, 단일 센서에서 간헐적으로 발생되는 부정적인 바이어스로 인한 퓨전 정확도 하락을 개선하기 위하여 단일 센서에서 추출된 데이터의 합리성을 판단하는 알고리즘의 연구 수행할 예정이다.