The Journal of Korean Institute of Electromagnetic Engineering and Science

The Korean Institute of Electromagnetic Engineering and Science

J. Korean Inst. Electromagn. Eng. Sci. 2025; 36(5):518-527

pISSN: 1226-3133, eISSN: 2288-226X

DOI: https://doi.org/10.5515/KJKIEES.2025.36.5.518

논문/REGULAR PAPERS

저고도 표적추적을 위한 다중주파수 다중빔을 이용한 각도추정 방법

임재혁^†

, 이의혁

, 정대교

, 오선진

Angle Estimation Technique Using Multi-Frequency Multi-Beam for Low-Altitude Target Tracking

Jaehyuk Lim^†

, Euihyuk Lee

, Daekyo Jeong

, Sunjin Oh

국방과학연구소

Agency for Defense Development

^†Corresponding Author: Jaehyuk Lim (e-mail: limjehunk@gmail.com)

© Copyright 2025 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Feb 19, 2025; Revised: Mar 09, 2025; Accepted: Mar 31, 2025

Published Online: May 31, 2025

요 약

레이다를 이용한 저고도 표적 추적시, 해수면·지상과 가까워 다중경로 간섭이 크게 발생하고, 이로 인해 모노펄스 각도추정에 큰 오차가 생긴다. 본 논문에서는 이러한 문제를 해결하기 위하여 다중주파수(multi-frequency)와 다중빔(multi-beam)을 결합한 MFMB(multi-frequency multi-beam) 방법을 제안한다. 먼저, 주파수별 간섭 패턴이 서로 상쇄될 수 있도록 회기신호 기반 최적의 주파수 조합을 도출한다. 이후, 각 주파수에서 생성된 수신신호를 합성하고 다중빔을 적용함으로써 각도추정 정확도를 높일 수 있다. 시뮬레이션 결과, 제안된 MFMB 방법은 모노펄스 대비 각도추정 오차를 크게 줄임을 확인하였다.

Abstract

When tracking low-altitude targets using radar, significant multi-path interference occurs because of their proximity to the sea surface or ground, leading to substantial errors in the monopulse angle estimation. To address this issue, this study proposes the multi-frequency multi-beam (MFMB) technique that combines the multi-frequency and multi-beam approaches. First, an optimal frequency combination is derived using linear regression to ensure that the interference patterns at different frequencies cancel one another out. Subsequently, the received signals at each frequency are synthesized, and multi-beam processing is applied to enhance the angle estimation accuracy. The simulation results confirm that the proposed MFMB method significantly reduces angle estimation errors compared with monopulse techniques, thereby contributing to improved detection and tracking of low-altitude targets in maritime and complex terrain environments.

Keywords: Radar; Low-Altitude Target; Multi-Frequency Multi-Beam (MFMB); Monopulse

I. 서 론

고도 표적 탐지는 해상이나 지상 등 지면에 매우 가까운 높이에서 비행하는 물체를 정확히 추적해야 한다는 점에서 현대 레이다 시스템에서 특히 중요한 이슈로 대두되고 있다. 예를 들어, 해상의 저고도 비행 표적은 해수면 반사에 의해 다중경로 현상이 발생하게 되는데, 이때 직접경로(direct path)와 간접경로(indirect path)로부터 들어오는 신호가 상호 간섭을 일으켜 각도 및 거리 추정에 큰 오차를 유발할 수 있다. 이러한 문제는 해수면만이 아니라 전파 반사가 일어날 수 있는 여러 환경(육지, 건물, 산악지형 등)에서도 유사하게 나타나며, 정확한 저고도 표적 탐지와 추적을 어렵게 만든다^[1]. 기존에 제안된 저고도 표적 추적 방법 중 대표적인 방법으로 모노펄스 각도추정 방법이 있다^[2]. 모노펄스는 수직 및 수평 방향의 빔 신호를 이용해 표적 각도를 추정하는 방식으로, 일반적으로 단일주파수에서 높은 정확도와 빠른 추적 성능을 보여 준다. 그러나 저고도 표적의 경우 해수면 반사 등에 기인한 간섭 영향이 각도추정 오차를 급격히 증가할 수 있다.

이러한 문제를 해결하기 위해, 다양한 저고도 표적 추적 방법들이 제안되었으며^[3]~[11]. 대표적으로 3차원 빔도메인 최대우도추정(3D-BDML) 방법을 기반한 연구들이 있다^[3]~[6]. 먼저, 센서 배열 신호처리를 빔도메인으로 옮겨 최대우도추정을 수행함으로써 모노펄스 대비 정확한 저고도 추적이 가능함을 보인 연구가 제시되었다^[3]. 또한, 다중경로현상이 적은 상황에서는 각도추정 성능이 떨어지는 문제를 개선하기 위해, 빔 세기의 비 보정과 같은 하이브리드 방법을 제안되었다^[4]. 또한 아주 낮은 고각에서 추정 오차 증가 문제를 개선하기 위해 선택적으로 지수 평활화를 적용하여 실시간 추적 성능을 높이는 방안^[5]과 수신 다중빔 환경에서의 고각 추정 성능에 대한 연구^[6] 또한 제안되었다. 마지막으로 근접전계 패턴 측정이 어려운 능동위상배열(AESA) 레이다에서도 안정적으로 적용가능한 3D-BDML 알고리즘이 제안되었다^[7].

한편, 다중 경로의 기하학적 관계를 활용하는 refined ML 방법을 통해서도 저고도 표적 추적의 다중경로 간섭 문제를 효과적으로 완화할 수 있다^[8]~[10]. 먼저, 해수면 반사 특성과 지구 곡률 등을 고려한 다중경로 신호 모델을 사용하여 정확한 고각을 추정하는 방법이 제안되었으며^[8], 주파수 가변 신호를 이용하여 평균제곱오차(MSE)가 가장 작아지는 주파수를 선택하여 저고도 추적 성능을 극대화하는 refined ML 방법이 제안되었다^[9]. 마지막으로, 복잡한 환경에서 적용 가능하도록 계산 부하를 줄이는 refined ML 알고리즘이 제안되었다^[10].

최대우도추정 방법을 기반한 기존 연구들과는 달리 다중 주파수 신호의 정보를 이용한 모노펄스 방식 기반 표적의 고각울 추정하는 연구가 제안되었다^[11]. 해당 연구에서는 표적 거리 및 모노펄스 신호비만 필요하기 때문에, 기존 모노펄스 레이더 시스템에 추가적인 하드웨어 구성없이 쉽게 적용 가능하다는 장점을 지닌다. 다만, 각 주파수별로 추정각도에 따른 계산값 테이블을 모두 가지고 있어야 되기 때문에, 장비에 적용하는데 걸리는 시간이 늘어날 수 있으며, 반사 환경의 변화에 따라 해당 계산값은 바뀔 수 있다는 단점이 있다.

현재 레이다의 개발 추세는 AESA 레이다를 넘어 복사소자 채널의 송수신 신호를 모두 디지털화 한 완전 디지털 AESA 레이다로 진화하고 있다^[12]. 이러한 방식의 레이다는 측정한 수신데이터로부터 동시에 다중빔을 형성할 수 있는 장점을 갖고 있다. 본 논문에서는 수신 다중빔 형성이 가능한 완전 디지털 AESA 레이다에서 별도의 하드웨어 구성없이 적용 가능한 다중주파수 수신신호와 다중빔 신호를 결합한 MFMB(multi-frequency multi-beam) 각도추정 방법을 제안한다. MFMB를 이용한 각도추정 방법에서는 별다른 계산값 테이블 준비 없이 다중주파수 수신신호를 결합하여 다중경로 간섭에 의해 생기는 변동성을 최소화하여 신호의 신뢰성을 높힐수 있으며, 이는 다중빔 형성을 통한 각도추정을 가능하게 한다. 제안한 방법의 유효성을 확인하기 위해, 먼저 다중경로 환경에서의 레이다 신호 모델링를 통해 모노펄스를 통한 각도추정의 한계에 대해 살펴본다. 이후 제안하는 MFMB 방법을 통해 저고도 표적 각도추정 오차를 효과적으로 개선하는 과정을 모의실험 결과와 함께 제시한다.

II. 다중경로에서의 모노펄스 각도 추정

2-1 신호 모델링

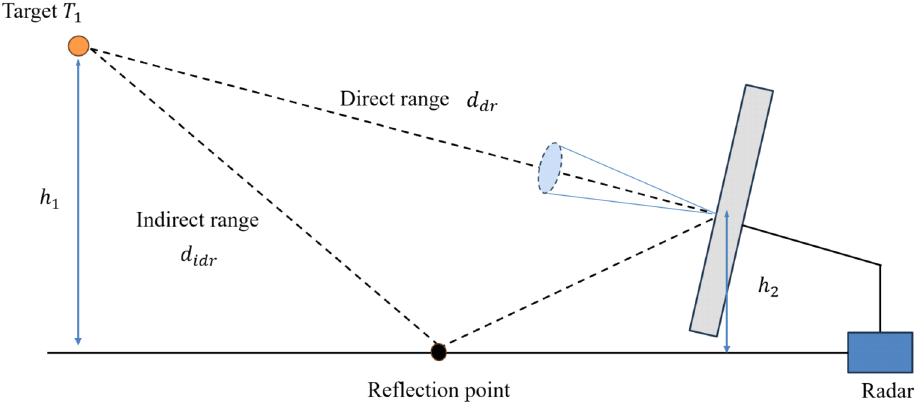
저고도 표적에 의해 발생하는 신호를 모의하기 위해, 저고도 표적 T₁가 고도 h₁의 위치한다고 가정하였으며, 이는 그림 1과 같다. 특히 저고도 표적에 대해서는 직접거리 d_dr 에 의해 발생하는 수신신호뿐만 아니라 해수면에 의한 반사 영향이 고려된 간접거리 d_idr 에 의해 발생하는 수신신호를 고려해야 한다.

그림 1. | Fig. 1. 저고도 표적 및 레이다 시나리오 | The scenario of radar and low-altitude target.

Download Original Figure

우선 표적 T₁ 의 직접거리 d_dr,에 의해 생성되는 수신신호의 SNR(signal-to-noise ratio) 값 A_i,dr 는 식 (1)과 같이 표현할 수 있으며, 레이다 파라미터로 표 1의 파라미터들을 사용하였다^[13].

A i, d r = P t n e l e m e n t G t G r λ 2 σ (4 π) 3 d d r 4 k T 0 F B

(1)

표 1. | Table 1. 레이다 파라미터 | Radar parameters.

	Parameter	Value	Unit
P_t	Transmit power	20	W
n_element	Number of elements	5,760	-
G_t	Transmit gain	-	dB
G_r	Receive gain	-	dB
λ	Wavelength	-	m
σ	RCS	1	m²
d_dr	Direct path distance	-	m
d_idr	Indirect path distance	-	m
k	Boltzmann constant	1.380649×10⁻²³	J/K
T₀	Standard temperature	290	K
F	Noise figure	3	dB
B	Bandwidth	1	MHz

Download Excel Table

여기서 A_i,dr 는 표적 T₁ 의 직접거리 d_dr,뿐만 아니라 i번째 주파수 f_i에 의해 결정된다. A_i,dr 가 결정되면, 직접거리 d_dr 에 대한 레이다 수신신호 R_i,dr 는 아래와 같이 표현할 수 있다.

R i, d r = A i, d r ⋅ exp j 2 π d d r λ

(2)

또한 간접거리 d_i,dr 로부터 SNR 값 A_i,dr 은 아래와 같이 얻을 수 있다.

A i, i d r = P t n e l e m e n t G t G r λ 2 σ (4 π) 3 d i d r 4 k T 0 F B

(3)

식 (1) 및 식 (2)와 마찬가지로, 레이다 수신신호 R_i,idr 는 아래와 같이 얻을 수 있다.

R i, i d r = A i, i d r ⋅ Γ exp j 2 π d i d r λ

(4)

여기서 Γ 는 해수면과 전파간 반사계수로, 다중경로 현상을 보다 명확하게 보기 위해 Γ = 1로 설정하였다. 최종적으로 저고도 표적에 의해 생성되는 수신신호 R_i는 식(1)~식 (4)를 이용해 얻은 R_i,dr, R_i,idr 를 이용하여 식 (5)와 같이 표현할 수 있다.

R i = R i, d r + R i, i d r + n i

(5)

여기서 n_i는 i번째 주파수의 가우시안 잡음이다.

2-2 수신신호 모의 및 모노펄스 각도추정 결과

정확한 수신신호를 생성하기 위해서는 레이다를 구성하고 있는 안테나의 형상을 먼저 설정하여야 한다. 본 논문에서는 안테나의 형상을 72×80개의 사각배열로 구성된 안테나로 설정하였으며, 배열소자 간격은 편의상 λ/2 로 설정하였다. 이로부터 direction cosine u, v에 대한 이득패턴 G(u,v)를 얻을 수 있다. 이러한 이득패턴으로부터 표적 위치에 따른 정확한 R_i,dr, R_i,idr 및 R_i값을 얻을 수 있다. 표적 T₁ 및 레이다의 위치를 표 2와 같이 설정하였으며, 표적 T₁ 의 마지막 위치에서의 구성은 그림 2와 같다. 신호 모의간격은 100 m마다 R_i,dr, R_i,idr 값을 생성하여, 표 2의 시나리오의 경우, 201번의 신호모의가 모의된다. 또한 실제 표적의 위치를 정확히 안다고 가정하고 해당 위치에 빔 조향을 적용하였다. 또한 주파수 f_i 는 레이다 운용시 적용되는 주파수 값으로, f_i = 9 + (i − 1)Δf GHz, Δf = 100 MHz이다. 또한 주파수세트 F에 대해, f_i∈F로, F = [f₁,f₂, ··· ,f₁₀] 이다.

표 2. | Table 2. 레이다 및 표적 위치 | Radar and target position.

	Initial position (m)	Final position (m)
T ₁	(0,10,000,50)	(0,30,000,50)
Radar	(0,0,0)	(0,0,0)

Download Excel Table

그림 2. | Fig. 2. 표적 T₁ 마지막 위치의 시뮬레이션 시나리오 | Simulation scenario at the target T₁’s final position.

Download Original Figure

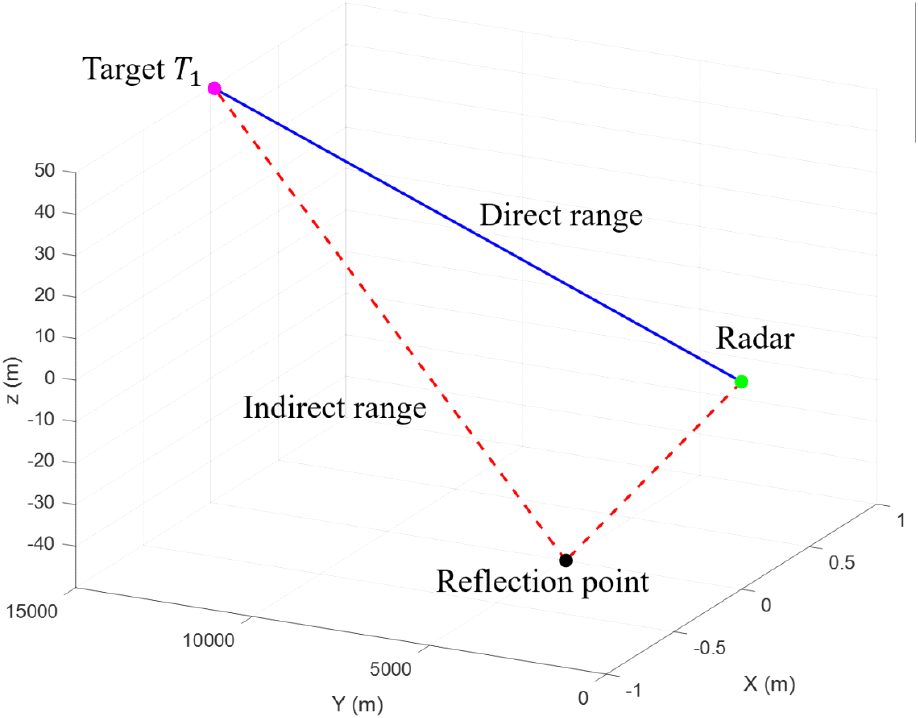
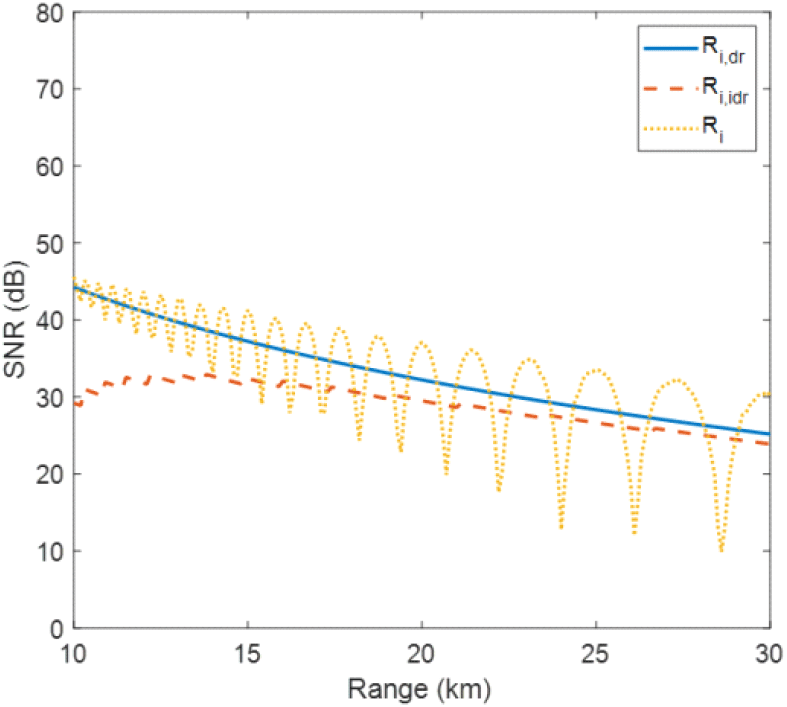
그림 3은 주파수 f₁을 적용해 얻은 수신신호 R_i,dr, R_i,dr 및 R_i의 SNR 결과이다. R_i,dr의 경우, 표적의 거리가 멀어짐에 따라, A_i,dr 값 영향에 의해 SNR 값이 감소함을 확인할 수 있다. R_i,idr 의 경우, 출발시점에 가까울수록 직접거리 방향과의 각도 차이에 의한 수신이득 차이로, R_i,dr과의 SNR 차이가 최대 12 dB 나는 것을 확인할 수 있으며, 거리가 멀어질수록 이러한 값 차이는 줄어든다. 의 경우, SNR 값이 주기적으로 변함을 확인할 수 있으며, 이는 식 (2) 및 식 (4)의 위상 항에 의해 R_i,dr, R_i,idr 는 서로 in-phase 또는 out-phase 상태가 되고, 이러한 위상 차이로 상쇄 또는 보강간섭을 일으킨 것으로 보인다. 뿐만 아니라, 주기적인 변곡점이 발생하는 것을 확인할 수 있다. 여기서 발생하는 수신신호의 변화는 모노펄스 방법을 이용한 각도추정 시 큰 오차를 유발할 수 있으며, 자세한 내용은 2-3절에서 다룬다.

그림 3. | Fig. 3. R_i,dr, R_i,idr 및 R_i 의 SNR 결과 | SNR results of R_i,dr, R_i,idr and R_i.

Download Original Figure

2-3 모노펄스를 이용한 각도추정 결과

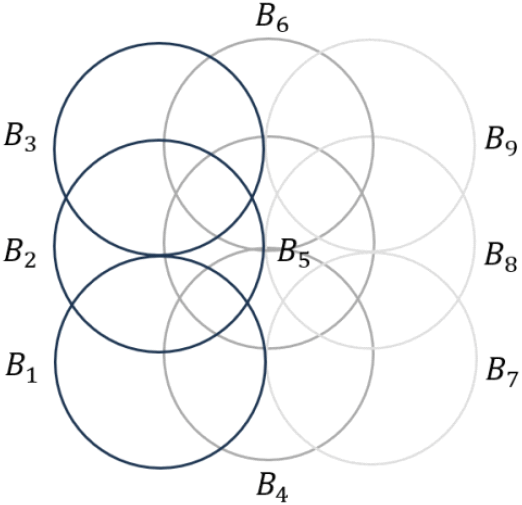
완전 디지털 AESA 레이다는 수신신호에 대해 원하는 방향으로의 다중빔 형성이 가능하다^[12]. 본 논문에서는 수신 다중빔을 그림 4와 같이 9개를 생성하였으며, 각 수신빔은 [B₁,B₂,B₃,B₄,B₅,B₆,B₇,B₈,B₉]과 같이 정의한다. 이때 수신빔을 생성을 위해 적용하는 조향벡터 $a s → u B n, v B n$ 는 다음 식으로 표현할 수 있다.

a 0 → u B n, v B n = β 0, 0 u B n, v B n, β 0, 1 u B n, v B n, ⋯, β 0, M − 1 u B n, v B n, ⋯, β L − 1, M − 1 u B n, v B n T

(6)

그림 4. | Fig. 4. 레이다의 다중빔 형성 | Multi beam generation of radar.

Download Original Figure

여기서 $u B n, v B n$ 값은 각 n번째 수신빔 B_n에서의 조향 값이며, L과 M은 각각 사각배열 안테나의 가로, 세로 크기로, 본 논문에서는 L = 72, M = 80이기 때문에, $a s → u B n, v B n$ 는 1 × 5760의 차원을 갖는다. 또한 β_l,m(u,v)은 아래와 같이 정의한다.

β l, m (u, v) = exp j 2 π λ l u ⋅ exp j 2 π λ m v

(7)

각 빔별 조향값은 표 3과 같이 설정하였다.

표 3. | Table 3. 다중빔 조향값 | Multi-beam steering values.

	$u B n, v B n$
B ₁	(−0.011, −0.01)
B ₂	(−0.011, 0)
B ₃	(−0.011, 0.01)
B ₄	(0, −0,01)
B ₅	(0, 0)
B ₆	(0, 0,01)
B ₇	(0.011, −0.01)
B ₈	(0.011, 0)
B ₉	(0.011, 0,01)

Download Excel Table

이때, 모노펄스 각도추적 방법은 다음의 순서로 이루어진다: 1) Δ_u 및 Δ_v 빔의 수신신호 크기를 구한다. 여기서 Δ_u = B₈ − B₂, Δ_v = B₆ − B₄ 이다. 2) 식 (8)을 이용해 정규화 신호 r_u 와 r_v 를 계산한다. 3) 식 (9)을 이용하여 지향점 기준 표적 추정치 δu, δv를 계산한다. 여기서 Slope_u, Slope_v는 각각 Δ_u/B₅, Δ_v/B₅의 선형구간 기울기를 의미한다. 4) 식 (10)과 같이, 지향방향 u_steer, v_steer값을 기준으로 실제 표적 각도 u_tgt, v_tgt를 추정한다.

r u = Δ u B 5, r v = Δ v B 5

(8)

δ u = r u S l o p e u, δ v = r v S l o p e v

(9)

u t a t = u s t e e r + δ u, v t a t = v s t e e r + δ v

(10)

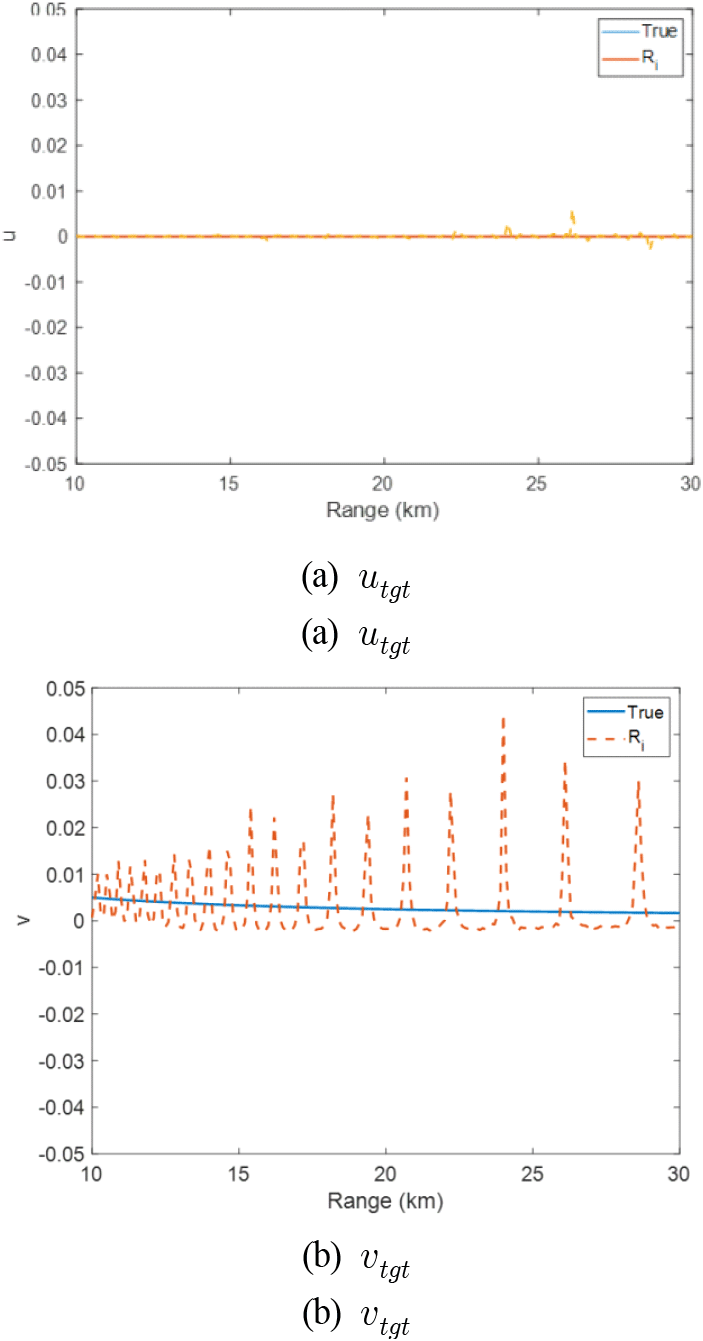
Slope_u, Slope_v는 사전에 측정을 통해 알고 있는 값이기 때문에, 실제 표적 각도 u_tgt, v_tgt는 정규화 신호 r_u와 r_v로부터 결정된다. 따라서 그림 3과 같이 다중경로로 인해 수신신호 R_i값이 주기적으로 변하는 경우, r_u와 r_v 값 또한 Slope_u, Slope_v 에 따라 움직이지 않고 예측과 다르게 변하게 되며, 이는 표적의 각도를 추정하는데 큰 오차를 발생시킨다. 그림 5는 2-2절에서 생성한 수신신호 R_i값을 이용하여 추정한 u_tgt, v_tgt 결과이다. 그림 5(a)에서와 같이, 추정한 u_tgt는 정답 표적위치와 차이가 거의 없음을 확인할 수 있으며, 이는 다중경로를 통한 각도추정 영향이 주로 수직 방향, δv에 영향을 크게 미치기 때문이다. 따라서, 앞으로의 분석결과에서 u_tgt는 더 이상 다루지 않겠다. v_tgt의 경우, 그림 5(b)에서와 같이, 다중경로의 영향을 매우 크게 받으며, 최대 0.04의 오차를 보인다. 여기서 중요한 부분은 그림 3과 같이, R_i의 변화가 큰 구간일수록 각도오차 또한 크게 발생한다는 점이다.

그림 5. | Fig. 5. R_i 을 이용한 모노펄스 각도추정 결과 | Monopulse angle estimation results using R_i.

Download Original Figure

III. MFMB 기반 각도추정 방법

3-1 다중주파수를 이용한 신호 합성

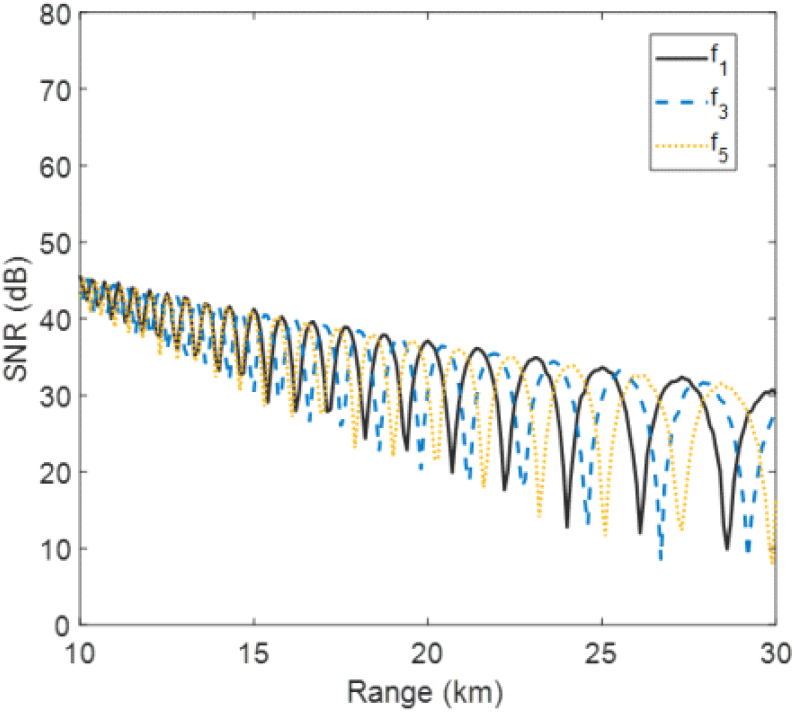
앞서 언급했듯이, 각 주파수별 R_i,dr의 변곡점 주기는 식 (2) 및 식 (4)의 위상 항에 의해 결정되기 때문에 주파수별로 다르다. 그림 6은 주파수 세트 중 f₁, f₃, f₅ 주파수에서의 각 R_i로부터 SNR 값을 도시한 결과이며, 여기서도 주파수가 변함에 따라 변곡점을 포함한 신호의 모양이 서로 다름을 알 수 있다.

우리는 II장의 결과와 그림 6의 결과로부터 다음의 사실을 확인할 수 있다. 1) 모노펄스 기반 각도추정의 오차는 R_i의 변화가 클수록 각도오차가 크게 발생한다. 2) 식 (2) 및 식 (4)로부터, 수신신호 R_i의 주기적 변화는 위상의 변화로부터 기인되며, 이는 주파수에 큰 의존성이 있다. 이러한 성질로부터 다양한 주파수에서의 신호를 최적의 조합으로 합성하면 각도추정 시 오차를 유발하는 신호의 변화를 줄일 수 있다. 따라서, 우리는 다양한 주파수 조합에 대해 정량적으로 성능을 평가하기 위한 방법론을 제시하고자 하며, 제시한 방법을 이용하여 최적의 주파수 조합을 선택한다.

그림 6. | Fig. 6. 주파수별 R_i의 SNR 결과 | SNR results of R_i with respect to f_i.

Download Original Figure

수신신호의 주파수에 대한 의존성과 변동성을 줄이기 위해, 다중주파수 합성신호 R_total를 아래 식 (11)과 같이 정의하였다.

R t o t a l = 1 N F' ∑ f i ∈ F' R i

(11)

이때, 주파수별 수신신호 R_i는 시간에 동시에 얻은 신호로 가정한다. 여기서 주파수조합 F′는 주파수세트 F내에서 선택한 주파수들의 집합으로 F′ ⊂ F이며, 만약 f₁, f₃, f₅ 주파수를 선택한다면 F′ = [f₃, f₅]이다. N_F′는 합성에 사용된 주파수 개수를 의미하며, 값에 따라 사용가능한 주파수 조합이 달라진다. 선택한 주파수 조합에 따라 식 (9)를 이용해 얻어진 합성신호 R_total로부터 정량적 성능평가를 위해, R_total를 재귀신호 R_ls을 least squres approximations 방법을 이용해 얻으며^[14], 자세한 방법은 다음과 같다: 합성신호 R_total의 거리 값을 $x →$ , SNR 값을 $y →$ 벡터로 치환하여 행렬 V를 식 (12)과 같이 얻는다. 식 (13)을 이용하여 행렬 P를 얻을 수 있으며, P의 계수값을 통해 재귀신호 R_ls를 얻을 수 있다.

V = 1 ⋮ x → x → ∘ x → 1

(12)

P = V T V − 1 V T y →

(13)

여기서 ° 는 원소별 곱을 의미한다.

최종적으로, 각 주파수조합 R_total에 대해 R_ls를 이용하면 각 합성신호 R_total별로 주파수에 대한 의존성과 변동성이 얼마나 줄어들었는지 손실값을 통해 평가가 가능하며, LSE(least squre error)를 이용하여 다음과 같이 얻을 수 있다.

L o s s = L S E R t o t a l − R l s

(14)

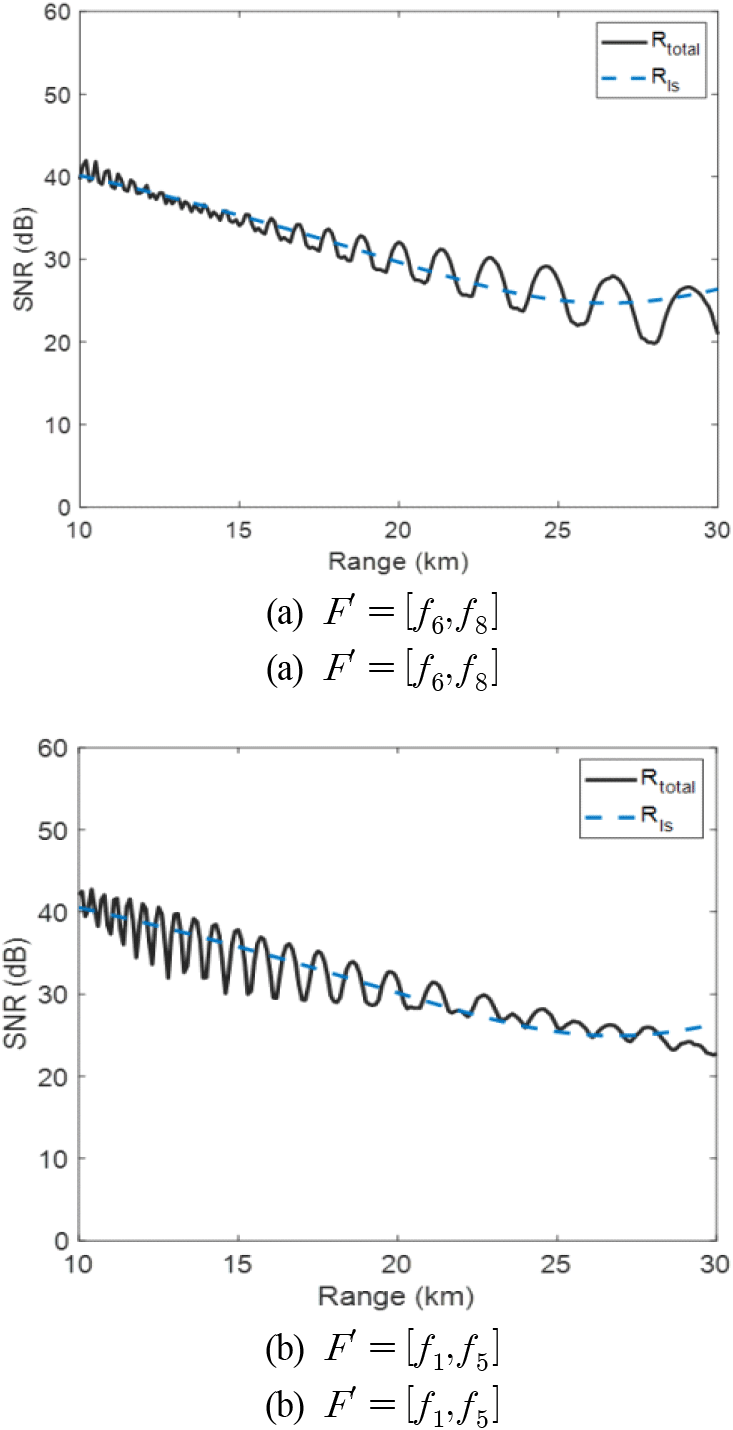
주파수 세트는 F = [f₁,f₂, ···, f₁₀] 로 10개이기 때문에 주파수 조합 F′의 경우의 수는 45개가 존재한다. 식 (12)를 통해 각 조합별 손실값을 계산하였다. 결론적으로, f₆, f₈ 주파수를 조합하였을 때 8.36·10³로 최솟값을 가졌으며,f₁, f₅ 주파수를 조합하였을 때 30.96·10³로 최댓값을 가졌다. 그림 7은 각 주파수 조합 F′ = [f₆,f₈], F′ = [f₁,f₅]에 대한 합성신호 R_total, 재귀신호 R_ls의 SNR 결과이며, 손실값이 가장 큰 F′ = [f₁,f₅]에서의 R_total과 비교했을 때, F′ = [f₆,f₈]에서의 R_total 값은 거리에 따른 신호의 변동성이 확실히 줄어든 것을 확인할 수 있다.

그림 7. | Fig. 7. 주파수 조합 f′ 에 따른 R_total 및 R_ls 의 SNR 결과 | SNR results of R_total and R_ls with respect to f′.

Download Original Figure

3-2 다중빔을 이용한 각도추정 결과

앞의 연구결과에서는 f′ = [f₆,f₈]에서의 합성신호가 주파수에 대한 의존성과 변동성이 가장 작음을 정량적으로 확인하였다. 본 절에서는 f′ = [f₆,f₈]에서의 합성신호에 대해, 식 (6)을 통해 만든 다중빔을 결합한 MBMF 방법을 이용하여 다중경로 환경에서의 수신신호 각도추정을 수행한다.

다중빔 생성은 그림 4와 같으며, R_total,n은 생성된 수신빔 [B₁,B₂,B₃,B₄,B₅,B₆,B₇,B₈,B₉] 중 n번째 빔 B_n에서의 합성신호 R_total을 의미한다. 우리는 다중빔의 빔별 합성신호 크기 정보를 이용하여 빔 별 가중치 $w B n$ 를 계산하며, 이는 식 (15)와 같다.

ω B n = R t o t a l, n 2 ∑ n = 1 9 R t o t a l, n 2

(15)

이는 각 빔 별 신호크기를 보고 신호가 강한 채널의 각도정보를 상대적으로 더 신뢰하겠다는 것을 의미한다. 이렇게 얻은 가중치 $w B n$ 와 표 3의 다중빔 조향값 $u B n, v B n$ 을 이용하여 지향점 기준 각도 추정치 δu, δv 를 아래와 같이 얻을 수 있다.

δ u = ∑ n = 1 9 w B n u B n, δ v = ∑ n = 1 9 w B n v B n

(16)

식 (16)을 통해 얻은 각도추정치를 식 (10)에 대입하여 최종 표적 각도를 추정할 수 있다.

그림 8은 F′ = [f₆,f₈], F′ = [f₁,f₅] 를 이용한 MFMB 방법과 모노펄스를 이용하여 각도추정 결과이다. F′ = [f₁,f₅] 에서의 각도추정 결과의 경우, 거리 10 km부터 16 km 구간에서의 각도추정 변화가 커졌는데, 이는 그림 7(b)와 같이 합성신호 R_ls가 해당 거리구간에서 신호 변동이 큰 영향으로 보인다. 그에 반해, F′ = [f₆,f₈]에서의 R_ls는 식 (14)의 손실값이 가장 작은 경우로, 전 구간에서의 신호 변동이 적기 때문에 각도추정에서도 변화가 적으며, 실제 위치에 매우 근접함을 알 수 있다. 또한 모노펄스의 경우, 최대 0.04의 오차를 보인 반면, F′ = [f₆,f₈] 에서의 MFMB 방법을 이용한 각도추정의 경우, 최대 0.003의 각도오차를 보였다. 따라서, MFMB 방법은 다중경로 간섭의 영향에도 불구하고 정확한 각도 추정이 가능하다.

그림 8. | Fig. 8. 모노펄스 및 F′ = [f₆,f₈], F′ = [f₁,f₅] 를 이용한 MFMB 방법을 이용한 각도추정 결과 | Angle estimation results for monopulse and MFMB methods using F′ = [f₆,f₈], F′ = [f₁,f₅].

Download Original Figure

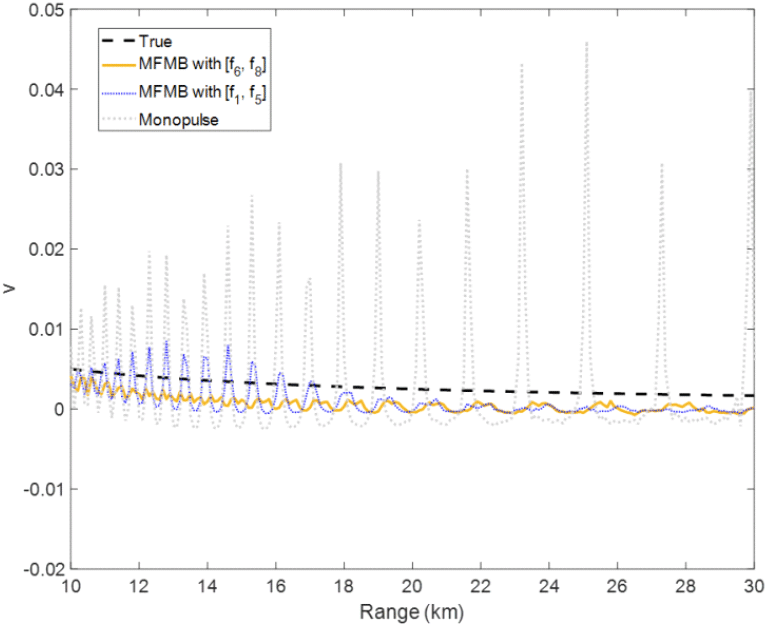
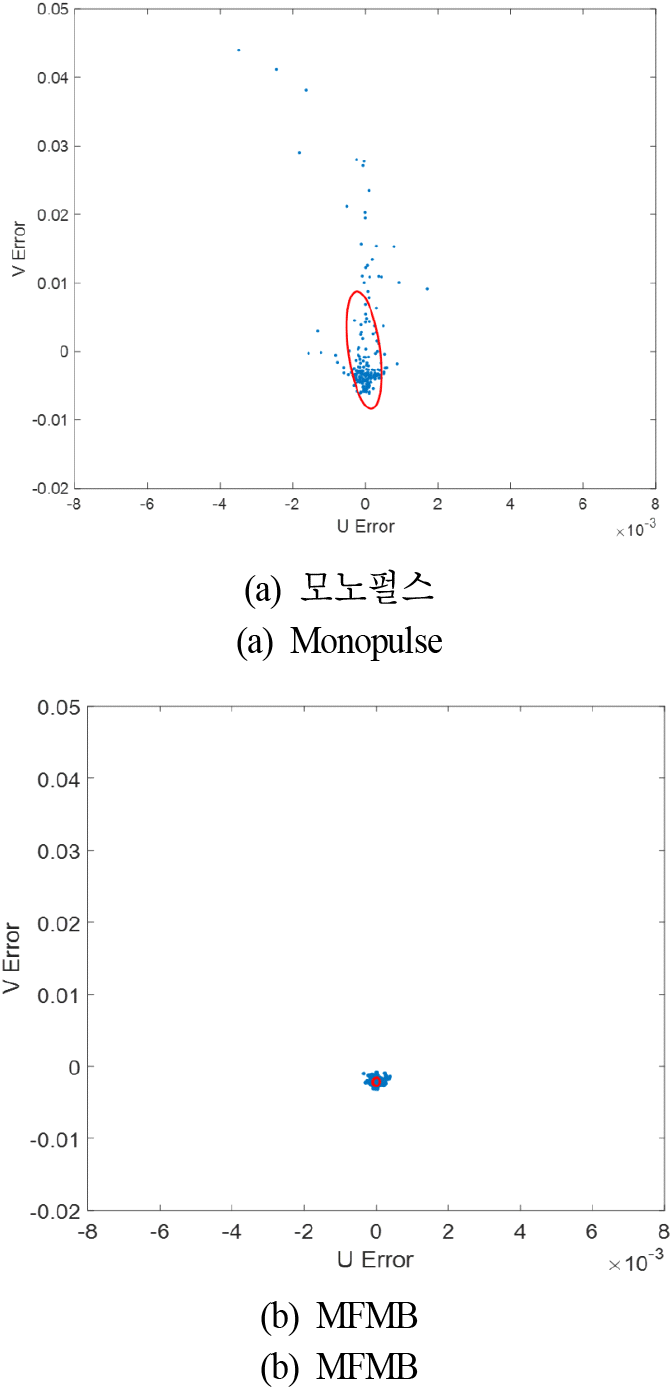
그림 9는 모노펄스 및 MFMB 방법에 대한 각각의 각도추정 결과에 대한 오차 결과이다. 그림 9(a)은 모노펄스를 이용한 각도추정 오차 결과이며, 추정오차의 평균값은 u,v 에 대해 각각 −0.0356·10⁻³ 며, 이는 다중경로 효과로 v 에 대한 각도오차가 매우 크게 나타난 것으로 보인다. 그림 9(b)는 MFMB 각도추정 오차 결과로, 추정오차의 평균값은 u,v 에 대해 각각 0,−0.0021 이다. 따라서 모노펄스에서의 각도추정 오차 평균 대비하여 에 대한 오차가 약 99% 감소하였다. 다만, 대략적인 고각 추정오차가 아래쪽 고각으로의 편향 특성을 보이는데, 이는 다중경로를 통해 들어오는 간섭 신호가 대부분 아래쪽으로 들어오는 것에 영향으로 보인다. 흥미롭게도, u 방향에 대한 오차 또한 일부 감소한 것을 확인할 수 있는데, 이는 신호 누적으로 인한 잡음 영향 감소가 신호오차를 감소시키는데 영향을 준 것으로 보인다.

그림 9. | Fig. 9. 모노펄스 및 MFMB 방법에 대한 각도추정 오차 결과 | Angle estimation error results for monopulse and MFMB methods.

Download Original Figure

IV. 결 론

본 논문에서는 저고도 표적 추적 시 해수면 반사로 인한 다중경로 간섭으로 인한 각도추정 해결하기 위해, 다중주파수와 다중빔을 결합한 MFMB(multi-frequency multi-beam) 방법을 제안하였다. 우선, 주파수별로 상이하게 나타나는 간섭 패턴을 다중주파수 신호합성을 통해 최소화하고자, 회기신호 기반 최적의 주파수 조합을 찾았으며, 이를 다중빔으로 확장하여 표적의 각도를 추정하였다. 이러한 주파수별 신호 누적 및 가중치 적용 과정을 통해 기존 모노펄스 대비 u,v 방향에 대한 각도추정 오차를 현저히 감소시킬 수 있음을 확인하였다.

References

[1].

H. Darvishi, M. A. Sebt, “Adaptive hybrid method for low-angle target tracking in multipath,” IET Radar, Sonar & Navigation, vol. 12, no. 9, pp. 931-937, Jul. 2018.

[2].

M. A. Richards, J. A. Scheer, and W. A. Holm, Principles of Modern Radar: Basic Principles, Raleigh, NC, SciTech, 2010.

[3].

M. D. Zoltowski, T. S. Lee, “Maximum likelihood based sensor array signal processing in the beamspace domain for low angle radar tracking,” IEEE Transactions on Signal Processing, vol. 39, no. 3, pp. 656-671, Mar. 1991.

[4].

K. S. Kim, M. S. Chung, and C. S. Jung, “Hybrid compensation technique on low elevation angle errors for multibeam surveillance radar in multipath environment,” Journal of the Korea Institute of Military Science and Technology, vol. 16, no. 3, pp. 365-372, Jun. 2013.

[5].

D. Kwon, H. Ko, S. Hong, B. L. Cho, K. S. Kim, and C. H. Kim, “Research of selective exponential smoothing method for estimating low-altitude target elevation in marine multipath environment,” Journal of Korea Institute of Information Technology, vol. 20, no. 9, pp. 115-123, Sep. 2022.

[6].

D. Kwon, B. Cho, K. S. Kim, and B. Lee, “Performance analysis of elevation estimation with respect to received beam grid in multipath environment,” The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 34, no. 3, pp. 190-196, Mar. 2023.

[7].

D. Kwon, H. Ko, S. Hong, K. Yoon, B. Cho, and K. S. Kim, “Elevation estimation algorithm for low-altitude targets in multipath environment,” Journal of Electromagnetic Engineering and Science, vol. 24, no. 4, pp. 341-349, Jul. 2024.

[8].

T. Lo, J. Litva, “Use of a highly deterministic multipath signal model in low-angle tracking,” IEE Proceedings F (Radar and Signal Processing). vol. 138. no. 2, pp. 163-171, Apr. 1991.

[9].

Y. Zhu, Y. Zhao, and P. Shui, “Low-angle target tracking using frequency-agile refined maximum likelihood algorithm,” IET Radar, Sonar & Navigation, vol. 11, no. 3, pp. 491-497, Mar. 2017.

[10].

J. W. Kim, J. S. Kang, J. Park, M. Park, and W. Yang, “Study of two-target elevation estimation techniques using refined ML in a multipath environment,” The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 35. no. 7, pp. 595-603, Jul. 2024.

[11].

C. H. Lee, S. M. Chon, J. Park, H. K. Na, and S. H. Kim, “Multi-frequency monopulse direction detection method for suppression of multipath effects in low-altitude sea target tracking,” The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 32, no. 3, pp. 306-314, Mar. 2021.

[12].

J. M. Joo, J. H. Lim, S. H. Hwang, J. Park, Y. D. Kang, and I. T. Han, et al., “Receiving near-field measurement of active phased array antennas applicable to full-digital multifunction radars,” The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 31. no. 2, pp. 188-199, Feb. 2020.

[13].

D. Kim, A. J. Park, U. S. Suh, D. Goo, D. Kim, and B. Yoon, “Accurate clutter synthesis for heterogeneous textures and dynamic radar environments,” IEEE Transactions on Aerospace and Electronic Systems, vol. 58, no. 4, pp. 3427-3445, Aug. 2022.

[14].

G. Strang, Introduction to Linear Algebra, Wellesley, MA, Wellesley-Cambridge Press, 2022.