압축센싱을 이용한 FMCW 레이다의 손실 신호 복원

I. 서 론

주파수 변조 연속파(FMCW, frequency-modulated continuous-wave) 레이다는 근거리 측정을 위한 레이다로써 근접신관(proximity fuze)과 전파고도계(radar altimeter)에 활용된다. 최근에는 산업 분야에서 다양한 응용 사례가 개발되고 있는데, 환자의 심장 박동과 호흡을 측정하는 실내 건강관리(indoor healthcare) 센서 제품과 자율 주행(autonomous driving)을 위한 자동차용 레이다가 대표적인 응용 사례라고 할 수 있다^[1]~[4].

FMCW 레이다는 주파수 변조를 통해 송신파에 시각 기준(timing reference)을 인코딩(encoding)하고 시간 지연된 수신파와 주파수 혼합하여 비트(beat) 신호를 측정함으로써 표적까지의 거리를 계산한다^[5],[6]. 전자파를 이용하여 표적 거리를 측정하므로 FMCW 레이다에는 외부 전자파로 인한 잡음(noise)이나 간섭(interference)이 인가될 수 있다. 군사 분야에서는 표적 탐지를 방해하기 위해 적대적 재밍(jamming)과 같은 전자파 간섭이 있을 수 있고, 산업 분야에서는 다수의 레이다 센서가 동시 운용됨으로써 각 센서 서로 간의 전자파 간섭을 일으킬 수 있다.

FMCW 레이다에서 전자파 간섭을 회피하는 방법으로는 주파수 호핑(hopping) 방법^[7]과 chirp의 기울기를 변경하는 방법^[8], 위상 코딩된(PC, phase-coded)-FMCW 신호를 송수신하는 방법이 있다^[9],[10]. 송신파의 중심주파수나 chirp의 기울기를 빠르게 변경함으로써 IF(intermediate frequency) 대역에서 전자파 간섭에 의한 비트주파수는 배제하거나, 실제 표적의 비트주파수와 전자파 간섭에 의한 비트주파수 차이를 크게 만들어 실제 표적을 구분할 수 있다. PC-FMCW 신호를 적용한 레이다는 송신파의 위상을 의사 난수 이진 수열(PRBS, pseudo random binary sequence)과 같은 코드로 변조하여 송신한 후 수신된 신호를 복조하여 전자파 간섭을 배제하고 실제 표적 신호만을 탐지할 수 있다.

기존 연구에서는 FMCW 레이다에 인가되는 협대역의 강한 전자파 간섭을 시간 축에서 실제 표적 신호와 구분하여 손실 처리함으로써 전자파 간섭이 있어도 표적 탐지·추적이 가능한 신호대잡음비(SNR, signal-to-noise ratio)를 확보하였다^[11]. 그러나 시간 축의 표적 신호가 손실된 상태로 주파수 축으로 변환하면 비트주파수 스펙트럼이 왜곡되어 표적 거리의 정확도가 낮아진다. 전자파 간섭이 있을 때도 표적 거리를 정확히 측정하고 싶다면 시간 축에서 손실 처리한 부분을 높은 정확도로 복원해야 한다. 한편, FMCW 레이다에 전자파 간섭이 인가되는 시점이나 간섭되는 주파수가 바뀜에 따라 시간 축 표적 신호의 손실과 비 손실 부분의 양상이 달라지기 때문에 비 손실 부분에서 특정 부분을 선택하여 손실 부분에 불연속 없이 이어 붙이기는 불가능하다.

아날로그 신호인 FMCW 레이다의 표적 신호는 아날로그-디지털 변환기(ADC, analog-to-digital converter)의 샘플링(sampling)을 통해 디지털 신호로 변환된다. 일반적으로 FMCW 레이다는 표적 신호를 손실 없이 복원하기 위해 나이퀴스트 샘플링(nyquist sampling)이론에 따라 최대 비트주파수의 2배보다 고속으로 샘플링한다. 만약, 복원하고자 하는 신호가 희소할 경우 낮은 차원의 관측값(measurements)만으로 높은 차원의 신호를 복원할 수 있다는 압축센싱(CS, compressive sensing)이론이 소개되었다^[12]~[13]. FMCW 레이다의 표적 신호는 시간 축에서는 희소하지 않지만, 주파수 축으로 변환하면 대부분의 값이 0(바닥 잡음 수준)이고 몇 개의 주파수 성분만 가지는 희소한(sparse)한 신호가 된다. 압축센싱 이론에 따르면 FMCW 레이다의 표적 신호를 Nyquist rate보다 적게 샘플링 하더라도 정확도 높은 비트주파수 신호를 복원할 수 있다. 압축센싱을 통한 FMCW 레이다 표적 신호의 복원을 위해서는 sub-Nyquist 샘플링이 ‘무작위(random)’로 되어야 한다. 대표적으로 random demodulator와 modulated wideband converter가 활용되며, 아날로그 신호를 고속 PRBS와 혼합(mixing), 압축(integration)한 후에 저속 샘플링 함으로써 무작위성이 구현된다^[14],[15]. 본 연구의 FMCW 레이다에는 무작위의 sub-Nyquist 샘플링 가능한 회로가 구성되지 않았기 때문에, 고속 샘플링된 표적 신호 중 무작위로 일부만 선택하여 전체 표적 신호를 복원해보았다. 특히, FMCW 레이다의 시간 축에서 표적 신호와 전자파 간섭을 구분하여 전자파 간섭을 손실 처리하였을 때 비 손실 부분 중 일부를 무작위로 선택한 후 손실 부분을 포함한 전체 표적 신호를 복원하는데 압축센싱을 적용하였다. 이를 통해 재밍 등의 전자파 간섭 시에도 표적 탐지·추적 및 정확한 거리 측정이 가능한 FMCW 레이다를 구현하였다.

서론에 이어 II장에서는 FMCW 레이다에 전자파 간섭이 인가될 때 표적 신호 일부를 의도적 손실 처리하였던 기존 연구 결과를 소개한다. III장에서는 표적 신호를 복원하기 위한 압축센싱 이론에 대해 정리한다. IV장에서는 전자파 간섭 시험을 수행하여 표적 신호의 손실을 모의한 후 압축센싱을 통해 전체 표적 신호를 복원한 결과를 기술한다. V장에서는 전체 내용을 종합하고 결론을 맺는다.

II. 전자파 간섭에 의한 표적 신호 손실 처리

FMCW 레이다는 주파수 축에서 신호대잡음비가 문턱값(threshold) 이상인 비트주파수를 표적 거리로 측정하는데, 전자파 간섭 때문에 바닥 잡음 준위가 상승하면 비트주파수의 신호대잡음비가 낮아져 표적 탐지에 실패할 수 있다. FMCW 레이다의 변조 대역폭 내 재밍이 인가되었을 때 시간 축 신호를 그림 1(a), 주파수 축 신호를 그림 1(b)에 나타내었다. 재밍과 같은 전자파 간섭이 인가되었을 때 주파수 축에서는 그림 1(b)와 같이 IF-대역 전체의 잡음 준위가 상승한다. 이때 주파수 축 신호만으로는 표적 탐지에 실패하는 원인이 전자파 간섭으로 인해 잡음 준위가 높아져서인지 표적 신호의 크기가 작아서인지 구분할 수 없다.

그림 1. | Fig. 1. FMCW 레이다에 재밍이 인가되었을 때 표적 신호 파형 | Target signal waveform when jamming is applied to the FMCW radar.

Download Original Figure

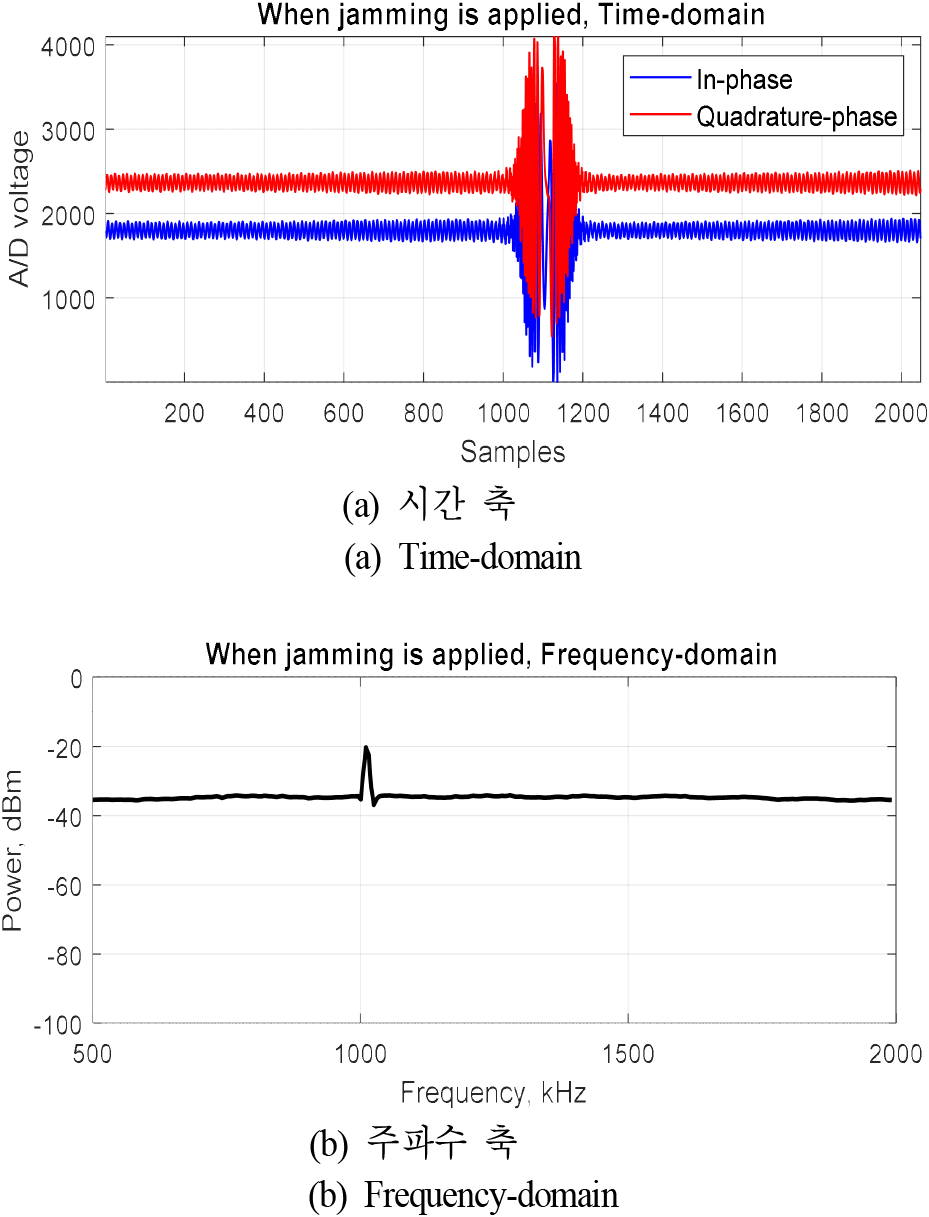
시간 축에서는 그림 1(a)와 같이 재밍이 변조 시간 대비 짧은 시간 동안 큰 진폭으로 나타난다. 시간 축에서는 표적 신호와 전자파 간섭 신호의 크기를 비교하여 임계값(critical value)을 설정할 수 있고, 임계값 이상의 신호는 전자파 간섭 신호로 보아 손실(0으로 대체)로 처리할 수 있다. 재밍이 인가되지 않은 상태로 상온(25 °C)과 고온(71 °C), 저온(−40 °C) 시험을 통해 최고 잡음 전력값(noise peak power)을 100,000번 측정하여 평균값(m)과 표준편차(σ) 값을 구하였다. 임계값은 m+3σ에 여유 10 dB를 더해 설정하였다. 최고 잡음 전력이 정규분포를 이룬다면, m+3σ 이상에는 0.14 %만 포함되고, 10배에 해당하는 안전여유가 있으므로 오경보율(false alarm rate)을 줄일 수 있다. FMCW 레이다가 재밍을 손실 처리하였을 때 시간 축 신호를 그림 2(a), 주파수 축 신호를 그림 2(b)에 나타내었다. 이처럼 시간 축에서 전자파 간섭을 손실 처리한 후 주파수 축 신호로 변환하면, 비트주파수 스펙트럼의 주업이 퍼지고(spread), 부엽(sidelobe)이 증가하는 등 파형의 왜곡이 있기는 하나 표적 탐지가 가능한 신호대잡음비를 얻을 수 있다. 하지만 신호의 일부 손실로 인해 무게중심점(centroid) 검출 등의 기법 적용 시 표적 거리의 정확도는 저하된다^[11].

그림 2. | Fig. 2. FMCW 레이다가 재밍을 손실 처리한 표적 신호 파형 | Target signal waveform when the FMCW radar discards the jamming.

Download Original Figure

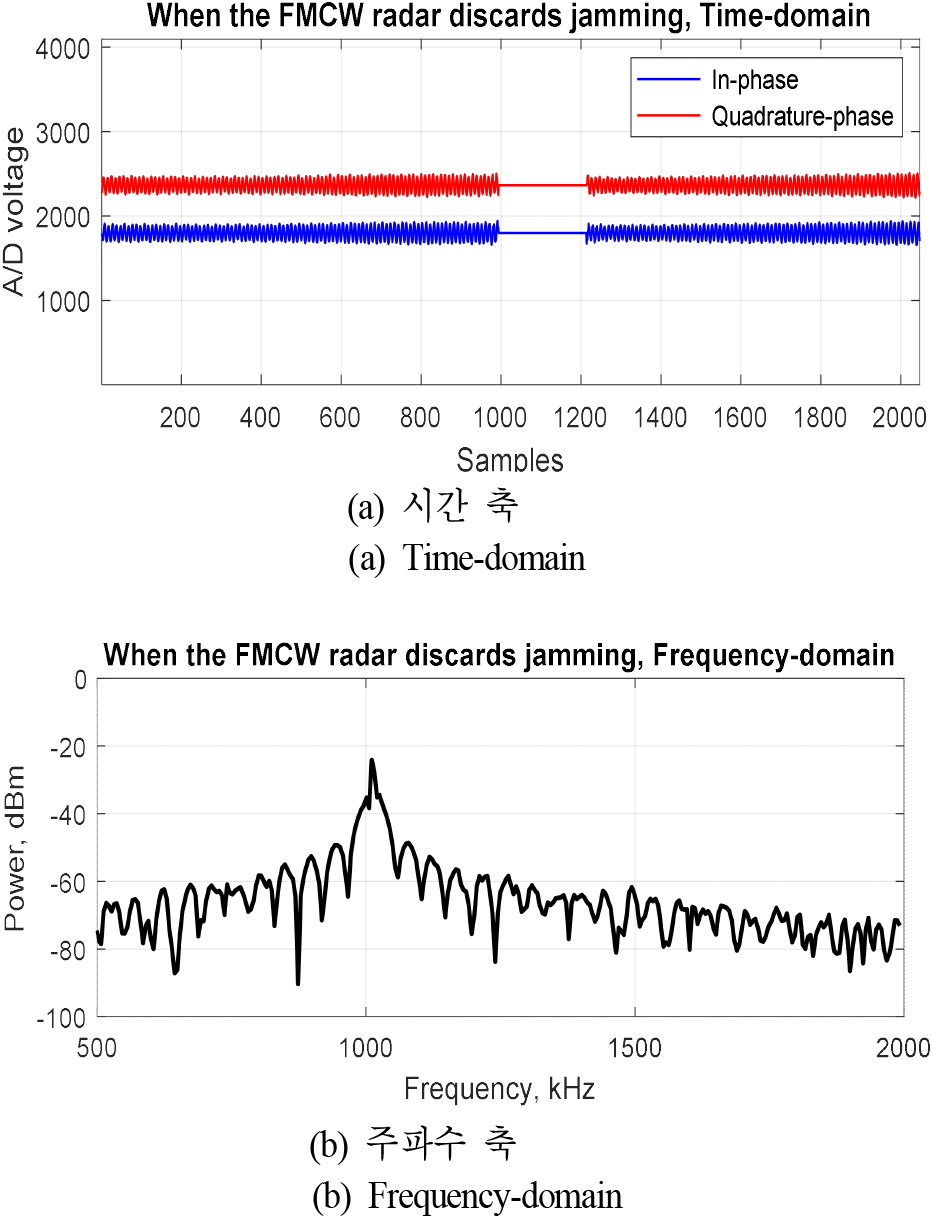
만약, 비 손실 부분의 일부 표적 신호만으로 손실된 부분을 포함한 전체 표적 신호를 원신호에 근사하게 복원한 후, 주파수 축 신호로 변환하여 전자파 간섭이 없을 때의 비트주파수 스펙트럼과 유사한 파형을 얻을 수 있다면 재밍 등의 전자파 간섭이 있을 때도 FMCW 레이다는 표적 탐지 및 정확한 표적 거리 측정이 가능할 것이다.

III. 압축센싱 이론

FMCW 레이다의 비트주파수 스펙트럼은 선형 시스템의 해이다. m개의 방정식과 n개의 미지수를 가지는 선형 시스템은 식 (1)로 표현할 수 있다.

여기서, $\overrightarrow{x}\in R^m$ 은 시간 축 표적 신호 벡터, Ψ ∈ R^{m × n}는 시스템 행렬(역[inverse] 이산 푸리에 변환의[discrete fourier transform] 기저 행렬), ψ_i ∈ R^m는 기저(역 이산 푸리에 변환 행렬의 열벡터), $\overrightarrow{s}\in R^n$ 는 주파수 축 표적 신호 벡터이다. 시간 축 표적 신호 벡터 $\overrightarrow{x}$ 는 행렬 Ψ의 열벡터(기저)의 선형 결합(linear combination)으로 표현될 수 있고, $\overrightarrow{x}$ 는 Ψ로 구성되는 부분공간(subspace) 내에 존재한다.

나이퀴스트 샘플링(nyquist sampling) 이론에 따라 최고 비트주파수의 2배(nyquist rate) 이상으로 샘플링하면, 식 (1)은 과잉결정(over-determined) 시스템이 되므로 시간 축 표적 신호 벡터로부터 주파수 축 표적 신호 벡터를 정확하게 복원할 수 있다.

FMCW 레이다의 비트주파수 스펙트럼은 각 bin의 주파수를 갖는 코사인(cosine)함수를 기저(basis)로 하는 희소 벡터(sparse vector)로 볼 수 있다. 시간 축에서 측정한 표적 신호 벡터는 희소한 성질을 갖지 않지만, 주파수 축에서는 표적 신호 벡터가 표적 거리에 해당하는 기저(주파수)에서만 큰 값을 갖고, 대부분의 다른 기저에서는 바닥 잡음 수준의 작은 값을 갖는다. 주파수 축 표적 신호 벡터 중에서 크기가 작은 bin을 모두 0으로 간주하면 희소 벡터가 된다.

압축센싱 기법에 따르면 표적 신호 벡터가 주파수 축에서 희소성을 가진다면, 시간 축에서 Nyquist rate 이상으로 샘플링하지 않아도 주파수 축의 표적 신호를 복원할 수 있다^[12]. 이 경우 식 (1)은 시간 축 샘플 수(m)가 주파수 축 bin의 수(n)보다 훨씬 적은 과소결정(under-determined) 시스템이 되는데, 이 경우 일반적으로는 해가 무수히 많아서 주파수 축 표적 신호 벡터를 복원하기 어렵다. 의 영 공간(null space)을 이용하여 설명하면, 주파수 축 표적 신호 벡터 $\overrightarrow{s}$ 와 Ψ의 영 공간에 있는 모든 벡터 $\overrightarrow{u}$ 의 합인 벡터 $(\overrightarrow{s}+\overrightarrow{u})$ 도 식 (1)의 과소결정 시스템의 해가 된다. 압축센싱 기법은 복원하고자 하는 주파수 축 표적 신호 벡터가 희소 벡터라는 성질을 추가로 활용하여 $(\overrightarrow{s}+\overrightarrow{u})$ 중에서 가장 희소한(sparse) 해를 찾는다^[13].

식 (1)의 과소결정 문제는 식 (2)에 따라 제약조건을 만족하면서 l₂-norm을 최소화하는 해를 구하는 방법이 보편적으로 사용된다.

여기서, $\Vert \overrightarrow{s}{\Vert }_2={\left(\sum _{i=1}^N{\left|s_i\right|}^2\right)}^{1/2}$ 이다.

식 (2)와 같은 최적화 문제의 해는 라그랑주 승수법(Lagrangian multiplier)을 이용하여 $\overrightarrow{x}={\text{Ψ}}^T{\left({\text{ΨΨ}}^T\right)}^{-1}\overrightarrow{s}$ 와 같이 구할 수 있다. 그러나 l₂-norm의 최소화는 일반적으로 희소하지 않은(non-sparse) 해를 찾는다. 이 같은 해는 주파수 축 표적 신호 벡터의 희소성에 기반한 압축센싱에는 적합하지 않은 해이다.

제약조건을 만족하면서 가장 희소한 주파수 축 표적 신호 벡터 $\overrightarrow{s}$ 를 찾는 문제는 l₀-norm 최소화 문제로 식 (3)과 같다.

여기서, $\Vert \overrightarrow{s}{\Vert }_0$ 는 l₀-norm으로 주파수 축 표적 신호 벡터 $\overrightarrow{s}$ 가운데 0이 아닌 원소의 개수를 나타낸다.

FMCW 레이다에서 식 (3)의 해는 측정된 시간 축 표적 신호에 대해 수신전력이 0(바닥 잡음 수준)이 아닌 bin의 개수가 가장 적은 주파수 축 표적 신호로 가장 희소한 해가 된다.

식 (3)의 최적화 문제는 제약조건은 컨벡스(convex)하지만 목적함수인 $\Vert \overrightarrow{s}{\Vert }_0$ 가 컨벡스 하지 않으므로, 조합 탐색(combinatorial search)을 해야 하는 np-hard(non-deterministic polynomial time hard) 문제가 된다. 즉, 제약조건을 만족하는 희소도 1인 해를 찾고, 해가 존재하지 않으면 희소도 2인 해를 찾는 과정을 반복하면서 회소도가 최소인 해를 구할 수 있으나 $\overrightarrow{s}$ 의 차원이 증가하면 계산량이 기하급수적으로 증가하기 때문에 풀기 어렵다^[12].

l₀-norm을 식 (4)와 같이 l₁-norm으로 완화하면 컨벡스 최적화를 통해 이 문제를 해결할 수 있다.

여기서, $\Vert \overrightarrow{s}{\Vert }_1=\sum _{i=1}^N\left|s_i\right|$ 이며, l₁-norm은 l₀-norm에 가장 가까운 컨벡스 함수이다. 식 (4)는 목적함수와 제약조건이 모두 컨벡스 함수인 컨벡스 최적화 문제가 되며 탐욕 알고리즘(greedy algorithm)이나 컨벡스 프로그래밍(convex programming)을 이용하여 해를 구할 수 있다^[16],[17].

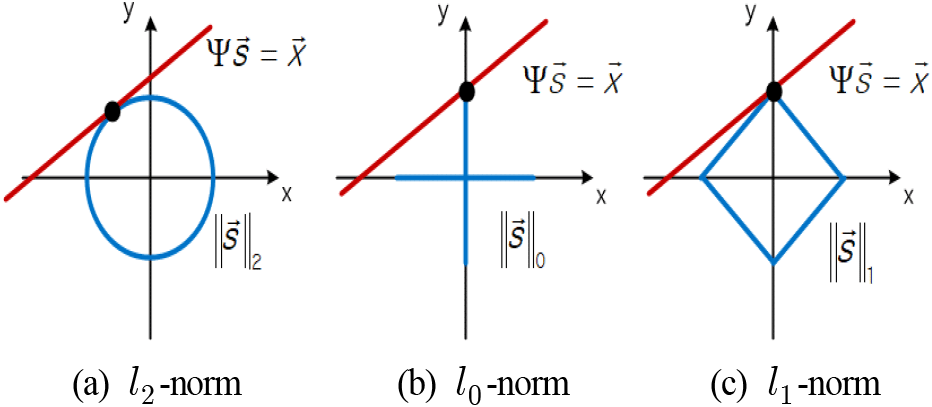
식 (2)~식(4)의 l₂,l₀,l₁-norm 최소화 문제를 그림 3과 같이 2차원 공간에 나타내었다. l₂-norm이 일정한 벡터의 집합은 둥근 l₂-구(ball)의 표면에 위치하고, l₀-norm이 일정한 벡터의 집합은 축 상에 위치한다. l₁-norm이 일정한 벡터의 집합은 마름모형의 l₁-구의 표면에 위치한다. 제약조건은 행렬 Ψ에 의해 가능한 해의 집합으로 그림 3에서 직선으로 표현된다. 식 (2)의 l₂-norm 최소화 문제에서는 이 직선이 최소 크기의 l₂-구와 만나는 지점이 해가 되는데 이 경우 제약조건을 만족시키는 해가 축 상에 나타난다는 보장이 없다. 식 (3)의 l₀-norm 최소화에서는 축 상에 해를 찾아서 원신호를 복원할 수 있다. 식 (4)의 l₁-구는 마름모꼴이기 때문에 제약조건을 만족시키는 해가 마름모의 꼭지점인 축 상에 나타난다. 이는 l₁-norm 최소화 문제의 해가 희소하다는 것을 의미하고, 이를 통해 식 (3)의 l₀-norm 최소화 문제를 식 (4)의 l₁-norm 최소화 문제로 완화해서 풀 수 있다는 것을 알 수 있다.

그림 3. | Fig. 3. l₂,l₀,l₁-norm 최소화 문제의 시각화 | Visualization of the l₂,l₀,l₁-norm minimization problems.

Download Original Figure

IV. 전자파 간섭 시험 및 손실 신호 복원

FMCW 레이다 운용 중 재밍이 인가되는 상황을 가정하고 전자파 간섭 시험을 수행하여 표적 신호에 손실이 발생하는 과정을 모의한 후, 압축센싱 기법을 적용함으로써 비 손실 부분만으로 원신호에 가깝게 표적 신호를 복원해 보았다.

4-1 FMCW 레이다의 전자파 간섭 시험

전자파 간섭(재밍) 시험에 사용한 FMCW 레이다는 최대 300 MHz의 변조 대역폭을 가지며, 표적 거리에 따라 변조 대역폭이 변경된다. FMCW 레이다는 표적 거리를 측정하기 위해 두 번의 주파수 변조 스윕(sweep)을 수행한다. 첫 번째 스윕 시에는 전자파를 송신하지 않고, 수신만 하면서 재밍 등의 전자파 간섭 신호가 있는지 확인하고, 두 번째 스윕 때만 전자파를 송신하며, 표적에서 반사되는 신호를 수신하여 표적 거리를 측정한다. FMCW 레이다의 변조 주기는 250 μs이고, IF-대역은 500~2 MHz 비트 신호의 최고 주파수가 2 MHz이다. 아날로그-디지털 변환기(ADC, analog-to-digital converter)는 12 bit 해상도, 10 MHz의 주파수로 샘플링하고, 변조 주기 내에 샘플 수가 2,048개이다. 전자파 간섭이 없다면, 나이퀴스트 샘플링 이론에 따라 최고 주파수의 2배보다 훨씬 큰 10 MHz의 주파수로 샘플링했으므로 앞 장에서 논의하였던 과잉결정 시스템이 되어 시간 축 표적 신호로부터 주파수 축표적 신호를 완전히 복원할 수 있다. 그러나 전자파 간섭이 있는 경우 그림 1과 같이 시간 축 표적 신호에 큰 진폭의 잡음이 혼재하여 주파수 축에서 표적 신호의 신호대잡음비가 감소하고, 그림 2에 나타낸 바와 같이 시간 축에서 임계값 이상의 잡음을 전자파 간섭으로 간주하여 손실 처리하면 주파수 축 표적 신호가 왜곡되어 표적 거리 측정에 오차가 발생할 수 있다.

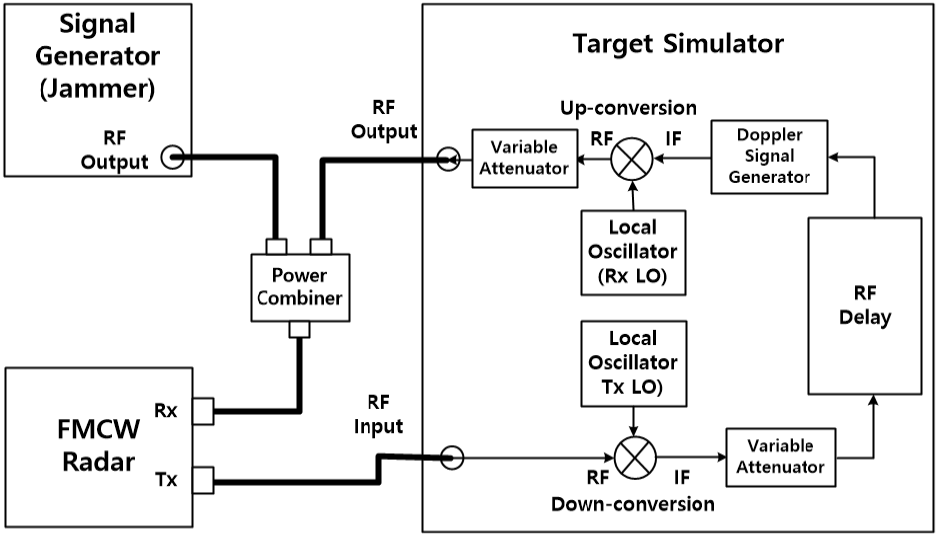
FMCW 레이다의 전자파 간섭 시험을 위한 구성을 그림 4에 나타내었다. 표적모의장치(target simulator)는 FMCW 레이다의 송신기로부터 RF 신호를 받아 RF 신호지연부를 통해 시간 지연해 표적 거리를 모의하고, 도플러 신호발생기를 통해 표적의 속도를 모의한다. 가변 감쇠기를 활용하여 표적의 레이다 단면적(RCS, radar cross section) 및 표적 거리에 따른 신호의 감쇠를 모의한 후 FMCW 레이다의 수신기로 표적 모의 신호를 인가한다. 신호발생기(signal generator)를 이용하여 FMCW 레이다의 수신기로 변조 주파수 대역 내에 협대역의 재밍을 인가한다. 표적 모의 신호와 재밍을 전력 결합기(power combiner)를 통해 결합하여 FMCW 레이다의 수신기에 인가한다. 표적모의장치를 이용하여 표적 거리를 200 m로 설정하고, 상대속도에 의한 도플러 편이는 설정하지 않았다. 표적 거리 200 m일 때 FMCW 레이다의 변조 대역폭은 115.4 MHz이다. FMCW 레이다는 변조 주기 250 μs 동안 f₀~f₀ + 115.4 MHz를 스윕하고, 변조 대역폭 내 중심주파수와 같은 f₀ + 57.7 MHz 주파수의 연속파(continuous wave) 재밍 신호를 수신기 내 I/Q(in-phase/quadrature-phase)-혼합기(mixer)의 P1dB를 고려하여 −50 dBm의 전력으로 인가하였다. 표적 신호의 수신전력은 −50 dBm 재밍에 의해 잡음 준위가 상승하여 표적 탐지에 실패하는 수준이 되는 −70 dBm을 인가하였다. 수신기의 수신 이득은 50 dB이다.

그림 4. | Fig. 4. 전자파 간섭(재밍) 시험 구성 | Configuration of the electromagnetic interference (jamming) test.

Download Original Figure

4-2 압축센싱에 기반한 손실 신호 복원

FMCW 레이다는 첫 번째 스윕에서 표적 신호가 없을 때 시간 축에서 임계값 이상의 큰 진폭의 잡음이 인가되면 이를 재밍 등 전자파 간섭으로 간주하고, 이 시점을 저장해두었다가 두 번째 스윕 시 시간 축 표적 신호와 전자파 간섭이 혼재할 때 첫 번째 스윕에서 저장하였던 시점에 해당하는 부분을 의도적으로 손실 처리한다. 그림 5(a)에는 아날로그-디지털 변환기의 오프셋(offset) 전압 제거하고, 재밍 때문에 왜곡된 부분을 손실 처리한 후의 시간 축 표적 신호와 압축센싱을 위해 무작위로 선택한 데이터를 표시하였다. 총 250 μs 변조 주기 내 2,048개 샘플 가운데 약 11 %에 해당하는 220개 샘플이 임계값을 넘어 손실 처리되었다. 변조 시간 250 μs 동안 변조 대역폭 115.4 MHz 중 11 %가 손실 처리되었으므로, 재밍 대역폭은 12.7 MHz라 볼 수 있다. 비 손실로 남은 1,828개 샘플 가운데 10 %인 182개의 샘플을 압축센싱 연산을 위해 무작위로 선택하였다. 컨벡스 프로그래밍을 풀 수 있는 CVX 패키지에 선택된 샘플을 입력하여 식 (4)의 l₁ - norm 최소화 계산을 수행하였다^[17]. 그림 5(b)는 압축센싱 연산 결과 복원된 시간 축 표적 신호를 나타낸 것으로 220개의 손실된 샘플을 포함하여 전체가 복원된 것을 알 수 있다. In-phase 표적 신호의 경우 양 끝 쪽 샘플의 복원 결과에 오차가 있어 보이는데, 무작위 선택 시 양 끝 쪽 샘플이 비교적 적게 선택된 결과로 생각된다. 이산 푸리에 변환 시 해닝 윈도우(hanning window)를 적용한 후 변환하므로 양 끝 쪽의 샘플이 비트주파수 스펙트럼에 미치는 영향은 미미하다.

그림 5. | Fig. 5. 시간 축 표적 신호 | Time-domain target signals.

Download Original Figure

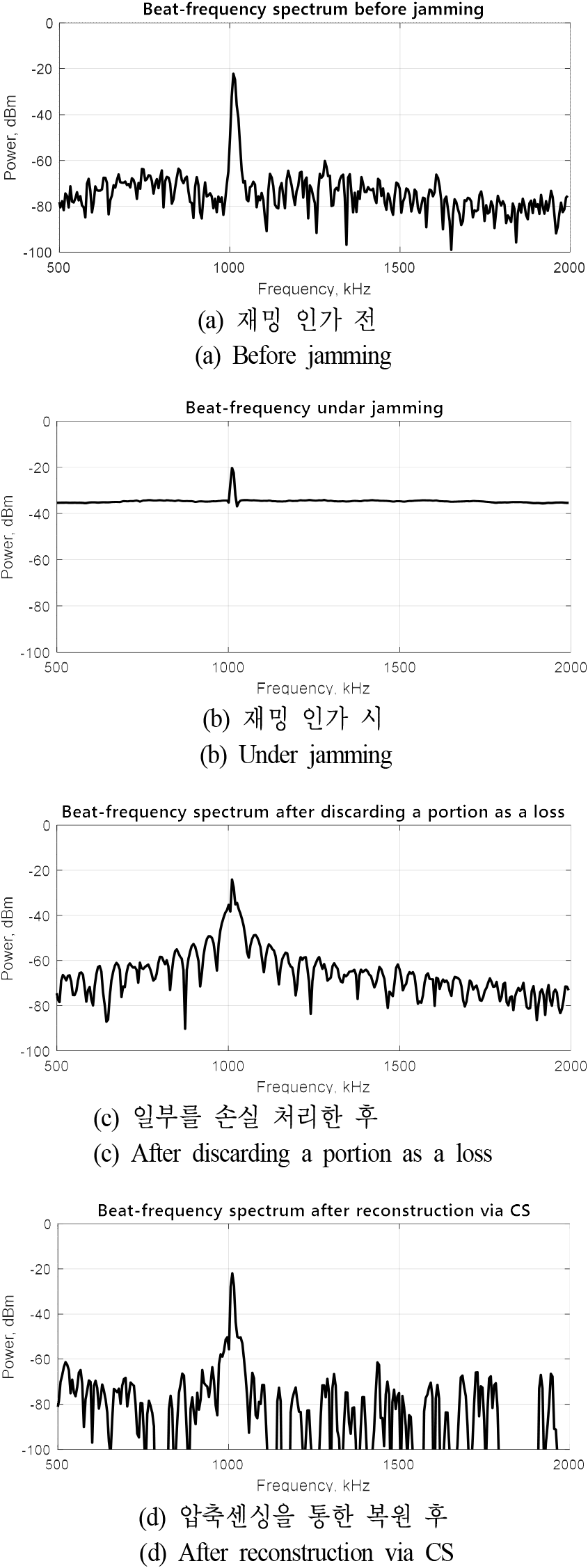
FMCW 레이다는 시간 축 표적 신호를 이산 푸리에 변환하여 비트주파수 스펙트럼으로 나타낸 후 신호대잡음비가 큰 비트주파수를 표적 거리로 측정하므로, 재밍 인가 전과 재밍 인가 후, 압축센싱을 통한 복원 후의 비트주파수 스펙트럼을 비교해야 표적 신호의 복원 성능을 확인할 수 있다. FMCW 레이다가 200 m 거리의 모의 표적을 추적하는 중 재밍 인가 전의 비트주파수 스펙트럼을 그림 6(a)에, 재밍 인가 시의 비트주파수 스펙트럼을 그림 6(b)에, 재밍 인가 시 임계값 이상을 손실 처리한 후의 비트주파수 스펙트럼을 그림 6(c)에, 압축센싱을 통해 복원된 후의 비트주파수 스펙트럼을 그림 6(d)에 나타내었다. 그림 6(a) 및 그림 6(b)를 비교하면 재밍 인가 시 바닥 잡음 준위의 상승으로 인해 신호대잡음비가 38 dB에서 14 dB로 감소하였다. 그림 6(b) 및 그림 6(c)를 비교하면, 재밍을 손실 처리한 후 신호대잡음비가 24 dB 수준으로 개선되었으나, 비트주파수 스펙트럼의 파형 왜곡이 발생한다. 이에 반해 그림 6(a) 및 그림 6(d)를 비교하면 양쪽 모두 비트주파수의 첨두전력은 −22 dBm 수준이었고, 잡음의 첨두전력이 −60 dBm 수준으로 압축센싱을 통한 표적 신호 복원 결과 38 dB의 신호대잡음비가 유지되었다. 압축센싱 연산 시에는 데이터가 무작위로 선택되므로 매번 비트주파수 스펙트럼이 조금씩 달라지지만, 여러 번을 시행해도 신호대잡음비가 저하되는 정도가 재밍 인가 전과 비교하였을 때 3 dB 이하였다. 첨두전력을 포함하고 있는 스펙트럼의 형태가 조금 달라졌지만, 무게중심점 검출 기법 적용 시 그림 6(a)의 재밍 인가 전의 표적 거리는 200.7 m이고, 그림 6(d)의 압축센싱을 통한 복원 후의 표적 거리는 199.9 m로 표적 거리의 차이가 해상도(resolution)인 1.6 m 이내였다. 이에 비해 그림 6(b)에서는 문턱값이 바닥 잡음보다 낮아 표적 거리 측정이 되지 않았으며, 그림 6(c)에서는 표적 거리가 193.3 m로 계산되었다. 비트주파수 스펙트럼의 주엽의 퍼짐과 부엽의 증가가 표적 거리 오차의 원인이다.

그림 6. | Fig. 6. 비트주파수 스펙트럼 | Beat-frequency spectrum.

Download Original Figure

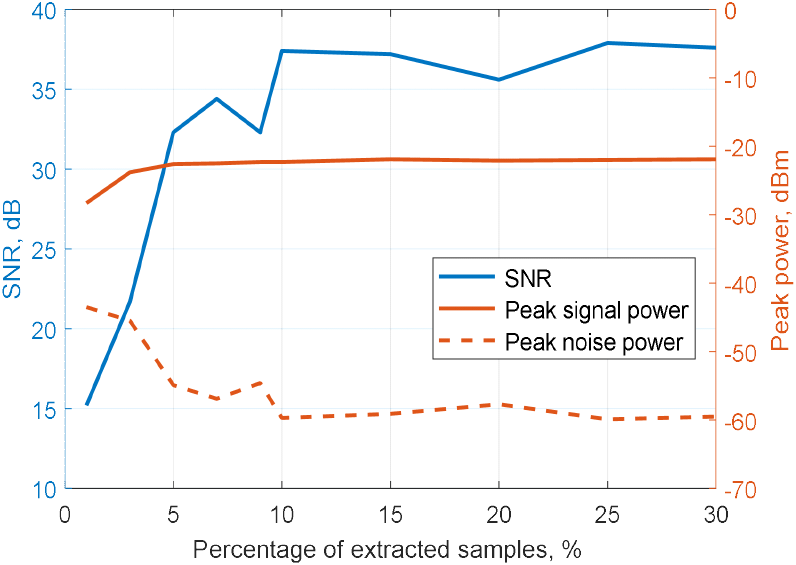
시간 축 표적 신호 내 비 손실 부분의 샘플을 선택하는 비율 대 비트주파수 스펙트럼의 신호대잡음비를 그림 7에 나타내었다. 비 손실 부분에서 전체 샘플 수 대비 선택하는 샘플 수의 비율을 변경하며 계산해 본 결과 10 % 이상 선택하면 재밍 인가 전과 유사한 신호대잡음비를 얻을 수 있었다.

그림 7. | Fig. 7. 선택된 샘플의 비율 대 신호대잡음비 | Proportion of selected samples vs. SNR.

Download Original Figure

주파수 축 표적 신호 벡터 $\overrightarrow{s}$ 의 차원(bin 수)은 2,048이고, 각 원소의 크기가 10⁻³ 이하이면 0으로 간주하였을 때 $\overrightarrow{s}$ 의 희소도는 in-phase에 대해서는 102, quadrature-phase에 대해서는 86이었다. 압축센싱 이론에 따르면 l₁ - norm 최소화를 이용할 때 길이가 N이고 희소도가 K(K-sparse)인 신호에 대해 식 (5)와 같이 M개 이상의 무작위 관측값이 있으면 높은 확률로 정확한 신호의 복구가 가능하다^[12].

$$M\ge Klog\left(\frac{N}{K}\right)$$

(5)

여기서, M은 관측값의 개수, N은 신호의 차원, K는 신호의 희소도이다.

식 (5)에 따라 계산하면 희소도 102, 86의 표적 신호의 경우 필요한 관측값의 개수는 305개, 273개이다. 이는 시간 축 표적 신호의 전체 샘플 수 2,048개 대비 13~15 % 수준으로 재밍 인가에 의해 일부 신호 손실이 있었음에도 비 손실 부분의 10 %의 샘플을 선택하였을 때 재밍 인가 전과 유사한 비트주파수 스펙트럼이 복원되었던 그림 6의 결과를 설명할 수 있다.

이 결과는 FMCW 레이다에 무작위로 샘플링 할 수 있는 sub-Nyquist 아날로그-디지털 변환기를 적용하여 샘플링 속도를 현재의 1/5~1/10 수준으로 감소시켜도 정확성 높은 비트주파수 스펙트럼을 얻을 수 있음을 의미한다. 향후 FMCW 레이다 신호처리의 연산 능력 향상에 따라 이러한 기술이 적용되면, 고속 샘플링에 대한 하드웨어적인 부담은 줄이고 소프트웨어적인 방법으로 성능 향상을 꾀할 수 있을 것이다.

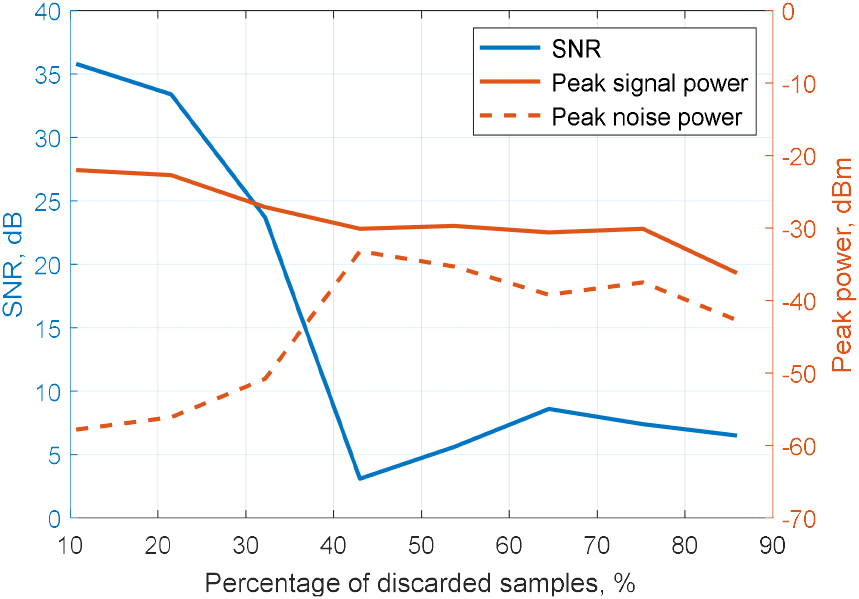
재밍에 의해 손실로 처리되는 시간 축 표적 신호의 비율 대 비트주파수 스펙트럼의 신호대잡음비를 그림 8에 나타내었다. 시간 축 표적 신호와 재밍이 혼재할 때 변조 대역폭 115.4 MHz이고 재밍 대역폭이 변조 대역폭의 30 %인 34.6 MHz 이상이면, 변조 시간 250 μs 동안 204.8 μs (2,048 샘플) 중 61.4 μs (615 샘플) 이상이 손실로 처리되어 신호대잡음비가 급격히 저하될 것임을 예상할 수 있다. 표적 거리가 멀어져 변조 대역폭이 줄어들면, 재밍 대역폭이 협대역이라 하더라도 전체 샘플 수 대비 재밍에 의해 손실 처리되는 샘플 수의 비율이 높아져 압축센싱을 이용한 표적 신호 복원 성능이 저하될 것이므로 주파수 호핑(frequency hopping)의 등 추가적인 전자파 간섭회피 방안도 고려하여야 할 것이다.

그림 8. | Fig. 8. 손실 처리되는 샘플의 비율 대 신호대잡음비 | Proportion of discarded samples vs. SNR.

Download Original Figure

V. 결 론

FMCW 레이다에 전자파 간섭이 인가될 때 시간 축에서 표적 신호와 전자파 간섭 신호를 구분하여 의도적 손실 처리한 후 주파수 축 변환하면 비트주파수 스펙트럼의 신호대잡음비가 확보되어 표적 탐지가 가능하지만, 주엽의 퍼짐과 부엽 상승 등 비트주파수 스펙트럼 파형의 왜곡으로 인해 표적 거리의 정확도는 저하된다. FMCW 레이다의 표적 신호에 손실이 발생하였을 때 압축센싱 기법을 활용하여 전체 표적 신호를 복원할 수 있다면 전자파 간섭이 있을 때도 정확한 표적 거리 측정이 가능하다. 비 손실 부분의 표적 신호 일부를 무작위로 선택하여 l₁-norm 최소화 연산을 수행하면 시간 축 표적 신호의 손실 부분을 포함한 전체 표적 신호를 복원할 수 있고, 이를 이산 푸리에 변환함으로써 전자파 간섭이 없을 때와 유사한 비트주파수 스펙트럼 파형과 신호대잡음비를 얻을 수 있다.

표적모의장치와 신호발생기를 이용하여 FMCW 레이다가 200 m 거리의 표적을 탐지하는 중 재밍과 같은 전자파 간섭 신호가 인가되는 상황을 모의하였다. FMCW 레이다의 변조 대역폭 내 중심주파수와 같은 주파수를 갖는 협대역 재밍을 인가하였을 때 수신 신호에 시간 축 표적 신호와 재밍 신호가 혼재하는 상황에서 총 샘플 수의 11 %에 해당하는 임계값 이상의 샘플이 손실 처리되었다. 남은 비 손실 샘플 중에서 10 %를 무작위 선택하고 압축센싱을 통해 표적 신호를 복원한 결과 재밍 인가 전과 유사한 비트주파수 스펙트럼과 신호대잡음비를 얻을 수 있었다. 선택되는 무작위 샘플의 수를 바꾸어 가며 계산해 본 결과 비 손실 샘플의 개수 중 10 % 이상 선택하여 복원하면 재밍 인가 전과 유사한 신호대잡음비를 얻을 수 있었다. 전체 샘플 수 대비 재밍 때문에 손실 처리되는 샘플 수의 비율을 변경하며 계산해 본 결과 변조 대역폭 대비 재밍 대역폭이 30 % 이하일 때 손실 처리되는 샘플이 30 % 이하가 되어 신호대잡음비의 유지가 가능하였다.