Ⅰ. 서 론
전력증폭기(PA, power amplifier)는 전력 이용 효율의 관점에서 디지털 무선 전송 시스템을 구성하는 중요한 요소 중 하나이다. 예를 들어 5G 기지국에서 PA는 기지국 전체 전력 소비의 약 50~80 %를 차지한다[1]. 전력 효율적인 PA의 운용은 현저한 비선형 동작 특성을 동반하며, 따라서 PA의 선형성 개선을 위한 여러 가지 방식의 다양한 연구가 수행되고 있다[1],[2]. 그중 범용성과 우수한 선형성 개선 효과로 디지털 사전왜곡기(DPD, digital predistorter) 방식이 널리 사용되고 있다. DPD의 설계 및 구현에는 다양한 모델이 적용되고 있으며, 메모리 다항식(MP, memory polynomial) 모델과 심층 신경망(DNN, deep neural network) 모델이 주류를 이루고 있다[2]. 머신 러닝 분야에서는 PA 입력 신호에 대한 출력을 측정하여 DPD 모델 학습을 위한 훈련 데이터로 이용한다. PA 특성이 변하면 새로 측정한 데이터를 기반으로 DPD 모델의 재학습이 필요하며, 이를 보완하기 위해 PA 동작 중 획득한 부분 데이터를 활용한 온라인 학습 방식이 고려된다. DPD에 MP 모델을 적용하는 경우, 온라인 또는 실시간 학습이 가능한 시스템을 FPGA 등으로 구현하려는 다양한 연구가 수행되고 있다[1]. 그러나 DNN 모델의 경우 합성곱 신경망(CNN, convolutional neural network), 순환 신경망(RNN, recurrent neural network) 등 다양한 신경망 구조의 도입으로 PA 선형화 성능은 개선되고 있으나, 학습 알고리즘의 복잡도가 증가함에 따라 여전히 오프라인 학습에 의존하고 있다[2].
PA의 특성 변화는 인위적 요인과 자연적 요인으로 구분할 수 있다. 입력 신호 대역폭, 반송파 주파수, PA 공급 전압의 변경은 특정 목적에 따라 발생하는 인위적 요인에 해당한다. 반면, 시간 경과에 따른 PA 동작 환경의 변화나 계측 오차로 인한 입력 신호 레벨의 변화는 자연적 요인으로 볼 수 있다. 대부분의 DNN 기반 DPD 연구에서는 PA 출력 신호를 측정해 DPD를 학습시킨 후, PA 특성이 일정하게 유지되는 조건에서 성능을 평가한다. 하지만 오프라인 학습에 의존하는 특성상, PA 특성 변화로 인한 선형화 성능 저하는 피할 수 없으며 이에 대한 정량적 분석이 요구된다. 본 논문에서는 한 달 구간에서 측정된 PA 출력 데이터를 이용하여 DPD를 학습시킨 후, 측정 시점이 다른 데이터로 학습한 PA 모델에 적용하여 시간 경과에 따른 PA 특성 변화가 선형화 성능에 미치는 영향을 분석한다. 또한, 계측 오차로 인한 입력 신호 레벨 변화가 선형화 성능에 미치는 영향도 고찰한다.
Ⅱ. 블록 처리 DNN 구조
PA 및 DPD 모델링을 위해 DNN 기반의 다양한 신경망 구조가 활용되고 있다. DNN에서 입력 데이터는 샘플 단위 또는 블록 단위로 처리될 수 있다. 특히, 신호 처리 시스템에서 블록 단위 처리는 특정 알고리즘의 고유 특성에 따라 필수적으로 요구되기도 한다. 또한, 시스템을 하드웨어로 구현 시 DMA(direct memory access) 채널을 이용하는 경우에도 블록 처리 방식은 효율적인 구현 방안으로 간주된다.
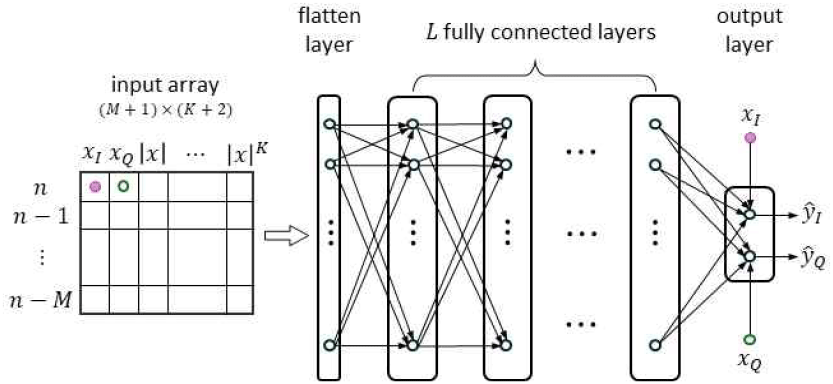
그림 1에 PA 및 DPD에 대한 DNN 모델 구조를 나타내었다. 시점 n에서 입력 샘플 x(n)=xI(n)+jxQ(n)으로 표시하면, DNN에 대한 입력은 PA 비선형성에 대한 차수 K와 메모리 효과에 대한 시간 지연 M을 고려하여 그림 1에서와 같이 크기가 (M+1)×(K+2)인 2차원 배열로 나타낼 수 있다. DNN은 입력 배열과 연결된 은닉층(L개 층)과 출력층으로 구성된다. 각 은닉층은 D개의 뉴런을, 출력층은 2개의 뉴런을 포함한다. 모든 층들은 이전 층들과 가중치로 완전 연결(fully connected)되어 순방향 DNN 구조를 형성한다. 입력 배열에 포함된 모든 데이터를 첫 번째 층에 연결하기 위해 flatten layer를 사용하였다. 또한, 입력 신호가 출력에 직접 연결되는 바이패스 경로를 추가하여, DNN은 출력과 입력의 차이, 즉 비선형 왜곡 성분만을 집중적으로 모델링하도록 설계되었다.
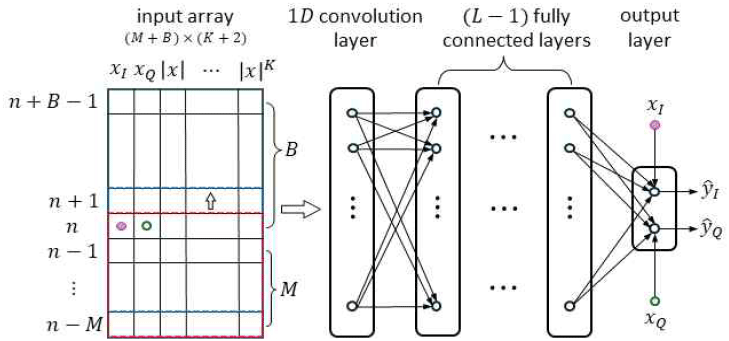
그림 2에 블록 처리를 위해 수정된 DNN 구조를 도시하였다. 점선으로 표시된 사각형 안의 데이터가 입력 샘플 x(n)에 해당하며 사각형이 한 번에 한 칸씩 위로 이동하면서 B개의 입력 샘플을 차례로 처리하는 블록 구조를 형성한다. 이러한 방식으로 동작하기 위해서 그림 1에서 입력 배열과 연결된 첫 번째 완전 연결 층을 그림 2와 같이 1차원 합성곱 층(1D convolution layer)으로 대치하였다. 합성곱 층은 일반적으로 가중치 공유(weight sharing)를 통한 특성 추출에 주로 사용되지만, 이 경우에는 입력 배열의 크기를 줄이기 위하여 가중치 재사용(weight reuse)의 개념으로 도입하였다[3]. 그림 1의 DNN에서는 입력 샘플당 요구되는 입력 배열의 크기는 블록의 크기와 상관없이 (M+1)(K+2)가 된다. 그러나 그림 2의 합성곱 층을 이용한 DNN에서는 B개의 샘플을 블록 처리하기 위한 입력 배열의 크기는 (M+B)(K+2)가 되며, 따라서 샘플당 요구되는 입력 배열의 크기는 (M/B+1)(K+2)가 된다. 블록의 크기 B를 메모리 효과 관련 상수 M보다 충분히 크게 설정하는 경우, 입력 배열을 저장하기 위한 메모리 공간이 약 (M+1)분의 1로 크게 감소하는 효과를 얻을 수 있다.
Ⅲ. DPD 기반 PA 성능 분석
PA 및 DPD에 대한 DNN 모델을 학습하기 위한 훈련용 데이터는 실제 PA 데이터를 원격으로 측정할 수 있는 RF WebLab을 이용하여 수집한다[4]. 전력증폭기의 최대 출력은 약 6 W이며, 중심주파수 2.14 GHz에서 최대 대역폭 160 MHz로 운용이 가능하다. 본 논문에서 PA 입력 신호는 10,000개의 1024-QAM 심볼 블록을 rolloff factor 0.2의 square-root raised cosine 펄스를 이용하여 생성하였으며 신호의 대역폭은 40 MHz로 설정하였다. 기본 측정에서 입력 신호 레벨은 −21 dBm으로 설정하여 PA 출력은 약 29 dBm으로 측정되었다. DPD 기반 PA 선형화 성능은 두 가지 항목으로 구분하여 대역내 전송 신호에 대한 성능은 EVM으로, 대역외 스펙트럼 누설에 의한 인접 채널 간섭 성능은 ACPR로 평가한다.
DNN 모델의 은닉층은 2개 층으로 구성되며, 각 층은 20개 뉴런을 포함한다. PA 비선형성에 대한 차수 K는 0으로, 메모리 효과에 대한 시간 지연 M은 신호의 해당 대역폭에서의 PA 특성을 반영하여 4로 설정하였다. DNN 학습에서 학습율은 초깃값 0.001에서 1,000회 학습마다 1/2, 1/3, ··· 로 감소하는 방식을 사용하였으며 조기 종료 관련 파라미터 tolerance=10−10, patience=50으로 설정하였다. 미니 배치의 크기는 32, 훈련 데이터 중 검증용 데이터 비율은 20%, 고속 옵티마이저로는 Adam을 사용하였다. DNN 학습에는 완전 연결형 DNN 모델을 사용하였으며, 학습 후에는 블록 처리 방식의 합성곱 DNN 모델로 변환하여 성능 평가에 이용하였다.
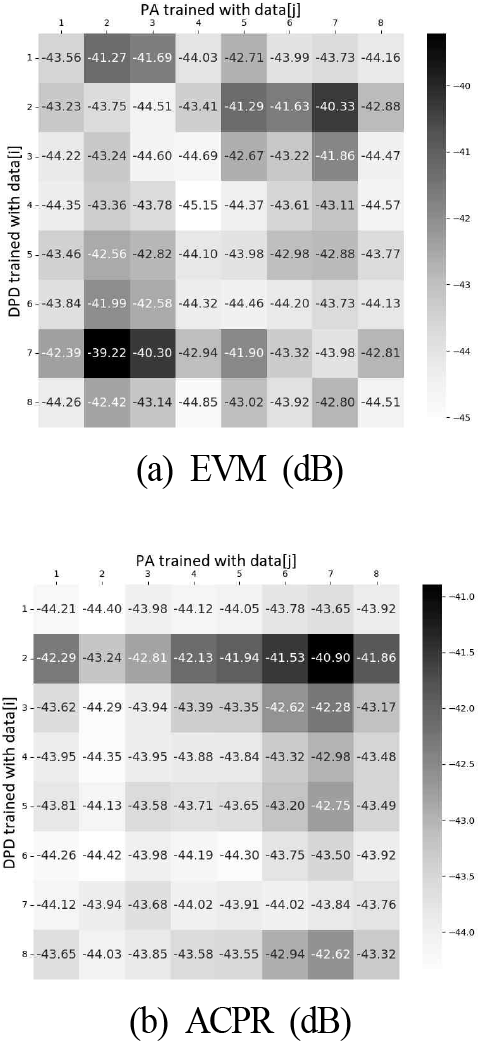
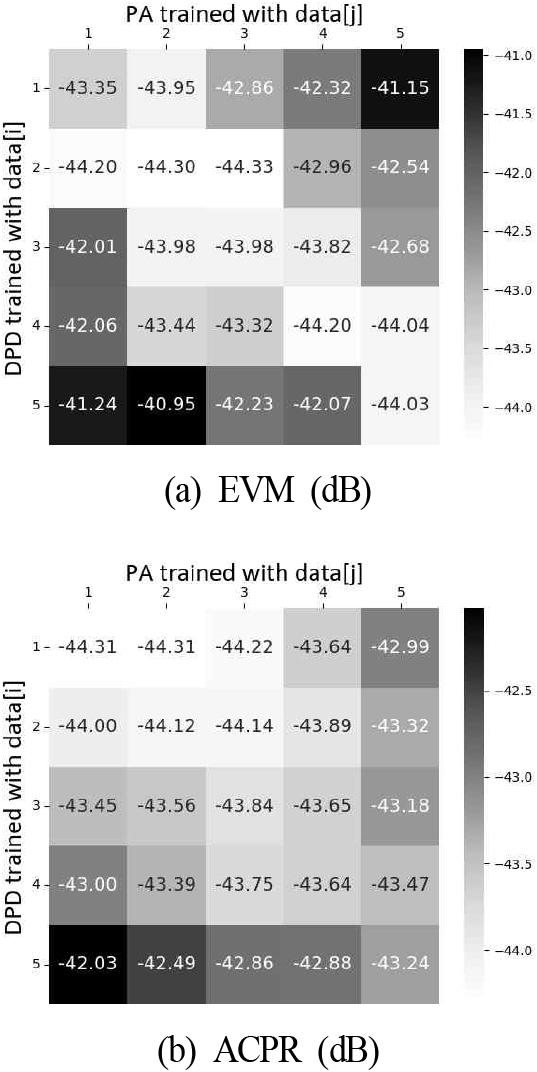
PA 출력 데이터는 한 달 구간에서 총 8회에 걸쳐 무작위 시점에서 측정하였다. 각 측정 시마다 2번 반복 측정하여 하나는 훈련용 데이터로 다른 하나는 시험용 데이터로 사용하였다. 총 8회 측정한 PA 데이터를 편의상 측정 시간 순서로 data [1], ··· , data [8]로 표시한다. 그림 3에 시간 경과에 따른 전송 신호의 EVM과 ACPR 변화를 나타내었다. 그림 3에서 data[i]로 학습한 DPD를 사용하여 data[j]로 학습한 PA로 평가한 EVM과 ACPR 값을 (i,j) 위치에 표시하였다. PA 특성 변화가 발생하지 않은 조건에서 평균 EVM은 −44.22dB로 평가되었다. 반면, PA 특성 변화가 발생한 경우의 평균 EVM은 −43.13 dB로 분석되었으며, 이는 특성 변화에 따른 1.09 dB의 EVM 성능 저하를 의미한다. PA 특성 변화가 EVM 성능에 가장 크게 영향을 미친 경우는 data [7]로 학습된 DPD 모델에 data [2]로 학습된 PA 모델을 적용하여 성능을 평가한 사례이다. 이 경우, 성능 저하는 4.76 dB로 최대 증가하였다. PA 특성 변화가 발생하지 않은 조건에서 평균 ACPR은 −43.73 dB이며, 특성 변화가 발생한 경우의 평균 ACPR은 −43.48 dB로 평가되어 특성 변화에 따른 0.25 dB의 ACPR 성능 저하를 나타내고 있다. PA 특성 변화가 ACPR 성능에 가장 크게 영향을 미친 경우는 data [2]로 학습된 DPD 모델에 data [7]로 학습된 PA 모델을 적용하여 성능을 평가한 경우이며 이에 따른 성능 저하는 2.35 dB이다. 그림 4에 입력 신호 레벨의 변화에 따른 전송 신호의 EVM과 ACPR 변화를 나타내었다. 입력 신호 레벨을 −22.0 dBm부터 −20.0 dBm까지 0.5 dB 간격으로 5단계 변화시키며 PA 출력을 측정하였다. 측정된 데이터는 편의상 data [1], ··· , data [5]로 표시한다. EVM의 평균 성능 저하는 1.16 dB, 최댓값은 3.08 dB이며, ACPR의 평균 성능 저하는 0.42 dB, 최댓값은 1.31 dB이다. CNN, RNN 등을 적용했을 때 EVM과 ACPR의 성능 개선 효과가 1~3 dB 정도[2]인 것과 비교하면 PA 특성 변화가 선형화 성능에 상당히 큰 영향을 미치는 것으로 판단된다.
Ⅳ. 결 론
PA의 특성 변화는 시간 경과에 따른 동작 환경 변화 또는 계측 오차에 의한 입력 신호 레벨 변화 등에 의해 발생할 수 있다. 본 논문에서는 이러한 특성 변화가 DPD 기반 PA 선형화 성능에 미치는 영향을 분석하였다. 한 달 구간에서 총 8회 무작위 시점에서 측정한 PA 출력 데이터와 입력 신호 레벨을 0.5 dB 간격으로 5단계 변화시키며 측정한 데이터를 DPD 및 PA 모델 학습에 이용하였다. 시간 경과에 따른 EVM과 ACPR의 최대 성능 저하는 각각 4.76 dB와 2.35 dB이며, 입력 신호 레벨 변화에 따른 최대 성능 저하는 각각 3.08 dB와 1.31 dB로 분석되었다.