I. 서 론
공항 저고도 대기에서의 급격한 바람 변화와 난류는 항공기 이착륙 안전을 직접적으로 위협한다. 이에 따라 공항 인근의 바람장을 높은 시공간 해상도로 실시간 관측하는 기술은 항공운영과 기상 경보 시스템의 핵심이다. 도플러라이다(Doppler lidar)는 안구 안전(eye-safe) 파장대의 1.5~1.6 μm 레이저를 사용하고, 지상 설치가 용이하며, 청천에서의 산란을 이용해 바람 정보를 제공할 수 있어 도심 및 공항 환경에서도 안정적으로 운용된다[1]. 상용 기종(예: Leosphere, Halo Photonics 등)의 보급으로, 도플러라이다는 연구용을 넘어 공항 활주로 주변 감시와 풍력단지 운영 등 다양한 현장 응용으로 활용 범위가 확장되었다.
라이다는 펄스 에너지를 기준으로 두 종류로 구분할 수 있다. 하나는 mJ 라이다로, 펄스 에너지가 커서 원거리(수 km에서 10 km 이상)까지의 바람장을 관측할 수 있다. 다만 장비가 크고 무거워 이동성이 떨어지므로, 주로 공항과 같은 현장에서 상시로 고정되어 운용하는 경우가 많다. 다른 하나는 μJ 라이다로, 펄스 에너지가 상대적으로 작아 최대 유효 관측거리가 짧은 편이지만, 장비가 소형 및 경량이어서 설치와 철거가 용이하다는 장점이 있다. 이러한 특성 때문에 μJ 라이다는 대기경계층 연구나 풍력단지의 감시 등, 현장 전개와 회수가 잦은 응용분야에 널리 활용된다.
단일 라이다는 빔 방향의 시선속도(radial velocity)만을 측정하므로, 풍향과 풍속을 재구성하기 위해서 VAD(velocityazimuth display)나 DBS(Doppler beam swinging)와 같은 관측기법이 널리 사용된다[2]. 그러나 이러한 단일 라이다 기반 기법들은 스캔 시간 동안의 균질 혹은 정상상태(steady-state)의 바람장에 대한 가정이 필요하고, 난류에 의한 변동이 큰 대류경계층(convective boundary layer)과 같은 환경에서는 체계적 편차가 발생할 수 있다[3]. 특히 라이다가 다수의 방위각에 대해 순차적으로 관측해야 한다는 점은 비정상 흐름에서의 대표성 저하로 이어진다.
이와 대조적으로 이중도플러(dual-Doppler) 라이다는 서로 독립된 두 라이다가 동시에 상이한 방향의 시선속도를 관측함으로써, 가정 의존성을 낮추고 수평 혹은 준3차원 바람장을 복원할 수 있다. 1982년 JAWS(joint airport weather studies) 프로젝트에서 10.6 μm 파장의 mJ 라이다 2대를 동시에 PPI(plan position indicator) 스캔으로 운용하여 수평 바람장을 복원하고 풍속계와의 비교를 통해 레이다의 이중도플러 기법을 라이다로 확장할 수 있음이 처음 입증되었다[4]. 이후 여러 야외 관측 캠페인—JU2003(joint urban 2003), ISB52(invest-to-save budget project 52), T-REX(terrain-induced rotor experiment), 일본 나토리 현장 관측—에서 기관 간 장비를 한시적으로 결합한 이중도플러 라이다 관측이 수행되었다[5~10]. 한편 참고문헌 [11]은 홍콩국제공항에서 활공경로(glide path) 감시를 위한 현업 관측전략을 활용하여 이중도플러 바람 정보를 산출하는 방법을 제시하였다. 그럼에도 공항에서 주로 운용되는 mJ 라이다를 활용한 이중도플러 바람장에 대한 체계적 정확도 평가와 오차요인에 대한 실험 및 분석은 부족하다.
본 연구는 제주국제공항에서 운용한 두 대의 mJ 라이다를 이용해 이중도플러 바람장을 산출하고, 공항 현장에서 활용할 수 있는 다중센서—공항기상관측장비, 저층바람시어경보시스템과 윈드프로파일러(WPR, wind profiler radar)—를 활용하여 정확도를 정량 평가하였다. 아울러 이중도플러 바람장의 추정 절차를 단계별로 정리하고, 주요 오차 원인을 진단하였다. 본 논문은 II장 자료와 방법, III장 결과, IV장 결론으로 이루어진다.
II. 연구 자료 및 방법
제주공항에 설치된 독일 Leonardo 사의 SKIRON3D 라이다 자료를 사용하였다. 해당 라이다는 약 1.55 μm의 파장을 사용하며, 속도 관측 범위는 ±70 m s−1이다. 대기 조건에 따라 수평적으로 10 km 이상 관측이 가능하며, 거리해상도는 조절할 수 있다. 본 연구에서 활용한 거리 해상도는 50 m다. 이중도플러 바람장 검증에는 세 종류의 외부 자료를 활용하였다. 지점관측으로는 공항기상관측장비(AMOS, aerodrome meteorological observation system)와 저층바람시어경보시스템(LLWAS, low-level windshear alert system)의 평균 바람을 사용하였다. AMOS는 1분 평균, LLWAS는 10초 평균 자료를 제공한다. 본 연구에서는 LLWAS 자료에 대해 1분 창(window)을 적용한 10초 간격의 이동평균을 적용하여 AMOS와 평균 창의 길이를 일치시켰다. 또한, 이중도플러 바람장의 고도 의존성을 진단하기 위해 독일 Scintec 사의 LAP-3000 윈드프로파일러를 통해 관측한 연직바람프로파일 자료를 사용하였다.
그림 1은 제주공항 인근의 기상 관측장비, 활주로의 위치와 지형을 나타낸다. WPR은 윈드프로파일러, DL는 라이다를 의미한다. 그 외에 빨간색과 노란색의 십자 표식은 각각 AMOS와 LLWAS의 위치를 나타낸다. 배경의 색상은 지형의 해발고도를 나타낸다.
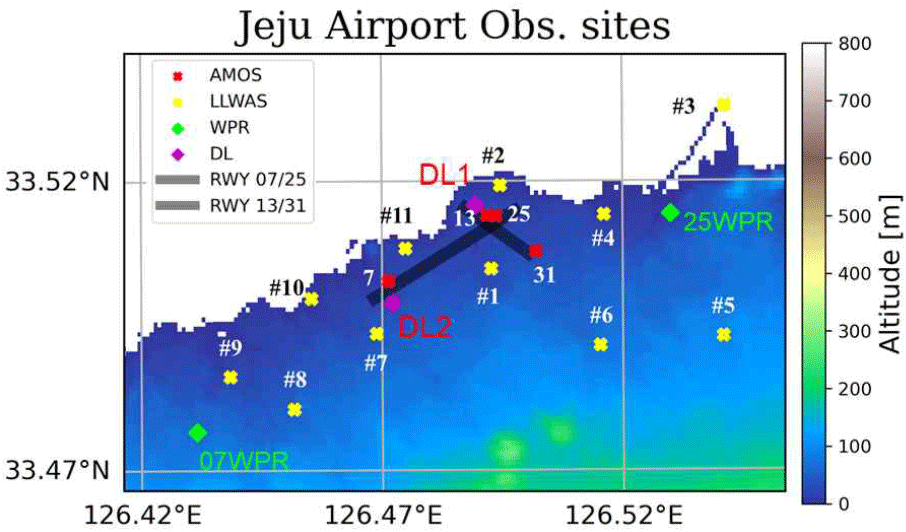
지점관측 자료를 활용한 이중도플러 바람장의 검증 시 오차를 최소화하기 위해서 각각의 라이다는 동시간에 검증에 활용할 장비의 위치를 정확히 관측해야 한다. 각 장비들의 위도, 경도, 고도를 먼저 확보하고, 구면 삼각법 및 하버사인(Haversine) 공식을 적용하여 라이다로부터 각각 검증장비를 향한 극좌표계 기반의 관측 목표점(고도각, 방위각, 거리)을 계산하여 관측전략에 반영하였다. 각각의 목표점에 대해 라이다는 약 5초간 관측하였다. 이때 독일 레이저 장비 규격(DIN EN 60825:2015)의 안전 기준을 충족하기 위해 5초간 같은 위치를 관측하지 않고, 관측 목표점의 방위각을 중심으로 ±5° 고도각 범위에서 RHI(range-height indicator) 스캔을 수행하였다. RHI 스캔 시에 안테나 회전 속도는 2.2° s−1을 적용하여 고도각 방향으로 고해상도의 관측자료를 수집하였다.
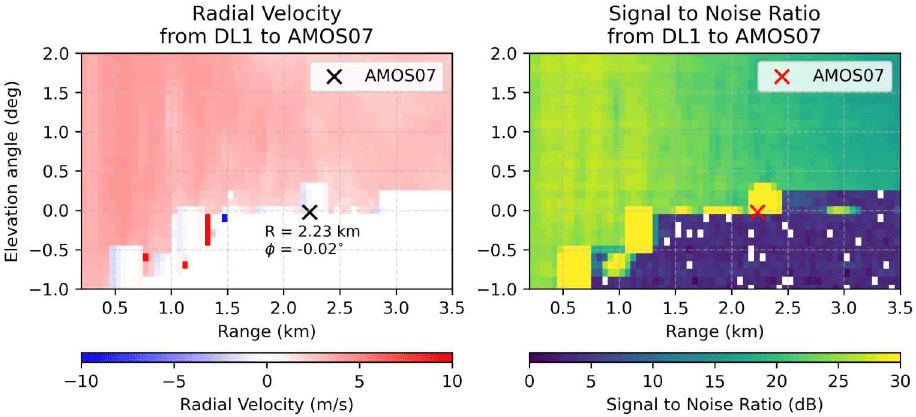
실제 라이다 관측 시에 지형 및 공항 구조물 차폐로 검증 장비가 위치하는 지점에 대한 관측이 어려울 수 있다. 그림 2는 2025년 4월 7일 09:12 UTC에 첫 번째 라이다(DL1)로부터 AMOS07에 대해 관측한 시선속도와 신호대잡음비(SNR, signal to noise ratio)이다. 세로축은 고도각, 가로축은 라이다로부터 거리에 해당한다. 십자 표시한 본래 관측 목표점은 고도각 −0.02°와 거리 2.23 km이다. 그러나 목표점 근처인 거리 2.2~2.4 km, 고도각 0.0~0.4° 영역에서 시선속도가 공간적으로 불연속적이고 0 m s−1에 가깝게 나타난다. SNR 또한 불연속적이고 30 dB 이상의 큰 값이 나타난다. 이는 지형으로부터 신호가 관측된 것이며, 해당 지점의 자료는 사용할 수 없다. 차폐가 발생하는 관측지점을 제외하여 최종적으로 검증을 위해 활용한 지점은 AMOS13과 LLWAS01이다.
WPR과의 비교를 위해서 라이다는 활주로 동편의 25WPR 상공 약 7 km까지 관측하도록 RHI 스캔을 수행하였다. WPR 관측자료는 하층 관측에 유리한 low 모드와 상층 관측에 유리한 high 모드로 구성되어 있다. 본 연구에서는 두 관측자료를 병합하여 133~783 m 고도에서 low 모드 자료를 사용하고 그 이상 고도에서는 high 모드를 사용하였다. 산출된 이중도플러 바람장의 고도 해상도는 약 20 m로 WPR가 50 m인 것에 비해 높은 해상도를 가진다. 두 자료의 고도를 일치시키기 위해 WPR 관측자료의 고도를 기준으로 ±25 m의 고도 범위에서 라이다 자료를 평균하여 분석하였다.
본 연구에는 다음 두 기간의 자료를 활용하였다:
기간 1에는 AMOS․LLWAS 전 지점과 25WPR을 대상으로 관측을 수행하였으며, 기간 2에는 차폐 영향을 받는 지점을 제외하고 AMOS13, LLWAS01, 25WPR에 대해서만 집중적으로 관측을 실시하였다.
두 대의 라이다에서 동시에 같은 지점을 관측한 시선속도를 활용하면 해당 지점에서의 수평 바람을 추정할 수 있다. 고도각이 0°에 가까워 수평성분이 지배적인 시선속도를 가정하면 바람의 연직성분 w를 무시할 수 있으며, w를 제외한 각각의 라이다에서 관측한 시선속도는 식 (1) 및 식 (2)와 같이 나타낼 수 있다.
이때 Vr,1, Vr,2는 각각 첫 번째와 두 번째 라이다에서 관측한 시선속도, u와 v는 각각 바람의 동서성분과 남북성분이다. θ1와 φ1는 첫 번째 라이다의 관측 방위각과 고도각이며, θ2와 φ2는 두 번째 라이다의 관측 방위각과 고도각이다. 두 식을 u와 v에 대해 각각 정리하면 식 (3) 및 식 (4)와 같이 이중도플러 관측을 통한 바람 u, v를 계산할 수 있다.
검증지표로서 편향오차(bias), 평균제곱근오차(RMSE, root mean squared error), 표준편차(STD, standard deviation), 상관계수(CORR, correlation coefficient)를 계산하였다. 풍향 통계의 경우 순환변수의 특성을 반영한 절차가 필요하며, 풍속․풍향에 대한 각 검증지표의 계산 과정은 참고문헌 [12]을 참조하였다.
III. 연구 결과
이 절에서는 지점관측 자료를 통해 추정된 이중도플러 바람장을 검증한 결과를 보인다. 그림 3은 이중도플러로 추정한 바람장과 지점관측 바람장의 시계열 비교이다. 좌측은 풍속, 우측은 풍향을 나타내며, 상단 두 행은 AMOS13 기반의 두 사례, 하단 두 행은 LLWAS01 기반의 두 사례를 각각 제시한다. 2025년 4월 7일 16:00 UTC부터 8일 09:00 UTC 사이에 풍속이 약 10 m s−1 이상으로 증가한 강풍 구간이 확인되며, 특히 16:00 UTC 무렵에는 풍속이 약 2 m s−1에서 10 m s−1 수준으로 급격히 상승하였다. 이 시점 전후로 풍향이 남동(≈135°)에서 남서(≈225°)로 급변하였다. 해당 기간의 지상일기도 분석 결과, 저기압과 동반된 전선 통과에 의해 바람장이 급격히 변화한 것으로 해석된다. 두 지점관측 자료와 비교했을 때 이중도플러 바람장은 이러한 급격한 바람의 변동을 전반적으로 잘 재현하였다. 그러나 강풍 구간에서 풍속은 분산이 상대적으로 커지고 일부 이상치가 나타나 지점관측과 불일치하는 경우가 관찰되었다.
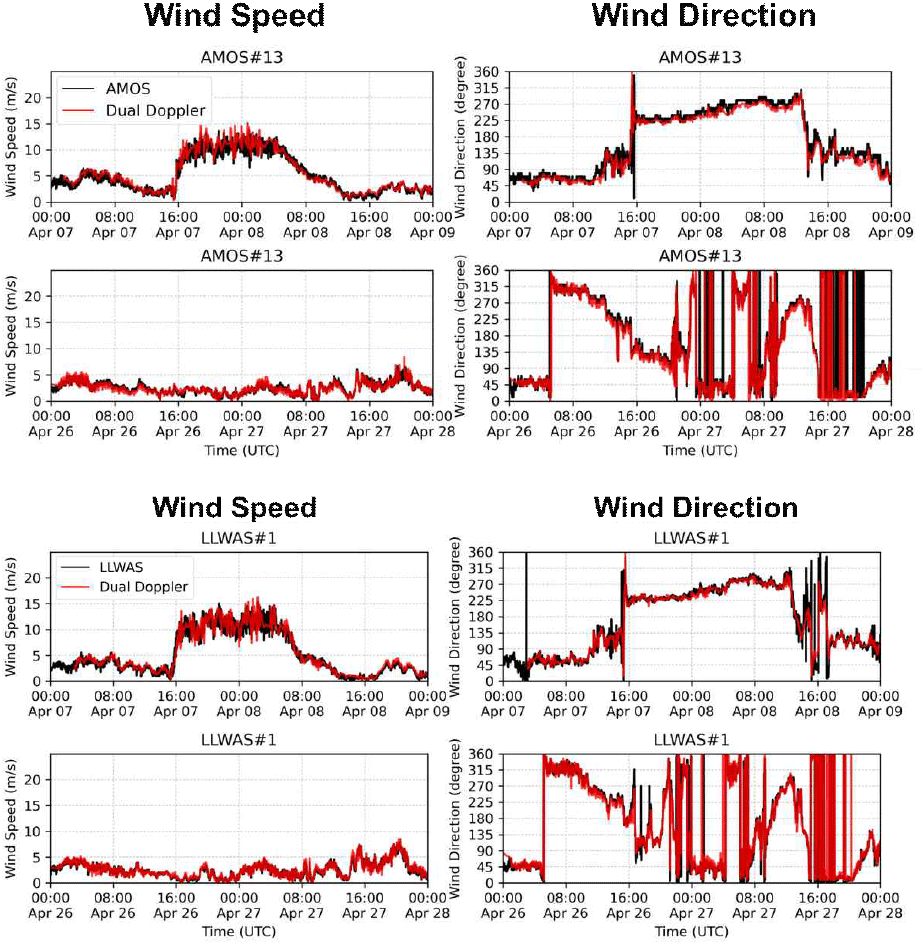
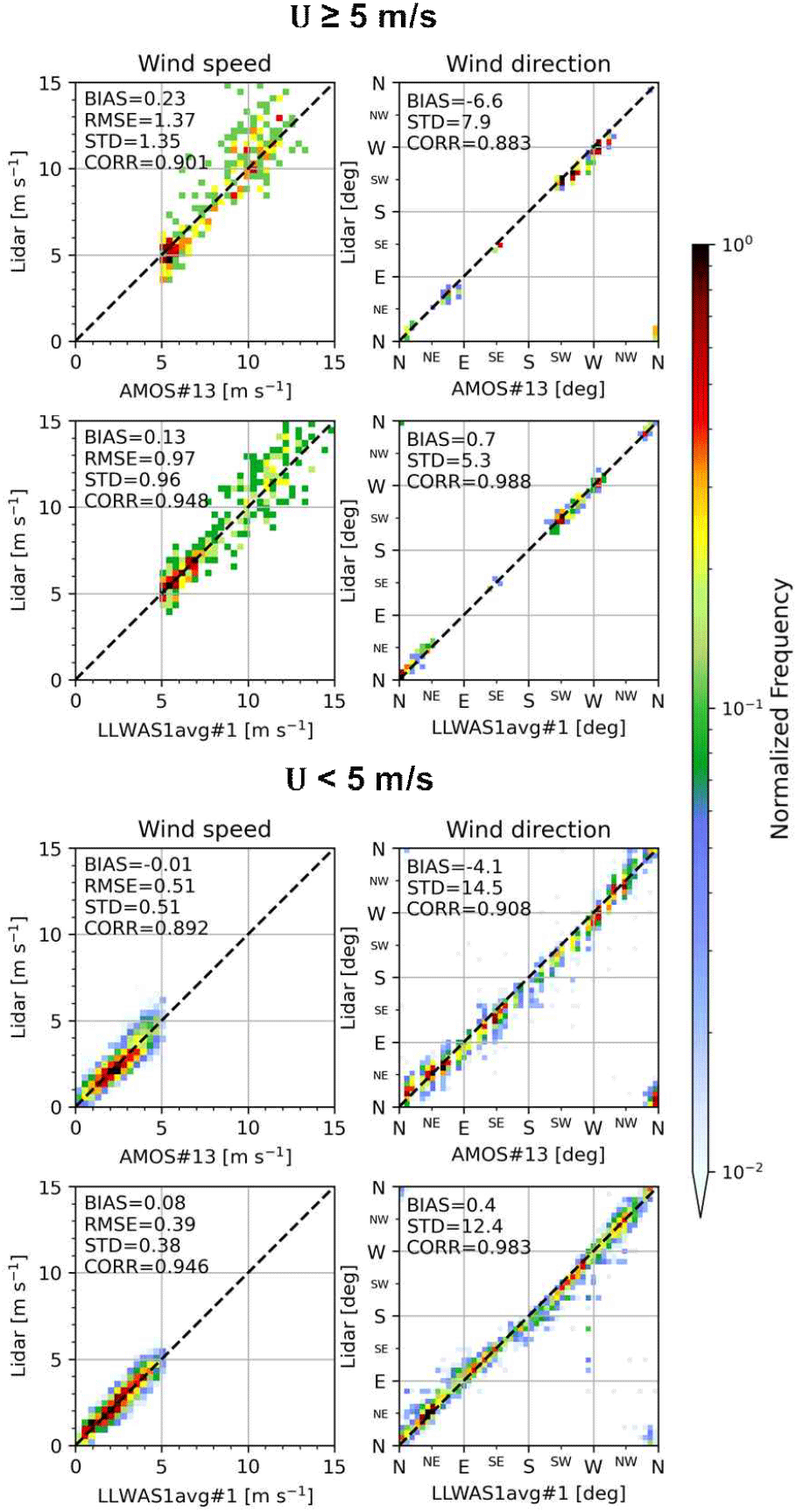
그림 4는 전체 기간에 대해 이중도플러 추정 바람장을 지점관측과 비교한 산포도와 검증지표를 제시한다(좌: 풍속, 우: 풍향; 상단: AMOS, 하단: LLWAS). 풍속의 경우 이중도플러 추정값은 관측과 매우 잘 일치하며, 편향오차가 0 m s−1에 근접하고 CORR도 0.95 이상으로 높다. STD와 RMSE는 대체로 약 0.5 m s−1 수준이며, AMOS가 LLWAS 대비 약 0.1 m s−1 더 큰 산포를 보이나 그 차이는 미미하다.
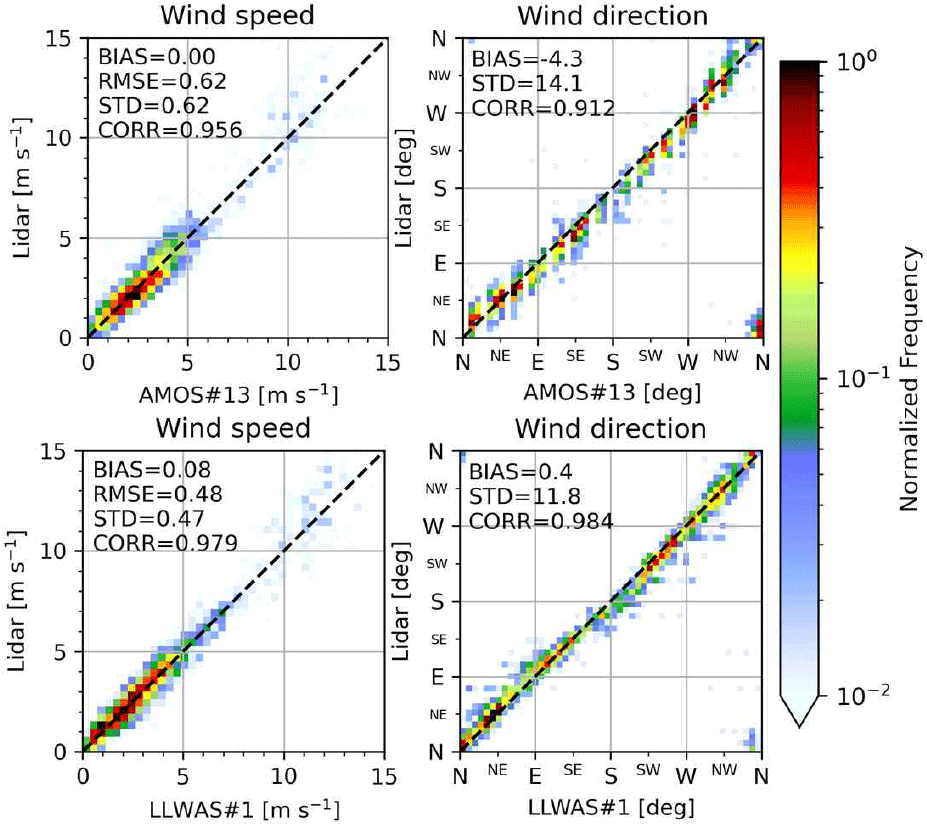
풍향의 경우에도 CORR≥0.9로 전반적 일치도는 높지만, 산포도에서 일부 이상치가 관찰되며 두 관측과의 비교 모두 STD가 11° 이상으로 나타났다. 편향은 AMOS −4.3°, LLWAS 0.4°로 AMOS의 절대 편향이 더 크며, 다른 지표들 역시 LLWAS가 AMOS보다 이중도플러 결과와의 일치도가 다소 우수한 경향을 보인다. 이는 항공 운용 편의를 위해 AMOS의 1분 평균 풍향이 10° 간격으로 양자화되어 제공되기 때문으로 해석되며, 산포도에 나타나는 불연속 또한 이 양자화 효과에 기인한 것으로 판단된다. AMOS 풍향의 10° 해상도로 인한 오차를 반올림 양자화에 따른 균등잡음으로 근사하면 추가 STD는 σq≈Δ/√12≈2.89°이고, 이는 자료에서 관찰된 AMOS와 LLWAS 간 STD 차이(≈2.3°)와 유사하다. 종합하면 본 검증에서 풍향 오차 규모는 대략 11~12° 수준으로 평가된다.
강풍 구간에서 나타난 이중도플러 바람장의 불일치를 진단하기 위해, 지점관측 풍속 기준 5 m s−1로 자료를 구분하여 그림 5에 산포도와 검증지표를 제시하였다(좌: ≥5 m s−1, 우: <5 m s−1). 풍속이 5 m s−1 이상일 때는 산포도의 분산이 뚜렷이 확대되고, 두 지점관측 모두에서 STD와 RMSE가 각각 약 0.6 m s−1 이상 증가하였다. 반대로 풍향은 5 m s−1 미만 구간에서 분산이 더 크게 나타나며, 해당 구간의 오차가 대략 4° 이상 증가한다.
강풍 구간에서 풍속 오차가 큰 경향은 관측 방향 오차(direction error)와 오차 전파(error propagation) 특성으로 설명될 수 있다. 실제 라이다 빔이 취하는 관측지점은 지점관측기의 위치와 정확히 일치하지 않으며(설치 오프셋, 방위․고도각/거리 해상도의 한계 등), 관측된 시선속도는 라이다 기기 자체의 오차뿐 아니라 관측 방향의 오차가 시선속도의 국지적 기울기를 통해 증폭되는 구조를 갖는다. 위의 오차 성분들의 전파를 고려한 관측 시선속도 오차는 다음과 같다:
여기서 σest는 기기 오차, σφ, σθ, σr은 각각 고도각․방위각․거리의 오차이며, ∂Vr/∂(•)는 해당 방향의 시선속도 기울기이다. 전선이 통과 시 동반되는 높은 풍속과 비균질성으로 ∂Vr/∂(•) 항이 커지면 시선속도의 오차가 증가하므로, 강풍 구간에서 풍속의 분산이 크게 나타난 결과와 정합적이다. 다만 강풍 사례에서 실제 시어 강도에 대한 정량적 평가는 별도의 분석이 요구된다.
반면 풍향 오차는 바람 벡터의 크기 에 대한 상대 민감도를 가진다. 참고문헌 [13]에서 작은각 근사를 적용하여 유도된 풍향 오차는 식 (6)과 같다:
σv는 평균류 방향과 수직인 방향의 풍속 오차를 나타낸다. 즉 수평 풍속 U가 작을수록 미소한 잡음에도 풍향이 크게 요동하며, 본 연구에서 U<5 m s−1 구간에서 풍향 분산과 오차가 더 크게 나타난 이유를 제공한다. 요약하면, 강풍 시에는 시선속도의 국지적 기울기와 관측 방향 오차의 결합으로 시선속도의 오차가 증폭되어 풍속 지표가 악화되고, 약풍 시에는 벡터 크기 감소로 인해 풍향의 잡음이 커질 수 있다. 이러한 두 기작이 그림 5에서 나타난 풍향과 풍속의 대비적인 경향을 설명한다.
이 장에서는 WPR를 통해 추정된 이중도플러 바람장을 검증한 결과를 보인다. 그림 6은 전선 통과가 있었던 기간 1에 대해, 이중도플러 바람장과 WPR 바람장을 시간-고도 단면으로 비교한 것이다. 가독성을 위해 표출 간격을 조정하여 고도 방향은 200 m, 시간 방향은 25분 간격으로만 표시하였다. 두 자료는 전반적으로 유사한 시공간적 변화를 보인다. 4월 7일 06 UTC부터 4월 8일 12 UTC 사이 1 km 고도에서, 전선 통과 시점인 약 16 UTC 전후로 풍속이 15 m s−1 이상으로 강화된 뒤 다시 약화되며, 풍향은 남서풍에서 서풍을 거쳐 북서풍으로 전형적인 저기압 통과 패턴을 따른다. 4월 7일 18 UTC에는 고도가 높아질수록 풍향의 순전(veering)이 뚜렷하며, 2 km 이하에서 12 m s−1 이상의 강한 바람이, 그 상층에서는 비교적 약한 바람이 나타난다. 다만 같은 시각(18 UTC) 2~3 km 고도에서 이중도플러 바람장은 WPR에 비해 풍속이 다소 크게 나타나는 양의 편차를 보인다.
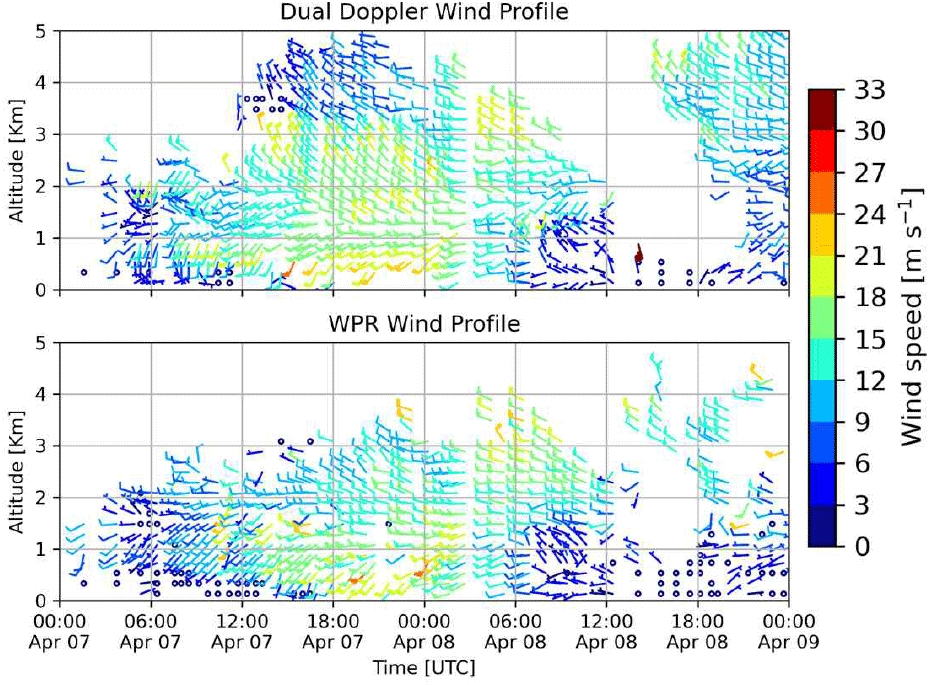
그림 7은 전체 기간에 대해 WPR을 기준으로 이중도플러 바람장을 검증한 산포도와 검증지표를 제시한다. 고도 의존성을 정량화하기 위해 100~500, 500~1,000, 1,000~1,500, 1,500~2,000 m의 네 구간으로 나누어 비교하였다. 2 km 이상 고도에서는 비교할 수 있는 자료 개수가 2,000개 이하로 감소하여 활용하지 않았다. 이중도플러 풍속은 전 고도에서 WPR 대비 양의 편차를 보였고, 고도가 높아질수록 STD는 증가하고 CORR는 감소하였다. 풍향의 경우 100~500 m 구간에서 정확도가 가장 높았으며, 그 외 구간에서는 다소 부정확한 결과를 보인다. 전반적으로 풍향 STD는 43° 이상으로 크게 나타났고, 100~500 m를 제외하면 CORR는 0.4 이하로 낮았다.
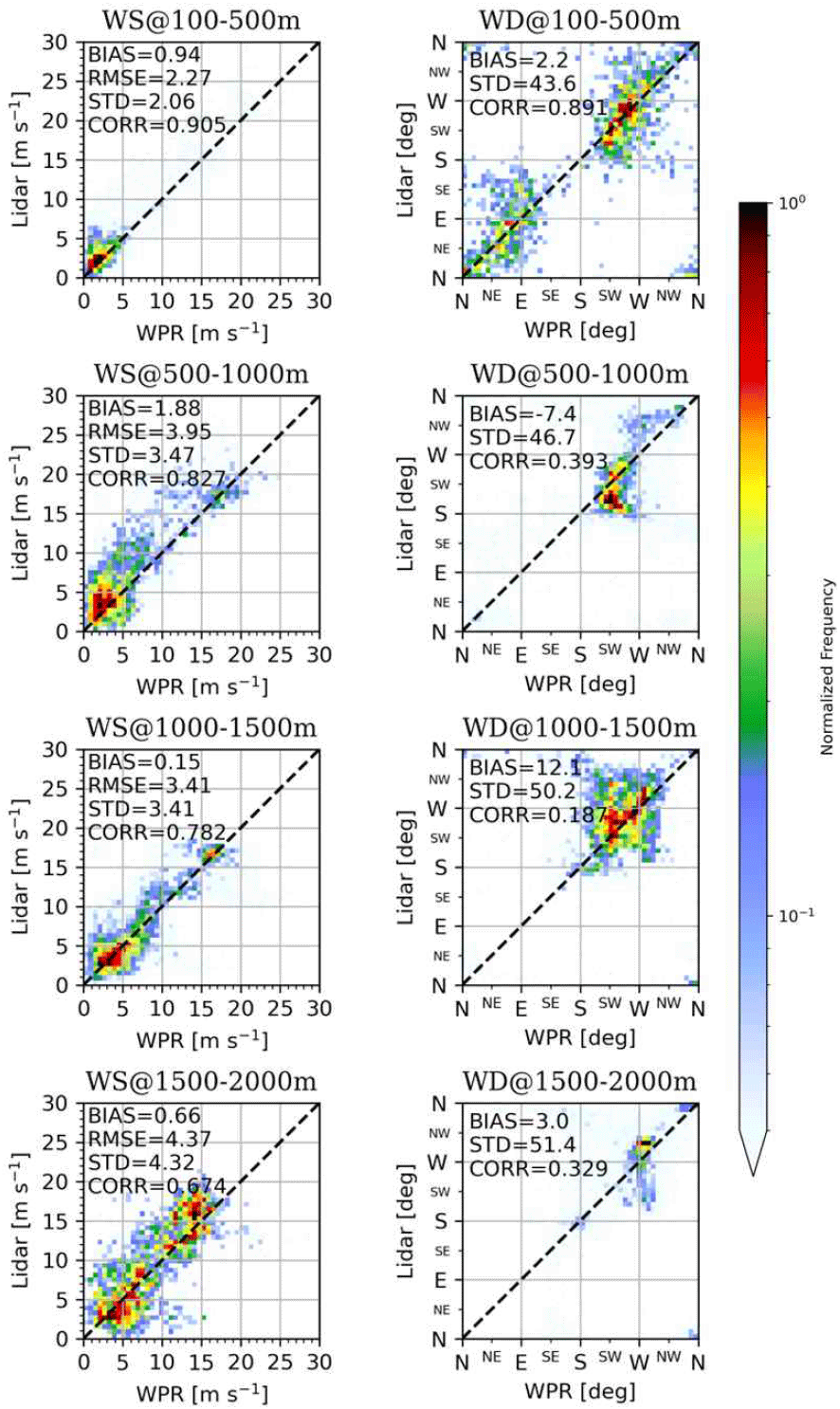
이중도플러 바람장은 지점관측 검증 결과에 비해 WPR과 비교에서 큰 분산도를 보였다. 이와 같은 큰 분산도는 관측 기하의 영향—특히 이중도플러 바람장 추정에서의 빔 교차각(β)—으로 설명될 수 있다. 참고문헌 [14]의 오차 전파 분석에 따르면 이중도플러 바람의 오차는 1/sin β에 비례하여, β가 90°일 때 오차가 가장 작고 β가 90°에서 멀어질수록 오차가 증폭된다. 본 사례에서 지점관측의 교차각은 AMOS13과 LLWAS1이 각각 83°와 95.5°로 90°에 근접한 반면, WPR은 20.3°로 작다. 따라서 WPR과의 비교에서 나타난 이중도플러 바람장의 큰 분산과 상관계수 감소는 작은 교차각에 따른 오차의 증폭이 주된 요인으로 해석된다.
이중도플러 바람장은 대체로 100~500 m 구간에서 가장 정확하며, 고도가 높아질수록 오차가 커지는 경향을 보였다. 이는 (1) WPR 운용 모드에 따른 특성 차이, (2) 라이다 시선속도에서 연직성분 기여의 증가, (3) 라이다와 WPR의 빔 폭(beamwidth) 차이라는 세 요인의 복합적 영향으로 해석된다.
WPR은 활용 목적에 따라 펄스 폭(pulse width)이 상이한 low 모드와 high 모드를 운용한다. 일반적으로 high 모드는 더 긴 펄스 폭을 사용하여 적분 평균하는 에코가 많아지며 평균화 오차가 커진다. 본 연구에서는 783 m 미만에서 low 모드, 783 m 이상에서 high 모드 관측을 사용하였으므로, 500~1,000 m 이상의 구간에는 high 모드 특성이 반영된 WPR 오차가 작용한 것으로 해석된다.
그리고 관측 목표 고도가 올라갈수록 라이다에 요구되는 관측 고도각이 커져 시선속도에서 연직성분의 비중이 증가한다. 본 연구는 이중도플러 계산 과정에서 w를 무시하는 가정을 두었으므로, 고도각이 증가할 때 오차가 증가할 수 있다.
또한 두 장비 간 빔 폭 차이에 따른 관측부피의 불일치가 존재한다. 라이다는 수십 μrad 수준의 매우 좁은 빔 폭으로 인해 작은 부피에 대해 평균하는 반면, WPR은 수 도(°) 수준의 넓은 빔 폭으로 비교적 큰 부피를 평균한다. 더불어 고도가 높아질수록 WPR은 빔 퍼짐(beam broadening)의 영향으로 관측부피가 더 커지고, 라이다는 빔 퍼짐의 영향을 거의 받지 않는다. 또한 WPR의 경우 5개의 빔 방향 (고도각 90°와 동서남북 방향으로 고도각 75 °)에서 관측한 시선속도를 이용하여 균질바람 가정에 기반하여 바람을 산출한다. 즉, 고도가 증가함에 따라 균질바람을 가정한 공간 규모가 증가하게 된다. 따라서 두 관측 값은 서로 다른 공간에 대한 평균을 나타내고, 이러한 공간대표성의 차이가 시어가 존재하는 비균질한 바람장에서 분산 증가 및 상관계수 감소를 유발할 수 있다.
이 절에서는 지점관측 및 WPR로부터 산출한 시선속도와 라이다 시선속도를 직접 비교한다. 이러한 비교는 이중도플러 바람장 추정에 활용되는 초기 자료인 시선속도의 정확도를 점검하여, 이후 수평풍으로 전파되는 오차의 근원과 전파 경로를 규명하기 위해 필요하다. 검증 장비에서 관측한 바람과 해당 장비의 위치에 대한 라이다 관측 방위각과 고도각을 식 (1)에 대입하여 시선속도를 계산할 수 있다.
그림 8은 전체 기간에 대해 각각 라이다의 관측 시선속도를 지점관측 자료와 비교한 결과이다. 모든 지점과 라이다 조합에서 CORR는 0.97~0.99, STD는 약 0.6 m s−1, 편향오차의 절대값은 0.3 m s−1 이하로 나타나 시선속도 수준의 관측 오차는 매우 작다. 이는 지점관측(AMOS13, LLWAS01)과 이중도플러 바람장의 높은 일치성과 일관되며, 강풍 시 관측된 분산 확대의 대부분은 시선속도 자체의 측정오차가 아니라 앞서 논의한 관측 방향 오차의 증폭에서 기인한 것으로 해석된다.
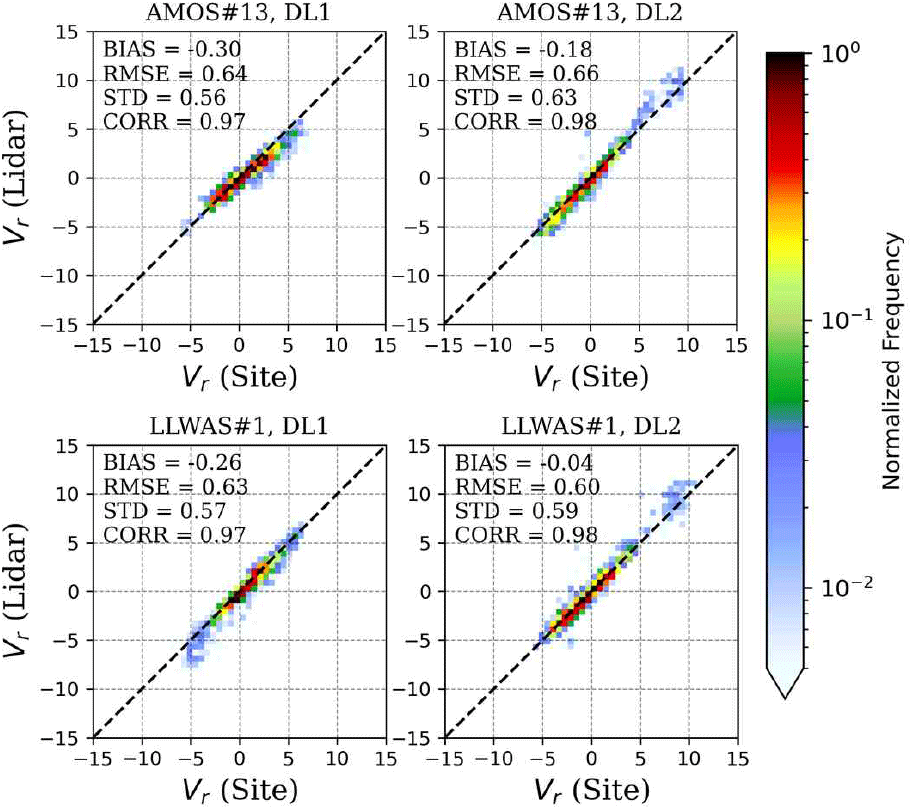
그림 9는 전체 기간에 대해 WPR로부터 산출한 시선속도와 각 라이다의 관측 시선속도를 비교한 결과이다. 편향오차의 절대값은 0.3 m s−1 이하로 매우 작지만, STD는 지점관측 대비 약 2.0 m s−1로 크게 나타난다. 이는 고정 지점에서의 순간값을 측정하는 지점관측과 달리, WPR이 유한한 관측부피를 갖는 특성 때문에 시공간 변동성에 대한 평균화가 발생하고, 이로 인해 라이다 단일 시선속도와의 일치도가 낮아질 수 있기 때문이다.
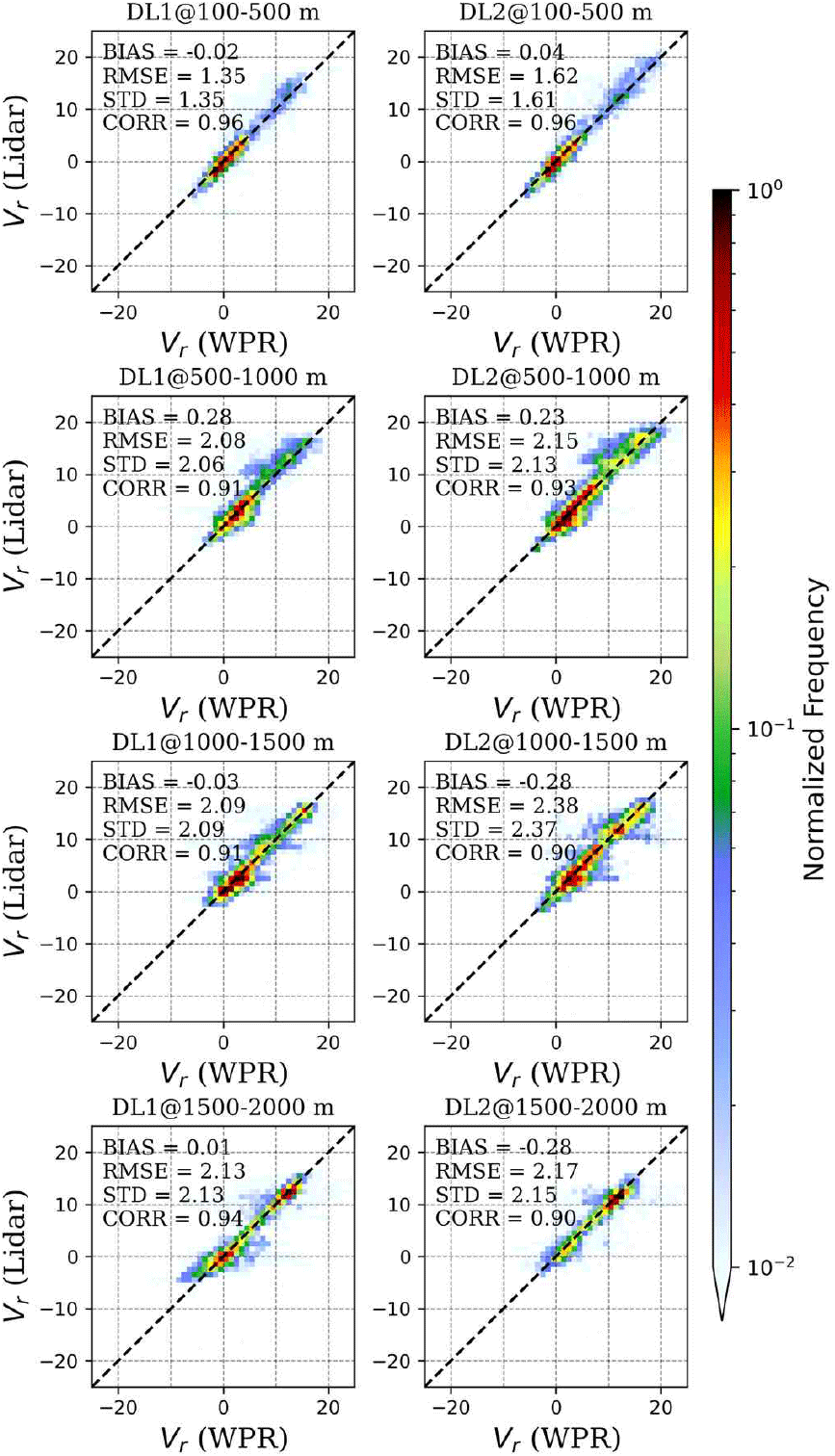
고도별로 보면 100~500 m 범위에서 STD가 약 1.5 m s−1로 가장 작고, 그 이상 고도에서는 약 2.1 m s−1로 증가한다. 이는 그림 7에서 확인한 WPR 운용 모드(low/high)에 따른 정확도 차이와 일관된다. 한편 이중도플러 검증과 달리 여기서는 고도에 따른 체계적 오차 증가 경향이 나타나지 않는데, WPR 시선속도 산출 시 연직성분 w을 포함했기 때문이다. 이 결과는 이중도플러 바람장에서 고도각 증가로 인해 w 기여를 무시한 가정이 오차를 키운다는 점을 뒷받침한다.
다음에서는 시선속도 오차가 이중도플러 바람장으로 전파되는 양을 정성적으로 추정하였다. 두 라이다의 관측 고도각이 0°로 같고, 시선속도 오차가 서로 독립이면서 크기가 같다고 가정하면 식 (3) 및 식 (4)로부터 식 (7) 및 식 (8)과 같이 오차 전파식을 얻을 수 있다:
여기서 σWS는 풍속 오차, σWD는 풍향 오차, σVr는 시선속도의 오차를 의미한다.
그림 8에서 지점관측과의 비교로 얻은 시선속도 STD는 σVr≈0.6 m s−1이며, AMOS13과 LLWAS01처럼 교차각 β가 90°에 근접한 경우 식 (7)에 따라 σWS≈0.6 m s−1가 예상된다. 풍향에 대해서도 식 (8)을 적용하면, 풍속 U=3~6 m s−1에서 σWD≈11~6°가 추정되며, 이는 이중도플러 바람 검증에서 확인된 풍속과 풍향 오차의 규모와 정성적으로 일치한다. 즉, 지점관측을 통한 검증에서 나타난 이중도플러 바람의 높은 일치도는 시선속도 수준의 작은 오차가 교차각이 90°에 가까운 관측전략에서 거의 그대로 수평풍으로 전달된 결과로 해석된다.
반면 그림 9의 WPR 비교에서는 라이다와 WPR 간의 시선속도 STD가 지점관측 대비 크게 나타나고, 교차각이 작아 식 (7)의 분모 항이 크게 작용한다. 100~500 m 고도 범위에서 나타난 σVr≈1.35 m s−1와 교차각 β=20.3°를 식 (7)과 (8)에 대입하면 σWS≈3.89 m s−1이며, U=3~6 m s−1에서 σWD는 74~37° 범위로 추정된다. 교차각이 작아짐에 따라 전파되는 오차의 양이 커진 것을 알 수 있다. 동일한 고도 범위에서 그림 7을 통해 확인한 실제 이중도플러 풍속과 풍향의 STD는 2.1 m s−1와 43.6°였으므로 전파식을 통해 정성적으로 추정한 값보다 대체로 작다. 이는 그림 9에서 나타난 시선속도의 STD에 라이다가 기인한 오차와 더불어 3장 2절에서 언급한 WPR의 관측오차가 추가로 작용한 결과로 해석된다. 실제 이중도플러 계산을 통해 전파되는 라이다 관측 시선속도에서 발생한 오차는 그림 9에서 나타난 것보다 작을 수 있다.
IV. 논의 및 결론
본 연구는 제주국제공항에서 두 대의 mJ 도플러라이다를 동시 운용하여 이중도플러 바람장을 산출하고, 지점관측(AMOS, LLWAS)과 윈드프로파일러(WPR)로 정량 검증하였다. 검증지표를 요약하여 표 1에 제시하였다. 지점관측과의 비교에서 이중도플러 풍속은 전반적으로 높은 일치도를 보였으며(편향≈0 m s−1, CORR≥0.95, STD․RMSE≈0.5 m s−1), 풍향은 STD가 대략 11~12° 수준으로 평가되었다. 강풍(≥5 m s−1)에서는 관측 방향 오차와 국지적 시어에 따른 오차 전파로 풍속 지표의 분산이 뚜렷이 확대되었고, 약풍(<5 m s−1)에서는 벡터 크기 감소에 따른 풍향 오차의 민감도가 커지는 대비적 경향을 확인하였다.
WPR을 기준으로 한 검증에서는 교차각 β의 제약(본 연구에서 WPR 방향 β≈20.3°)으로 인해 이중도플러 바람장의 분산이 커지고 상관이 약화되는 한계를 보였다. 이는 이중도플러 바람 오차가 1/sinβ에 비례한다는 이론과 일치하며, 지점관측 기반 검증보다 낮은 성능의 주요 원인이었다. 한편 시선속도 자체의 정확도는 매우 양호하여, 지점관측 유도 시선속도 대비 라이다 시선속도의 상관계수 0.97~0.99, STD≈0.6 m s−1, |bias|≤0.3 m s−1를 확인하였다. WPR 유도 시선속도 대비로는 관측 부피 평균화 차이로 STD가 1.3 m s−1 이상으로 크게 나타났으며, 고도 상승에 따라 WPR 모드 특성(low/high) 및 이중도플러 연직성분 오차가 복합적으로 반영되었다.
본 연구의 한계는 다음과 같이 정리된다. 우선, 이중도플러 바람 추정에서 연직성분 w를 무시한 근사를 사용했다는 점이다. 이에 대해서는 제3 라이다를 추가해 3성분 바람을 직접 복원하거나[15], 비압축 연속방정식 제약을 선형계/비용함수에 도입한 변분적 방법으로 w를 간접 추정하는 접근이 대안이 될 수 있다[8]. 둘째, 교차각과 관측 방향 오차에 따라 발생하는 오차의 정량화가 수행되지 못했다. 이중도플러 바람장의 오차 전파를 정리한 참고문헌 [14]의 방법을 적용하면, 본 연구에서의 관측 기하에 따른 불확실도를 정량화하고 결과 해석의 신뢰도를 높일 수 있다. 셋째, WPR 운용 모드 전환에 따른 체계오차를 명시적으로 보정하지 않아, 고도별로 모드가 혼용되는 구간에서 이중도플러 바람장 오차의 고도 의존성에 대한 해석이 모호해졌다. 향후에는 모드별 오차 특성을 정량화하고, 검증 시 모드 일치 또는 보정 절차를 도입할 필요가 있다. 마지막으로, 신호대잡음비(SNR)에 따른 시선속도 오차를 고려하지 않았다. 관측 거리가 증가하거나 산란체 농도가 낮아질수록 SNR 저하로 속도 오차가 커지는 특성을 고려하여[16], 민감도 분석이 추가되어야 한다. 이러한 보완점에 관한 추가적인 연구를 수행하여 이중도플러 바람장의 정확도와 해석 가능성을 높일 수 있을 것이다.
이중도플러 바람장 추정의 정확도를 높이기 위한 실무적 개선 방안도 제시하였다. 첫째, 관측 방향 오차를 줄이기 위해 고정 표적(hard target)을 활용한 스캐너 재정렬이 활용될 수 있다. 위치가 명확히 알려진 원거리 표적에 대해 PPI 또는 RHI 스캔을 수행하고, 표적의 실제 방위각 혹은 고도각과 라이다가 관측한 각도의 차이를 이용해 오프셋을 보정한다. 둘째, 구름, 안개 및 강수 환경에서는 강한 감쇄로 인한 오염으로 관측이 어렵거나, 강수입자의 낙하속도가 관측에 포함될 위험이 있어 해당 수상체 영역에 대해 자료를 배제하는 과정이 필요하다. 그리고 강수 혹은 구름이 존재하는 환경에 대한 라이다의 제약을 고려하여 AMOS, LLWAS, WPR 및 공항기상레이다를 통합한 운용이 요구된다. 셋째, 도플러라이다는 대기 중 에어로졸을 관측 표적으로 하므로 에어로졸의 농도에 따라 자료 품질이 좌우된다. 참고문헌 [17]이 제시한 저농도의 에어로졸 환경에서 SNR을 보정하는 기법을 활용하면 자료의 가용성을 높일 수 있다.
종합하면, 본 연구는 공항 환경에서의 이중도플러 라이다 검증 절차를 실제 운용 제약과 함께 제시하고, 여러 관측장비를 활용하여 교차각과 시어 환경이 오차 요인임을 보였다. 제시한 검증 과정은 이중도플러 기반 운항지원 및 경보 시스템의 현장 적용성을 높이고, 향후 난류 및 급변풍 감시로의 확장에도 기반을 제공한다.







